Тема урока : «Уравнение процессов в колебательном контуре. Период колебания»

Вид материала

Урок

Содержание C – ёмкость конденсатора (Ф) L 0,2 Гн, а амплитуда колебаний силы тока 40 мА 3. Объяснение нового материала. Лекция учителя. Запись конспекта. Формула Томсона

Подобный материал:

• 172. Электрические колебания в колебательном контуре заданы уравнением. Какова циклическая, 133.13kb.
• Гармонические колебания в контуре, 42.15kb.
• Урок учителя математики Гукасовой А. П. Тема урока: «Уравнение касательной», 52.29kb.
• План-конспект Тема урока : Движение жидкостей и газов. Уравнение Бернулли, 43.29kb.
• Вынужденные электромагнитные колебания, 39.6kb.
• Гармонические колебания. Уравнение гармонических колебаний (вывод). Сложение колебаний., 27.62kb.
• План-конспект урока. Тема урока: «Период колебания математического и пружинного маятников», 86.71kb.
• Лекция №1 «Общие сведения о моделировании систем», 97.61kb.
• Решение дифференциального уравнения затухающих колебаний, график затухающих колебаний,, 68.04kb.
• Задача Свободные колебания в контуре имеют начальную амплитуду напряжения 40В, 21.48kb.

Физика 11 класс

Тема урока: «Уравнение процессов в колебательном контуре.

Период колебания»

Цель урока: Изучение колебательного процесса в колебательном контуре и вывод

формулы Томсона для вычисления периода колебания.

Ход урока:

1. Организационный момент.
   
2. Проверка домашнего задания. Опрос по вопросам:
   

1. Свободные и вынужденные колебания. Параметры колебания.
   
2. Колебательный контур. Зарядка конденсатора.
   
3. Разрядка конденсатора через катушку. Полная энергия цепи.
   
4. Решение задачи № 983 из сборника задач А.П. Рымкевича.
   

3. Объяснение нового материала. Лекция учителя. Запись конспекта.

4. Решение заданий ЕГЭ.

5. Домашнее задание: § 30, упр. 4 № 2.


Проверка домашнего задания.

a. Свободные и вынужденные колебания. Параметры колебания.

Свободными называются колебания, которые возникают после выведения системы из равновесия.

Вынужденными называются колебания, которые происходят под действием внешней периодической силы.

Параметры колебательного процесса:

Рассмотрим на графике зависимости электрического заряда q от времени t

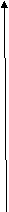q

(Кл)


q_max




t (сек)


T
-q_max

1) q_max – амплитуда электрического заряда (Кл)

2) T – период (сек)

3) - циклическая частота (рад/с)

4) 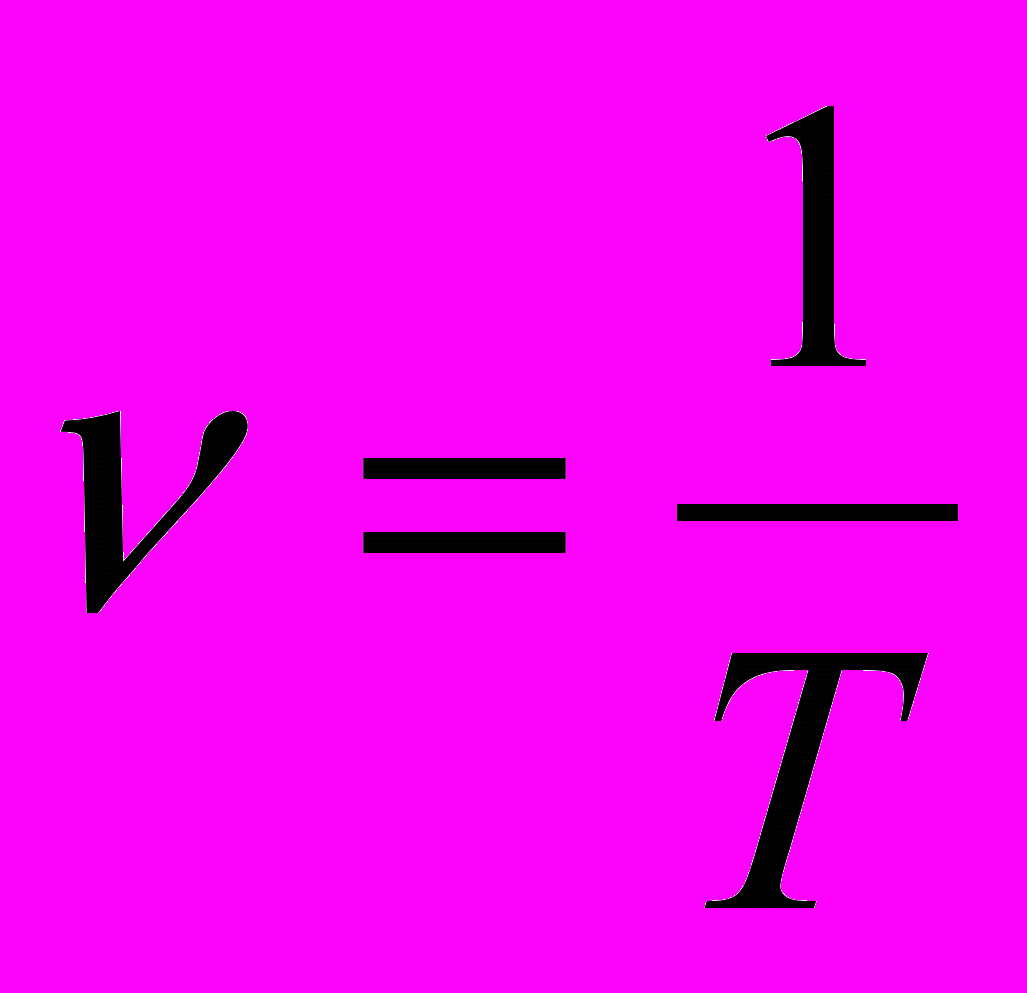- частота (Гц)


b. Колебательный контур


Колебательный контур – это электрическая цепь, в которой энергия электрическая превращается в магнитную и обратно.

C – ёмкость конденсатора (Ф)

L – индуктивность катушки (Гн)


Рассмотрим процессы зарядки и разрядки конденсатора:





Процесс зарядки конденсатора. Ключ в пол.1.


Конденсатор заряжается от источника питания до напряжения источника.





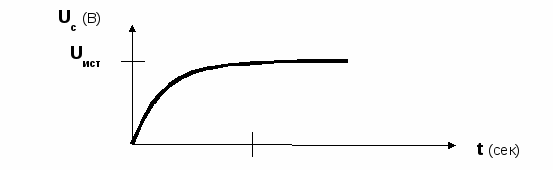
U_с – напряжение между обкладками конденсатора (В)

I_с – ток, протекающий через конденсатор (А).


Конденсатор накапливает электрическую энергию:

Из формул:


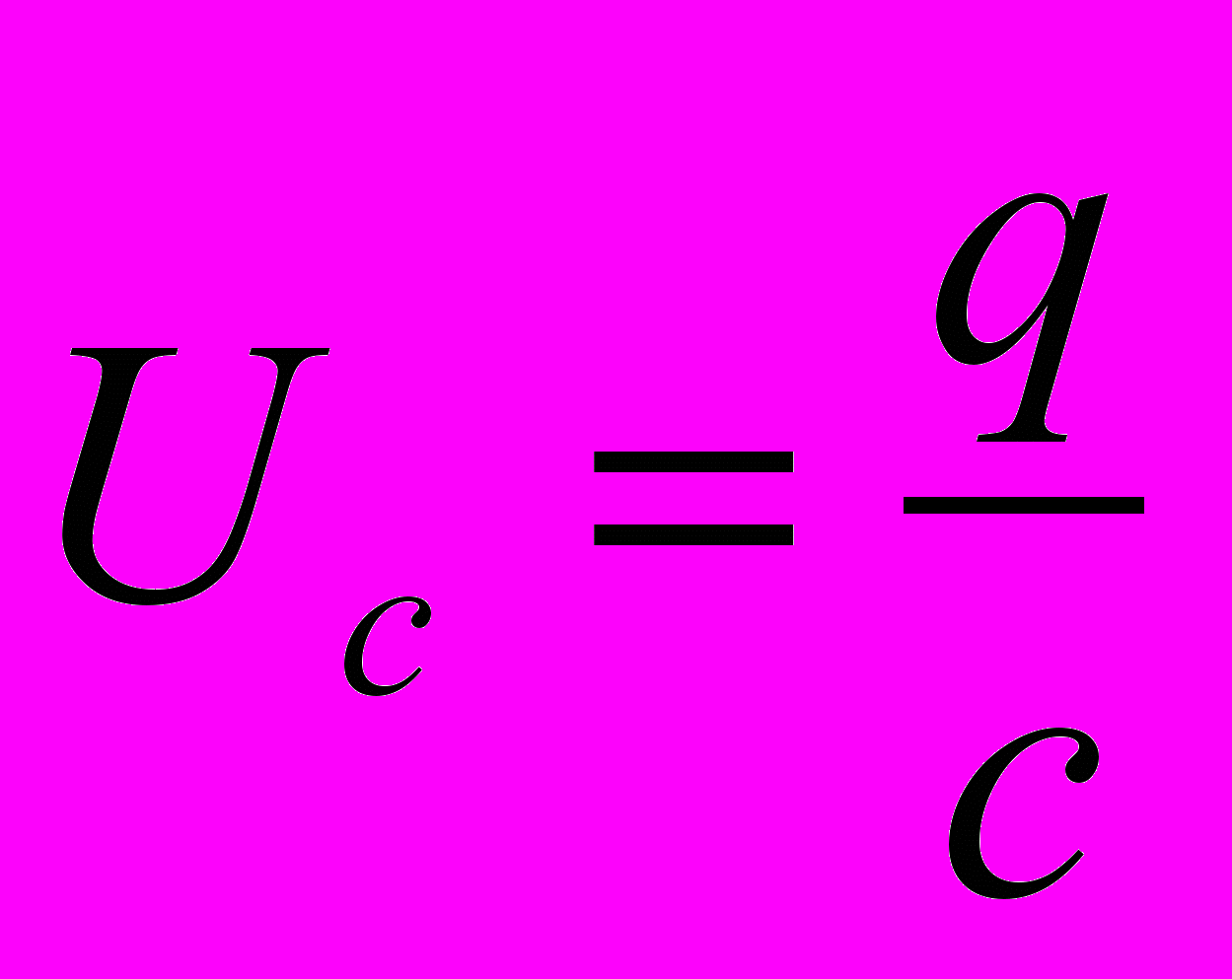
получим:

, где W_эл- электрическая энергия конденсатора.

c. Процесс разрядки конденсатора. Ключ в пол. 2.

Конденсатор начинает разряжаться через катушку






В катушке создается E_c, которая препятствует нарастанию тока.

Когда I=I_max напряжение на конденсаторе будет U_c=0.

В этот момент: W_эл=0, т.к.

Вся энергия накапливается в катушке:

до значения

В следующий момент конденсатор начинает перезаряжаться, сила тока при этом уменьшается, а напряжение на конденсаторе увеличивается. Магнитная энергия катушки превращается в электрическую.

Полная энергия цепи:


d. Решение задачи № 983 Сборник задач (А.П. Рымкевич).

В колебательном контуре индуктивность катушки равна 0,2 Гн, а амплитуда колебаний силы тока 40 мА. Найти энергию электрического поля конденсатора и магнитного поля катушки в тот момент, когда мгновенное значение силы тока в 2 раза меньше амплитудного значения.


3. Объяснение нового материала. Лекция учителя. Запись конспекта.

Тема: «Уравнение колебательного процесса в колебательном контуре»

Полная энергия цепи:

Найдем скорость изменения тока или ускорение, с которым меняется заряд в колебательном контуре. Для этого возьмем первую производную полной энергии по времени:




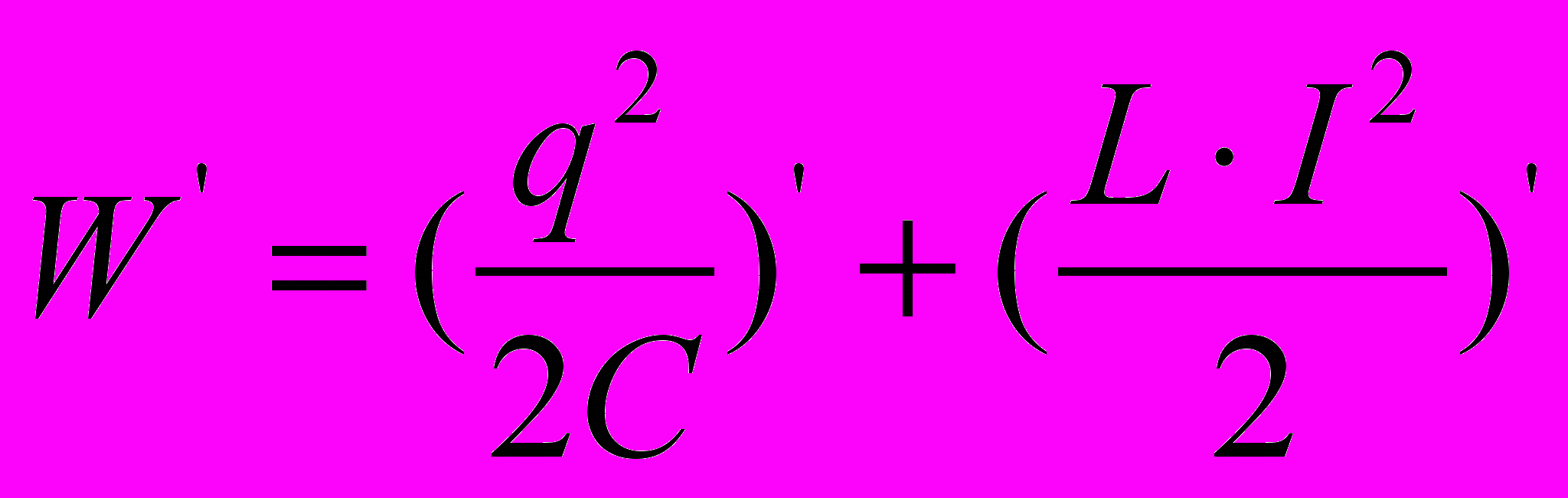
W ^'=0, т.к. W=const

Получим: как производную сложной функции


подставим в предыдущую формулу, получим: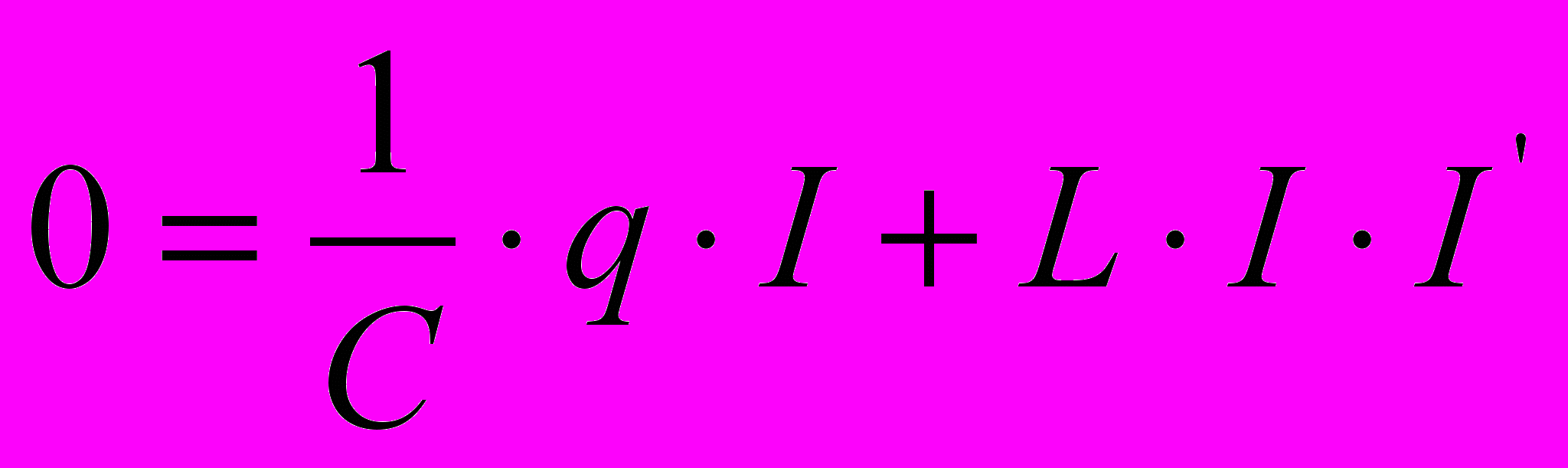



или

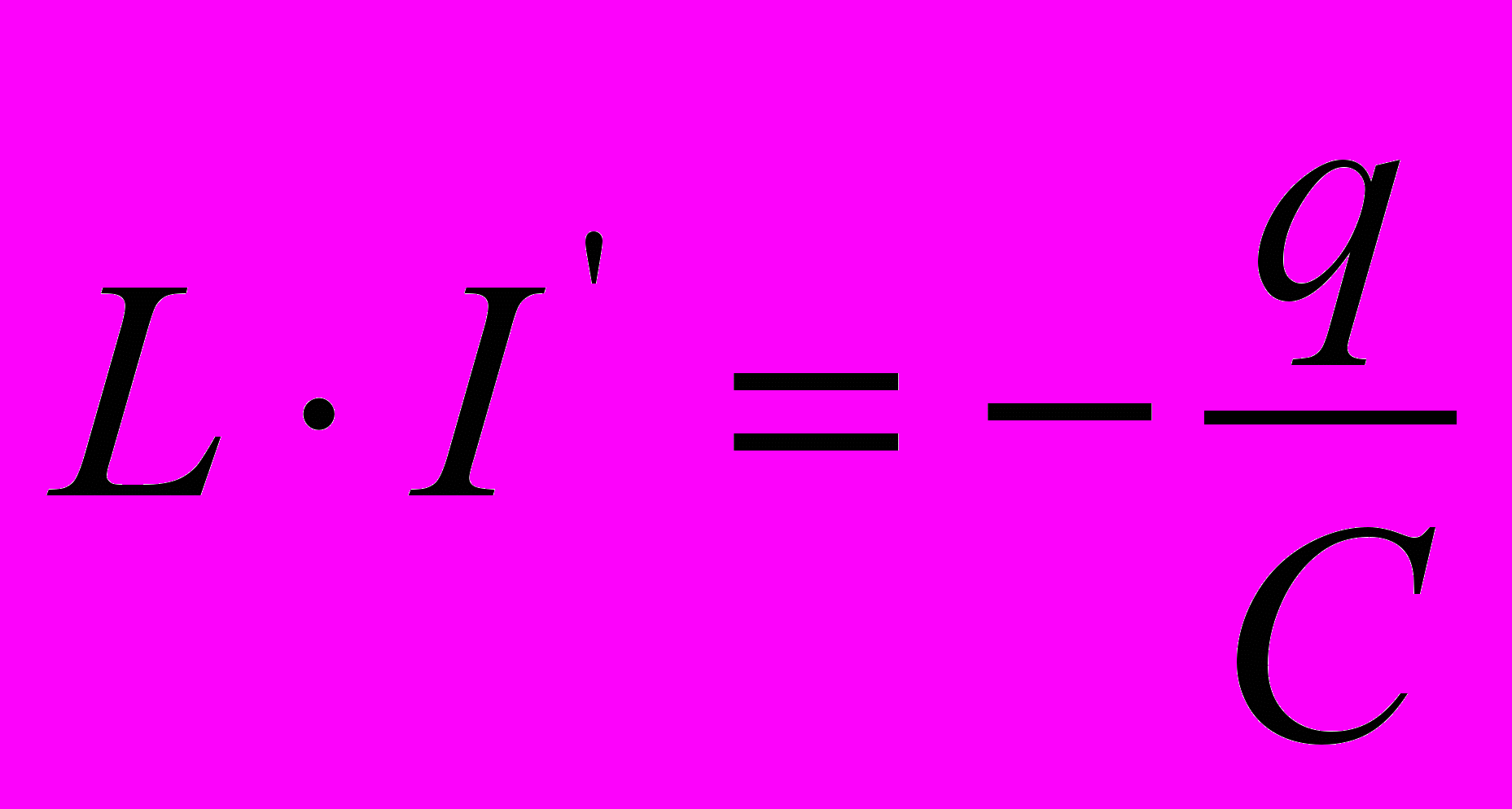
(1)


Так как , следовательно (2)


Формулы 1 и 2 – это уравнение колебательного процесса. Уравнение показывает, как быстро меняется сила тока в колебательном контуре и с каким ускорением происходят колебания электрического заряда.


Формула Томсона

По аналогии с механическим колебанием определим циклическую частоту и период колебательного процесса в контуре:







, следовательно, собственная циклическая частота будет равна








- Период колебательного процесса

в колебательном контуре. Формула Томсона.

4. Решение заданий ЕГЭ



5. Домашнее задание: § 30, упр. 4 № 2.