Задача Свободные колебания в контуре имеют начальную амплитуду напряжения 40В

Вид материала

Задача

Подобный материал:

• Гармонические колебания в контуре, 42.15kb.
• Лабораторная работа 3 свободные механические колебания (математический маятник и груз, 101.5kb.
• Тема урока : «Уравнение процессов в колебательном контуре. Период колебания», 85.02kb.
• 172. Электрические колебания в колебательном контуре заданы уравнением. Какова циклическая, 133.13kb.
• Вынужденные электромагнитные колебания, 39.6kb.
• Контрольная работа № Механические колебания и волны Задача, 352.68kb.
• Вопросы к теоретическому зачету по физике за Iполугодие, 17.24kb.
• Радиоэлектроника, 285.63kb.
• 1. 1 Индукция и напряженность, 153.53kb.
• Занятие №57 Механические колебания. Гармонические колебания. Резонанс. Колебания, 227.41kb.

Задача

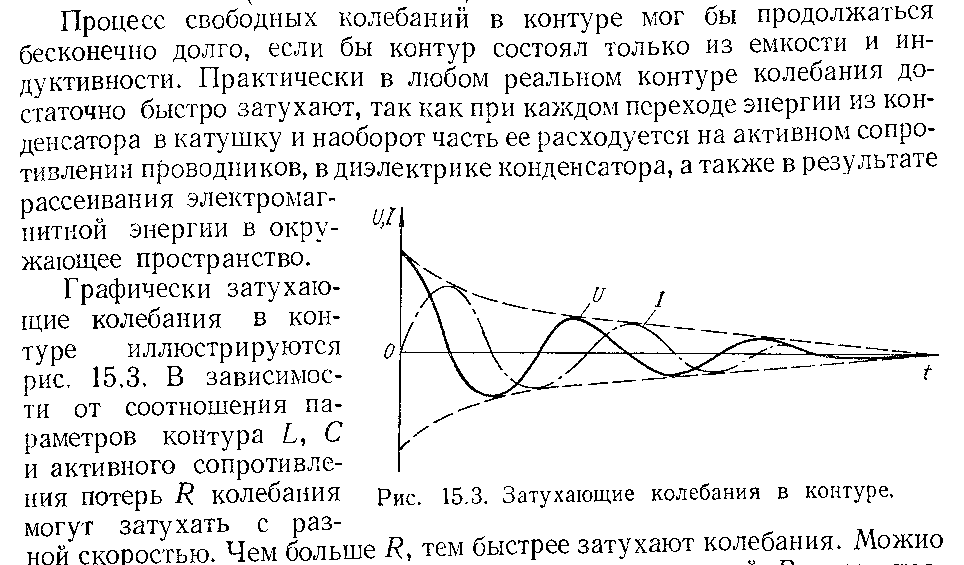
Свободные колебания в контуре имеют начальную амплитуду напряжения 40В,

начальную амплитуду тока 80 мА и период 1 мкс. Определить L, C и r, добротность,

логарифмический декремент затухания и постоянную времени цепи при затухании контура 0,008. Изобразить график колебаний.

РЕШЕНИЕ

1. Период свободных колебаний Т₀=10^-6с, следовательно частота свободных колебаний f₀=10⁶Гц и круговая частота ω₀=2πf₀ = 6.28*10⁶Гц.
   
2. Графики напряжения и тока в контуре [1]:
   

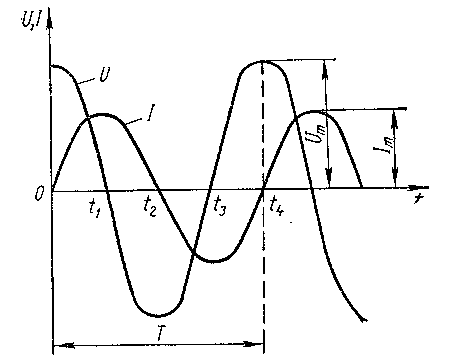
Между амплитудой тока Im и амплитудой напряжения Um существует зависимость [1]:

Im = Um* ω₀*С,

Тогда емкость контура С:

С= Im/ Um* ω₀ = 80*10^-3/(40*6,28*10⁶) = 0,318*10^-9 Ф.

3. Определяем индуктивность контура, например из резонансной частоты [1],[2]:
   

ω₀ = 1/√( L*C),

тогда

L = 1/( ω₀²*C) = 1/(6,28²*10¹²*0,318*10^-9) = 0,0795*10^-3 Гн.

Аналогичный результат можно получить из уравнения для цепи переменного тока [1]:

Im= Um / L * ω₀ => L = Um /Im * ω₀ .

4. Определяем волновое или характеристическое сопротивление контура [1]:
   

ρ = Um /Im = √( L*C) = ω₀ *L= = 1/(ω₀*C) .


ρ = Um /Im = 40/80*10^-3 = 0,5*10³ Ом.

5. 
   

В задании указана безразмерная величина затухания контура υ = 0,008. Из последней формулы [1] определим сопротивление R контура:


R = (υ*ρ)/π = (0.008*0.5*10³)/3.14 = 1.27 Ом.

6. Определяем добротность контура Q [1], [2]:
   

Q = ρ/R = 0.5*10³/1.27 = 393.7

Контур имеет высокую добротность.

7. Логарифмический декремент затухания показывает степень затухания колебаний на отрезке времени равным периоду колебаний [2]:
   

Δ = Ln(Uc(t)/Uc(t+T₀)) = υ*T₀ = 0.008*10^-6 = 8*10^-9.

8. Постоянная времени цепи:
   

τ = 2* R*C = 2* 1.27*0.318*10^-9 = 0.8*10^-9 c.

9. График колебаний напряжения на емкости контура. Формула для расчета через параметры контура [2]:
   

Uc(t) = Um*EXP(-υ*t)*SIN(ω₀ *t + χ).


Начальная фаза определяется из уравнения [2]:


Tg(χ) = ω₀ /υ . => χ = ARCTg(ω₀ /υ) = ARCTg(6.28*10⁶/0.008) = 1.57 рад или 90⁰.


Формула для расчета напряжения на емкости контура имеет окончательный вид:


Uc(t) = 40*EXP(-0,008*t)*SIN(6,28 *t + 1,57).


Текущее время t задается в микросекундах. Расчет по формуле на участке от 0 до 50 мкс выполнен в программе MathCAD 14 и представлен ниже:



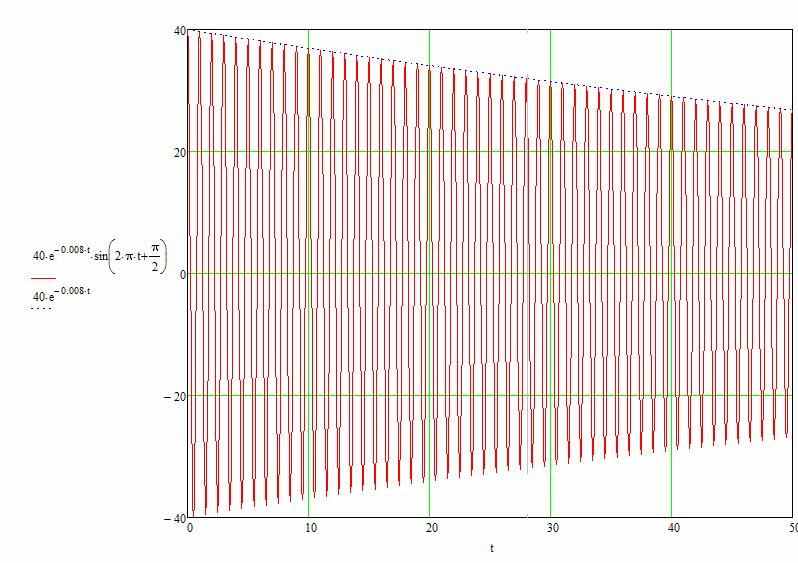
Пунктирной линией показан график огибающей.


Литература:

1. 
   
2.