Виктору Георгиевичу Лазуткину за огромную проделанную работу, без ознакомления с его исследованиями данная работа появилась бы значительно позже исследование
| Вид материала | Исследование |
- Данная работа предоставлена в целях ознакомления и изучения, незаконное копирование,, 8313.83kb.
- Методические указания к написанию курсовой работы по дисциплине «теория государства, 149.83kb.
- Учреждениями всех форм собственности, ежегодно проводит большую работу по трудоустройству, 81.79kb.
- -, 211.22kb.
- Дипломной работы, 234.14kb.
- Прежде всего, выражаю благодарность за инициативу и настойчивость Виктору, автору идеи, 31.29kb.
- Игорь блудилин-аверьян тень титана, 3253.71kb.
- Сергею Георгиевичу Бочарову. Его научные труды полностью отражают его профессиональное, 6648.51kb.
- Экономический Институт" Тема дипломной работы:, 145.41kb.
- Рекомендации по составлению доклада к защите дипломного проекта по специальности 240305, 13.09kb.
Александр Новицкий
ЛРАА «Гелиос»
Автор глубоко признателен Виктору Георгиевичу Лазуткину
за огромную проделанную работу,
без ознакомления с его исследованиями данная работа
появилась бы значительно позже.
Исследование зависимости Солнечной активности от взаимных положений (аспектов) планет.
Содержание:
Исследование зависимости Солнечной активности от взаимных положений (аспектов) планет. 1
Содержание: 1
Вступление. 2
Методика исследований. 4
Интерполяция графика Солнечной активности только с учётом планет-гигантов. 6
Интерполяция графика Солнечной активности с учётом Плутона 7
Анализ причин расхождений. Введение фазовых сдвигов. 8
Поиск одного оптимального фазового угла. 10
Поиски трансплутоновых объектов. 13
Возникающие проблемы. 15
Результаты поисков. Множественность вариантов. 17
Предварительные выводы. Проблема так просто не решается 18
Поиск решения… Исключая Плутон, но учитывая P06 19
Исправление формулы для случая 6 планет. 20
Приведение формулы к удобному для анализа виду. 23
W=A(t)*sin(AЮпиСат +F(t)) 23
Литература: 25
Вступление.
В наши дни влияние Солнечной активности на процессы, происходящие на Земле, уже ни у кого не вызывает сомнения [3], спектр этого влияния достаточно широкий, начиная с обострения сердечно-сосудистых заболеваний и заканчивая повышением количества дорожно-транспортных происшествий.
Вместе с тем, в вопросах понимания причин и прогнозировании Солнечной активности и поныне очень много «белых пятен», нет надёжной, и главное – долгосрочной методики прогнозирования, разные специалисты дают очень разные прогнозы даже на ближайший цикл. В связи с этим возникает впечатление, что эти неудачи связаны с тем, что не учитывается какой то важный фактор, имеющий существенное влияние на Солнечную активность.
Мы согласны с В.Г.Лазуткиным [1] в том, что необходимо учитывать взаимное расположение планет, в первую очередь планет-гигантов Юпитера, Сатурна, Урана и Нептуна. Исторически, ещё Рудольф Вольф (профессор астрономии и директор Бернской обсерватории, автор одноименного индекса Солнечной активности) полагал, что причиной Солнечной активности являются планеты.
К сожалению, позже по идеологическим причинам официальная наука принципиально отказалась рассматривать влияние планет на Солнечную активность, видимо это слишком напоминало астрологию. Действовали по принципу «этого не может быть, потому что этого не может быть никогда». Ведь если будет доказано влияние планет на Солнечную активность, тем самым будет доказано и влияние планет на происходящее на Земле – а ведь это основополагающее утверждение астрологии, которую материалистически настроенные учёные назвали «лженаукой». Соответственно, плачевное состояние с прогнозированием Солнечной активности, по нашему мнению, связано с тем, что влияние планет на Солнечную активность просто принципиально не исследуется, на эти исследования наложено «табу», по той простой причине, что успех такого исследования реанимирует статус астрологии - как науки о влиянии планет на земные процессы.
Глубокое рассмотрение физических моделей влияния планет на Солнечную активность выходит за рамки данной работы. Заметим, что мы согласны с тем, что смещение Солнца относительно барицентра Солнечной системы под влиянием различных конфигураций планет может приводить к смещению или изменению параметров вращения Солнечного ядра, что в свою очередь может приводить к изменению Солнечной активности.
Таким образом, важной характеристикой планеты, позволяющей судить о силе её влияния на Солнечную активность, является момент M=r*m, где r – расстояние от центра масс Солнечной системы до планеты, m – масса планеты. Как известно из астрономии, моментов планет гигантов Юпитера, Сатурна, Урана и Нептуна вполне достаточно, чтобы при определённых положениях этих планет барицентр Солнечной системы отклонился от центра Солнца настолько, чтобы даже выйти за пределы солнечного диска. Более подробно относительно физики процесса можно посмотреть в [1].
Целью данной работы является изучение, как именно Солнечная активность зависит от положений планет, и построение математической модели, которая бы позволяла на основании известных положений планет с достаточной точностью интерполировать уже имеющиеся данные, и делать прогнозы.
Методика исследований.
Виктор Георгиевич Лазуткин в своём исследовании [1] приводит зависимость Солнечной активности от пары планет Юпитер-Сатурн, с модулирующим влиянием на эту зависимость пары планет Уран-Нептун, называя это «Законом креста» и Би-Бинарным взаимодействием. Также он приводит замечание, что хотя это и является основным фактором влияния планет на солнечную активность, но для более точной корреляции необходимо также учитывать и транс-Нептуновые объекты. Произведём независимое исследование этого вопроса, применяя метод наименьших квадратов для поисков параметров данной закономерности.
Математический вид формулы предлагается таким:
Обозначения:
Юпи – Юпитер
Сат – Сатурн
Ура – Уран
Неп – Нептун
АЮпиСат – аспект Юпитер – Сатурн, то есть угол между Юпитером и Сатурном по эклиптике, AЮпиСат = LЮпи – LСат, где LЮпи и LСат - эклиптические долготы Юпитера и Сатурна, соответственно;
АУраНеп – аспект Уран-Нептун;
И так далее, рассматриваем все возможные варианты аспектов.
В.Г.Лазуткин предлагает искать формулу влияния аспектов планет в виде комбинаций би-бинарных влияний, для 4-х планет она может иметь вид:
Формула №1:
W=A1*sin(АЮпиСат+АУраНеп)+ А2*sin(АЮпиСат-АУраНеп)+ А3*sin(АЮпиУра+АСатНеп)
То есть, аспект одной пары планет модифицируется (фазовый сдвиг) аспектом другой пары планет. Коефициенты A1…A3 находим при помощи метода наименьших квадратов.
Почему слагаемых только 3, и не рассматриваются, например, варианты АЮпиУра-АСатНеп, АЮпиНеп+АCатУра, АЮпиНеп –АСатНеп? Потому что, на самом деле, они не являются независимыми, и сводятся к предыдущим трём вариантам. Например:
АЮпиУра-АСатНеп = LЮпи-LУра-(LСат-LНеп) = LЮпи – LСат – LУра + LНеп = АЮпиСат - АУраНеп
Можна модифицировать формулу №1, учитывая так же транс-Нептуновые обьекты. А так же добавлять не только sin но и cos данных би-бинарных соотношений, делая возможным фазовые сдвиги. Так же для удобства применения метода наименьших квадратов, формулу №1 можна преобразовать (что так же предложено в [1]):
Sin(A+B)=Sin(A)Cos(B)+Cos(А)Sin(B)
В заключение, следует обратить внимание на то, что предложенный В.Г.Лазуткиным метод отображать графики чисел Вольфа таким образом, чтобы чётные и нечётные циклы имели противоположный знак, очень удобен, так как значительно упрощает математику. Кроме того, нам показалось удобным так же нормировать эти графики, разделив значения на величину стандартного среднеквадратического отклонения StDev. Данные по Солнечной активности брались из [4], с выполнением вышеприведенных преобразований. В работе использовались среднегодичные числа Вольфа за период с 1749 по 2010 год.
Координаты планет брались не средние, как у [1], а истинные, но приведенные на средину соответствующего года (так как число Вольфа, усреднённое за год, так же можна относить к средине данного года).
С учётом вышесказанного график Солнечной активности приобретает следующий вид, График №1:
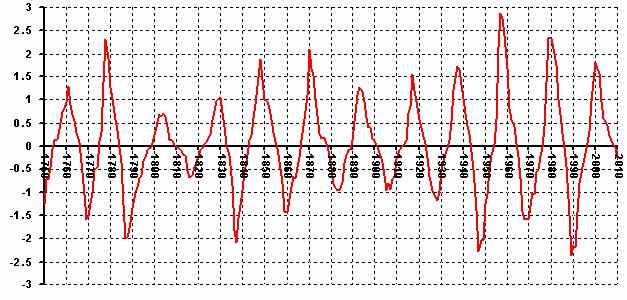
Минимуму солнечной активности соответствует пересечение графиком 0, максимумам – екстремумы графика, независимо от знака – «+» или «-».
Для приведения графика к «привычному» виду, нужно умножить на величину стандартного среднеквадратического отклонения StDev = 66.496, и взять значение по модулю.
Интерполяция графика Солнечной активности только с учётом планет-гигантов.
Попробуем найти коефициенты для формулы №1, используя метод наименьших квадратов, чтобы посмотреть насколько точно может быть апроксимирован наш график чисел Вольфа, с учётом влияний только наибольших планет – Юпитера, Сатурна, Урана и Нептуна. Транс-Нептуновые объекты пока не учитываем. Планеты Земной группы не учитываем вообще – они могут влиять на среднемесячные числа Вольфа, а на среднегодичных их влияние будет гначительно сглаживаться вследствие усреднения за год. К тому же, их вклад в смещение барицентра Солнечной системы значительно скромнее, чем планет-гигантов, следовательно и влияние на Солнечную активность так же значительно меньше.
Результат применения метода наименьших квадратов,
Таблица №1:
-
Формула
A
Sin(LЮпи-LСат-LУра+LНеп)
0.9912
Sin(LЮпи-LСат+LУра-LНеп)
-0.2835
Sin(LЮпи+LСат-LУра-LНеп)
-0.0609
В результате получаем коефициент корреляции 0.7214, что совсем неплохо для такой простой формулы. Заметим так же, что с достаточной точностью можна ограничиться двумя первыми членами, третий имеет маленький коефициент и соответственно, незначительно влияет на корреляцию, и поведение нашей апроксимирующей функции. С учётом только первых двух членов коефициент корреляции составит 0.7201.
График №2
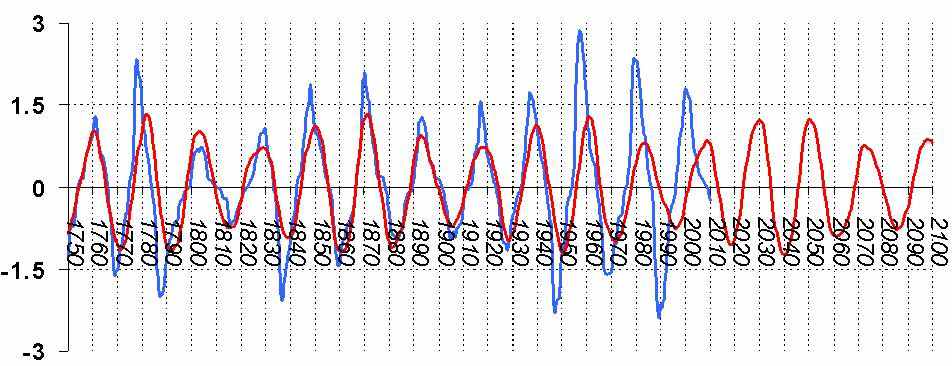
На данном графике синим представлены числа Вольфа, красным – наше приближение по Формуле №1. Видно неплохое совпадение, впрочем наша формула несколько заниживает реальные максимумы чисел Вольфа, особенно в 19-20-х столетиях, так же бросается в глаза наявность систематического расхождения, в виде медленного сдвига максимумов. Поэтому, несмотря на осмысленное поведение нашей функции на интервале после 2010 года, её напрямую нельзя использовать для прогноза, необходимо провести некоторые коррекции, например проверить, не устраняет ли данное расхождение учёт транс-Нептуновых планет, например Плутона.
Интерполяция графика Солнечной активности с учётом Плутона
Проверим, значительно ли улучшиться ситуация, если мы задействуем в расчётах так же и Плутон. Напомним, что влияние пары Уран-Нептун на основное взаимодействие Юпитер-Сатурн проявляется именно в виде фазового сдвига, так как приблизительно формула может быть представлена в виде Sin(АЮпиСат±АУраНеп), то есть можна предположить, что без влияния пары Уран-Нептун Солнечная активность просто совпадала бы с ходом АЮпиСат. Наше расхождение реальных данных с рассчётными показывает небольшое и систематическое расхождение именно по фазе, так что есть основание надеяться, что совпадение будет улучшено с учётом дополнительных планет.
Таблица №2:
-
№
Формула
A
1
Sin(LЮпи-LСат-LУра+LНеп)
0.9915
2
Sin(LЮпи-LСат-LНеп+LПлу)
-0.3143
3
Sin(LЮпи-LСат+LУра-LНеп)
-0.3027
4
Sin(LЮпи-LСат+LУра-LПлу)
0.2248
5
Sin(LЮпи-LСат-LУра+LПлу)
-0.2036
6
Sin(LЮпи-LСат+LНеп-LПлу)
0.1149
7
Sin(LСат-LУра+LНеп-LПлу)
-0.1005
8
Sin(LЮпи+LСат-LУра-LНеп)
-0.0561
9
Sin(LСат-LУра-LНеп+LПлу)
0.0401
10
Sin(LЮпи-LУра-LНеп+LПлу)
-0.0280
11
Sin(LСат+LУра-LНеп-LПлу)
0.0252
12
Sin(LЮпи+LСат-LНеп-LПлу)
0.0248
13
Sin(LЮпи-LУра+LНеп-LПлу)
0.0147
14
Sin(LЮпи+LУра-LНеп-LПлу)
0.0022
15
Sin(LЮпи+LСат-LУра-LПлу)
0.0009
Из Таб. №2 видно, что при учёте Плутона колличество независимых комбинаций увеличилось до 15. Жёлтым выделены элементы формулы, которые мы использовали для описания взаимодействия с учётом только планет-гигантов. Радует, что числовые значения этих коэффициентов почти не изменились после того, как мы добавили к рассмотрению ещё одну планету. Кроме того, бросается в глаза, что наибольшие коеффициенты имеют те элементы формулы, которые включают в себя AЮпиСат = LЮпи-LСат, поэтому без особого ущерба для поведения нашей функции мы можем оставить только первые 6 элементов формулы. Таким образом, с учётом Плутона и наших упрощений, формула может быть сведена к членам вида:
Sin(АЮпиСат±АУраНеп), Sin(АЮпиСат±АУраПлу), Sin(АЮпиСат±АНепПлу).
Коеффициент корреляции при учёте всех 15 слагаемых равен 0.7945, при учёте только 6 основных слагаемых – 0.7888.
Таблица №3 (перерассчитанны коефициенты, с учётом только членов содержащих АЮпиСат):
-
№
Формула
A
1
Sin(LЮпи-LСат-LУра+LНеп)
0.9959
2
Sin(LЮпи-LСат-LНеп+LПлу)
-0.3098
3
Sin(LЮпи-LСат+LУра-LНеп)
-0.3044
4
Sin(LЮпи-LСат+LУра-LПлу)
0.2227
5
Sin(LЮпи-LСат-LУра+LПлу)
-0.2067
6
Sin(LЮпи-LСат+LНеп-LПлу)
0.1119
Из Таб.№3 мы видим что максимальные коефициенты у пары Уран-Нептун, аспекты Уран-Плутон и Нептун-Плутон влияют меньше, что неплохо согласуется с нашей физической моделью.
График №3

Сравнивая График №2 и График №3 мы видим что совпадение значительно улучшилось, расхождение хоть и не исчезло совсем, но значительно уменьшилось.Так же бросается в глаза небольшие значения максимума текущего цикла, и нескольких последующих, что согласуется с выводами [1]
Однако, некоторое запаздывание нашей формулы по отношению к текущему циклу не позволяет остановиться на достигнутом, и заставляет искать дополнительные причины этого расхождения.
Анализ причин расхождений. Введение фазовых сдвигов.
Некоторое остаточное расхождение между нашей формулой и реальными данными заставляет задуматься над причинами, которые могут приводить к такому расхождению. В качестве эксперимента попробуем учитывать не только Sin но и Cos, таким образом мы позволим фазовый сдвиг екстремумов нашей функции относительно углов 0, 90, 180, 270 на произвольную величину. Используем тот факт, что:
A*sin(X)+B*cos(X) = C*sin(X+F)
Посмотрим, сможет ли это кардинально поменять ситуацию и устранить расхождение.
Таблица №4.
-
№
Формула
A
1
Sin(LЮпи-LСат-LУра+LНеп)
0.9981
2
Sin(LЮпи-LСат-LНеп+LПлу)
-0.4554
3
Sin(LЮпи-LСат+LУра-LНеп)
-0.4496
4
Sin(LЮпи-LСат+LУра-LПлу)
0.2584
5
Sin(LЮпи-LСат-LУра+LПлу)
-0.2131
6
Sin(LЮпи-LСат+LНеп-LПлу)
-0.0973
7
Cos(LЮпи-LСат-LУра+LНеп)
0.6673
8
Cos(LЮпи-LСат+LУра-LНеп)
-0.2425
9
Cos(LЮпи-LСат+LНеп-LПлу)
0.1755
10
Cos(LЮпи-LСат-LНеп+LПлу)
0.1738
11
Cos(LЮпи-LСат-LУра+LПлу)
-0.1495
12
Cos(LЮпи-LСат+LУра-LПлу)
0.1037
Коефициенты при членах с Sin поменялись не сильно и сохранили свой знак, исключение составил только Sin(АЮпиСат+АНепПлу). Однако наявность довольно большого коефициента при Cos(АЮпиСат-АУраНеп) заставляет серьёзно задуматься.
Действительно, если бы все коефициенты при членах с Cos были малыми, это бы означало, что никакими фазовыми поворотами улучшить корреляцию уже не удасться. По сути, поворот по фазе и отличие экстремумов функции от углов 0, 90, 180 и 270 градусов говорит о том, что есть какая то физическая причина, какое то дополнительное взаимодействие.
Ведь, если вспомнить, например ситуацию с приливами на Земле и их зависимостью от фаз Луны, то максимальные приливы получаются во время новолуний и полнолуний (АСолнцеЛуна 0 и 180 градусов), минимальные – во время квадратур (АСолнцеЛуна – 90 и 270 градусов). Эсли бы эти углы были другими, и были бы смещены на какой то угол, это заставило бы задуматься о природе этого угла, о дополнительных силах и обьектах, способных создать такое смещение.
Коеффициент корреляции при учёте Сos возрастает значительно, и составляет аж 0.9160, графики по сути совпадают теперь очень хорошо. Но остаётся вопрос в правомерности такого решения, то есть не является ли такая хорошая корреляция попросту математическим фокусом, ведь для того чтобы её достичь мы посути ввели 6 независимых фазовых углов, для каждой пары взаимосвязанных Sin і Cos. Какая их физическая суть, и можна ли уменьшить колличество этих фазовых сдвигов, например только до одного – общего для всех пар Sin і Cos? Тогда это могло бы иметь физический смысл – взаимодействие с каким то обьектом, и можна было бы пытаться искать параметры такого взаимодействия.
График №4.

График №4 демонстрирует отличное совпадение. Если бы оно было достигнуто без введения пока что абстрактных фазовых смещений, работу на этом можна было бы считать законченной.
Поиск одного оптимального фазового угла.
Поставим задачу следующим образом. Попробуем найти оптимальное значение одного фазового угла, одинакового для всех членов формулы, и сравним, значительно ли ухудшиться коефициент корреляции (по сравнению с тем, что мы получили введя члены с Cos).
Формула 2:
W=A1*Sin(АЮпиСат+АУраНеп+F)+A2*Sin(АЮпиСат-АУраНеп+F)+ A3*Sin(АЮпиСат+АУраПлу+F)+A4*Sin(АЮпиСат-АУраПлу+F)+ A5*Sin(АЮпиСат+АНепПлу+F)+A6*Sin(АЮпиСат-АНепПлу+F)
Таким образом, от 12 неизвестных коеффициентов мы вернулись к 6 плюс фазовый сдвиг F. Посмотрим, намного ли ухудшиться корреляция.
Одновременное нахождение коеффициентов A1 – A6 и F методом наименьших квадратов не очень удобно, так как теперь уже задача не сводиться к решению системы линейных уравнений. Поэтому мы действовали методом перебора F, при поиске оптимальных коефициентов A1-A6 для каждого варианта. Ищем такое значение F, при котором среднеквадратичное отклонение будет минимально.
График №5

Как оказалось, график зависимости среднеквадратических отклонений нашей функции от значения фазового угла F имеет очень чётко выраженный характер и два абсолютных минимума.
Таким образом, оптимальное значение F:
F1=27.84036
F2=F1+180=207. 84036
Для данного значения фазового угла F1 найдём набор коэффициентов:
Таблица №5
-
№
Формула
A
1
Sin(LЮпи-LСат-LУра+LНеп+F)
1.0662
2
Sin(LЮпи-LСат+LУра-LНеп+F)
-0.4219
3
Sin(LЮпи-LСат-LНеп+LПлу+F)
-0.3614
4
Sin(LЮпи-LСат+LУра-LПлу+F)
0.2800
5
Sin(LЮпи-LСат-LУра+LПлу+F)
-0.1872
6
Sin(LЮпи-LСат+LНеп-LПлу+F)
0.1384
Коеффициент корреляции составил для данной формулы 0.8882, и хотя это меньше чем 0.9160 при использовании Сos, но мы достигли этого результата путём уменьшения колличества членов формулы почти вдвое, при не очень значительном уменьшении корреляции. Кроме того, этот результат может иметь физический смысл, например F это среднее положение какого либо неизвестного объекта за исследуемый период, либо среднее значение угла между этим объектом и какой либо из известных планет, например Нептуном.
Предположительно эта величина меняется очень медленно, так как имеет отношение к транс-Плутоновым объектам, поэтому и возможно с достаточной точностью представить это влияние с помощью константы.
График №6
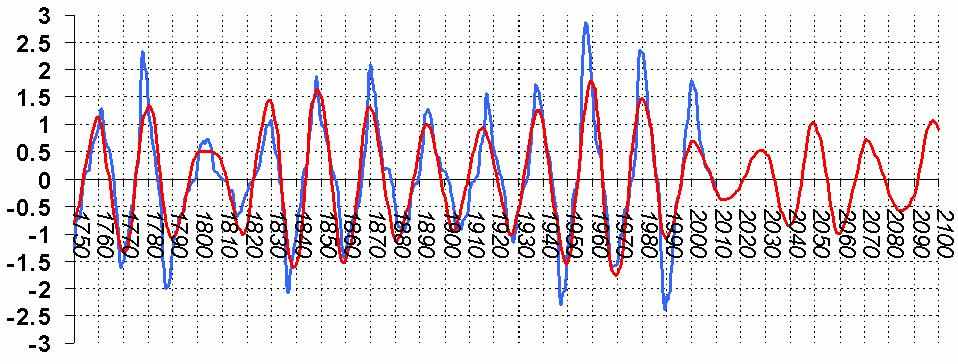
Визуально совпадение нашей функции с реальными данными не хуже, чем при использовании cos, поведение после 2010 года тоже не сильно отличается. Поэтому следует считать Формулу №2 с коеффициентами из Таб.№5 и фазовым углом F1 пока что наиболее работоспособной из всех рассмотренных вариантов.
Следующее соображение по поводу применимости Формулы №2 к прогнозам Солнечной активности. Рассматриваемый период с 1749 по 2010 - составляет 261 год. На протяжении этого периода F можна рассматривать как константу. Следовательно, период изменения F значительно больше чем 261 год. Кроме того, хороший результат на указанном периоде позволяет надеяться на прогноз ±260 лет за граници интервала 1749 – 2010 (или хотя бы 260/2=±130 лет), то есть можна пробовать делать прогноз примерно до 2140 года.
Напомним: в формулу №2 следует подставлять не средние долготы планет, которые изменяются линейно, а истинные долготы (с учётом эллиптичности орбит), найденные на средину года. Для планет от Юпитера до Нептуна средняя долгота может значительно отличаться от истинной, среднеквадратическое отклонение может составлять примерно 3-5 градуса. А для Плутона вследствие большого эксцентриситета орбиты среднеквадратическое отклонение истинной долготы от средней может составлять до 20 градусов. Коэфициенты в Таб.№5 были найдены при использовании именно истинных, а не средних долгот.
Поиски трансплутоновых объектов.
Тот факт, что с помощью введения фазового сдвига F мы кардинально смогли улучшить корреляцию нашего графика с реальными данными, говорит в пользу того, что такая систематическая ошибка, которую мы попытались устранить введением фазового угла F может возникать от неучтения нами влияния каких то дополнительных объектов.
Выше было показано что учёт планет земной группы вряд ли улучшит ситуацию вследствии их малых периодов обращения, в то время как нам нужен очень медленный (и следовательно очень удалённый) объект.
Мы уже учли планеты гиганты – Юпитер, Сатурн, Уран, Нептун, а так же Плутон, но этого всё равно не оказалось достаточно, пришлось вводить параметр F. Следовательно это должен быть один или несолько транс-Нептуновых, или даже транс-Плутоновых объектов.
Это может быть какой то из уже известных транснептуновых объектов (в последнее время их открыто достаточно много), или же это может быть ещё неизвестный объект.
В работе [1] В.Г.Лазуткин рассматривает много гипотез о существовании новых транс-Нептуновых объектов, выдвинутых другими авторами в процессе поиска планеты Плутон, на основании анализа возмущений орбиты Урана и Нептуна, которые не обьясняются иначе небесной механикой, нежели гравитационным влиянием какого то пока неизвестного обьекта. Как известно, Нептун и позже Плутон были найдены именно благодаря таким вычислениям. Также известно, что масса Плутона, вычисленная после открытия его спутника Харона, оказалась намного меньше, чем та, которая была нужна для обьяснения возмущений в движении Нептуна [5]. То есть не было исключено существования и других транснептунов, которые впоследствии и были открыты – Куаоар, Эрис и т.д.
Задача предсказания существования новых объектов Солнечной системы, на основании отклонений Солнечной активности от ожидаемого, ещё сложнее, чем такое же предсказание по отклонениям в движении планет, хотя бы потому что законы движения планет мы знаем значительно лучше, чем механизмы Солнечной активности. Тем не менее В.Г.Лазуткин выдвигает ряд смелых гипотез, по поводу параметров гипотетических планет, анализирует гипотезы других авторов [5], и делает попытку сверхдолгосрочных прогнозов. Поэтому, читателей заинтересованных в данном вопросе мы можем отослать к работе [1] а так же [5]
Целью данной работы не является поиск новых планет, или свергдолгосрочные прогнозы Солнечной активности. Мы хотели просто найти хорошую рабочую формулу Солнечной активности, и показать зависимость Солнечной активности от угловых положений (аспектов) планет Солнечной системы. По сути нами было независимо проведено исследование, которое уже ранее провёл В.Г.Лазуткин в [1], и которое полностью подтвердило его результаты относительно связи положений планет с Солнечной активностью, а так же необходимость рассмотрения дополнительных объектов Солнечной системы, так как влияния известных планет немножко не хватает.
Так как в наших формулах всё же присутствует загадочный параметр F, который учитывает влияние неизвестного (или нескольких неизвестных ) объектов, попробуем несколько усложнить нашу модель, и ввести вместо F какой то движущийся объект, с учётом которого мы могли бы описать Солнечную активность как минимум, не хуже чем по простой Формуле №2.
Точный учёт всех элементов орбиты нашего гипотетического объекта видиться слишком сложным и не очень нужным, тем более что даже простым подбором фазового сдвига мы доcтигли хорошего результата. Поэтому, попробуем просто учесть влияние нашего объекта, в виде линейной формулы для средней долготы:
Формула 3:
LP06 = L0 + L1 * (Y – 2000)
Здесь Y – год, на средину которого рассчитывается положение гипотетической планеты, L0 – её положение на средину 2000 года, L1 – угловая скорость движения планеты.
Параметры L0 и L1 нам как раз и предстоит найти, L0 может изменяться от 0 до 360º, L1 будем искать от 1.46º/год до 0º/год (то есть, от орбиты Плутона, и дальше). Период обращения нашей планеты, следовательно будет равен 360º/L1.
Следуя принципу разумной достаточности, вводим пока что только один такой объект. Поскольку мы получили достаточно хороший результат с введением параметра F, который описывает влияние очень медленно двигающегося (в данном приближении стационарного) объекта, если мы позволим объекту двигаться с какой то скоростью L1, результат должен быть как минимкм не хуже, в крайнем случае L1 может быть равно 0, и наша задача сведётся к случаю c F.
Возникающие проблемы.
Период, за который у нас есть данные по Солнечной активности, немногим больше одного оборота Плутона. Искомый объект движеться, по определению, ещё медленней Плутона. Стало быть, не будет и одного его оборота. Поэтому метод наименьших квадратов уже не будет гарантировать хорошую сходимость коефициентов при формулах, куда входят аспекты этой планеты. Так же может возникать нереалистичное поведение функции за границами интерполируемого интервала. Например, если сумма по модулю всех коеффициентов даст в каком то решении 10, то это будет означать, что в какой то момент Солнечная активность предсказываемая нашей функцией, будет составлять 10*66.496=664 единиц чисел Вольфа, что маловероятно и пока в природе не наблюдалось.
Следовательно, нам будет недостаточно минимизировать среднеквадратические отклонения, а нужно будет ещё и пытаться минимизировать сумму (по модулю) коеффициентов при наших формулах, и отбрасывать те результаты, где коеффициенты неправдоподобно завышены.
Другой подход нормализации поведения функции вне интервала интерполяции – пытаться подбирать параметры движения новой планеты так, чтобы функция апроксимации вела себя осмысленно и давала минимумы при известных удалённых минимумах Солнечной активности (например, минимум Маундера), других геологических событиях типа глобальных похолоданий, ледниковых периодов и т.д.(как событий, возможно связанных с глобальными минимумами Солнечной активности). В таком случае нужны, во первых, дополнительные данные, во вторых – задание краевых условий, в дополнение к минимизации квадратических отклонений на периоде 1749 – 2010.
Кроме того, следует заметить, что введение не одной а нескольких гипотетических объектов ещё более усугубляет проблему, и невозможно без введения таких краевых условий, поэтому остаётся вне предмета рассмотрения данной работы.
И последнее замечание, по поводу объекта описываемого Формулой 3. Это может быть либо какой то реальный объект, либо это может описывать движение барицентра нескольких транснептуновых объектов. Наперёд неизвестно что это такое. Это координаты точки, учитывая взаимодействие которой с остальными известными планетами, тем же способом что и для взаимодействий между ними (по принципу би-бинарного взаимодействия четвёрок планет), мы получим наилучшее совпадение с нашим графиком чисел Вольфа, и разумное поведение нашей функции, причём при более долговременном прогнозе, чем нам бы это позволила приближённая Формула 2 с учётом параметра F.
По поводу вида нашей функции, сейчас нам будет удобно воспользоваться формулой:
Sin(A±B)=Sin(A)Cos(B) ±Cos(А)Sin(B)
Cохраняем условие что в каждый елемент формулы должен быть включён AЮпиСат и угол (аспект) между какими то другими планетами, включая гипотетическую P06, причём беруться только взаимонезависимые комбинации.
Таким образом, мы будем искать коефициенты для формулы, представленной в следующем виде:
Таблица №6:
-
N
Формула
A
1
Sin(LЮпіСат)Cos(LУраНеп)
?
2
Cos(LЮпіСат)Sin(LУраНеп)
?
3
Sin(LЮпіСат)Cos(LУраПлу)
?
4
Cos(LЮпіСат)Sin(LУраПлу)
?
5
Sin(LЮпіСат)Cos(LУраP06)
?
6
Cos(LЮпіСат)Sin(LУраP06)
?
7
Sin(LЮпіСат)Cos(LНепПлу)
?
8
Cos(LЮпіСат)Sin(LНепПлу)
?
9
Sin(LЮпіСат)Cos(LНепP06)
?
10
Cos(LЮпіСат)Sin(LНепP06)
?
11
Sin(LЮпіСат)Cos(LПлуP06)
?
12
Cos(LЮпіСат)Sin(LПлуP06)
?
Теперь, при таком подходе, мы должны определить 12 параметров A1 – A12, а также параметры L0 и L1, которые описывают движение объекта P06.
Результаты поисков. Множественность вариантов.
При поиске наилучшего решения для параметров нового объекта P06, движение которого описывается Формулой 3, а взаимодействие с другими планетами – таблицей №6, действительно возникли ожидаемые проблемы.
Так, нам уже нужно осуществлять поиск наименьшего квадратического отклонения не по одному параметру, как с F, а по двум L0 и L1, и для кажного варианта рассчитывать оптимальные коеффициенты A1 – A12 методом наименьших квадратов. Для того чтобы не пропустить каких то вариантов решений, был применён метод Монте-Карло, с последующим уточнением значения L0 и L1 методом квадратической интерполяции.
К сожалению теперь среднеквадратическое отклонение ведёт себя не так чётко, как при случае с F (график №5), то есть при значительных изменениях L0 среднеквадратическое отклонение изменяется незначительно, минимумы выглядят скорей как мелкие блюдца, поэтому несмотря на довольно большие коэффициенты корреляции, есть довольно большая неопределённость с определением в первую очередь L0.
Для взаимодействий, заданных таблицей №6, было найдено три устойчивых решения для параметров движения P06:
Вариант №1:
L0= 30.3899220 (или 210.3899220)
L1= 0.7244936 º/год
Период = 360º/L1 = 496.90 лет.
Корреляция: 0.9322
Макс. амплитуда: 10.4087
Вариант №2:
L0= 173.4115880 (или 353. 4115880)
L1= 0.3492329 º/год
Период = 360º/L1= 1030.83 лет.
Корреляция: 0.9231
Макс. амплитуда: 8.0446
Вариант №3:
L0= 64.5316896 (или 244.5316896)
L1= 0.2809188º/год
Период = 360º/L1= 1281.51 лет.
Корреляция: 0.9268
Макс. амплитуда: 7.1698
Предварительные выводы. Проблема так просто не решается
Вариант №1 удивил относительно большой скоростью среднего движения, и не типичным повышением Солнечной активности после 2050 года, что идёт вразрез с выводами [1] о общей тенденции к глобальному понижению Солнечной активности (а так же со всеми другими вариантами поведения графика после 2010 года, включая наилучший наш вариант с учётом фазового сдвига F по формуле №2).Можна было бы конечно порадоваться по поводу того что глобального похолодания не будет, если бы не подозрительно большое значение максимальной амплитуды 10.4087, которое соответствует совершенно нереальной активности в 697 единиц Вольфа.
Вариант №2 показал более привычное поведение функции после 2010 года, максимумы не превышают ±1 (≈ 67 единиц Вольфа), что хорошо соответствует выводам [1]. Но максимально возможная амплитуда 8.0446 слишком большая – это соответствует ≈ 539 единиц Вольфа, как максимально возможный предел Солнечной активности, что безусловно так же слишком завышено.
Вариант №3 несмотря на маленькую скорость среднего движения всё равно даёт нетипичную и противоречащую [1] картину роста Солнечной активности в районе 2049 года, вплоть до 2.5 (≈168 единиц Вольфа). И хоть и самую маленькую из всех трёх вариантов, но всё же довольно большую максимально возможную амплитуду 7.1698 – что соответствует ≈ 480 единиц Вольфа.
Неприятным сюрпризом оказалась большая чувствительность поведения графика после 2010 года, от параметров гипотетического объекта P06, так как это противоречит нашим представлениям о том, что основные влияния на Солнечную активность всё таки производят планеты-гиганты Юпитер, Сатурн, Уран и Нептун. Соответственно от других планет ожидается только корректировка графика, а не кардинальное его изменение. Такое было бы возможно только при очень большом моменте неизвестной планеты (и следственно, большой масивности), порядка моментов планет-гигантов, или больше, но тогда такая планета вряд ли была бы неоткрыта до сих пор.
Так что, по видимому, такое поведение графика являет собой скорее математическую проблему из за недостаточной продолжительности рядов данных, чем физическую реальность, и стало быть нам следует поискать решения, которые ближе к тому, что даёт учёт только четырёх планет гигантов. На это указывают и завышенные значения максимальных амплитуд графика.
В связи с слишком завышенными максимальными амплитудами, напрашивается вывод о слабой приемлимости всех трёх найденных решений, видимо данных за период с 1749 по 2010 год не хватает для того чтобы, метод наименьших квадратов корректно подобрал коеффициенты для объектов со столь малой скоростью углового движения, периоды обращения которых значительно превышают 260 лет.
Второй возможный вариант напрашивается в связи с тем, что масса Плутона оказалась слишком мала, чтобы объяснить отклонения в движении Нептуна. Возможно и отклонения в движении Нептуна, и наше отклонение в поведении Солнечной активности обьясняются влиянием этого неизвестного объекта, а Плутон вообще не причём в силу своей малой массы, и его следует вообще исключить и заменить объектом P06, и тогда у нас не будет возникать проблем с завышенными значениями коеффициентов, и как следствие, с завышенным значением максимальной амплитуды?
Поиск решения… Исключая Плутон, но учитывая P06
Попробуем заменить всюду в наших уравнениях Плутон на P06 и посмотрим что у нас выйдет. Действительно, если Плутон всё таки нужен, мы можем получить решение с параметрами L0 и L1 близкими к движению Плутона, и тогда корреляция не будет значительно ниже, чем при учёте Плутона, но без дополнительной планеты и сдвига по фазе F. Но возможно, мы получим результат значительно лучше, методом подбора других значений параметров L0 и L1?
Методом Монте-Карло, с последующим уточнением значения методом квадратической интерполяции мы получили, на этот раз одно решение:
L0= 168.015143 (или 348.015143)
L1= 0.311813º/год
Период = 360º/L1= 1154.54 лет.
Корреляция: 0.8470
Макс. амплитуда: 3.5278
В результате, мы получили объект, не очень похожий на Плутон, но очень похожий на вариант №2, только при отсутствии Плутона.
Радует нормальное значение максимальной амплитуды, корреляция хотя и выше чем при учёте Плутона вместо P06, но всё же хуже чем при учёте Плутона и фазового сдвига F.
Полученный результат заставляет задуматься. Видимо проблема с нереальными коефициентами и завышенными амплитудами связан с взаимодействием P06 и Плутона, так как по отдельности учёт либо P06, либо Плутона к таким результатам не приводит. Проблема так же не в конкретных значениях L0 и L1, как можна было подумать, так как без Плутона мы пришли решению очень близкому по значению к варианту №2, однако там при учёте Плутона эти значения вызывали проблемы, в нашем последнем варианте с теми же значениями – проблем не возникло.
Попробуем в таком случае проанализировать ещё раз таблицу №6 – кто то из её членов портит картину, сильно искажает значение коэффициентов, и сильно завышает максимальную амплитуду формулы.
Исправление формулы для случая 6 планет.
По видимому, какой то один, или несколько членов, приведенных в таблице №6 сильно искажает картину, завышая свои коэффициенты, и искажая коэффициенты при других членах формулы. Попробуем разобраться, кто бы это мог быть. Будем исходить из своих физических представлений о влиянии планет на Солнечную активность, а так же из соображений здравого смысла. Например, отбрасываемый член формулы с одной стороны должен иметь значительные по величине коэффициенты, а с другой стороны – его исключение не должно существенно ухудшать коэффициент корреляции. То есть, несмотря на большой коэффициент, искомый угол должен иметь такое значение, чтобы на интервале 1749-2010 не сильно проявляться, то есть давать максимальные значения за пределами наших данных. Значит он должен изменяться медленно, и не принимать всех возможных значений на протяжении 260 лет, так как иначе метод наименьших квадратов запретил бы ему принимать нереально большие значения.
Естественно, нам следует оставить члены формулы с аспектами между Ураном и Нептуном, они вносят максимальный вклад в формулу, но делают это обоснованно, Уран и Нептун имеют максимальные после Юпитера и Сатурна масы и моменты.
Аспекты Урана и Нептуна к Плутону, а так же к P06 можна оставить, так как они не дают таких больших коеффициентов, и сами по отдельности, как мы видели, не приводят к негативному результату.
Итак, методом исключения, у нас остались только члены включающие аспект между Плутоном и P06. Действительно, Плутон имеет период порядка 250 лет, P06 по определению ещё больший период, поэтому коэффициенты не могут быть корректно определены методом наименьших квадратов. Кроме того здесь наблюдаются действительно довольно большие коэффициенты – порядка величины как у Урана с Нептуном. Плутон не имеет большого момента. Можна было бы думать что такие большие коэффициенты являются следствием большого момента объекта P06, однако коэффициенты при взаимодействии Уран-P06 и Нептун-P06 меньше, чем при взаимодействии Плутон-P06. Так что такие большие коэффициенты при AПлуP06 противоречат нашим физическим представлениям о механизмах влияния планет на Солнечную активность.
Поэтому попробуем исправить картину, просто исключив члены включающие AПлуP06. У нас остануться только взаимодействия Плутона и P06 с Ураном, либо с Нептуном. Это и есть основное исправление формулы. Теперь у нас выделенное положение не только пары Юпитер-Сатурн, но и выделенное положение пары Уран-Нептун.
Интересно, что теперь мы получили новое решение для L0 и L1.
L0= 43.3139 (или 223.3139)
L1= 0.1751 º/год
Период = 360º/L1= 2056.30 лет.
Корреляция: 0.9166
Макс. амплитуда: 5.4779 (или 367 единиц Вольфа)
Корреляция не пострадала, она даже больше чем при использовании варианта с Cos, максимальная амплитуда слегка завышена, хотелось бы не выше 3, но поведение функции после 2010 года приемлемое, не превышает значительно 1, возможно что в действительности Солнечная активность бывает выше, чем та что мы наблюдали за 260 лет, либо же экстремальные значения углов бывают крайне редко. При необходимости, можна пробовать отбросить так же взаимодействие P06 с Ураном, так как P06 ближе к Нептуну, и коефициент взаимодействия Нептун-P06 выше.
Таблица №7:
-
N
Формула
A
1
Sin(LЮпіСат)Cos(LУраНеп)
0.8136
2
Cos(LЮпіСат)Sin(LУраНеп)
-1.4330
3
Sin(LЮпіСат)Cos(LУраПлу)
-0.0676
4
Cos(LЮпіСат)Sin(LУраПлу)
0.5299
5
Sin(LЮпіСат)Cos(LУраP06)
0.1905
6
Cos(LЮпіСат)Sin(LУраP06)
-0.3502
7
Sin(LЮпіСат)Cos(LНепПлу)
-0.4454
8
Cos(LЮпіСат)Sin(LНепПлу)
0.4489
9
Sin(LЮпіСат)Cos(LНепP06)
0.8179
10
Cos(LЮпіСат)Sin(LНепP06)
-0.3811
Обращает на себя внимание большое значение коефициентов при LНепP06. А в целом, можна признать это решение удовлетворительным. Интересны еще и слелующие факты:
- Период 2056.30 лет. По данным радиоуглеродного анализа, на больших периодах наблюдаются климатические колебания, с периодом порядка 2000 лет.
- Если посчитать среднее значение LP06 на всём интервале 1749-2010, у нас получиться среднее положение 30.09385, что довольно близко к найденному значению для F=27.84036
Поведение графика после 2010 года тоже не очень сильно расходиться с тем, что мы имели для варианта с фазовым сдвигом F.
График №6
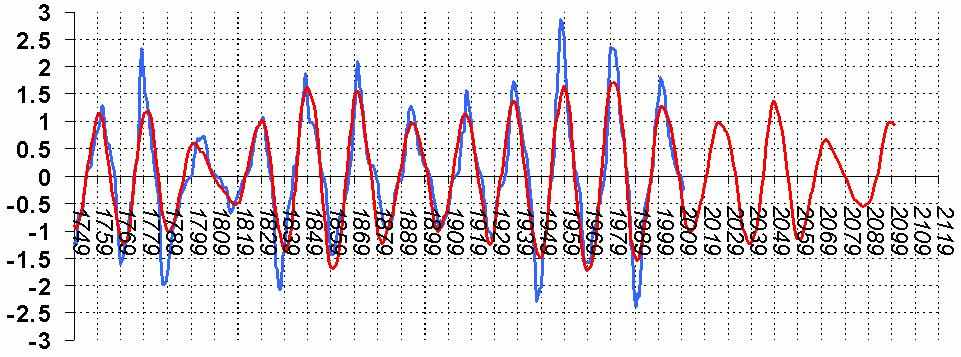
Интересно так же отметить, что поведение графика после 2069 года похоже на поведение графика после 1799 года, то есть так же имеют место очень низкие значения максимумов.
Приведение формулы к удобному для анализа виду.
Стоит обратить внимание, что мы можем привести нашу формулу к виду:
Формула 4:
W=A(t)*sin(AЮпиСат +F(t))
Где A(t) – амплитуда, и F(t) – фазовый сдвиг, которые в свою очередь зависят от времени, а именно - только от углов между Ураном, Нептуном, Плутоном и P06. Поэтому, с одной стороны можна посмотреть, как именно зависит амплитуда A(t) от времени, а с другой – проанализировать при каких значениях аспектов между планетами она становиться максимальной или минимальной.
Приведение к виду Формулы 4 довольно просто, достаточно вынести за скобки Sin(АЮпиСат) и Сos(АЮпиСат), а потом преобразовать формулу
A*Sin(АЮпиСат) +B* Сos(АЮпиСат)
к виду А1* Sin(АЮпиСат+F). Так как А и В будут у нас функциями положений планет Урана, Нептуна, Плутона и P06, то и A1=A(t) и F=F(t) будут функциями только положения этих планет, и следовательно функциями времени.
A1=Sqrt(A*A+B*B)
F=Atan(A/B)
Функция изменения амплитуды представляет особый интерес потому, что показывает долговременные циклы изменения Солнечной активности, и может быть связана с глобальными климатическими изменениями [1]. В связи с этим интересен тот факт, что амплитуда в нашей формуле зависит только от взаимного расположения Урана, Нептуна, Плутона и P06.
График №7 – изменение амплитуды Солнечной активности во времени:
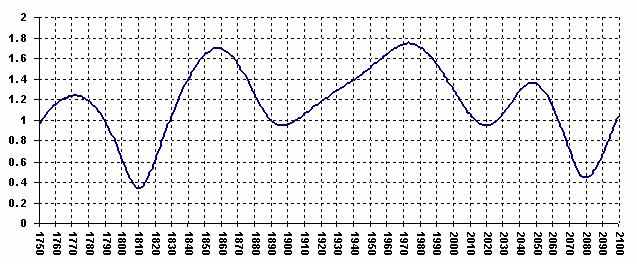
По поводу изменений амплитуды Солнечной активности – обращает внимание факт минимума в районе 1810 года, и тенденция к уменьшению на промежутку 1970 -2080 год, с локальным минимумом примерно в наше время, что обьясняет невысокие значения Солнечной активности в текущем цикле.
График №8 – фазовый сдвиг относительно угла Юпитер-Сатурн
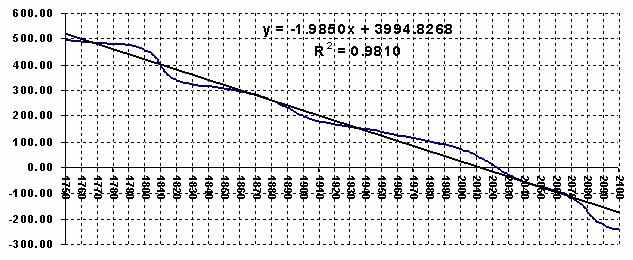
Что касается фазы, то мы видим что имеет место медленный, примерно -1.985 º/год сдвиг максимумов графика Солнечной активности относительно угла Юпитер-Сатурн. По большому счёту, этот сдвиг фазы с достаточной точностью изменяется линейно (квадрат коефициента корреляции при линейной интерполяции составил 0.981). Этот фазовый сдвиг так же зависит только от Урана, Нептуна, Плутона и P06, и является результатом их взаимодействия с основной парой Юпитер-Сатурн.
Литература:
1. Авторский сайт В.Г.Лазуткина, посвящённый вопросам связи влиянии планет на солнечную активность ссылка скрыта
2. Лазуткин В.Г., Тихонов А.А.. Аппроксимация, ретропрогноз и прогноз среднегодичных чисел Вольфа с 1000 до нашей эры по 2300 годы. Биоэнергоинформатика том 1, Барнаул, 1998.
3. Чижевский А.Л., Космический пульс жизни. Земля в объятиях Солнца. Гелиотараксия. М.: Мысль, 1995.
4. База данных по солнечной активности с 1749 по 2011 г.: ссылка скрыта
5. Уайт А., Планета Плутон. М.: Мир, 1982. ссылка скрыта
