Методическое пособие по лабораторным работам для студентов специальности 201400 «аудиовизуальная техника» Санкт-Петербург

Вид материала

Методическое пособие

Содержание Цифровые фильтры с конечной импульсной характеристикой (КИХ-фильтры) N – порядок фильтра (длина импульсной характеристики). Операция свертки может быть представлена в виде структурной схемы (рис. 2 КИХ-фильтры с линейной фазой N существует толь­ко одна фазовая задержка - , при которой может достигаться строгая линейность фазовой характеристики, причем 3. Порядок выполнения работы N и параметр соответствующего окна. Использовать только нечетные значения N 4. Оформление результатов A() – заданная частотная характеристика; – частотная характеристика фильтра; W() P() представляет собой линейную комбинацию из М P() определяется выражением (20), а Q() N – нечетно, h(n) М + 1 частоте существует равновеликая, знакочередующаяся ошибка  3. Описание документа "MathCad" "Расчет оптимального КИХ-фильтра по алгоритму Ремеза" P в относительном и логарифмическом масштабах и график функции ошибки Е 5. Оформление результатов 1. Цель работы 2. Основные теоретические положения M  N. В этом случае фильтр называется фильтром N T(s) в передаточную функцию цифрового фильтра H(z) I, ранжированную переменную i ... Полное содержание

Подобный материал:

• Санкт-петербургский государственный университет кино и телевидения, 301.8kb.
• Рабочая программа по дисциплине «Проблемы социальной работы с молодежью» (наименование, 128.96kb.
• Методическое пособие к лабораторным работам по физической и коллоидной химии для студентов, 4131.07kb.
• Методические указания к лабораторным работам для студентов специальности 210100 "Автоматика, 536.56kb.
• Методические указания к лабораторным работам №1-­5 для студентов специальности 210100, 363.6kb.
• Методические указания к лабораторным работам по физике по практикуму «Вычислительная, 138.12kb.
• Методическое пособие для студентов Института массовых коммуникаций Санкт-Петербург, 2088.04kb.
• Учебно-методическое пособие по организации и проведению занятий с персоналом образовательных, 287.8kb.
• Учебное пособие для студентов среднего профессионального образования Санкт-Петербург, 777.31kb.
• Учебно-методическое пособие Санкт-Петербург 2001 удк 681. 3 Бобцов А. А., Лямин, 1434.37kb.

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО КУЛЬТУРЕ И КИНЕМАТОГРАФИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕНГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ КИНО И ТЕЛЕВИДЕНИЯ»


КОМПЬЮТЕРНОЕ ПРОЕКТИРОВАНИЕ УСТРОЙСТВ ЦИФРОВОЙ ОБРАБОТКИ ЗВУКОВЫХ СИГНАЛОВ


ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ ФИЛЬТРОВ


МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО
ЛАБОРАТОРНЫМ РАБОТАМ


ДЛЯ СТУДЕНТОВ СПЕЦИАЛЬНОСТИ 201400 «АУДИОВИЗУАЛЬНАЯ ТЕХНИКА»


Санкт-Петербург


2006

Состовитель – ст. препод. А.Н. Мышенский

Рецензент – доц. А.В. Белозерцев (каф. видеотехники)


Рекомендовано к изданию

Советом факультета аудиовизуальной техники.

Протокол № 1 от 28.09.06 г.


© СПбГУКиТ, 2006


Цифровые фильтры с конечной импульсной характеристикой (КИХ-фильтры)

Общие положения


Ц
ифровой фильтр можно представить некоторым функциональным блоком, на вход которого поступает входной сигнал x(n) в виде последовательности чис­ловых отсчетов, а с выхода снимаются числовые отсчеты выходного сигнала y(n) (см. рис. 1).

Этот фильтр должен обладать вполне определенной частотной харак­те­рис­ти­кой – H(), требования к которой задаются анологично требованиям к час­тот­ным характеристикам аналоговых фильтров, за исключением того, что харак­тер­ные частоты должны быть заданы в нормированных единицах по отно­ше­нию к частоте дискретизации или должна быть задана частота дискретизации.

Д

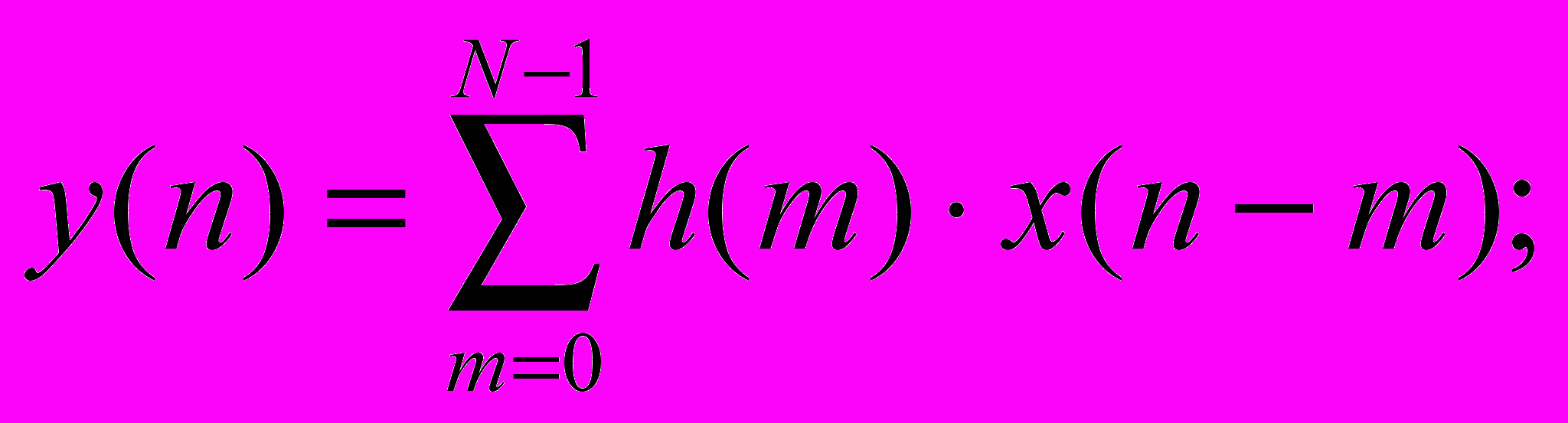
(1)
ля того чтобы реализовать цифровой фильтр в виде аппаратного или программно-аппаратного устройства, необходимо знать его передаточную функцию, а для фильтров с конечной импульсной характеристикой достаточно знания от­сче­тов импульсной характеристики h(n), так как каждый отсчет выходного сиг­на­ла может быть вычислен как результат свертки входного сигнала с им­пуль­сной характеристикой:

где N – порядок фильтра (длина импульсной характеристики).

Операция свертки может быть представлена в виде структурной схемы (рис. 2), где z^–1 обозначает элемент задержки на интервал дискретизации.

Т
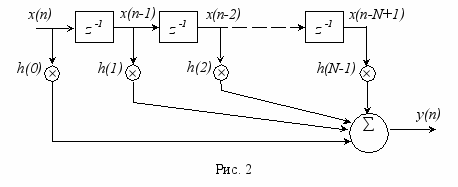
аким образом, для того чтобы рассчитать цифровой КИХ фильтр, не­об­хо­ди­мо определить порядок фильтра N и рассчитать значения всех от­сче­тов им­пуль­сной характеристики. При этом следует отметить, что всегда жела­тель­но иметь минимальное N, при котором еще удовлетворяются тре­бо­ва­ния к час­тот­ной характеристике фильтра. Тогда для реализации фильтра потребуется мень­шая вычислительная мощность, т.е. будут меньше затраты времени и па­мя­ти.

Цифровые КИХ фильтры обладают рядом достоинств по сравнению с циф­ро­выми фильтрами с бесконечной импульсной характеристикой (БИХ филь­тры). Они всегда устойчивы, менее чувствительны к точности пред­ста­­вления числовых параметров фильтра и, главное, могут быть спро­ек­ти­ро­ваны та­ким образом, что их фазочастотная характеристика будет строго линейной, что обычно бывает желательно, а иногда необходимо. Недос­тат­ком КИХ фильтров является то, что для получения частотных характеристик с крутыми пере­па­да­ми между областями пропускания и задерживания требуются фильтры высоких порядков, т.е. с длинной импульсной характеристикой.


КИХ-фильтры с линейной фазой


Р

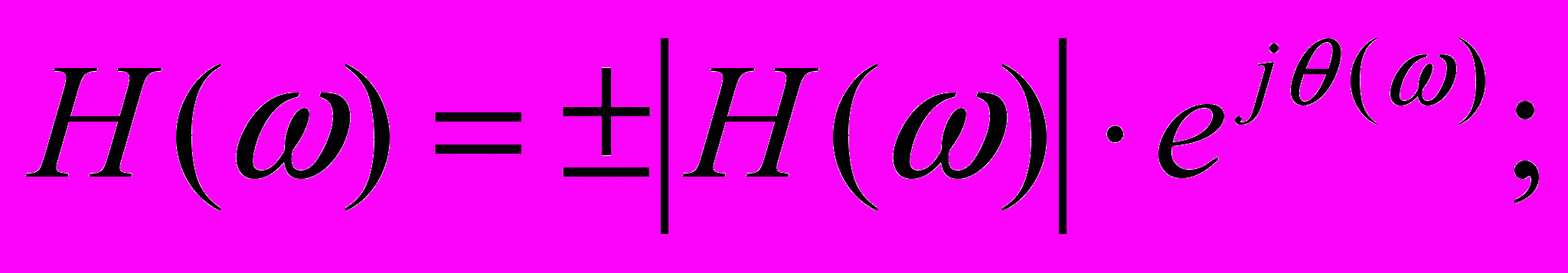
(2)
ассмотрим свойства, которыми должна обладать частотная характеристика КИХ фильтра с линейной фазой.Такая харак­те­рис­тика должна иметь вид:

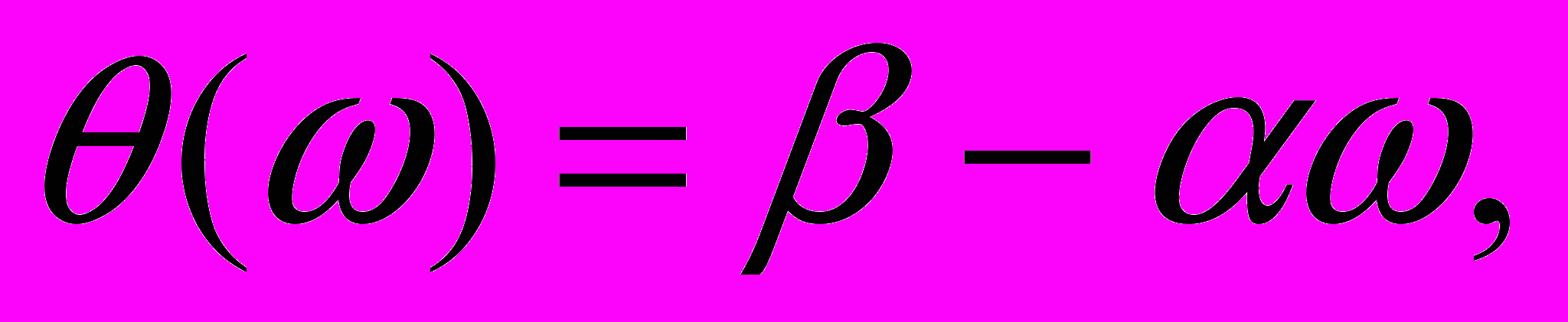
г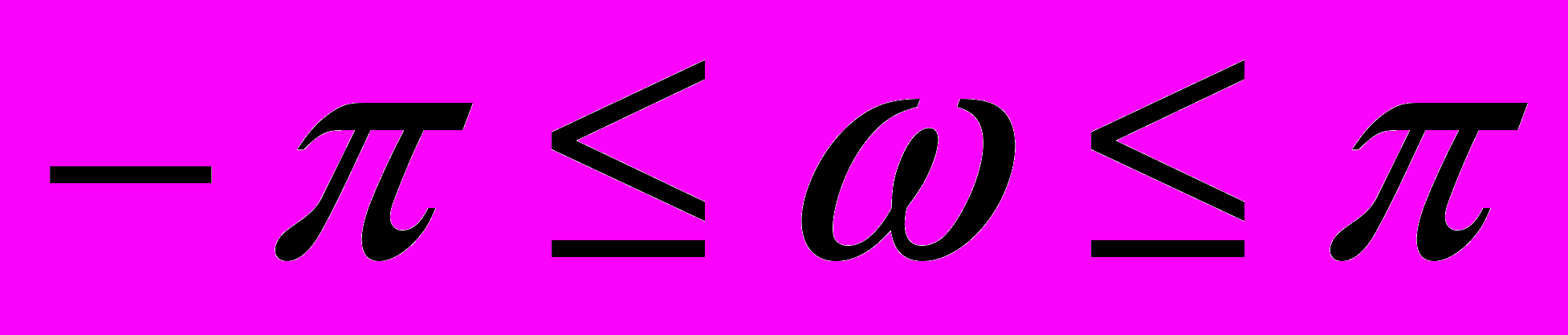де - фаза частотной харак­те­рис­тики,

 - время групповой задержки,

 - дополнительный фазовый сдвиг.

С

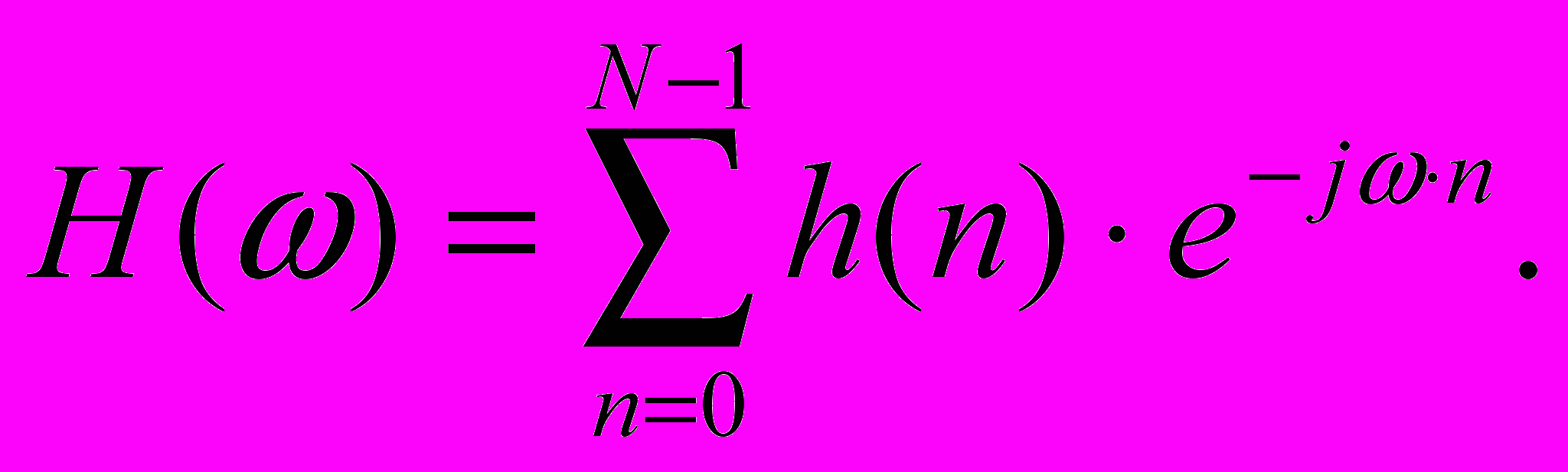
(3)
другой стороны, частотная характеристика цифрового фильтра определяется преобразованием Фурье дискретной импульсной характеристики:

Приравнивая правые части этих выражений друг другу, можно получить ус­ло­вия, которым должны удовлетворять параметры фазы и отсчеты импульсной ха­рактеристики для фильтров с линейной фазовой характеристикой. Ока­зы­ва­ет­ся возможны два случая:


1
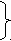
0  n  N-1

(4)
)  = 0;  = (N-1)/2; h(n) = h(N-n-1);

2)  = /2;  = (N-1)/2; h(n) = h(N-n-1);


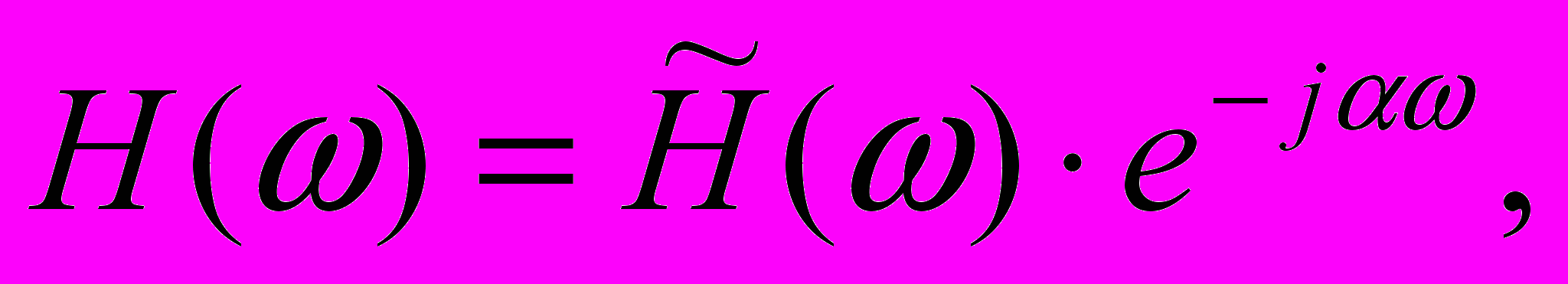С
(5)
мысл этих условий заключается в том, что для каждого N существует толь­ко одна фазовая задержка - , при которой может достигаться строгая линейность фазовой характеристики, причем в первом случае (=0) частотная ха­рак­теристика будет иметь вид:

г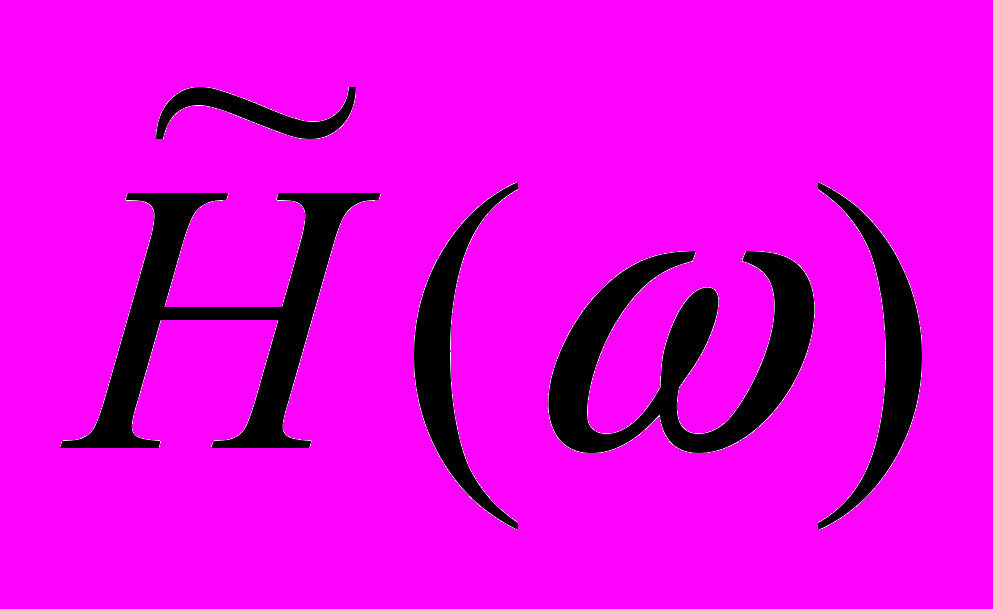де является действительной функцией, а импульсная ха­рак­те­рис­тика будет симметрична относительно своего центра.

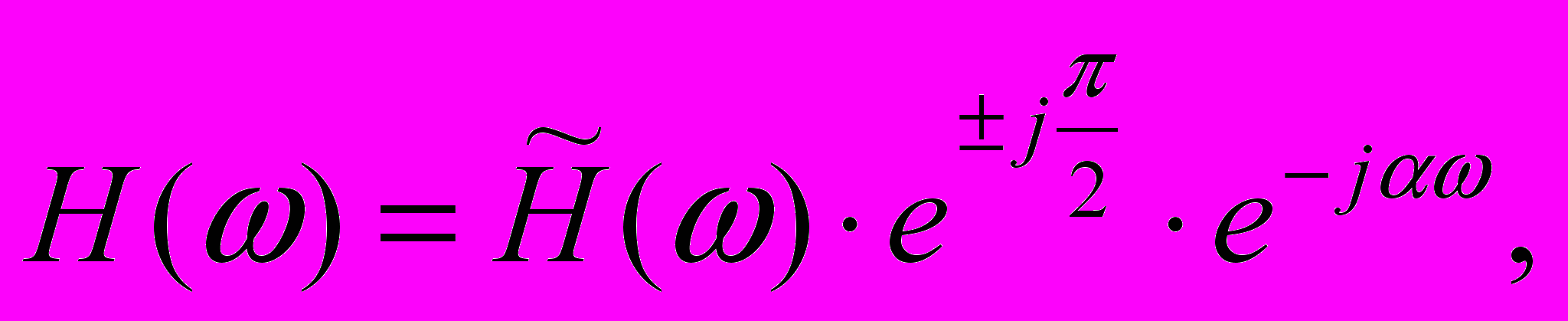В
(6)
о втором случае (= /2) частотная характеристика будет иметь вид:

а импульсная характеристика будет антисимметрична относительно центра. Фильтры с харак­те­ристиками второго типа могут использоваться для построения диф­фе­рен­ци­а­то­ров или преобразователей Гильберта. Кроме того, в каждом из этих случаев N может быть нечетным или четным. В случае нечетного N время групповой задержки оказывается равно целому числу интервалов дискретизации, а в случае четного N выходной сигнал фильтра будет задержан на нецелое число интервалов, что иногда может вызвать затруднения.

Для каждого из этих случаев могут быть записаны выражения, определяющие частотную характеристику через значения отсчетов импульсной характеристики.

1. 
   
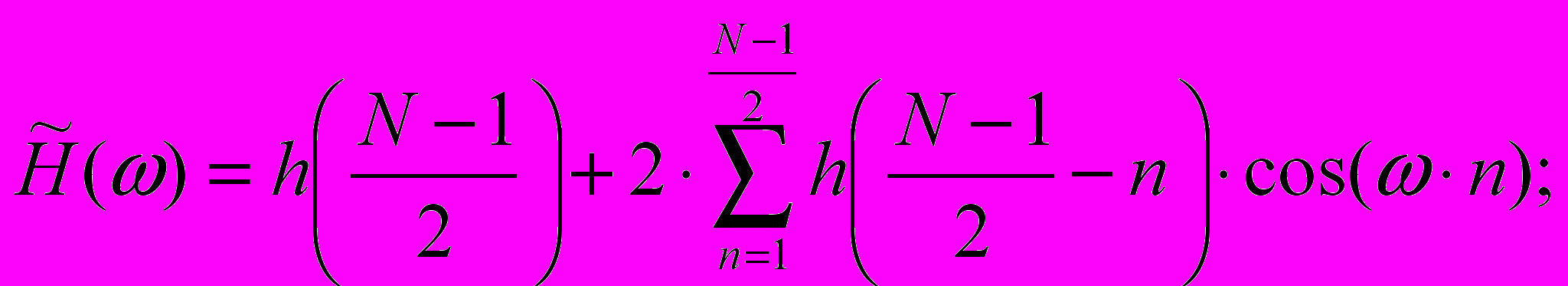
   (7)
   = 0; N – нечетно
   
2. 
   
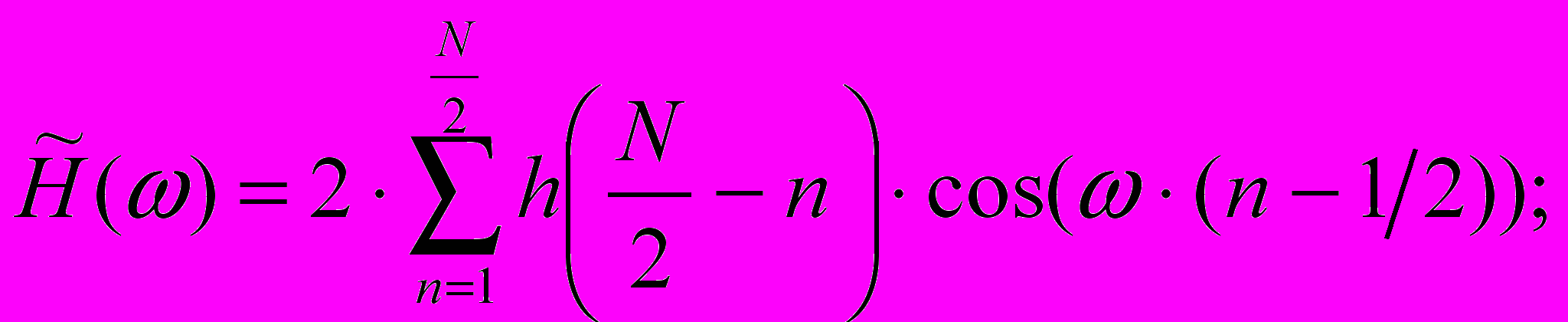
   (8)
   = 0; N – четно
   
3. 
   
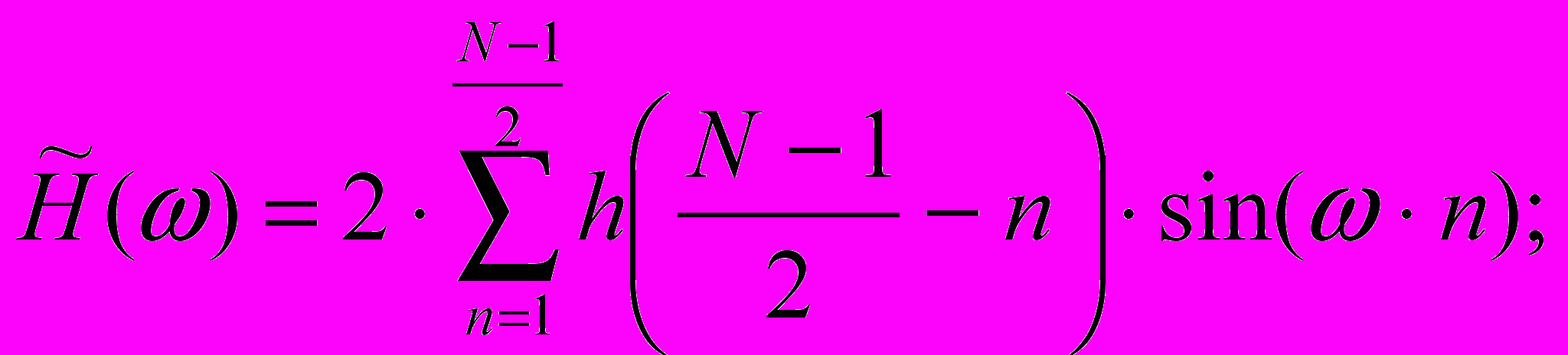
   (9)
   = /2; N – нечетно
   

4. 
   
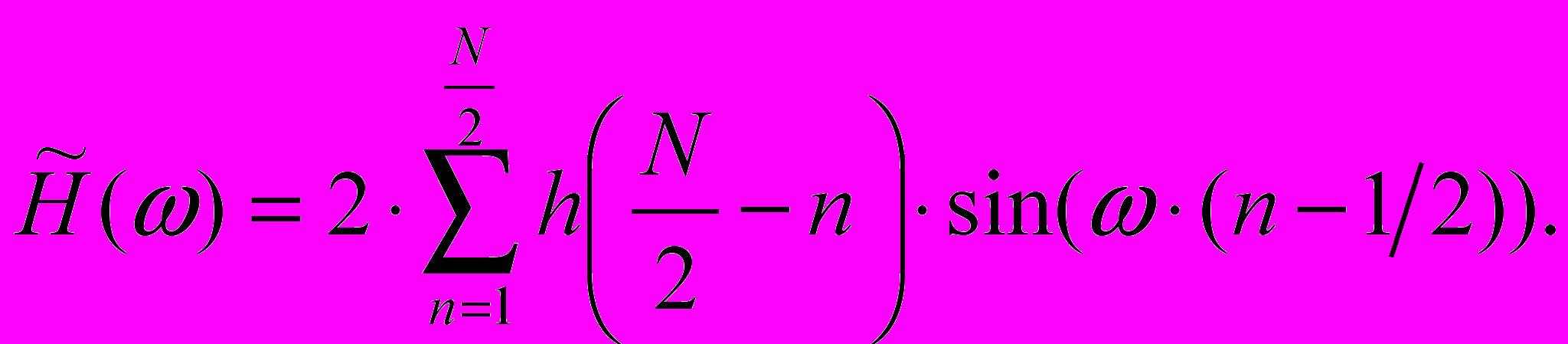
   (10)
   
   (10)
   = /2; N – четно
   

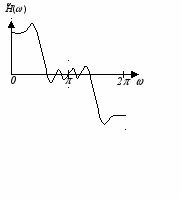
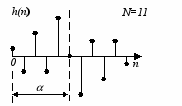
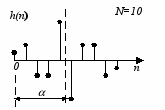
Таким образом, можно выделить четыре типа фильтров. Типичные виды импульсных и частотных характеристик для этих случаев представлены на рис.3, а, б, в, г соответственно. Следует отметить, что для фильтров второго типа ( = 0; N четно) значение частотной ха­рак­те­рис­ти­ки при  =  всегда равно 0 вне зависимости от N, и, следовательно, фильтры этого типа не могут использоваться для построения фильтров верхних частот. У фильтров третьего типа ( = /2; N нечетно) частотная характеристика равна нулю как при  = 0, так и при  = , а у фильтров четвертого типа ( = /2; N четно) значение частотной характеристики всегда равно 0 при  = 0.


г)









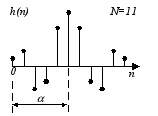
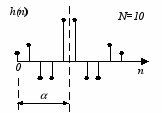
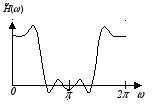
Симметричная импульсная характеристика


а)


б)






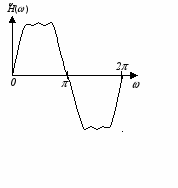
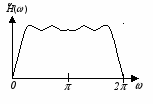
в)


Антисимметричная импульсная характеристика

Нечетное N

Четное N

Рис. 3


б)

г)

в)

Нечетное N

Четное N

рис. 3
Р
N=10
АБОТА 1. Изучение синтеза цифровых КИХ-фильтров методом взвешивающих функций (методом "окна")


1. Цель работы


Целью работы является практическое освоение метода, закрепление теоретических знаний и исследование частотных и переходных характеристик, синтезированных фильтров.


2. Основные теоретические положения


П

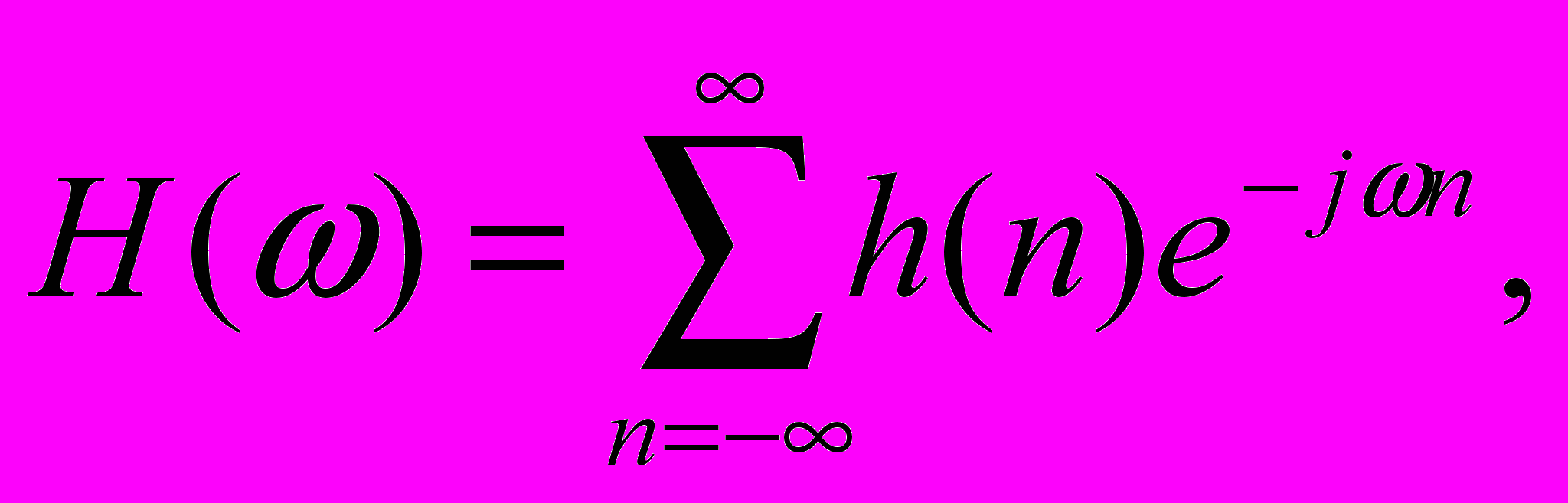
(11)
оскольку частотная характеристика любого цифрового фильтра является периодической функцией частоты, ее можно разложить в ряд Фурье:

в

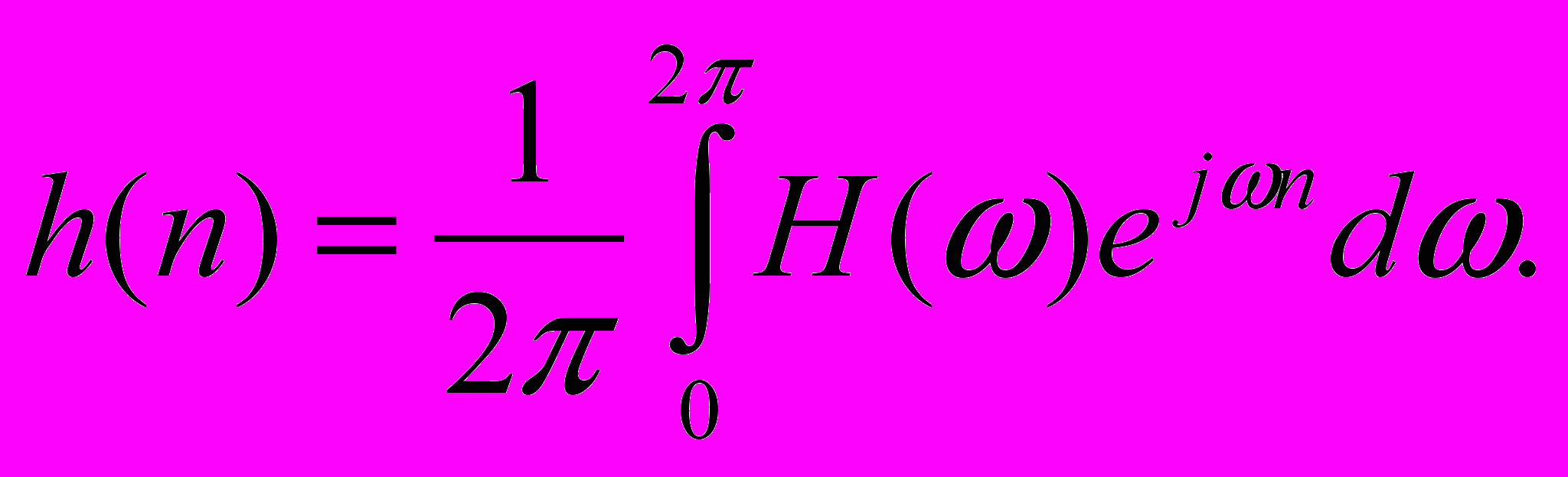
(12)
котором отсчеты импульсной характеристики являются коэффициентами ряда Фурье и, если частотная характеристика задана, могут быть определены по соответствующей формуле:

Непосредственное использование этого соотношения для проектирования КИХ-фильтров с типовыми частотными характеристиками невозможно, так как разложение в ряд Фурье получается бесконечным, причем n изменяется в пределах от   до .

Один из возможных методов получения КИХ-фильтра, аппроксимирующего заданную частотную характеристику, заключается в усечении бесконечного ряда до конечной длины N. Однако простое усечение ряда приводит к так называемому явлению Гиббса, которое проявляется в виде выбросов и пульсаций частотной характеристики определенного уровня до и после точек ее разрыва. Так, например, при аппроксимации идеального фильтра нижних частот максимальная амплитуда этих пульсаций составляет около 9%, а общая неравномерность составляет 12% и не умень­ша­ет­ся с увеличением длины импульсной характеристики. Вместо этого по мере увеличения N уменьшается ширина выброса. Вследствие этого данный метод не пригоден для проектирования фильтров с более-менее высокими требованиями к неравномерности частотной характеристики.

Д

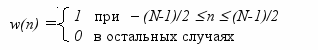
(13)
ля сглаживания пульсаций применяют метод, основанный на использовании весовой последовательности конечной длины w(n), называемой окном, которое служит для модификации отсчетов импульсной характеристики, полученных по формуле (12). Модификация заключается в умножении отсчетов импульсной характеристики на соответствующие отсчеты окна. При этом общая частотная характеристика, в соответствии со свойствами рядов Фурье, получается в результате свертки частотной характеристики идеального фильтра и частотной характеристики окна. Простейшим окном, которое соответствует обсуждавшемуся выше усечению импульсной характеристики, является прямоугольное окно. Это окно показано на рис. 4а (при N = 11) и может быть задано в виде:

Его частотная характеристика показана на рис. 4б и задается выражением:


W
(14)
_N() = sin (N/2)/Nsin (/2).


В результате свертки частотной характеристики окна с частотной характеристикой идеального фильтра, последняя, во-первых, приобретает неравномерность из-за колебательного характера боковых лепестков и, во-вторых, переходную полосу конечной ширины в местах разрыва частотной характеристики идеального фильтра из-за конечной ширины главного лепестка частотной характеристики окна. Из этого следует, что желательно иметь временное окно такого вида, чтобы его частотная характеристика, по возможности, имела минимальную ширину главного лепестка и минимальные амплитуды боковых лепестков. К сожалению, эти требования противоречивы, и оконные функции разрабатываются на основе некоторого компромисса.

Б
(15)

ыло предложено большое количество оконных функций разной степени сложности. В приложении П1 приведены выражения для ряда таких функций. Одним из простейших окон является окно Хэмминга, которое определяется следующим выражением:


w_H = 0,54 +0,46cos (2n/N); – (N –1 )/2  n  (N – 1)/2 .


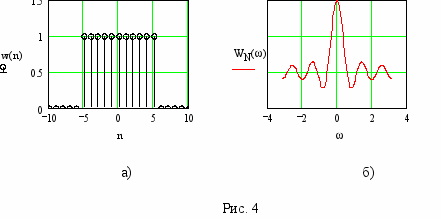
Вид этого окна представлен на рис.5а, а вид его частотной характеристики – на рис. 5б.

Ширина главного лепестка частотной характеристики обратно пропорциональна ширине окна и, следовательно, длине импульсной характеристики и зависит от типа окна. В формулах для некоторых типов окон присутствует параметр, с помощью которого можно регулировать компромисс между шириной главного лепестка и уровнем пульсаций боковых лепестков.

В
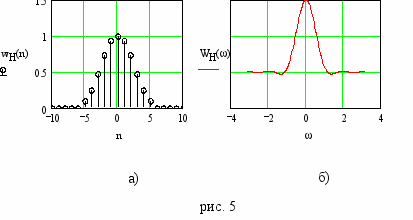
исходных данных на проектирование фильтров обычно указываются граничные частоты полос пропускания и задерживания, а также неравномерности частотной характеристики в этих полосах. Из этих данных можно определить минимальную ширину переходной полосы заданного фильтра – f . При этом оказывается, что при достаточно больших N произведение Nf практически не зависит от граничной частоты полосы пропускания, около которой находится переходная полоса, а зависит от вида используемого окна и значения его параметра, если таковой имеется. Существуют графики таких зависимостей. В приложении П2 приведены такие графики для окон Ланцоша и Кайзера. С помощью этих графиков можно определить примерный порядок проектируемого фильтра.

Общий порядок расчета КИХ-фильтров методом взвешивания заключается в следующем:

1. Выбрать тип оконной функции и по графикам приложения П2 определить примерный порядок фильтра N и начальное значение параметра функции, если это требуется.
   
2. Определить ряд Фурье по заданной частотной характеристике. Это можно сделать аналитически по формуле (12), если частотную характеристику можно описать достаточно простым выражением. В приложении П3 приводятся формулы таких рядов для стандартных типов фильтров. Если математически описать заданную частотную характеристику затруднительно, то можно воспользоваться обратным дискретным преобразованием Фурье (ОДПФ). Для чего синтезируемую частотную характеристику нужно дискретизировать с достаточно малым интервалом дискретизации по частоте, чтобы длина ДПФ превышала ожидаемую длину импульсной характеристики в несколько раз. Это позволит избежать наложения во временной области. Затем произвести ОДПФ полученной частотной выборки и получить длинную импульсную характеристику. Эту характеристику, как и характеристику, полученную по формуле (12), ограничивают прямоугольным окном в пределах – (N-1)/2  n  (N-1)/2 для нечетных N и – (N/2-1)  n  N/2 для четных N.
   
3. Привести полученную импульсную характеристику к каузальному виду (без отрицательных значений n ) путем сдвига вправо на (N-1)/2 отсчетов для нечетного N и на N/2 отсчетов для четного.
   
4. Рассчитать значения отсчетов выбранной оконной функции (для четного N аргумент n заменить на n - 1).
   
5. Привести полученную оконную функцию к каузальному виду.
   
6. Модифицировать импульсную характеристику, полученную в пункте 2, используя значения отсчетов оконной функции.
   
7. Построить график частотной характеристики фильтра, используя одну из формул (7) – (10).
   
8. Проверить по графику, удовлетворяет ли полученная частотная характеристика заданным требованиям.
   
9. Изменяя порядок фильтра, параметры оконной функции и граничные частоты полосы пропускания (для типовых фильтров ФНЧ, ФВЧ и ППФ) или полосы задерживания (для фильтров ПЗФ) и повторяя действия по пп. 1 – 9, добиться соответствия полученной характеристики заданным требованиям при минимальном N.
   

Этот алгоритм расчета легко реализуется в математическом пакете "Mathcad" версий 6.0 и выше.

Полученные таким способом фильтры не оптимальны, так как метод окна не использует какие-либо условия оптимальности. Однако он достаточно универсален и прост, а полученный порядок фильтра не слишком сильно отличается от оптимальных фильтров, рассчитанных по критерию Чебышева (минимаксному критерию).


3. Порядок выполнения работы

1. Получить у преподавателя вариант требований для расчета цифрового фильтра методом взвешивания. При расчете используется окно Ланцоша или окно Кайзера в соответствии с заданием. Оба окна имеют параметр.
   
2. В соответствии с пунктом 1 предыдущего раздела определить начальные порядок фильтра N и параметр соответствующего окна. Использовать только нечетные значения N.
   
3. Загрузить в ПК программу "Mathcad -2001" и задать в ней исходные данные, используя соответствующие обозначения. При задании данных, введении формул, построении графиков и визуализации результатов снабжать эти действия текстовыми комментариями.
   
4. Задать ранжированную переменную n в пределах от – (N-1)/2 до (N-1)/2 для получения некаузальной формы временных характеристик.
   
5. Задать функцию импульсной характеристики, определяемой через ряд Фурье, и функцию заданного окна.
   
6. Построить графики этих функций в некаузальной форме. Графики построить с применением линий типа "stem" или "bar".
   
7. Получить значения отсчетов импульсной характеристики и оконной функции в виде векторов в каузальной форме. Для этого в левой части выражения присваивания записать индексированную переменную h_n+(N-1)/2 со сдвигом вправо на половину длины импульсной характеристики, а в правой – обозначение заданной выше функции для импульсной характеристики от n. Аналогичным способом получить вектор для отсчетов окна. Для работы с этими векторами задать ранжированную переменную n1 в пределах от 0 до N 1.
   
8. Построить график частотной характеристики фильтра с импульсной характеристикой, ограниченной прямоугольным окном. Для этого задать ранжированную переменную для оси частот в пределах от 0 до 1 и с шагом 0,005 и функцию частотной характеристики (см. формулу (7)).
   
9. Измерить неравномерность полученной характеристики в областях пропускания и задерживания с помощью маркерных линий. Увеличить порядок фильтра вдвое. Сравнить полученную неравномерность с предыдущей. Результаты зафиксировать. Вернуться к прежнему порядку.
   
10. Получить вектор модифицированной импульсной характеристики hm путем перемножения соответствующих элементов векторов характеристики с прямоугольным окном и вектора окна. В качестве индексной переменной использовать n1 . Построить график этой импульсной характеристики.
    
11. Построить два графика частотной характеристики фильтра с импульсной характеристикой, ограниченной заданной оконной функцией в относительном и логарифмическом масштабе по оси ординат. На первом графике маркерными линиями обозначить полосу пропускания и заданную неравномерность в ней. На втором – полосу задерживания и неравномерность в этой полосе. Расположить их таким образом, чтобы их можно было наблюдать на экране одновременно.
    
12. Рядом с графиками задать значения порядка фильтра N, параметра окна L или  (окно Ланцоша и окно Кайзера соответственно) и граничные частоты, входящие в выражения для ряда Фурье, с помощью знака глобального присваивания “” (Shift + ~ на клавиатуре). Затем отключить их задание в начале "Mathcad"-овского документа, щелкнув правой кнопкой “мыши” на отключаемом выражении, и в открывшемся меню активизировать команду “ Disable Evaluation”.
    
13. Меняя значения этих параметров и наблюдая за изменениями графиков частотной характеристики, добиться, чтобы она удовлетворяла заданным требованиям при минимально возможном N.
    
14. Сохранить полученные результаты (т.е. вектор импульсной характеристики) в текстовом файле с помощью встроенной функции “WRITEPRN”.
    
15. Определить количество десятичных разрядов после запятой в представлении отсчетов импульсной характеристики, при котором еще выполняются требования к частотной характеристике фильтра.
    

1. Для этого использовать функцию "Mathcad" - round(x,n), которая округляет действительное число x до n десятичных знаков. С ее помощью округлять значения отсчетов импульсной характеристики до различного количества разрядов и наблюдать за частотной характеристикой, построенной по округленным значениям.
   

1. Построить графики частотных характеристик фильтра при минимальном количестве разрядов, при котором требования к фильтру еще удовлетворяются, и при количестве разрядов на единицу меньше, при котором требования уже не выполняются.
   
1. Реализовать фильтрацию сигнала рассчитанным фильтром с помощью операции свертки. Исследовать переходной процесс на выходе фильтра
   

1. Для этого задать входной сигнал для фильтра в виде суммы двух дискретизированных синусоид с частотами f1 и f2, первая из которых лежит в полосе пропускания фильтра, а вторая – в полосе задерживания, и с амплитудами А1 и А2 равными 1. Входной сигнал задать в виде вектора длиной N1, которая в 3...4 раза больше чем длина импульсной характеристики., для чего задать ранжированную переменную n.
   

1. Построить график входного сигнала.
   

1. Задать ранжированную переменную n1 для выходного сигнала длиной N + N1 - 1.
   

1. О
   
   (16)
   пределить выходной сигнал y, реализовав операцию свертки в "Mathcad" в следующем виде:
   Условные пределы суммирования необходимы, так как операция выполняется над векторами и индексы не должны выходить за размеры векторов.
   

1. Построить график выходного сигнала.
   

1. Определить по графику задержку сигнала.
   

1. Задавая по очереди А1 и А2 равными нулю, определить особенности переходного процесса для сигнала в полосе пропускания и в полосе задерживания.
   

4. Оформление результатов


Результаты работы оформляются в виде работающего документа в пакете "Mathcad", который должен иметь заглавие работы, номер группы и фамилии и инициалы студентов, выполнявших работу в подгруппе. Документ должен содержать результаты выполнения операций, приведенных в разделе "Порядок выполнения работы", снабженные комментариями. Пример выполнения и оформления работы приведен в приложении П4. Документ следует сохранить в виде файла с именем, имеющим вид: "ЦУОЗС_Р1_<фамилия одного из студентов подгруппы>", в папке с номером группы.


5. Контрольные вопросы


1. Каким образом может быть получена импульсная характеристика цифрового КИХ-фильтра?

2. Для чего нужны взвешивающие (оконные) функции?

3. Какое явление возникает при применении прямоугольного окна?

4. Какие окна вы знаете?

5. Для чего служит параметр окна?

6. На что влияет четность или нечетность порядка фильтра?

7. Каковы достоинства и недостатки цифровых фильтров с конечной импульсной характеристикой?

8. Какую задержку вносят КИХ-фильтры с линейной фазой?

9. Какие величины требуется варьировать, чтобы получить частотную характеристику, удовлетворяющую заданным требованиям?

10. Как выглядит и для чего используется знак глобального присваивания в пакете "Mathcad"?

11. Результатом какой операции является выходной сигнал КИХ-фильтра?

12. Что является результатом расчета КИХ-фильтра?

13. Как можно изменять оформление графиков в пакете "Mathcad"?


РАБОТА 2. Изучение синтеза оптимальных цифровых КИХ-фильтров по алгоритму Ремеза


1. Цель работы


Целью работы является практическое освоение метода, закрепление теоретических знаний и исследование скорости сходимости алгоритма.


2. Основные теоретические положения


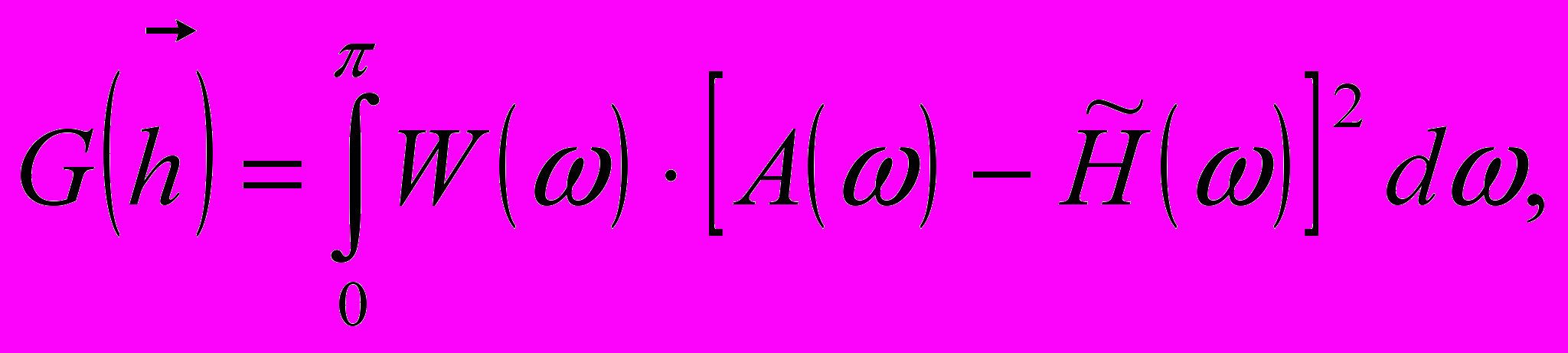П
(17)
ри синтезе цифровых фильтров по заданной частотной характеристике могут быть определены различные критерии оптимальности. Все они, так или иначе, должны быть связаны с минимизацией ошибки, которая возникает при аппроксимации заданной частотной характеристики частотной характеристикой синтезируемого фильтра. В частности, при оптимизации по методу наименьших квадратов минимизируется целевая функция:

г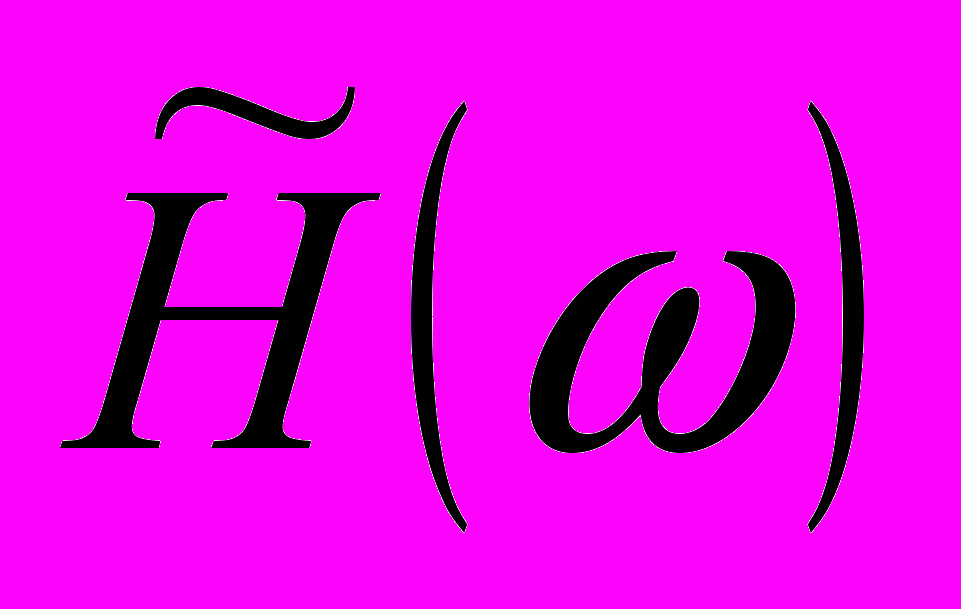де A() – заданная частотная характеристика;
– частотная характеристика фильтра;

W() – весовая функция ошибки, которая позволяет регулировать точность аппроксимации в различных частотных областях. Там, где значения этой функции велики, точность аппроксимации оказывается выше, чем в тех частотных областях, где ее значения малы.

Ф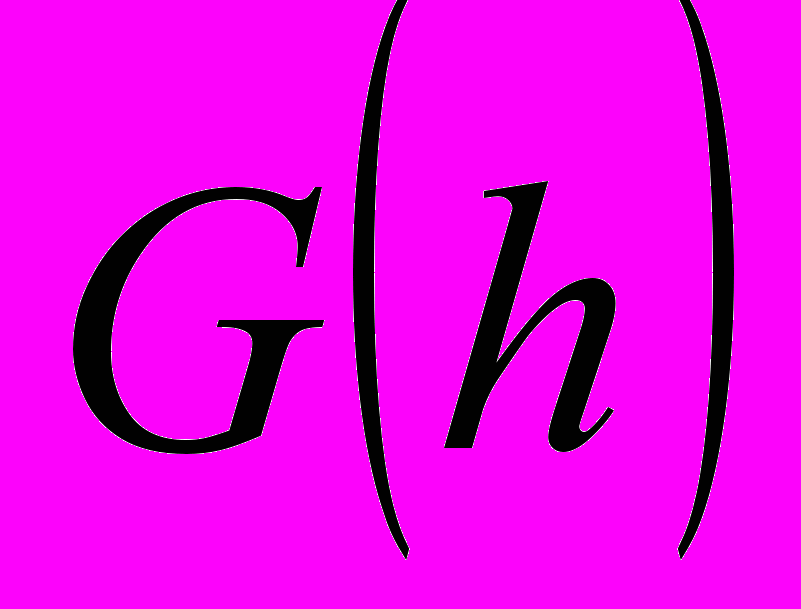ункция зависит от значений отсчетов импульсной характеристики, которые здесь обозначены в виде вектора. Чтобы определить ее минимум, необходимо найти частные производные по каждому из этих отсчетов (с учетом их симметрии), приравнять производные нулю и решить полученную систему уравнений [1]. По существу, в этом случае минимизируется площадь, ограниченная взвешенной функцией ошибки, или взвешенная площадь фигуры, полученной как разность между заданной частотной характеристикой и ч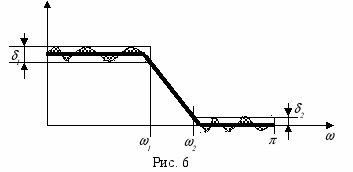
астотной характеристикой фильтра. На рис.6 эта площадь показана в виде заштрихованной области.

При этом о максимальных отклонениях АЧХ фильтра от заданной характеристики ничего определенного сказать нельзя.

Д

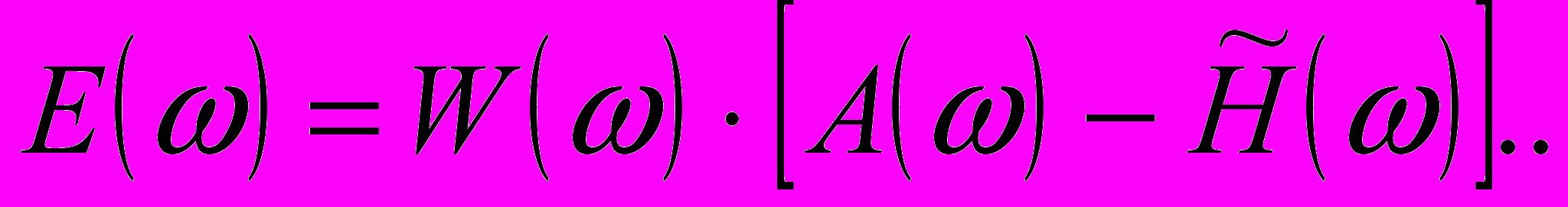
(18)
ругой подход при проектировании оптимального фильтра заключается в минимизации максимальной ошибки отклонения частотной характеристики фильтра от заданной. В этом случае взвешенная функция ошибки определяется выражением:

В

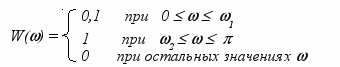
(19)
звешивающая функция W() определяет отношение максимальных ошибок в различных частотных областях и может быть, например для ФНЧ, задана в следующем виде:

При этом максимальная ошибка в полосе пропускания будет в десять раз больше, чем в полосе задерживания. Максимальная ошибка напрямую связана с требованиями по неравномерности частотной характеристики в различных областях. Здесь следует отметить, что в полосе пропускания неравномерность ₁ будет равна удвоенной максимальной ошибке, в то время как в полосе задерживания неравномерность ₂ будет равна модулю ошибки (см. рис. 6).

Возможность получения такого оптимального фильтра базируется на теореме о чебышевском альтернансе. Поэтому оптимальные фильтры этого вида называют фильтрами с наилучшей равномерной (чебышевской) аппроксимацией или фильтрами с минимаксной ошибкой. Сама теорема может быть сформулирована следующим образом: