Методическое пособие по лабораторным работам для студентов специальности 201400 «аудиовизуальная техника» Санкт-Петербург

Вид материала

P() представляет собой линейную комбинацию из М
P() определяется выражением (20), а Q()
N – нечетно, h(n)
М + 1 частоте существует равновеликая, знакочередующаяся ошибка 
3. Описание документа "MathCad" "Расчет оптимального КИХ-фильтра по алгоритму Ремеза"
P в относительном и логарифмическом масштабах и график функции ошибки Е
5. Оформление результатов
1. Цель работы
2. Основные теоретические положения
M  N. В этом случае фильтр называется фильтром N
T(s) в передаточную функцию цифрового фильтра H(z)
I, ранжированную переменную i

Подобный материал:

1 2 3

Т

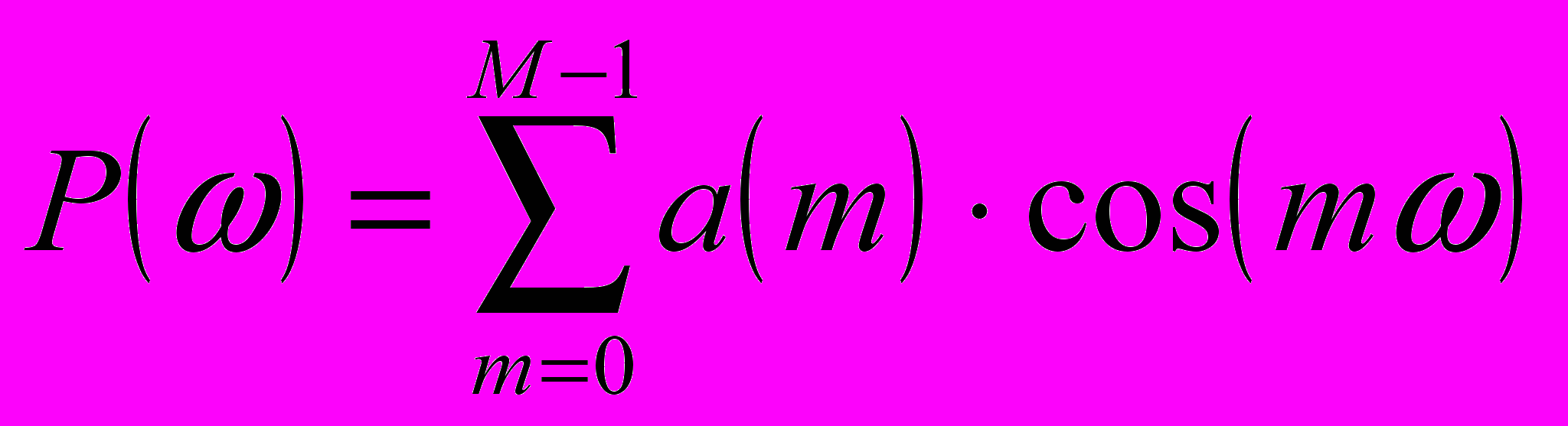
, (20)
еорема. Если функция P() представляет собой линейную комбинацию из М косинусных функций, т. е.

то необходимое и достаточное условие того, что P() является единственной и наилучшей аппроксимацией со взвешиванием непрерывной функции A() на множестве частотных областей B, в которых производится аппроксимация, состоит в том, что взвешенная функция ошибки Е() имеет, по крайней мере, М + 1 экстремальных частот на множестве частотных областей, т.е. в этих частотных областях должны существовать М + 1 точек _i , таких, что


| E(_i) | = max[E()].

  B

₀ < ₁ <  < _Mи Е(_i) = – E( _i₊₁), i = 0, 1,  M и

Э

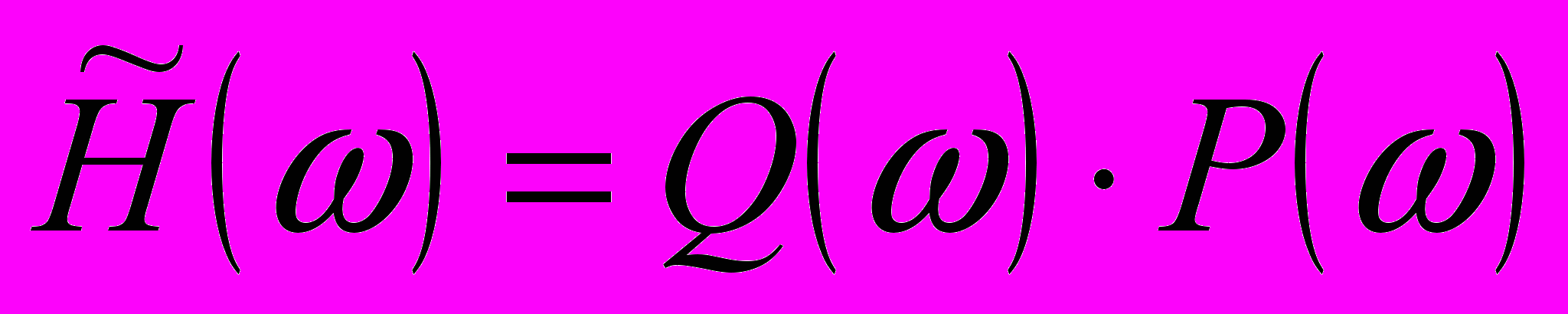
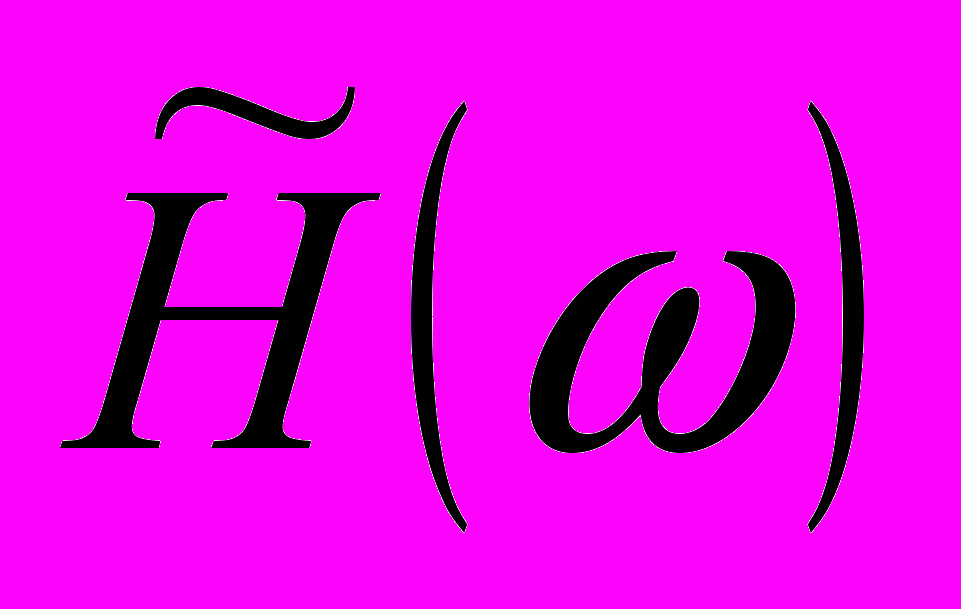
, (21)
та теорема дает необходимые и достаточные условия для получения решения, оптимального в чебышевском смысле. При этом необходимо в формуле, определяющей частотную характеристику фильтра выделить множитель, который являлся бы линейной комбинацией косинусных функций, т.е. необходимо представить в виде:

г

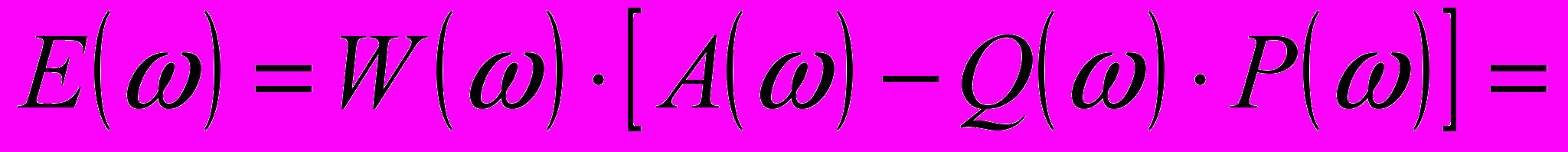
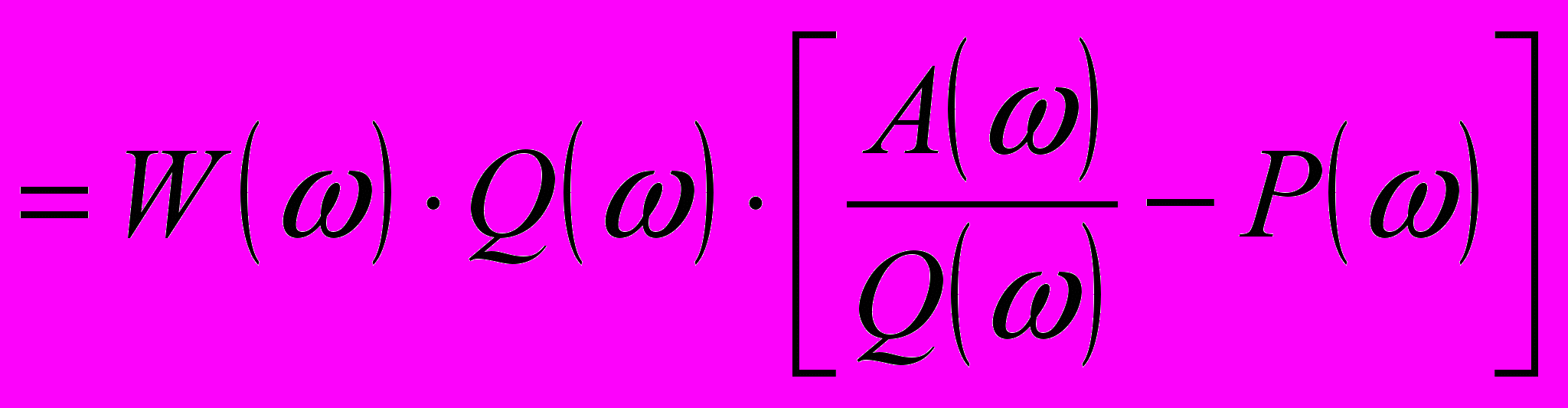
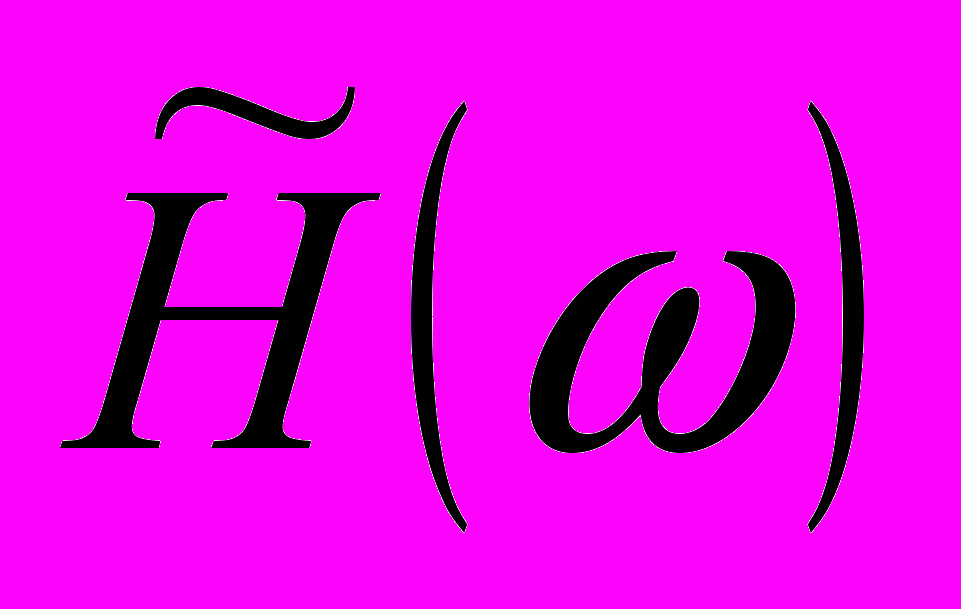
. (22)
де P() определяется выражением (20), а Q() не зависит от импульсной характеристики. В этом случае выражение для ошибки (18) можно переписать в виде:

В
(23)

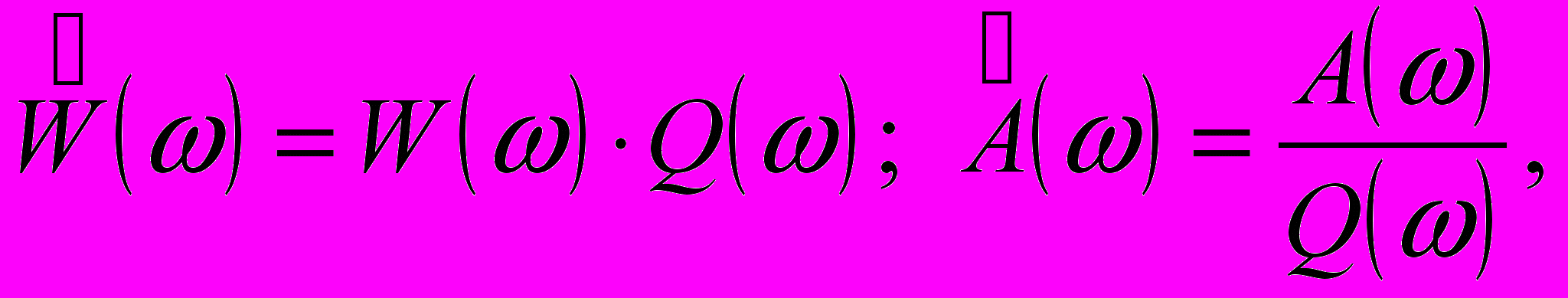ведя обозначения:

м

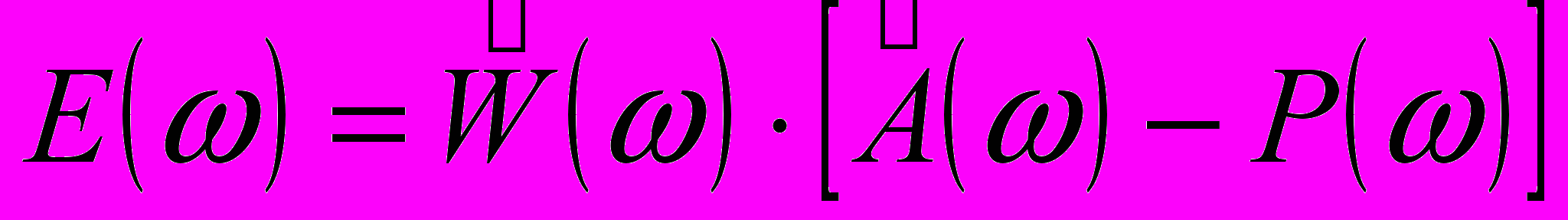
, (24)
ожно придти к прежнему виду выражения для ошибки:

которое удовлетворяет требованиям теоремы.

Можно показать, что выражения для частотных характеристик всех четырех типов фильтров приводятся к виду (24), а именно:

Т
(25)
ип 1. N – нечетно, h(n) – симметрична.

Т
(26)

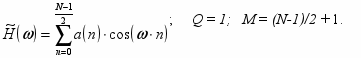
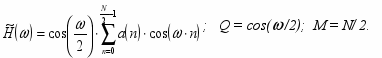
ип 2. N – четно, h(n) – симметрична.

Т

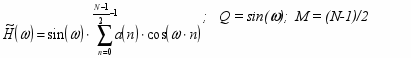
. (27)
ип 3. N – нечетно, h(n) – антисимметрична.

Т

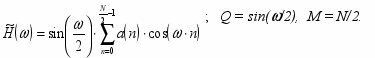
(28)
ип 4. N – четно, h(n) – антисимметрична.

Во всех выражениях для частотных характеристик значения весовых коэффициентов a(n) жестко связаны со значениями отсчетов импульсной характеристики h(n). Таким образом, для всех типов КИХ-фильтров с линейной фазой существуют фильтры оптимальные в чебышевском смысле.

Для построения фильтров, имеющих ошибку с таким равноколебательным поведением, было предложено несколько методов. Наиболее эффективный с вычислительной точки зрения основан на итерационной процедуре, известной под названием второго алгоритма Ремеза.

И

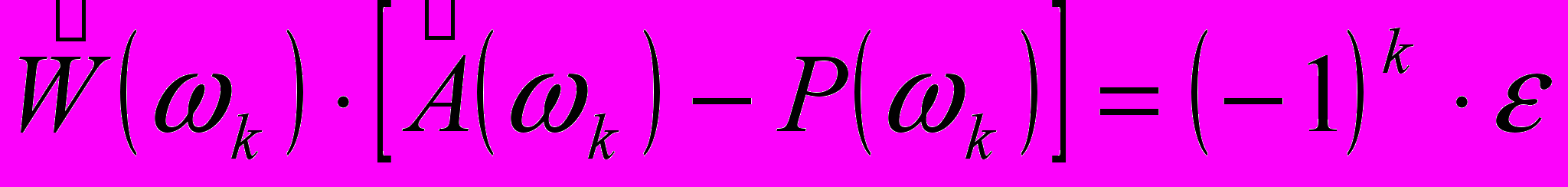
. (29)
з условий теоремы следует, что в оптимальном фильтре, по крайней мере, на М + 1 частоте существует равновеликая, знакочередующаяся ошибка . Если в частотных областях, где производится аппроксимация, произвольным образом задать частоты _k, k = 0, 1, , M, то можно записать следующие
М + 1 уравнения:

Э

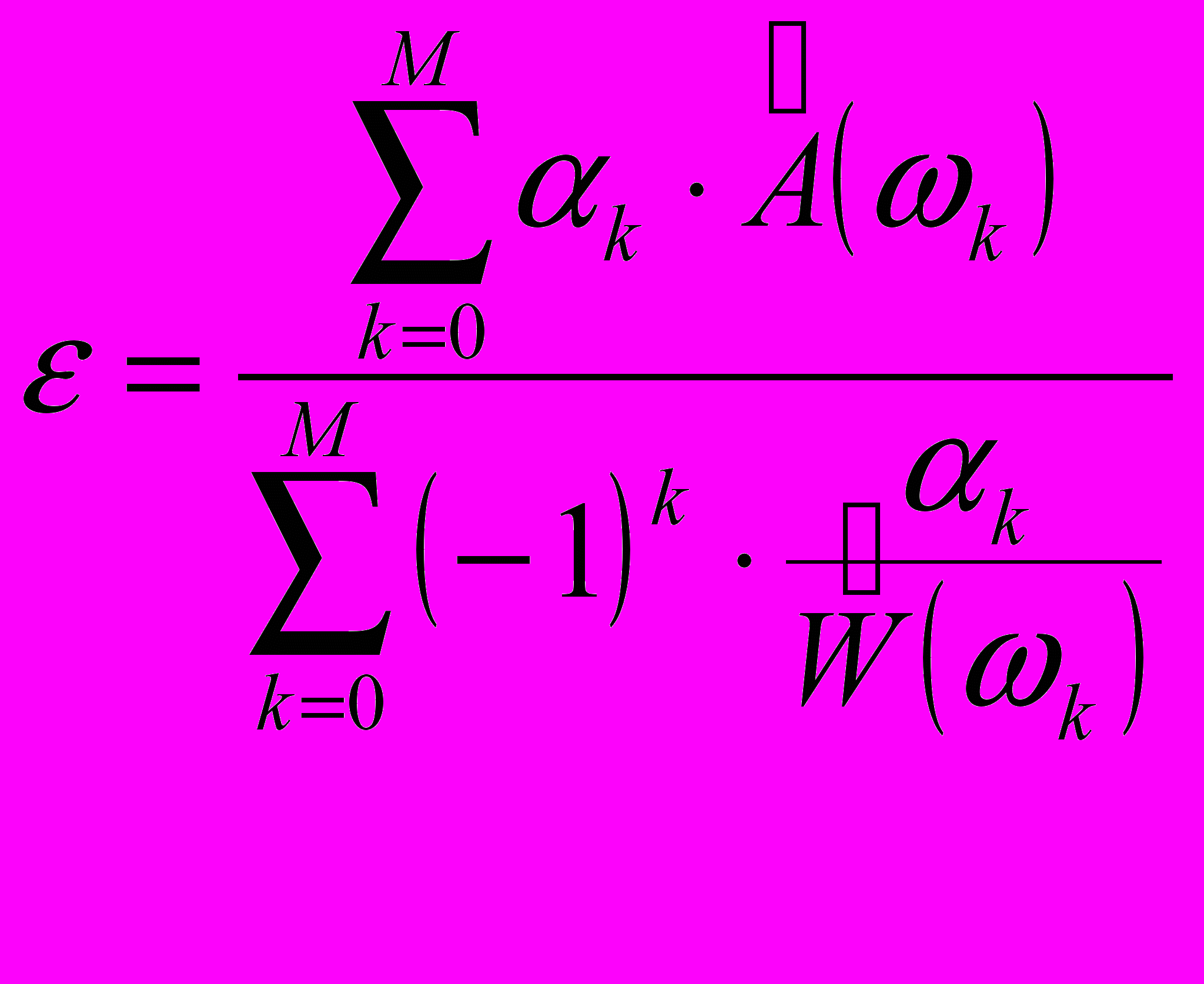
, (30)
ту систему можно решить относительно ошибки , исключив коэффициенты a(n). Это решение определяется формулой:

г

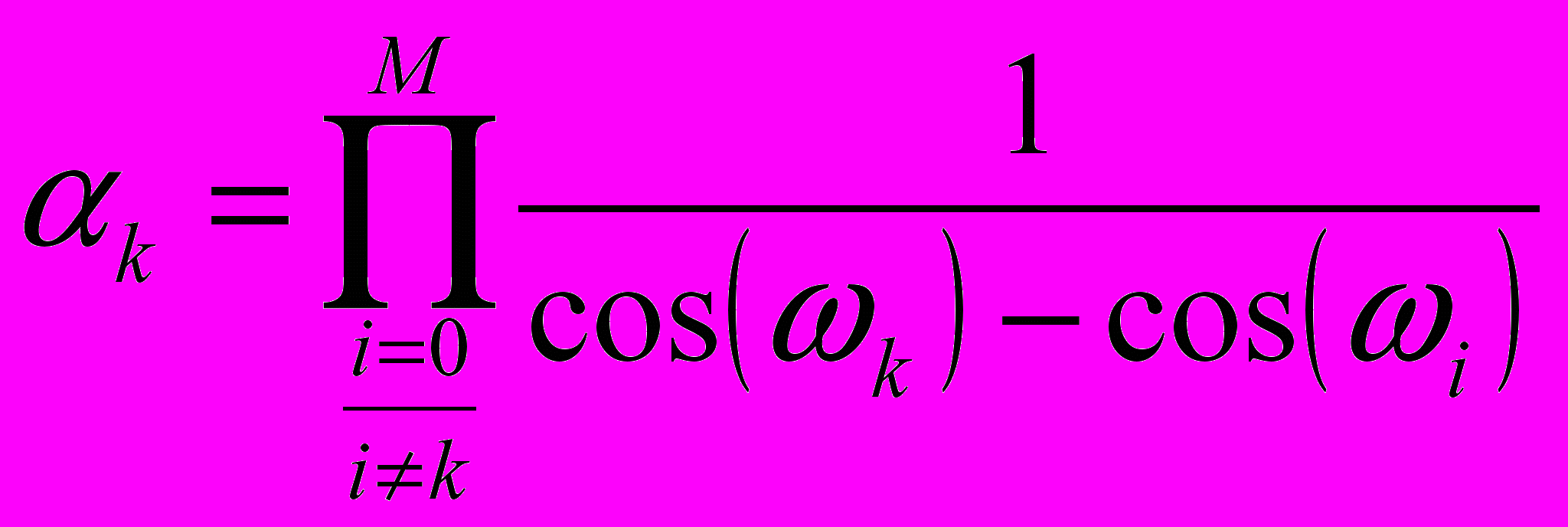
. (31)
де

З

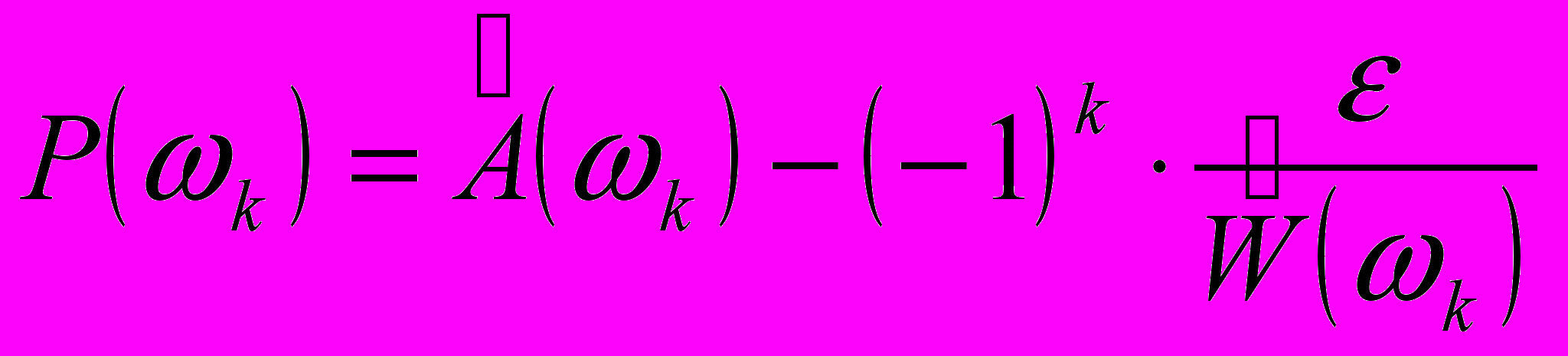
. (32)
ная ошибку в заданных точках _k, можно определить значения аппроксимирующей функции в этих точках:

З

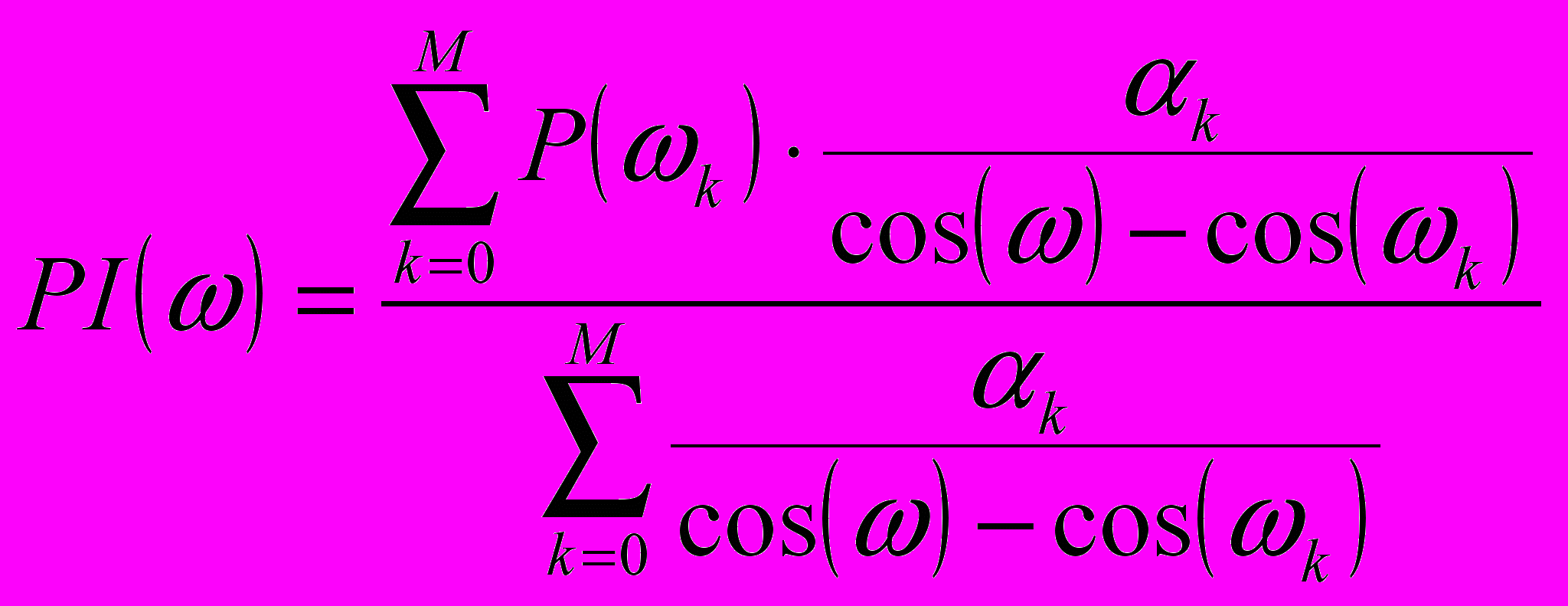
, (33)
атем по этим точкам можно построить интерполирующий полином на основе интерполяционной формулы Лагранжа:

где _k определено в выражении (31).

На следующем этапе задается плотная сетка частот _i,
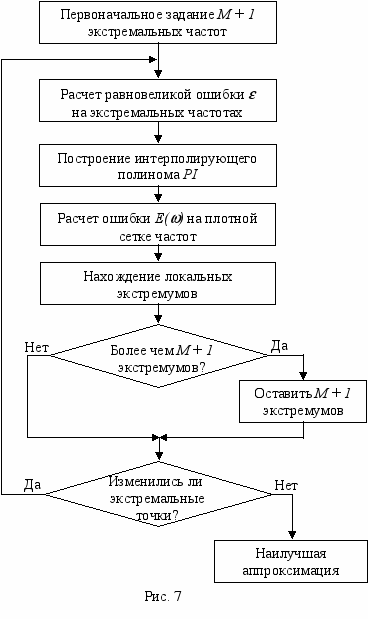
i = 0, 1,2, , I, I >> M. Вычисляются значения ошибки Е(_i) на этой сетке частот, находятся ее экстремальные значения и соответствующие им частоты. Из этих частот выбирается новая совокупность М + 1 экстремальных частот с наибольшими значениями модулей ошибки и так, чтобы они имели знакочередующийся характер. После этого снова находится равновеликая ошибка , и процесс повторяется. Этот процесс сходится к оптимальному фильтру с минимаксной ошибкой. Если |E()|   для всех частот плотной сетки и новая совокупность экстремальных частот совпадает с совокупностью, полученной на предыдущем этапе итерационного процесса, то получена оптимальная аппроксимация. Если второе условие выполняется, а первое, с требуемой точностью, – нет, то необходимо увеличить количество частот на плотной сетке. Блок схема алгоритма Ремеза показана на рис. 7.

После того как получена оптимальная аппроксимация при заданном порядке фильтра, следует проверить, удовлетворяет ли полученная максимальная ошибка заданной неравномерности частотной характеристики фильтра в какой-нибудь частотной области. Если взвешивающая функция ошибки задана правильно, то в других областях соотношение сохранится.

Если требования к частотной характеристике фильтра не выполняются, то следует увеличить порядок фильтра и повторять аппроксимацию до тех пор, пока они не будут выполнены. Если имеется некоторый запас по ошибке, то можно уменьшить порядок фильтра.

После того как требования к фильтру удовлетворены, следует рассчитать импульсную характеристику фильтра. Это делается с помощью обратного дискретного преобразования Фурье. Для этого ось частот на интервале от 0 до 2 делится на бины в соответствии с порядком фильтра:

b_k =2k/N k = 0, 1, , N – 1.

З

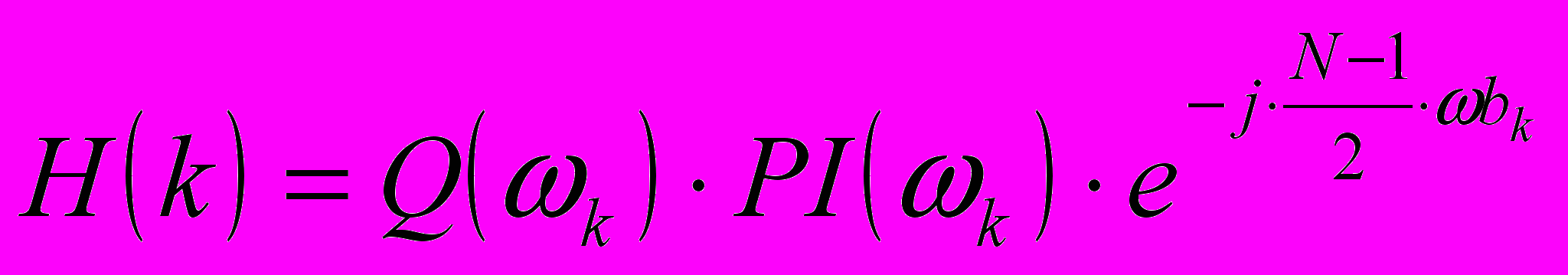
(34)
атем, используя интерполяционный полином PI(), в соответствии с формулой (34) находят комплексные отсчеты частотной характеристики на биновых частотах

и

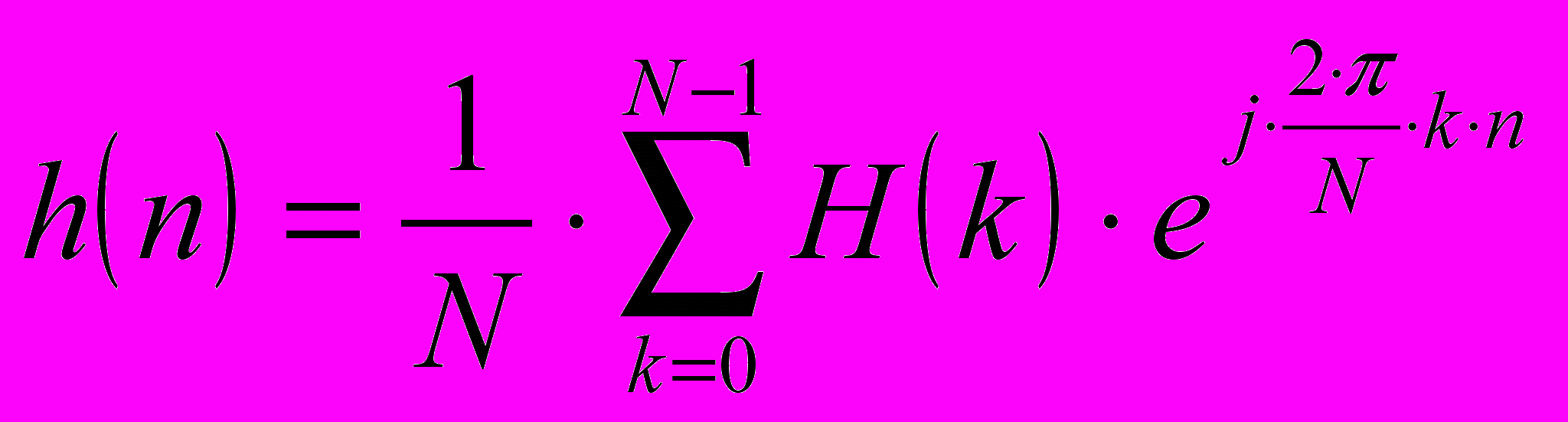
. (35)
определяют импульсную характеристику с помощью ОДПФ:

В общем виде процедура проектирования оптимального фильтра с минимаксной ошибкой включает следующие этапы:

Задание частотной характеристики А(), весовой функции W() и длины импульсной характеристики фильтра N.
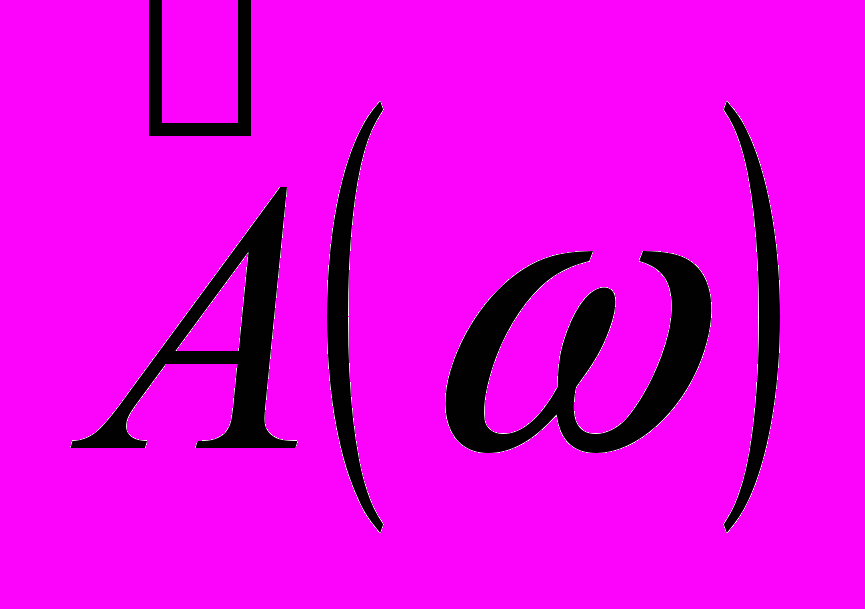
Ф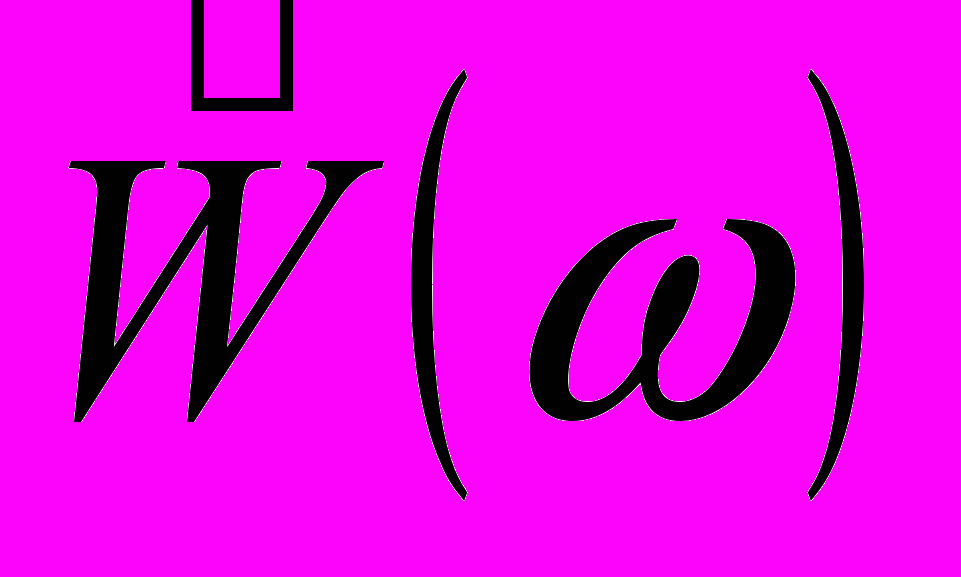ормулировка соответствующей эквивалентной задачи аппроксимации, т. е. задание , и P().
Решение задачи аппроксимации с использованием алгоритма Ремеза.
Расчет импульсной характеристики фильтра.

Итерационная процедура алгоритма Ремеза реализована в пакете "MathCad". Все операции снабжены комментариями.

3. Описание документа "MathCad" "Расчет оптимального КИХ-фильтра по алгоритму Ремеза"

В исходном документе в качестве примера рассчитывается полосовой фильтр. В начале документа приводятся исходные данные для расчета фильтра. Они выделены цветом и при расчете нового фильтра требуют приведения в соответствие с новыми требованиями. Затем, в соответствии с требованиями, задаются аппроксимируемая частотная характеристика и взвешивающая функция ошибки. Эти величины заданы программными блоками, что позволяет задавать различные значения для разных частотных областей.

Затем для заданного порядка фильтра N (N – должно быть нечетным), в соответствии с теоремой Чебышева, определяется количество экстремальных точек и они распределяются по частотным областям примерно пропорционально их ширине, и в этих областях им назначаются частоты. Здесь необходимо учитывать, что в каждой частотной области, где производится аппроксимация, должна присутствовать, по крайней мере одна точка. Затем все экстремальные частоты объединяются в один вектор начальных экстремальных частот fn с помощью функции "stack". При выполнении работы описанные операции должны быть приведены в соответствие с типом рассчитываемого фильтра и заданными требованиями.

Затем в документе реализованы действия, выполняемые во время одной итерации алгоритма Ремеза. В результате рассчитываются значения интерполирующего полинома P и взвешенной функции ошибки E на плотной сетке частот (500 точек). Далее, с помощью программного блока, определяется массив Extr, содержащий два столбца; в нулевом – значения всех экстремумов, в первом – соответствующие частоты. Затем из найденных экстремальных точек отбираются знакочередующиеся экстремумы (точки альтернанса), из которых формируется массив TAlt. И, наконец, определяется, имеется ли лишний экстремум, и если таковой присутствует, удаляется наименьший крайний. В результате последней операции формируется массив TAlt1, который содержит координаты требуемого количества экстремумов.

Ниже, в документе выводятся графики интерполирующего полинома P в относительном и логарифмическом масштабах и график функции ошибки Е. По этим графикам можно наблюдать ход итерационного процесса. Под графиками выводятся значения равновеликой ошибки и абсолютного максимума ошибки на данной итерации. Для того чтобы можно было контролировать сходимость, ниже выделена область, куда эти значения можно копировать на каждом шаге итерационного процесса. Это позволяет после получения оптимального фильтра проследить ход процесса и определить количество итераций.

Далее располагается область запуска итерационного процесса, так как при запуске каждой следующей итерации используются значения экстремальных частот, полученных на предыдущем этапе. В этой области находится оператор глобального присваивания значений рабочему вектору экстремальных частот f. В начале процесса оптимизации этому вектору путем копирования присваиваются значения вектора начальных экстремальных частот, которые выведены справа от оператора. На каждом следующем шаге итерационного процесса, тем же способом, ему присваиваются значения первого столбца матрицы TAlt1, в котором содержатся новые значения экстремальных частот. Этот столбец выведен слева от оператора глобального присваивания.

Ниже располагается область расчета импульсной характеристики оптимального фильтра. Затем по ней рассчитывается и строится график частотной характеристики фильтра, который служит для окончательного контроля результата.

4. Порядок выполнения работы.

Запустить программу "MathCad" и открыть в ней файл Remez.mcd. Изучить документ, используя теоретические знания и комментарии, которые в нем содержатся.
В качестве задания для расчета фильтра использовать те же исходные данные, что и в работе 1.
В документе "MathCad" изменить исходные данные, задание частотной характеристики, задание взвешивающей функции ошибки и начальное задание экстремальных частот в соответствии с выполняемым вариантом.
Перейти к области запуска итерационного процесса. Отключить автоматический режим счета. Скопировать значения вектора начальных экстремальных частот fn в буфер обмена и затем вставить их в правую часть оператора глобального присваивания значений рабочему вектору экстремальных частот f.
Прокрутить документ так, чтобы на экране были видны графики интерполирующего полинома и взвешенной функции ошибки. Установить на них маркерные линии в соответствии с вариантом (при первом выполнении пункта). Запустить счет.
Наблюдать результаты на графиках. Во время каждой итерации сохранять значения равновеликой ошибки и максимальной ошибки путем копирования соответствующих значений в область ниже вывода результатов итерации. Если функция ошибки не носит колебательного характера с равновеликими знакочередующимися экстремумами, то снова перейти к области запуска итерационного процесса. Скопировать новую совокупность экстремальных частот, которая находится в первом столбце матрицы TAlt1, в рабочий вектор – f и перейти к пункту 5.
Если функция ошибки имеет равновеликие экстремумы, то получен оптимальный или близкий к оптимальному фильтр. Это следует проверить по новой совокупности экстремальных частот. Если частоты изменились, то следует выполнить еще одну итерацию, если нет, то фильтр – оптимален. В этом случае следует проверить, удовлетворяет ли частотная характеристика заданным требованиям.
Если требования к АЧХ удовлетворяются, то следует скопировать экстремальные частоты, и сохранить их на полях документа. Затем уменьшить порядок фильтра на 2 (N – должно быть нечетным) и повторить процедуру оптимизации с пункта 4.
Если максимальная ошибка оптимального фильтра превышает заданную неравномерность, то предыдущий вариант является наилучшим оптимальным фильтром для заданных требований. Нужно путем копирования вернуть значения экстремальных частот в рабочий вектор f, запустить счет и перейти к расчету импульсной характеристики фильтра.
Импульсная характеристика рассчитывается с помощью ОДПФ, и в документе "MathCad" это происходит автоматически. Необходимо зафиксировать результат и проверить частотную характеристику, рассчитанную по импульсной характеристике, на соответствие требованиям.

5. Оформление результатов

Результаты работы оформляются в виде работающего документа в пакете "Mathcad", выполненного на основе файла "Remez.mcd", который должен иметь заглавие работы, номер группы и фамилии и инициалы студентов, выполнявших работу в подгруппе. В документе должны быть сделаны изменения в соответствии с заданным вариантом. Документ должен содержать результаты последней выполненной итерации, при которой получен оптимальный фильтр, удовлетворяющий заданным требованиям. Пример выполнения и оформления работы приведен в приложении П5. Документ следует сохранить в виде файла с именем, имеющим вид: "ЦУОЗС_Р2_<фамилия одного из студентов подгруппы>", в папке с номером группы.

6. Контрольные вопросы

Что понимается под оптимальным фильтром?
Какой критерий оптимальности используется при проектировании оптимального фильтра с минимаксной ошибкой?
Как формулируется теорема о чебышевском альтернансе?
Каким требованиям должна удовлетворять аппроксимирующая функция?
Каковы основные этапы алгоритма Ремеза?
Каким образом получается выражение для равновеликой ошибки?
Для чего задается плотная сетка частот?
Что служит критерием окончания процесса оптимизации?
Для чего нужна взвешивающая функция?
Как ведет себя равновеликая ошибка от итерации к итерации?
Какой характер имеет функция взвешенной ошибки у оптимального фильтра?
Каким образом рассчитывается импульсная характеристика у оптимального фильтра?
Каким образом минимизировать порядок фильтра для заданных требований?

РАБОТА 3. Изучение синтеза цифровых фильтров с бесконечной импульсной характеристикой (БИХ-фильтров) методом билинейного преобразования передаточной характеристики аналогового прототипа

1. Цель работы

Целью работы является практическое освоение метода расчета, освоение команд символьного преобразования в пакете с закреплением теоретических знаний и экспериментальное изучение влияния точности представления коэффициентов передаточной характеристики на частотную характеристику фильтра и его устойчивость.

2. Основные теоретические положения

Для того чтобы фильтр с бесконечной импульсной характеристикой был устойчивым и физически реализуемым, на его импульсную характеристику накладываются следующие ограничения:

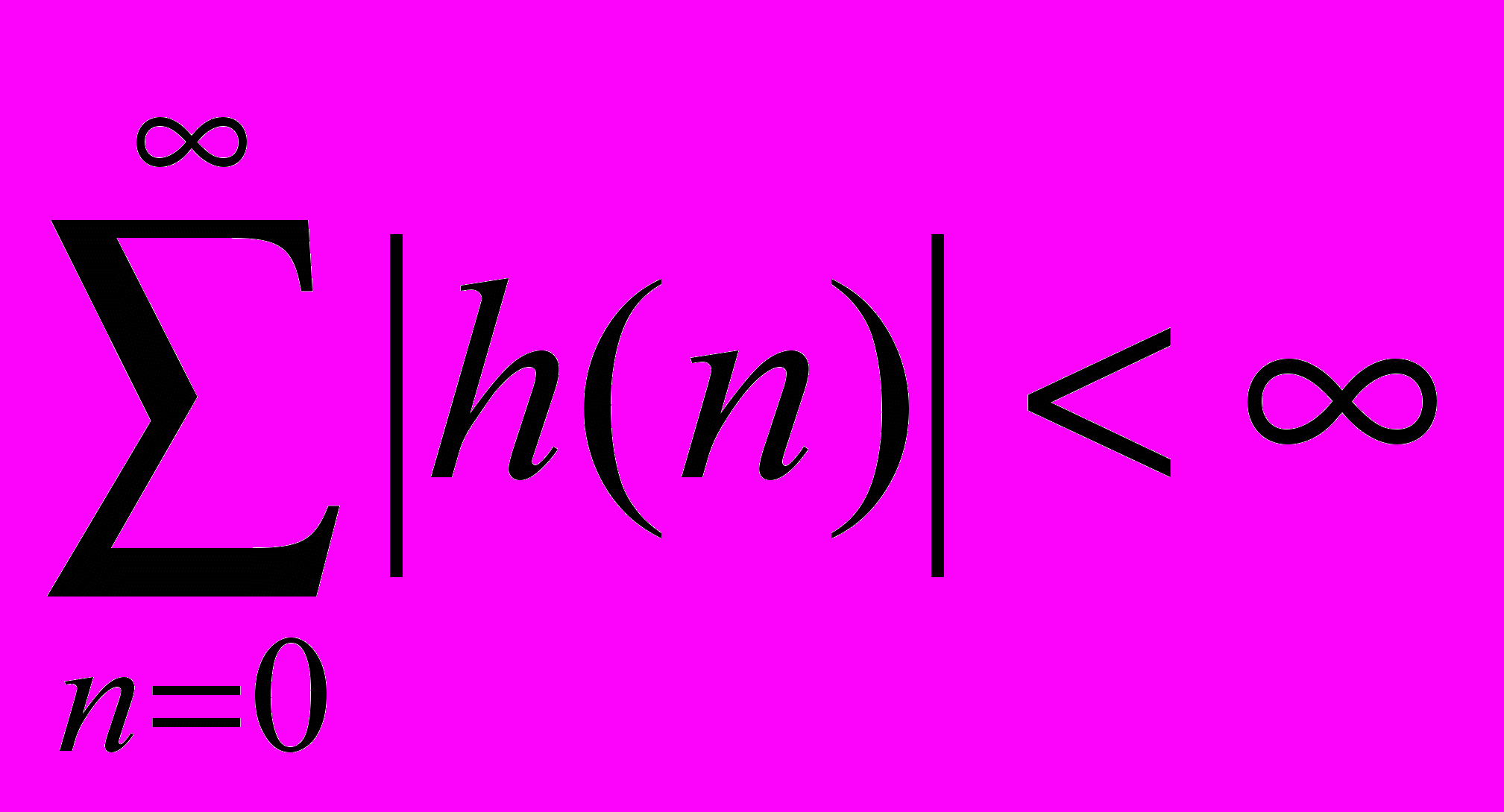h
. (36)
(n) = 0 при n < 0 ,

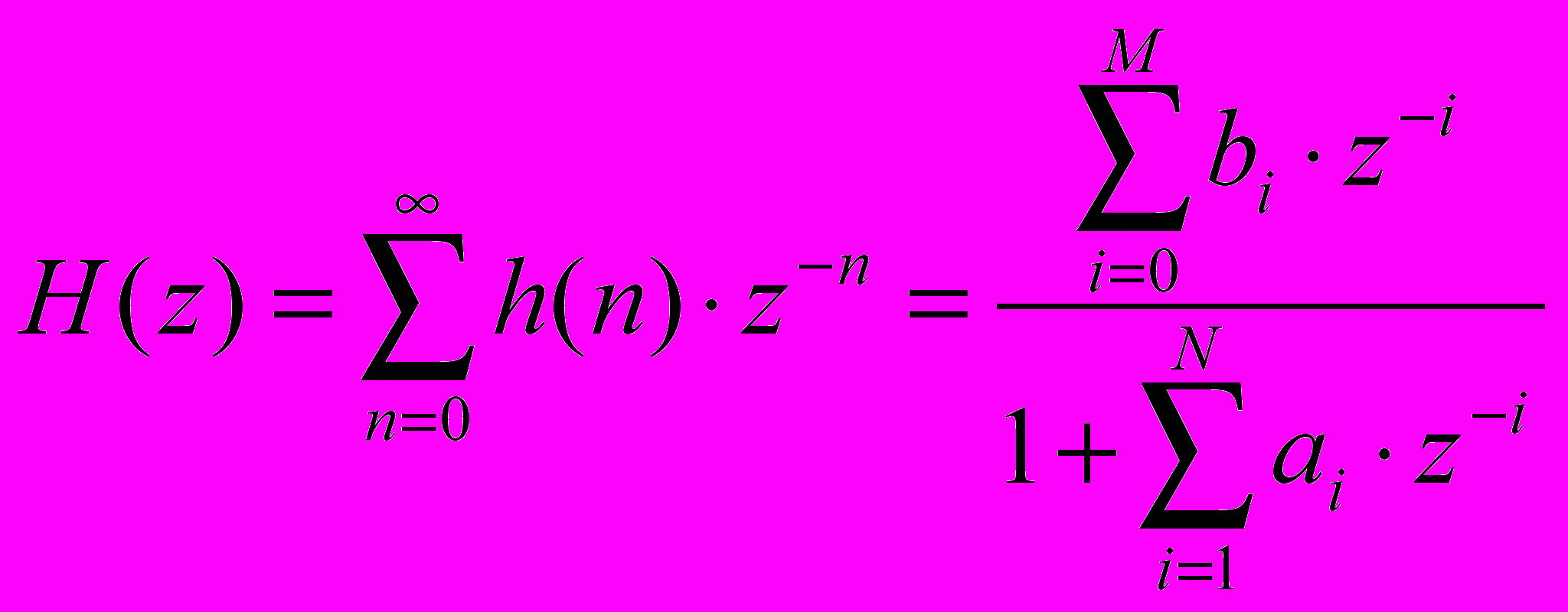П
. (37)
ередаточная функция БИХ-фильтра определяется как Z-преобразование импульсной характеристики и в общем случае имеет следующий вид:

При этом предполагается, что M  N. В этом случае фильтр называется фильтром N-ого порядка. В случае M > N, систему можно представить в виде последовательно соединенных БИХ-фильтра N-ого порядка и КИХ-фильтра M – N-ого порядка. Для того чтобы БИХ-фильтр был устойчивым, его полюса (т. е. корни полинома знаменателя) должны лежать внутри единичной окружности на комплексной плоскости.

При определении передаточных функций БИХ-фильтров используются три класса методов:

методы преобразования аналоговых фильтров в цифровые;
прямые методы расчета БИХ-фильтров;
методы, использующие алгоритмы оптимизации.

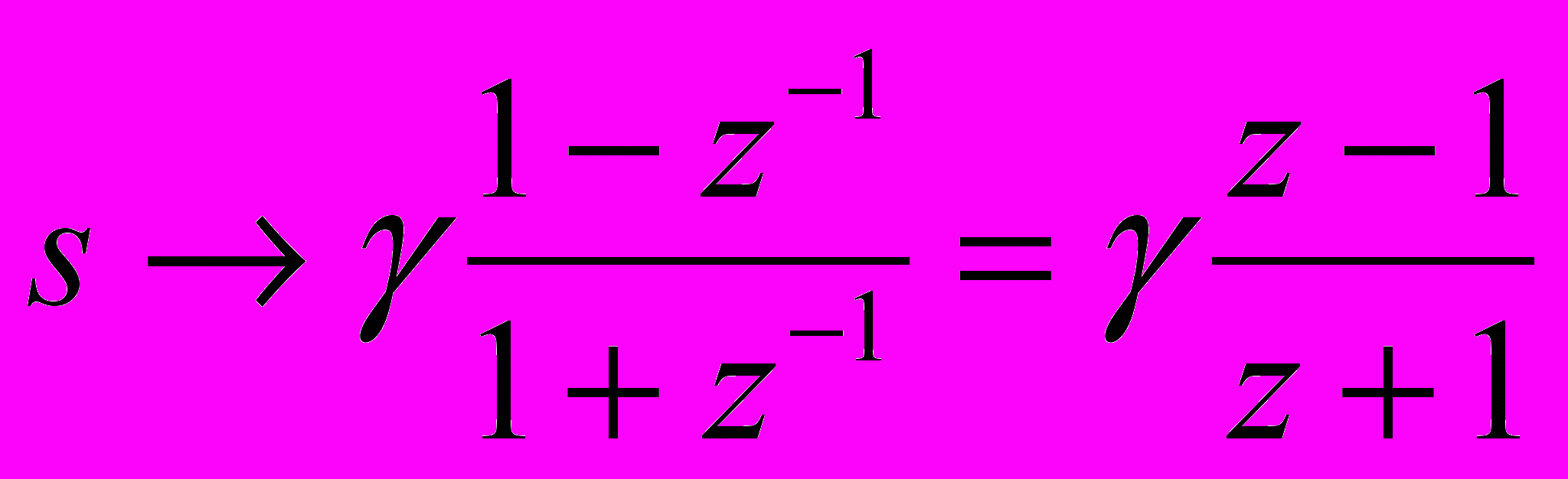Д
, (38)
ля расчета избирательных БИХ-фильтров со стандартными характеристиками (ФНЧ, ФВЧ, ПФ, РФ) наиболее простым и широко используемым является метод билинейного преобразования. С помощью этого метода передаточная функция T(s) аналогового фильтра-прототипа преобразуется в передаточную функцию H(z) цифрового БИХ-фильтра. Это осуществляется с помощью простой замены комплексной переменной s передаточной функции аналогового фильтра на следующее выражение от z:

где  – постоянный параметр, который определяет соответствие аналоговых и цифровых частот. О его выборе будет сказано позднее.

Использование этой подстановки обеспечивает однозначное преобразование передаточной функции аналогового фильтра T(s) в передаточную функцию цифрового фильтра H(z). При этом оказывается, что вся мнимая ось j s-плоскости отображается в единичную окружность z-плоскости (значения передаточных функций на этих линиях и определяют частотные характеристики аналогового и цифрового фильтров соответственно), левая полуплоскость s отображается внутрь единичного круга на z-плоскости, а правая полуплоскость s – в область, расположенную вне единичного круга на z-плоскости. Таким образом, устойчивый аналоговый фильтр преобразуется в устойчивый цифровой фильтр. Эти свойства легко проиллюстрировать, если из выражения для подстановки определить z :

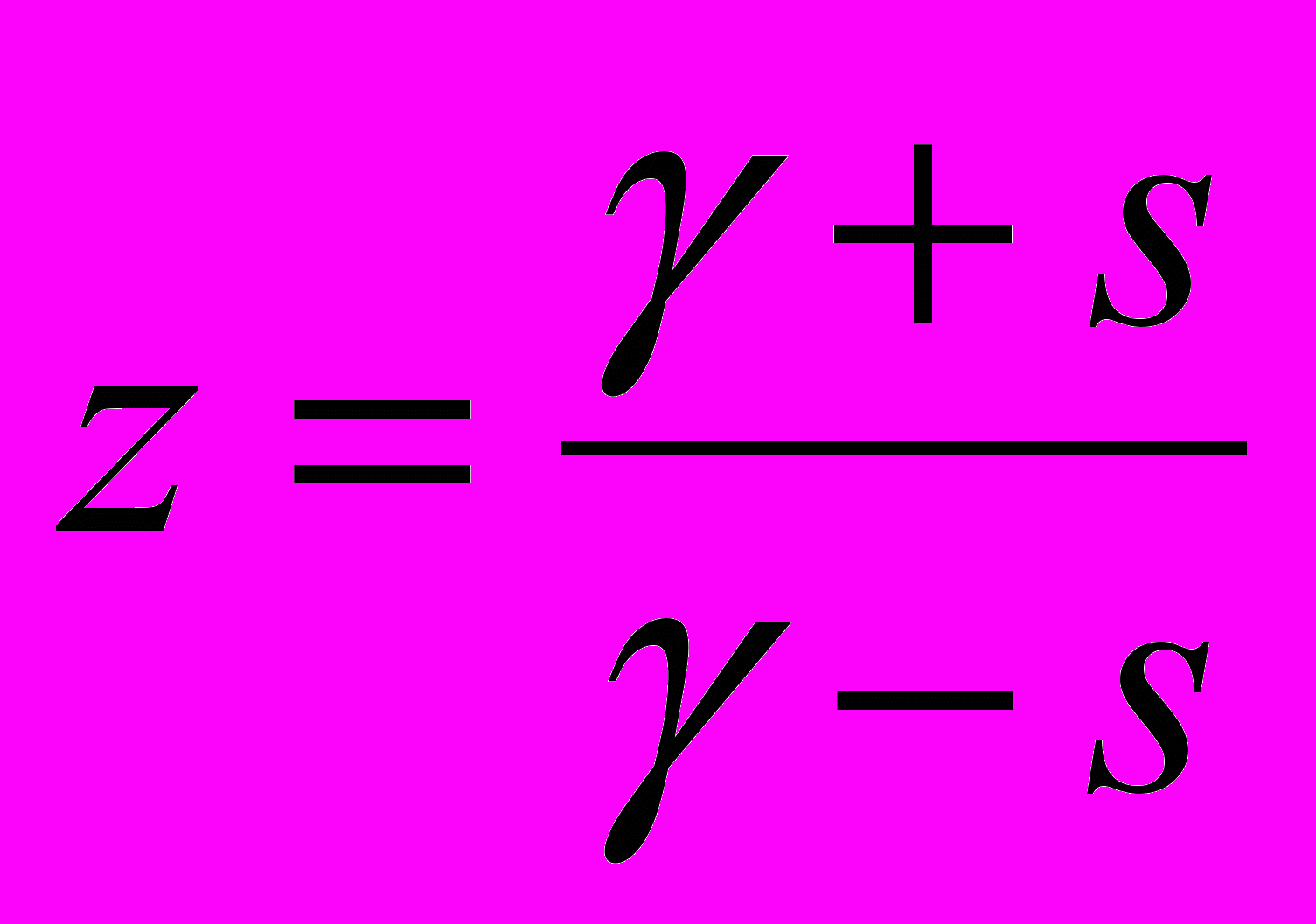П
. (39)

, (41)

. (40)
ри s = j  имеем:

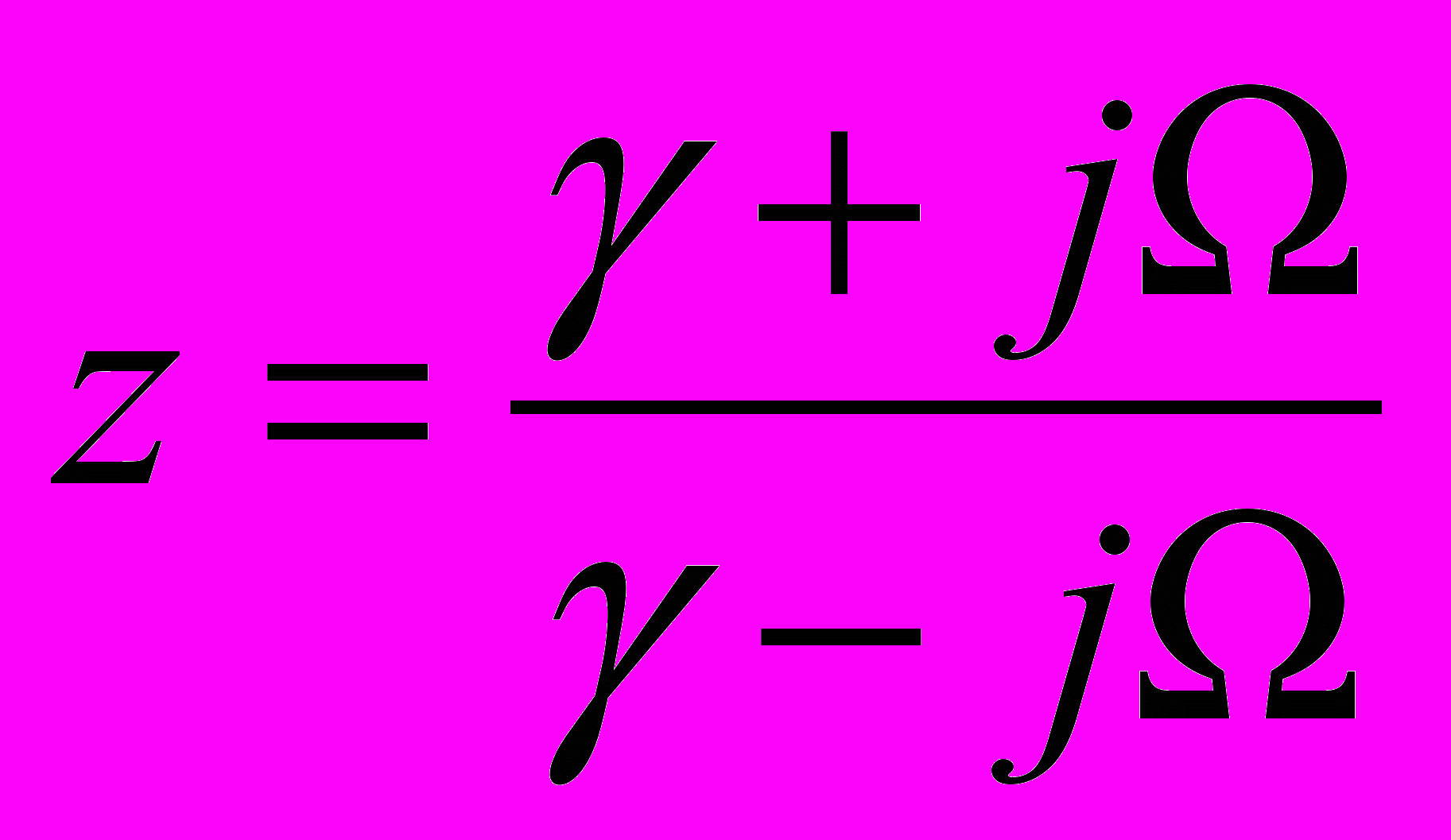
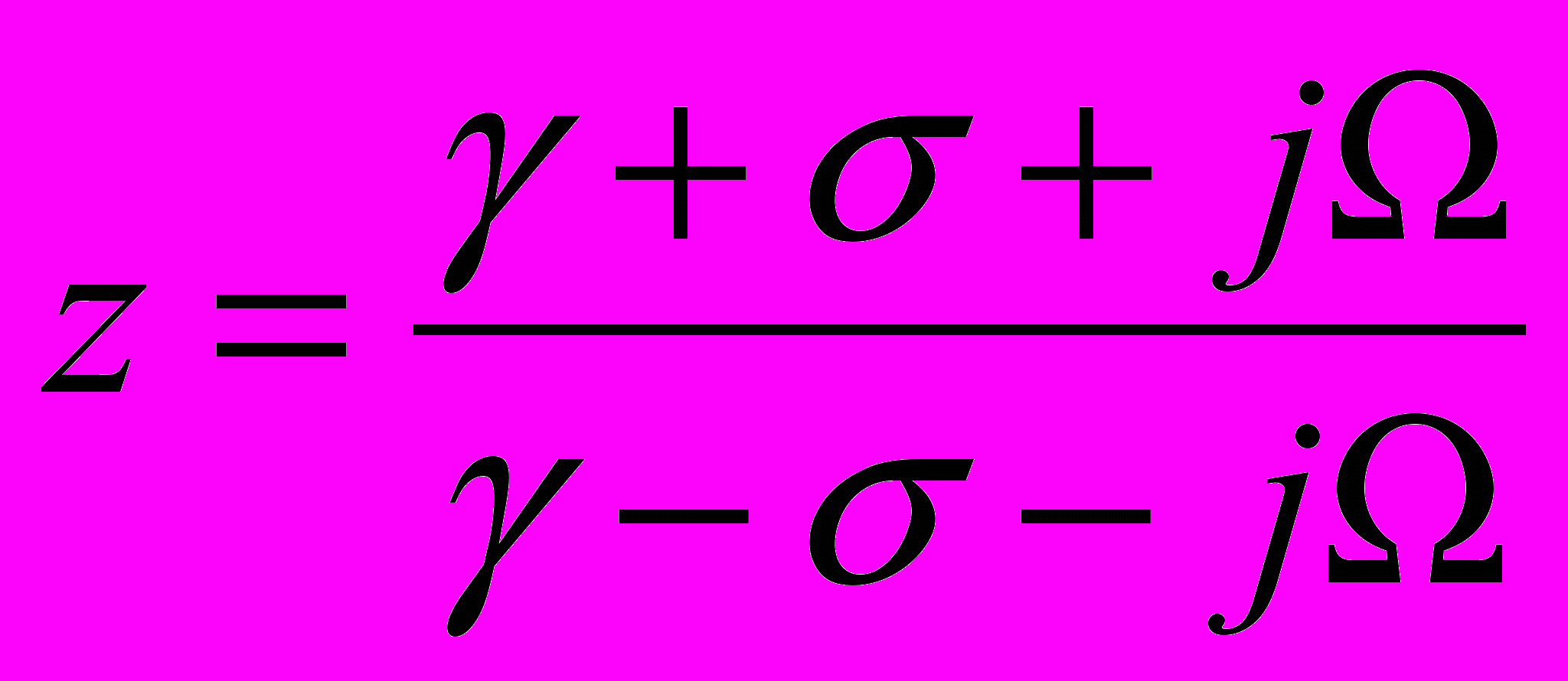Отсюда видно, что | z | = 1 при всех значениях . При  = 0 имеем z = 1 и при  =  z = –1, таким образом, при монотонном изменении аналоговой частоты  от - через 0 до + аргумент комплексной переменной z, являющийся частотой цифровой системы – , монотонно изменяется от - через 0 до +.

При s =  + j

При  < 0 (для левой полуплоскости s) | z | < 1, т.е. все точки левой полуплоскости располагаются внутри единичной окружности.

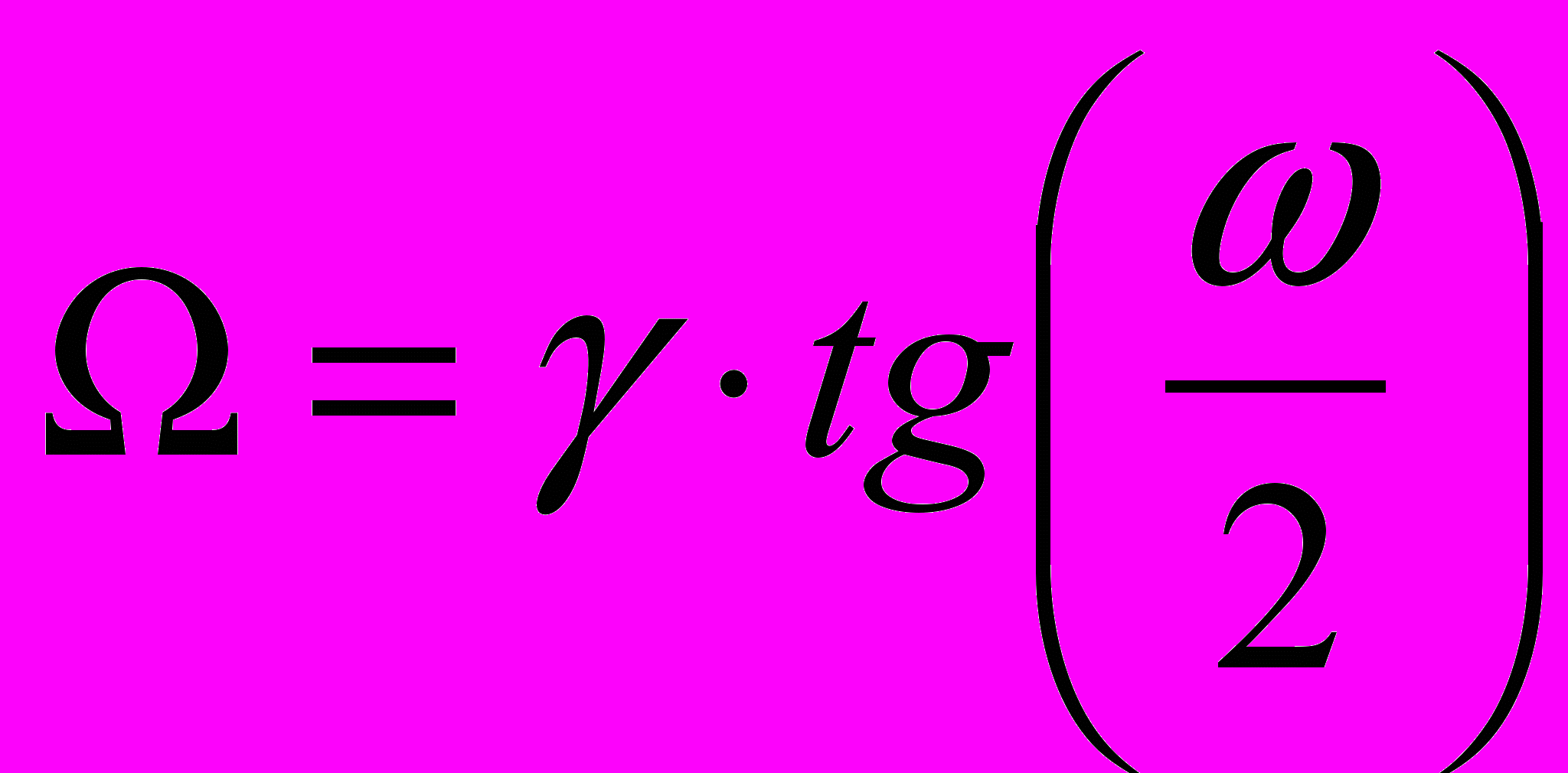Т
. (42)
ак как вся мнимая ось s-плоскости отображается на единичную окружность, то все минимумы и максимумы АЧХ аналогового фильтра (|T(j)| ) сохраняются и в АЧХ цифрового фильтра (| H(ej)|). Сохраняется также и неравномерность АЧХ для соответствующих диапазонов частот. Таким образом, избирательные аналоговые фильтры преобразуются в соответствующие цифровые фильтры. Однако соотношение между частотами аналогового фильтра  и цифрового фильтра  оказывается существенно нелинейным. Это соотношение можно получить из формулы подстановки, заменив s на j , а z – на e^j^ и воспользовавшись формулой Эйлера:

Таким образом, имеет место деформация шкалы частот при переходе от аналогового фильтра к цифровому. Это ограничивает область применения билинейного преобразования. Тем не менее, для стандартных типов избирательных фильтров (ФНЧ, ФВЧ, ППФ и ПЗФ), АЧХ которых имеет вид кусочно-постоянной функции, деформация шкалы частот может быть скомпенсирована с помощью предыскажений в аналоговом фильтре. При этом характерные частоты аналогового фильтра необходимо определять по приведенной выше формуле (40). Метод компенсации нелинейности соотношения частотных осей иллюстрируется на рис. 8.

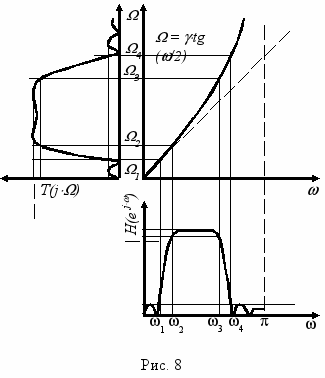
Параметр  выбирается из соображения удобства при проведении билинейного преобразования. В частности при р
, (43)
асчете цифрового фильтра нижних частот удобно определить  п

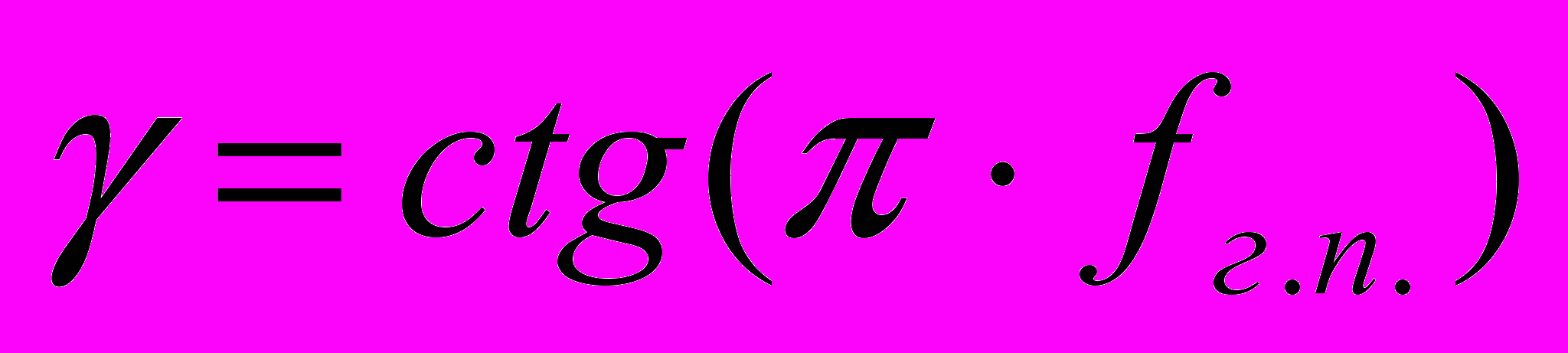
о формуле:

где f_г.п.нормированная граничная частота полосы пропускания.

В этом случае в качестве прототипа надо использовать нормированный аналоговый фильтр с частотой среза _с = 1, а параметры именно таких фильтров приводятся в литературе по проектированию аналоговых фильтров. При расчете аналоговых фильтров других типов, в качестве прототипа также используется нормированный фильтр нижних частот, который затем преобразуется в фильтр нужного типа с помощью соответствующей подстановки комплексной переменной s. При этом требуется, чтобы аналоговые полосовые и режекторные фильтры были бы геометрически симметричны. Для того чтобы не производить двойных преобразований при расчете цифровых БИХ-фильтров соответствующих типов, было разработано обобщенное билинейное преобразование, позволяющее преобразовывать аналоговый ФНЧ в цифровой фильтр любого стандартного типа (ФНЧ, ФВЧ, ППФ и ПЗФ). Формулы для соответствующих преобразований приведены в приложении П6. При преобразовании аналогового ФНЧ в ППФ или ПЗФ появился дополнительный параметр , формулы для которого приведены в соответствующей графе таблицы приложения. Кроме того, для обеспечения геометрической симметрии аналогового прототипа, коэффициент прямоугольности рассчитывается по двум формулам и выбирается наименьший по абсолютной величине.

При реализации аналоговых фильтров высоких порядков их обычно разбивают на звенья второго и первого порядков, которые включаются последовательно. Это делается для того, чтобы упростить схемную реализацию фильтров и их настройку, уменьшить чувствительность к разбросу параметров элементов схемы и другим дестабилизирующим факторам. При реализации цифровых фильтров большинство дестабилизирующих факторов отсутствуют. Однако при прямой реализации вычислений по передаточной функции БИХ-фильтра высокого порядка, характеристики фильтра оказываются очень чувствительны к точности представления ее коэффициентов. Поэтому передаточную функцию цифровых БИХ-фильтров также обычно разбивают на звенья первого и второго порядков, включаемых последовательно.

Общий порядок расчета передаточной функции цифрового БИХ-фильтра этим методом заключается в следующем:

Расчет нормированных цифровых частот границ полос пропускания и задерживания.
Расчет параметра преобразования  (и  для полосовых и режекторных фильтров).
Нахождение коэффициента прямоугольности аналогового ФНЧ.
Определение передаточной функции аналогового нормированного фильтра-прототипа нижних частот требуемого типа (Баттерворта, Чебышева, Кауэра и т.п.). Соответствующие методы излагаются в курсе аналоговой схемотехники. Запись передаточных функций звеньев первого и второго порядка.
Определение передаточных функций соответствующих звеньев первого, второго или четвертого порядка цифрового фильтра с помощью билинейного преобразования в зависимости от его типа.
Разложение звеньев четвертого порядка (если они есть) на звенья второго порядка.
Контрольный расчет и построение графиков АЧХ полученного БИХ-фильтра.
Исследование влияния точности представления коэффициентов передаточных функций звеньев второго порядка на общую частотную характеристику фильтра.

Этот алгоритм реализуется в пакете "MathCad 2001" с использованием символьных вычислений. Расчет звеньев передаточной функции аналогового прототипа может быть выполнен в документах "MathCad" "Фильтр Чебышева.mcd" или "Фильтр Баттерворта.mcd" в зависимости от типа фильтра. Значения коэффициентов полиномов знаменателя всех звеньев содержатся в результирующей матрице.

3. Порядок выполнения работы

В качестве исходных данных для расчета фильтра использовать данные работы 1. Расчет вести в пакете "MathCad 2001".
В соответствии с пп. 2 и 3 предыдущего раздела рассчитать параметр преобразования  и  (если требуется) и коэффициент прямоугольности _k , используя формулы из таблицы приложения.
Используя документ "MathCad" "Фильтр Чебышева.mcd", рассчитать порядок и коэффициенты полиномов передаточных функций звеньев первого и второго порядка аналогового фильтра-прототипа.
С помощью копирования перенести матрицу с коэффициентами в документ по расчету цифрового фильтра, присвоив ее значения матрице b.
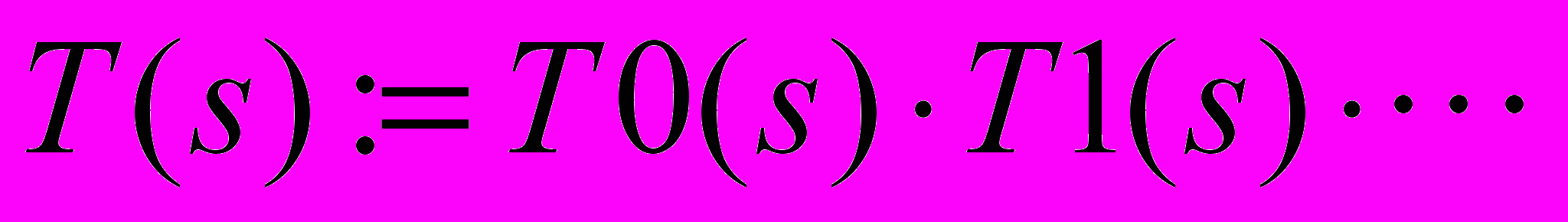З
, (44)

(45)
аписать передаточные функции от s для каждого аналогового звена, используя элементы матрицы b в виде:
где первый индекс элемента матрицы b определяет номер звена аналогового фильтра, а второй – является номером коэффициента в полиноме. Затем записать передаточную функцию всего аналогового фильтра в виде произведения передаточных функций звеньев:
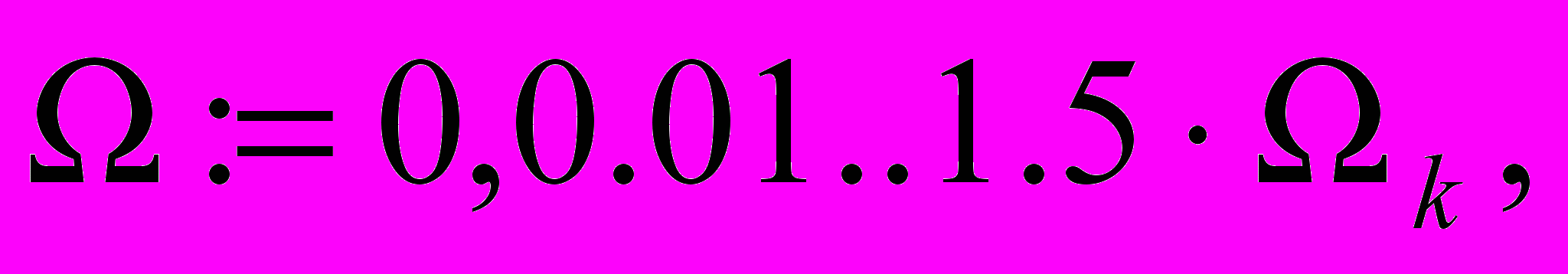П
(46)
остроить частотные характеристики всех звеньев аналогового фильтра и всего фильтра в целом на одном графике. Для этого задать аналоговую частоту  в виде ранжированной переменной:
и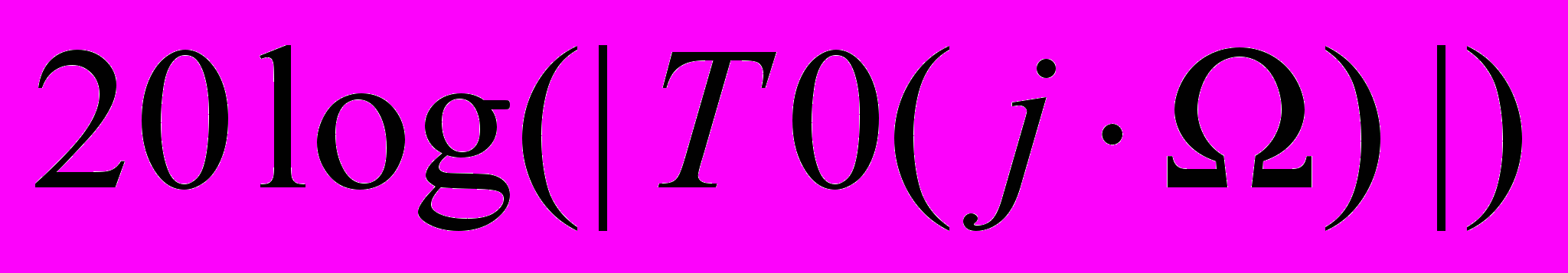

, (47)
использовать ее в качестве аргумента графика. Функции для построения задавать в виде:
где j – мнимая единица. Проверить соответствие частотной характеристики требованиям к аналоговому прототипу.
Записать в скобках выражение для билинейного преобразования требуемого типа фильтра.
Скопировать и вставить в документ выражение для передаточной функции аналогового звена.
Заменить путем копирования и вставки переменную s на выражение билинейного преобразования. Вызвать панель инструментов с командами символьного преобразования "Simbolic". Выделить курсором переменную z. Нажать на кнопку "simplify" (упростить). Справа от выражения, после стрелки, появится преобразованное выражение в виде двухэтажной дроби, в которой выполнены вычисления над числовыми значениями параметров исходного выражения, произведены упрощения и приведение подобных членов.
Если выполнялось преобразование для полосового или режекторного фильтра и в знаменателе передаточной функции цифрового фильтра получен полином четвертой степени, то такую передаточную функцию нужно разбить на два звена второго порядка. Для этого нужно скопировать полином знаменателя в буфер обмена, а затем вставить его документ в виде отдельного выражения. Затем выделить курсором комплексную переменную z, в меню "Simbolics" выделить пункт "Variable" (переменная) и в этом пункте выполнить подпункт "solve". Ниже записи полинома появится матрица с четырьмя попарно сопряженными комплексными корнями полинома.

И
(z – z₀)(z – z₁)

, (48)
спользуя значения этих корней, следует построить полиномы второго порядка. Для этого надо записать выражение следующего вида:
где z₀ и z₁ – пара комплексно сопряженных корней. Значения корней в выражение лучше вставить с помощью операции копирования из матрицы решения. Затем следует выделить все выражение и выполнить в меню "Simbolics" в пункте "Evaluate" подпункт "Complex". Ниже выражения появится запись квадратного трехчлена, который будет являться знаменателем передаточной функции второго порядка.
Такую же операцию следует повторить для второй пары корней.

Повторить пункты 8, 9 и 10 для всех звеньев аналогового фильтра.
Сгруппировать коэффициенты всех полиномов знаменателя в матрицу d, а коэффициенты числителя в матрицу с, аналогично матрице b с коэффициентами аналогового фильтра. Отмасштабировать коэффициенты знаменателя так, чтобы свободные члены были равны 1. Для этого можно значения элементов в строках матриц d и c разделить на значения соответствующих свободных членов. Это можно сделать непосредственно при задании матрицы, в позициях соответствующих элементов.
Для дальнейшего исследования влияния точности значений коэффициентов на свойства фильтра, задать количество знаков после запятой k := 10 и выполнить округления элементов матрицы с помощью функции r
ound() и операции векторизации:
З

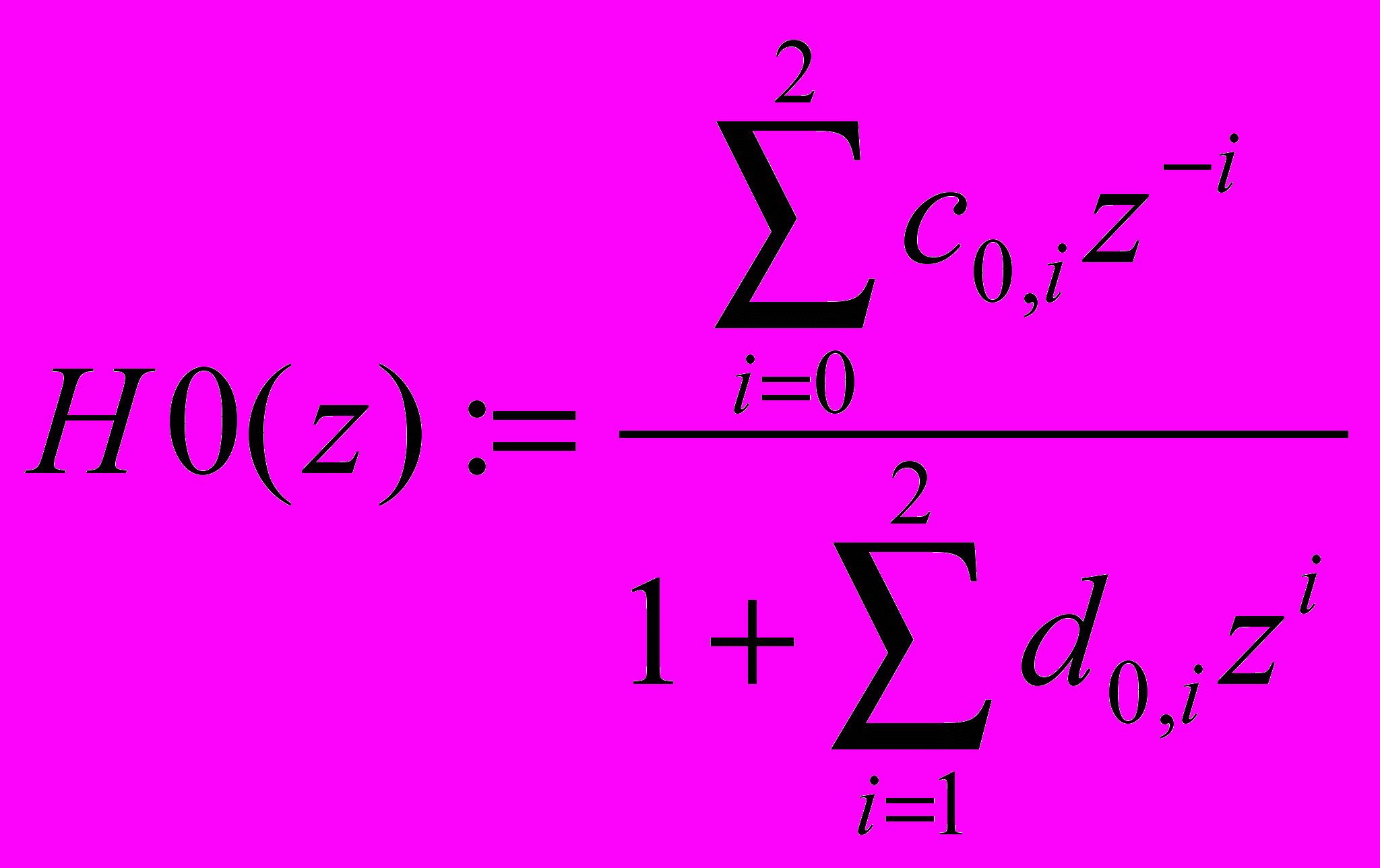
. (50)

. (49)
аписать выражения для передаточных функций всех цифровых звеньев в виде:
Построить частотные характеристики всех звеньев цифрового фильтра и всего фильтра в целом на одном графике. Для этого задать количество точек на оси ц
(51)

. (52)
ифровых частот I, ранжированную переменную i, п
I := 500 i := 0

Blog

Методическое пособие по лабораторным работам для студентов специальности 201400 «аудиовизуальная техника» Санкт-Петербург