1 Расчет линейной электрической цепи постоянного тока Задание

Вид материала

Закон

Содержание 1.2 Определение токов во всех ветвях методом контурных токов 1.3 Определение показания вольтметра 1.4 Баланс мощностей 2 Расчет электрической цепи однофазного переменного тока 2.1 Определение комплексов действующих значений токов во всех ветвях схемы 2.2 Определение показаний приборов 2.3 Определение полной комплексной мощности цепи 2.4 Компенсация реактивной мощности 2.5 Построение векторной диаграммы токов и напряжений

Подобный материал:

• Задача № расчет линейной электрической цепи постоянного тока по заданной обобщенной, 87.8kb.
• Электрические цепи постоянного тока, 1039.6kb.
• Экзаменационная программа Электротехника и электроника Раздел Цепи постоянного тока, 19.14kb.
• Расчет сложных цепей постоянного тока, 93.75kb.
• Урок физика-математика «Расчет комплексных сопротивлений в электрических цепях переменного, 117.95kb.
• Программа вступительных экзаменов в магистратуру по специальности 6М071800 «Электроэнергетика», 590.06kb.
• Задача расчет линейной цепи при постоянных токах и напряжениях, 61.22kb.
• Электрический ток в проводниках, 75.18kb.
• 1 Как зависит от напряжения сила постоянного тока в замкнутой электрической цепи, 43.86kb.
• Математики и программирования пояснительная записка к курсовой работе по курсу «Введение, 151.91kb.

1 Расчет линейной электрической цепи постоянного тока


Задание:


Составить систему уравнений по законам Кирхгофа для определения токов во всех ветвях цепи

Определить токи во всех ветвях цепи методом контурных токов

Определить показания вольтметра

Составить баланс мощностей и проверить его подстановкой числовых значений


Исходные данные:


Е₃=55 В; Е₅=32 В; Е₆=-55 В;

R₁=52 Ом; R₂=36 Ом; R₃=68 Ом;

R₄=45 Ом; R₅=77 Ом; R₆=60 Ом.





Рисунок 1.1 – Исходная схема цепи


1.1 применение законов Кирхгофа для определения токов во всех ветвях схемы


1.1.1 Выберем направление токов в ветвях и направления обхода контуров. Составим систему уравнений по 1-у закону Кирхгофа для узлов a, b и c, и по 2-му закону Кирхгофа для контуров abca, abda, и cbdc.





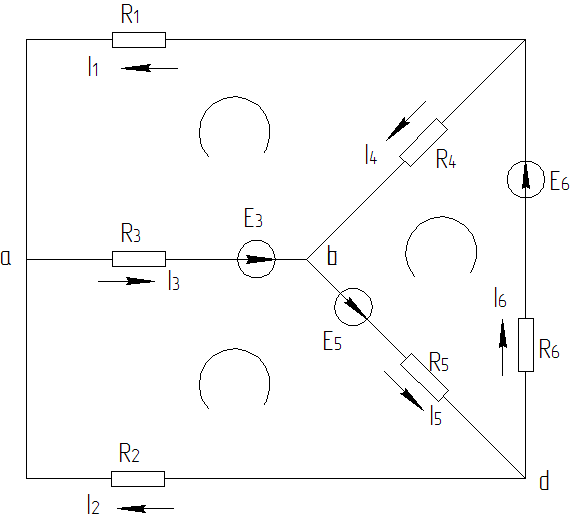
Рисунок 1.2 – Схема цепи для расчета методом уравнений по законам Кирхгофа


I₁-I₃+I₂=0

I₃+I₄-I₅=0

I₆-I₄-I₁=0

-R₁I₁+R₄I₄-R₃I₃=-E₃

-R₄I₄-R₆I₆-R₅I₅=-E₅-E₆

R₅I₅+R₂I₂+R₃I₃=E₅+E₃


Подставив значения получим:


I₁-I₃+I₂=0

I₃+I₄-I₅=0

I₆-I₄-I₁=0

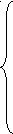-52*I₁+45*I₄-68*I₃=-55

-45*I₄-60*I₆-77*I₅=-32+55

77*I₅+36*I₂+68*I₃=32+55


1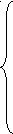.1.2 Решив систему уравнений получим значения токов в ветвях цепи


I₁=-0,072 A; I₂=0,694 A; I₃=0,622 A;

I₄=-0,366 A; I₅=0,256 A; I₆=-0,438 A.


Значит направление токов I₁; I₄ и I₆ противоположно первоначально принятому.


1.2 Определение токов во всех ветвях методом контурных токов





Рисунок 1.3 – Схема для расчета методом контурных токов


1.2.1 Выберем направления контурных токов I₁₁, I₂₂ и I₃₃ в контурах abca, abda и cbdc соответственно. Составим уравнения по 2-му закону Кирхгофа для нахождения значений контурных токов.


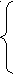(R₁+R₄+R₃)*I₁₁-R₃*I₂₂-R₄*I₃₃=-E₃

(R₃+R₅+R₂)*I₂₂-R₃*I₁₁-R₅*I₃₃=E₃+E₅

(R₅+R₄+R₆)*I₃₃-R₅*I₂₂-R₄*I₁₁=-E₆-E₅


1.2.2 Подставим числовые значения


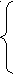(52+45+68)*I₁₁-68*I₂₂-45*I₃₃=-55

(68+77+36)*I₂₂-68*I₁₁-77*I₃₃=55+32

(77+45+60)*I₃₃-77*I₂₂-45*I₁₁=55-32


1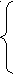65*I₁₁-68*I₂₂-45*I₃₃=-55

181*I₂₂-68*I₁₁-77*I₃₃=87

182*I₃₃-77*I₂₂-45*I₁₁=23


1.2.3 Вычислим определители получившейся системы уравнений


165 -68 -45

∆= -68 181 -77 =2777812

-45 -77 182




-55 -68 -45

∆₁= 87 181 -77 =200215

23 -77 182




165 -55 -45

∆₂= -68 87 -77 =1927775

-45 23 182




165 -68 -55

∆₃= -68 181 87 =1216143

-45 -77 23


1.2.4 Определим значения контурных токов


I₁₁=∆_1/∆=2000215/2777812=0,072 A

I₂₂=∆₂/∆=1927775/2777812=0,694 A

I₃₃=∆₃/∆=1216143/2777812=0,438 A


1.2.5 Вычислим значения токов в ветвях цепи


I₁=-I₁₁=-0,072 A

I₂=I₂₂=0,694 A

I₃=I₂₂-I₁₁=0,694-0,072=0,622 A

I₄=-I₃₃+I₁₁=-0,438+0,072=-0,366 A

I₅=-I₃₃+I₂₂=-0,438+0,694=0,256 A

I₆=-I₃₃=-0,438


1.3 Определение показания вольтметра





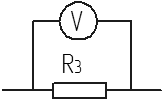
Рисунок 1.4 – Схема включения вольтметра


1.3.1 Определим показания вольтметра


U=R₃*I₃=68*0,622=42,296 В


1.4 Баланс мощностей


1.4.1 Найдем суммарную мощность источников


∑P_ист=E₃*I₃+E₅*I₅+E₆*I₆=55*0,622+32*0,256+(-55)*(-0,438)=66,492 Вт


1.4.2 Найдем суммарную мощность нагрузок


∑P_нагр=R₁*I₁²+R₂*I₂²+ R₃*I₃²+ R₄*I₄²+ R₅*I₅²+ R₆*I₆²=

=52*(-0,072)²+36*0,694²+68*0,622²+45*(-0,366)²+

+77*0,256²+60*(-0,438)²=66,5 Вт


1.4.3 Баланс мощностей выполняется, т.к. ∑P_ист ≈ ∑P_нагр


2 Расчет электрической цепи однофазного переменного тока


Задание:


Определить комплексы действующих значений токов во всех ветвях схемы

Определить показания приборов

Вычислить полную комплексную мощность цепи

Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента X

Построить векторную диаграмму токов и напряжений


Исходные данные:


U=350 В; f=100 Гц;

R₁=28 Ом; R₂=42 Ом;

L₁=73 мГн;

C₁=11 мкФ; С₂=254 мкФ





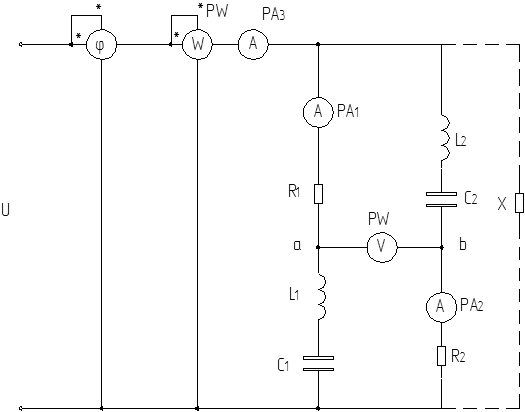
Рисунок 2.1 – Исходная схема

2.1 Определение комплексов действующих значений токов во всех ветвях схемы





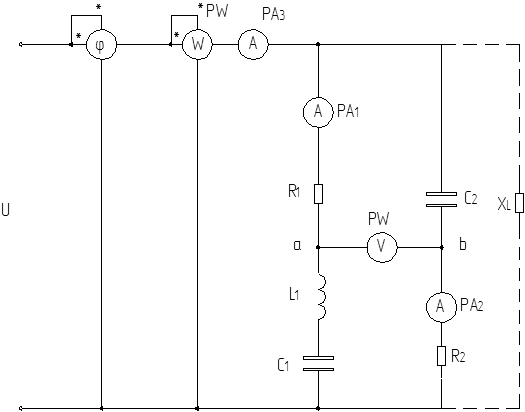
Рисунок 2.2 – Комплексная схема замещения цепи


2.1.1 Определим сопротивления реактивных элементов цепи


X_L1=ω*L₁=2*π*f*L₁=2*3,14*100*73*10^-3=45,867 Ом

X_C1=1/(ω*C₁)=1/(2*π*f*C₁)=1/(2*3,14*100*11*10^-6)=144,686 Ом

X_C2=1/(ω*C₂)=1/(2*π*f*C₂)=1/(2*3,14*100*254*10^-6)=6,266 Ом


2.1.2 Найдем комплексные значения полных сопротивлений ветвей цепи


Z₁=R₁+jX_L1-jX_C1=28+j45,867-j144,686=28-j98,819=102,709*e^-j74,18°

Z₂=R₂-X_C2=42-j6,266=42,465*e^-j8,485°


Определим комплексное значение полного сопротивления всей цепи


Z=(Z₁*Z₂)/(Z₁+Z₂)=

=(102,709*e^-j74,18۫ *42,465*e^-j8,485۫ )/(28-j98,819+42-j6,266)=

=(4361,538*e^-j82,665۫ )/(70-j105,085)=( 4361,538*e^-j82,665۫ )/(126,265*e^-j56,331۫ )=

=34,543*e^-j26,334° =30,958-j15,323


2.1.3 Определим ток на неразветвленном участке цепи


İ=U/Z=350/(34,543*e^-j26,334°)=10,132*e^j26,334°=(9,08+j4,495)А


2.1.4 Найдем ток в ветвях цепи


İ₁=U/Z₁=350/(102,709*e^-j74,18°) =3,408*e^j74,18°=(0,929+j3,279)А

İ₂=U/Z₂=350/(42,465*e^-j8,485°)=8,242*e^j8,485°=(8,152+j1,216)А


2.2 Определение показаний приборов


2.2.1 Амперметры PA, PA₁ и PA₂ показывают действующие значения токов:

I=10,132 А; I₁=3,408 А; I₂=8,242


2.2.2 Определим напряжение между точками a и b


Ú_ab=φ_a-φ_b=R₁*İ₁+jX_C2*İ₂=

=28*(0,929+j3,279)+j6,266*(8,152+j1,216)=

=18,393+j142,892=(144,07*e^j82,665°)В


Вольтметр PV показывает действующее значение напряжения:


U=144,07 В


2.2.3 Определим показание ваттметра


P_w=Re[U*İ]=Re[350*10,132*e^j26,334°]=Re[3632*e^j26,334°]=

=Re[3255,083+j1611,166]=3255,083 Вт


2.2.4 Фазометр показывает величину угла сдвига по фазе между напряжением и током цепи:


φ=26,334°


2.3 Определение полной комплексной мощности цепи


2.3.1 Определим полную комплексную мощность цепи


Š=U*İ=350*10,132*e^j26,334°=3546,2*e^j26,334°=(3178,187+j1573,105) ВА


Активная и реактивная мощности цепи:


P=3178,187 Вт; Q=1573,105 Вар


2.3.2 Найдем коэффициент мощности цепи


сosφ=cos(26,334)=0,896 или

cosφ=P/S=3178,187/3546,2=0,896


2.4 Компенсация реактивной мощности


2.4.1 Повысим cosφ до значения 0,98 , включив параллельно цепи компенсирующее индуктивное сопротивление X_L. При этом величина сдвига по фазе между напряжением и током цепи:


φ׳ =arcos(0,98)=11,478°


2.4.2 Определим реактивную мощность цепи после компенсации


Q׳=P*tgφ׳=3178,187*tg(11,478°)=645,339 Вар


2.4.3 Найдем мощность подключаемого реактивного элемента


Q_L=Q׳-Q=645,339-1573,105=-927,766 Вар


2.4.4 Определим полную комплексную мощность цепи после компенсации


Š׳=P+jQ׳=3178,187+j645,339=(3243,044*e^j11,478°) ВА


2.4.5 Найдем ток, сопряженный току на неразветвленном участке


İ׳=Š׳/U=3243,044*e^j11,478°/350=9,26584*e^j11,478°=(9,08+j1,8438) А


2.4.6 Определим ток через компенсирующее индуктивное сопротивление X_L


İ_L=İ׳-İ₁-İ₂=(9,08+j1,844)-(0,929+j3,279)-(8,152+j1,216)= -j2,651=

=(2,651*e^-j90°) А


2.4.7 Найдем сопротивление компенсирующего реактивного элемента


X_L=U/İ_L=350/(2,651*e^-j90°)=132,026*e^j90°=(j132,026) Ом


2.4.8 Определим индуктивность компенсирующего реактивного элемента


L=X_L/ω=132,026/(2*3,14*100)=0,210126 Гн = 210,126 mГн


2.5 Построение векторной диаграммы токов и напряжений


2.5.1 Определяем комплексы действующих значений напряжений на всех элементах цепи


Ú_R1=R₁*İ₁=25*3,408*e^j74,18°=(85,2*e^j74,18°) В

Ú_L1=X_L1*İ₁=45,867*e^j90°*3,408*e^j74,18°=(156,315*e^j164,18°) В

Ú_C1=X_C1* İ₁=144,686*e^-j90°*3,408*e^j74,18°=(493,09*e^-j15,82°) В

Ú_C2=X_C2*İ₂=6,266*e^-j90°*8,242*e^j8,485°=(51,644*e^-j81,515°) В

Ú_R2=R₂* İ₂=42*8,242*e^j8,485°=(346,164* e^j8,485°) В


2.5.2 Построим векторную диаграмму токов и напряжений цепи.


Выбираем масштабы: m_U=25 В/см; m_I=1 А/см





Рисунок 2.3 – Векторная диаграмма токов и напряжений цепи