Задача расчет линейной цепи при постоянных токах и напряжениях
| Вид материала | Задача |
- Задача № расчет линейной электрической цепи постоянного тока по заданной обобщенной, 87.8kb.
- 1 Расчет линейной электрической цепи постоянного тока Задание, 93.15kb.
- Лекция №11. Нелинейные цепи переменного тока в стационарных режимах. Особенности нелинейных, 122.96kb.
- Тема магнитные цепи и их расчет, 69.42kb.
- Контрольная работа (типовой расчет) №2 "расчет сложной цепи периодического синусоидального, 29.02kb.
- Контрольная работа выполняется на тему «Основные законы теории цепей, анализ установившегося, 35.6kb.
- Тема: «теория матриц» Основная задача линейной алгебры, 28.88kb.
- Лекция № Нелинейные магнитные цепи при постоянных потоках. Основные понятия и законы, 207kb.
- Задача 1 посвящена анализу линейной электрической цепи однофазного синусоидального, 157.7kb.
- Реферат работа содержит 22 листа, 12 рисунков, 4 таблицы, 7 источников литературы, 160.62kb.
ЗАДАЧА
РАСЧЕТ ЛИНЕЙНОЙ ЦЕПИ ПРИ ПОСТОЯННЫХ ТОКАХ И НАПРЯЖЕНИЯХ
Для электрической схемы, соответствующей номеру варианта и изображенной на рис. 1, выполнить следующее:
1. Написать систему уравнений для расчета неизвестных токов в ветвях при помощи законов Кирхгофа (решать эту систему уравнений не следует).
2. Определить токи во всех ветвях схемы методом контурных токов.
3. Определить токи во всех ветвях схемы методом узловых потенциалов.
4.Результаты расчета токов, выполненного двумя методами, свести в таблицу и сравнить их между собой.
5. Применяя теорему об эквивалентном генераторе (активном двухполюснике), определить ток в одной (любой) из ветвей.
6. Составить баланс мощностей.
7. Построить потенциальную диаграмму для любого замкнутого контура, включающего в себя обе ЭДС.
Числовые значения ЭДС и сопротивлений даны в табл. 1
Таблица № 1.
| Номер строки | Е1, В | r1, Ом | Е2, В | r2, Ом | Е3, В | r3, Ом | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом |
| 3 | 220 | 2 | 110 | 1 | 110 | 2 | 4 | 5 | 6 | 12 | 8 | 10 |
Примечание. Из табл. 1 записываются данные только двух источников ЭДС, обозначенных на схеме рис. 1.
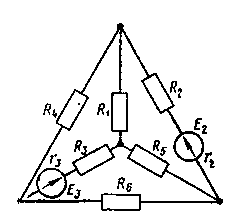
Рис 1
Решение:
- Написать систему уравнений для расчета неизвестных токов в ветвях при помощи законов Кирхгофа
Для составления уравнения путем непосредственного применения законов Кирхгофа зададим направления токов во всех шести ветвях схемы, а также укажем направления обхода контуров.

Составим уравнения по законам Кирхгофа:
Число узлов цепи: у=4
Число ветвей цепи: в=6
Число ветвей с источником тока Ви=0
Количество уравнений по 1 закону Кирхгофа: N1=у-1=3
Количество уравнений по 2 закону Кирхгофа: N2=в-Ви-(у-1)=3
С
 истема уравнений по законам Кирхгофа:
истема уравнений по законам Кирхгофа:- –I1+I3-I5=0
- I1+I2-I4=0
- I4-I3+I6=0
1. I1*R1+I4*R4+I3*(R3+r3)=E3
2. -I1*R1+I2*(R2+r2)+I5*R5=Е2
3. I3*(R3+r3)+I5*R5+I6*R6=E3
- Определить токи во всех ветвях схемы методом контурных токов

В основу метода контурных токов положено использование понятия контурного тока, под которым понимают условный ток, замыкающийся только по своему контуру: I11, I22, I33.
Количество независимых контуров: N2=в-(у-1)=3
Д
 ля каждого из этих контуров записывается уравнение по второму закону Кирхгофа, совокупность этих уравнений образует систему линейных алгебраических уравнений, решением которой являются значения контурных токов.
ля каждого из этих контуров записывается уравнение по второму закону Кирхгофа, совокупность этих уравнений образует систему линейных алгебраических уравнений, решением которой являются значения контурных токов.I11*R11+I22*R12+I33*R13=E11
I11*R21+I22*R22+I33*R23=E22 , где
I11*R31+I22*R32+I33*R33=E33
Е11,Е22,Е33 – собственные эдс контура;
R11,R22,R33 – собственные сопротивления контура;
R12,R21,R13,R31,R23,R32 – взаимные сопротивления контуров.
Найдем собственные эдс контура.
Е11=E3=110 В
Е22=E2=110 В
Е33=Е3=110 В
Найдем собственные сопротивления контура:
R11=R1+R3+r3+R4=24 Oм
R22=R1+R2+r2+R5=18 Ом
R33=R3+r3+R5+R6=26 Ом
Найдем взаимные сопротивления контуров:
R12=R21=-R1=-4 Ом
R23=R32=R5=8 Ом
R13=R31=R3+r3=8 Ом
П
 олучили систему уравнений:
олучили систему уравнений:24*I11-4*I22+8*I33=110
-4*I11+18*I22+8*I33=110
8*I11+8*I22+26*I33=110
Решим систему уравнений методом Крамера.
Найдем определитель главной матрицы.
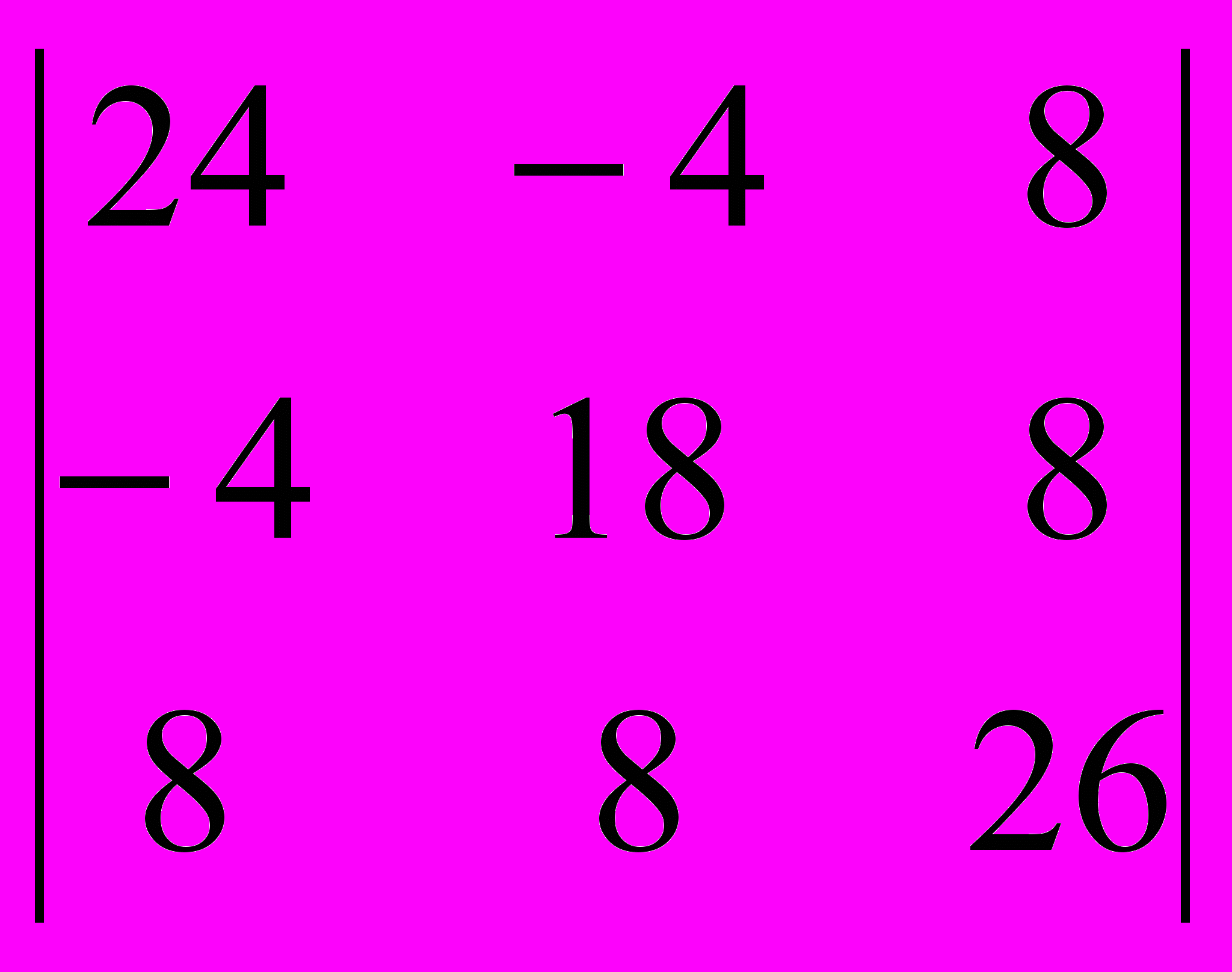
 =24*18*26-4*8*8-4*8*8-8*18*8-24*8*8-4*4*26=7616
=24*18*26-4*8*8-4*8*8-8*18*8-24*8*8-4*4*26=7616 Определитель главной матрицы системы уравнений не равен нулю, следовательно, данная система уравнений имеет единственное решение. Найдем его.
Составим определители, заменив в каждом столбце, коэффициенты на коэффициенты стоящие за знаком равенства в системе уравнений.
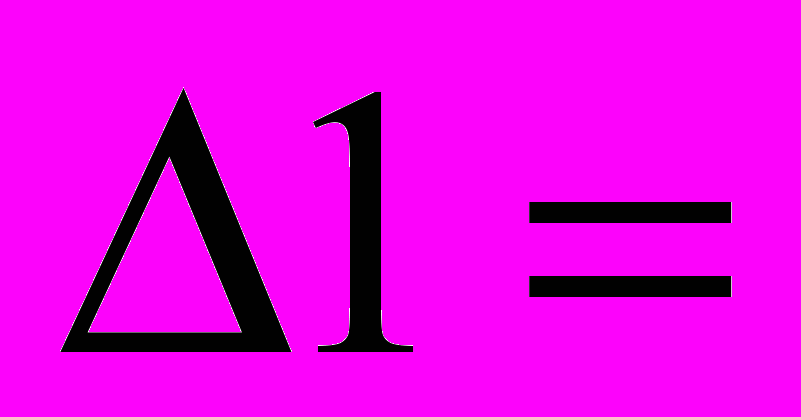
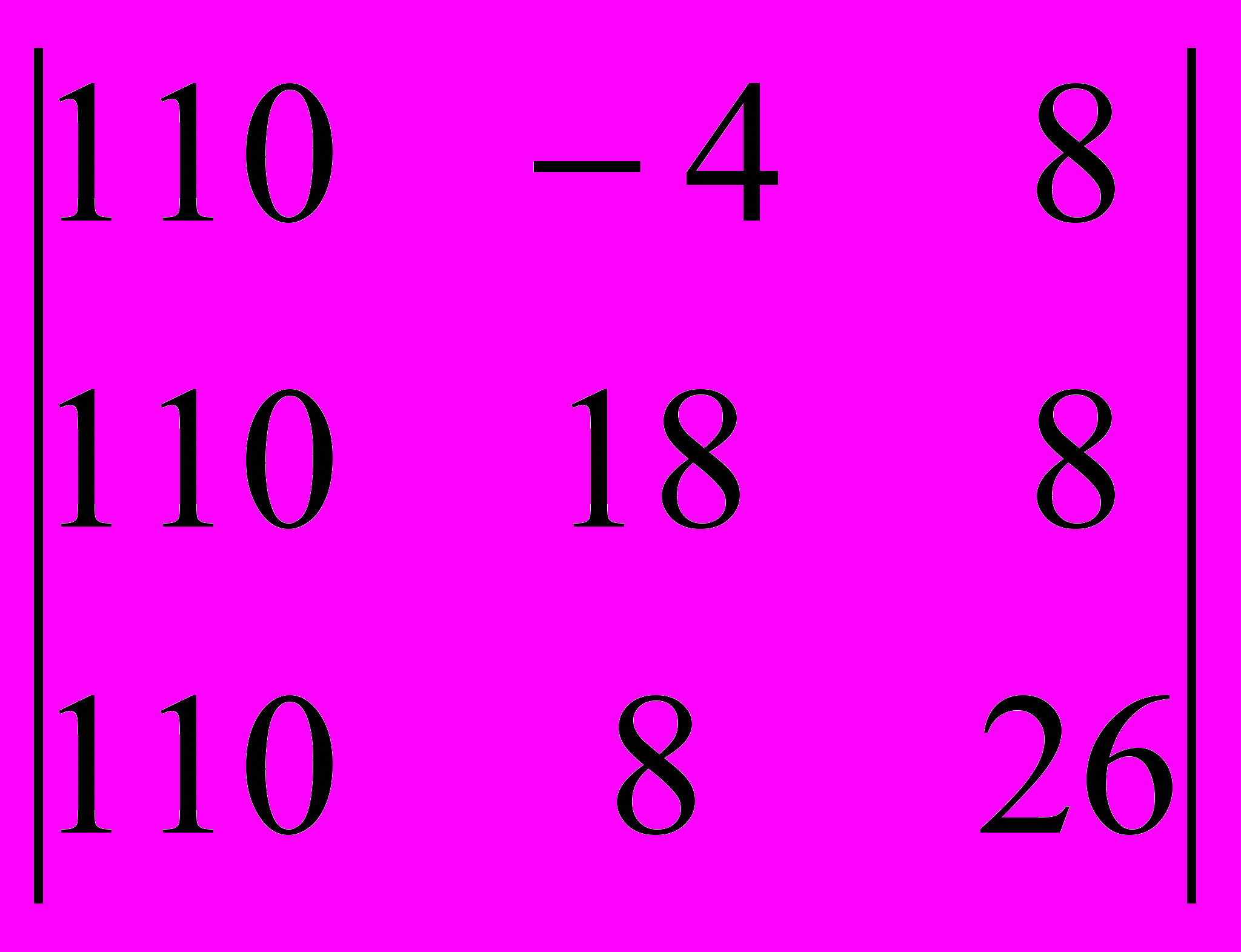 =43560
=43560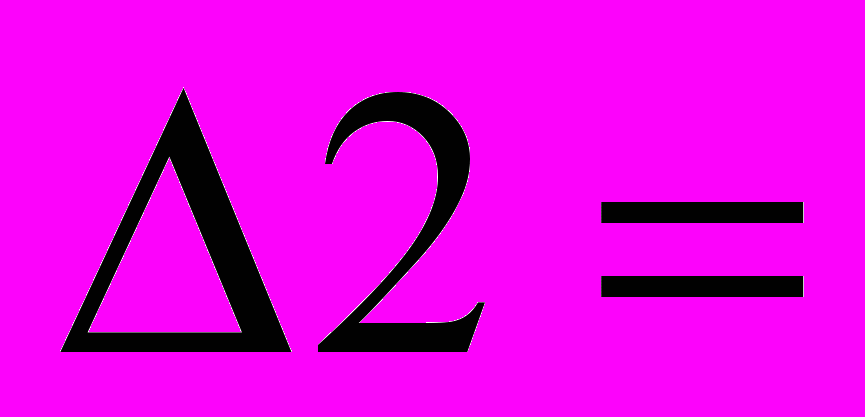
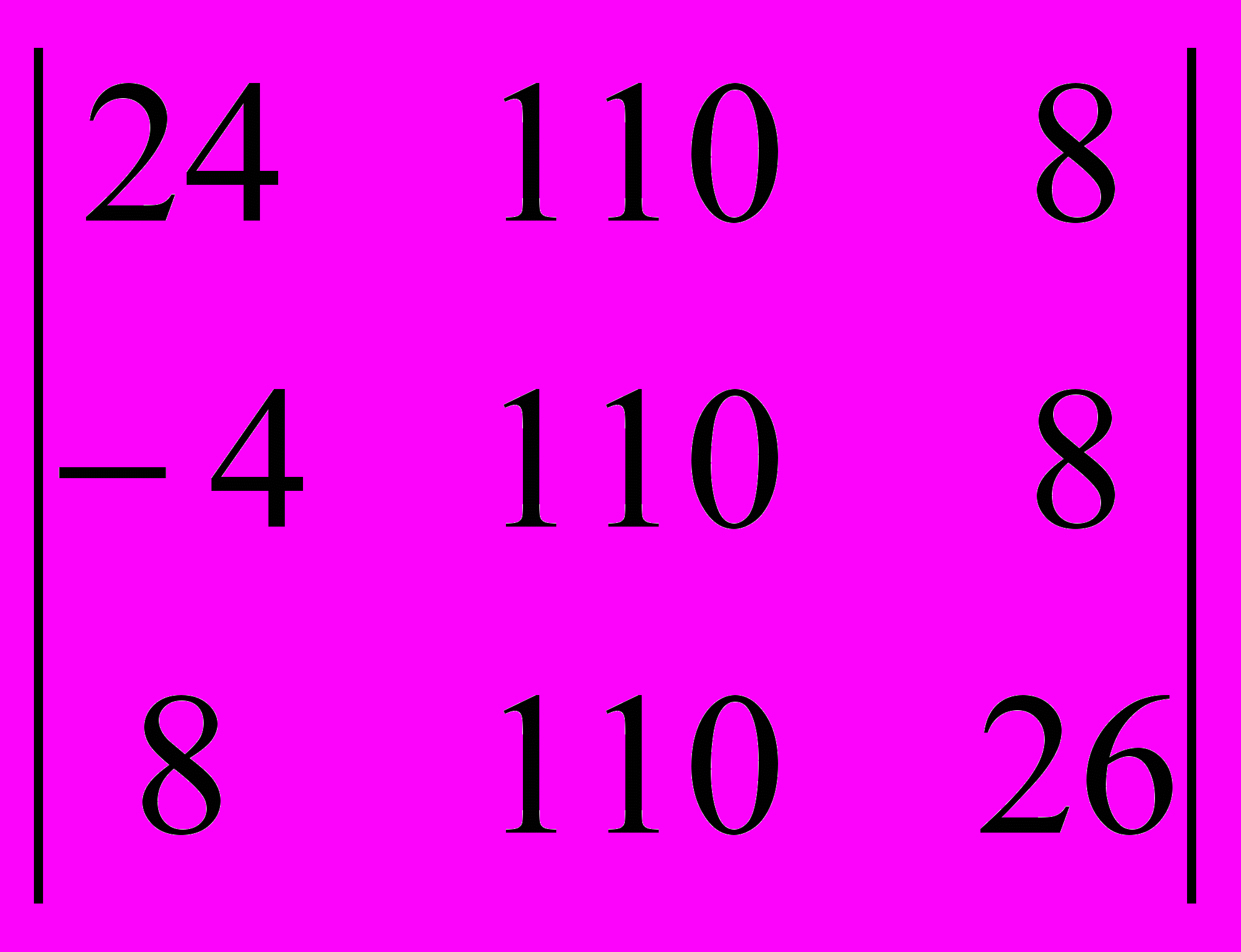 =55440
=55440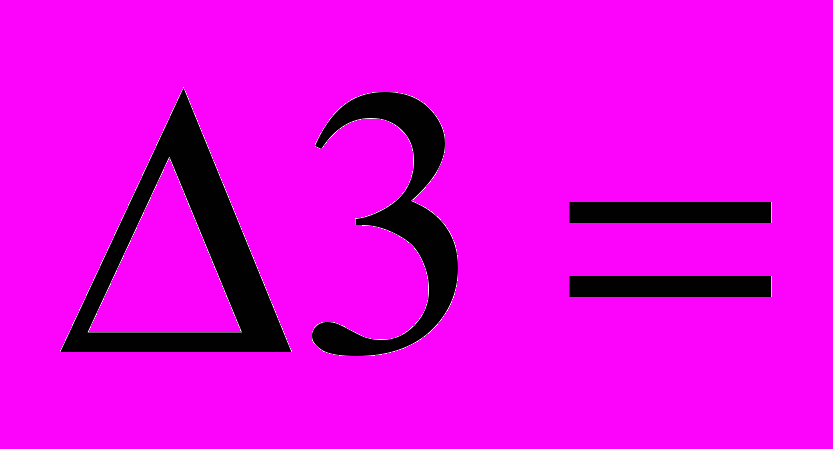
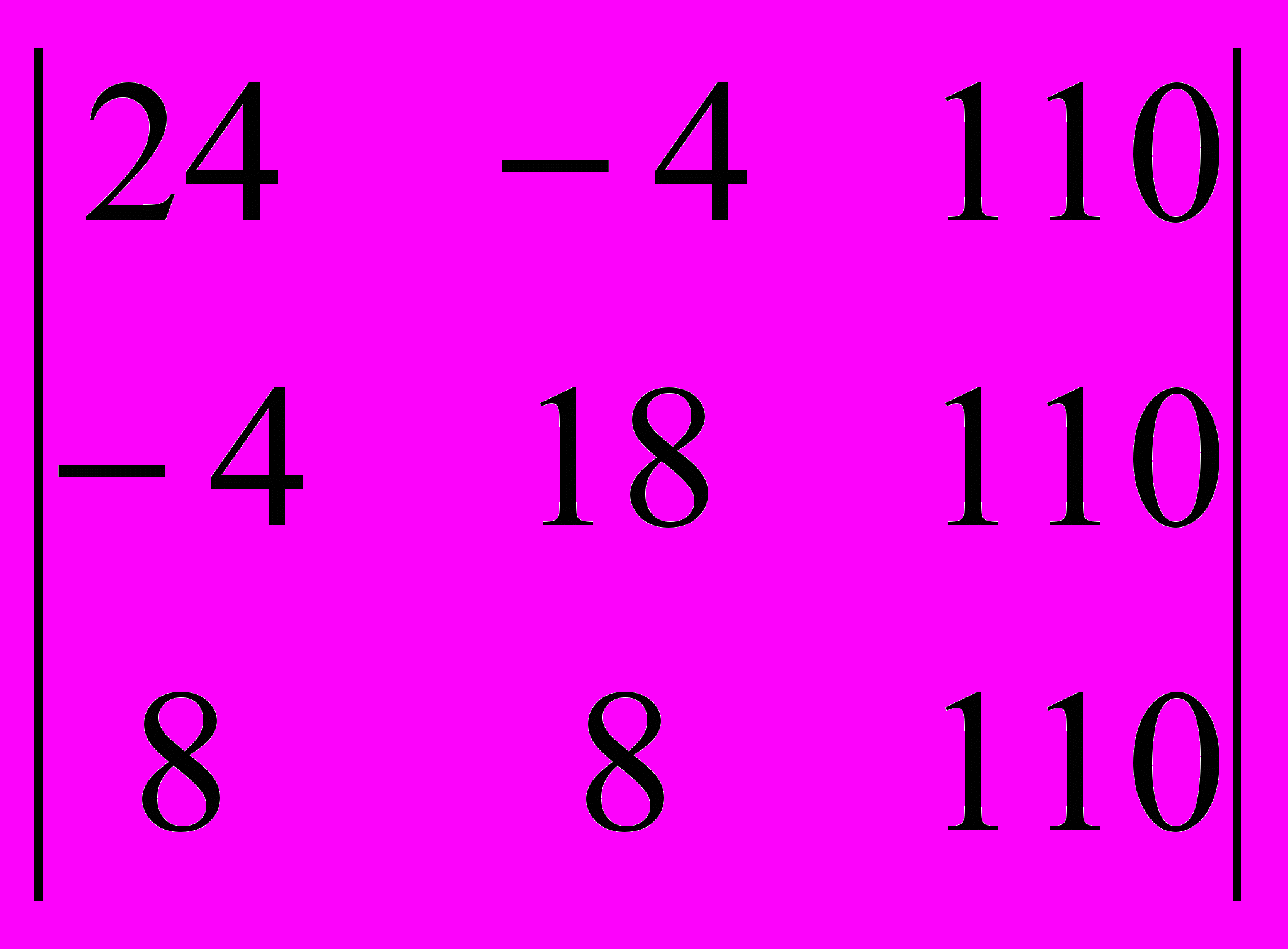 =1760
=1760Найдем решение системы уравнений:
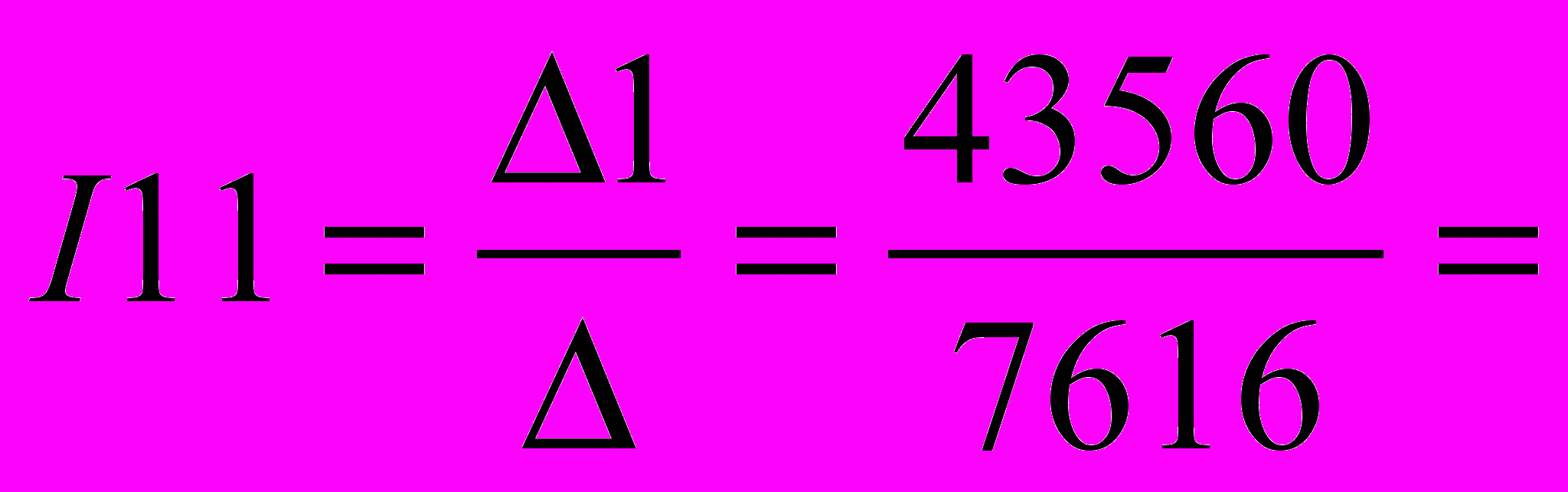 5.72 А
5.72 А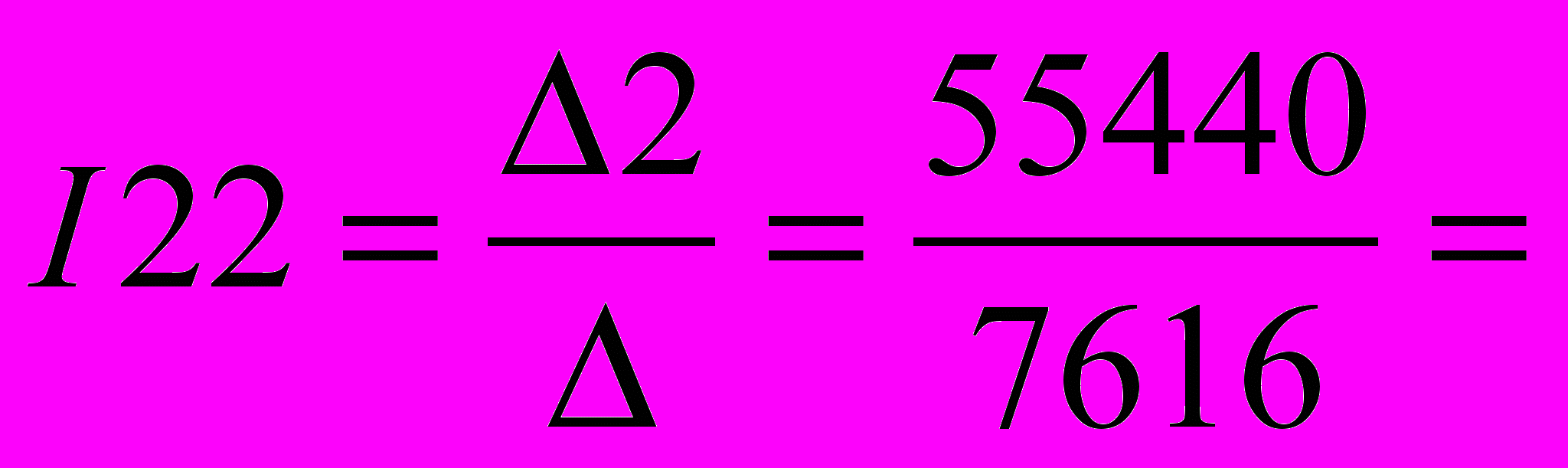 7.28 А
7.28 А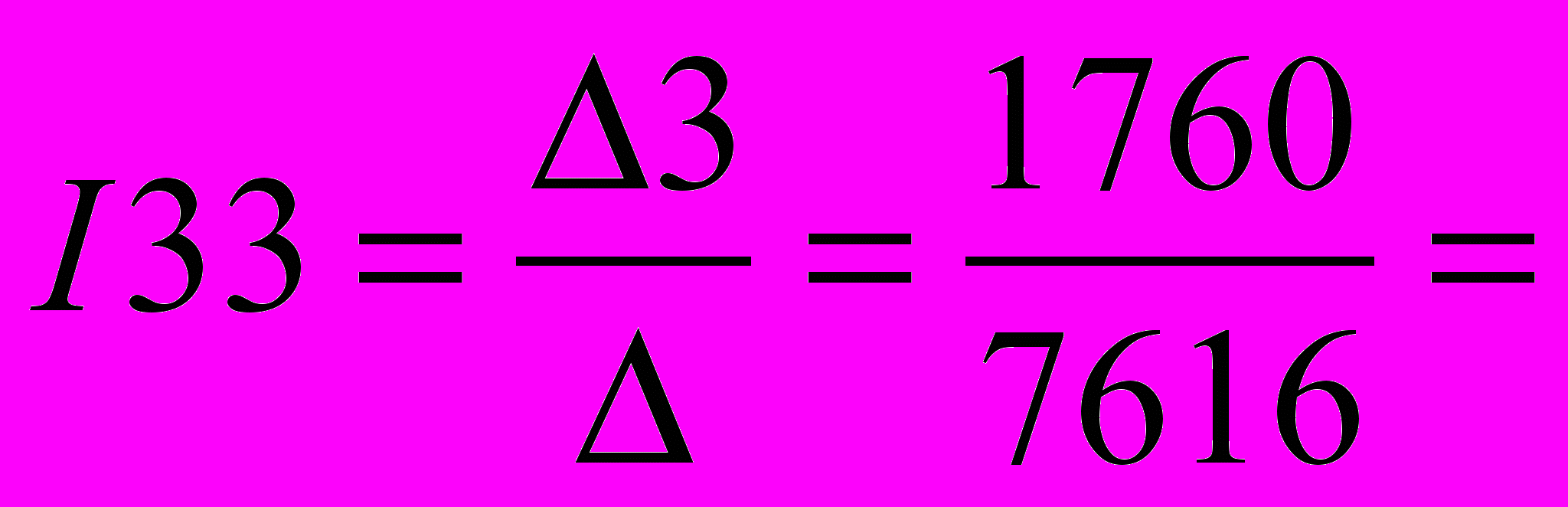 0.23 А
0.23 АДействительные токи в ветвях находят сложением всех контурных токов, протекающих в данной ветви.
I1=I11-I22=-1.56 A
I2=I22=7.28 A
I3=I11+I33=5.95 A
I4=I11=5.72 A
I5=I22+I33=5.71 A
I6=I33=0.23 A
Знак минус говорит о том, что ток I1 в схеме должен быть направлен в противоположную сторону.
- Определить токи во всех ветвях схемы методом узловых потенциалов
П
 римем φ4=0. Запишем систему уравнений по МУП:
римем φ4=0. Запишем систему уравнений по МУП:G11*φ 1 + G12*φ 2+G13* φ 3=I11
G21*φ 1+ G22*φ 2+ G23*φ 3=I22 , где
G31*φ 1+ G32*φ 2+ G33*φ 3=I33
I11,I22,I33 – узловые токи;
G11,G22,G33 – собственные проводимости узлов;
G12,G21,G13,G31,G23,G32 – взаимные проводимости узлов.
Найдем узловые токи:
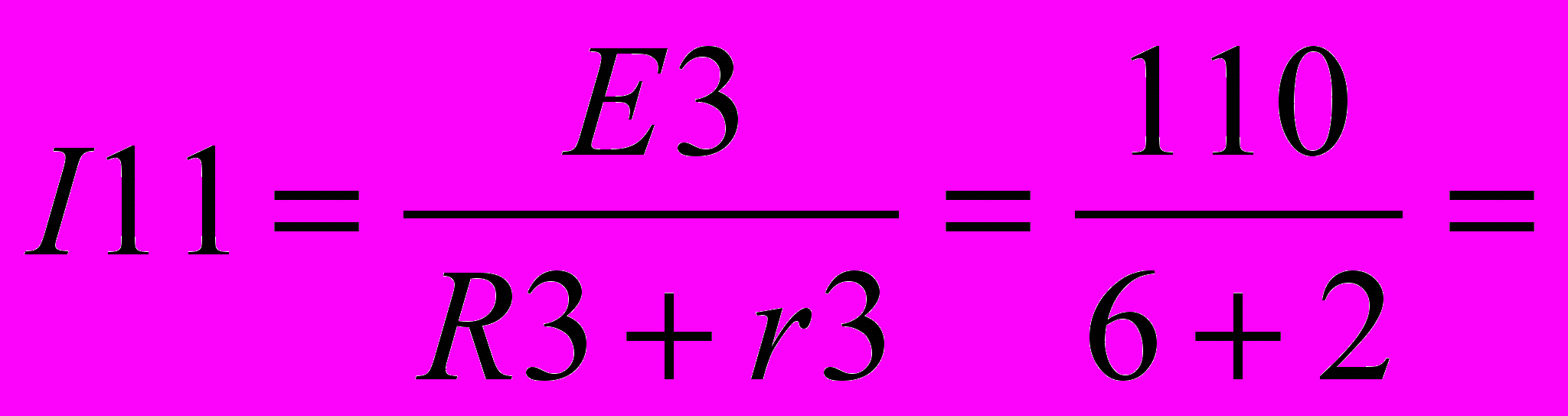 13.75 А
13.75 А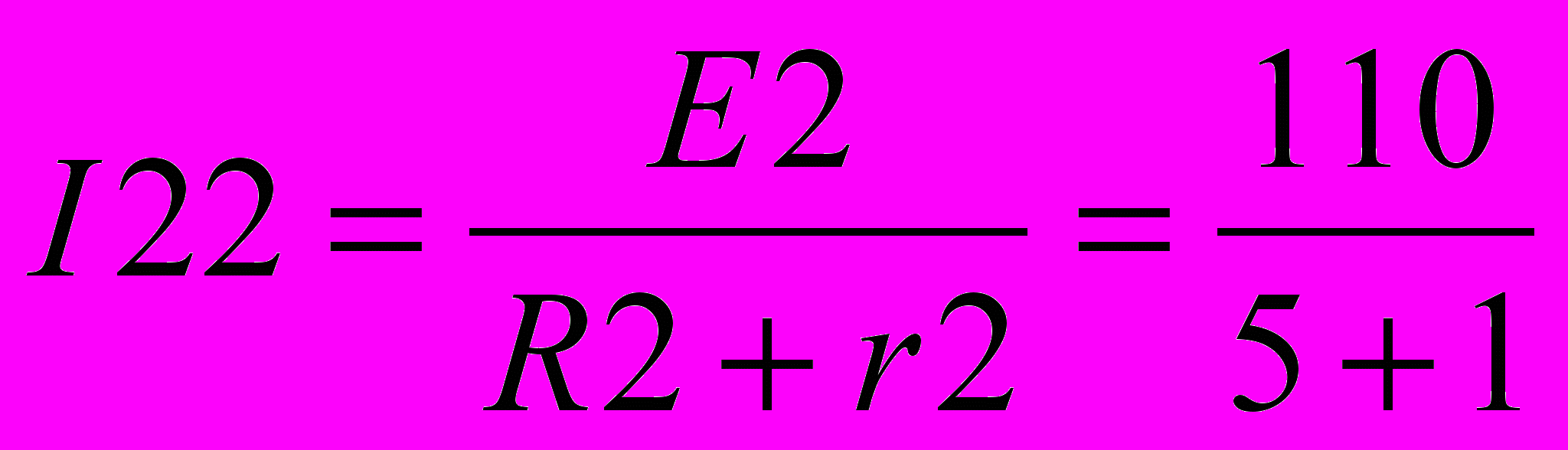 =18,33 A
=18,33 A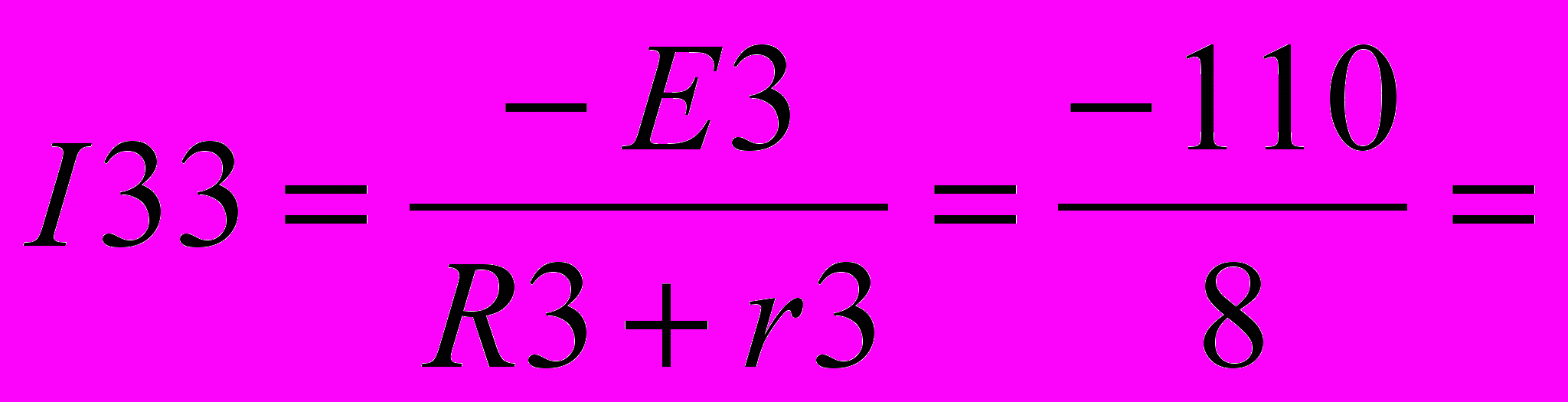 -13,75 A
-13,75 AНайдем собственные проводимости узлов:
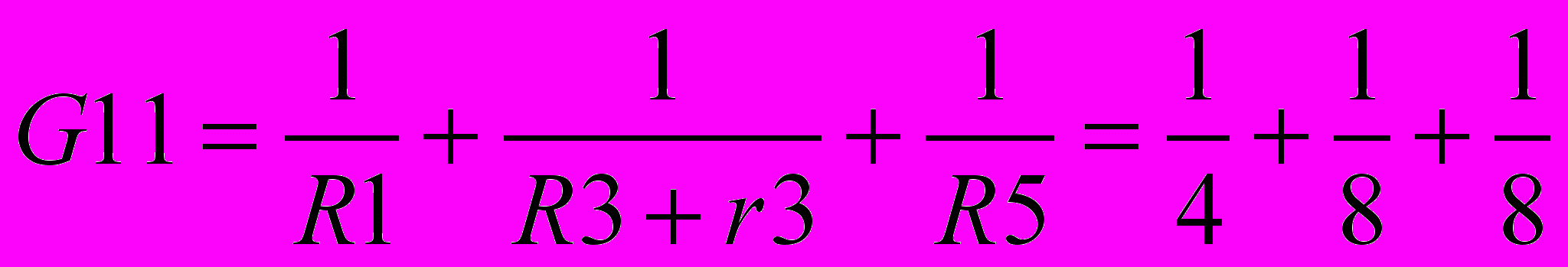 =0.25+0.125+0.125=0,5 См
=0.25+0.125+0.125=0,5 См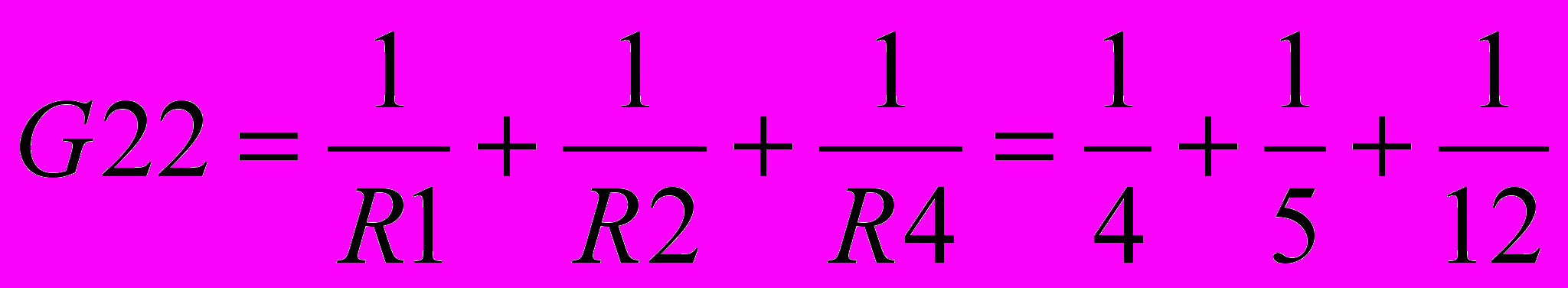 =0,25+0,2+0,083=0,533 См
=0,25+0,2+0,083=0,533 См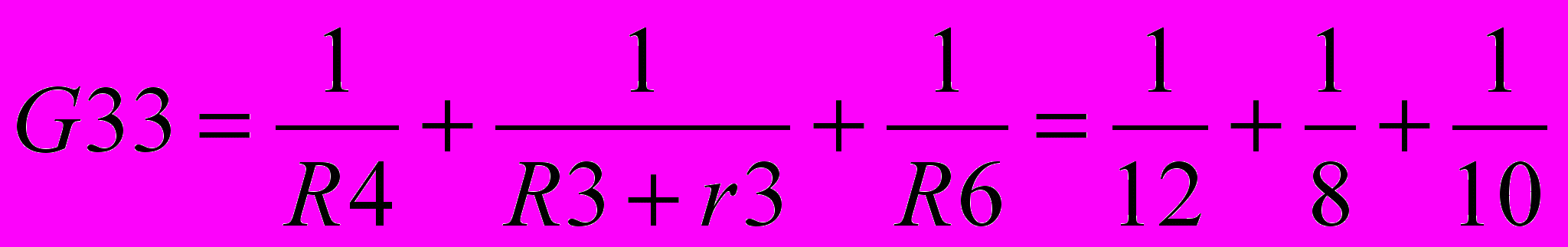 =0.083+0.125+0.1=0,308 См
=0.083+0.125+0.1=0,308 СмНайдем взаимные проводимости узлов:
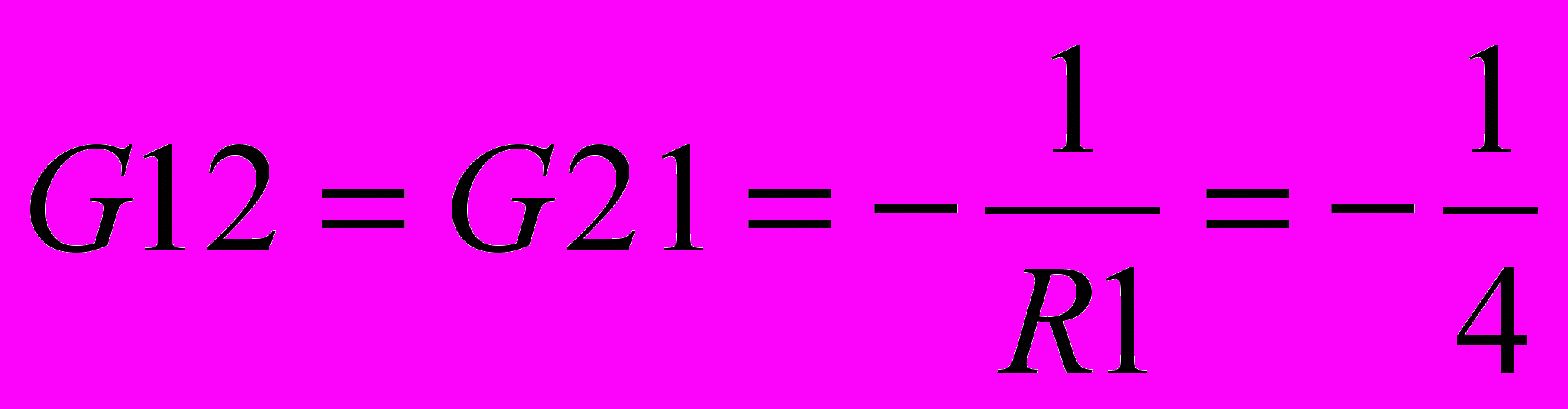 =-0.25 См
=-0.25 См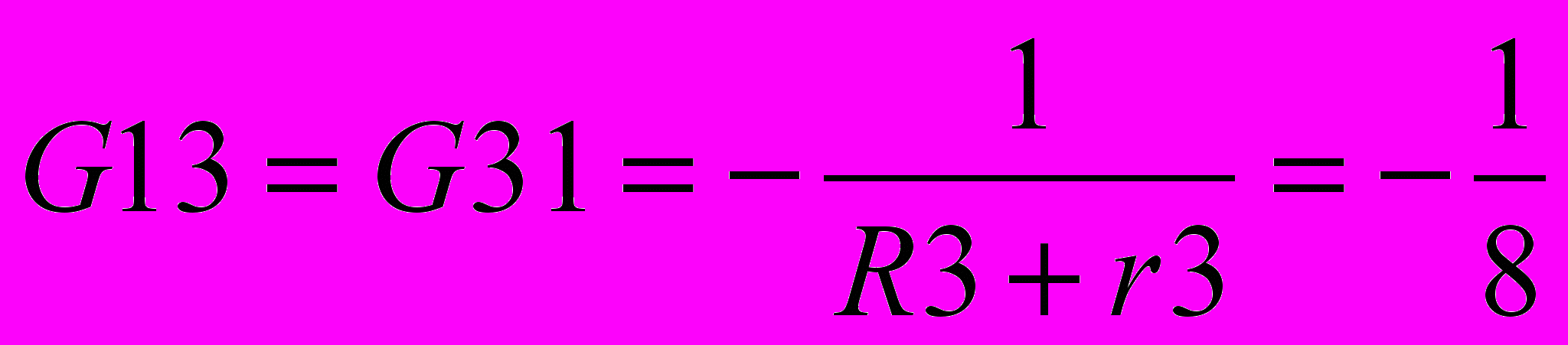 =-0.125 См
=-0.125 См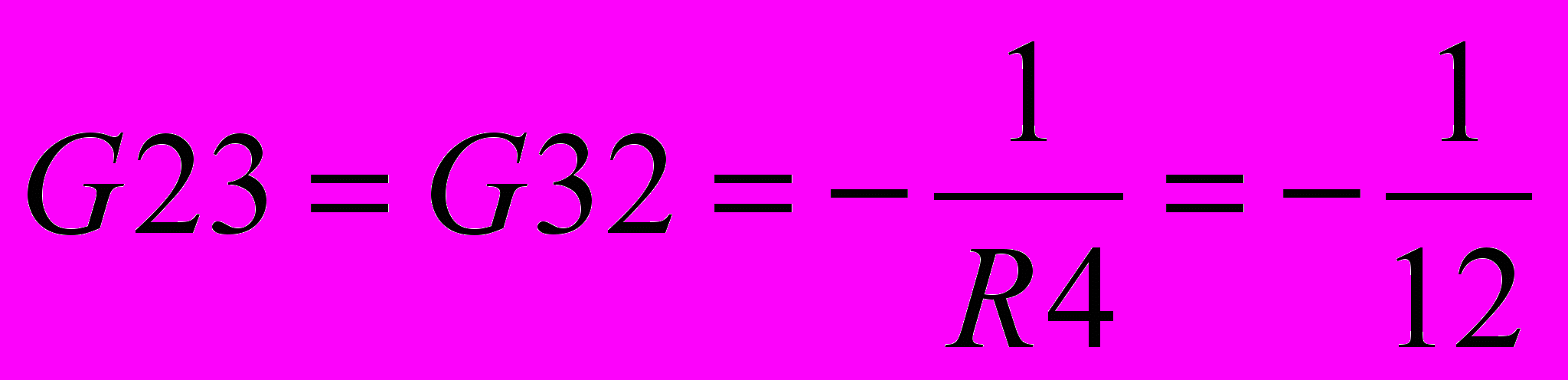 =-0.083 См
=-0.083 СмП
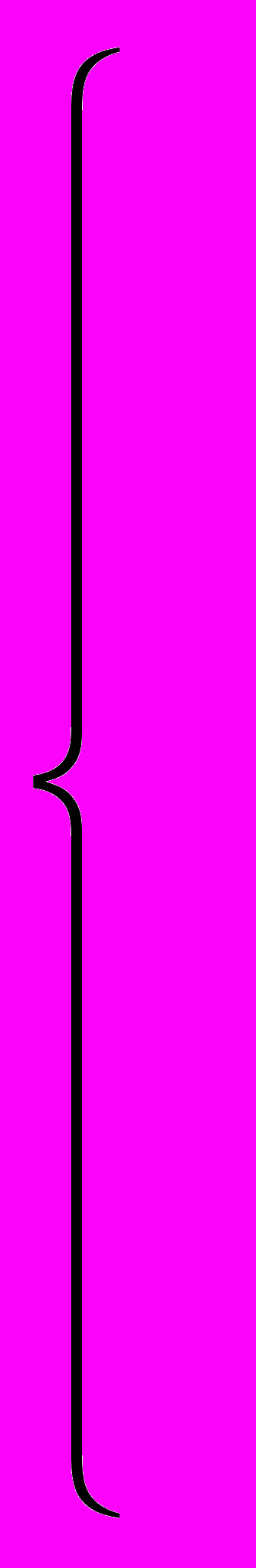 олучим систему уравнений по МУП:
олучим систему уравнений по МУП:0,5φ 1 -0,25φ 2-0,125 φ 3=13,75
-0,25φ 1+ 0,533φ 2-0,083φ 3=18,33
-0,125φ 1-0,083φ 2+ 0,308φ 3=-13,75
Решим систему уравнений методом Крамера.
Найдем определитель главной матрицы.
 =
= 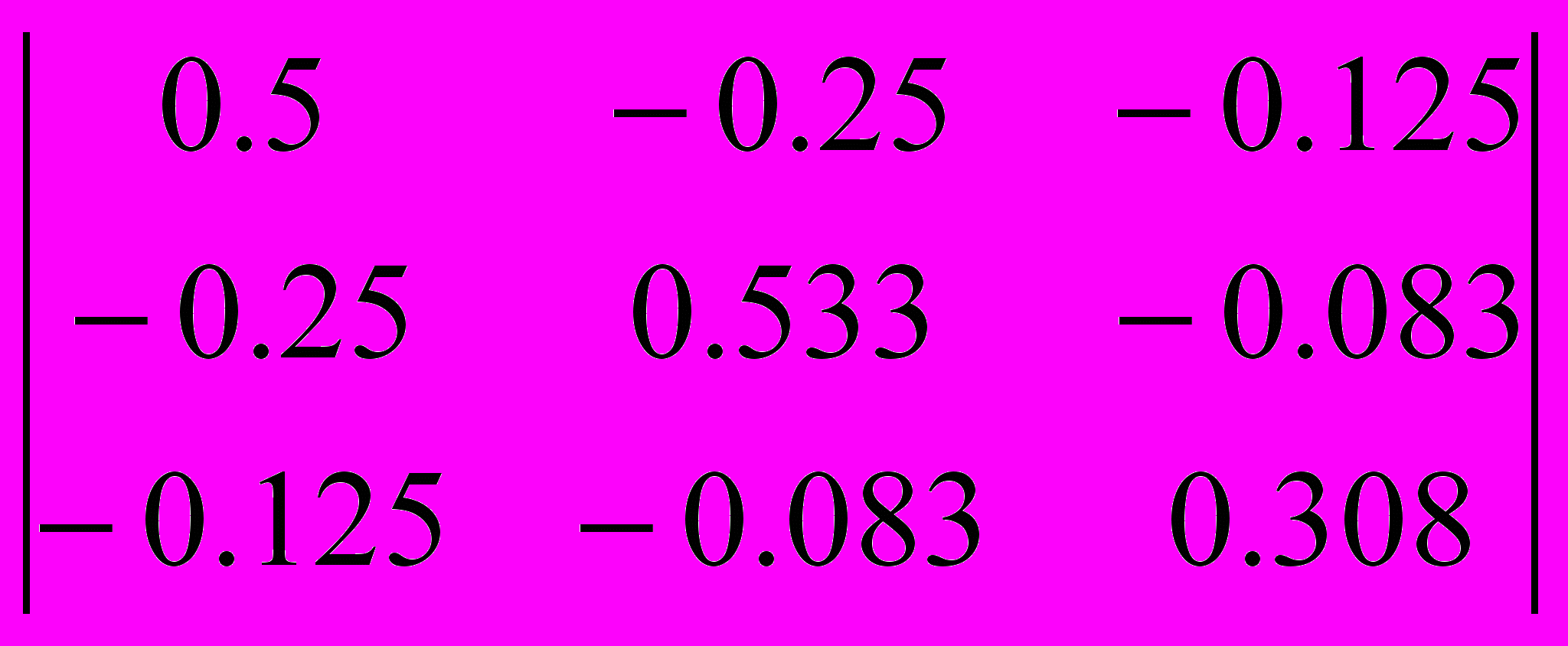 =0,04587
=0,04587Определитель главной матрицы системы уравнений не равен нулю, следовательно, данная система уравнений имеет единственное решение. Найдем его.
Составим определители, заменив в каждом столбце, коэффициенты на коэффициенты стоящие за знаком равенства в системе уравнений.
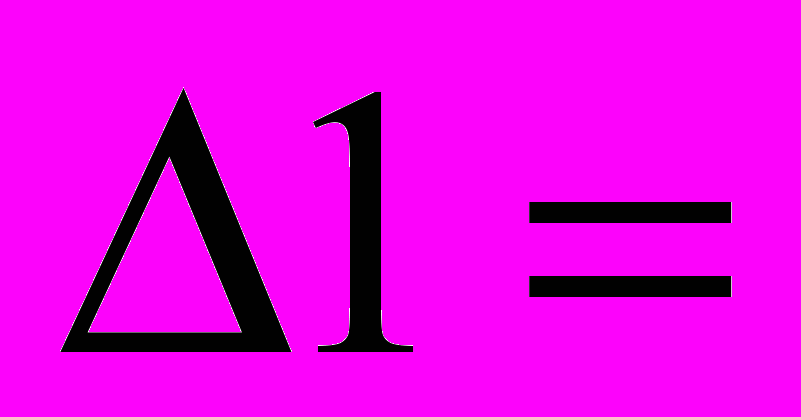
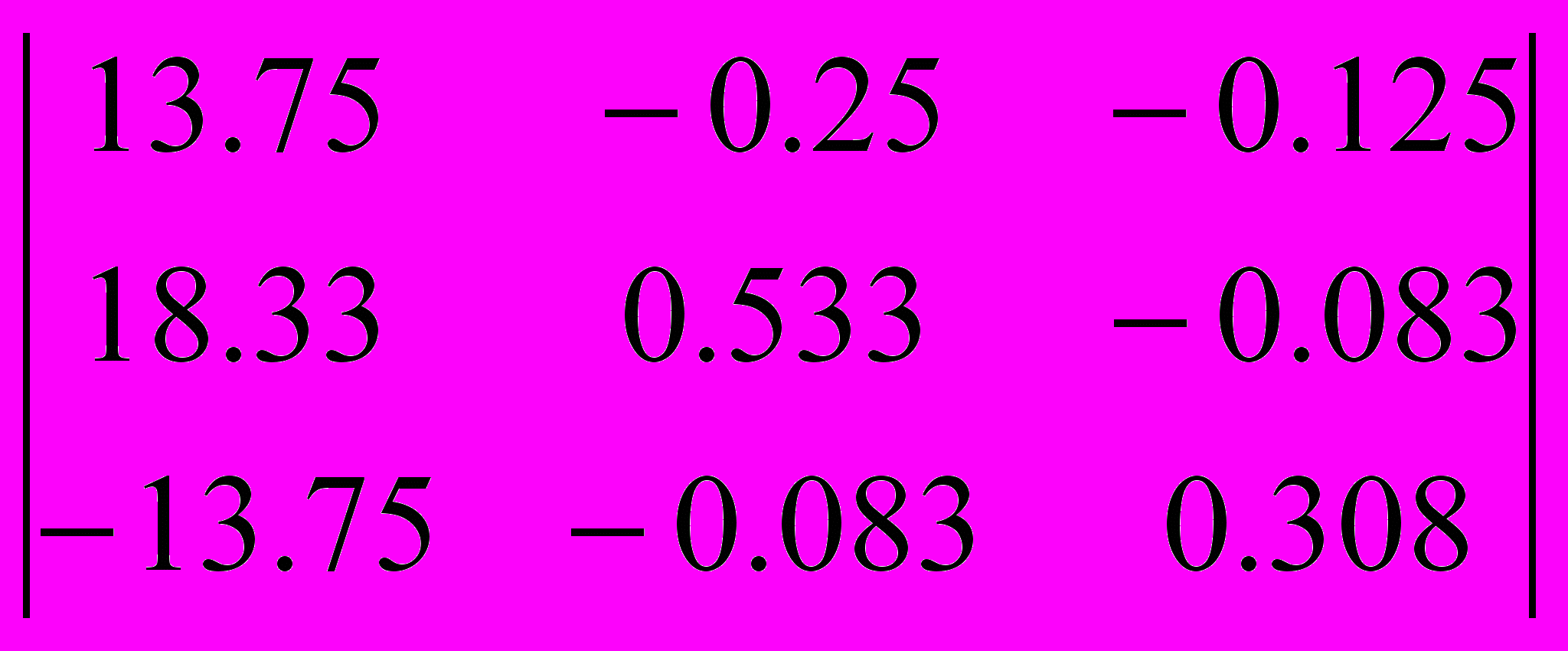 =2,5627
=2,5627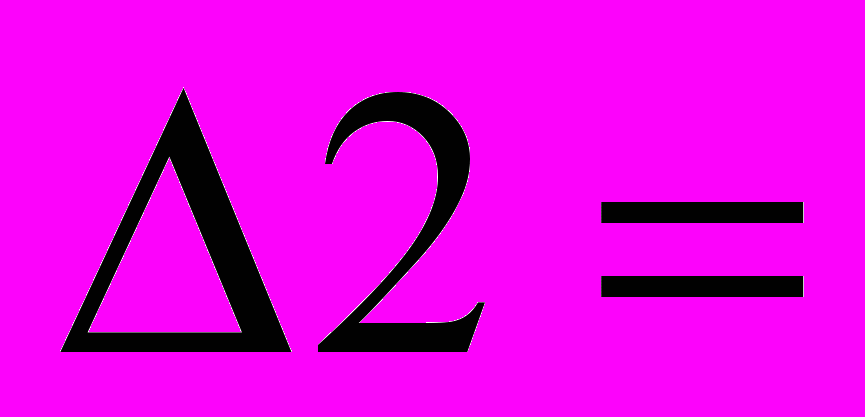
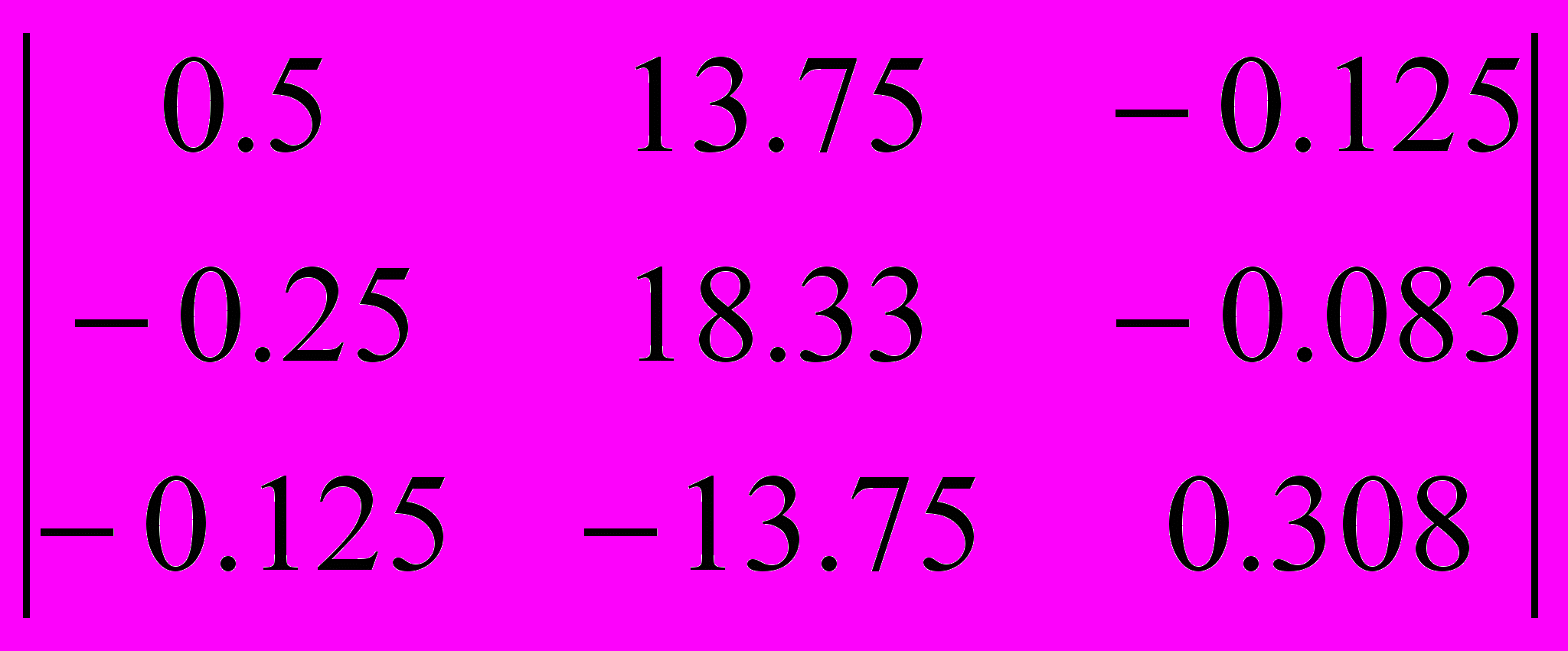 =2,7375
=2,7375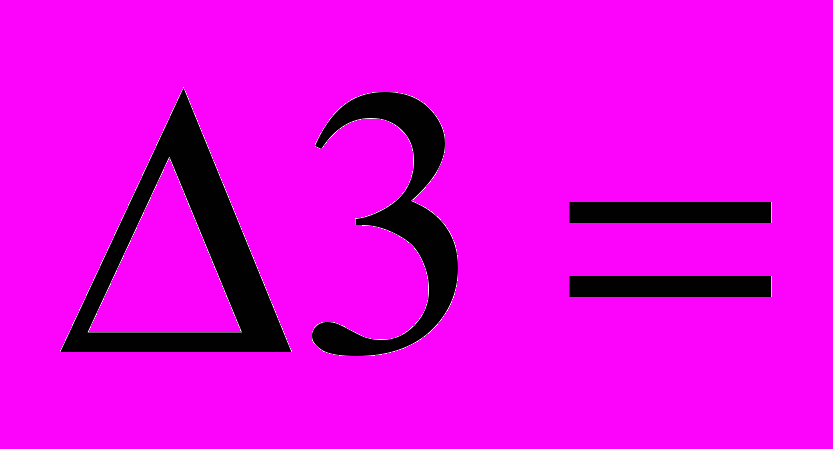
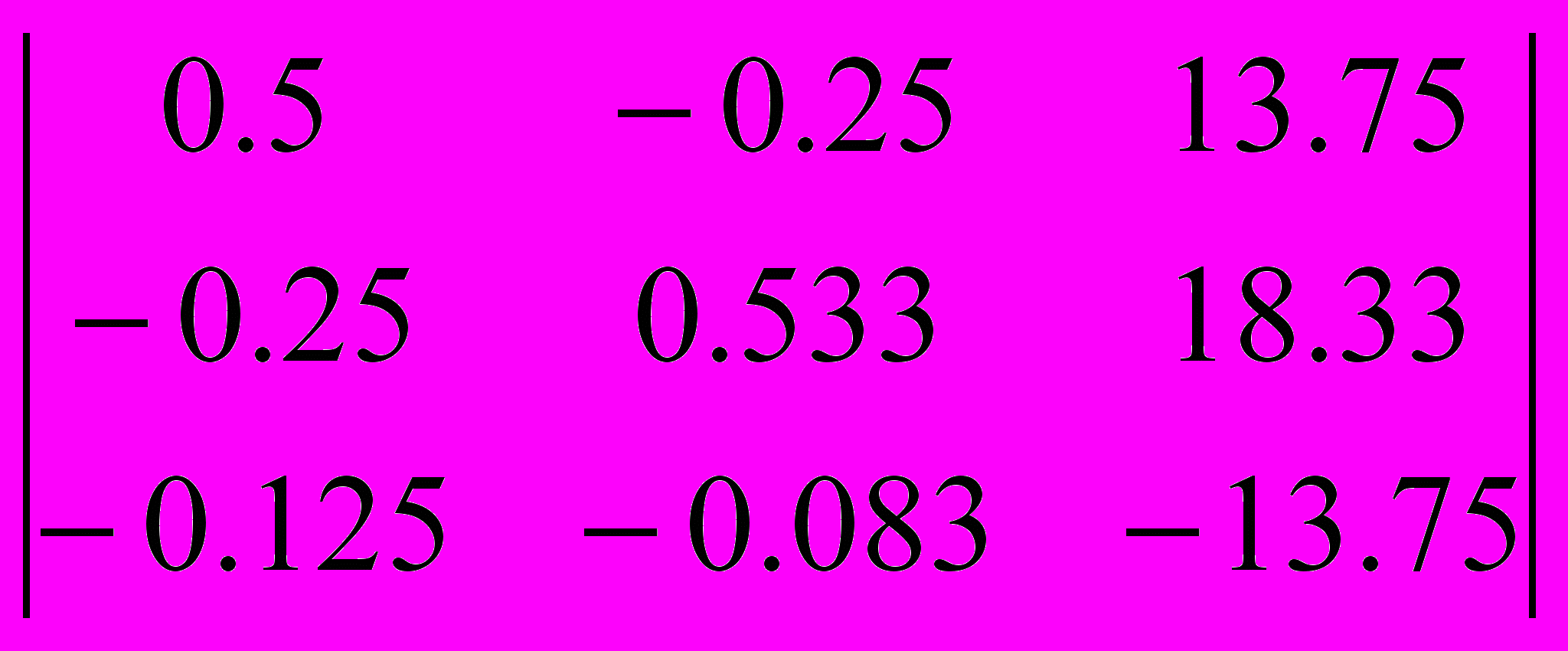 =-0,27
=-0,27Найдем решение системы уравнений:
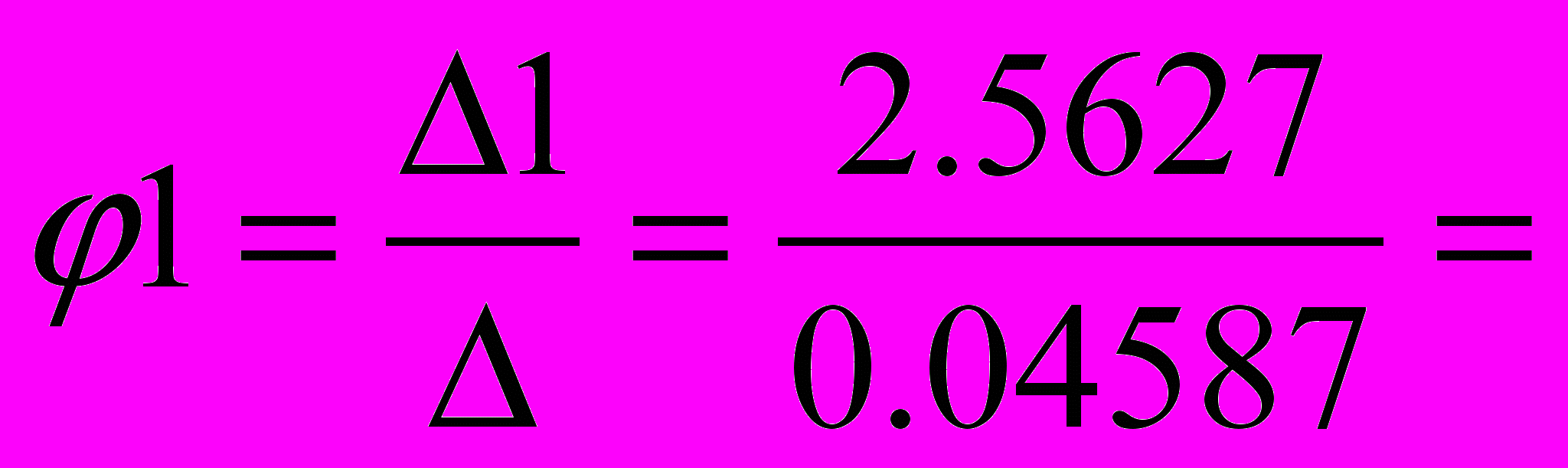 55,87 А
55,87 А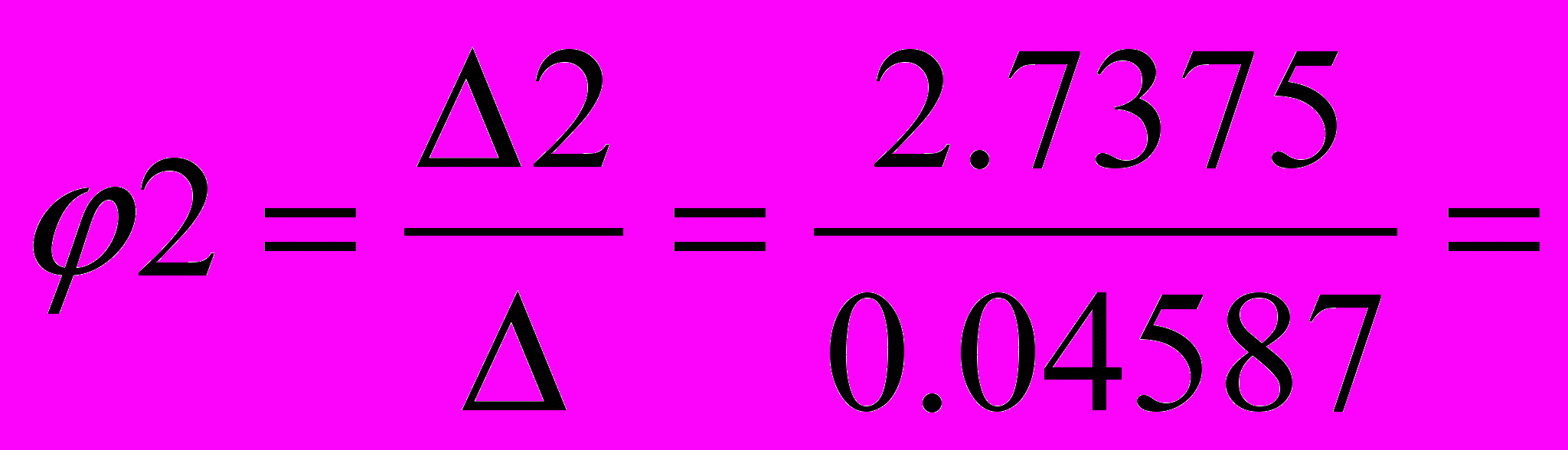 59,68 А
59,68 А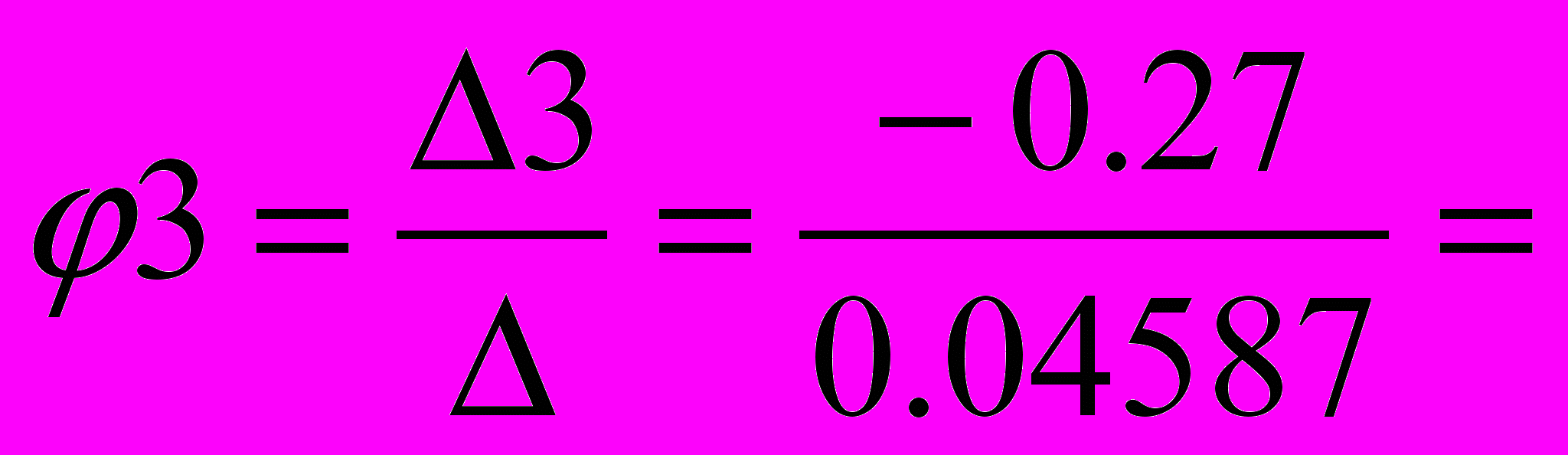 -5,89 А
-5,89 АТоки в ветвях находят, используя закон Ома:
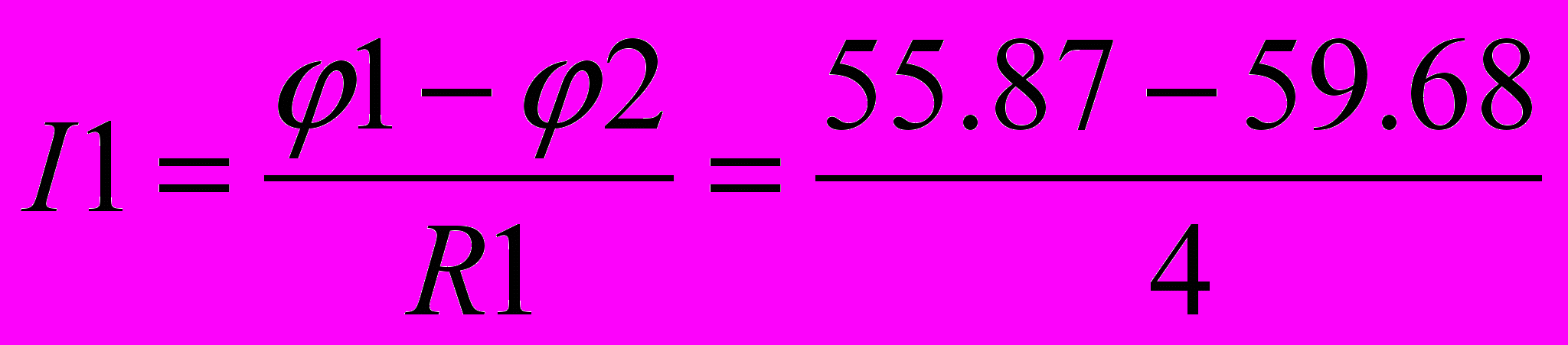 =-0,95 А
=-0,95 А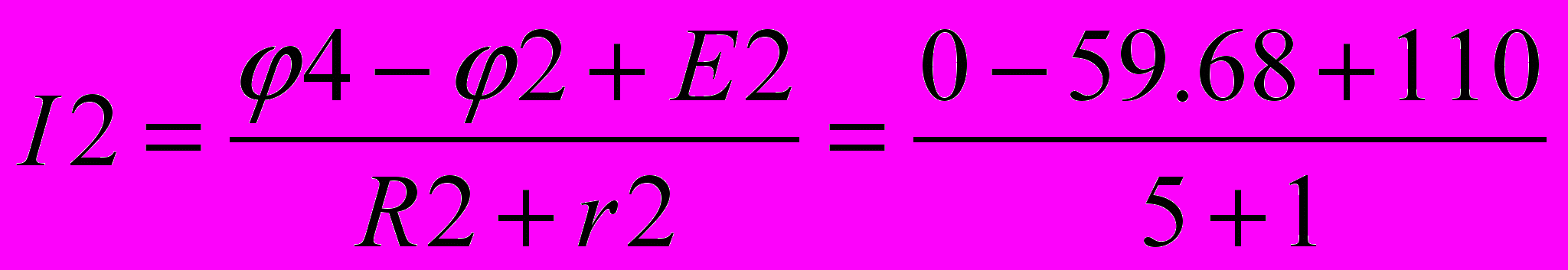 =8,387 А
=8,387 А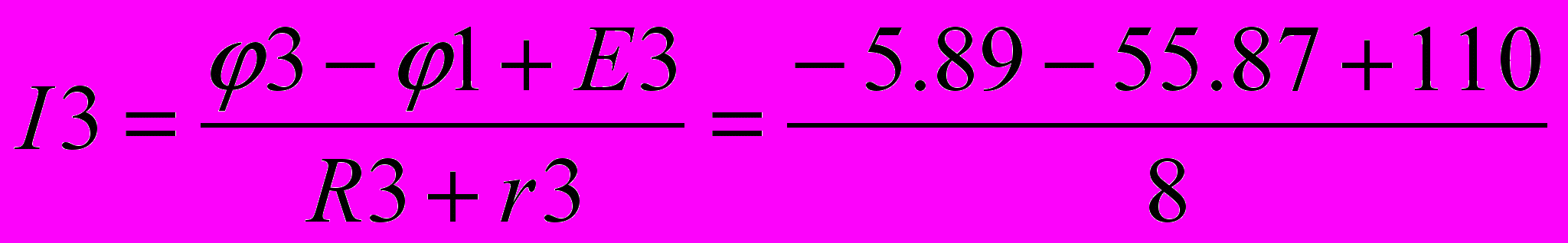 =6,03 А
=6,03 А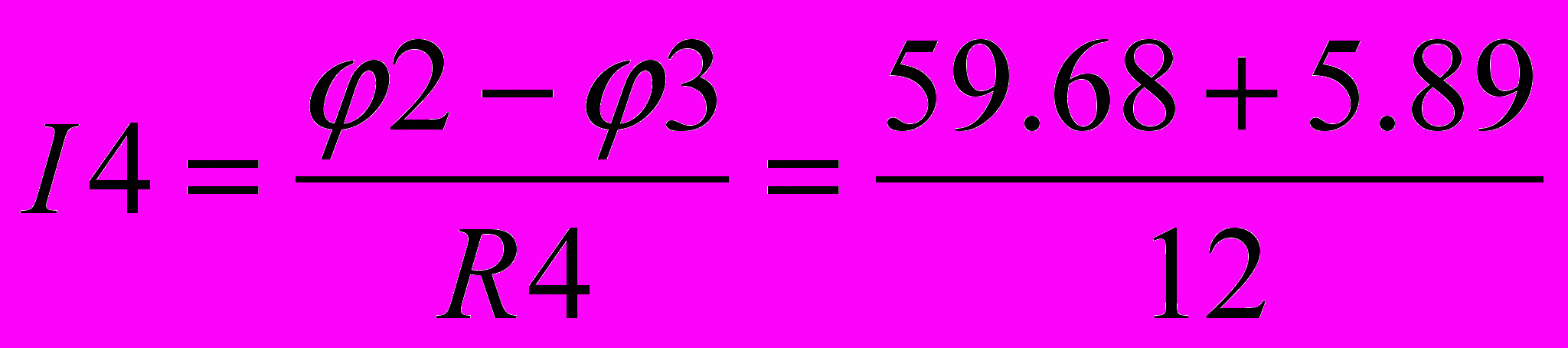 =5,46 А
=5,46 А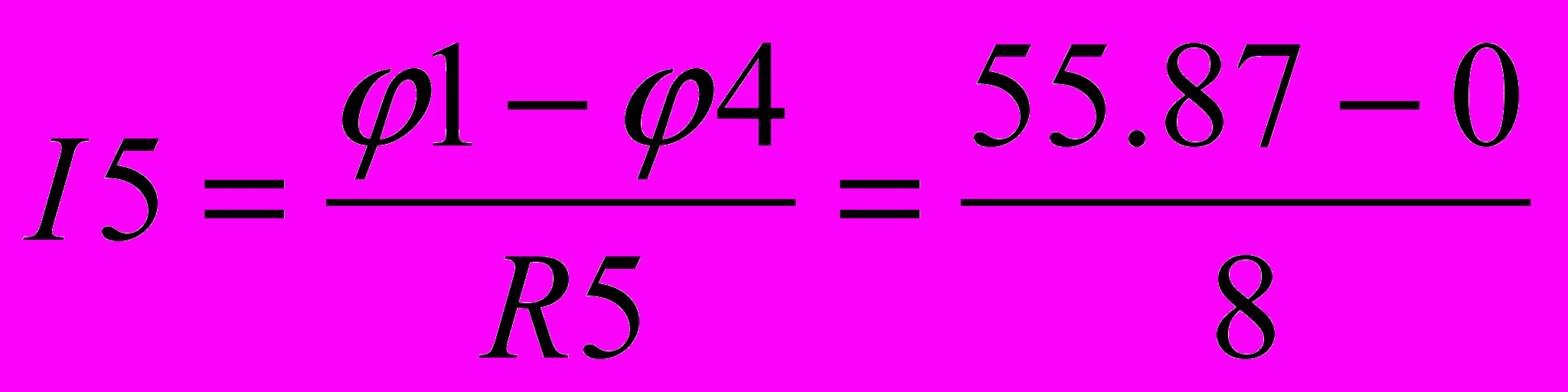 =6,98 А
=6,98 А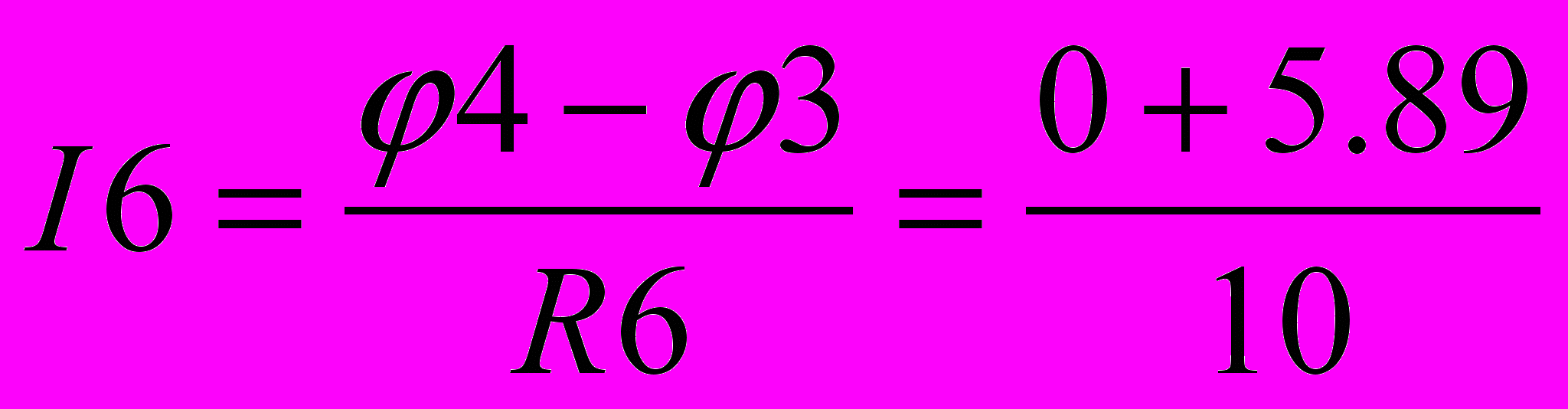 = 0,589 А
= 0,589 АЗнак минус, говорит о том, что действительное направление тока I1 противоположно указанному на схеме.
- Результаты расчета токов, выполненного двумя методами, свести в таблицу и сравнить между собой.
| Метод расчета | I1, A | I2, A | I3, A | I4, A | I5, A | I6, A |
| МУП | | | | | | |
| МКТ | | | | | | |
