Электрический ток в проводниках

Вид материала

Лекция

Подобный материал:

• Самостоятельная работа «Переменный электрический ток» Вариант 1 Когда магнитное поле, 29.04kb.
• Электрический ток в различных средах, 106.22kb.
• Разработка урока физики в 10 классе Тема урока: «Электрический ток в различных средах», 134.4kb.
• А. С. Попов и Г. Маркони шли от одной схемы радиоприемника, используя принцип когерера., 287.2kb.
• Домашнее задание 17 января физика электрический ток. Источники электрического тока., 5.6kb.
• Тест : Как взаимодействуют два параллельных проводника, если электрический ток в них, 730.09kb.
• Если полюсы соединить проводником, то под действием поля свободные заря-женные частицы, 76.01kb.
• Дут выравниваться, при этом заряды на проводниках перераспределяются, а в соединительной, 221.73kb.
• Альтернативный электрический ток “холодное” электричество Эдвина Грея, зарядка, разряда, 264.32kb.
• Тема зачёта, 26.51kb.

ЭЛЕКТРИЧЕСКИЙ ТОК В ПРОВОДНИКАХ


Характеристики электрического тока. Классическая теория электропроводности металлов. Законы Ома и Джоуля-Ленца в дифференциальной форме. Законы постоянного тока в интегральной форме. Характеристики электрической цепи, э.д.с. Соединения сопротивлений и э.д.с. Правила Кирхгофа.

1. Электродинамика – раздел учения об электричестве, в котором рассматриваются явления и процессы, связанные с движением электрических зарядов или заряженных тел.
   
2. Электрический ток – всякое упорядоченной движение электрических зарядов.
   
   1. Электрический ток в проводящих средах под действием электрического поля – ток проводимости.
      
   2. Механическое движение в пространстве макроскопических объектов – конвекционный ток.
      
   3. Направление электрического тока – направление движения положительных зарядов.
      
   4. Условия существования электрического тока в проводниках:
      

• - наличие свободных носителей тока;
  
• - существование в проводящей среде электрического поля, энергия которого расходуется на перемещение зарядов и восполняется от источников электрической энергии.
  

3. Силой электрического тока называется скалярная величина, равная отношению зарядя dq, переносимого сквозь рассматриваемую поверхность за малый промежуток времени dt, к величине этого промежутка
   

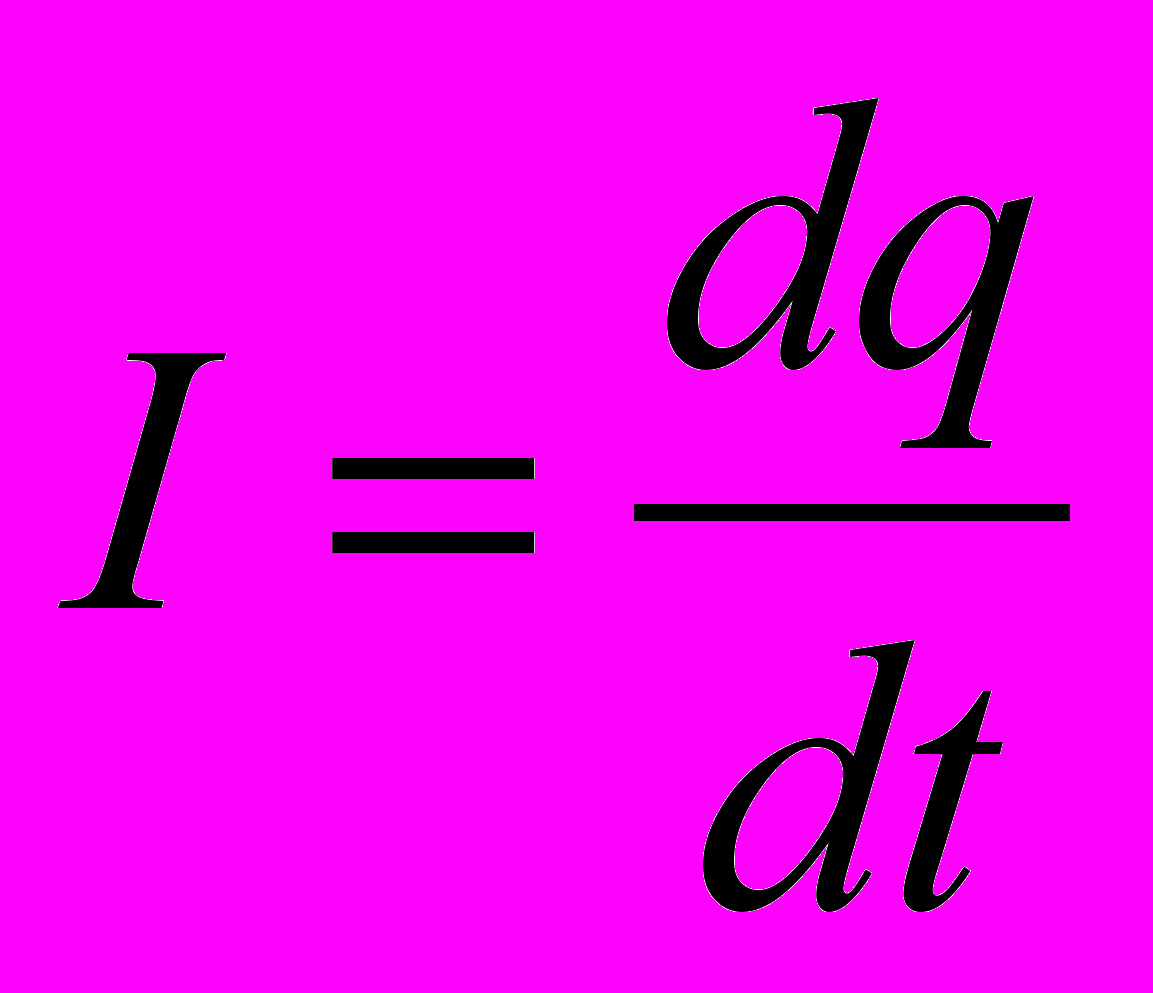
Для постоянного тока

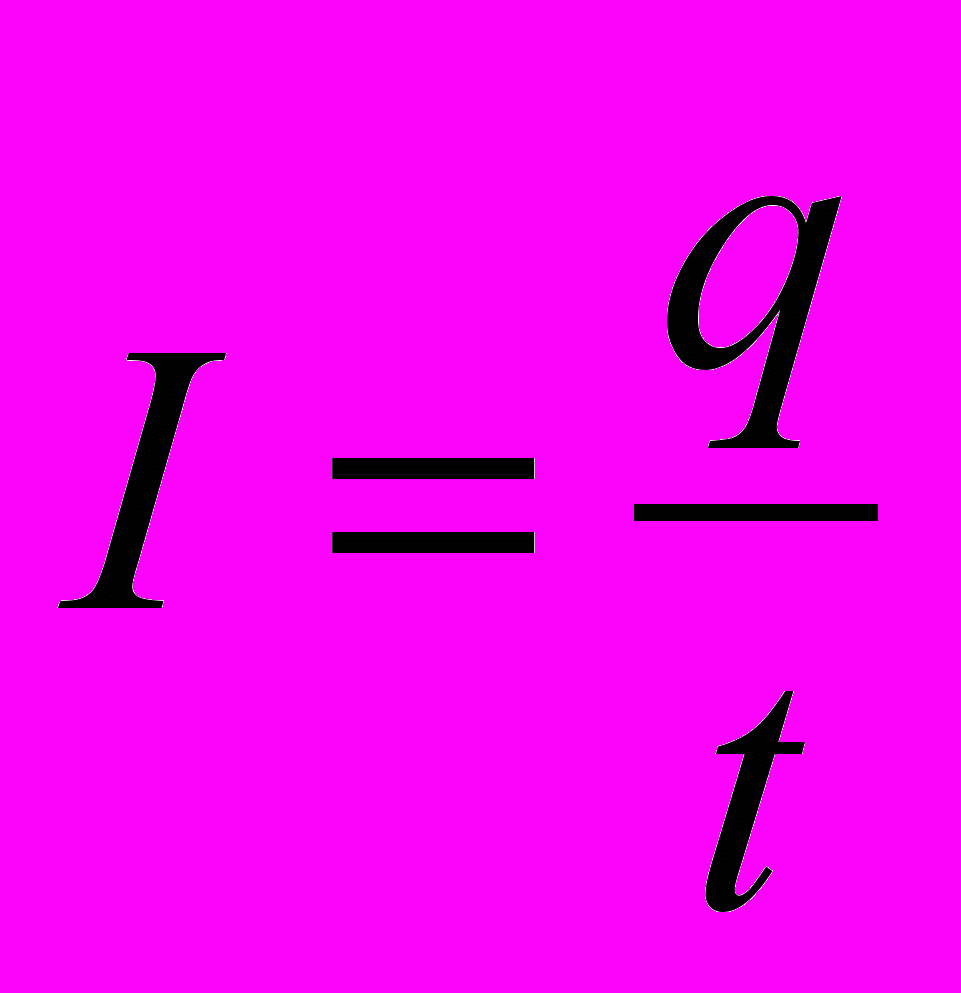
4. Направление электрического тока определяется вектором плотности тока j, который направлен вдоль вектора напряженности электрического поля и численно равен отношению силы тока dI сквозь малый элемент поверхности dS, нормальный к направлению движения заряженных частиц, к величине площади этого элемента
   

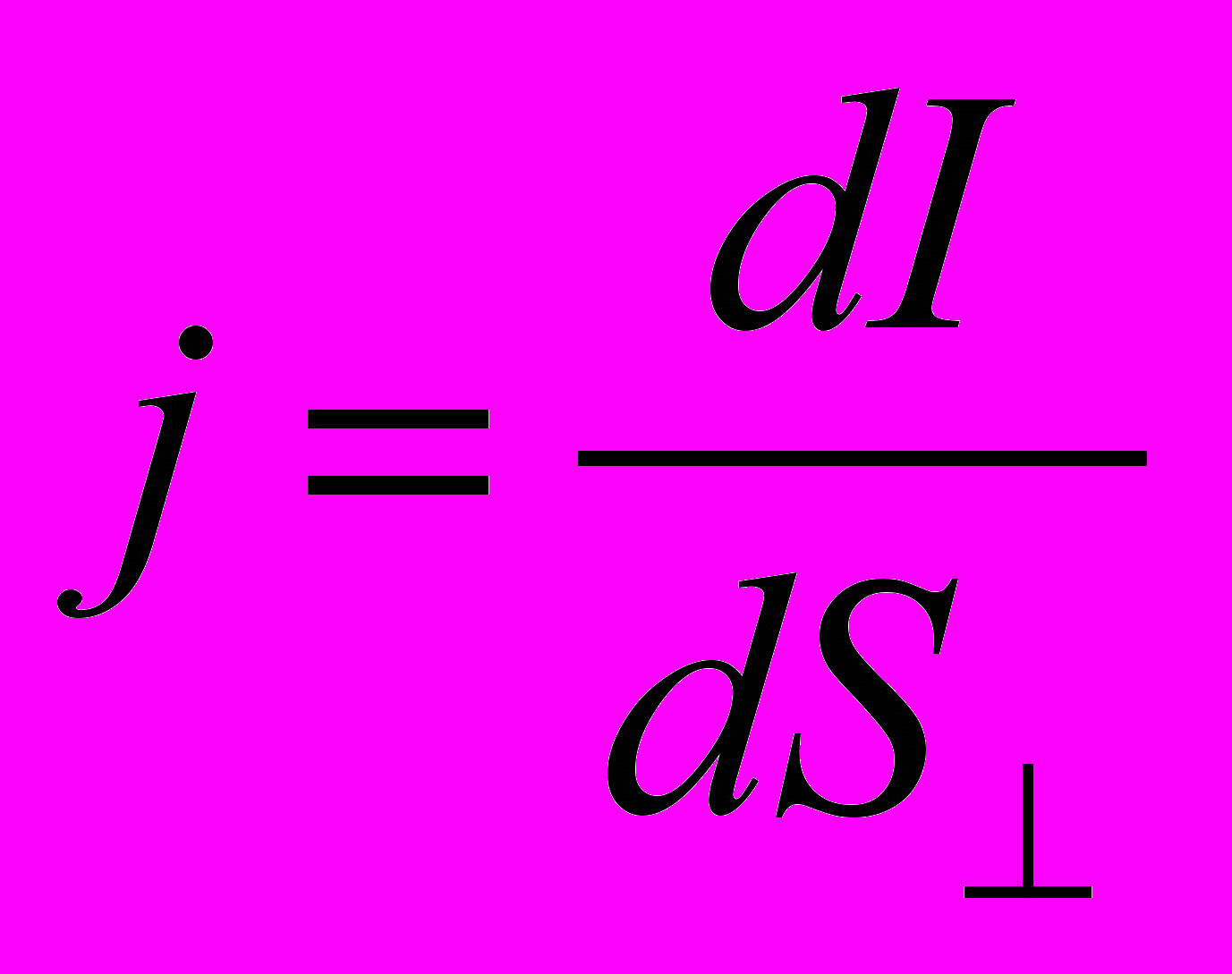
В общем виде вектор плотности тока определяется из соотношения

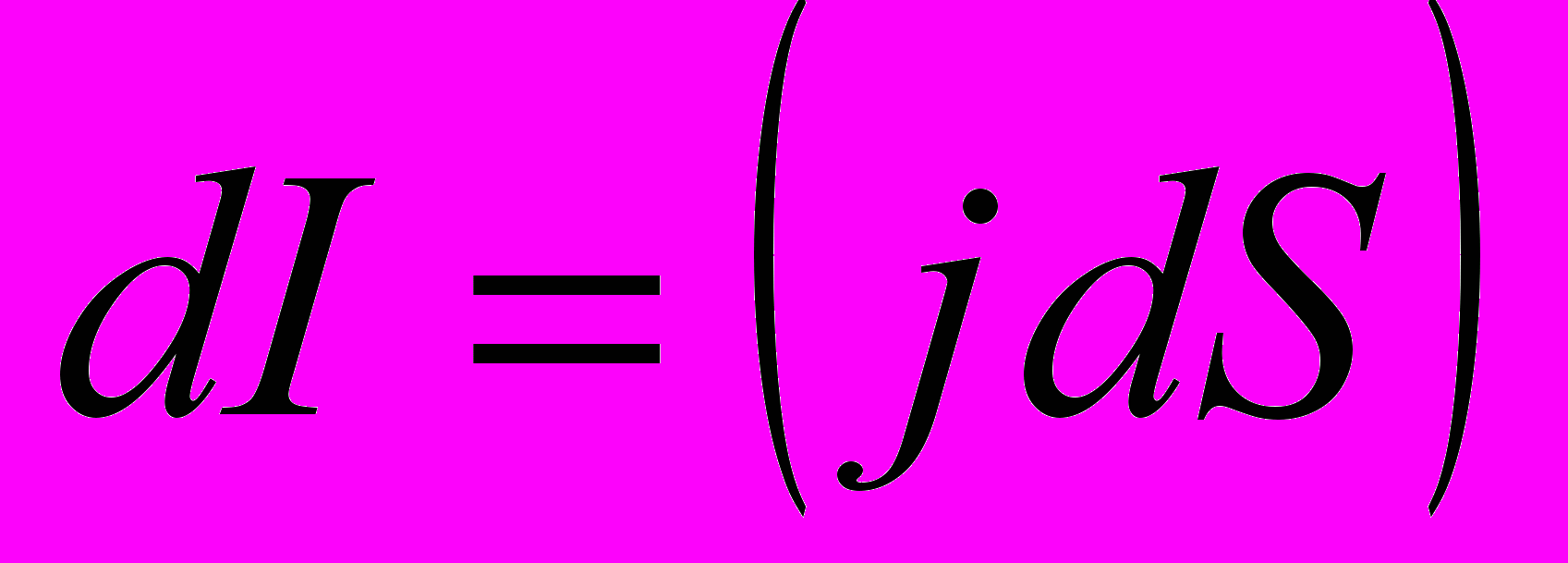
1. Сила тока через произвольную поверхность S определяется
   

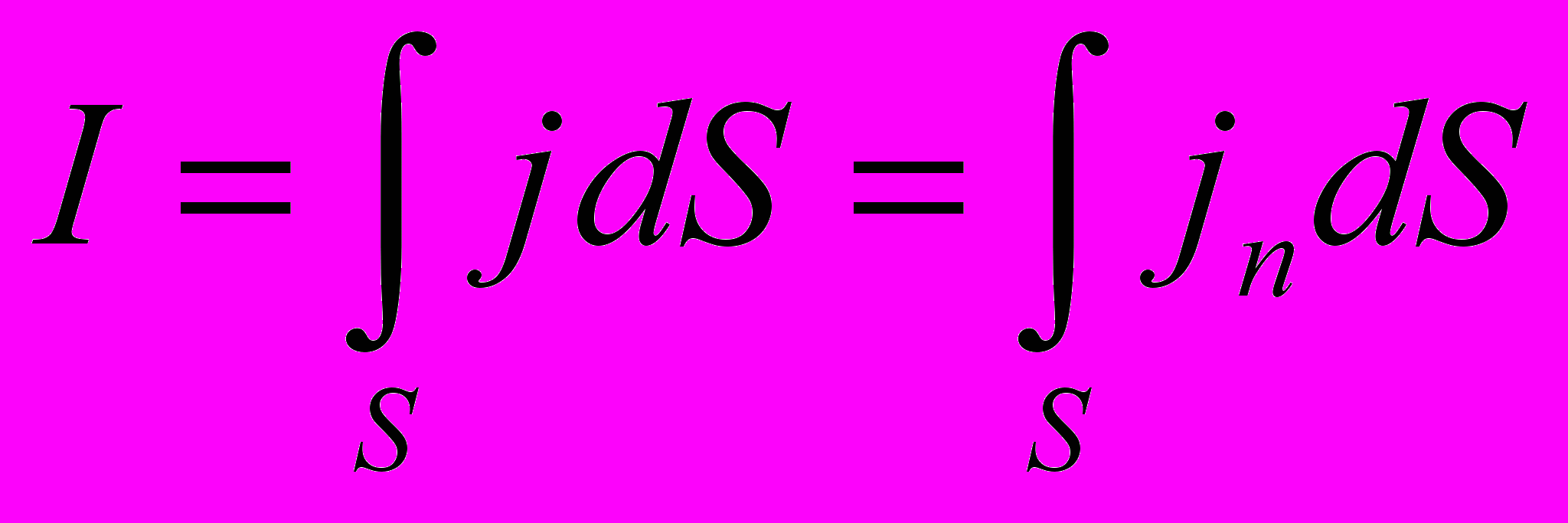
Для постоянного тока

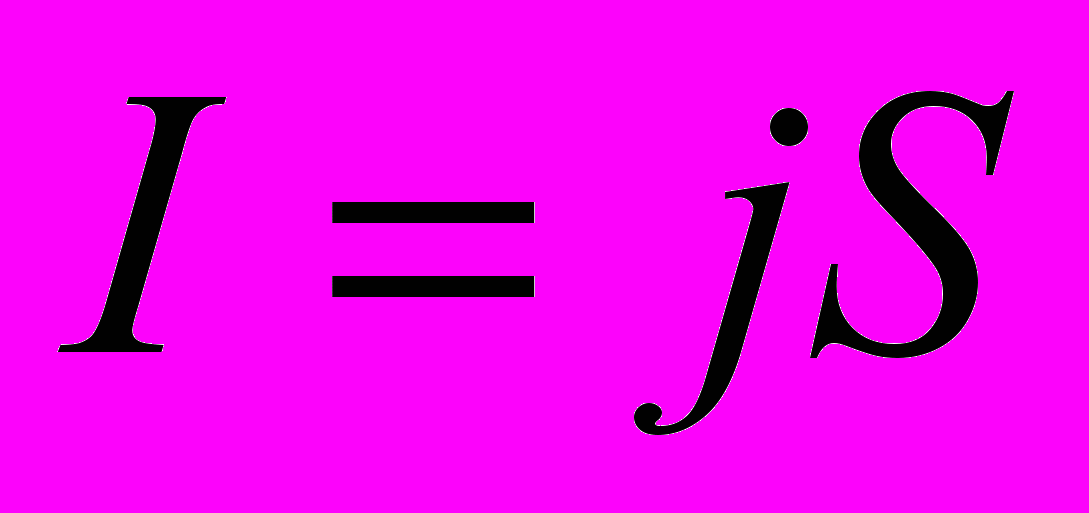
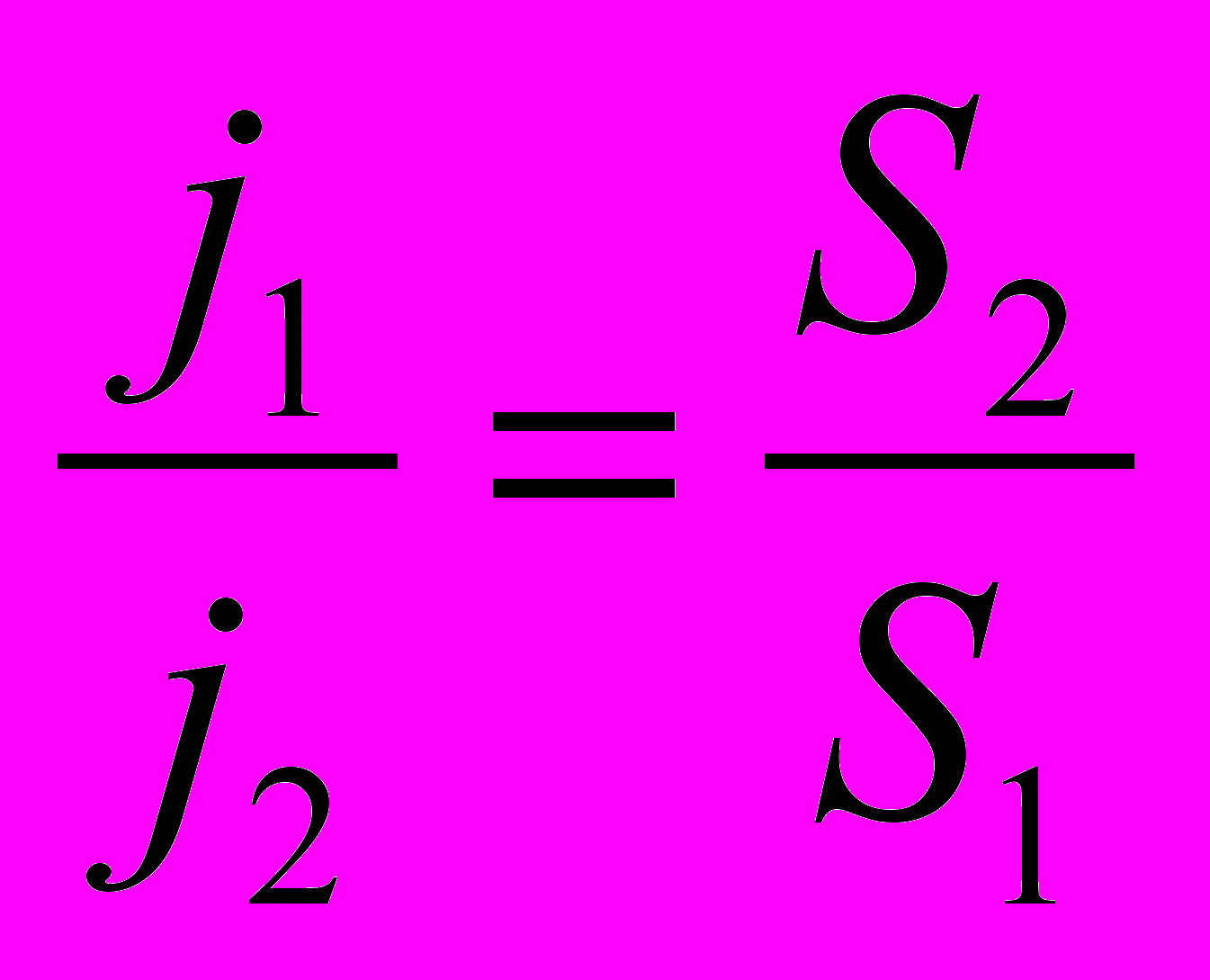
2. Плотность электрического тока пропорциональна напряженности Е электрического поля в проводнике и совпадает с ней по направлению (закон Ома в дифференциальной форме)
   

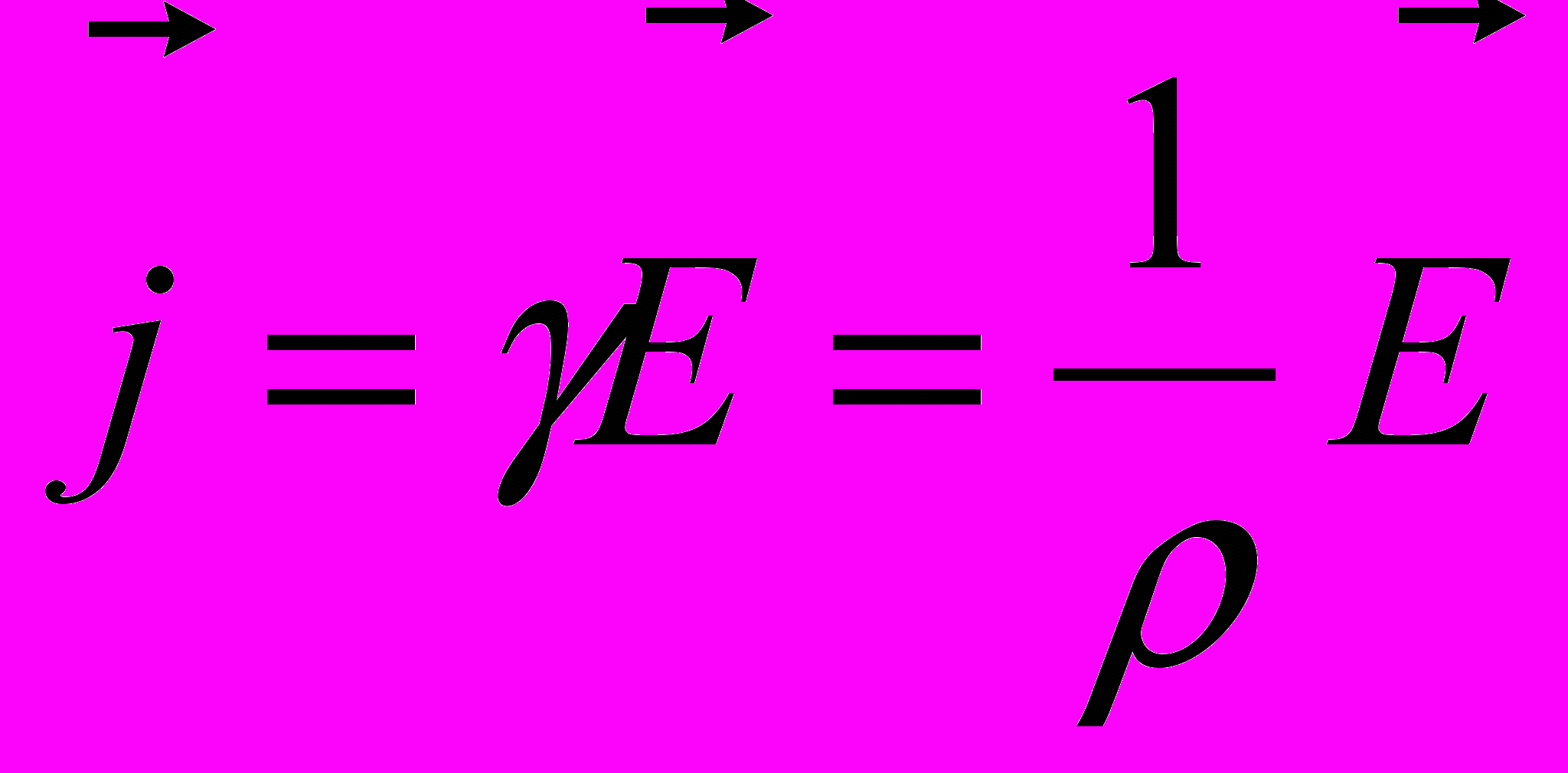
где γ – удельная проводимость среды (удельная электропроводность); ρ – удельное эектрическое сопротивление среды.

3. Закон Ома основан на двух предположениях:
   

а) концентрация электронов проводимости не зависит от напряженности электрического поля в проводнике;

б) средняя скорость упорядоченного движения электронов во много раз меньше средней скорости их теплового движения



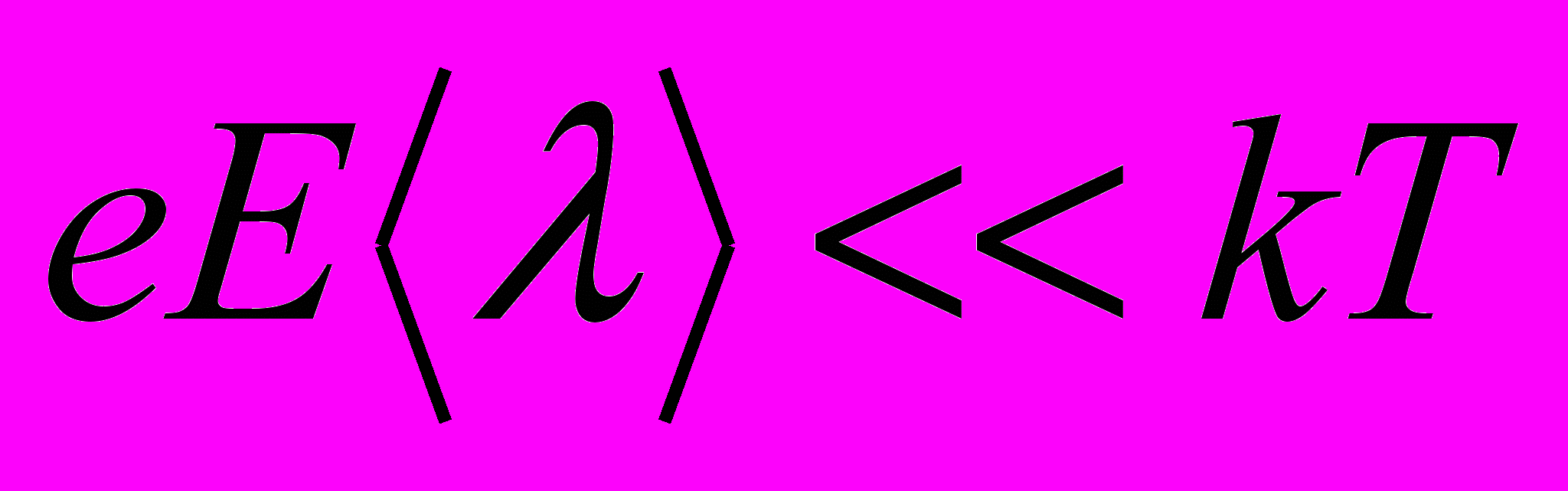
где 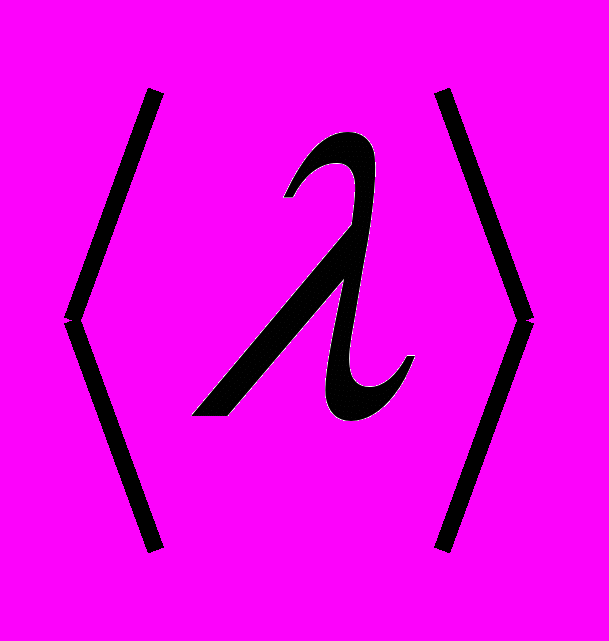– средняя длина свободного пробега электронов; е – заряд электрона.

5. Электропроводность металлов обеспечивается большим количеством свободных носителей заряда – электронов проводимости – коллективизированных электронов.
   
   1. В классической теории Друде-Лоренца электроны проводимости рассматриваются как электронный газ, обладающий свойствами идеального газа.
      
   2. Концентрация электронов проводимости пропорциональна концентрации атомов
      

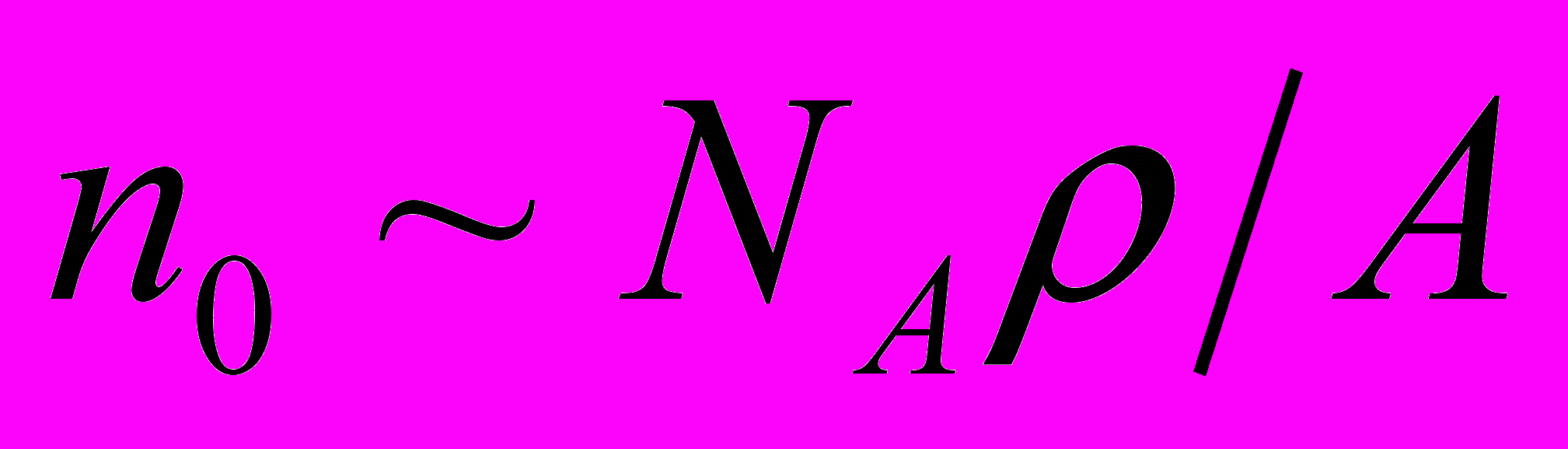(10²⁸ ÷ 10²⁹ м³)

где N_A – постоянная Авогадро, А – атомная масса металла, ρ – его плотность.

3. Средняя кинетическая энергия теплового (хаотического) движения электронов
   

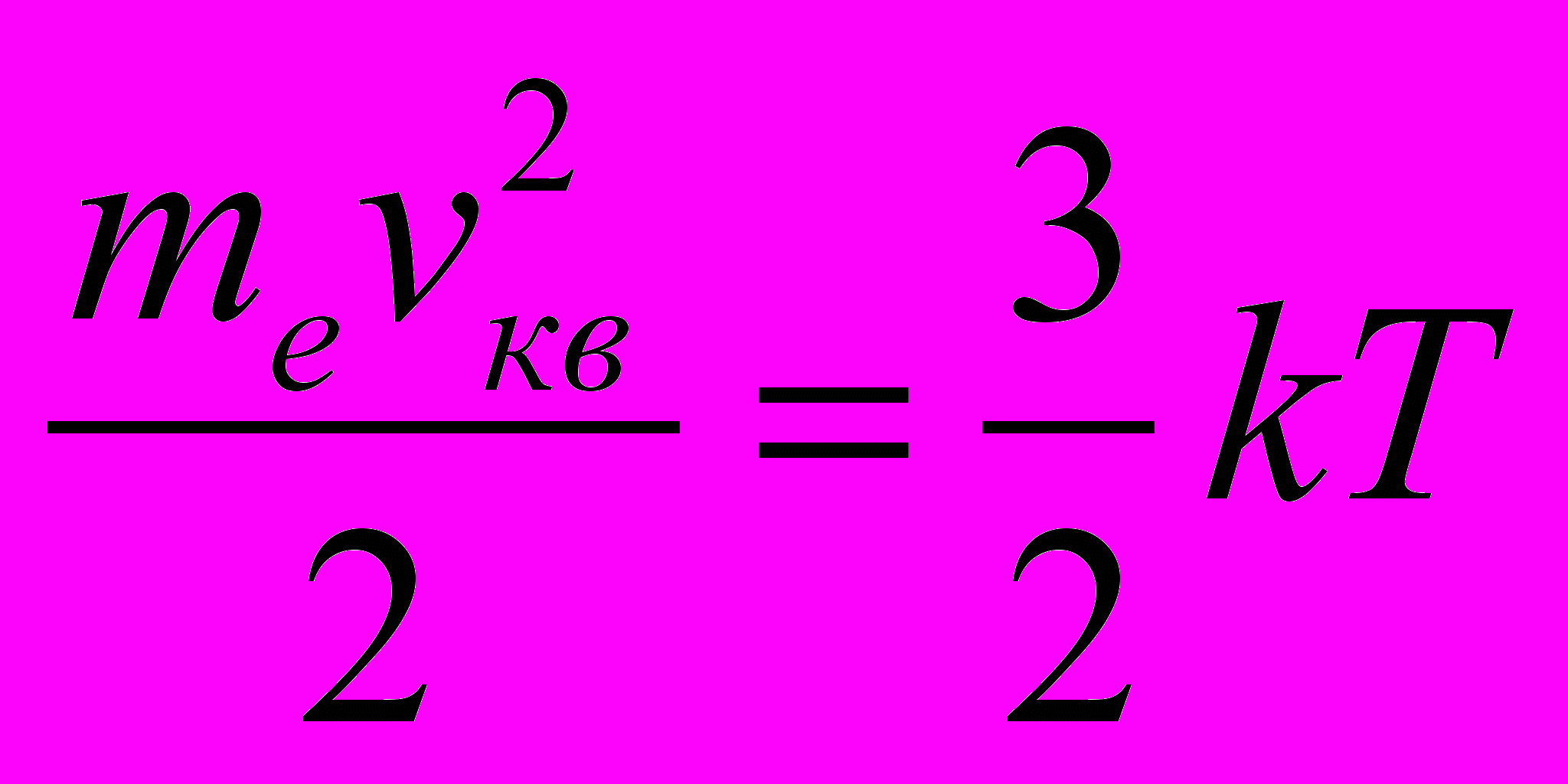v_кв ~ 10⁵ м/с

4. Электрическое поле вызывает упорядоченное движение (дрейф) электронов. Плотность тока определяется
   

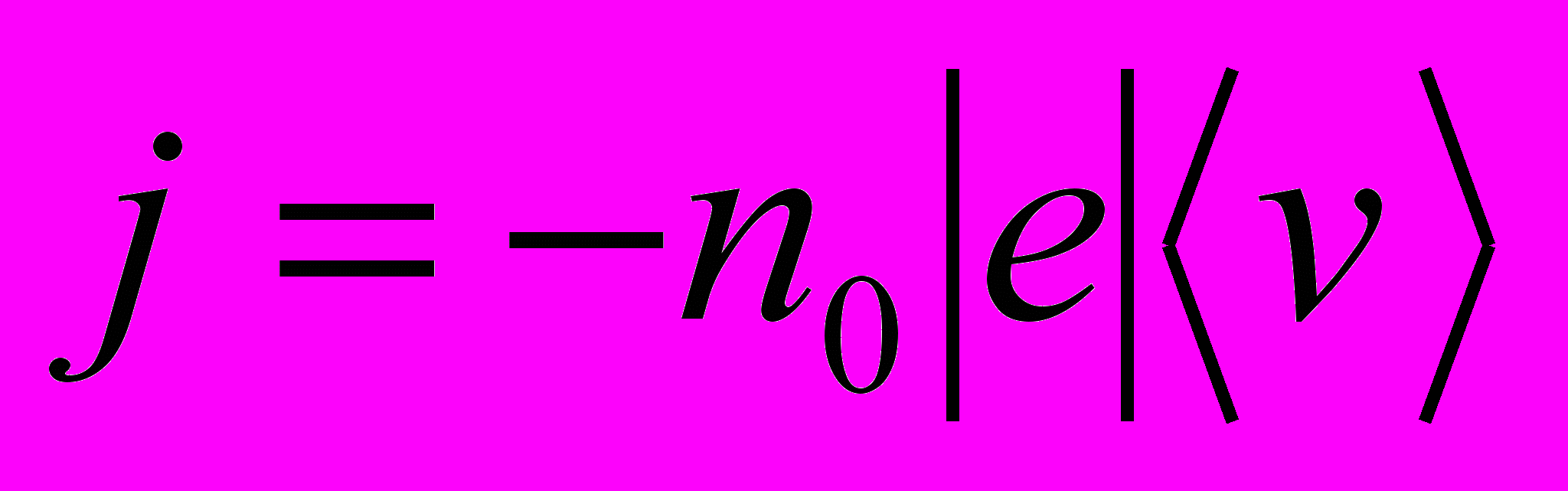
где 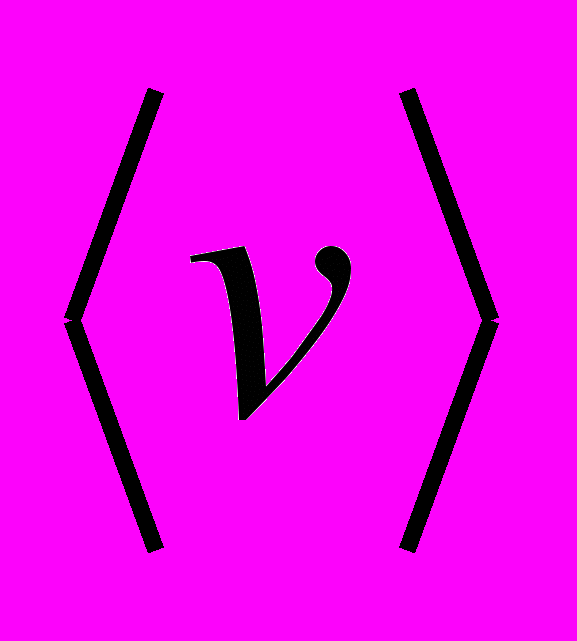– средняя скорость дрейфа электронов (< 10^-4 м/с)

5. Электрический ток в цепи устанавливается за время
   

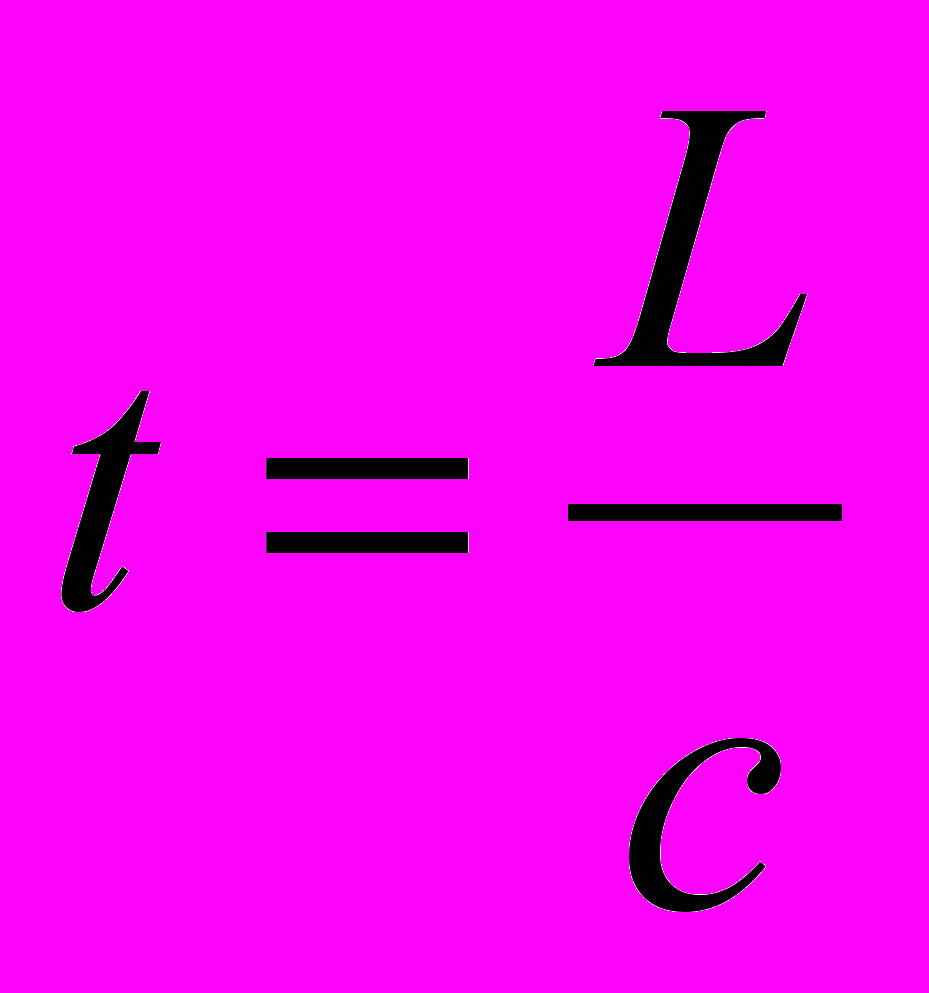
где L – длина цепи, с – скорость света.

6. В соответствии с классической теорией получается
   

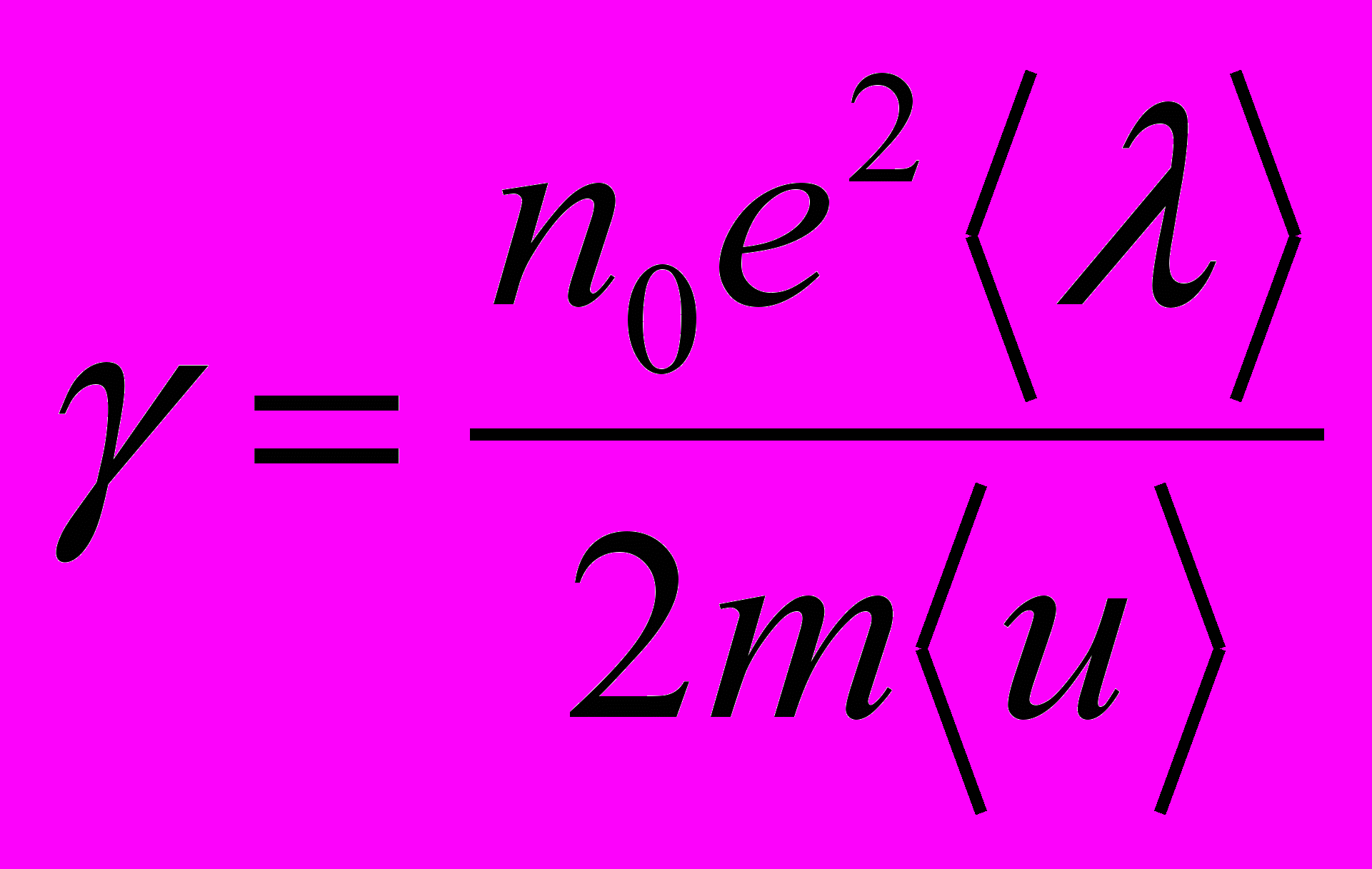и

где m – масса электрона; u – средняя скорость теплового движения электронов.

6. На длине свободного пробега электрон под действием электрического поля приобретае скорость v_max. При соударении с ионом электрон теряет эту энергию, которая переходит во внутреннюю энергию проводника (проводник нагревается).
   
   1. Величина, численно равная энергии, выделяющейся в единице объема проводника за единицу времени, называется объемной плотностью тепловой мощности электрического тока.
      
   2. Объемная плотность тепловой мощности электрического тока равна скалярному произведению векторов плотности тока и напряженности электрического поля (закон Джоуля-Ленца)
      

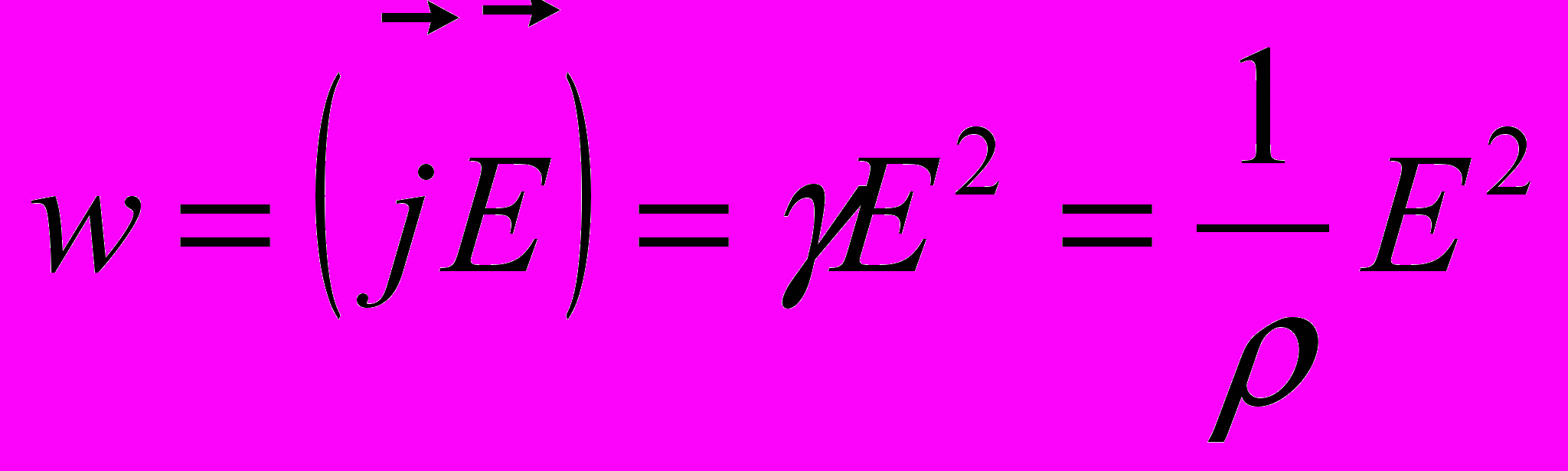
• объемная плотность тепловой мощности электрического тока не зависит от характера соударений электрона;
  
• из законов сохранения энергии и импульса следует, что при столкновении иону передается только малая часть энергии электрона
  

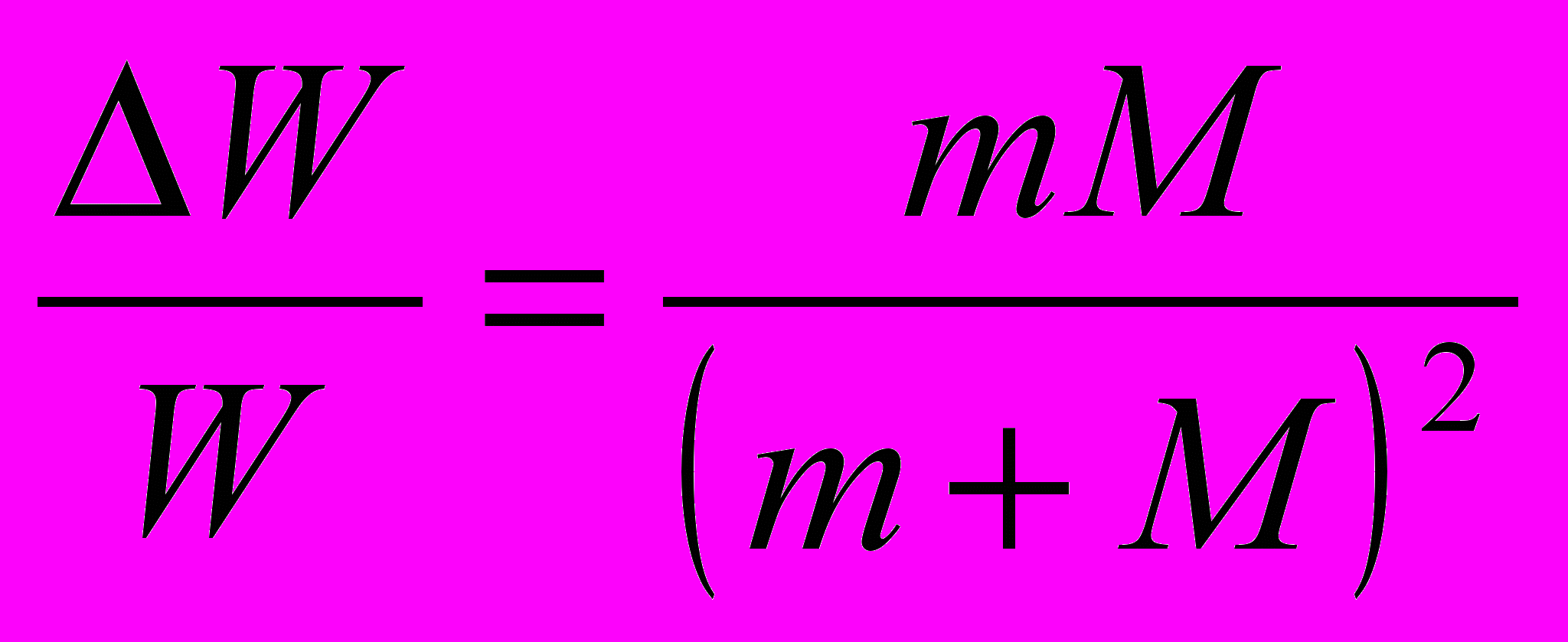- при неупругом столкновении;

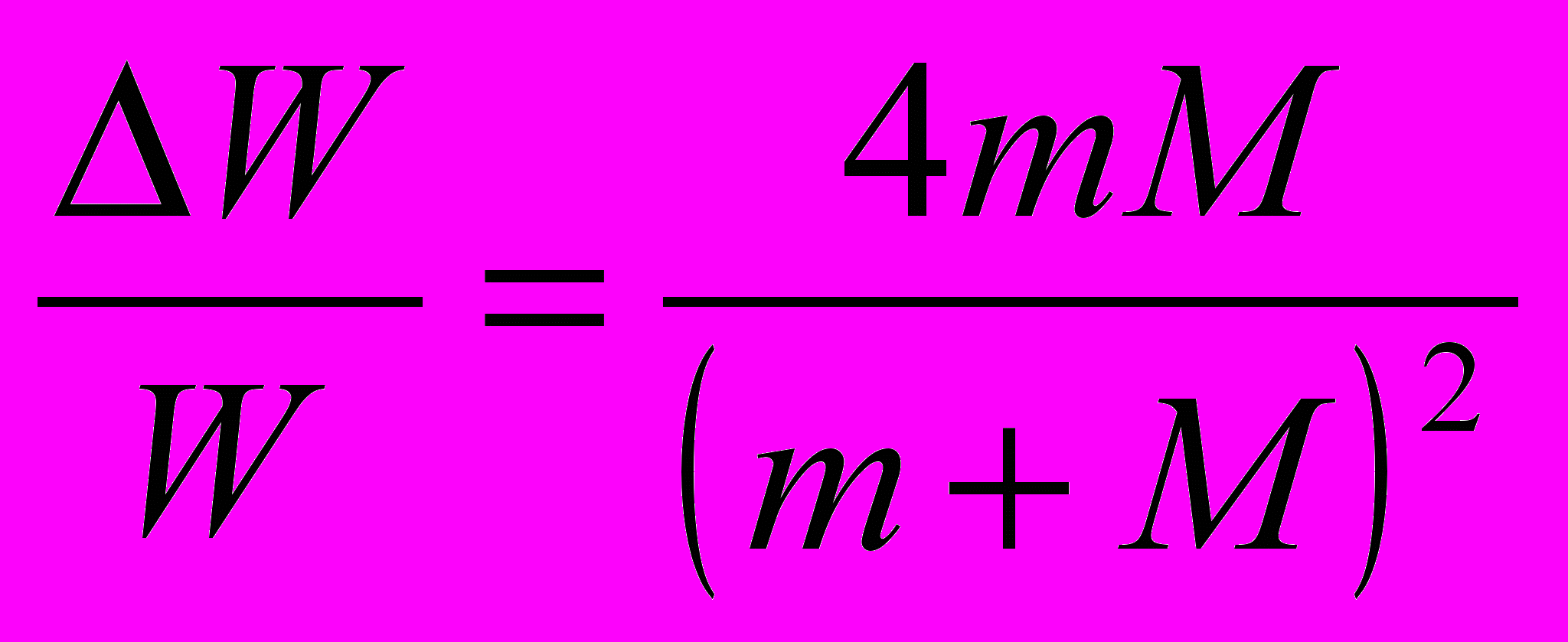- при упругом столкновении.

7. Для всех металлов отношение коэффициента теплопроводности λ к удельной электрической проводимости γ прямо пропорционально температуре Т (закон Видемана-Франца)
   

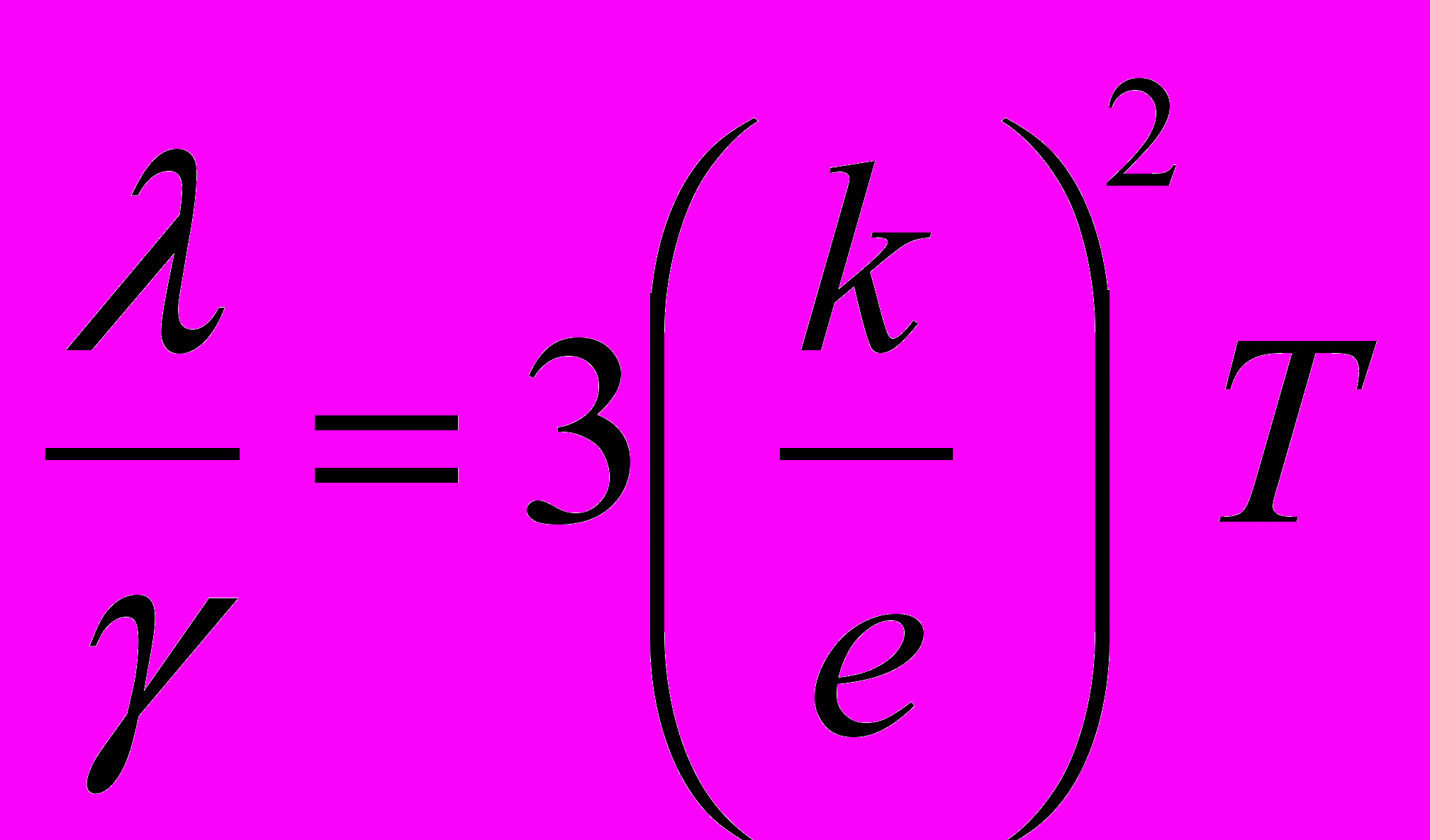
8. Недостатки классической теории электропроводности металлов:
   
   1. Невозможно объяснить экспериментально наблюдаемую линейную зависимость удельного электросопротивления от температуры.
      
   2. Неправильное значение молярной теплоемкости металлов, которавя должна складываться из теплоемкости кристаллической решетки (3R) и теплоемкости электронного газа (3R/2). Однако в соответствии с законом Дюлонга-Пти молярная теплоемкость металлов мало отличается от 3R.
      
   3. Экспериментальные значения удельного электросопротивления и теоретические значения средней скорости движения электронов приводят к значению длины свободного пробега, на два порядка превышающего период кристаллической решетки металла.
      
9. Силы кулоновского взаимодействия вызывают такое перераспределение зарядов в проводнике, при котором потенциалы во всех точках проводника выравниваются и напряженность поля внутри проводника становится равной нулю.
   
   1. Для поддержания в цепи постоянного тока нужно, чтобы на носители тока действовали не только кулоновские силы, но и неэлектростатические силы, поддерживающие заданное значение напряженности электрического поля в проводнике. Такие силы называются сторонними силами.
      
   2. Сторонние силы действуют внутри источников электрической энергии на носители тока, которые движутся против сил электростатического поля.
      
10. Если проводник содержит источник электрической энергии, то в произвольной точке проводника существует электростатическое поле кулоновских сил с напряженностью Е_кул и поле сторонних сил с напряженностью Е_стор=F_стор/q, а напряженность результирующего поля
    

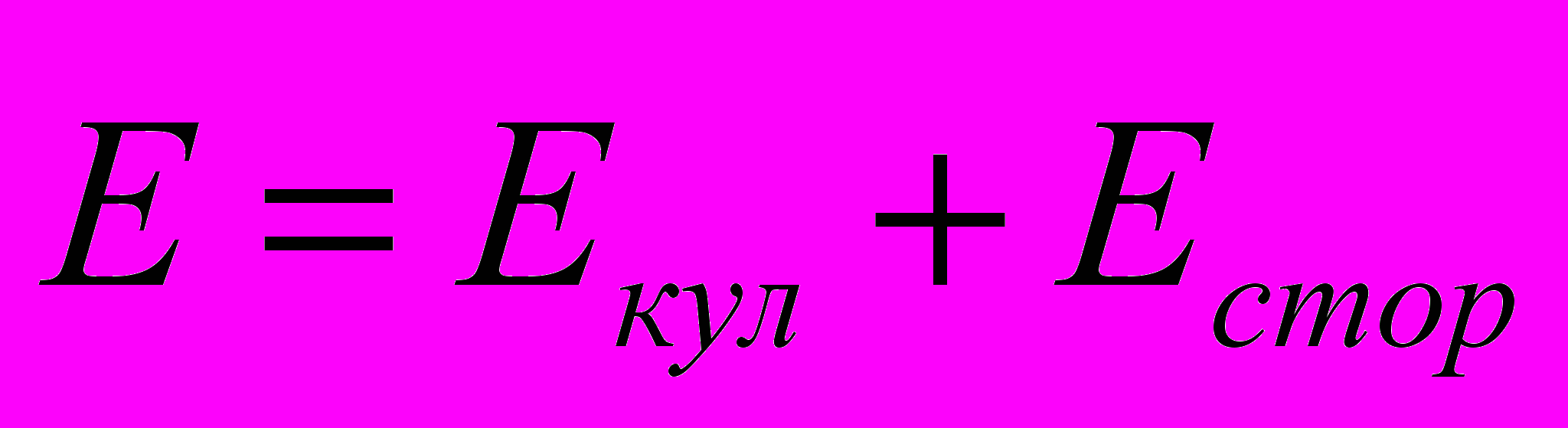
1. По закону Ома плотность тока
   

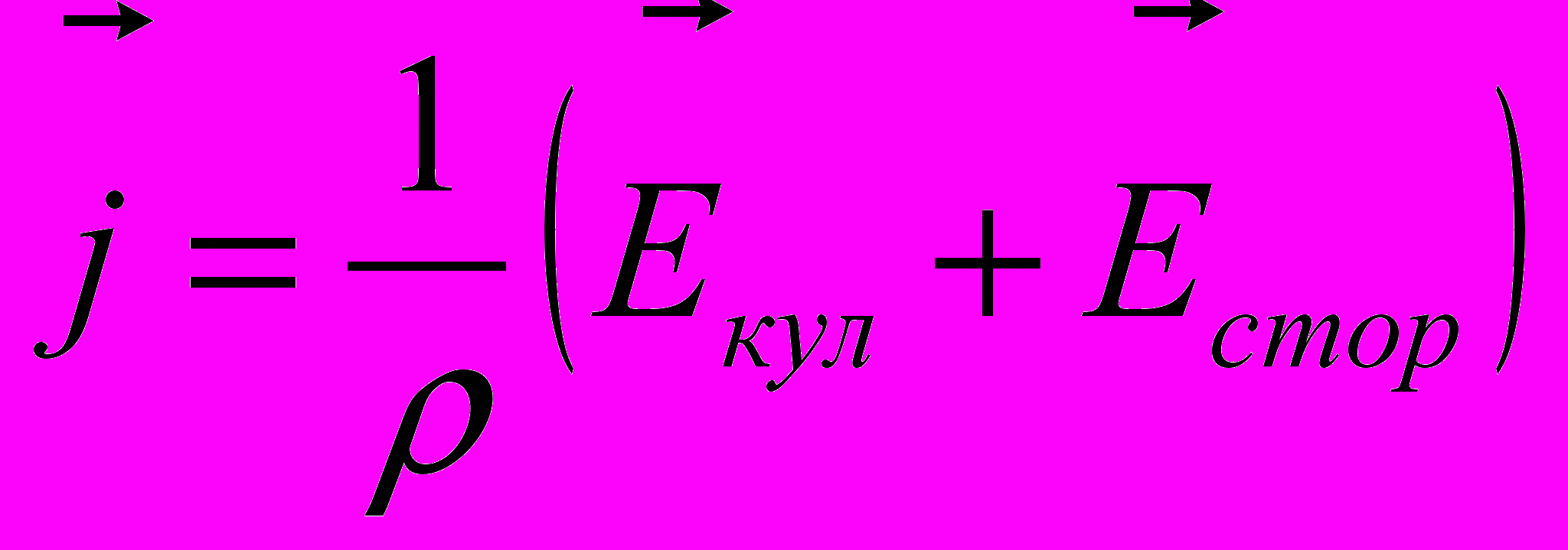
2. Домножим обе части на ρ и на длину dl малого участка цепи. Для участка цепи между точками 1 и 2 (с учетом I=jS)
   

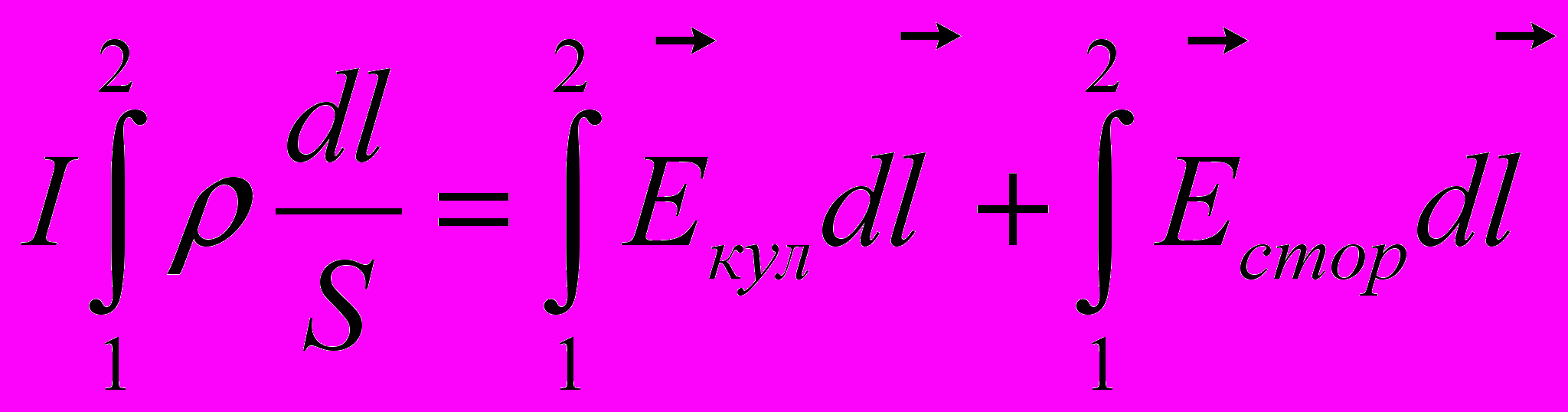
3. Интеграл 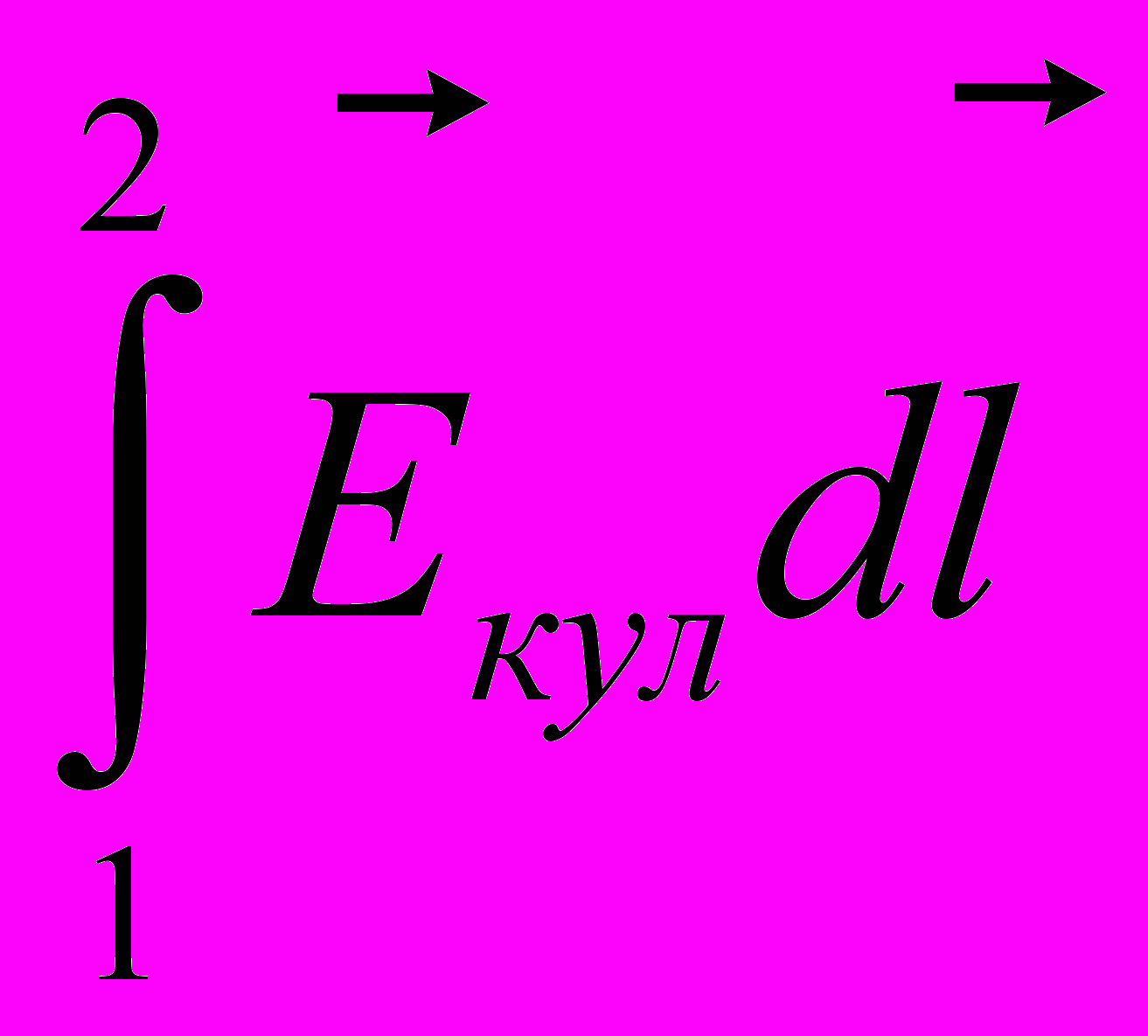численно равен работе, которую совершают кулоновские силы по перемещению единичного положительного заряда из точки 1 в точку 2
   

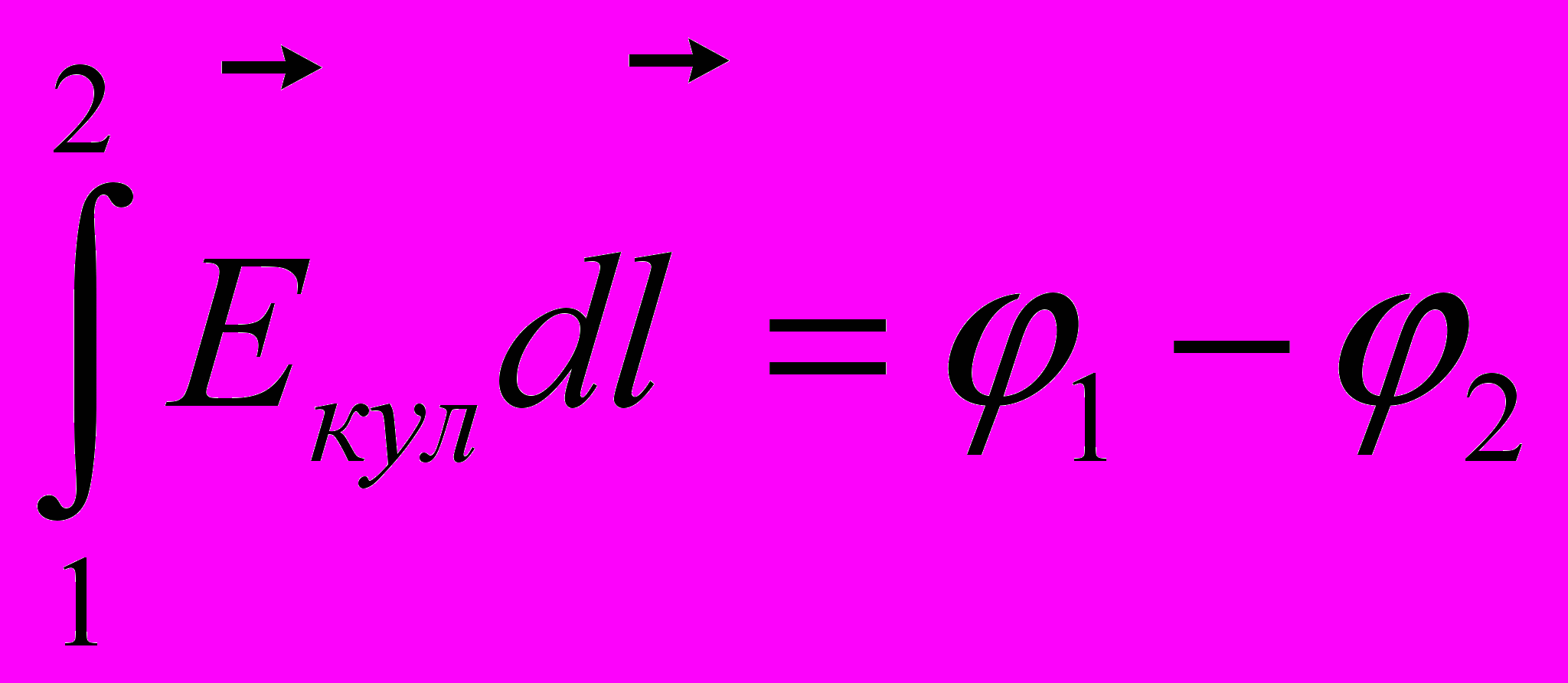
4. Второй интеграл численно равен работе сторонних сил по перемещению единичного положительного заряда из точки 1 в точку 2. Этот интеграл определяет понятие электродвижущей силы
   

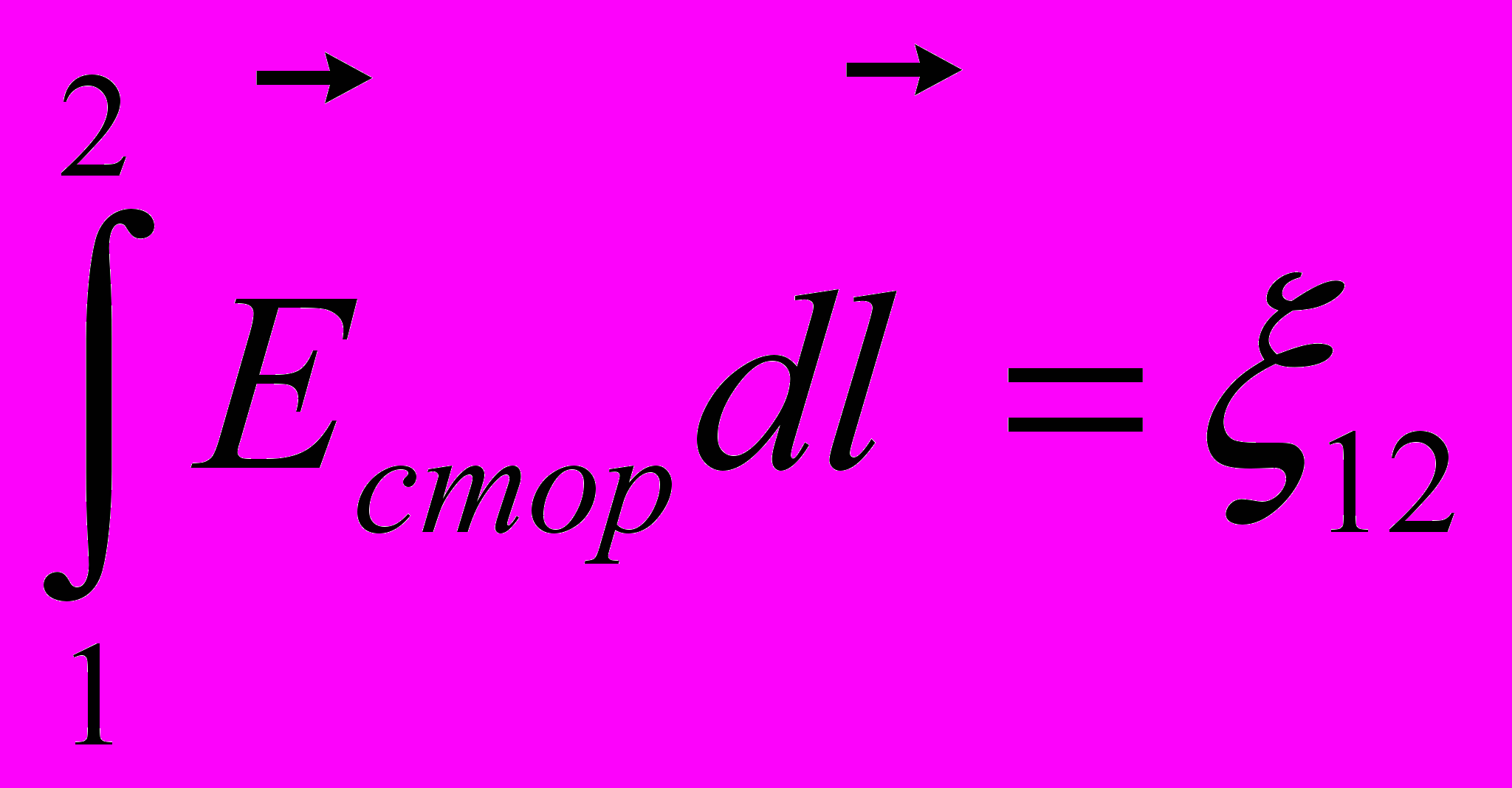
5. Напряжением U₁₂ на участке цепи 1 – 2 называется физическая величина, численно равная работе, совершаемой кулоновскими и сторонними силами при перемещении единичного положительного заряда из точки 1 в точку 2
   

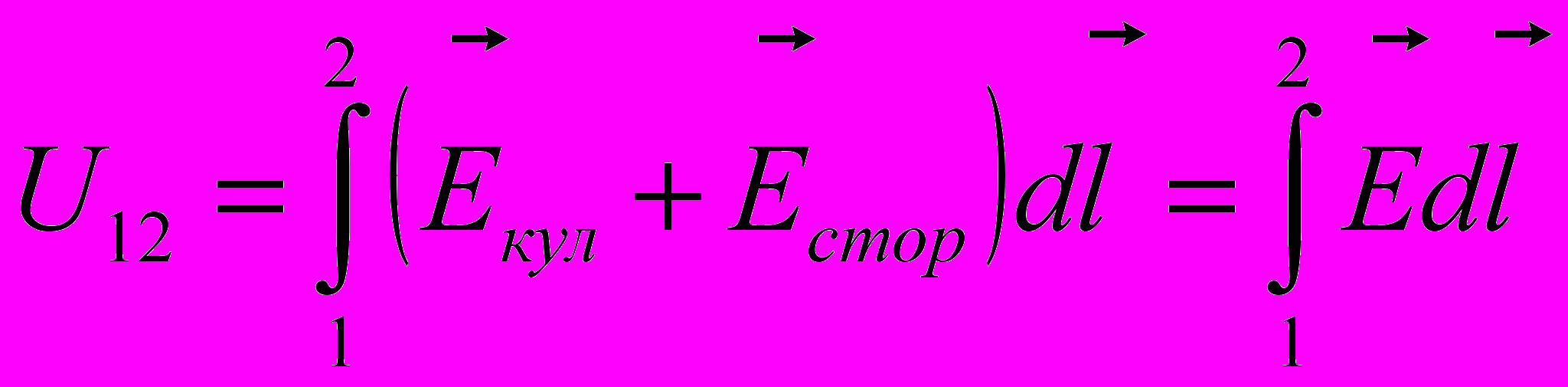
6. Сопротивлением R₁₂ участка цепи между точками 1 и 2 называется интеграл
   

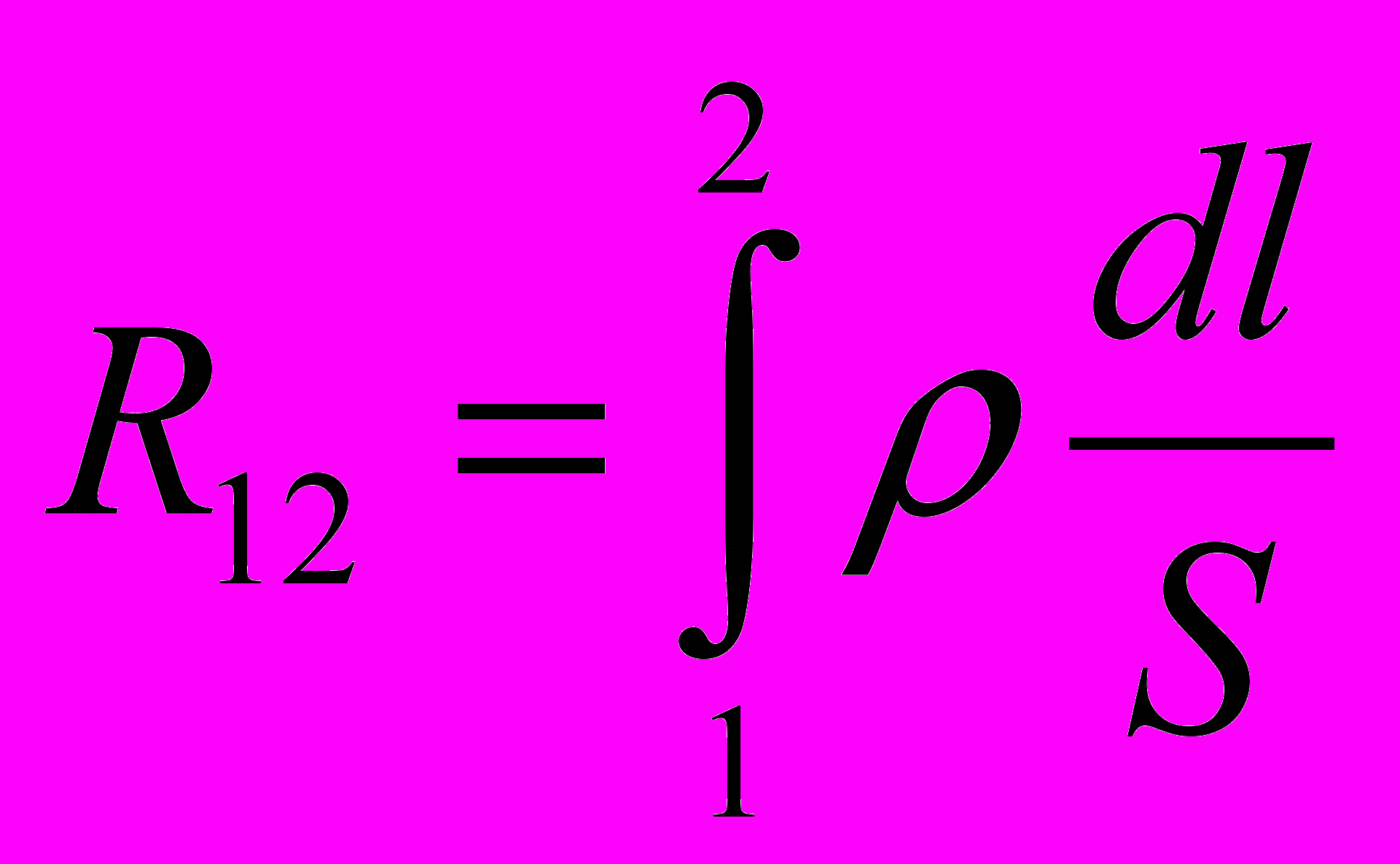
Для однородного проводника постоянного сечения

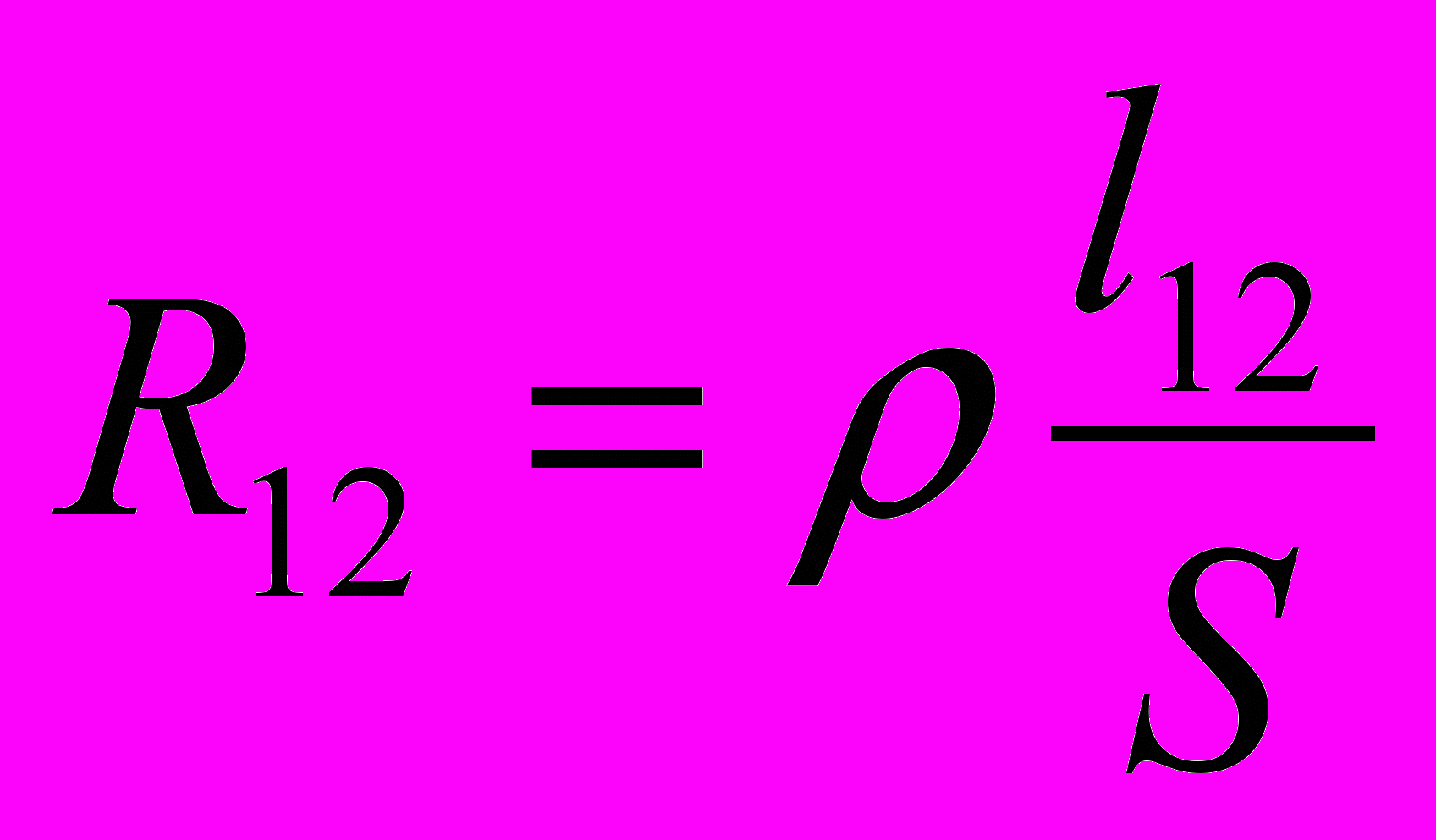
7. Обобщенный закон Ома (закон Ома в интегральной форме) для произвольного участка цепи
   

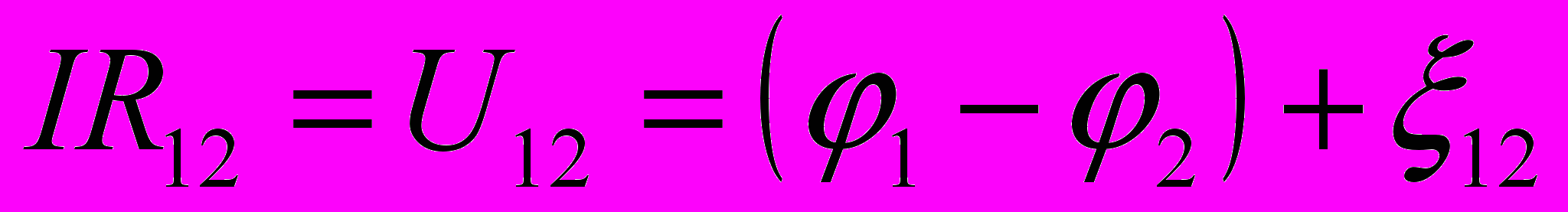
8. В неразветвленной замкнутой электрической цепи сила тока во всех сечениях одинакова, а сама цепь является участком с совпадающими концами.
   

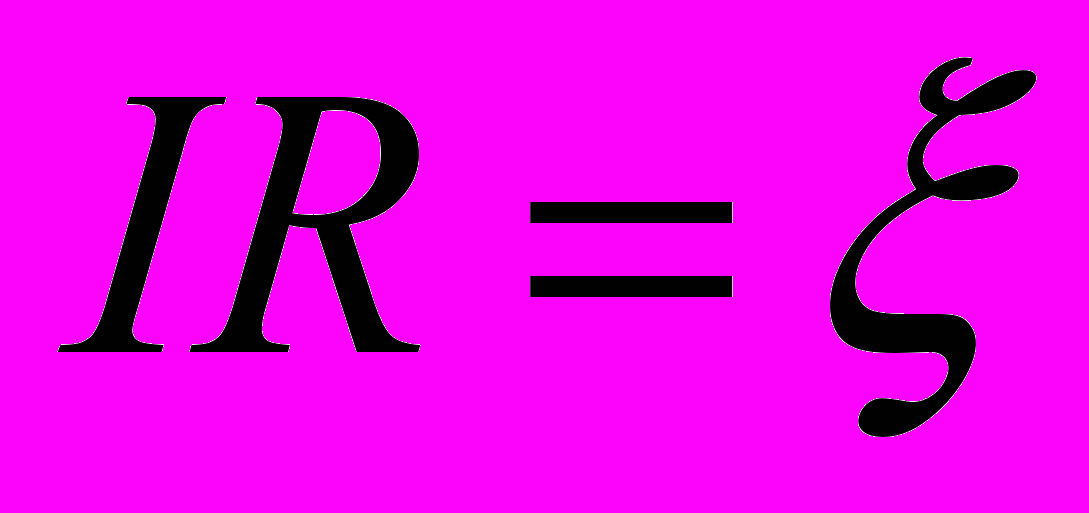
где ξ – алгебраическая сумма всех ЭДС, приложенных в цепи.

9. Если замкнутая цепь состоит из источника электрической энергии с ЭДС ξ и внутренним сопротивлением r, а сопротивление внешней части цепи равно R, то закон Ома имеет вид
   

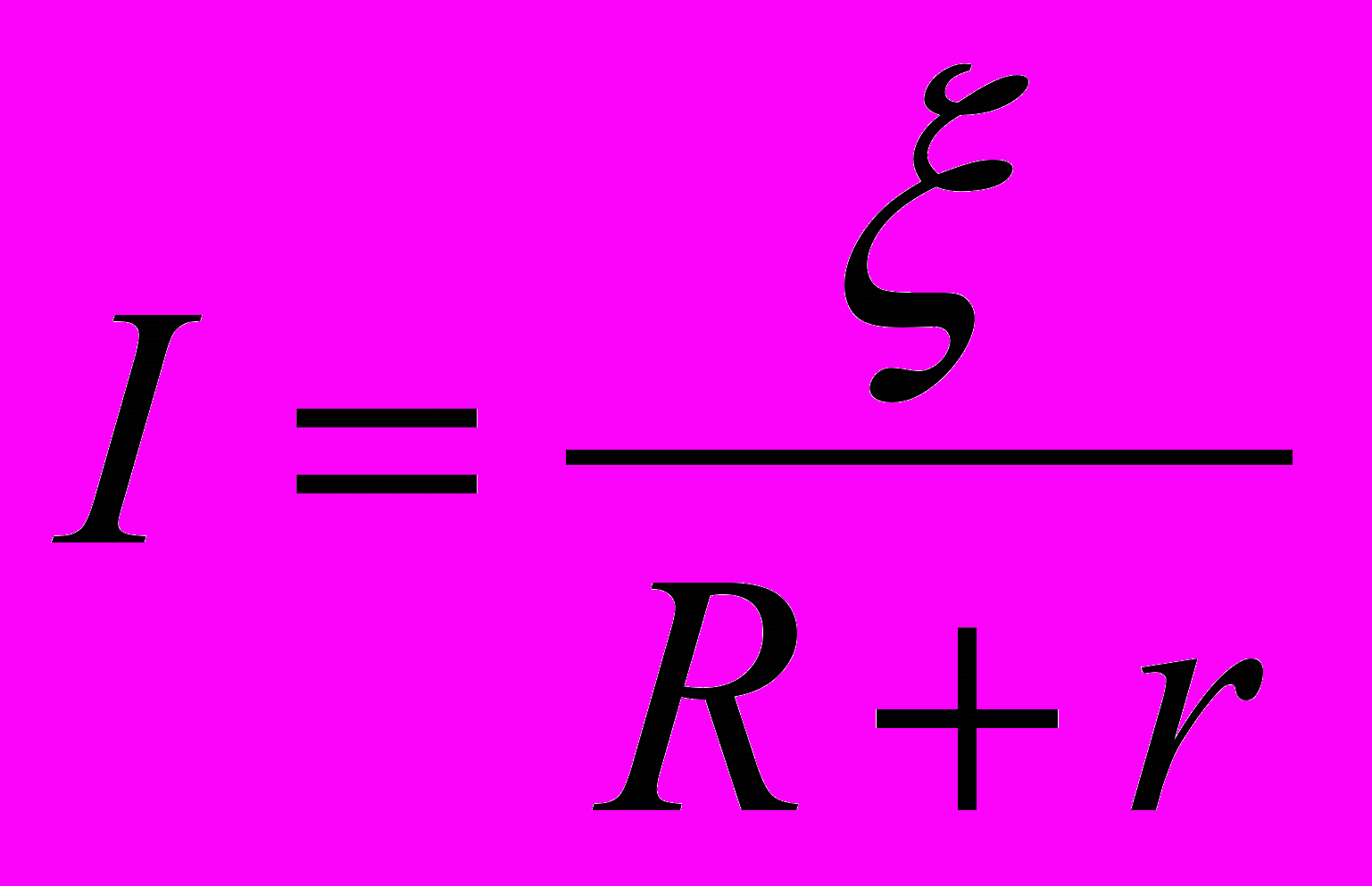
а разность потенциалов на клеммах источника равна напряжению на внешней части цепи

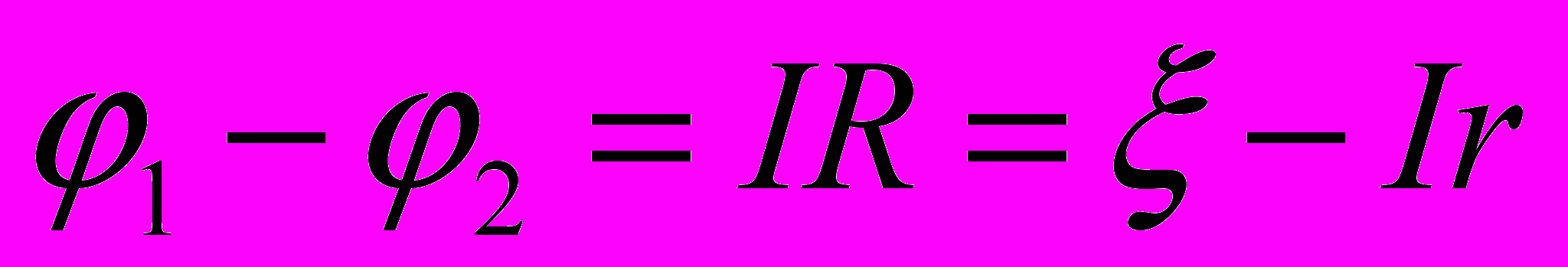
10. Если цепь разомкнута, то в ней тока нет и
    

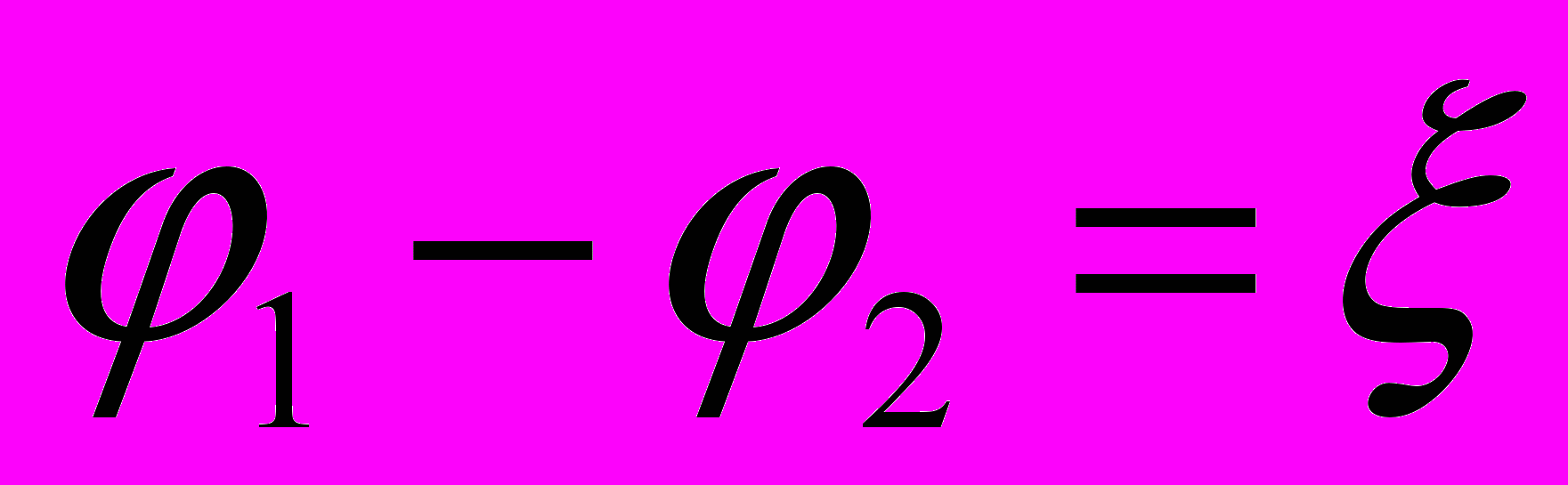
11. При прохождении тока по проводнику в соответствии с законом Джоуля-Ленца выделяется теплота
    

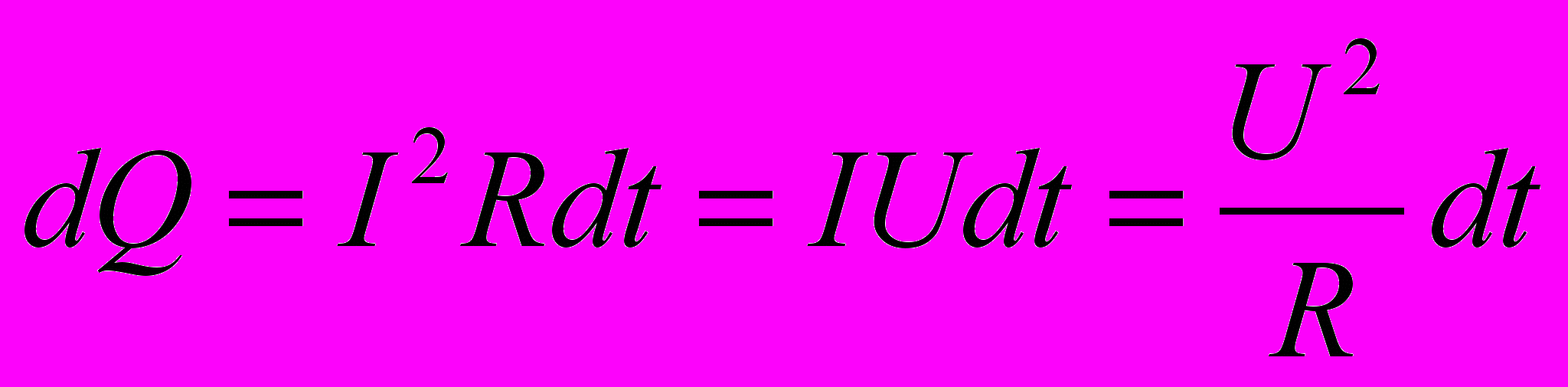
11. Расчет разветвленных цепей состоит в отыскании токов в различных участках таких цепей по заданным значениям сопротивления участков цепи и приложенным в них ЭДС.
    
    1. Узлом называется точка разветвленной цепи, в которой сходится более двух проводников.
       
    2. Первое правило Кирхгофа (правило узлов): алгебраическая сумма токов, сходящихся в узле, равна нулю.
       

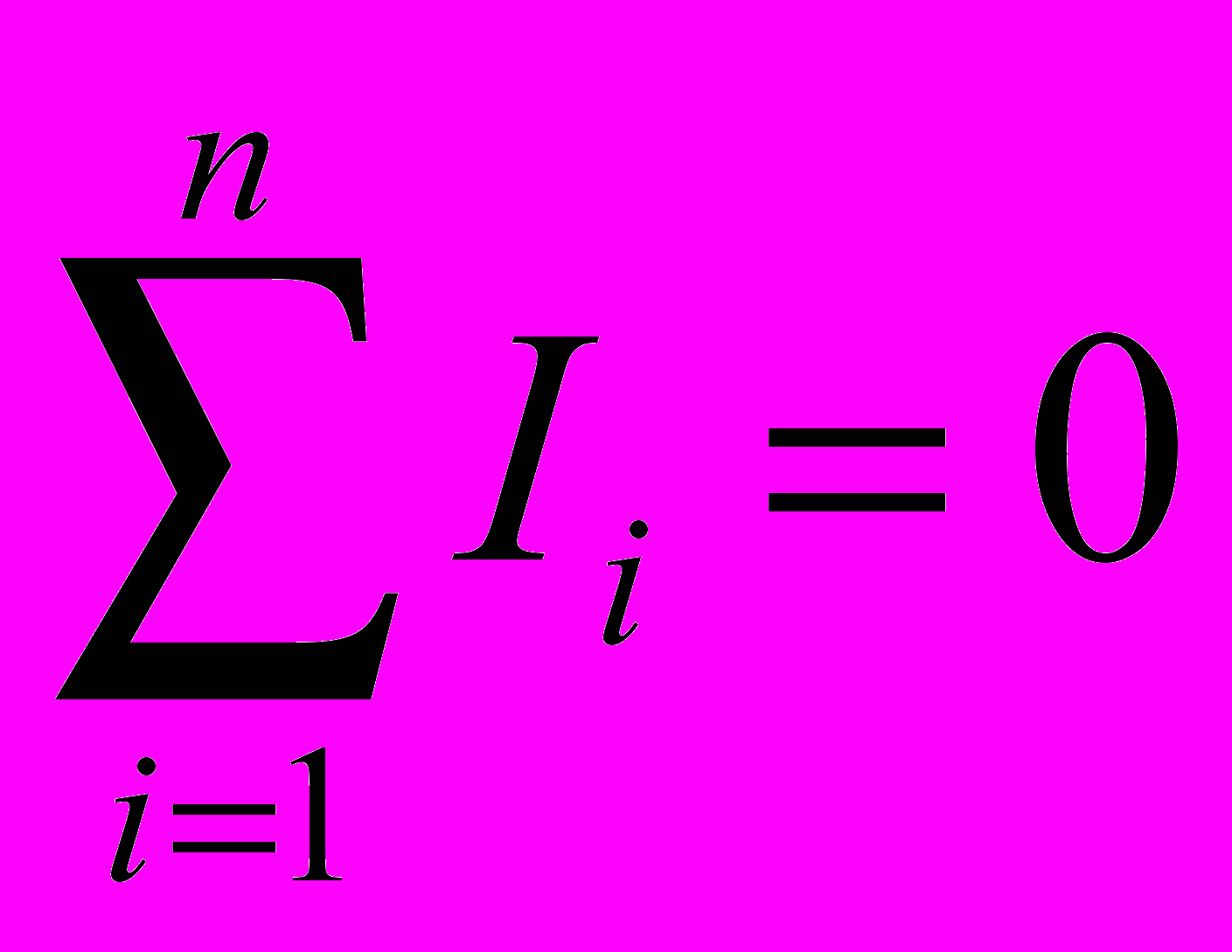
3. Второе правило Кирхгофа (правило контуров): в любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений токов I_i на сопротивления R_i соответствующих участков этого контура равна алгебраической сумме ЭДС в контуре
   

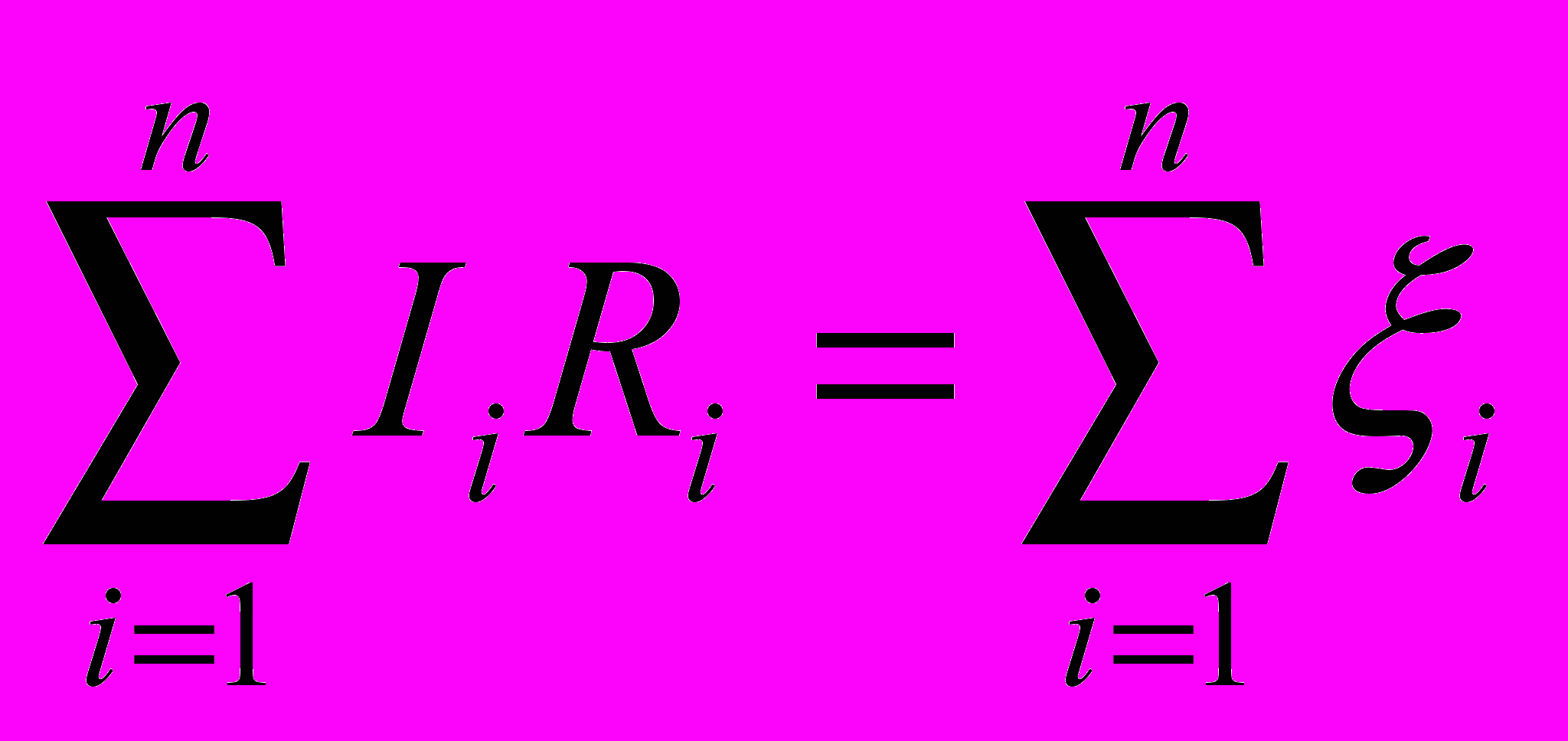
4. Второе правило Кирхгофа позволяет рассчитывать величины токов и сопротивлений в сложных участках электрических цепей
   
   1. При последовательном соединении проводников с сопротивлениями R1, R2 и R3 можно записать
      

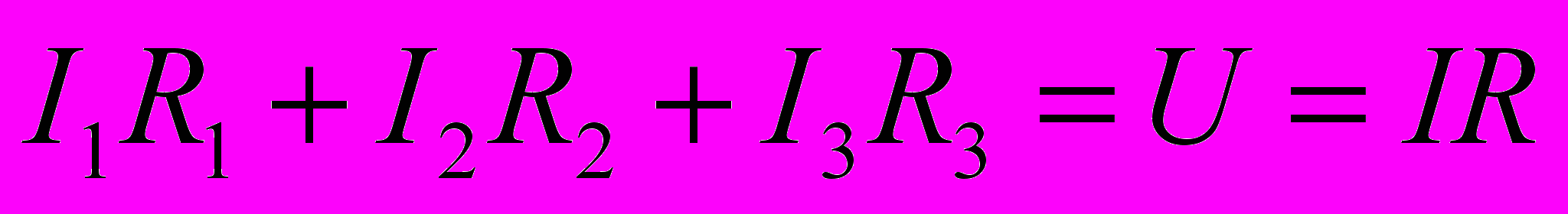
но для неразветвленной цеп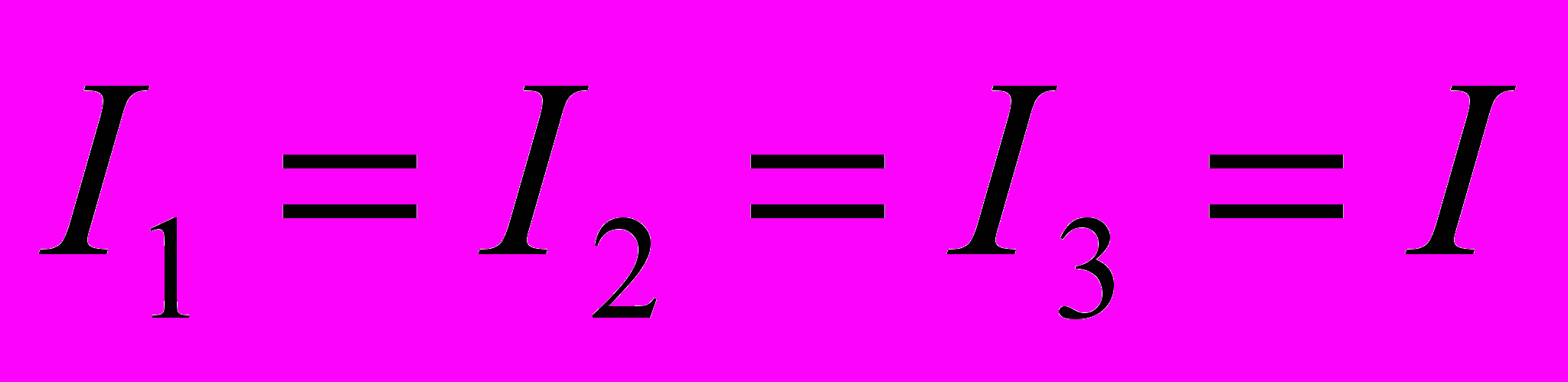и и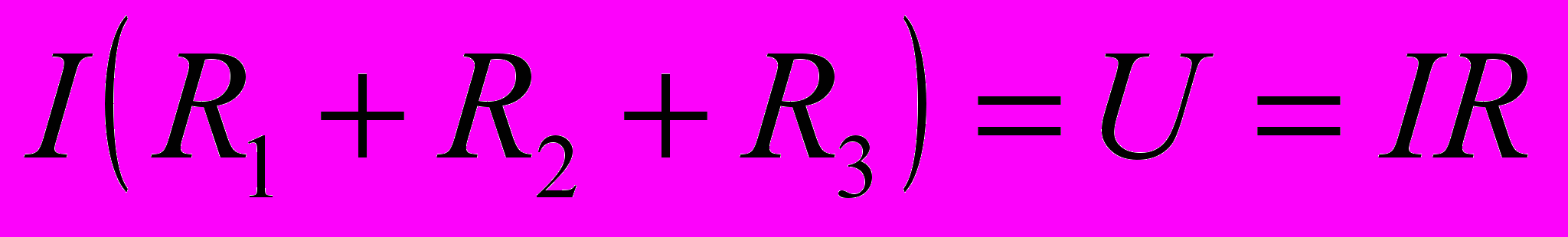



Это означает, что при последовательном соединении проводников сопротивление цепи равно сумме сопротивлений проводников, составляющих цепь.

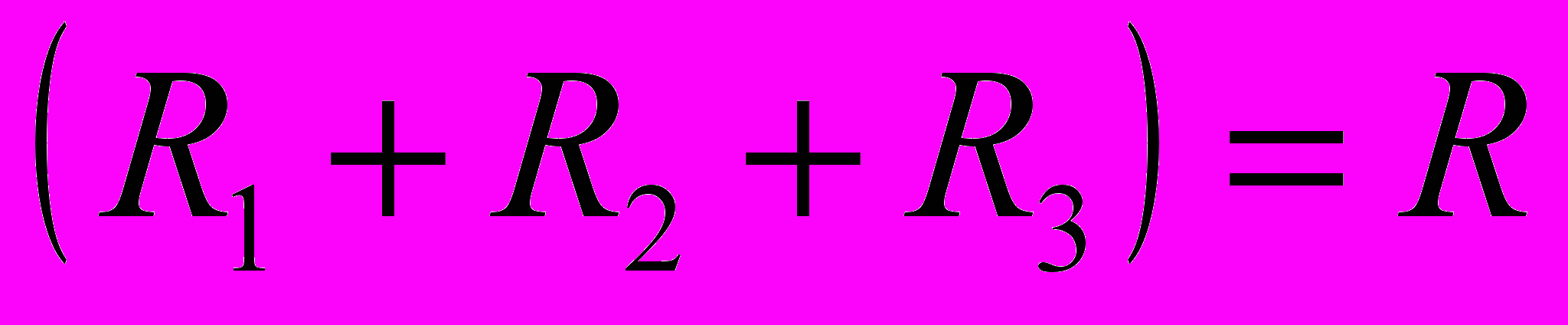
2. При параллельном соединении проводников с сопротивлениями R1, R2 и R3 можно записать
   

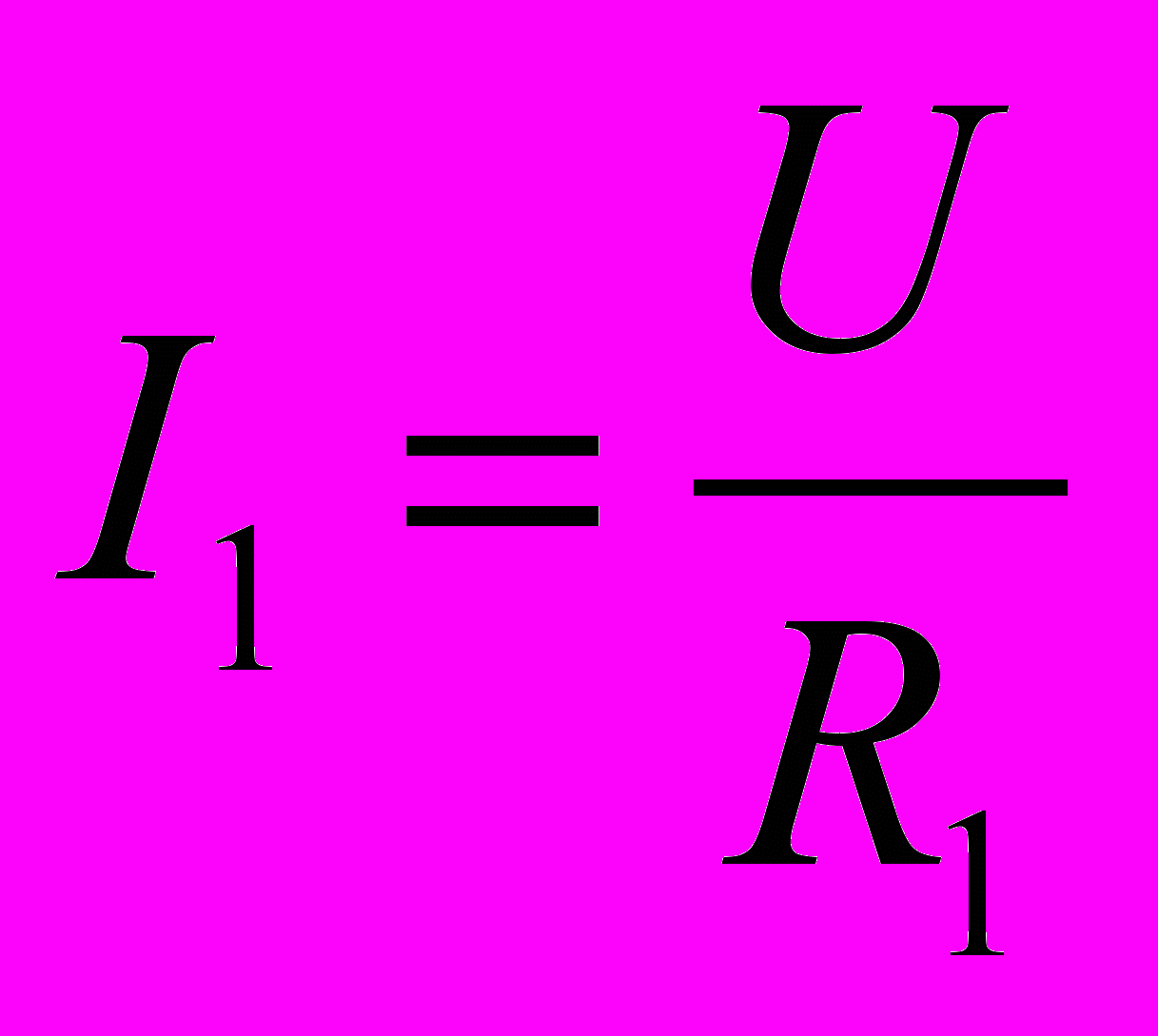
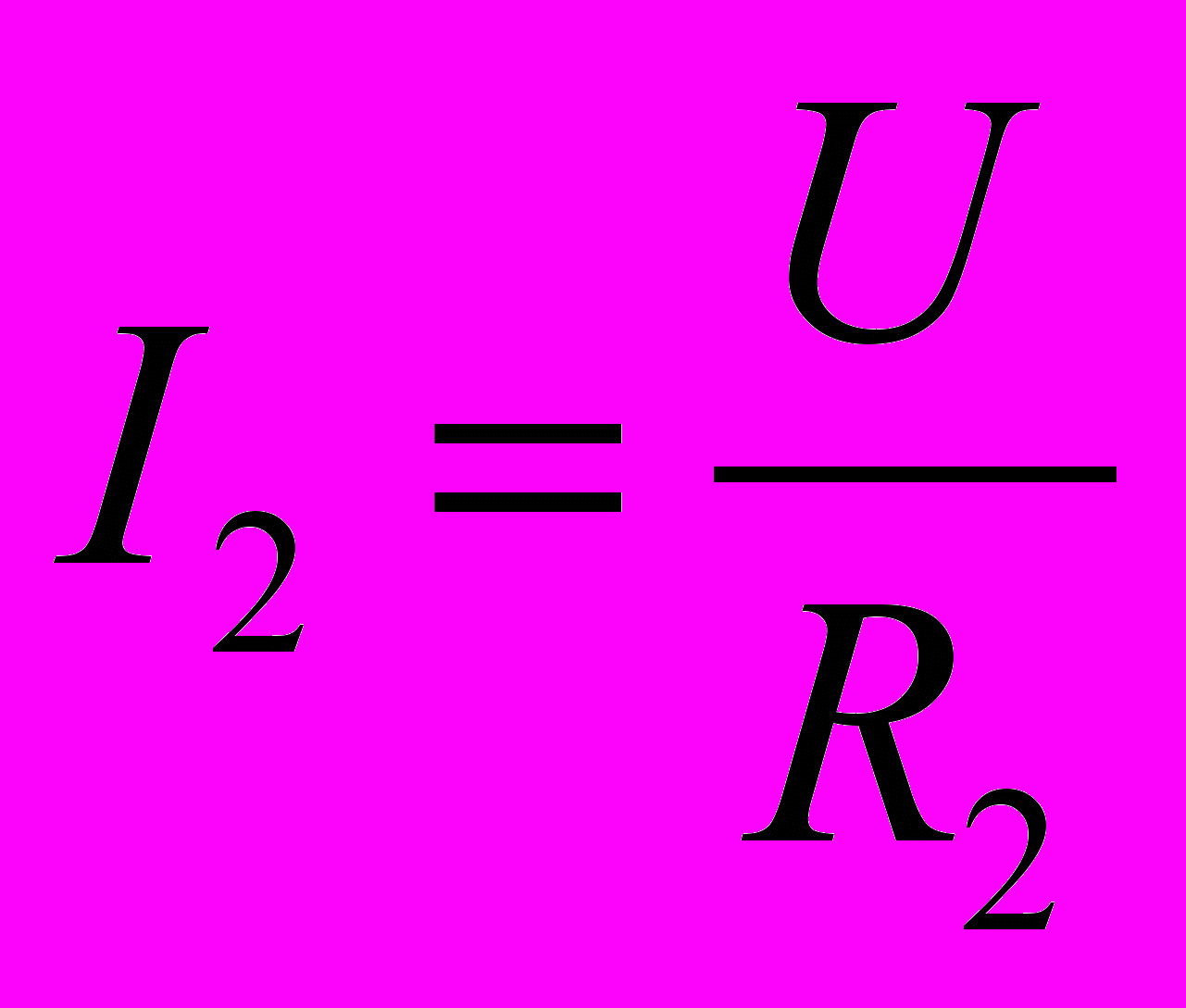
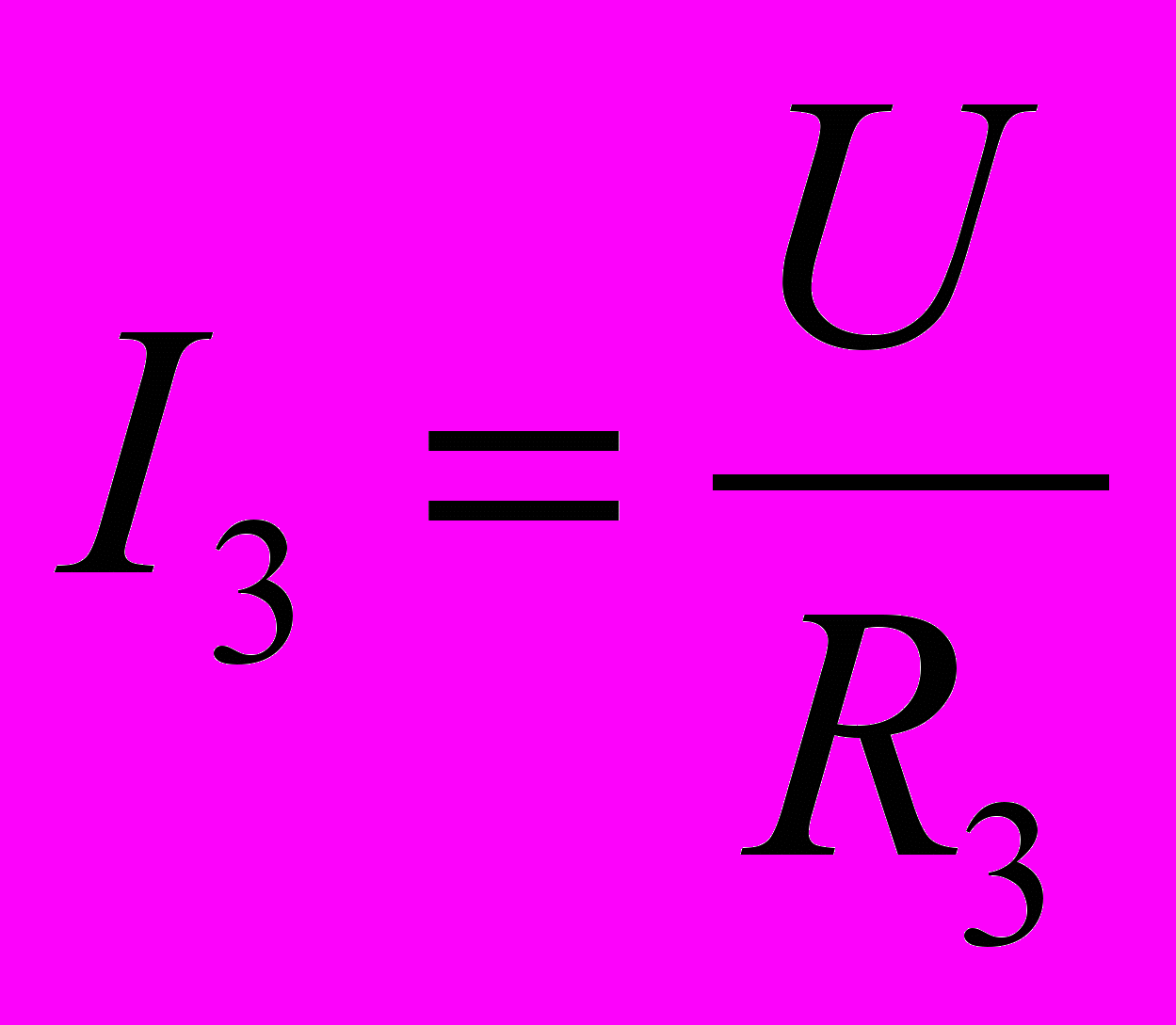
но, применяя первое правило Кирхгофа для любого узла, получим



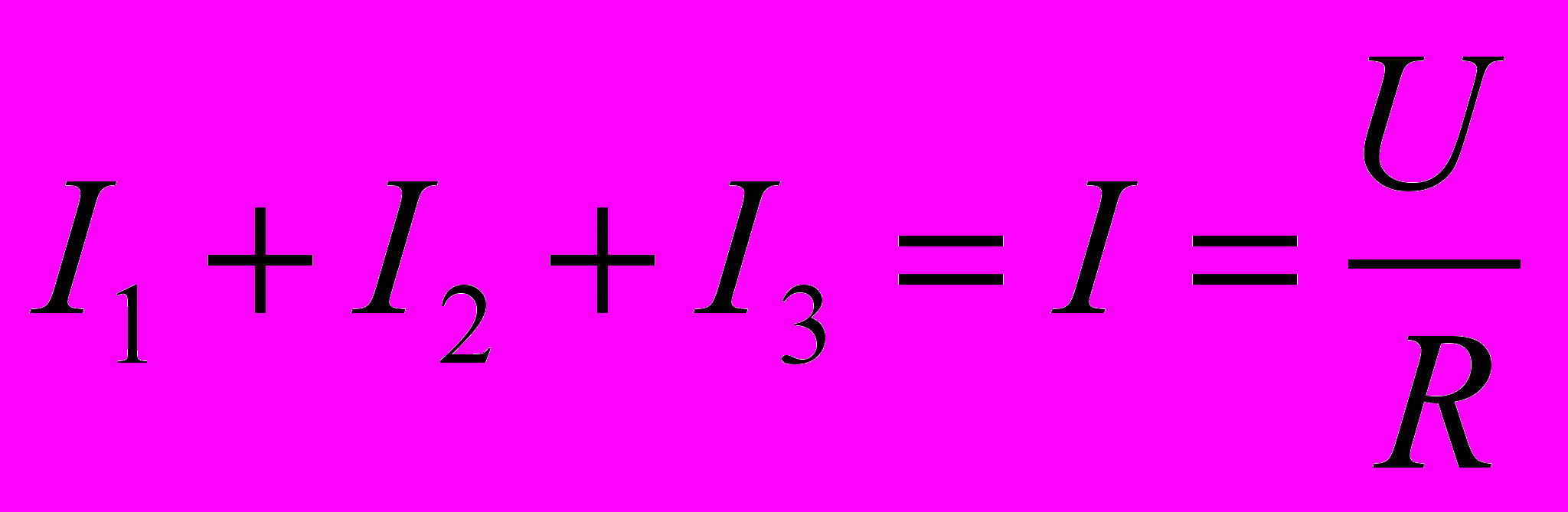
и тогда



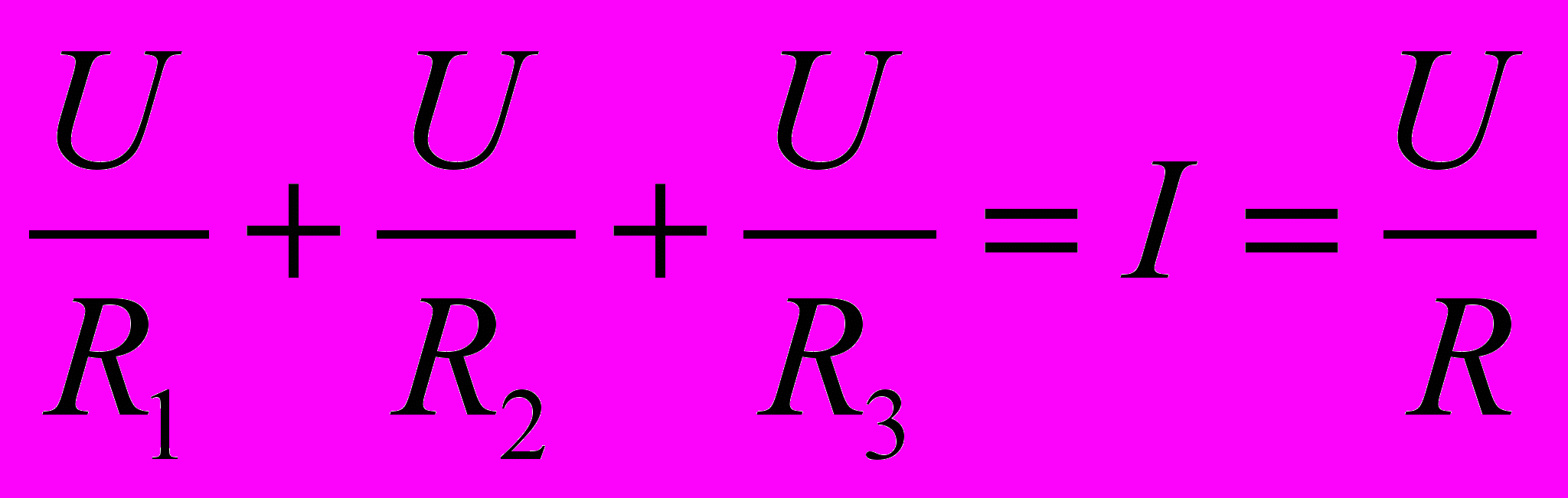
Это означает, что при параллельном соединении проводников сопротивление цепи равно сумме обратных величин сопротивлений проводников, составляющих цепь.