Метод определения отказовых состояний в сложных электроэнергетических системах

Вид материала

Документы

Содержание Zmax) и наименьшим диагональным элементом (Z Nк – количество подсетей; Z

Подобный материал:

• История разработок теории и приложений количественного системного анализа, 266.41kb.
• Описание требований в контексте модели прецендентов, 605.08kb.
• Заявка участника Всероссийского молодежного конкурса наукоёмких инновационных идей, 244.53kb.
• Программа спецкурса "Дополнительные главы электродинамики сред с дисперсией", 33.42kb.
• Рабочая учебная программа дисциплины для специальности 1-53, 114.04kb.
• 3. Лекция: Методы поиска решений, 336.6kb.
• Х вычислительных комплексов специального назначения определяет права доступа по комбинированному, 10.03kb.
• Переходные процессы в электрических системах рабочая программа, методические указания., 137.38kb.
• Примерный учебный план 2 "Электрические станции и подстанции" 3 "Электромагнитные переходные, 200.27kb.
• Источники ошибок в программных средствах, 166.29kb.

УДК 621.311.019.3


МЕТОД ОПРЕДЕЛЕНИЯ ОТКАЗОВЫХ СОСТОЯНИЙ В СЛОЖНЫХ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМАХ.


Фокин Ю. А.; Осипов¹ Я. Н.


В настоящее время проведена реформа электроэнергетики, возникло большое количество собственников энергообъектов, в существующих энергосистемах появились границы балансовой принадлежности, однако параллельная работа источников сохранилась, электроэнергетические системы (ЭЭС) большого размера и очень большого остались, также как и проблемы управления надежностью их функционирования.

В докладе предлагается развитие методов анализа с элементами синтеза надежности функционирования сложных ЭЭС. Предложения обоснованы проведением большого количества вычислительных экспериментов на реальных ЭЭС большого размера.

ЭЭС состоит из относительно высоконадёжных элементов, поэтому вероятность одновременного отказа более чем двух, а для систем очень большого размера более чем трёх независимых элементов, пренебрежимо мала. Ранее в промышленных компьютерных программах определение параметров надёжности осуществлялось на основе структурного анализа. Метод структурного анализа, учитывает только первый закон Кирхгофа, и этого нередко недостаточно при необходимости учета режимных ограничений в анализе послеаварийных, аварийных и состояниях преднамеренного отключения.

С помощью методов структурного анализа можно было решать достаточно сложные комбинаторные задачи надежности [2,3] при небольших затратах памяти и ресурсов ЭВМ. Но неучёт ограничений, связанных со вторым законом Кирхгофа, не всегда позволяет получить адекватные показатели надёжности, а приёмы, используемые для учёта этих ограничений, не всегда оказываются эффективными.

Методы, основанные на использовании обобщённых параметров схем, дают полную информацию о структурно-функциональных характеристиках ЭЭС [1, 2, 3] и её элементах, а при правильном их применении и об отказовых состояниях [1] .

Недостатком обобщенных параметров [2,4] является их исключительно большая размерность для больших схем, следовательно, и трудоемкость цифрового анализа. Поэтому первоочередной необходимостью является декомпозиция сложных ЭЭС, причем желательно автоматическая и не только по структуре, но и по функциям - в данном случае по режимам.

В докладе излагаются некоторые результаты первой попытки решения этой комбинаторной задачи большого размера не только с точки зрения анализа, но и синтеза.

Достаточно информационноемкой структурой обобщённых параметров, характеризующей ЭЭС, является матрица узловых сопротивлений Z_у. Основным недостатком, например, расчёта режима с помощью матрицы узловых сопротивлений Z_у, является трудоёмкость её получения. Для небольших схем расчёты матриц Z_у не составляют особого труда, но для схем состоящих из нескольких тысяч узлов это занимает уже десятки- сотни минут. Поэтому наиболее целесообразной в этом случае является коррекция матрицы Z_у при изменении коммутационного состояния сети [2] . Так как используемая для расчётов режимов (установившихся, аварийных, послеаварийных) матрица узловых сопротивлений достаточно просто корректируется при изменении коммутационного состояния сети.

Использовавшийся ранее подход [2,3] предполагал отдельный расчёт структурной надёжности, при котором обычно не учитывались или учитывались приближенно ограничения по режимам и отдельный расчет функциональной надежности.

Такой подход прагматичен при определении показателей надёжности относительно небольшой сети (предел - несколько десятков тысяч элементов).

В том случае, когда просто и достаточно быстро определяется структурная надёжность, а по расчётам режимов - функциональная. Но в этой ситуации происходит решение последовательно двух задач. Сначала определяются сечения относительно узлов в сети, а потом для различных коммутационных состояний рассчитываются режимы и определяется недоотпуск электроэнергии. При этом определяется потокораспределение для каждого из коммутационных состояний, что является достаточно трудоёмкой задачей, так как для каждого состояния заново определяется матрица коэффициентов распределения C [2,3].

Как известно [2-4], матрицы С и Z_у взаимосвязаны:

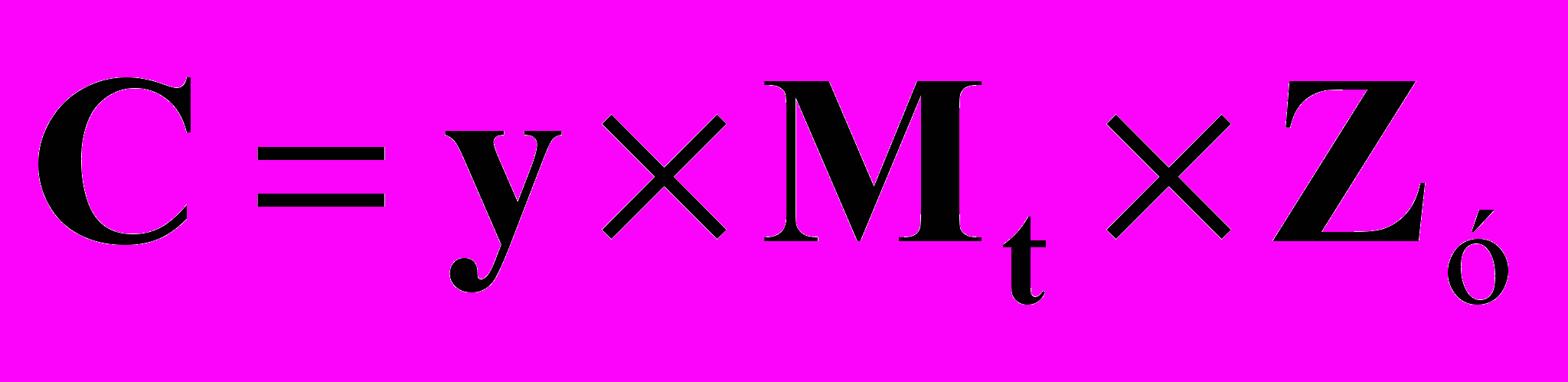, (1)

где y - диагональная матрица проводимостей ветвей,

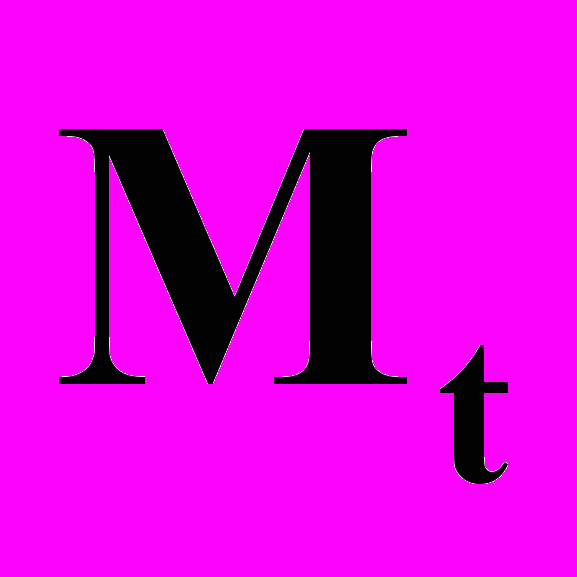- транспонированная первая матрица инциденций.

При использовании единого подхода к расчёту надёжности и режима с использованием обобщённых параметров схем определяется матрица узловых сопротивлений. Она определяется для состояния нормального режима в сети. Важной особенностью является использование так называемой базовой схемы замещения и матрицы 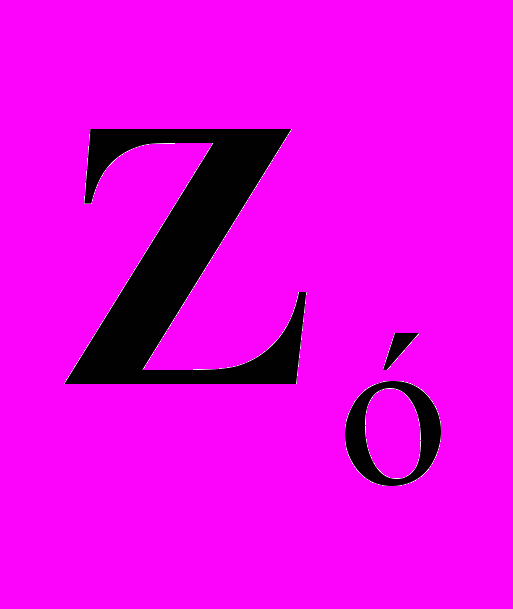для расчётов режима и коррекции её при изменении коммутационных состояний. Благодаря [1] взаимнооднозначному переходу от схемы электрических соединений к схеме замещения, возможна коррекция матрицы 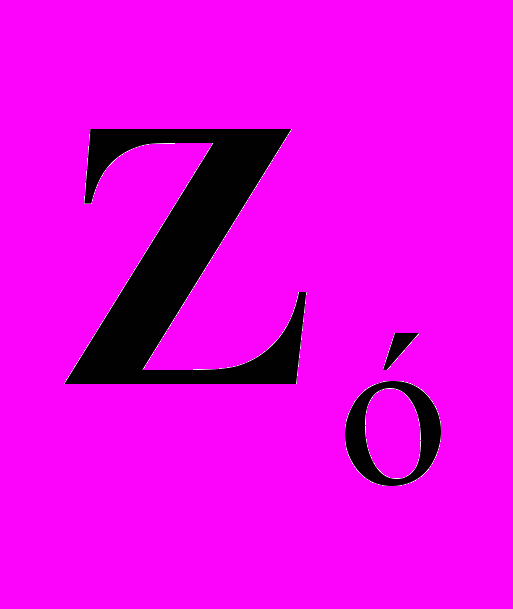при различных коммутационных состояниях. И, соответственно, возможен расчёт режима в каждом из коммутационных состояний.

При изменении сопротивлений ветвей меняются значения матрицы Z_у. Изменения сопротивлений, в том числе при наличии в системе регулирующих, преобразовательных устройств, например, «гибкие» ЛЭП, ВПТ влияют на значения сопротивлений элементов (не дискретное изменение) матрицы узловых сопротивлений: Z_ij и Z_ii – взаимные и собственные сопротивления между узлами i, j и i, i.

В таких ситуациях следует корректировать матрицу узловых сопротивлений. При изменении ветви схемы замещения, например, между узлами , i и j на величину необходимо к рассматриваемым узлам подключить ветвь с сопротивлением:

, (2)

где 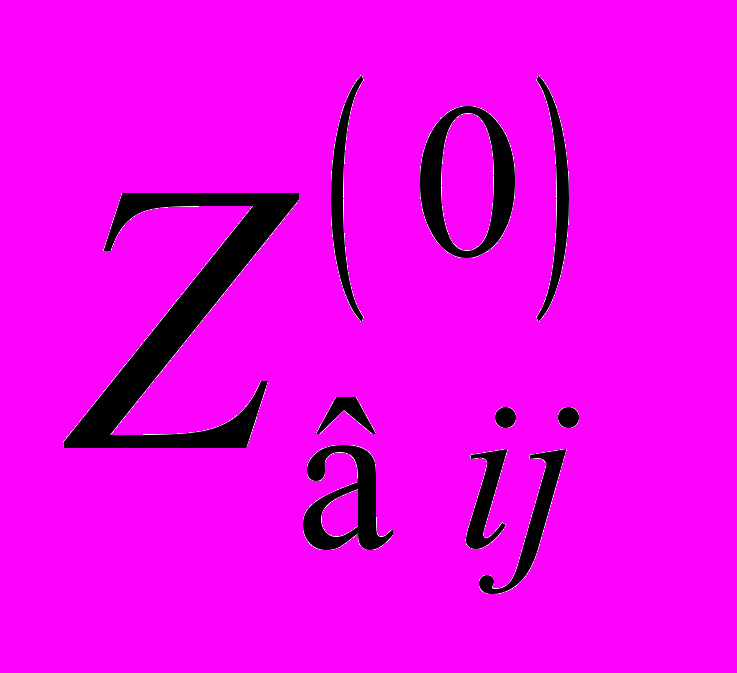- исходное сопротивление ветви. Знак плюс в формуле (2) означает отрицательное приращение сопротивления ветви, а минус – положительное.

Таким образом, коррекция матрицы узловых сопротивлений при изменении сопротивлений элементов ветви схемы замещения сводится к подключению ветви параллельной рассматриваемой с сопротивлением, полученным по формуле (2).

Декомпозиция сложной сети ранее была необходима в связи с недостаточной производительностью вычислительной техники. Для этого при различных критериях декомпозиции сложная схема делилась на несколько более простых меньшего размера. Сейчас производительность вычислительной техники намного возросла. Но, ввиду комбинаторного характера задач надежности, декомпозиция при анализе сложной схемы необходима, так как, например, при определении показателей надёжности ЭЭС, состоящей из 20000 элементов, и вычислении, например, вероятности отказа элемента при учёте безотказной работы всех остальных элементов (формальном подходе) вероятность отказа будет равна примерно 2,043·10^-12 (при учёте того, что вероятность отказа одного элемента равна ≈10^-3, а вероятность безотказной работы остальных элементов ≈ 0,999¹⁹⁹⁹⁹). Поэтому необходимо выделять только те элементы, которые реально влияют на надёжность функционирования ЭЭС.

При схеме 2-х отказов [2] - двухэлементные сечения в гораздо меньшей степени влияют на вероятность безотказной работы остальных элементов, так как количество таких сечений гораздо больше, а вероятность их отказа в среднем в 10^-3 раз меньше, чем одноэлементных сечений.

Схема «одного отказа» [2] имеет большую значимость, потому что для одноэлементное сечение эквивалентно сотне двухэлементных сечений. Но так как в сотни двухэлементных сечений входят также наложения отказов одних элементов на преднамеренные отключения других, то значимость двухэлементных сечений с учётом этого фактора возрастает. Большая часть элементов системы (особенно сети 35 кВ и выше) обычно резервирована. Поэтому нередки ситуации, когда одноэлементных сечений практически не бывает. (Например, для ЭЭС выполняется известный критерий «N-1»).

В том случае когда, анализируется схема большой электроэнергетической системы, учёт всех взаимосвязей между элементами не всегда возможен и не всегда имеет смысл. Понятие «большая» ЭЭС не совсем однозначно. Но, как правило, таковыми являются схемы, в которых содержится более 1000-5000 узлов, и присутствуют сети различных номинальных напряжений. Территориально схема сети может охватывать несколько энергосистем, включающих, например, сети 500 кВ, и сети 10 кВ, работающие по своей сути независимо друг от друга. В этом смысле параметры режимов, например, сети 500 кВ практически не зависят от параметров режима сети 10 кВ. Поэтому при расчёте режима в сети большим количеством номинальных напряжений целесообразно вести расчёт части сети, а не всей сети полностью. В случае с большой ЭЭС декомпозиция оказывается наиболее эффективной, так как анализ полностью всей сети и расчёт режима, является достаточно трудоёмкой задачей.

В общем случае декомпозиция подразумевает разделение одной большой задачи на несколько подзадач. В случае с ЭЭС разделение большой сети на подсети (кластеры) даёт возможность считать их независимыми и вести расчёт режимов, коротких замыканий и определения показателей надёжности для каждой подсети отдельно, то есть независимо.

В действительности параметры режимов элементов сети, удалённых друг от друга электрически можно считать практически независимыми. При этом с точки зрения электрической удалённости подсети будут объединять элементы, которые находятся близко друг от друга электрически.

В предлагаемом методе декомпозиция осуществляется по матрице узловых сопротивлений Z_у, являющейся матрицей обобщённых параметров схем. Для большой ЭЭС декомпозиция представляет собой разделение большой схемы на подсхемы, то есть кластерный анализ (анализ подсетей). Исходной информацией для декомпозиции сети выбрана матрица Z_у, так как она наиболее полно учитывает электрическую удалённость элементов друг от друга.

Декомпозиция по матрице узловых сопротивлений Z_у проводится следующим образом:

1. В матрице узловых сопротивлений Z_у, полученной для всей сети, анализируются все диагональные элементы (Z_ii). Из этих n-элементов выделяются элементы, имеющие наибольшее и наименьшее значения сопротивления.
   
2. Определяется разность между наибольшим диагональным элементом ( Z_max) и наименьшим диагональным элементом (Z_min).
   
3. Эмпирически (вычислительные эксперименты на больших ЭЭС) была получена формула по определению количества подсетей, на которое необходимо поделить схему сети большой ЭЭС. Данная формула применима при числе узлов n > 500. Количество подсетей получается равным:
   

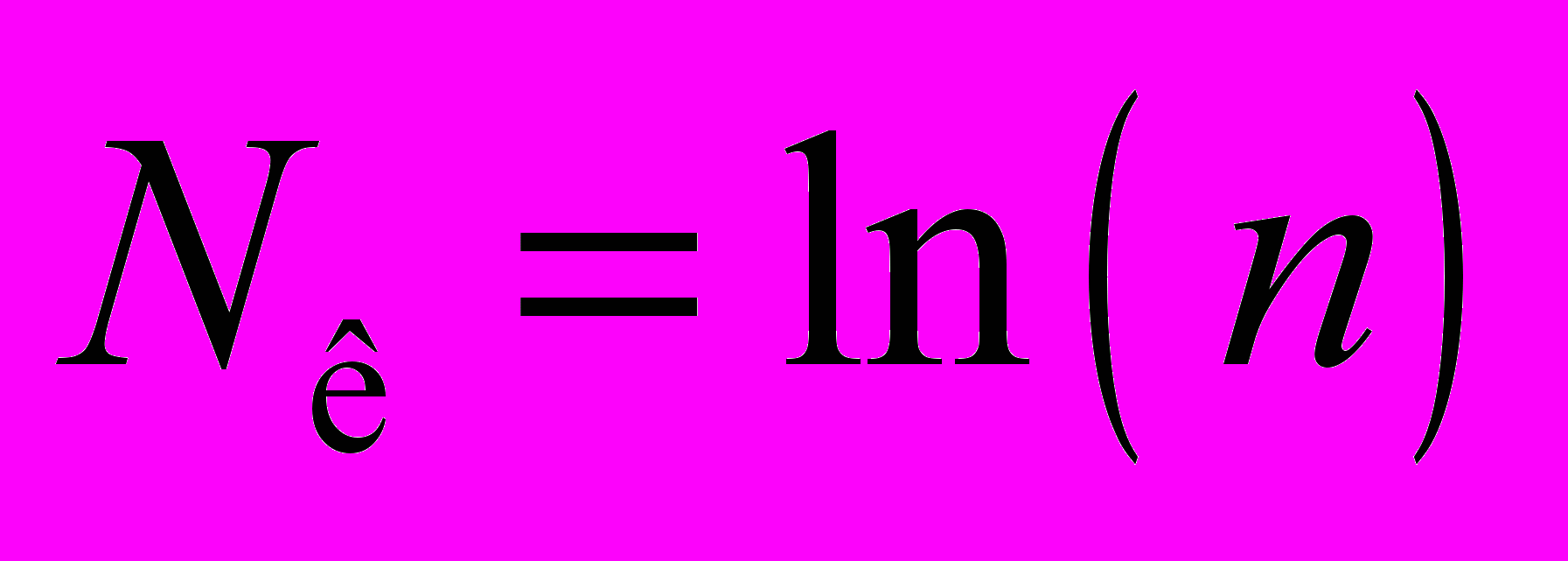, (3)

где n – число узлов в схеме.

Полученное значение N_к округляется до наименьшего целого.

4. По найденному количеству подсетей определяется величина интервала 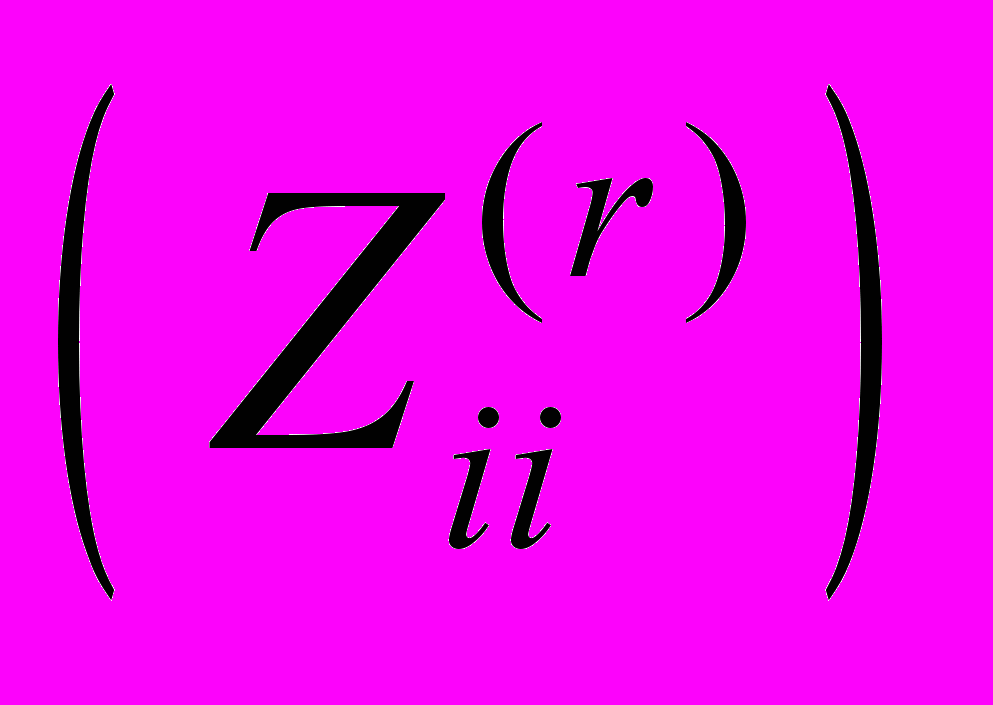, на которые будет разделена вся сеть.
   

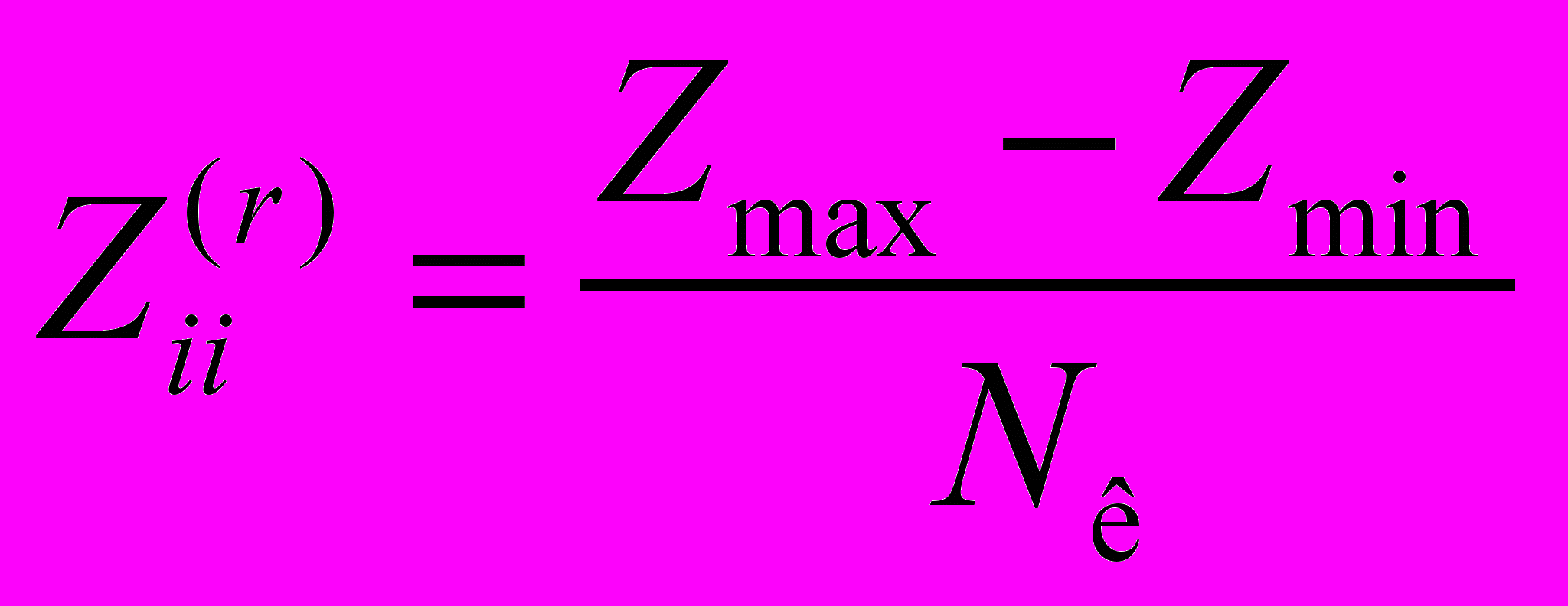, (4)

где N_к – количество подсетей; Z_max – наибольший диагональный элемент матрицы Z_у; Z_min – наименьший диагональный элемент матрицы Z_у.

А по полученной величине интервала определяются сами интервалы:

1-й интервал [; 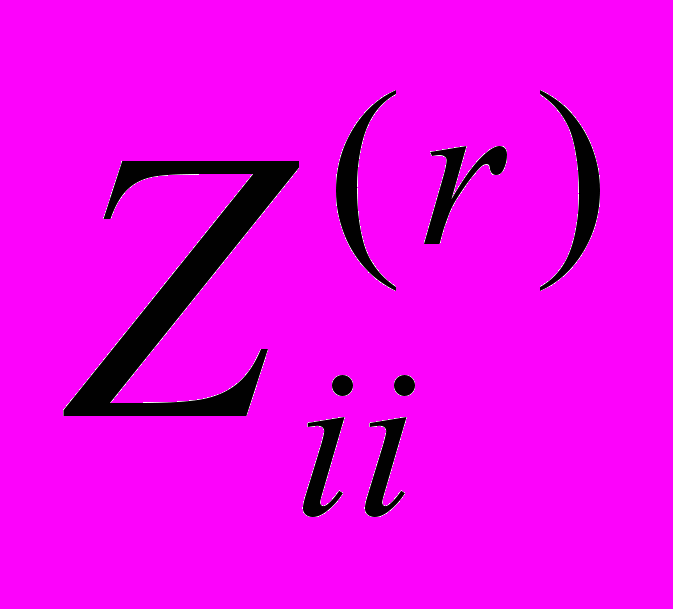], 2-й интервал [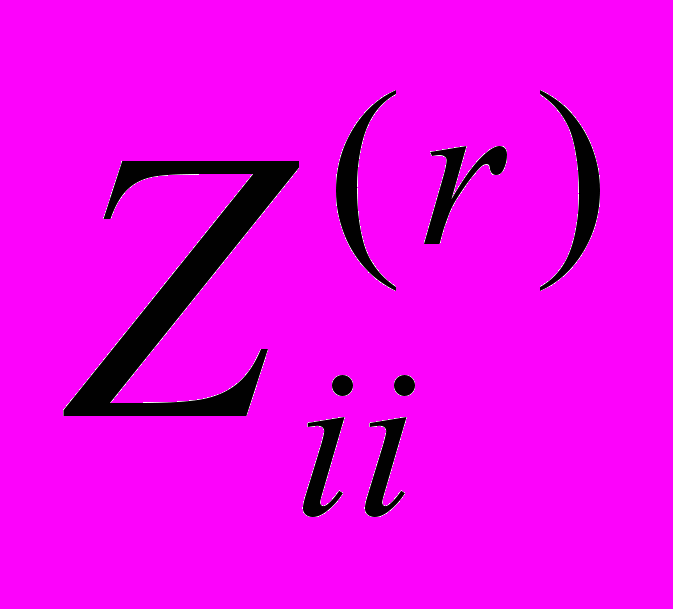; 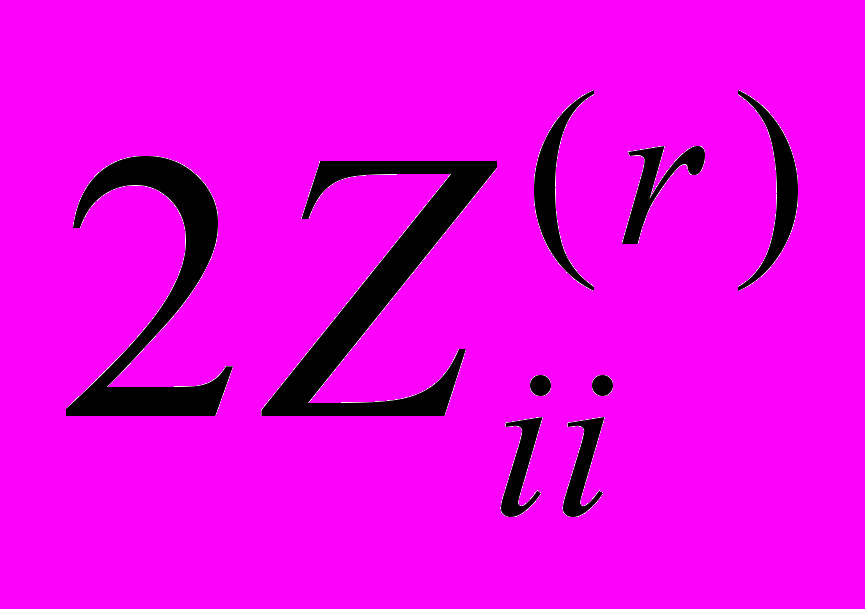], 3-й интервал [; ],

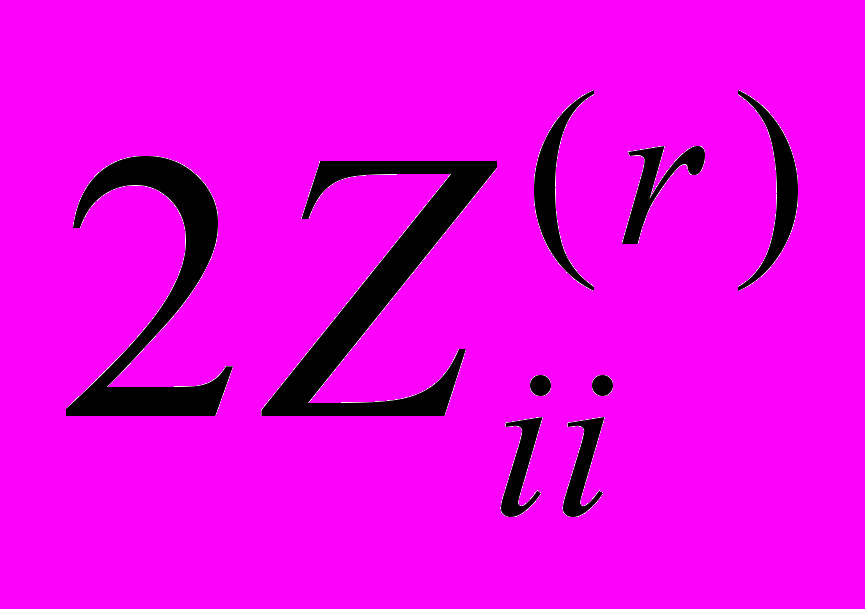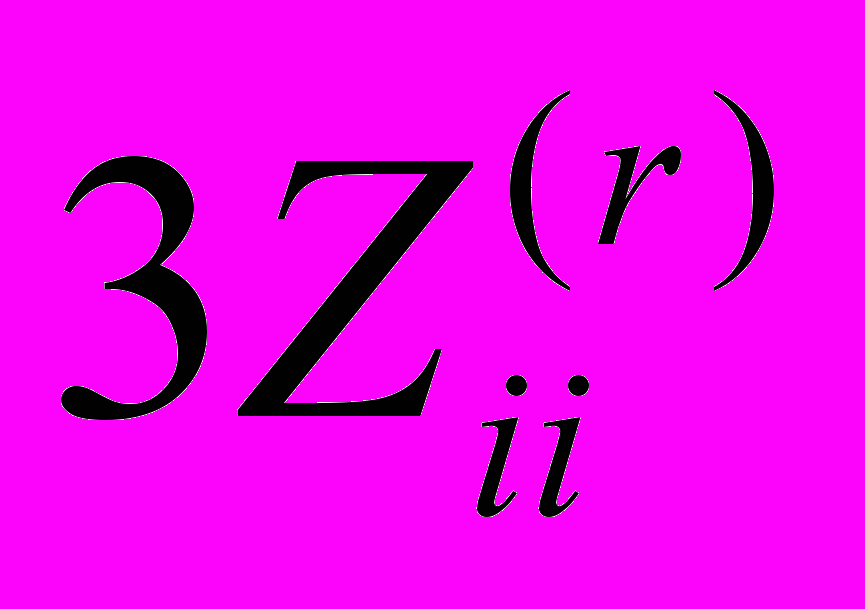N_к-й интервал [; ].

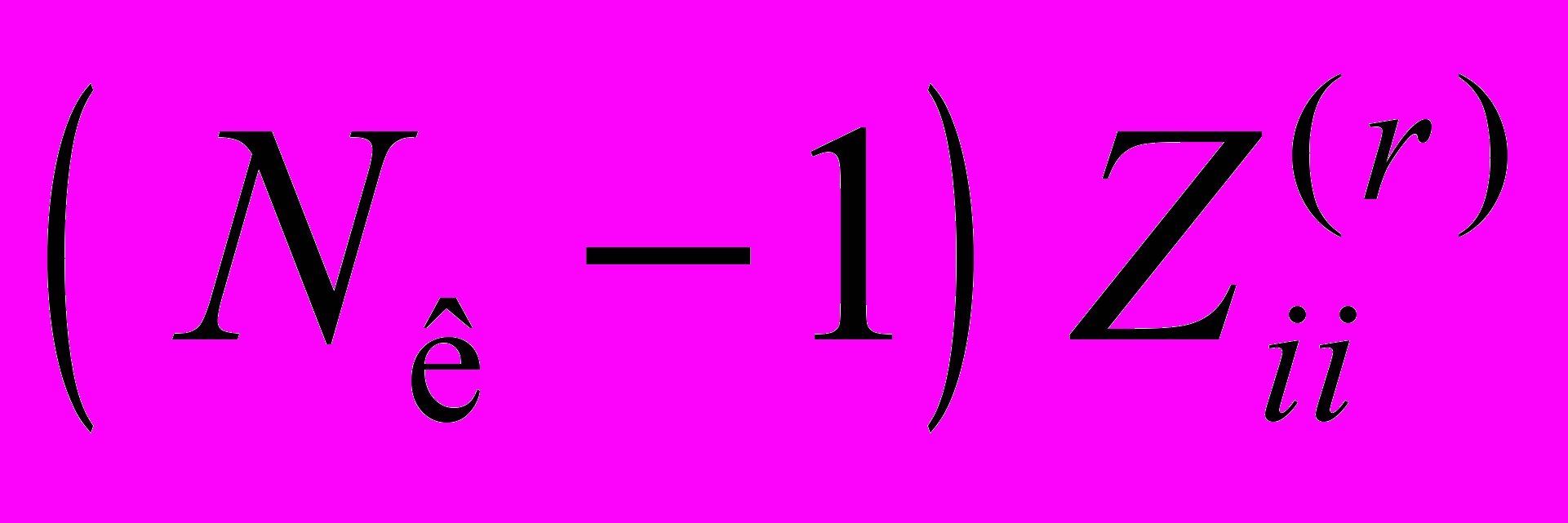Например, при n = 20000, Z_max = 300000 Ом, Z_min = 0,1 Ом 9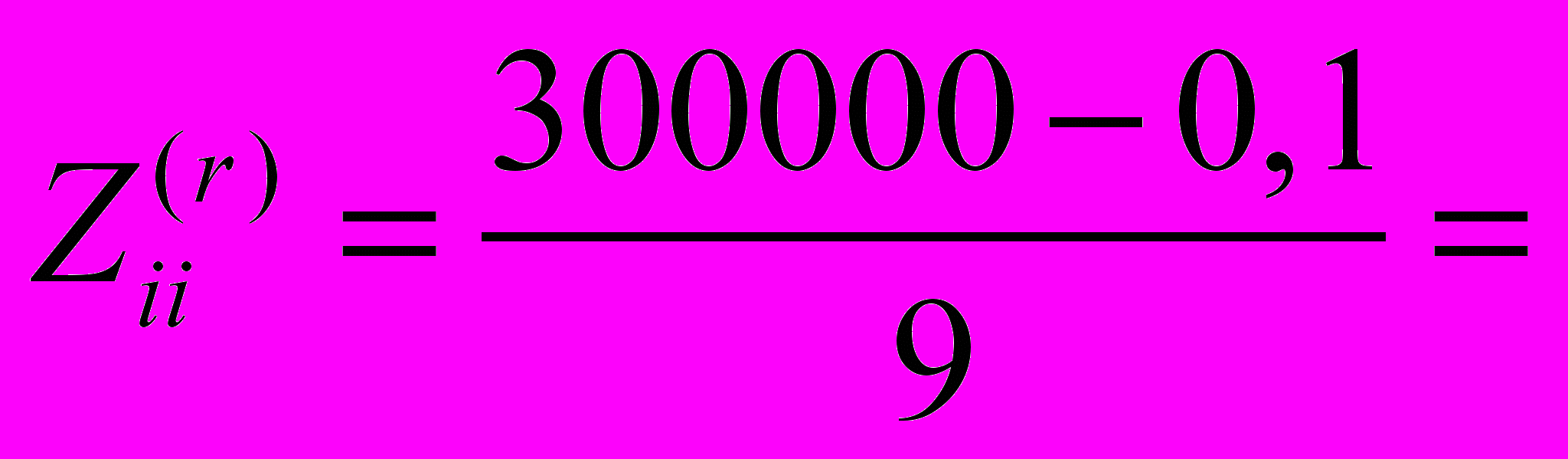

33333,32 Ом.

Определяются интервалы. 1-й интервал [0,1 Ом; 33333,32 Ом] ([; 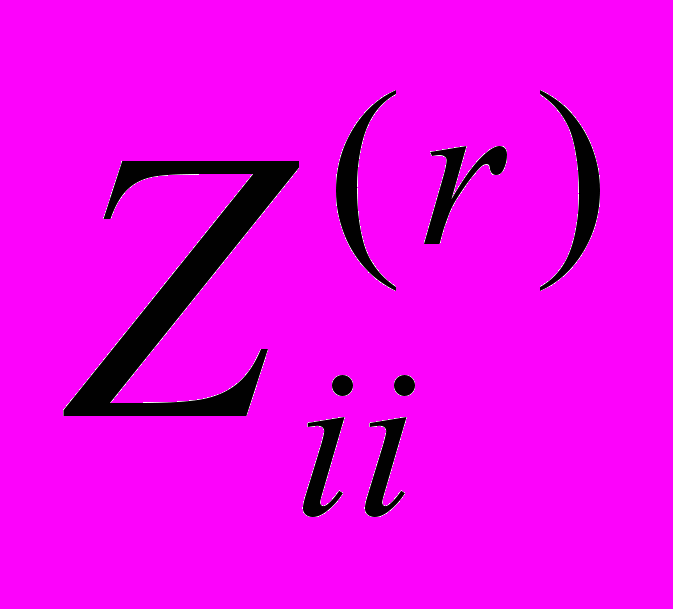]), 2-й интервал [33333,32 Ом; 66666,64 Ом] ([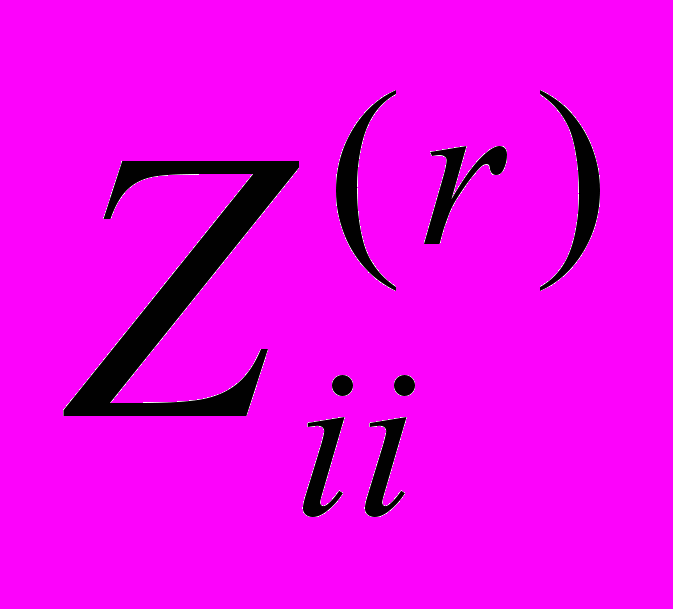; 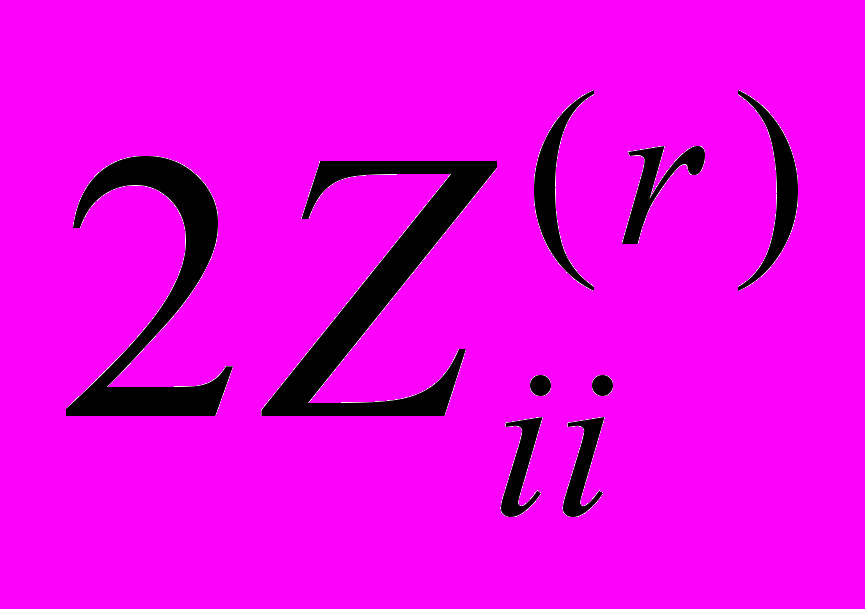]) и т. д. (для всех 9 интервалов). Например, в первый интервал попадут элементы, для которых:

0,1 Ом 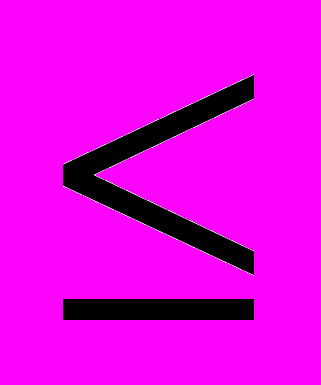Z_ii < 33333,32 Ом.

5. По величине диагональных элементов матрицы Z_у определяются те узлы, которые попадают в полученные интервалы. Таким образом, происходит декомпозиция схемы по узлам.
   

Затем «просматриваются» все диагональные элементы и определяется принадлежность каждого элемента к одному из кластеров (к подсети). Несмотря на то, что в единицах сопротивлений интервалы одинаковы (длина одинакова), количество элементов в каждом интервале будет разное, другими словами размеры кластеров (подсетей) будут различны.

6. По полученным диагональным элементам для каждого кластера определяются остальные элементы для каждой подсети (недиагональные элементы). В матрице Z_у элементы Z_ij выбираются таким образом, чтобы один и тот же элемент входил только в один кластер. Таким образом, исходная матрица Z_у разделяется на N_к кластеров.
   
7. По полученным кластерам определяются элементы структуры сети – матрица Г[4]. Матрица Г для кластера получается по матрице Г для всей сети. Так как известны номера узлов, которые относятся к кластеру, то по ним можно определить ветви, относящиеся к искомому кластеру, (в матрице Г для полной схемы это будут те, ветви, которые начинаются (-y) и заканчиваются (+y) в той части схемы, которая выделяется в кластер). Если в какой-то строке матрицы Г полученной подматрицы есть строка только с +y или только -y, то эта ветвь также войдёт в кластер. Такие ветви будем называть «граничными». Но в дальнейшем при окончательном формировании кластера возможно либо исключение этой ветви, либо определение принадлежности этой ветви кластеру (определяется по матрице коэффициентов распределения С). Если строка матрицы Г нулевая, то такие строки не входят в матрицу Г для кластера. В противном случае строка, относящаяся к полной матрице Г, будет относиться и к матрице Г для кластера. При нумерации базисный узел обозначается нулевым. Вышеприведённое правило получения матрицы Г для кластера в случае его применения к базисному узлу будет работать не совсем корректно. Для корректировки при рассмотрении ветви, связанной с базисным узлом необходимо (для неё будет строка только с +y или только –y) эту ветвь включить в матрицу Г для кластера.
   
8. Для «граничных» ветвей, которые входят и в один, и в другой кластер (в связи с тем, что определение ветвей, связывающих разные кластеры, носило предварительный характер) по матрице коэффициентов распределения C определяется принадлежность ветви к одному из кластеров. Это осуществляется по величине элементов матрицы C, полученной для каждого из кластеров. Ветвь, входящая в оба кластера (исходя из определения ветвей по матрице Z_у), окончательно должна входить только в один кластер.
   

В полученных матрицах C для обоих кластеров, в которые входит одна и та же ветвь (только в одном случае эта ветвь, например, выходит из узла (-y), относящегося к одному из кластеров, а в другом случае входит в узел (+y), относящийся уже к другому кластеру), сравниваются значения элементов матрицы C, которые относятся к этой ветви.

Та «граничная» ветвь, у которой значение элемента матрицы C по модулю больше, окончательно определяется в один из кластеров. В другом кластере (в котором эта ветвь также была) эта ветвь не рассматривается. Так как при этом теряется информация об узле, который связывала эта ветвь, то узел другого кластера заменяется при этом так называемым фиктивным узлом.

Фиктивный узел – узел, показатели надёжности которого равны нулю, и он не учитывается при определении сечений в этом кластере. Получившиеся ветви, связывающие вновь образовавшиеся фиктивные узлы с реальными узлами, не будут одноэлементными сечениями относительно фиктивных узлов. Они будут показывать связь между кластерами.

При расчёте режима в большой ЭЭС в элементах могут возникать перегрузки. Для снятия этих перегрузок предлагается метод определения ветвей-кандидатов на переключение для снижения аварийной перегрузки в элементах сложной сети, основанный на количественных взаимосвязях между элементами (режимами ветвей).

Для получения коэффициентов корреляции между нагрузками ветвей необходима информация о коэффициенте корреляции между нагрузками узлов. Коэффициент корреляции показывает, как режим в одной ветви влияет на другую ветвь. Это является исходной информацией. Но, как правило, такого рода информация на практике отсутствует.

Для решения данной задачи можно использовать приближённый метод, который основывается на моделировании нагрузок узлов независимыми случайными величинами (пренебрежение вероятностными взаимосвязями между режимами электропотребления узлов). Это вполне допустимо, так как обычно перегрузки допускаются на короткое время, а на коротких интервалах времени нагрузки узлов можно считать независимыми случайными величинами.

Поэтому для определения кандидатов на переключение при перегрузке одной или нескольких ветвей необходимо в цифровом виде определить взаимозависимость между перегруженными ветвями (ветвью) и всеми остальными в послеаварийном состоянии системы. Для исследуемой системы, чтобы в «чистом» виде оценить влияние изменения нагрузки одной ветви на другую, нагрузки узлов задаются интегральными характеристиками задающих токов узлов независимых случайных величин. Далее по формуле [2] определяется матрица корреляционных моментов.

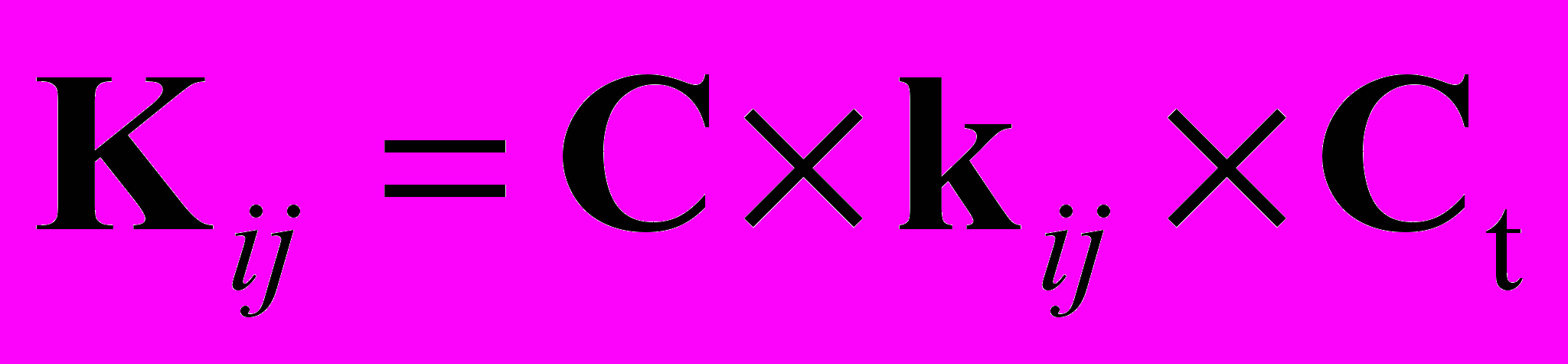, (5)

где 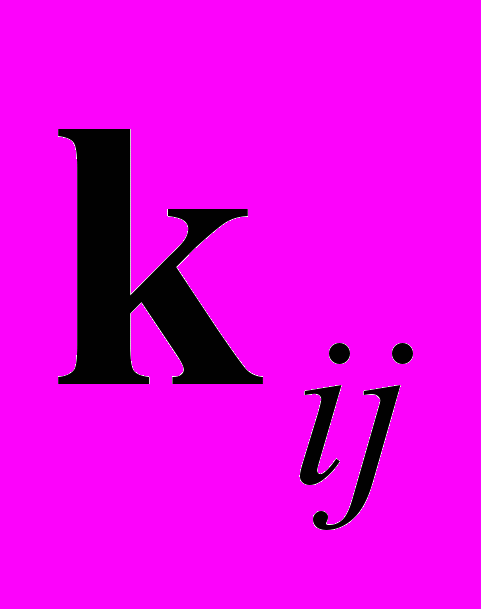- матрица корреляционных моментов токов узлов (квадратная и симметричная относительно главной диагонали).

- матрица корреляционных моментов токов ветвей. По матрице корреляционных моментов находим коэффициенты корреляции: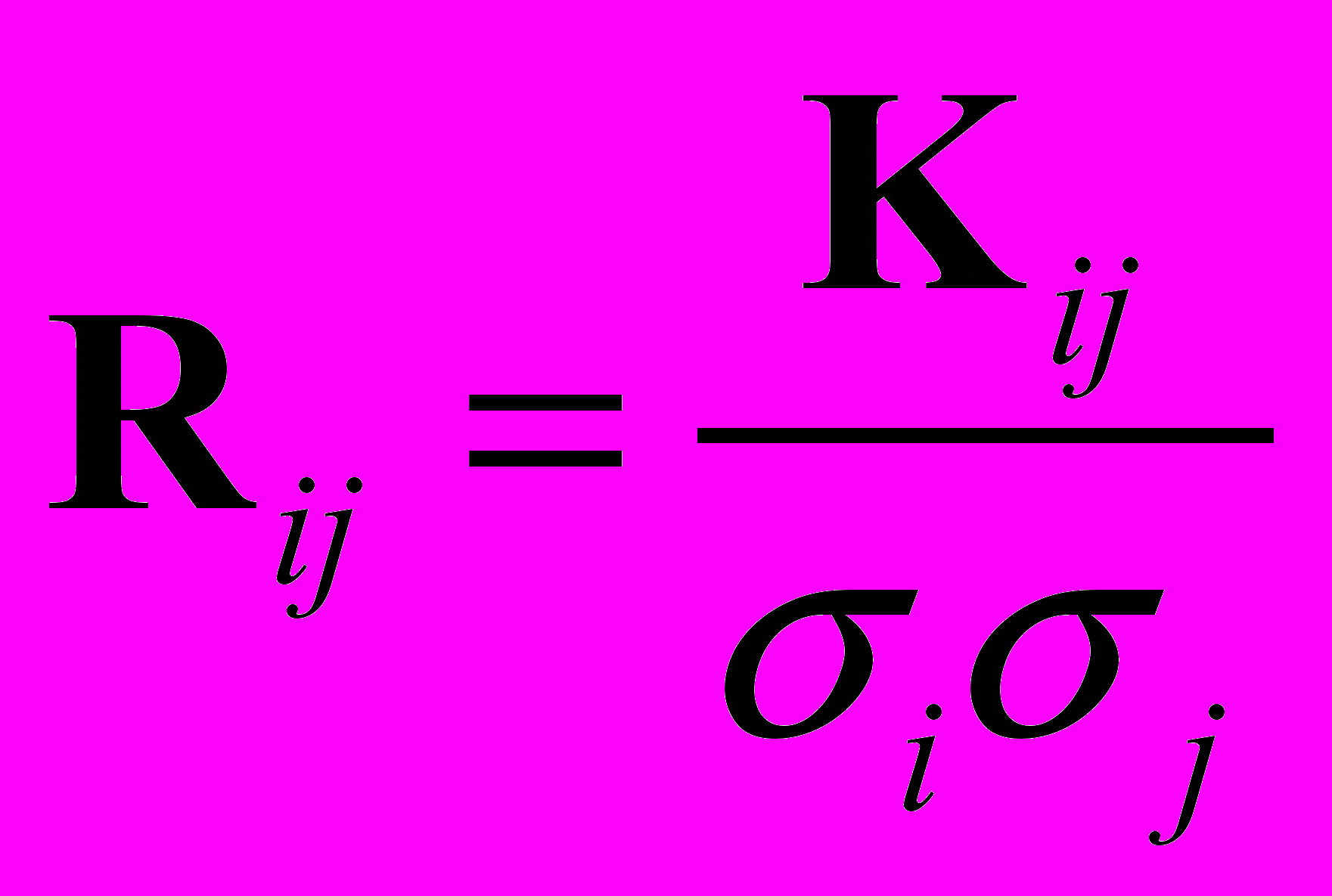

, (6)

R_ij – коэффициент корреляции между нагрузками ветвей.

При выявлении перегруженной ветви необходимо найти те ветви в сети, которые наименее всего загружены. Для этого анализируются все коэффициенты корреляции перегруженной ветви с остальными ветвями. Ветвями – кандидатами на отключение будут те ветви, коэффициент корреляции которых с перегруженной ветвью по модулю наибольший. То есть это будет означать, что корреляционная взаимосвязь между этими ветвями будет наибольшей.

При определении ветвей – кандидатов на включение (при рассматриваемой перегруженной ветви) необходимо найти минимальный коэффициент корреляции между этими ветвями и, кроме того, проверить возможность включения этой ветви. Отключённая ветвь моделируется большим сопротивлением, ориентировочно 10⁶ Ом. (Получено в результате вычислительных экспериментов на ЭЭС большого размера) В этом случае эта ветвь будет входить в матрицу коэффициентов распределения С, и будет возможность включить в работу эту ветвь.

Аналогичный подход используется для определения ветвей- кандидатов на отключение.


Выводы.

1. Ресурсы современных ПЭВМ позволяют успешно решать режимно-надежностные задачи комбинаторного характера для ЭЭС большого размера с использованием обобщённых параметров за приемлемое время.
   
2. Обоснован, разработан и прошел апробацию практически универсальный «механизм» структурно функциональной декомпозиции сложной ЭЭС, на основе обобщенных параметров схем, обеспечивающий достаточную точность расчётов ЭЭС.
   
3. Предложенный алгоритм декомпозиции по матрице узловых сопротивлений Z_у, основан на цифровом анализе параметров, характеризующих электрическую удалённость элементов ЭЭС.
   
4. Предложен один из возможных алгоритмов снижения перегрузок элементов ЭЭС с использованием также обобщённых параметров, а именно, матрицы C.
   

Литература.

1. Фокин Ю.А., Осипов Я.Н. Применение обобщенных параметров схем в расчетах структурной и функциональной надежности сложных электроэнергетических систем. Сб. науч. трудов: Методические вопросы исследования надежности больших систем энергетики, вып. 58, отв. ред. Н.И. Воропай – М.-Н.-Новгород, 2008 г., с.36-42 – 446 с.
   
2. Электротехнический справочник: В 4 т. Т. 3 Производство, передача и распределение электрической энергии / Под ред. В.Г. Герасимова и др. – 8-е изд., испр. и доп. – М.:, Издательство МЭИ, 2002 г., 964 с.
   
3. Фокин Ю.А. Вероятностно-статистические методы в расчетах систем электроснабжения – М. Энергоатомиздат, 1985 г., 240 с.
   
4. Фокин Ю.А. Методика оценки параметрической надежности систем электроснабжения. Под ред. Е.В. Путятина. – М.:, Издательство МЭИ, 1987 г., 92 с.
   

УДК 621.311.019.3

«Метод определения отказовых состояний в сложных

электроэнергетических системах»

В докладе проводится анализ методов оценки надёжности, существовавших ранее и показываются их недостатки и преимущества. Показывается недостаточность учёта только первого закона Кирхгофа при расчёте надёжности и определении отказовых состояний.

Предлагается применение обобщённых параметров схем, а именно матрицы коэффициентов распределения, для определения структурной и функциональной надёжности. Применительно к схемам большой размерности предлагается метод декомпозиции сети по признаку электрической удалённости элементов.

Использование обобщенных параметров удобнее, так как позволяет использовать единую информационную базу как для расчётов надёжности, так и при расчётах режима.


Ответ на рецензию.

1. Текст соответствует докладу, сделанному на конференции.
   
2. Фиктивные узлы, упомянутые в докладе, приняты для учёта связей между кластерами(подсетями). Показатели надёжности этих узлов приняты равными для исключения двойного счёта(учёта показателей надёжности реального узла и фиктивного).
   
3. Доклад отредактирован в соответствии с требованиями.
   

Фокин Ю. А.; Осипов Я. Н.


Просим опубликовать данный доклад в сборнике «Методические вопросы исследования надёжности больших систем энергетики».