При обработке информации, связанной с изображением на мониторе, принято выделять три основных направления: распознавание образов, обработку изображений и машинную графику

Вид материала

Задача

Содержание Закраска гранично-связной области 1-2. Начнём формировать новый список вершин. В соответствии с ориентацией ребра занесём в выходной список вершину 2 => {2}. Дале Определение яркости в точке пересечения с областью вывода. 3.1. Координаты и преобразования P = [x y] -- вектор-строка исходных координат,P` 3.4. Трехмерные геометрические преобразования 3.4.4 Движение по рельефу

Подобный материал:

• Конспект Лекций Лекция 1 Введение в компьютерную геометрию и графику Основные направления, 1002.69kb.
• Задачи обработки изображения : Устранение дефектов изображения (напр., устранение снега, 98.28kb.
• Белорусский государственный университет применение информационных технологий при анализе, 187.23kb.
• Лабораторная работа № Нейросетевое распознавание печатных символов. Дисциплина: «Распознавание, 74.04kb.
• Распознавание и преобразование образов указатель документов описания первоисточников., 52.79kb.
• 7. западноевропейский тип культуры, 587.09kb.
• Нелинейная цифровая фильтрация лазерных изображений при регистрации и обработке, 242.95kb.
• Алгоритмы восстановления изображений при томографической обработке проекций, 48.43kb.
• Доклад посвящен методам сопоставления образов с шаблоном в системе автоматической обработки, 31.12kb.
• Программа по дисциплине "Распознавание образов/(по выбору)" для подготовки студентов, 89.53kb.

Закраска гранично-связной области

Существует несколько алгоритмов закраски такой области. Рассмотрим два из них.

1)      Использует рекурсию. Метод прост для программирования, однако крайне неэффективен. От затравочной точки просматривают все точки. Если они не граничные, закрашивают и посылают в стек. Далее вытаскивают из стека, и если точка не является граничной и закрашенной, делают то же самое. См. блок-схему рис.2.9.3.



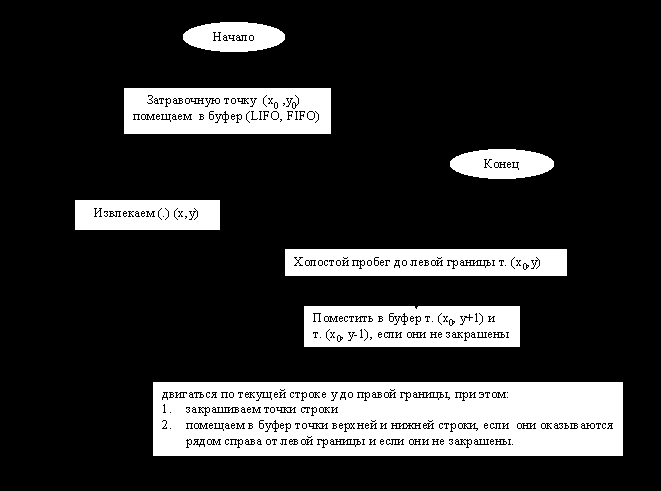
рис. 2.9.3.



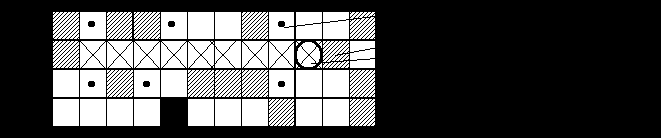
Рис. 2.9.4.

Алгоритм закраски областей, заданных списком вершин

(метод построчного сканирования)

Интерполяция яркости при закраске областей

О линейной интерполяции яркости при закраски области можно говорить, если закрашиваемая фигура плоская т.е. лежит в одной плоскости, например (ХУ).



Рис. 2.9.5.

Плоскость определяется по трём точкам:



Рис. 2.9.6.

   

 

|| || - определитель матрицы;

  A·x + B·y + D A В D

V = - ¾¾¾¾¾¾¾ = a·x + b·y + g, где a = - ¾, b = - ¾ , g = - ¾;

  C С C C

 

V = V₁ + α (х - х₁)+β (у - у₁), где

V – яркость в произвольной точке, V₁ – яркость известная.

Предварительно производится отсечение многоугольника по полю вывода. Существуют различные задачи закраски: выпуклых многоугольников и многоугольников произвольной формы. Начнем с закраски произвольного многоугольника.



Рис.2.9.7.

Сначала находят y_max и y_min. Далее для текущей у-координаты находят крайнее левое и крайнее правое ребро. Начинают с крайнего левого ребра: идут вправо (и закрашивают соответствующие точки) до пересечения со следующим ребром. Также необходим анализ на наличие локальных экстремумов. В этих точках режим закраски не меняется. Солнечный пляж египта - отдых для вашей семьи

Алгоритм работает с помощью 2-х таблиц:

1.       таблица ребер (ТР);

2.       таблица активных ребер (ТАР);

В ТР заносятся все ребра, а в ТАР лишь те ребра, которые мы пересекаем.

Составление ТР:

 Все ребра делятся на группы по нарастанию у-координаты, а внутри группы рёбра упорядочиваются в соответствии с нарастанием х_нач. Ребро в таблицу заносится только 1 раз, горизонтальные ребра игнорируются.

A (1, 2) B (4, 8) C (8, 6) D (7, 2) E (5, 4)

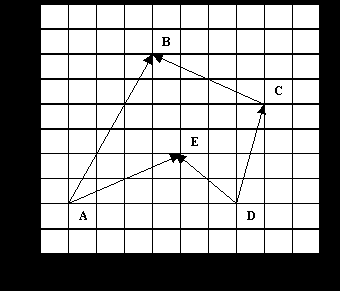
Таблица рёбер:

Группа, №	Ребро	ymin	ymax	хНАЧ	хКОН	∆x	VНАЧ	VКОНЕЧ	∆V
1	АВ	2	8	1	4	0.5
	АЕ		4	1	5	2
	DC		6	7	8	0.25
	DE		4	7	5	-1
2	CB	6	8	8	4	-2

 х_КОН ¾  х_НАЧ V_{КОНЕЧ  ¾}  V_НАЧ

Dх = ¾¾¾¾¾¾; DV = ¾¾¾¾¾¾¾;

  y_max ¾ y_min y_max ¾  y_min

Алгоритм

1.       Сформировать ТР и подготовить ТАР

2.       Выбор первой координаты сканируемой строки: у = min {y_min};

3.       Если у = у_min, то перенос группы из ТР в ТАР.

Таблица активных ребер (ТАР)

Ребро	уНАЧ	хНАЧ	∆х	VНАЧ	∆V
AB	2	1	0.5
AE	2	1	2
DC	2	7	0.25
DE	2	7	-1

4. Упорядочивание ребер в ТАР по возрастанию х_НАЧ.

5. Сканирование (проводят сканирующую строку).
а) переключение режимов по х_НАЧ

б) учёт прохождения через вершины – локальные экстремумы. Если точка – локальный экстремум, то режим следует сохранить. Для отслеживания данной ситуации можно включить в ТР у_max, при совпадении необходим дополнительный анализ.

в) проводить линейную интерполяцию яркости при закраске от (х_НАЧ , V_НАЧ)_i  до (х_НАЧ , V_НАЧ)_i+1

6. Удалить из ТАР те ребра, для которых справедливо у = у_max

7. Для всех элементов в ТАР произвести: х_НАЧ = х_НАЧ + ∆х;  V_НАЧ = V_НАЧ + ∆V;

8. Переход к следующей сканирующей строке: y=y+1;

9. Проверка на окончание: если y>max{у_max}, то конец, иначе осуществить переход к п.3).

2.10. Отсечение плоских фигур (алгоритм Коэна-Сазерленда)



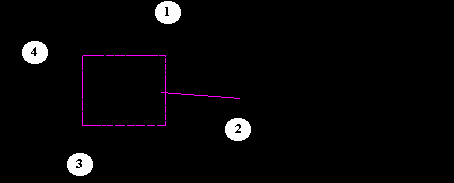
Предварительно необходимо договориться о направлении обхода вершин (по часовой стрелке или против неё). Фигура должна быть замкнутой.

Последовательно производят отсечение многоугольника по четырём границам.

.

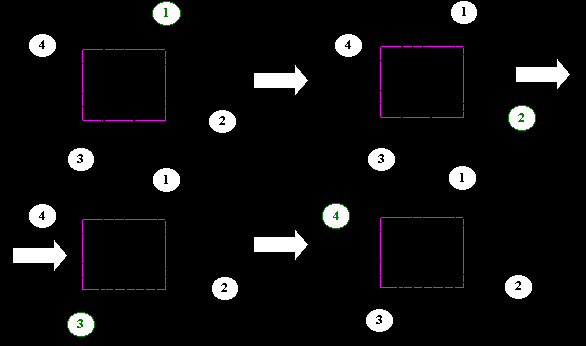
Анализ ребер: возможно 4 варианта расположения ребра в пространстве:



Может также возникнуть вариант, когда ребро совпадает с границей.

В случае 1: Добавить в список рисуемых вершин Р;

  2: Добавить в список Q;

 3:  Ничего не добавляется;

 4: Добавить в список Р,Q;

Пример: многоугольник задан списком вершин {1,2,3,4,5,6,7,1}



Последовательно переберём все рёбра. Начнем процесс с точки 1 и ребра 1-2. Начнём формировать новый список вершин. В соответствии с ориентацией ребра занесём в выходной список вершину 2 => {2}. Далее рассмотрим ребро 2-3: добавляется точка 8 => {2, 8}

3-4: {2, 8, 9, 4}.

4-5: {2, 8, 9, 4, 10}.

5-6: {2, 8, 9, 4, 10}. Ребро полностью оказалось вне, поэтому ничего не добавляется.

6-7: {2, 8, 9, 4, 10, 11, 7}.

7-1: {2, 8, 9, 4, 10, 11, 7, 1}.

Таким образом, новый список вершин: {2, 8, 9, 4, 10, 11, 7, 1}.

Определение яркости в точке пересечения с областью вывода.



Вычисления проводятся по одной из двух формул:

(1)  

(2)   

Примечание:

По формуле (1) считают, если |у₂ – у₁| ³ |х₂ – х₁|, по формуле (2) - если 

|у₂ – у₁| < |х₂ – х₁|;

3.1. Координаты и преобразования

Описание, конструирование, манипулирование и представление геометрических объектов являются центральными работами в графических системах. Их поддержка в требуемом объеме за счет соответствующих математических методов, алгоритмов и программ оказывают существенное влияние на возможности и эффективность графической системы. В данном разделе будут рассмотрены математические методы для описания геометрических преобразований координат в двух и трехмерном случае, будут обсуждены некоторые вопросы эффективности, рассмотрены геометрические преобразования растровых картин.

Далее большими буквами x, y, z будут обозначаться обычные декартовые координаты, а маленькие буквы X, Y, Z будут использоваться для обозначения т.н. однородных координат.

3.2. Двумерные геометрические преобразования

Параллельный перенос



Параллельный перенос в плоском случае имеет вид:

 

   x` = x + Dx

 y` = y + Dy

[x’, y’] = [x, y] + [Dx, Dy]

 

 P’ P T

или в векторной форме:

P` = P + T,

где  P` = [x` y`] - вектор-строка преобразованных координат,

где x, y - исходные координаты точки,
Tx, Ty - величина сдвига по осям,
x`, y` - преобразованные координаты.
P = [x y] -- вектор-строка исходных координат,
P` = [x` y`] -- вектор-строка преобразованных координат,
T = [Tx Ty] -- вектор-строка сдвига.

Масштабирование



Преобразование масштабирования относительно начала координат имеет вид:

  x` = x ·Sx

 y` = y ·Sy или

 

  Sx 0

[x`, y`] = [x, y] ·

   0 Sy 

  P` P

  S 

или в матричной форме:

P` = P ·S,

где Sx, Sy -- коэффициенты масштабирования по осям, а

S - матрица масштабирования

Поворот



Преобразование поворота относительно начала координат имеет вид:

 

  x`= x·cos(φ) – y·sin(φ)

  y`= x·sin(φ) + y·cos(φ)

или

   cos(φ) sin(φ)

[x`, y`] = [x, y] ·

   –sin(φ) cos(φ) 

  P` P

  R 

Где R – матрица поворота

φ – положительный угол поворота

или в матричной форме:

P` = P ·R,

Столбцы и строки матрицы поворота представляют собой взаимно ортогональные единичные векторы. В самом деле квадраты длин векторов-строк равны единице:

cos·cos+sin·sin = 1

(-sin) ·(-sin)+cos·cos = 1,

а скалярное произведение векторов-строк есть

cos·(-sin) + sin·cos = 0.

Так как скалярное произведение векторов A ·B = A ·B ·cos, где A - длина вектора A, B - длина вектора B, а  - наименьший положительный угол между ними, то из равенства скалярного произведения двух векторов-строк длины 1 следует, что угол между ними равен 90^.

Аналогичное можно показать и для векторов-столбцов. Кроме того вектора-столбцы представляют собой такие единичные векторы, которые после выполнения преобразования, заданного этой матрицей, совпадут с осями. В самом деле, произведение первого столбца на матрицу есть

 

cos

-sin

·

cos

sin

=

1 0

,

-sin

cos

т.е. это единичный вектор вдоль оси X.

Аналогично, произведение второго столбца на матрицу даст вектор [ 0 1 ]. Это позволяет сформировать матрицу, если известны результаты преобразования.

3.4. Трехмерные геометрические преобразования

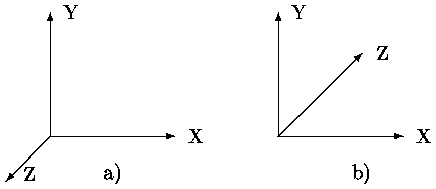
Далее при рассмотрении трехмерных преобразований, в основном, используется общепринятая в векторной алгебре правая система координат (рис. а). При этом, если смотреть со стороны положительной полуоси в центр координат, то поворот на +90^ (против часовой стрелки) переводит одну положительную ось в другую (направление движения расположенного вдоль оси и поворачивающегося против часовой стрелки правого винта и положительной полуоси совпадают). В некоторых, специально оговариваемых случаях, используется левая система координат (см. рис. б). В левой системе координат положительными будут повороты по часовой стрелке, если смотреть с положительного конца полуоси. В трехмерной машинной графике более удобной является левая система координат. Тогда если, например, поверхность экрана совмещена с плоскостью XY, то большим удалениям от наблюдателя соответствуют точки с большим значением Z (см. рис. б).




Работа с однородными трехмерными координатами и матрицами преобразования (формирование и композиция) подобна таковой для двумерного случая, поэтому здесь будут рассмотрены только матрицы преобразований сдвига, масштабирования и поворота и пример конструирования матрицы преобразования по известному его результату.

Подобно тому как в двумерном случае точка в однородных координатах представляется трехмерным вектором [ X Y W ], а матрицы преобразований имеют размер 3×3, для трехмерного случая точка представляется четырехмерным вектором [ X Y Z W ], где W не равно 0, а матрицы преобразований имеют размер 4×4.

Формулы для преобразования:

Если W не равно 1, то декартовые координаты точки (x,y,z) получаются из соотношения:

[ x y z 1 ] = [ (X/W) (Y/W) (Z/W) 1 ].

Параллельный перенос:

  Р` = Р∙Т;

1 0 0 0 

Где Т =

  0 1 0 0 - матрица переноса

0 0 1 0 
Tx Ty Tz 1

Масштабирование:

  Р` = Р∙S;

 

  Sx 0 0 0 

S =

 0 Sy 0 0 , S – матрица

  0 0 Sz  0
0 0 0 1

Поворот:

При повороте в 3-х мерном пространстве существует 3 поворота вокруг каждой из осей.

Кроме того, существует 2 системы координат: правая и левая.

Для обеих систем: Х: Y→Z Y: Z→X Z: X→Y

Ранее рассмотренная для двумерного случая матрица поворота является в то же время трехмерным поворотом вокруг оси Z. Так как при трехмерном повороте вокруг оси Z (поворот в плоскости XY) размеры вдоль оси Z неизменны, то все элементы третьей строки и третьего столбца равны 0, кроме диагонального, равного 1:

Rz(z) =			cosz	sinz	0	0			.
			-sinz	cosz	0	0
			0	0	1	0
			0	0	0	1

При повороте вокруг оси X (в плоскости YZ) размеры вдоль оси X не меняются, поэтому все элементы первой строки и первого столбца равны 0, за исключением диагонального, равного 1:

Rx(x) =			1	0	0	0			.
			0	cosx	sinx	0
			0	-sinx	cosx	0
			0	0	0	1

При повороте вокруг оси Y (в плоскости XZ) размеры вдоль оси Y не меняются, поэтому все элементы второй строки и второго столбца равны 0, за исключением диагонального, равного 1:

Ry(y) =			cosy	0	-siny	0			.
			0	1	0	0
			siny	0	cosy	0
			0	0	0	1

В общем случае любой поворот в пространстве может быть описан с помощью некоторых комбинаций этих трех поворотов. Причём повороты не обладают свойством коммутативности:

R_X ∙ R_Y ∙ R_Z ≠ R_Z ∙ R_X ∙ R_Y.

Любой произвольный поворот может быть представлен 6 сочетаниями элементарных поворотов. Причем в каждом случае будут свои углы (за исключением вырожденных ситуаций).



P` = P ∙ R, где R – матрица поворотов.

P` = [X`, Y`, Z`, 1];

P  = [X, Y, Z, 1];

Элементы R – косинусы соответствующих углов.

 

   a₁ a₂ a₃ 0 cos(XOX`) cos(XOY`) cos(XOZ`)  0

==

R =

   b₁ b₂  b₃ 0 cos(YOX’) cos(YOY’) cos(YOZ’)  0

  c₁ c₂  c₃ 0 cos(ZOX’) cos(ZOY’) cos(ZOZ’) 0

   0 0 0 1 0 0 0 1

Элементы матрицы R можно также рассматривать в виде векторов:



`i, `j, `k – это вектора единичной длины.

`N<sub>1 =</sub> `i ·a₁ +`j ·b<sub>1</sub> +`k·c₁ `M<sub>1 =</sub> `i ·a₁ +`j ·a<sub>2</sub> +`k·a₃
`N<sub>2 =</sub> `i ·a₂ +`j ·b<sub>2</sub> +`k·c₂ `M<sub>2 =</sub> `i ·b₁ +`j ·b<sub>2</sub> +`k·b₃
`N<sub>3 =</sub> `i ·a₃ +`j ·b<sub>3</sub> +`k·c₃ `M<sub>3 =</sub> `i ·c₁ +`j ·c<sub>2</sub> +`k·c₃

Запишем векторное произведение:

`N<sub>1</sub> ´`N₂ =`N<sub>3</sub>  `M₁ ´`M<sub>2</sub> =`M₃  

`N<sub>2</sub> ´`N₃ =`N<sub>1</sub>  `M₂ ´`M<sub>3</sub> =`M₁  

`N<sub>3</sub> ´`N₁ =`N<sub>2</sub>  `M₃ ´`M<sub>1</sub> =`M₂  

Скалярное произведение:

`N<sub>1</sub> ·`N₂ =`N<sub>1</sub> ·`N₃ =`N<sub>2</sub> ·`N₃ = 0

Композиция 3D изображений

P` = P·M; P = P`· М^–1

Поворот вокруг произвольной оси, проходящей через начало координат:

  z

	l2+m2+n2=1,т.е. координата нормирована

 

j

P’

P

y

x

   (l, m, n) 

  

   

 

 

  

 

 l²+cos(j)·(1–l²) l·(1–cos(j))·m+n·sin(j) l·(1–cos(j))·n–m·sin(j) 0 

	M =

 

 l·(1–cos(j))·m m²+cos(j)·(1–m²) m·(1–cos(j))·n+l·sin(j) 0 

 l·(1–cos(j))·n+m·sin(j) m·(1–cos(j))·n–l·sin(j) n²+cos(j)·(1–n²) 0 

  0 0 0 1 

M – в общем случае не ортогональная матрица, т.е. М^–1≠ М^Т,

а R–ортогональная (R^–1=R^T).

В общем виде матрица преобразований имеет вид:

  m₁₁ m₁₂ m₁₃  0 

 m₂₁  m₂₂ m₂₃ 0

M = m₃₁ m₃₂ m₃₃  0

 m₄₁ m₄₂ m₄₃  1

Координаты точки вычисляются по следующим формулам:

X` = X*m₁₁+Y* m₂₁+ Z* m₃₁+ m₄₁ 

Y` = X*m₁₂+Y* m₂₂+ Z* m₃₂+ m₄₂

Z` = X*m₁₃+Y* m₂₃+ Z* m₃₃+ m₄₃

3.4.4 Движение по рельефу

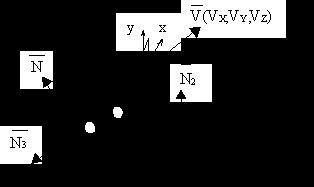Нормаль к поверхности определяет N₂ => a₂b₂c₂

V_z как правило не известен