Циклические алгоритмы 12 Вопросы для повторения: 17

Вид материала

Документы

Содержание Этапы решения задач на ЭВМ Моделирование и формализация Формы представления моделей Постановка задачи Результатом первого этапа Отладка и тестирование программы Компьютерный эксперимент I. Расписание Свойства алгоритма Линейный алгоритм Алгоритмическая структура «ветвление» Циклические алгоритмы Вопросы для повторения

Подобный материал:

• «Численные методы в химии» Общая трудоёмкость дисциплины составляет, 22.46kb.
• Методика обучения информатике Перечень примерных контрольных вопросов и заданий для, 158.15kb.
• Циклические алгоритмы. Цикл с предусловием, 297.88kb.
• 2008/2009 учебный год Вопросы для повторения: Философия, ее предназначение, смысл, 37.19kb.
• История Европы Нового времени. Проблемные вопросы (1) и вопросы для повторения (2), 8.95kb.
• Доклады, рефераты и вопросы для повторения, 40.59kb.
• Белая Холуница Кировская область Описание проекта Название проекта Алгоритмы и основы, 179.54kb.
• Лекция: Алгоритмы синхронизации, 244.5kb.
• Вопросы для повторения: Политическая карта Западной Европы (XI-XV вв.), 123.79kb.
• Вопросы для повторения к зачету по дисциплине, 27.32kb.

ТКК им. Л.С.Дёмина





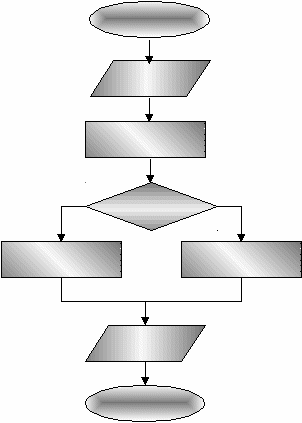
Учитель информатики

Спиридонова Н.Е.


Содержание

Этапы решения задач на ЭВМ

Моделирование и формализация

С различными моделями и модельными представлениями мы встречаемся каждодневно и ежечасно. Моделями являются фотография, карта дорог, географическая карта, рисунок, картина, различные описания и т.д.

Модели незаменимы в физике, химии, биологии, математике, информатике. Выбор модельных представлений часто определяет успех научных исследований, т.к. от него зависит точность и достоверность получаемых выводов, прогнозов и рекомендаций.

Моделирование – это метод познания, состоящий в создании и исследовании моделей.

Модели по своей сути – чисто информационное понятие.

Модель – отражение наиболее существенных признаков, свойств, отношений, явлений, объектов или процессов предметного мира (фотографии и рисунки – это представление внешнего вида предметов, а чертежи раскрывают их структуру (внутреннюю организацию)).

Для одних и тех же объектов, процессов и явлений можно построить различные модели, а разные объекты могут описываться одной моделью. Многообразие модельных представлений, связываемых с одними и теми же объектами, отражает различие точек зрения, интересов, потребностей людей в изучении этих объектов. В математике и информатике модели служат основой для постановки задачи.

Формы представления моделей

Все модели можно разбить на два больших класса: модели предметные (материальные) и модели информационные. Пред­метные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме (глобус, анатомические муляжи, модели кристаллических решеток, макеты зданий и сооружений и др.).

Информационные модели представляют объекты и про­цессы в образной или знаковой форме.

Образные модели (рисунки, фотографии и др.) представ­ляют собой зрительные образы объектов, зафиксированные на каком-либо носителе информации (бумаге, фото- и кино­пленке и др.). Широко используются образные информаци­онные модели в образовании (учебные плакаты по различным предметам) и науках, где требуется классифи­кация объектов по их внешним признакам (в ботанике, био­логии, палеонтологии и др.).

Знаковые информационные модели строятся с использо­ванием различных языков (знаковых систем). Знаковая ин­формационная модель может быть представлена в форме текста (например, программы на языке программирования), формулы (например, второго закона Ньютона Р = т•а), таб­лицы (например, периодической таблицы элементов Д.И. Менделеева) и так далее.

Работа по решению задач с использованием компьютера проходит через следующие этапы:



Эту последовательность называют технологической цепочкой решения задачи на компьютере. Дадим описание каждого из перечисленных этапов.

Постановка задачи

На этапе постановки задачи должно быть четко определено, что дано, и что требуется найти. Так, если задача конкретная, то под постановкой задачи понимают ответ на два вопроса: какие исходные данные известны и что требуется определить. Если задача обобщенная, то при постановке задачи понадобится еще ответ на третий вопрос: какие данные допустимы. Таким образом, постановка задачи включает в себя следующие моменты: сбор информации о задаче; формулировку условия задачи; определение конечных целей решения задачи; определение формы выдачи результатов; описание данных (их типов, диапазонов величин, структуры и т. п.).

Поиск решения любой задачи начинается с анализа ее условий. Результатом анализа условий должна стать четкая постановка задачи, в которой должны быть ответы на четыре вопроса:

1. Что дано? Что требуется? Какие данные допустимы? Какие результаты будут правильными, а какие нет?
   

Результатом первого этапа должно стать построение описательной информационной модели.

Формализация

Правильность результатов решения задачи с помощью компьютера зависит, прежде всего, от правильности выбранного метода решения. Метод решения является правильным, если для любых допустимых исходных данных он приводит к получению результатов, соответствующих постановке задачи. Для решения задач с помощью компьютера соответствующим методам необходимо дать математическую интерпретацию.

На этом этапе строится математическая модель - система математических соотношений - формул, уравнений, неравенств и т. д., отражающих существенные свойства объекта или явления. Необходимо отметить, что при построении математических моделей далеко не всегда удается найти формулы, явно выражающие искомые величины через данные. В таких случаях используются математические методы, позволяющие дать ответы той или иной степени точности.

В случае большого числа параметров, ограничений, возможных вариантов исходных данных модель явления может иметь очень сложное математическое описание (правда, реальное явление еще более сложно), поэтому часто построение математической модели требует упрощения требований задачи. Необходимо выявить самые существенные свойства объекта, явления или процесса, закономерности; внутренние связи, роль отдельных характеристик. Выделив наиболее важные факторы, можно пренебречь менее существенными.

Итак, создавая математическую модель для решения задачи, нужно: выделить предположения, на которых будет основываться математи­ческая модель; определить, что считать исходными данными и результатами; записать математические соотношения, связывающие результаты с исходными данными.

Алгоритмизация

Наиболее эффективно математическую модель можно реализовать на компьютере в виде алгоритмической модели. Для этого может быть использован язык блок-схем или какой-нибудь псевдокод, например учебный алгоритмический язык. Разработка алгоритма включает в себя выбор метода проектирования алгоритма; выбор формы записи алгоритма (блок-схемы, псевдокод и др.); выбор тестов и метода тестирования; проектирование самого алгоритма.

Программирование

Первые три этапа - это работа без компьютера. Дальше следует собственно программирование на определенном языке в определенной системе программирования. Программирование включает в себя следующие виды работ: выбор языка программирования; уточнение способов организации данных; запись алгоритма на выбранном языке программирования.

Справедливости ради, надо сказать, что этот этап решения задачи было бы правильнее назвать "Компьютерным моделированием", т. к. при решении некоторых задач можно обойтись без составления программы на языке программирования, это можно успешно сделать, используя современные приложения (электронные таблицы, системы управления базами данных и пр.). В этом случае не понадобится и следующий этап - отладка и тестирование программы, а вот проведение расчетов и анализ полученных результатов следует проводить с особой тщательностью.

Отладка и тестирование программы

Под отладкой программы понимается процесс испытания работы программы и исправления обнаруженных при этом ошибок. Обна­ружить ошибки, связанные с нарушением правил записи программы на языке программирования (синтаксические и семантические ошибки), помогает используемая система программирования. Пользователь получает сообщение об ошибке, исправляет ее и снова повторяет попытку исполнить программу.

Проверка на компьютере правильности алгоритма производится с помощью тестов. Тест - это конкретный вариант значений исходных данных, для которого известен ожидаемый результат. Прохождение теста - необходимое условие правильности программы. На тестах проверяется правильность реализации программой запланированного сценария.

Таким образом, тестирование и отладка включают в себя синтаксическую отладку; отладку семантики (семантика определяет смысловое значение предложений алгоритмического языка) и логической структуры программы; тестовые расчеты и анализ результатов тестирования; совершенствование программы.

Компьютерный эксперимент

Последний этап - это использование уже разработанной программы для получения искомых результатов. Производится анализ результатов решения задачи и в случае необходимости - уточнение математической модели (с последующей корректировкой алгоритма и программы). Программы, имеющие большое практическое или научное значение, используются длительное время. Иногда даже в процессе эксплуатации программы могут исправляться, дорабатываться.

Алгоритм

Каждый из нас ежедневно использует различные алгоритмы: инструкции, рецепты, правила и т.п. Обычно мы это делаем не задумываясь. Примеры.

I. Расписание занятий	II. Открывание двери ключом	III. Маршрут движения
1. Физика 2. Математика 3. Русский язык 4. Физическое воспитание	1. Достать ключ 2. Вставить ключ в замочную скважину 3. Повернуть ключ 2 раза против часовой стрелки 4. Вынуть ключ	1. Выйти из дома 2. Повернуть направо 3. Пройти 2 квартала до автобусной остановки 4. Сесть в автобус 30, идущий к центру города 5. Проехать 3 остановки, выйти из автобуса.

Ha первый взгляд, эти 3 алгоритма не имеют между собой ничего общего. Однако при внимательном изучении можно заметить одно существенное сходство - строгий порядок выполнения действий. Правда, алгоритм 1 как частный случай выполняется при любом порядке действий, предложенных в нем. Но алгоритм 2 при перестановке, например, 2 и 3 действий может быть выполнен, но не приведет к желаемому результату - дверь не будет открыта. Если же в алгоритме 3 поменять местами 4 и 5 действия, он станет невыполняемым. Таким образом, для алгоритма важен не только набор действий, но и то, как они организованы, т.е. в каком порядке выполняются. Это общее свойство всех алгоритмов.

Теперь мы можем сказать, что А Л Г О Р И Т М - это организованная последовательность действий. Эта формулировка не может считаться определением алгоритма, т.к. не объяснены понятия «организованная» и «действия». Абсолютно строгого определения алгоритма не существует. Это - одно из фундаментальных понятий информатики. Такое же, как понятие точки, прямой и плоскости в геометрии, пространства и времени в физике, вещества в химии и т.д.

Понятие алгоритма возникло и используется давно, значительно раньше появления компьютеров. Само слово «алгоритм» происходит от латинской формы написания имени выдающегося математика средневекового Востока Мухаммеда Аль-Хорезми, который сформулировал правила выполнения арифметический действий. Но широким распространением это понятие обязано основополагающей идее - идее автоматизации поведения исполнителя - автомата, реализуемой на основе алгоритма. Предписание о выполнении отдельного законченного действия исполнителя называется командой алгоритма. Совокупность всех команд, которые могут быть выполнены некоторым исполнителем, образует СКИ – систему команд данного исполнителя. Задача обучения алгоритмизации заключается в том, чтобы научить составлять запись алгоритмов, причем делать это так, чтобы воображаемый исполнитель мог однозначно и точно следовать предписаниям алгоритма и эффективно получать определенный результат. Это накладывает на записи алгоритмов целый ряд обязательных требований, которые мы сформулируем в виде перечня свойств, которым должны удовлетворять все алгоритмы.

Свойства алгоритма

1. Дискретность (прерывность).

Описываемый процесс должен быть разбит на последовательность отдельных шагов. Возникающая при этом запись представляет собой упорядоченную совокупность четко разделенных друг от друга предписаний (директив, команд), образующих прерывную (дискретную) структуру алгоритма: только выполнив требования одного предписания, можно приступить к выполнению следующего.

2. Понятность.

Используемые на практике записи алгоритмов составляются с ориентацией на определенного исполнителя. Составляя алгоритм, нужно знать, какие предписания этот исполнитель может понять и исполнить, а какие нет. У каждого исполнителя имеется свой перечень предписаний, которые для него понятны и которые он может исполнить. Такой перечень называют системой команд исполнителя (СКИ). Составляя запись алгоритма для определенного исполнителя, можно использовать лишь те команды, которые входят в его СКИ.

3.Определенность (детерминированность).

Будучи понятным, алгоритм не должен содержать предписаний, смысл которых воспринимается неоднозначно, т.е. алгоритм не должен оставлять места для произвола исполнителя. Предписание типа "Взять 2-3 ложки сахарного песка" или "умножить х на одно из двух данных чисел a или b" недопустимы в записи алгоритма. Кроме того, в алгоритмах недопустимы ситуации, когда после выполнения очередного предписания исполнителю не ясно, какое предписание алгоритма должно выполняться на следующем шаге.

4. Массовость

Наиболее предпочтительными являются алгоритмы, обеспечивающие решение широкого класса задач данного типа. В простейшем случае алгоритм должен обеспечивать возможность использования различных допустимых значений исходных данных, например: решение квадратного уравнения ах²+bх+с=0 в области действительных чисел может быть найдено по формулам, которые применимы не для одного, а для многих квадратных уравнений с коэффициентами а,b,с, удовлетворяющими условию: D = b² -4ас > 0

5. Результативность

Это обязательное требование к алгоритмам, смысл которого состоит в том, что при точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен быть получен какой-либо определенный ответ на вопрос задачи.

Теперь с учетом рассмотренных свойств алгоритма (в частности, свойства 2) мы можем уточнить понятие алгоритма.

А Л Г О Р И Т М - это строго определенная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд.

Разработка алгоритма – трудоемкая задача, требующая от человека глубоких знаний и больших временных затрат. Решение задачи по готовому алгоритму требует от исполнителя только строгого следования заданным предписаниям. Исполнитель не обязан вникать в смысл того, что он делает, и рассуждать, почему он поступает так, а не иначе, т.е. он действует формально – по командам.

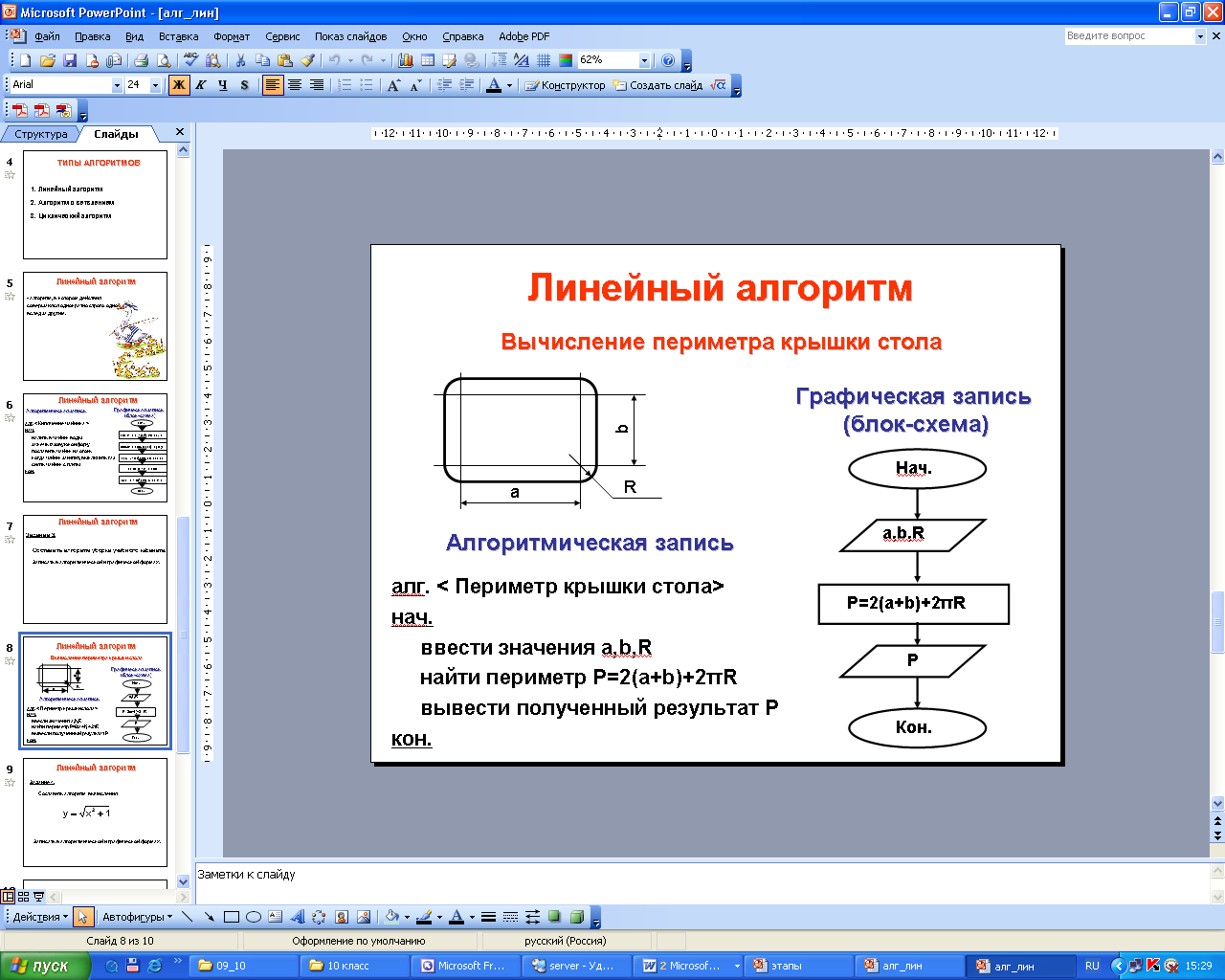
Линейный алгоритм

Алгоритм, в котором действия совершаются строго одно вслед за другим, называется ЛИНЕЙНЫМ.

Такими, например, будут алгоритмы вычислений по простейшим формулам: площадь круга, длина окружности, квадрат гипотенузы и т.д.

Алгоритмы бывают правильные и неправильные.

Для описания алгоритмов используют определенную форму записи - алгоритмический язык. Запись алгоритма должна оформляться по следующим правилам.

На первой строке записывается слово алгоритм или его трехбуквенное сокращение  алг. Далее за этим словом записывается название алгоритма.

На второй строке записывается слово начало или его сокращение  нач.

Далее в столбик записываются действия, составляющие алгоритм. Последней строкой описания алгоритма должно быть слово конец или  кон. в той же позиции, что и слово  начало. Общая форма записи:


алг. <название алгоритма>

нач. <составные команды>

действия

кон. <конец>

В алгоритмической форме можно записывать не только алгоритмы для вычислительных машин, но и различные инструкции, предписания и рекомендации для людей.

Например:

Кипячение чайника.

 алг. < Кипячение чайника.>

нач

налить в чайник воды

зажечь газовую конфорку

поставить чайник на огонь

когда чайник закипит, выключить газ

снять чайник с плиты

кон.

Очень часто алгоритмы описываются с помощью языка блок-схем. Блок-схемы являются графическим описанием алгоритма.


ЯЗЫК БЛОК – СХЕМ

Символ	Обозначение
	Начало, конец алгоритма
	Ввод и вывод данных
	Действие
	Проверка условия
	Начало цикла

Тогда алгоритм для кипячения чайника с помощью блок-схемы можно описать следующим образом:



Пример 2.

Алгоритмическая структура «ветвление»

Легко и просто было бы жить, если бы удалось раз и навсегда расписать какие поступки, и в какой последовательности совершать. На самом деле нам постоянно приходится принимать решения в зависимости от создавшейся ситуации. Если идет дождь, то мы берем зонт. Если жарко, то идем купаться. Разумеется, встречаются более сложные ситуации, когда надо делать выбор.

Логику принятия любого решения можно описать тремя ключевыми словами:

ЕСЛИ <условие> ТО <действия 1> ИНАЧЕ <действия2> - полная форма

Иногда <действия 2> могут отсутствовать:

ЕСЛИ <условие> ТО <действия 1> - неполная форма


Например:

ЕСЛИ хочешь быть здоров, ТО закаляйся, ИНАЧЕ валяйся весь день на диване

ЕСЛИ низко ласточки летают, ТО будет дождь, ИНАЧЕ дождя не будет

ЕСЛИ назвался груздем, ТО полезай в кузов.

Форма организации действий, при которой в зависимости от выполнения некоторого условия совершается та или иная последовательность действий, называется ветвлением.

Для обозначений ветвлений на блок-схемах используются ромбы, называемые блоками проверки условия.

Рассмотрим два примера.

1. Алгоритм покупки билетов в кино может выглядеть так:

1) подойти к кассе

2) если билеты на сеанс 18.00 имеются, то купить билеты

3) отойти от кассы

2. Алгоритм вечера выходного дня. Тогда:

1) если уроки выучены, то иди гулять,

2) иначе учи уроки.

Мы видим, что при выполнении каждого из этих алгоритмов наступает такой момент, когда появляется несколько направлений для продолжения.

Алгоритм как бы раздваивается, разветвляется. В этом случае говорят, что алгоритм содержит ветвление.


Алгоритмическая запись ветвления

Ветвление в неполной форме: Ветвление в полной форме:

 если  <условие>   если  <условие>

то серия 1   то серия 1

 все    иначе серия 2

  все

Графическая форма записи:









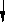
действия 1







Задание 1.

Записать рассмотренные примеры в алгоритмической форме и с помощью блок-схемы.

1) алг поход в кино нач подойти к кассе если билеты на сеанс имеются то купить билеты все кон

2) алг воскресный вечер нач если уроки выучены то иди гулять иначе учи уроки все кон

В качестве условий, по которым разветвляется алгоритм, могут использоваться операции сравнения между величинами

А<В	А меньше В
А<=В	А меньше или равно В
А=В	А равно В
А>В	А больше В
А>=В	А больше или равно В
А<>В или А><В	А не равно В

Здесь буквы А и В можно заменять на любые другие переменные, числа и арифметические выражения. Приведенные выше операции сравнения допускаются и для символьных переменных.

Условия, состоящие из одной операции сравнения, называются простыми. В качестве условий при организации ветвления можно использовать и т.н. составные условия. Составные условия получаются из простых с помощью связок И(AND), ИЛИ(OR), НЕ(NOT). Служебное слово И означает одновременное выполнение всех условий, ИЛИ – выполнение хотя бы одного условия, а НЕ означает отрицание условия, записанного за словом НЕ.

Например, алгоритм определения принадлежности точки Х отрезку [АВ]. Если точка принадлежит данному отрезку, то должен выводится ответ «ДА», в противном случае – «НЕТ».

Циклические алгоритмы

Вы легко заметите, что алгоритмы, которые мы составляли на предыдущих занятиях, обладают одним общим свойством: при их выполнении каждое действие совершается один раз или вообще не совершается. Однако человек постоянно встречается с ситуациями, для решения которых требуется многократно повторять одни и те же действия до тех пор, пока соблюдается некоторое заранее установленное условие. Используя только ветвление, такие алгоритмы не запишешь. Для этого нужна новая форма организации действий.

Предположим, нам необходимо письменно перевести английский текст на русский язык. Возможный алгоритм действий:

1. открыть текст;
   
2. прочесть предложение;
   
3. перевести это предложение на русский язык;
   
4. записать перевод в тетрадь;
   

{прочесть предложение;}

{перевести это предложение на русский язык;}

{записать перевод в тетрадь;}

5. если в тексте остались предложения, не переведенные на русский язык, то перейти к 1, в противном случае – завершить работу.
   

Ясно, что если мы соберемся писать этот алгоритм до конца, перевод придется отложить надолго.

Циклом (повтором) называется такая форма организации действий в алгоритме, при которой выполнение одной и той же последовательности команд повторяется до тех пор, пока истинно некоторое логическое выражение.

Циклический алгоритм – алгоритм, содержащий циклы.

Для организации цикла необходимо выполнить следующие действия:

• перед началом цикла задать начальное значение параметра;
  
• внутри цикла изменять параметр цикла с помощью оператора присваивания;
  
• проверять условие повторения или окончания цикла;
  
• управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из цикла в противном случае.
  

Ситуация, при которой выполнение цикла никогда не заканчивается, называется зацикливанием. Следует разрабатывать алгоритмы, не допускающие таких ситуаций.

Команда исполнителю многократно повторить указанную последовательность действий (тело цикла) называется командой повторения.

Различают следующие виды циклов:

Цикл с предусловием (цикл-пока), цикл с постусловием (цикл-до), цикл с параметром (цикл-для)

Составим блок-схему рассмотренного алгоритма: выделим последовательность действий, которые многократно повторяются при выполнении данного алгоритма. Очевидно, что это действия 2, 3 и 4. Последовательность этих действий называют телом цикла.



Проанализируем схему слева. Исполнитель сначала проверяет, выполняется ли условие. Если - да, то выполняется тело цикла, после чего условие проверяется снова, и т.д. Если же условие не выполняется, то исполнитель по ветви «нет» переходит к действию за пределом цикла.

Может случиться так, что условие не выполняется с самого начала (нет текста). Тогда действия, составляющие тело цикла, не совершаются ни разу.

Ту же самую работу можно описать и с помощью другого алгоритма. Набор действий будет тот же, однако порядок их выполнения будет иной.

Отличие данного алгоритма в том, что действия, составляющие тело цикла, сначала выполняются, и только потом проверяется условие. Оба эти алгоритма равноправны, но второй алгоритм имеет одно существенное отличие. При его выполнении, даже если условие сразу же не выполняется, тело цикла будет выполнено по крайне мере один раз. Это несущественное, на первый взгляд, отличие может иногда приводить к серьезным ошибкам. Предположим, что перевод текста будет поручена автомату, запрограммированному на выполнение второго алгоритма. Если окажется, что условие сразу не выполняется, то такой алгоритм не может быть исполнен, однако он предписывает перевести хотя бы одно предложение несуществующего текста: вряд ли автомат справится с решением этой простой задачи!

Для дальнейшей работы нам потребуется, чтобы выход из второго цикла осуществлялся по выходу «да».

Для этого, очевидно, проверяемое условие потребуется заменить на противоположное. Если в первом случае проверялось условие «непереведенные предложения есть?», то во втором случае проверяемое условие будет «непереведенных предложений нет?», или, в общем случае, если условие обозначим через P, то противоположное ему условие будет условие HE P. Кроме того, серию действий, составляющих тело цикла, обозначили в виде одного блока - т.ц. С учетом сказанного оба алгоритма (точнее, их циклическая часть), будут выглядеть следующим образом.

А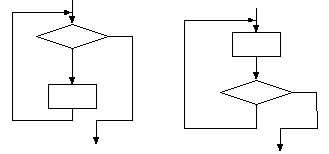лг.1 называется циклом с пред-условием (условие проверяется перед началом цикла) или циклом-пока.

Алг.2 называется циклом с пост-условием (условие проверяется после выполнения тела цикла) или циклом-до. В цикле-пока проверяемое условие является условием продолжения цикла. В цикле-до проверяемое условие есть условие выхода из цикла.

Задание на выполнение работы по переводу текста можно сформулировать и по-другому: перевести пять предложений, начиная с первого. В этом случае заранее известно число повторений. Такой цикл называют циклом-для, циклом с параметром, циклом со счетчиком.

Переменная k называется параметром (или счетчиком) цикла. Такой цикл оказывается весьма полезным при решении многих задач, поэтому важно рассмотреть его сокращенную форму записи: ПЦ – параметр цикла НЗ – начальное значение параметра (1) КЗ – конечное значение параметра (5) Ш – шаг (1)

К циклическим алгоритмам сводится решение многих задач, как вычислительного, так и чисто практического характера. В качестве примеров рассмотрим задачи по сортировке шаров по цвету, на нахождение НОД двух чисел, а также нахождение суммы заданного числа первых членов числовой последовательности.

ПРИМЕР 1. В урне хранится некоторое количество черных и белых шаров. Требуется сделать запись алгоритма рассортировки этих шаров по двум корзинам (черного и белого цвета) так, чтобы в результате выполнения алгоритма белые шары оказались в белой корзине, черные – в черной.

Составим сначала схему алгоритма выполнения этой работы. Очевидно, что для рассортировки шаров по корзинам с каждым шаром должны быть проделаны следующие действия: вынуть шар из урны (в соответствии с условием задачи предполагаем, что урна с самого начала не пуста), определить цвет вынутого шара и опустить его в соответствующую корзину. Если после этого в урне еще остаются шары, описанные выше действия повторить еще раз и т.д. Схема искомого алгоритма изображена на рисунке. Можно заметить, что группа повторяющихся в цикле блоков образует довольно-таки сложную конструкцию, так как включает разветвление.

Пользуясь схемой, легко составить словесную запись этого алгоритма:

1. вынуть из урны один шар

2. если шар белый, идти к 4

3. опустить шар в черную корзину; идти к 5

4. опустить шар в белую корзину

5. если урна не пуста, идти к 1

6. конец.

ПРИМЕР 2. Составить запись алгоритма Евклида нахождения наибольшего общего делителя (НОД) двух целых положительных чисел x и y.

Воспользуемся известным алгоритмом вычитания, суть которого состоит в следующем: заданные числа сравниваются между собой и в случае равенства одно из них объявляется результатом. Если же числа не равны, то из большего числа вычитается меньшее, после чего большее число заменяется полученной разностью. Вслед за этим процесс повторяется: снова числа сравниваются между собой и т.д.

Циклический характер этого алгоритма хорошо виден из его схемы, изображенной на рисунке.

Словесная запись:

1.чтение x,y 2.если x=y идти к 6 3.если x>y идти к 5

4.y:=y-x; идти к 2 5.x:=x-y; идти к 2 6.запись "НОД=",x 7.конец

ПРИМЕР 3. Составить алгоритм вычисления суммы первых 20 членов последовательности с общим членом a =k/(k² +1). Для циклического накопления сумм при составлении соответствующих алгоритмов используется предписание стандартного вида: сумма:=сумма+слагаемое.

Если повторить такое предписание требуемое количество раз, изменяя соответствующим образом слагаемое, то и будет получена искомая сумма. Понятно, что сумма перед началом работы цикла должна иметь нулевое значение. В схеме, изображенной на рисунке, роль суммы выполняет переменная S, а роль слагаемого - формула общего члена последовательности. Изменение слагаемого достигается увеличением в каждом обороте цикла номера члена k на единицу. Словесная запись этого алгоритма:

1.k:=1;S:=0

2.S:=S+k/(k2+1)

В этом циклическом алгоритме управление окончанием цикла осуществляется проверкой условия k<=20, и производится эта проверка всегда после выполнения рабочей части цикла (см.рис.). Такие циклы называют циклами с пост-условием. Этот же алгоритм можно организовать иначе: поставить проверку окончания перед рабочей частью цикла. Такие циклы называют циклами с пред-условием. Ниже приведена словесная запись алгоритма, соответствующего схеме, изображенной на рисунке. При составлении предписания условного перехода оказалось удобнее взять не условие k<=20, а его отрицание k>20.

В рамках рассмотренной задачи нахождения суммы 20 членов последовательности оба приведенных алгоритма равносильны в том смысле, что они дадут одинаковый результат. Впрочем, нужно отдавать себе отчет в том, что одинаковые по смыслу алгоритмы, составленные с пред-условием и пост-условием, все-таки различны. Очевидно, что рабочая часть (тело) циклов, построенных по схеме, всегда выполнится по меньшей мере один раз независимо от результатов проверки условия. В то же время тело цикла с пред-условием в определенной ситуации может не выполниться ни разу. Если допустить, что в задачах, подобно рассмотренной выше, верхняя граница параметра k заранее не известна и определяется, скажем, в результате предыдущего счета, то может оказаться, что алгоритм с пост-условием в этой ситуации даст нелепый результат. Действительно, если окажется, например, что заданная граница значения параметра k не положительна, то последовательность становится неопределенной. А алгоритм с пост-условием в этом случае выдаст в качестве значения суммы последовательности ее первый член.

Подобные ситуации требуют особого внимания при составлении программ, суммирующих последовательность.

Вопросы для повторения:

1. Что такое модель? Привести примеры.

2. Что такое моделирование?

3. На какие классы делятся модели?

4. Что воспроизводят предметные модели? Привести пример

5. Что представляют собой образные модели?

6. Что представляют собой знаковые модели?

7. В каких формах представляют объекты информационные модели?

8. Перечислить этапы решения задач на ЭВМ.

9. Что происходит на этапах при решении задач на компьютере?

10. Что такое алгоритм? Привести примеры.

11. Что и кто может быть исполнителем алгоритма?

12. Какой алгоритм называют неправильным? Примеры.

13. Перечислить свойства алгоритма. Привести примеры.

14. Что такое команда алгоритма? СКИ?

15. Формы записи алгоритмов.

16. Что такое «ветвление»

17. Какие существуют формы ветвления?

18. Как образуются составные условия?

19. Что такое «цикл»?

20. Что такое «тело цикла»?

21. Виды циклов.