Geum.ru

Universitatea liberă internaţională din moldova факультет экономических знаний Слесаренко Ольга, мастерат тема: Прогнозирование (Лабораторная работа)

Вид материалаЛабораторная работа
6. Методы, применяемые для уточнения прогноза
6.1. Метод адаптивного сглаживания
6.2. Метод Бокса — Дженкинса
6.3. Байесовские прогнозы
7. Изучение сферы сбыта
Подобный материал:
1   2   3

6. МЕТОДЫ, ПРИМЕНЯЕМЫЕ ДЛЯ УТОЧНЕНИЯ ПРОГНОЗА


Существует много различных методов прогнозирования, которые (при правильном их использовании) должны приводить практически к одному результату — выбору одного и того же варианта из ряда возможных и одинаковой оценке экономических последствий выбранного варианта. Правильное ведение прогнозирования предполагает, в частности, применение соответствующих критериев при пересмотре прогнозов. Известны три вида подходов, широко применяемых для пересмотра и уточнения прогнозов при анализе больших рядов, таких, как спрос на запасенные товары, курс акций или стоимость товаров. В данном разделе рассматриваются основные черты каждого из этих подходов, но, чтобы ознакомиться со всеми деталями, которые необходимы для практической работы, целесообразно обратиться к многочисленным- оригинальным источникам.

6.1. Метод адаптивного сглаживания

Основы метода адаптивного сглаживания были заложены при разработке метода экспоненциального сглаживания и затем развиты путем включения в рассмотрение сезонных моделей. Адаптивное сглаживание успешно применяется при прогнозировании спроса для управления запасами и поэтому вводится в соответствующие пакеты прикладных программ. Этот метод целесообразно использовать в тех случаях, когда модели спроса достаточно хорошо описываются с помощью постоянного уровня, тренда и сезонных моделей, которые не претерпевают резких изменений- для большинства рядов. Во многих случаях адаптивное сглаживание позволяет получать хорошие результаты в течение короткого промежутка времени, что иногда имеет более важное значение, чем получение более точного прогноза в течение длительного времени и с применением значительных усилий.

Математическое описание модели, позволяющей проводить, прогнозирование для любых рядов, имеет вид X = аF, где а — вектор т коэффициентов, вычисленных отдельно для каждого временного ряда, F — матрица соответствующих функций размерности т X Т, строки которой соответствуют каждому из т членов .модели и столбцы — каждому из Т интервалов прогнозирования. Компоненты вектора X представляют собой прогнозируемые, значения для каждого из интервалов.

Если в течение годового цикла имеется 12 наблюдений, то основная частота равна w = 2л/12 и существуют только семь возможных видов моделей. Простейшая модель включает только уровень и тренд, а наиболее сложная содержит также члены рядов Фурье вплоть до соs 6wt. Строки матрицы F привождятся ниже.



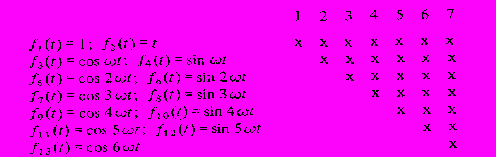
При других основных частотах, конечно, возможны и другие модели. Коэффициенты а вычисляются сначала по методу наименьших квадратов в соответствии с N исходными данными (т X N) матрицы F. Гармоники включаются в модель вплоть до топ частоты, при которой показатель степени (квадрат амплитуды) составляет по крайней мере 0,25) от величины дисперсии остатков, получаемых при подгонке этой модели с учетом имеющихся для ошибок степеней свободы.

С каждым новым наблюдением вектор а заменяется на вектор 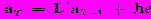, где L — матрица перехода, которая определяется с помощью выражения f (t) = Lf (t - 1) п переводит значения соответствующих функций из одного периода времени в следующий. Столбец матрицы F, имеющий номер t, обозначается как f (t). и е представляет собой ошибку (скаляр) самого последнего прогноза, сделанного на один интервал вперед: е = хТ — Хт-1. Вектор h характеризующий т постоянных сглаживания, определяется следующим образом. Используя z-преобразования и некоторые элементарные тригонометрические соотношения, можно вывести выражение для матрицы Н в замкнутом виде: 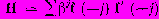. Так как B<1, то значимость более старых данных снижается и увеличивается вес, приписываемый более поздним данным.

Следовательно, вектор сглаживания можно записать как h, = Н-1f (0). Величины L и h необходимо вычислить только один раз, так как при дальнейшем пересмотре прогнозов они не изменяются.

Если прогнозы составляются для переменных интенсивности (например, таких, как спрос на запасенные товары) и результаты наблюдений получены в нерегулярные интервалы времени, то исходные данные преобразуются к величинам, характеризующим скорость их изменения на равномерных интервалах времени. Получаемые в результате прогнозы могут быть приведены в соответствие с величиной будущих интервалов времени. Заметим, что подобное использование сечения какой-либо входной переменной одинаково пригодно для любых рядов и не приводит к такому же увеличению дисперсии, какое имело бы место в случае получения сечения из данных предыстории.


6.2. Метод Бокса — Дженкинса

Основные положения и сам метод рассматриваются в работах. Согласно данному методу, прогнозы составляются па основе всестороннего анализа статистических свойств рядов. Для того чтобы в полной мере использовать его достоинства, требуются.достаточно длинные ряды (содержащие не менее 100 результатов наблюдений); это в значительной степени помогает понять изучаемый процесс с точки зрения получения предварительных данных относительно возможных изменений процесса в будущем. С помощью данного метода может быть проанализирован гораздо более широкий круг моделей, чем с помощью метода адаптивного-сглаживания. Кроме того, он особенно полезен в тех случаях, когда требуется получить как можно более точный прогноз.

Анализ моделей но методу Бокса — Дженкинса начинается с формирования разностей из исходных данных Zt и вычисления частных автокорреляционных функции φ для разностных рядов 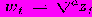. Затем разностные ряды вводятся в модель с соответствующим числом коэффициентов авторегрессии и скользящего среднего: 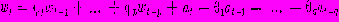, где φp— частные автокорреляционные функции. Для оценки коэффициентов в моделях такого типа и для вычисления дисперсии шума в результатах наблюдений используются методы наименьших квадратов.

Операторы разности скользящего среднего могут быть разложены таким образом, чтобы выразить модель прогнозов через исходные данные наблюдений:



По методу Бокса — Дженкинса сначала прогнозируется изменение преобразованных входных переменных, а затем осуществляется обратное преобразование.

Если необходимо проанализировать сезонные циклы, то вклад от каждого из них вычисляется путем составления разностей для определенных отрезков цикла. Для годового цикла, например, в качестве таких отрезков можно принять месяцы, и тогда прогноз для каких-то месяцев в будущем будет основываться на известных данных для этого месяца в прошлые годы.

Одно из основных применений метода Бокса — Дженкинса связано с управлением процессами в химической промышленности, где имеются ряды температур, давлений, скоростей потоков и т. п. с большим числом известных результатов наблюдений и неплохо известна возможная динамика изменения системы, подлежащей управлению. Цель управления состоит в том, чтобы наиболее рациональным образом менять технологические параметры— температуру, давление или скорость потока. Значительные усилия по разработке точных прогнозов для подобных производственных процессов вполне оправдываются достигаемым при этом экономическим эффектом.

6.3. Байесовские прогнозы

В работе предложена схема разработки прогноза, которая включает основные положения двух предыдущих подходов как частные случаи. Ниже (после небольшого вступления) приводится строгое изложение математических основ этого метода и руководство для его практического использования.

Пока результаты наблюдений согласуются с прогнозами, последние стабильны и ожидаемое распределение ошибок прогнозов ограничено узкими пределами в соответствии с шумом в результатах наблюдений. Появление хотя бы одного большого отклонения повышает чувствительность метода. Если последующие наблюдения подтверждают скачкообразное или постепенное изменение изучаемого процесса, прогнозы быстро корректируются с помощью новой модели. Однако, если указанное отклонение представляло собой случайный выброс, прогноз остается без изменения.

Объем вычислений при использовании рассматриваемого метода гораздо больше, чем при адаптивном сглаживании, так как успешное прогнозирование гарантируется и в тех случаях, когда могут возникнуть непредвиденные и существенные изменения в прогнозируемом процессе. Это справедливо даже в случае изучения спроса на товары широкого потребления, который особенно сильно подвержен влиянию моды или неконтролируемой рыночной конъюнктуры. Если есть предварительные сведения об ожидаемых событиях, то можно начать прогнозирование при весьма скромных данных или вообще при их отсутствии. Вместе с тем, если имеется большой объем результатов наблюдений, прогнозирование можно начать при отсутствии исходных предпосылок о поведении прогнозируемой величины. Применяемый алгоритм вычислений дозволяет построить модель процесса по данным его предыстории.

Типичная модель для результатов текущих наблюдений может быть представлена выражением 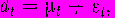где µ — уровень полезной составляющей и 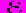— шум текущего наблюдения. Текущий уровень связан с трендом выражением и 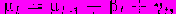где тренд изменяется по закону 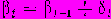. Предполагается, что скачкообразное изменение 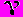основного уровня, изменение 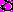тангенса угла наклона кривой, описывающей зависимость выходной переменной от времени, а также шум 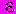независимы и распределены по нормальным законам с нулевым средним и известными (но не обязательно постоянными) дисперсиями .

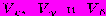В модели, которая описывает много состояний, обычно имеются два состояния для каждого возможного возмущения, причем каждое из них характеризуется своим значением дисперсии 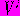В устойчивом состоянии дисперсия мала, а в состоянии изменения велика. Имеются также априорные вероятности 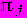того, что состояние j не изменяется. Ниже приведен пример четырех состояний и соответствующих им условных вероятностей и дисперсий, использованных авторами метода в качестве типичных начальных условий. Дисперсия шума 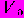зависит от соотношения между фактическими изменениями процесса и текущим прогнозом и описывается соотношением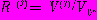



Пусть вектор 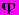содержит следующие элементы: ожидаемое значение уровня, ожидаемое значение тангенса угла наклона, дисперсию ошибок при определении уровня, ковариацию наклона и уровня, а также дисперсию ошибок при определении тангенса угла наклона. Тогда, если в момент времени t — 1 совместное распределение уровня и тангенса угла наклона является двумерным нормальным и характеризуется параметрами 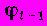, то соответствующее распределение в момент времени t также будет двумерным нормальным, а его параметры будут определяться вектором .

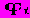Переменные, находящиеся в левой и правой частях приведенных ниже уравнений, относятся соответственно к текущей и предшествующей итерациям:



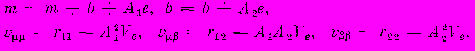
Пять постоянных сглаживания определяются следующим образом:



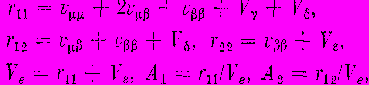
где е — ошибка, полученная при сравнении результата текущего наблюдения и самого последнего прогноза. Существуют также выражения для коэффициентов сезонных сечений, которые здесь не приводятся.

Если первоначально имелось N возможных состояний, то данному процессу соответствуют N² возможных комбинаций. Эти N² возможностей описываются N двумерными нормальными распределениями с одинаковыми (взвешенными) первыми и вторыми моментами, так что процедура корректировки прогноза может проводиться без ограничений.


7. ИЗУЧЕНИЕ СФЕРЫ СБЫТА

Ни в одном из статистических методов прогнозирования не может заранее предусматриваться изменение модели прогнозируемого процесса. Как уже отмечалось, имеется ряд изящных методов, быстрого обнаружения изменений в последующих процессах и соответствующей реакции на них. Модель прогноза может все более усложняться, когда это экономически оправдано и позволяет глубже проникнуть в механизм наблюдаемых явлений.

Во многих случаях изменения в изучаемом процессе можно предвидеть заранее, по в модель прогноза они тем не менее не включаются. Например, интенсивная кампания по подписке может увеличить число подписчиков на периодические издания; принятие проекта о дополнительном налоге вызывает волну покупок как раз до того, как он входит в действие; массовое ознакомление покупателей с новой продукцией типа Tange или Polariod SХ-10 не только позволяет продать ее, но и создает представление о типичной продукции такого рода и меняет спрос на старую продукцию; директивы Вашингтопа радикально меняют соотношение закупок и расхода нефтяных продуктов.

Последствия таких изменений в изделиях, в спроса на них, экономике и в правительственном регулировании не могут быть точно рассчитаны. Тем не менее опытные руководители на основе тщательного анализа различных вариантов могут предсказать характер изменений. И это все же лучше, чем полное игнорирование проблемы из-за отсутствия формальных методов ее решения. В подобной ситуации единственно неверным является прогноз, не предсказывающий никаких изменений. Поэтому руководителям необходимо иметь обзор статистических прогнозов, в который должны регулярно вноситься изменения, отражающие появление новой продукции, ее развитие, действия конкурентов, погодные условия, образование дефицита материалов и т. д.

Одной из функций любой действующей прогнозирующей системы должна быть подготовка отчетов по отдельным вопросам статистических прогнозов с учетом изменений всех параметров модели сферы сбыта. В таких отчетах данные могут быть сгруппированы по различным показателям: типам продукции, рынкам сбыта, периодам времени,— что облегчает их восприятие человеком. Иногда общие объемы продажи какой-либо корпорации или прогнозы доступных рынков не будут соответствовать сумме предсказанных объемов продажи отдельных видов продукции.

Если появляется несоответствие между зонами, заключенными в пределах от минимальных до максимальных значений прогноза, руководители должны рассмотреть причины этого несоответствия и факторы, учтенные при получении прогнозов. Далее, если для некоторой группы товаров требуется скорректировать прогнозы, чтобы привести их в соответствие с достигнутыми показателями продажи, то необходимо не только решить вопрос о том, как осуществить эту коррекцию по всей группе товаров, но также и о том, какие нужно принять специальные меры, чтобы гарантировать, реализацию этих прогнозов.

Если решения о производстве и распределении приняты на основе хорошего прогноза и торговые операции гарантируют соответствие действительных показателей продажи этому прогнозу, то издержки, связанные с ошибочностью прогноза, будут минимальны. Торговля при неточном прогнозировании может представлять собой более экономичный путь к правильным решениям, чем сложные попытки точного прогнозирования поведения рынка.

Для корректировки прогноза иногда применяют прием, заключающийся в обеспечении обратной связи. Проиллюстрируем его на конкретном примере.

Допустим, что по статистическому прогнозу объем продаж на март составляет 1000 ед. В то же время по субъективному прогнозу на этот же месяц, принятому ранее с учетом обеспечения достаточного количества товаров, объем продаж составлял 1500 ед. В апреле стало известно, что фактический объем продаж по отчетам за март равен 1375 ед. Если бы поступление товаров обеспечивалось на основании статистической модели, то имел бы место потенциальный дефицит в 375 ед. (смягченный, конечно, фондом запаса). Если бы компания руководствовалась данными субъективного прогноза, то был бы получен потенциальный избыток в 125 ед. Тогда при наличии потерь, обусловленных недостатком товаров, вдвое более весомых, чем от избытка товаров, чистый выигрыш за счет использования субъективного прогноза составил бы (2 - 375) — 125 = 625 ед. Чистый выигрыш может быть выражен в долларах или в виде нормирующего множителя для стандартного отклонения ошибок прогноза.

В любой отдельный период времени существует, очевидно, несколько серий прогнозов, отличных от простого описательного прогноза. Вместе с тем результаты изучения рынка, представленные цифрами значимости изменений, расположенными по порядку от высоких до низких, действуют на людей как положительная обратная связь, побуждающая к дальнейшим значительным и содержательным изменениям. Это также позволяет минимизировать время, затрачиваемое на внесение незначительных изменений, и активно вносить действительно существенные изменения. Независимо от того, вносятся ли изменения в прогноз или в результате прогноза принимаются более решительные действия при продаже, результатом является рост прибыли, повышение эффективности торговли и рост престижа организации.