Представление знаний в экспертных системах

Вид материала

Документы

Содержание Фрейм (англ. frame – рамка, каркас) – Продукционная модель Модели представления нечетких знаний

Подобный материал:

• Б. А. Кобринский Рассматриваются различные решения в экспертных системах 10 20-летней, 258.49kb.
• Ния инструментальной среды приобретения знаний для прикладных экспертных систем, сделаны, 112.06kb.
• Конспект лекций Представление знаний в информационных системах Лекция№1, 194.32kb.
• Экспертные системы и базы знаний, 42.45kb.
• Рабочая программа По дисциплине «Представление знаний в информационных системах», 210.06kb.
• Тарасюк А. П., Спасский, 109.74kb.
• Аний, связанных с разрешением проблемы неполноты в базах знаний интегрированных экспертных, 33.09kb.
• 6. Лекция: Методология построения экспертных систем, 291.07kb.
• Основы компьютерного представления экспертных знаний для мониторинга программно-целевой, 846.29kb.
• Вопросы для подготовки к экзамену по архитектуре ЭВМ, 79.1kb.

ПРЕДСТАВЛЕНИЕ ЗНАНИЙ В ЭКСПЕРТНЫХ СИСТЕМАХ

Хлебалкин И.В.

Российский химико-технологический университет им. Д.И. Менделеева


Развитие экономики в настоящее время в большой степени связано с практическим применением средств вычислительной техники и современных информационных интеллектуальных технологий, одной из которых является технология экспертных систем [1].

Экспертная система (ЭС) – это специальный программный комплекс, аккумулирующий знания специалистов в конкретной предметной области и обеспечивающий пользователя возможностями [2]:

- решения широкого круга неформализуемых задач в различных предметных областях, которые до недавнего времени считались малодоступными для использования вычислительной техники;

- трансформирования опыта специалистов-экспертов в память компьютера путем создания и развития базы знаний;

- достижения более устойчивых результатов в решении задач за счет исключения эмоциональных и других факторов человеческой деятельности;

- получения значительных доходов за счет низкой стоимости эксплуатации системы и привлечения менее квалифицированных специалистов.

Под неформализуемыми задачами понимаются задачи, которые невозможно представить в числовой форме ввиду неточной определенности исходной информации, а также операций и целей ее преобразования. К таким задачам относятся задачи классификации, диагностики, проектирования, принятия решений в условиях неопределенности и др.

Основными отличительными характеристиками экспертных систем по отношению к прикладным и другим интеллектуальным программным системам являются:

• формирование даже в случае неточной исходной информации выводов и рекомендаций по решению задачи на основе базы знаний (БЗ) с возможностью объяснения полученных результатов;
  
• использование для решения задач в основном эвристических методов поиска, которые, в отличии от алгоритмических методов, не всегда гарантируют полноту решения задачи;
  
• моделирование механизма мышления специалистов (экспертов) в данной предметной области реального мира;
  
• достаточно высокая производительность, т. е. практически приемлемая скорость получения достоверного решения задачи.
  

Исторически первыми экспертными системами были Heuristic DENDRAL и Meta-DENDRAL, разработанные в середине 60-х годов XX века в Станфордском университете и предназначенные для расшифровки структуры соединений органической химии.

Информационной основой экспертной системы являются база данных и база знаний.

База данных содержит формализованную информацию об отдельных фактах, характеризующих объекты, процессы и явления предметной области, а также их свойства (например, данные о производственной продукции, технологическом оборудовании, физико-химических свойствах веществ и т.д.).

На данных, полученных практическим путем, основываются знания, представляющие собой структурированные данные (метаданные), характеристическими признаками которых являются:

• активность - возможность программной генерации новых знаний (в отличии от данных, которые пассивно хранятся в памяти компьютера);
  
• интегрируемость - существование возможности разъяснения смысла знаний;
  
• связность - описание закономерностей относительно фактов, явлений, процессов и причинно-следственных отношений между ними, позволяя специалистам ставить и решать практические задачи в данной предметной области;
  
• структурированность - возможность декомпозиции сложных объектов и установления связей между составляющими объектами с использованием отношения типа «часть - целое".
  

Естественен переход от данных к знаниям как следствие развития и усложнения информационно-логических структур, обрабатываемых вычислительной техникой.

База экспертных знаний (знаний специалистов в соответствующей предметной области) является главной составной частью экспертной системы.

В настоящее время основными классами моделей представления знаний в экспертных системах являются фреймы, семантические сети, продукционные модели и модели нечетких знаний [3, 4].

Фрейм (англ. frame – рамка, каркас) – познавательная структура, дающая целостное представление об объектах, явлениях и их типах в виде абстрактных образов для представления стереотипа восприятия.

Структура фрейма представляется в виде:


N : {1,V₁.P₁>,...,k,V_k,P_k>,...,n,V_n,P_n>},


где N - имя фрейма; k,V_k,P_k> (k=1,...,n) – слот; S_k – имя слота; V_k – значение слота; P_k– процедура.

Слоты – это структурные элементы фрейма, заполнение которых приводится к тому, что фрейм ставится в соответствие некоторой ситуации, явлению, объекту или процессу.

Имена фреймов и слотов обеспечивают интерпретируемость хранящихся во фреймах значений. Фреймы имеют свойство вложенности, т.к. значениями слота могут быть имена слотов более глубокого уровня. Значениями слотов могут быть приказы вызова процедур для активизации программ на основе имеющихся значений. Различают фреймы-образцы (прототипы), хранящиеся в БЗ, и фреймы-экземпляры, отображающие реальные ситуации на основе поступающих данных. Знания предметной области представляются фреймами-объектами, фреймами-сценариями, фреймами-ролями, фреймами-ситуациями и др. Например, фреймами-объектами можно представить знания о веществах, процессах и аппаратах, производственных технологических схемах и т.д.

Фреймы математически представляются как ориентированные графы с помеченными вершинами и дугами. Они отражают концептуальную основу организации памяти человека, обладают наглядностью, модульностью, объединяют достоинства процедурного и декларативного представления знаний, эффективны при обработке семантической составляющей знаний.

Семантическая сеть – это ориентированный граф, вершины которого представляют понятия (объекты, события, явления), а дуги изображают отношения между понятиями (например, класс – элемент класса, свойство – значение, пример элемента класса).

Основными видами семантических отношений являются лингвистические, теоретико-множественные, логические и квантифицированные. Семантические сети можно классифицировать по количеству типов отношений (однородные, неоднородные) и по типам отношений (бинарные, N – арные). Они обеспечивают наглядность отображения объектов, связей и отношений, а также гибкость представления знаний за счет ассоциативности и иерархичности. Эффективно, например, представление семантической сетью знаний о совокупности технологических операций в различных производствах.

Недостатком семантических сетей и фреймов как моделей знаний является отсутствие универсальной процедуры их обработки, а также сложность организации процедур поиска вывода, что может привести к неэффективному использованию ресурсов вычислительной техники.

Продукционная модель позволяет представить знания в виде продукционных правил, т.е. предложений типа: ЕСЛИ <перечень условий>, ТО <перечень действий >.

«Условие» - это образное предложение, по которому идет поиск в базе знаний, а «действие» - это операция, выполняемая при успешном результате поиска.

Продукционное правило в общем случае представляется в виде:


i : S; C; A → B; P,


где i - номер продукции; S - описание класса ситуаций, в котором эта структура может использоваться; С – условие, при котором данная продукция активизируется; А→В – ядро продукции (например, «ЕСЛИ А₁,А₂,…,А_n, ТО В»); Р – постусловие продукционного правила, определяющее действия, которые необходимо произвести после выполнения В.

В зависимости от количества условий и действий в соответствующих перечнях различают следующие типы правил: простое – одно условие и одно действие, составное – много условий и действий, фиксирующее – много условий и одно действие, разветвляющееся – одно условие и много действий.

Продукционные модели (наряду с фреймами) являются наиболее распространенными средствами представления знаний (особенно в промышленных экспертных системах), так как обеспечивают простоту смысловой интерпретации, модульность, легкость корректировки и логического вывода. Применение продукционных правил способствует «прозрачности» экспертной системы, т.е. ее способности к объяснению принятых решений и полученных результатов. Недостатками продукционных моделей являются трудности при добавлении правил, зависящих от уже имеющихся в базе знаний, а также при отладке программ.

Модели представления нечетких знаний используются для формализации человеческих знаний, описывающих качественные характеристики (например, большой, сильный, очень сильный, высокий и т.п.) объектов предметной области, которые могут интерпретироваться неоднозначно, но содержат важную информацию.

Теоретической основой данного представления являются нечеткая (fuzzy) алгебра, нечеткая логика и теория нечетких множеств [5]. Одним из основных понятий в нечеткой логике является понятие лингвистической переменной (ЛП), которая определяется как переменная, значения которой описываются набором словесных (вербальных) характеристик некоторого свойства. Например, лингвистическая переменная «цена продукции» может определяться набором значений {очень высокая, высокая, средняя, низкая, очень низкая}. Совокупность значений (названий) лингвистической переменной образует так называемое терм-множество, а исходная переменная называется базовой. Различным термам могут соответствовать различные значения базовой переменной. Значения ЛП определяются через нечеткие множества, которые, в свою очередь, определены на базовой числовой шкале, имеющей размерность.

Если рассмотреть универсальное множество U как область рассуждений (диапазон), в которой может находиться величина, то нечеткое подмножество А множества U можно охарактеризовать функцией принадлежности μ_А : U→[0;1], ставящей в соответствие каждому элементу u є U число μ_А є [0;1].

Нечеткое подмножество представляется в виде:

А =

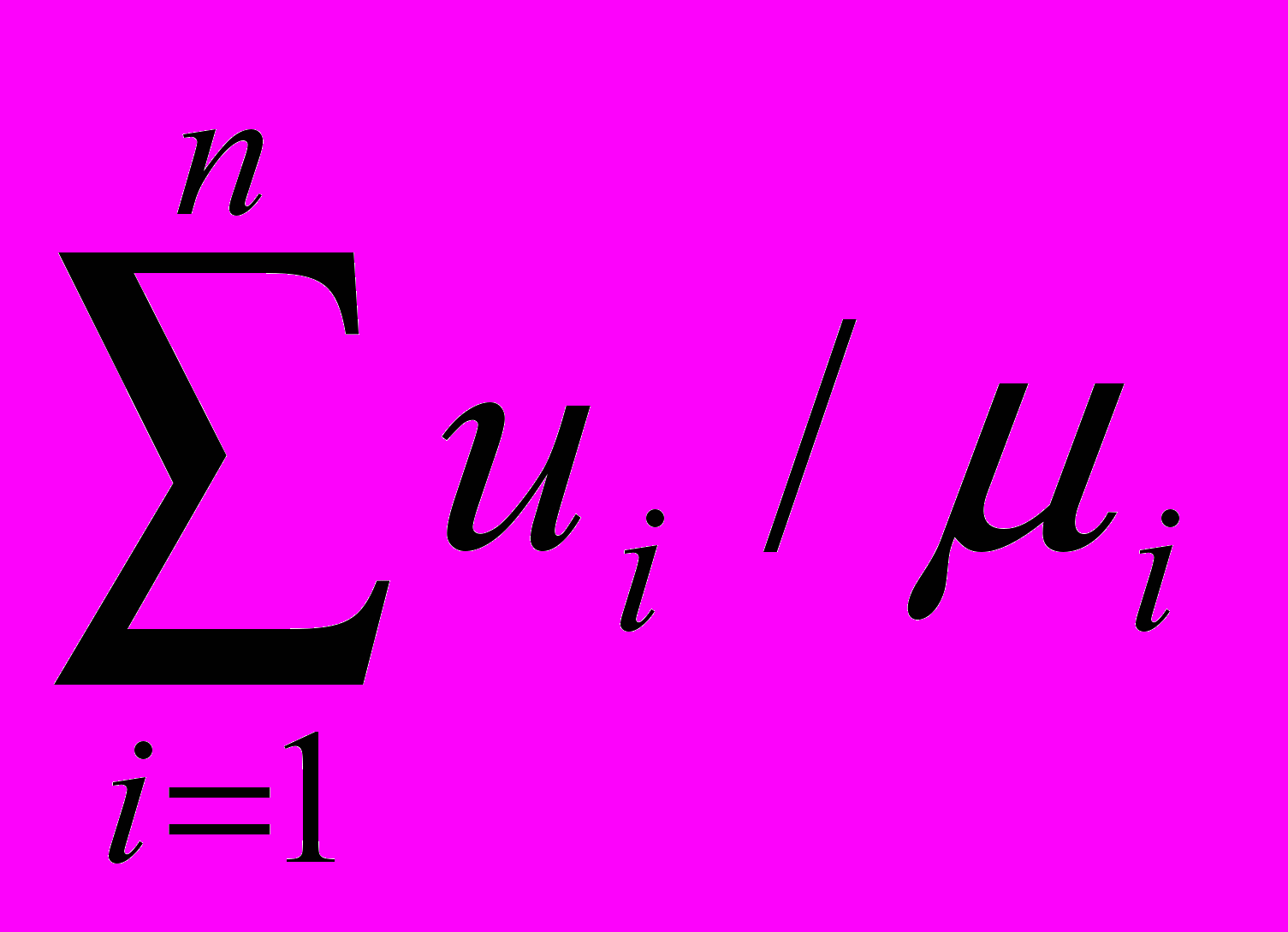
где μ_i - степень принадлежности элемента u_i подмножеству А; знак суммирования обозначает объединение одноточечных множеств u_i / μ_i ; черта не является символом деления.

Так, например, терму «высокий» для значения некоторого параметра химико-технологического процесса можно сопоставить нечеткое множество А универсального множества U = 0+1+2+3+4+5 (диапазона значений параметра):


A = 0/0 + 1/0,2 + 2/0,4 + 3/0,6 + 4/0,8 + 5/1


Если μ_i непрерывная функция, то нечеткое подмножество А представляется в виде:


А = ,

где знак интегрирования обозначает операцию объединения одноточечных множеств

u / μ_A(u).

Нечеткое множество можно представить в виде совокупности пар (x,μ_A(x)), образованной значениями базовой переменной х є Х и из функций принадлежности μ_А(х), устанавливающих связь между этими значениями и числами на отрезке [0;1].

Функция принадлежности характеризует степень субъективной уверенности эксперта в том, что данное значение базовой шкалы соответствует нечеткому множеству.

Для интерпретации, например, лингвистической переменной «возраст» можно использовать нечеткие множества «Детский», «Юный», «Молодой», «Зрелый», «Старый» и базовую шкалу в диапазоне от 0 до 120 лет. Функция принадлежности будет определять степень соответствия данного количества лет с данной категорией возраста.

На основе моделей представления нечетких знаний реализуются, в частности, методы принятия решений в условиях неопределенности.

Совершенствование методологии представления знаний обеспечивает дальнейшее развитие технологии экспертных систем.

Литература

1. Джексон П. Введение в экспертные системы. – М.: Издательский дом «Вильямс», 2001. – 624 с.
   
2. Попов Э.В., Фоминых И.Б., Кисель Е.Б., Шапот М.Д. Статические и динамические экспертные системы: Учебное пособие. – М.: Финансы и статистика, 1996. – 320 с.
   
3. Гаврилова Т.А., Хорошевский В.Ф. Базы знаний интеллектуальных систем. – СПб.: Питер, 2001. – 384 с.
   
4. Рыбина Г.В. Проектирование систем, основанных на знаниях: Учебное пособие. – М.: МИФИ, 1997. -104 с.
   
5. Кофман А. Введение в теорию нечетких множеств: Перевод с англ. – М.: радио и связь, 1982. – 432 с.