Тарасюк А. П., Спасский А. С

Вид материала

Подобный материал:

УДК 681.518:658.386

Тарасюк А.П., Спасский А.С.

ИСПОЛЬЗОВАНИЕ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ В ЭКСПЕРТНЫХ СИСТЕМАХ ДИАГНОСТИКИ УРОВНЯ КАЧЕСТВА ПОДГОТОВКИ СПЕЦИАЛИСТОВ

Одним из наиболее распространенных направлений развития искусственного интеллекта являются экспертные системы реального времени (ЭС) – системы объединяющие возможности программных и аппаратных средств со знаниями и опытом экспертов в некой предметной области в такой форме, что система может осуществить разумное решение поставленной задачи. Классы задач, решаемых экспертными системами реального времени таковы: мониторинг в реальном масштабе времени, диагностика, проектирование, составление расписаний, планирование, оптимизация, поиск, управление и т.д. ЭС представляется весьма эффективной в диагностике уровня качества подготовки специалистов в конкретной предметной области, в частности при проведении аккредитации специальностей.

Проблема затронутая в данной статье заключается однако не в контроле и оценке уровня качества подготовки специалиста, а в выявлении “слабых мест” – учебных элементов, содержательных модулей и блоков содержательных модулей, которые по каким то причинам усвоены не на достаточном уровне в масштабе конкретной специальности в конкретном учебном заведении. Это позволит разработать практические рекомендации по совершенствованию содержания и методов обучения, а также выявить неудачно сформированные тестовые задания.

Сердцевину любой экспертной системы составляет база знаний, которая накапливается в процессе ее построения. Знания выражены в явном виде и организованы так, чтобы упростить принятие решений. Для ЭС диагностики знания представлены в виде тестов, объединенных в направлении роста степени интеграции наименованиями учебных элементов, содержательных модулей блоков содержательных модулей и дисциплин (рис. 1).

Для контроля качества подготовки специалистов из базы знаний формируются наборы тестов, которые предлагаются испытуемым.

Для решения проблемы выявления “слабых мест”, при генерации тестовых последовательностей удобнее всего применить так называемые генетические адаптивные алгоритмы [1], которые основаны на стандартных моделях наследственности и эволюции из области популяционной генетики, являющихся модельным воплощением тех механизмов адаптации, которые имеются в живых системах. Применительно к проблеме генерации тестовых последовательностей суть генетического алгоритма заключается в следующем. В начальный момент времени (обычно случайным образом) генерируются тестовые последовательности (особи) и ряд тестовых последовательностей (популяция) (рис. 2). [2]

Рис. 1. Структура представления базы знаний в экспертной системе диагностики уровня качества подготовки специалистов

1	0	1	1	0	тест				0	1	0	1	0
0	1	0	1	1				1	0	1	0	1	1
0	0	0	1	1			0	0	1	1	1	1	1
0	1	0	0	1		1	0	1	1	0	0	0	0
0	1	1	1	0		0	1	0	1	1	1	0	1
1	0	1	0	1		0	0	0	1	1	0	1	0
						0	1	0	0	1	1
						0	1	1	1	0	0
						1	0	1	0	1
а) особь (тестовая последовательность для одного испытуемого)						б) популяция (ряд тестовых последовательностей для группы испытуемых)

Рис. 2. Кодирование особей и популяций

Далее, после тестирования испытуемых (нескольких групп), на основании некоторых критериев вычисляется оценочная функция каждой особи, характеризующая относительную способность решения поставленной проблемы (в нашем случае выявление тестов на которые даны неправильные ответы). Чем больше неправильных ответов в тестовой последовательности, тем выше оценка особи.

Далее из текущего поколения особей строится следующее с целью либо найти решение, либо улучшить оценку каждой особи. Цель данной операции – получение новых особей в популяции, обладающих новыми свойствами. Новое поколение строится следующим образом. Из популяции выбираются несколько особей (в зависимости от размера популяции). Вероятность выбора особи полагается пропорциональной оценочной функции. Копии выбранных особей сразу помещаются в новую популяцию. После этого к данным особям применяются модифицирующие операции. Обычно используют два вида таких операций: кроссинговера (скрещивание) и мутацию. Скрещивание производится в одной или нескольких точках (рис. 3).

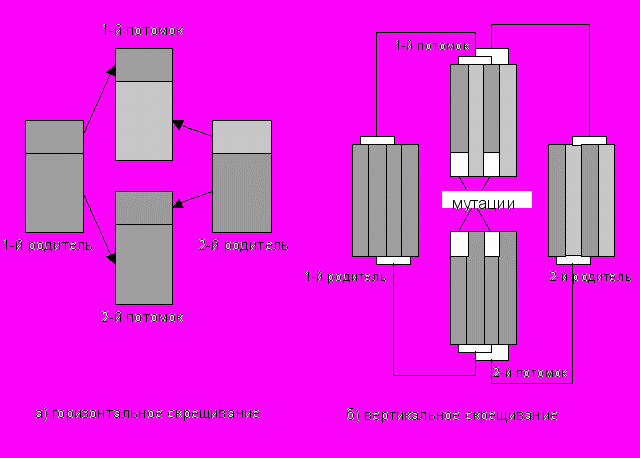
Рис. 3. Генетические операторы

Далее с некоторой вероятностью в двух новых особях происходит мутация битов: ноль изменяется на 1 и наоборот, после чего модифицированные особи помещаются в новую популяцию.

Так происходит до тех пор, пока в новой популяции не наберется необходимое число особей.

Далее проводится повторное тестирование испытуемых, которое обычно сопровождается снижением полученных оценок. После этого цикл повторяется. Порождение новых популяций и тестирование прекращается, когда тестовые оценки перестают снижаться (обычно это происходит после 35 раз). Популяция тестовых последовательностей, которая дала наиболее низкие оценки и определяет наиболее слабо усвоенные содержательные модули.

Основная парадигма более точно выражена на рис.4.

Рис. 4. Основной метод поиска

Чтобы как-то прочувствовать поведение такой поисковой стратегии, рассмотрим вероятности отбора, определенные на шаге 3.

Мы видим, что если m особей выбраны для участия в генерации новых особей в момент t, то среднее число новых особей, получаемых в текущей популяции, составит

,

где

- средняя полезность аргумента (оценочная функция особи). Таким образом эти вероятности обеспечивают селективное смещение в пользу особей, ведущих себя лучше среднего по сравнению с остальными особями в популяции (имеющими более низкую оценку).

В отсутствии других механизмов такое избирательное давление приведет к тому, что хорошо ведущие себя особи со временем будут занимать в популяции все больше и больше места.

Сила адаптивной стратегии поиска, описанной выше, состоит не в апробировании отдельных структур (особей), а в эффективном использовании той богатой информации, которую дает такое апробирование в отношении взаимодействия между компонентами этих структур. Специфические конфигурации значений компонент, которые дали заметный вклад в “хорошее поведение”, сохраняются и распространяются по структурам в базе знаний. А это, в свою очередь, создает предпосылки для последующего возникновения подобных конфигураций все большего и большего размера. Интуитивно мы можем рассматривать эти структурные конфигурации как регулярности в пространстве, которые проявляются по мере порождения и испытания отдельных особей. Встретившись однажды, они начинают служить в качестве “строительных блоков” при создании новых особей. Но поскольку структуры, принадлежащие специфическим разбиениям, обеспечивающим высокое качество функционирования, с малыми определяющими фрагментами со временем начинают преобладать в базе знаний, то произойдет эффективное уменьшение числа определяющих фрагментов других разбиений, ослабляющее разрушительное влияние оператора кроссинговера на темп, с которым последние выбираются. Оператор мутации оказывает незначительное влияние на фактор выбора, поскольку ему отводится в поиске фоновая роль.

В таком поиске могут возникнуть все те трудности, если существенные разбиения (т.е. примитивные строительные блоки) обладают длинными определяющими фрагментами. Эта проблема связана с представлением и возникает при неудачном выборе порядка структурных компонент. В этом случае продуктивность поиска повышается путем использования инверсии. Этот оператор изменяет характер связей между компонентами структуры. Он берет одну структуру, случайным образом выбирает на ней две точки разрыва и располагает в обратном порядке компоненты, попавшие между этими двумя точками разрыва. Благодаря изменению порядка компонент в структуре, его применение будет создавать тенденцию к уменьшению длины длинных определяющих фрагментов, благодаря чему открываются бльшие возможности применения кроссинговера. Заметим, что оператор инверсии не создает совсем другую структуру, а лишь альтернативное представление той же самой структуры (переупорядочивая составляющие ее компоненты).

Таким образом, чтобы задать генетический алгоритм, необходимо определить понятие особи, популяции, операции скрещивания и мутации, инверсии и задать оценочную функцию. Очевидно также, что эффективность генетического алгоритма зависит от целого ряда параметров: размера популяции, метода выбора особей из предыдущей популяции; скрещивания и мутации, а также вида оценочной функции.

Описанный выше подход можно использовать не только в экспертных системах диагностики уровня качества подготовки специалистов, но и для разработки и реализации алгоритмов генерации тестовых последовательностей для последовательных схем диагностики технических систем.

Литература

Экспертные системы. Под ред. Р.Форсайта. –М.: Радио и связь, 1987, - 222 с.
Иванов Д.Е., Скобцов Ю.А. Ускорение работы генетических алгоритмов при построении тестов./ Искусственный интеллект. №1. 2001 г. – Донецк. 2001. – с. 52-60.

Тарасюк А.П., Спаський А.С.

Використання генетичних алгоритмів в експертних системах діагностики рівня якості підготовки спеціалістів.

Розглядається проблема генерації тестових послідовностей для діагностики рівня якості підготовки спеціалістів. Основана на моделюванні генетична стратегія побудови тестів показує результати, що співставленні з детермінованими методами, та при цьому має ряд переваг: прозорість стратегії та простота реалізації.

Тарасюк А.П., Спасский А.С.

Использование генетических алгоритмов в экспертных системах диагностики уровня качества подготовки специалистов.

Рассматривается проблема генерации тестовых последовательностей для диагностики уровня качества подготовки специалистов. Основанная на моделировании генетическая стратегия построения тестов показывает сравнимые с детерминированными методами результаты, обладая рядом преимуществ: прозрачность стратегии и простота реализации.

Tarasyuk A.P., Spasski A.S.

The Use of Genetic Algorithms in Expert Systems of Quality Level Diagnostics of Specialists’ Training.

The problem is being considered of the generation of test sequences for quality level diagnostics of specialists’ training. Based on modelling, genetic strategy of test construction produce the results that can be compared. With the deterministic methods and have a number of advantages – strategy transparence and simplicity of implementation.

Blog

Тарасюк А. П., Спасский А. С