Конспект лекций Представление знаний в информационных системах Лекция№1

Вид материала

Содержание

Пример структуры
Примеры списков
Clauses - база фактов и правил. Содержит два вида предложений
Пример программы на прологе
1) Геометрическая интерпретация задачи.
2) Формирование исходных данных
Обработка списков
Логическая модель.
Задание: Разработать программу, объединяющую элементы двух списков в третий
Пошаговое выполнение программы принадлежит
Последовательность выполнения целей в запросе(условий в правиле), содержащих логическое (и), (или), отсечения (!).
Лекция №6.
Знания - это данные о данных. 1. Продукционная модель.
2. Семантическая сеть.
Алгоритм обучения без учителя.

Подобный материал:

Конспект лекций

Представление знаний в информационных системах

Лекция№1

Введение.

Задача курса – изучение моделей знаний: модели на основе нейронных сетей, фреймы, семантические сети, продукционные модели, логические модели.

Логические модели разрабатываются на основе декларативных языков программирования (Prolog, Lisp…).

Язык Пролог разрабатывался в 70-е годы, разработчик Келмэроу. Этот язык изучают по следующим причинам:

Пролог – представитель декларативных языков;
это язык управления, он применяется в Западной Европе;
пролог используется в робототехнике (Япония);
методология построения СУБД и языков запроса.

Основные объекты Пролога.

Существует приблизительно 20 диалектов Пролога. Отсутствует единый стандарт.

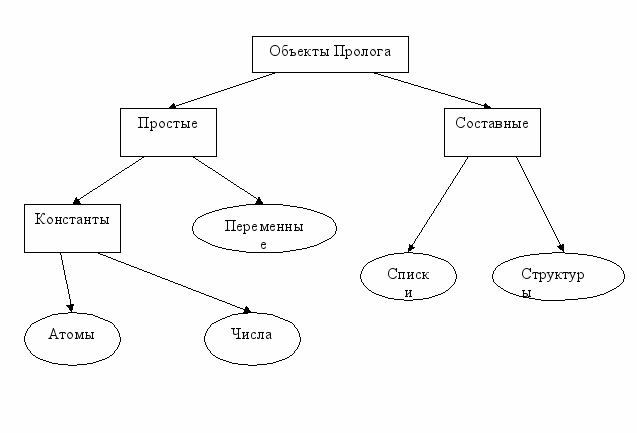
Атом. Синтаксически начинается с малой буквы латинского или русского алфавита, лексема атома может содержать буквы, цифры и знак подчеркивания. Атом несет информацию в своем наименовании (аналог строковой константы). Пример: лекция_1_введение.
Числа. Используются целые (integer) и действительные (real) числа. Пример: 1.2 и 38.
Переменная. Существуют следующие типы переменных:
1. именованные переменные – начинаются с большой буквы латинского или русского алфавита, лексема может содержать буквы, цифры и знак подчеркивания. Лексический диапазон (аналог зоны действия или области видимости) именованной переменной одно предложение, заканчивающееся точкой.
2. анонимные переменные – это переменные без имени, обозначаются знаком подчеркивания, лексический диапазон – момент работы с ней.

Переменная может находиться в одном из двух состояний:

конкретизированное – содержит терм (константу, структуру, список),

неконкретизированное – содержит все, что угодно или ничего одновременно.

Первоначальное состояние любой переменной неконкретизированное.

Лекция №2.

Структура. Структура в Прологе аналогична структуре в языке Си.

Структура характеризуется:

именем (функтор) – обычно атом,
количества аргументов (арность),
и аргументов структуры.

Аргумент структуры – любой объект Пролога – терм.

Пользовательские структуры должны быть описаны в области PREDICATES с указанием функтора, арности, типов данных аргументов:

Пример структуры лекция_2 (Основные_объекты, процедуры_пролога, часа_2).

Списки. Признаком списка являются скобки [], список содержит любое количество однотипных аргументов.

Примеры списков:

[] – пустой список, [1,2,3], [Один,2,3], [Один,Два,Три].

Допустимо представлять список, разбив его на голову и хвост.

[Гол1,Гол2|Хвост]

Голова списка должна содержать минимум один элемент. Если их несколько, то один от другого отделяются запятыми:

Хвост списка сам является списком.

Основные процедуры Пролога.

1. Проверка запроса на истинность. Проверка истинности происходит при сопоставлении цели запроса с утверждениями. Пролог осуществляет перебор утверждений. Сопоставление термов осуществляется на основе правил.

а) Сопоставление констант даёт истину если const тождественны

лекция1 v лекция_1 (-)

1 v 1.0 (-)

б) Сопоставление переменных

При сопоставлении не конкретизированных переменных с любым объектом пролога результат всегда истина. При этом переменная конкретизируется, принимает значение того объекта, с кот. было сравнение. Первоначальное состояние любой переменной нен конкретизировано.

Сопоставление конкретизированной переменной с термом определяется видом терма, которым переменная конкретизировалась.

A V [1,2,3] (+); A1 v лекция (+); A2 V B (+); A3(=лекция1) V 1 (-).

в) Сопоставление структур

Начинается с сопоставления имени структур (по правилу сопоставления атомов ), сравнивается арность структур, сопоставляются соответствующие аргументы структур между собой

г) Сопоставление списков

Начинается с сопоставления кол-ва элементов, затем сопоставляются между собой соответствующие элементы двух списков.

[1,2,3] v [Один, Два, Три] (+)

1 V Один (+) ; 2 V Два (+)

[1,2,3] v [Один, Два |Три] (-) Недоопр. Структура

Структура программы на Visual Prologe.

Область Domains - Может использоваться для описания типов данных, аргументов, структур.
Область Predicates – должны быть описаны пользовательские структуры с указанием имени структуры, кол-ва аргументов, тип данных аргументов, если они не описаны в области доменов.
Clauses - база фактов и правил.

Содержит два вида предложений.

<утверждение> - факт.

<утверждение>:-<условие> - правило

Утверждение является истиной !!!

Условие (также как и цель у запроса требует проверки на истинность)

В правиле может быть несколько условий.

В этом случае условия объединяются:

И (,)

ИЛИ(;)

Обычно утверждения и условия являются структурами

Область GOAL

<цель> Если целей несколько то они объединены лог. И/ИЛИ.

Обычно цель – структура.

Пример программы на прологе

:Задание Разработать программу, определяющую виды соединений двухполюсников в схеме (общий узел, параллельное соединение, звезда, последовательное соединение).

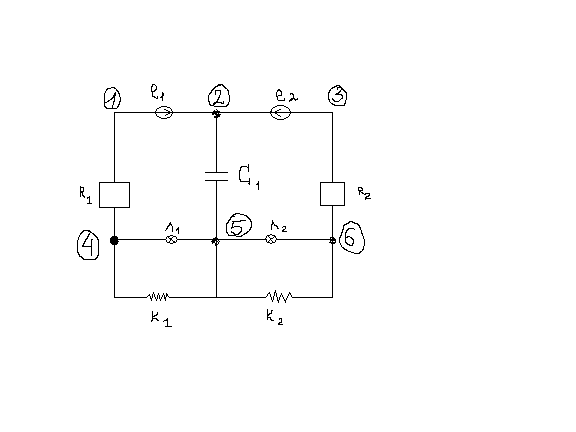
1) Геометрическая интерпретация задачи.

Выбрать схему, содержащую, как минимум, по 2 элемента с соединением каждого вида:

общий узел,

параллельное соединение,

звезда,

последовательное соединение.

2) Формирование исходных данных

Каждый элемент характеризуется:

а) наименованием, например, резистор, конденсатор

б) обозначением , например, r1, e1.

в) первым узлом подключения,

г) вторым узлом подключения.

Выберем вид терма

Для описания объекта используется несколько параметров, поэтому терм должен быть составным (структура или список)

Типы данных параметров – разнородны (symbol, integer), следовательно, для описания используем структуру.

Вводим структуру

% элемент(наименование, обозначение, узел1, узел2)

Структуру необходимо описать в области предикатов

Predicates

nondeterm элемент(symbol, symbol, integer, integer)

CLAUSES

элемент(резистор, r1,1,4). % факт1

элемент(резистор, r2, 3, 6). %факт2

элемент(источ, е1, 1, 2). % факт3

элемент(источ, е2, 2, 3). % факт4

элемент(конденс, с1, 2, 5). % факт5

элемент(лампа, л1, 4, 5). % факт6

элемент(лампа, л2, 5, 6). % факт7

элемент(катушка, к1, 4, 5). % факт8

элемент(катушка, к2, 5, 6). %aакт 9

Goal

% запрос

элемент(резистор, r2, 3, 6). % цель

Если запрос не содержит имени переменой то возможен ответ Yes, No

Пошаговое выполнение программы.

элемент(резистор ,_, Уз1, _) % Запрос 1.

Формулировка запроса. Какой номер первого узла подключения имеет элемент с наименованием резистор, с любым обозначением и любым номером подключения второго узла.

1.З v ф1

Найденное решение отправляет в стек. Переменная Узел1 в запросе снова становится не конкретизированой. И пролог с таким состоянием переменой продолжает отыскиват решения.

2.З v ф2

Получаем 2-ое решение

Лекция №3

Запрос может быть составным, содержащим несколько целей, которые объединяются (,), (;).

Последовательность выполнения целей в запросе

Объединённые логическим (или): выполняются все цели стоящие до (или), затем все решения у цели стоящие после (или). Данная модель соответствует последовательным циклам.
Объединённые логическим (и): Данная модель соответствует вложенным циклам. Первое решение первой цели, все решения второй цели, затем второе решение первой цели, все решения второй цели и т.д.

Правило общего узла

Геометрическая интерпретация.
Логическая модель.

понятие(Элемент, Наименование, Обозначение, Узел1, Узел2)

общ_узел(обозн1, обозн2, узел1)

Элементы с обозначением 1 и 2 в узле 1 соединены в общий узел, если есть элементы с об.1 и узел1 и есть элемент с об2 и узел1.

Разработка частного правила.

общий_узел(e1, r2, 1):-элемент(источник, e1, 1, 2), элемент(рез, r1, 1, 4).

Разработка общего правила

общий_узел(е1,е2,Уз1):-элемент(_, е1, Уз1, _), элемент(_,е2,Уз1,-).

Чтобы избавится от избыточных решений вводим ограничение(условие) Эл1<Эл2.

Анализ ограничений

Общ_узел(r1, у1 ,1) No % Из-за Э1<Э2

Необходимо в руководстве пользователя вводить ограничения на последовательность записей обозначений в запросе.

Как снять это ограничение?

Последовательное соединение

Два элемента с об1 и об2 соединены в узле последовательно, если эти два элемента в этом узле имеют общий узел и соединены в этом узле, не является звездой и данный узел не содержит звезды для любых трёх элементов.

not(звезда(_, _, _, Уз1))

Обработка списков

Обработка списков базируется на рекурсии хвоста списка.

Рекурсия в прологе – это обращение из правой части правила к левой части того же правила.

При обращении правой части правила к левой части того же правила, переменные в утверждении теряют конкретизацию, что эквивалентно обращению к новому предложению.

Пример рекурсивного обращения

PREDICATES

nondeterm пример_рекурсии(symbol)

CLAUSES

пример_рекурсии(а). %факт, выход из рекурсии

пример_рекурсии(А):- пример_рекурсии(А). % рекурсивное правило

GOAL

пример_рекурсии(А).

Необходимые условия возникновения рекурсии в одном предложении

Левая и правая часть должна содержать предикаты с одинаковыми именами
Результат сопоставления их должен быть (+)

Пример программ с рекурсией хвоста списка

Задание: Разработать программу, проверяющую принадлежность элемента списку.

Интерпретация.

a [a, b]

b [a, b]

c [a, b]

Логическая модель.

Элемент принадлежит списку, если он является первым элементом списка.

Элемент принадлежит списку, если он входит в хвост списка, полученный после отбрасывания первого элемента списка.

DOMAINS

список = symbol* % символьный список

PREDICATES

nondeterm принадлежит (symbol, список)

CLAUSES

принадлежит(X,[X|_]). % Факт 1

принадлежит(X,[_|Хвост]) :- принадлежит(X,Хвост)% правило 1

GOAL

принадлежит(c,[а,b,c]) .

Задание:

Записать программу в виде одного предложения

принадлежит(X, [Y|Хвост]):- X<>Y, принадлежит(Х, Хвост); Х=Y, !.

Лекция №4

Пошаговое выполнение программы принадлежит:

Запрос сопоставляем с фактом 1 (-)

X V c (+)

[Х(=c)|_] V [a,b,c] (-)

Х(=c) V a (-)

Запрос V левой частью правила 1

X V с (+); [_|Хвост] V [a,b,c] (+)

V а (+); Хвост V [b,c] (+)

правую часть правила сопоставляем с фактом 1 (-)

Х(=c) V X (не конкретизированным) (+);

Хвост(=[b,c]) v [X( =c)|_}]; (-)

правую часть правила сопоставляем с левой частью правила (+)

X(=с) V X (+); Хвост(=[b,c]) V [_|Хвост]; (+)

правую часть правила сопоставляем с фактом 1 (+)

X(=с) V X (+); [Х(=с)|_] V Хвост(=[с]) (+)

Варианты программы принадлежит

Можно проверять элементы, стоящие на чётном месте.

CLAUSES

% принадлежит(X,[_,X|_]).

%принадлежит(X[_,_|Хвост]):-……..

Самостоятельно отредактировать программу для проверки элементов, стоящих на нечётных местах

Если необходимо закончить проверку, не рассматривая 2 последних элемента, то факт преобразуем в правило, где к хвосту предъявляем требования

% принадлежит(X,[X|Хвост]):-Хвост=[_,_|_].

Задание: Разработать программу, объединяющую элементы двух списков в третий

Интерпретация.

[a, b] [c, d] [a, b, c, d]

Логическая модель

Если первый список пустой, то результирующий список равен второму списку.

Элемент принадлежит списку, если он входит в хвост списка, полученный после отбрасывания первого элемента списка.

DOMAINS

список = symbol* % символьный список

PREDICATES

nondeterm конкатенация (список, список, список)

CLAUSES

конкатенация ([], L1,L1). % факт 1

конкатенация ([X |L1], L2 ,[X |L3]) :- конкатенация (L1, L2 ,L3). % правило 1

GOAL

конкатенация ([a, b], [c, d],[a, b, c, d]).

Факт 1 обеспечивает занесение 2-ого списка в 3-ий целиком, когда первый список становится пустым.

Правило 1 производит поэлементное занесение первого списка в третий. При этом второй список остается неизменным.

Пошаговое выполнение программы принадлежит:

Запрос сопоставляем с фактом 1 (-)

[a, b] V [] (-)

Запрос сопоставляем с левой частью правила 1

[a, b] V [X |L1] (+);

[_|Хвост] V [a,b,c] (+)

V а (+); Хвост V [b,c] (+)

[c, d] V L2

[a, b, c, d]. V [X |L3]

правую часть правила сопоставляем с фактом 1 (-)

Х(=c) V X (не конкретизированным) (+);

Хвост(=[b,c]) v [X( =c)|_}]; (-)

правую часть правила сопоставляем с левой частью правила (+)

X(=с) V X (+); Хвост(=[b,c]) V [_|Хвост]; (+)

правую часть правила сопоставляем с фактом 1 (+)

X(=с) V X (+); [Х(=с)|_] V Хвост(=[с]) (+)

Варианты программы принадлежит

Свойства отсечений.

Зеленое отсечение:

Если убрать зеленое отсечение, то результат выполнения программы должен остаться неизменным при любом запросе
Декларативный смысл программы с зеленым отсечениями и без него одинаков
В программе с зеленым отсечением можно переставлять предложения местами и результат останется неизменным
Программа, как правило, содержит избыточные условия, т.е. условия, которые истинны всегда, когда мы их проверяем.

Красное отсечение:

Если удалить красное отсечение, то результат выполнения изменится хотя бы для одного запроса
При красном отсечении декларативный смысл изменится хотя бы в одном предложении по сравнению с программой без отсечения, дающей тот же результат
Перестановка предложений местами должна привести к изменению результата
Перестановка предложений местами должна привести к изменению результата хотя бы при одном запросе и при какой-то перестановке

В программе с красным отсечением избыточность, как правило, отсутствует

Последовательность выполнения целей в запросе(условий в правиле), содержащих логическое (и), (или), отсечения (!).

GOAL

P(X),!,P(Y),!; P(Z)

Чтобы отсечение заработало => его выполнить.
Отсечение запрещает в правиле блок «или»
Внутри целей, объединённых «и», отсечение запрещает поиск последующий после 2-ого решения слева от отсечения.

Марщрутизация

Задача марщрутизациии включает в себя выбор маршрута, (n), в метро, междугородних перевозок, движение по ж/д., с учётом критериев min, opt (min расстояние, время, пересадки, стоимости.)

Эти задачи сводятся к моделям описываемым графами.

Исходные данные: 5 узлов, 8 ветвей,

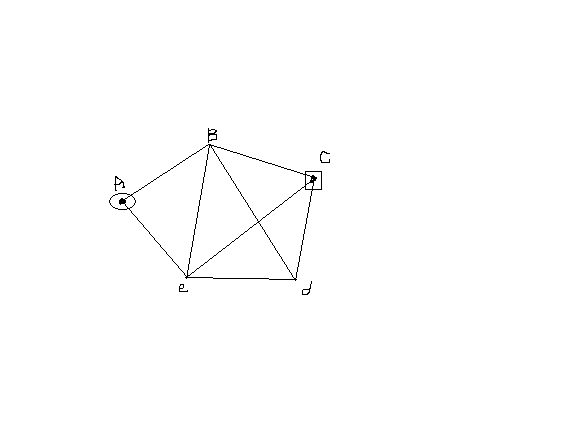задаётся начальный и конечный узел. Необходимо отыскать все пути из начального узла в конечный.

Без введения дополнительных ограничений – бесконечное число решений.

Ограничения.

Нельзя повторно проходить ветвь в том же направлении

(в обратном направлении).

2) Ограничение на повторное прохождение узла. Ограничение на вход(выход) из узла

3) Ограничение на кол-во ветвей в пути (маршруте)

Выбор алгоритма

Отыскиваем маршрут от начала к концу
Отыскиваем маршрут от конца к началу
Движение по одной ветви
Движение по последней ветви
Движение, исключая пройденную ветвь
Движение не исключая эту ветвь
Движение, сохраняя стратегию предыдущего шага
Движение, изменяя стратегию предыдущего шага + появление промежуточной ветви.

DOMAINS

список = symbol*

PREDICATES

nondeterm путь(symbol,symbol,список,список, integer)

nondeterm путь(symbol,список,список,список, integer)

nondeterm принадлежит(symbol, symbol, список)

nondeterm граф(список)

nondeterm смежные(symbol,symbol, список)

CLAUSES

граф([a,b,b,d,b,c,c,d,c,e,e,d,d,b,e]) % факт 1

% содержит описание всех 8-ми ветвей графа

% граф неориентированный => по ветви можно пройти

% как =>, так и <=

путь(A,Z,Граф,Путь,Номер):-путь1(A,[Z],Граф,Путь, Номер). % правило 1

% передаём из предиката «путь» в «путь1»

% передаём : A - начальный. узел

Z – конечный узел

Граф – ветви графа

% Номер - ограничение на кол-во ветвей

Лекция №5

CLAUSES

граф([a,b,b,d,b,c,c,d,c,e,e,d,d,b,e]) % факт 1

путь(A,Z,Граф,Путь,Номер):-путь1(A,[Z],Граф,Путь, Номер).

Путь1 (A[A|Путь1],_,Путь1,_). Факт2

% Описание пути – Путь1, в случае когда начальный узел равен конечному. Осуществляется выход из рекурсии, позволяющий находить ветви в маршруте. Выход происходит когда текущий промежуточный узел, будет равен начальному.

/*1*/

Убеждаемся что кол-во ветвей в маршруте не превышает заданное значение.

Путь1(A,[Z|Путь1], Граф, Путь, Номер):-

/*1*/ Номер > 0,

/*2*/ смежные(Y,Z, Граф)

/*3*/ not (принадлежит(Y,Z,Путь1)),

/*2*/

По заданному узлу Z среди списка, сод. Ветви граф, находим смежный узел Y.

/*3*/

Ограничение на повторное прохождение ветви в прямом направлении, т.е. убеждаемся, что ветвь Y,Z Пути 1 не принадлежит.

/*4*/

Номер1= Номер-1

Уменьшает значение счётчика на один

Выбираем ветвь.

/*5*/

Путь1(A,[Y,Y,Z|Путь1], Граф, Путь, Номер1). % Правило 2.

Рекурсивно обращаемся в левую часть правила, при этом текущий узел Z, заполнится конкретизацией Y, а в переменную Путь1 левой части правила попадает [Y, Z, Путь1]

Смежные (Y,Z,Граф):- принадлежит (Y, Z, Граф); принадлежит(Z,Y,Граф). % Правило 3

Обеспечивает направленность графов – ветвь Y,Z описана в графе 1 раз, а двигаться по ней можно в двух направлениях из Y в Z и из Z в Y/

Принадлежит(Y,Z,[Y,Z|_]). %факт 3

Принадлежит(Y,Z,[_,_|Хвост]):-принадлежит(Y,Z, Хвост). % Правило 4

GOAL

граф(Граф), путь(a, c, Граф, Путь, 3).

Пошаговое выполнение программы

(1) 1-ая цель v ф1 (+)

Граф V [a, b,…] (+)

(2) 2-ая цель v ф1 (-)

(3) 2 – ая цель v левая часть правила 1

A V a (+); Z V C (+); Граф (=[a, b,…]) V Граф (+)ж

Путь V Путь (+);

Номер V З (+)

(4-6) Правая часть правила 1 v ф2 (-)

(7)правая часть правила 1 v левая часть правила 2

A(=a) V A(+); [Z(C=)] v [Z|Путь1] (+);

Номер V Номер (=3) (+);

Граф (=[a,b]) V Граф (+); Путь1 v Путь (+);

(8) Номер(=3) > 0 (+)

(9-13)

2-ое условие правила 2 v левая часть правила 3

Y v Y (+); Z(=C) V Z (+);

Граф(=[a,b,…]) V Граф (+)

(14-19)

1-е условие правила 3 v ф3 (-)

Y V Y (+); Z(=C) V Z (+);

[Y,Z(=c)|_] v Граф (=[a,b,…]) (-)

Z(=C) v b (-)

правая часть правила 1 v левая часть правила 4

Y v Y (+); Z(=C) v Z (+);

[_,_|Хвост] v Граф (=[a,b,,,,])

(21-26)

правая часть правила 4 v ф3 (-)

Y V Y (+); Z(=C) V Z (+);

[Y,Z(=C)|_] v Хвост(=[a,b,….]) (-)

(27) правая часть правила 4 v левая часть правила 4 (+)

Y V Y (+); Z(=C) V Z (+);

Хвост(=[b,d,b,c]) v [_,_|Хвост] (+) [b,c,…]

Последовательность решения задач

Запись исходных данных
Геометрическая интерпретация
Ввод понятий и запись логических моделей – типы правил.
М.Б. введены ограничения на прохождение ветви в обратном направлении, например not принадлежит(Z, Y, Путь1)

Ограничение на выход из узла Y (Y,_,Путь1)

Ограничение на вход в Y (_,Y,Путь1)

(_,_,Путь1) – можем пройти из Y в Z, если мы идём в первой ветви.

Лекция №6.

Понятие данных и знаний.

Данные - это отдельные факты характеризующие объекты, процессы и явления в предметной области и их свойства.

Бывают: данные как результат измерений и наблюдений, данные в виде таблиц, протоколов и справочников, данные содержащиеся в базах данных.

Знания - выявленные закономерности предметной области - законы, принципы и связи.

Примеры: знания в памяти человека как результат мышления.

Знания - это структурированные данные.

Бывают: знания отображенные в учебниках и пособиях, знания в форме данных, знания в форме моделей знаний: продукционная модель, семантическая сеть, фреймы, нейронные сети.

Отличительная особенность знаний - получение новой информации.

Знания - это данные о данных.

1. Продукционная модель.

Данная модель базируется на правилах:

Если (условие), то <действие>.

Продукционная модель предполагает наличие машины вывода: а) прямой вывод - от данных к поставленной цели; б) обратный - от цели, для ее подтверждения, к данным (пролог).

Плюсы продукционной модели:

Наглядность
Модульность
Легкость редактирования
Простой механизм логического вывода .

2. Семантическая сеть.

Семантика - это наука устанавливающая отношения между символами объектами.

Семантическая сеть - это ориентированный граф, вершины которого - понятия, а дуги - отношения между ними.

Примеры отношений:

Класс - элемент класса
Свойство - значение этого свойства
Часть - целое
Количественные отношения: равенство,<,>
Пространственные отношения: рядом, далеко...

Семантическая сеть - это универсальная модель.

Пример: сюда рисунок

Семантическая сеть может отображать наследование (передача свойств от родительского объекта к дочернему). Существуют свойства передающиеся по наследству и не передающиеся.

Семантическая сеть на прологе описывается с помощью предикатов имеющих два аргумента.

Пример: предназначен (транспорт, для_перевозок).

является (авто_транспорт, транспорт ).

Каждый вид отношений должен быть записан в базу фактов.

Наследование свойств может происходить на основе правила:

свойства (Наследник, свойства):-

иерархия(Родитель, Наследник), свойства (Родитель, Свойства).

Плюс: соответствует современным представлениям об организации долговременной памяти человека.

минус: сложность вывода.

3. Фреймы.

Фрейм - (каркас, рамка) структура знаний для восприятия пространственных сцен. Под фреймом понимается пространственный образ или ситуация.

Состав фрейма:

Имя фрейма
Слот1
Значение слота1
Слот2
Значение слота2

На прологе фрейм целесообразно программировать на основе предиката содержащего имя фрейма, i-тый слот, значение i-того слота.

Лекция № 7

Нейросеть

Область эффективного применения

В случае если алгоритм решения задачи неизвестен. Пример: Построение модели.
При решение задач различной физической и математической природы, но однородных с точки зрения нейронных сетей. Распознавание надписи, отпечатков пальцев, сетчатки глаза.
При обработке больших массивов данных. Пример – для управления машиной.

История: Н.С. были предложены в 50-е годы 20 века как инструмент моделирования биологических нейронов. 1011 - нейронов 1013 –связей

В качестве модели искусственного нейрона используется

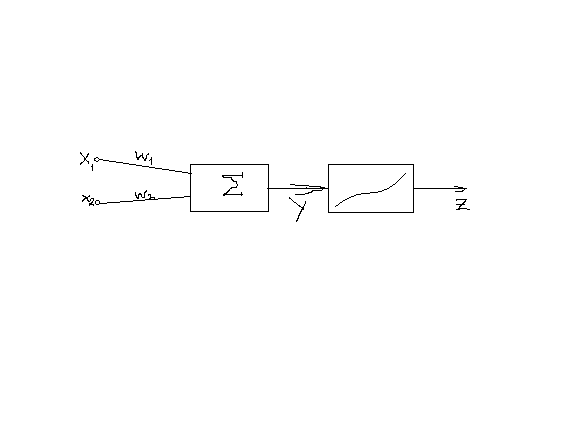
x1, x2 -входы нейрона min1 вход и до 10-ка тысяч.

Подаётся сигнал от другого нейрона(с выхода)
Из вне по нейронной сети
С входа этого же нейрона.

W1 ,W2 – блок весовых коэффициентов нейрона, в процессе обучения нейрона происходит подстройка значений весовых коэффициентов.

N – кол-во входов(весовых коэффициентов)

Функция активации: Нейрон может быть в двух состояниях активное и пассивное. В качестве фу-ии активации м.б. испорльзованы

Линейная зависимость. Равномерная чувствительность, лёгкий процесс обучения.dy=dz – соответствие

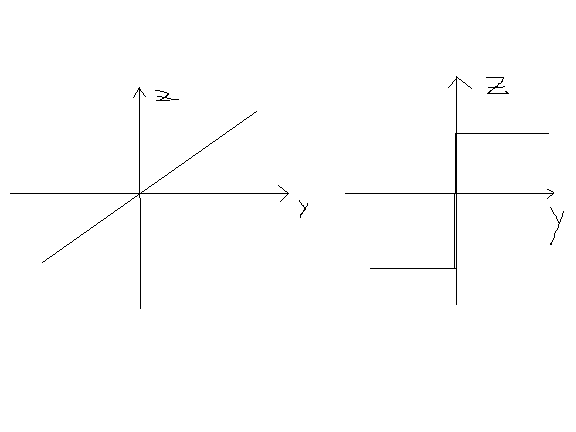
Ступенчатая ф-ия

«-» ф-ия не чувствительна к изменению аргумента, прорблемы с обучением

«+» высокие интеллектуальные способности.

Компромисс - Логическая кривая – в логической кривой есть зона с высокой чувствительностью – легкое обучение, находится около нуля. Дальше от нуль чувствительность резко падает.

Нейроны могут быть классифицированы по связи с входными и выходными сигналами сети.

Нейроны входного слоя – на вход которых подаётся сигнал из вне.
Выходные (Выходного слоя
Скрытые нейроны.

До 70-х годов использовалась однослойная нейронная сеть – персептрон

Однослойная нейронная сеть обучалась на основе алгоритма «Дельта правило»

Сложение двух чисел.

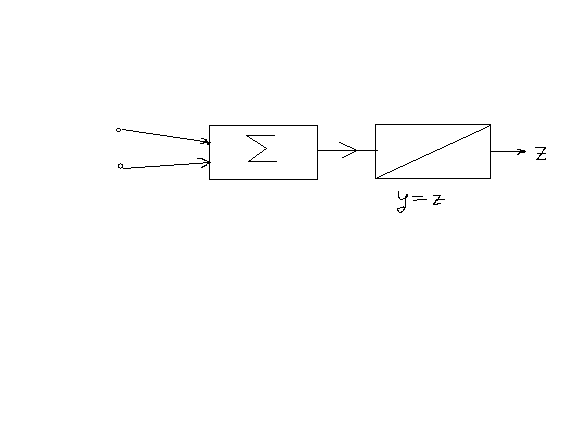
Шаг1: Формирование исходных данных. Исходные данные для обучения содержат : Входныеи тестовые значения на выходе.

1 0 1 - обучающая пара

2 3 5

1 2 3

Исходные данные должны соответствовать структуре нейронной сети.

Шаг2: Задаём начальное приближение.

Для весовых коэффициентов обычно в качестве начального приближения берутся значения из интервала близкого к нулю [0,1]. Вел задаётся случайным образом.

W1 = 0,1 W2 = 0,5.

Шаг3: Расчёт выходного значения нейронной сети при выходных сигналах соот. Первой обучающей паре. X1 = 1 X2 = 0 Y = x1w1+x2w2 = 1*0,1 +0*0,5 = 0,1

Шаг4: Осуществляем подстройку весовых коэффициентовна основе дельта правила.

D = t-y = 1- 0,1 =0,9

dWi= n dXi

n – норма, скорость обучения.

Процедура подстройки весовых коэффи циентов продолжается до тех пор пока не закончатся все записи при этом завершится эпоха. Подстройка нейронной сети требует сотен – тысяч эпох.

Лекия№8

Алгоритм обучения на основе d- правила применим для Н.С. содержащих входной и выходной слоя.

Di = Ti - Yi

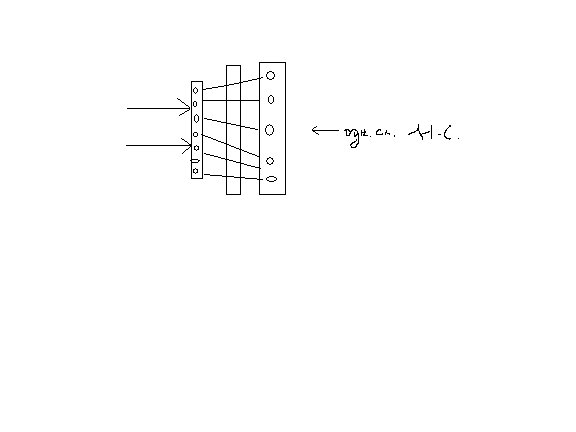
Однослойный персептрон обладает ограниченными возможностями моделирования.

В 70-ые годы эти ограничения были выявлены, но многослойные Н.С. не применяли т.к. отсутствовал алгоритм их обучения. В 80-ые были разработаны алгоритмы обратного распространения ошибки, который можно использовать для многослойной нейронной сети. Проблема связанна с невозможность применения дельта правила, обусловлена отсутствием тестовых сигналов на входе скрытого слоя.

Алгоритм обратного распространения ошибки предполагает перерасчёт ошибки, возникающей на выходе источника, эти ошибки пораждающего.

2 источника погрешности 1-й значений весовых коэффициентов у нейронов выходного слоя., 2-й – несоответствие значения на выходе на выходе нейронов скрытого слоя.

Даная процедура является итерацией.

Алгоритм обучения без учителя.

Не предполагает задание выходных значений в исходных данных..

Например: Задача кластеризации.

Этапа решения задач на основе нейронной сети.

Классификация задачи.
Выбор модели нейронной сети
Выбор пакета нейронных сетей
Выбор структуры нейронной сети
Выбор алгоритма обучения.
Переход в режим дообучения.
Анализ качества обучения

Экспертная система.

Назначение: Используется для тиражирования знаний высоко квалифицированных специалистов.

С ними работают

1) Эксперт – наситель знаний

2) Инженер – основной разработчик.

3) Программист – разрабатывает оболочку.

4) Пользователь

Представление знаний в ЭВМ

Лекции.

Волков Михаил Борисович

Blog

Конспект лекций Представление знаний в информационных системах Лекция№1

Содержание