Методы портфельного планирования инновационного развития предприятий болдарук И. И. Красноярский государственный аграрный университет, Красноярск, Россия

Вид материала

Документы

Содержание I [2]. Ковариация проектов i

Подобный материал:

• Методы оценки риска при планировании инновационной деятельности болдарук И. И. Красноярский, 118.08kb.
• Анализ проблем инновационного развития агропромышленного комлекса россии руденко, 34.58kb.
• Анализ проблем инновационного развития пищевой промышленности русских Ю. Н. Красноярский, 44.43kb.
• Отражение фактов хозяйственной жизни в бухгалтерском учете, 52.12kb.
• Проблемы, связанные с диагностикой лейкоза крупного рогатого скота люто А. А. Красноярский, 38.5kb.
• Дифференциальная рента и экономическая оценка земли курчанова Е. А. Красноярский государственный, 201.2kb.
• Методы обучения переводу на уроках иностранного языка в вузе дубинина Т. Г. Красноярский, 70.29kb.
• Основные направления развития малых форм хозяйствования в красноярском крае федосенко, 57.19kb.
• Информационная поддержка инновационной деятельности производственных предприятий рожкова, 59.68kb.
• Методы обучения чтению на английском языке чантурия Е. В. Красноярский государственный, 97.09kb.

МЕТОДЫ ПОРТФЕЛЬНОГО ПЛАНИРОВАНИЯ ИННОВАЦИОННОГО РАЗВИТИЯ ПРЕДПРИЯТИЙ


Болдарук И.И.

Красноярский государственный аграрный университет, Красноярск, Россия


The author of the article discusses methods of portfolio planning innovation development in enterprises. The article gives the analysis widely-distributed techniques of portfolio planning.


В отечественной экономической науке ведется активный поиск инновационных механизмов, которые позволили бы обеспечить рациональное использование всех имеющихся ресурсов АПК, а также обеспечить устойчивое развитие всех отраслей агропромышленного комплекса.

Механизмы инновационного развития АПК еще недостаточно полно проработаны, и поэтому требуется их научное и методологическое обоснование.

Для решения проблемы определения стратегии инновационного развития АПК, обеспечивающей повышение эффективности инновационной деятельности и устойчивости инновационного развития предприятий, предлагается использовать методы портфельного планирования.

Состав и структура оптимального портфеля инновационного проектов предприятий АПК, во многом определяется типом стратегии инвестора. В условиях обострения конкуренции приоритетной является такая стратегия инвестора, при которой производственный потенциал предприятий будет усилен, создадутся возможности для разработки новых технологий и продукции. При таком типе стратегии инвесторы вынуждены принимать рискованные решения. В этой связи при планировании инновационного развития предприятий возникает необходимость в ограничении размера риска.

Как следует из практики планирования инновационной деятельности на предприятиях, наиболее распространенной является стратегия умеренного риска, при которой критерием задачи формирования оптимального портфеля является показатель, учитывающий экономическую эффективность портфеля при ограничении рисков.

Выбор показателя максимизации стоимости бизнеса в качестве критерия формирования оптимального портфеля проектов, делает необходимым решение задачи определения множества допустимых инновационных проектов. Рассматриваемые инновационные проекты оцениваются на предмет способности обеспечить предприятиям максимальный экономический результат инновационной деятельности, при использовании ограниченных средств.

В настоящее время в специальной научной литературе и в практике планирования распространены различные методы, позволяющие решать задачу формирования оптимального портфеля инновационных проектов, которые можно представить в виде двух групп: точные и приближенные методы портфельного планирования.

Среди точных классических методов наибольшее распространение получили: модель Г. Марковица, методы линейного и динамического программирования.

Основой подхода к построению оптимального портфеля инновационных проектов с точки зрения современной портфельной теории является работа Гарри Марковица [2, 3]. В соответствии с подходом Г. Марковица для принятия решения о вложении средств инвестору не нужно проводить оценку всех портфелей, а достаточно рассмотреть лишь так называемое эффективное множество вариантов комбинации проектов.

Предприятие формирует свой оптимальный портфель инновационных проектов из множества допустимых инновационных портфелей, каждый из которых обеспечивает:

- максимальную ожидаемую экономическую эффективность инновационной деятельности для некоторого уровня риска;

- минимальный риск для некоторого значения ожидаемой экономической эффективности инновационной деятельности.

Набор инновационных портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством или эффективной границей.

Для построения эффективного множества инновационных проектов используется метод, основанный на принципах рыночной модели.

В соответствии с данной моделью [2], доходность портфеля оценивается на рыночный индекс. Затем для каждого проекта определяется коэффициент вертикального смещения 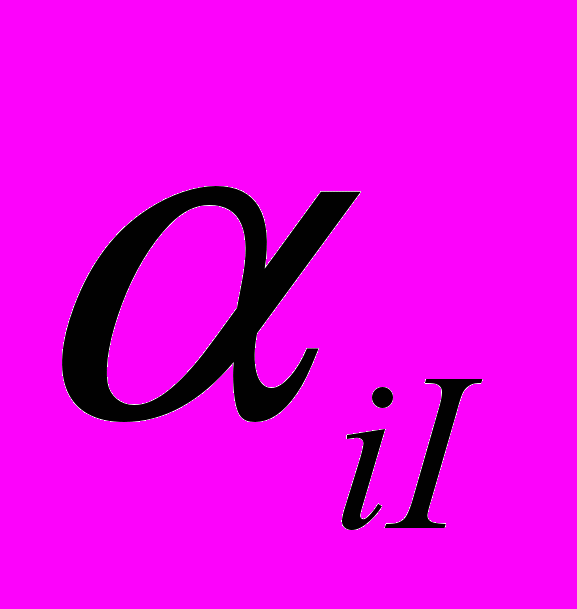и коэффициент «бета». Полученные значения используются для проведения оценок ожидаемой доходности каждого проекта с помощью уравнения: .

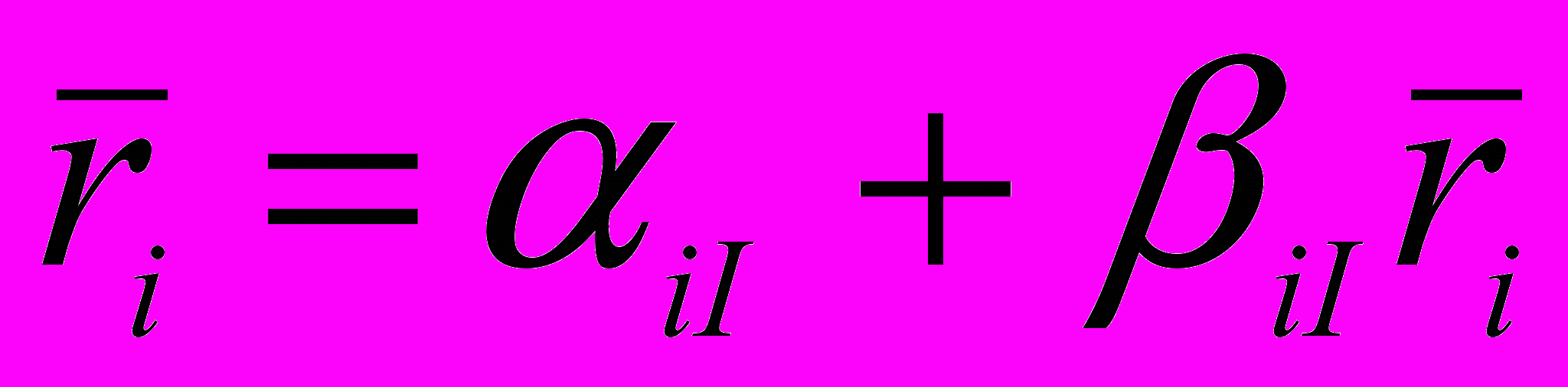Дисперсия проекта i может быть оценена по формуле: ,

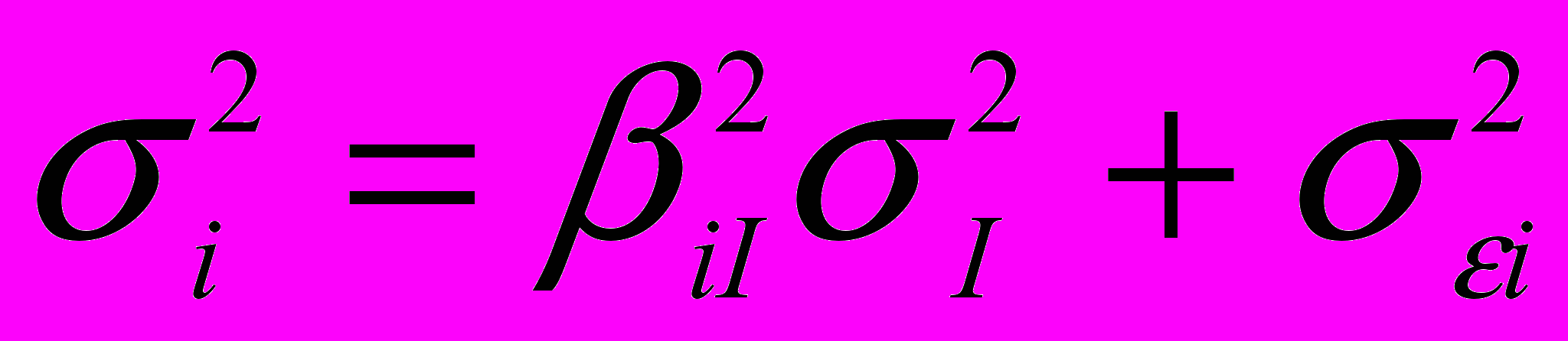где 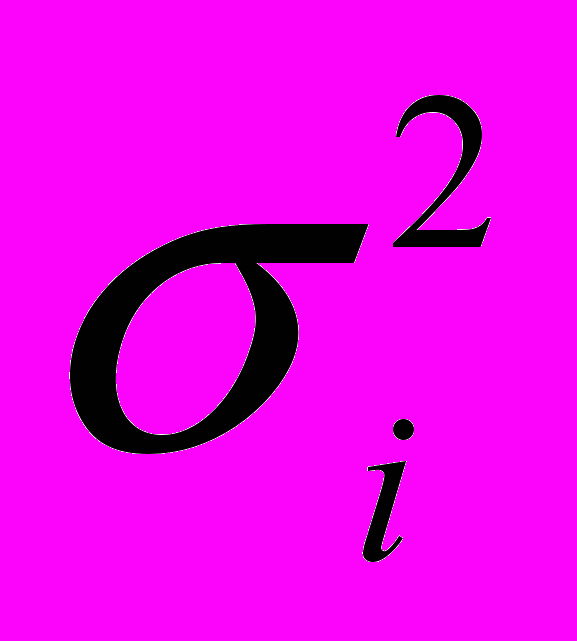обозначает дисперсию индекса и 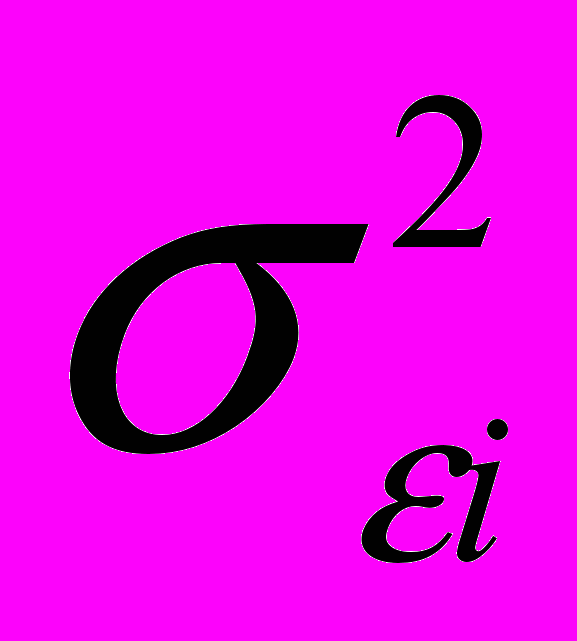обозначает дисперсию случайной погрешности для проекта I [2].

Ковариация проектов i и j оценивается произведением трех чисел: «бета» - коэффициента i-ого проекта, «бета» - коэффициента j-ого проекта и дисперсии индекса рынка [2]:

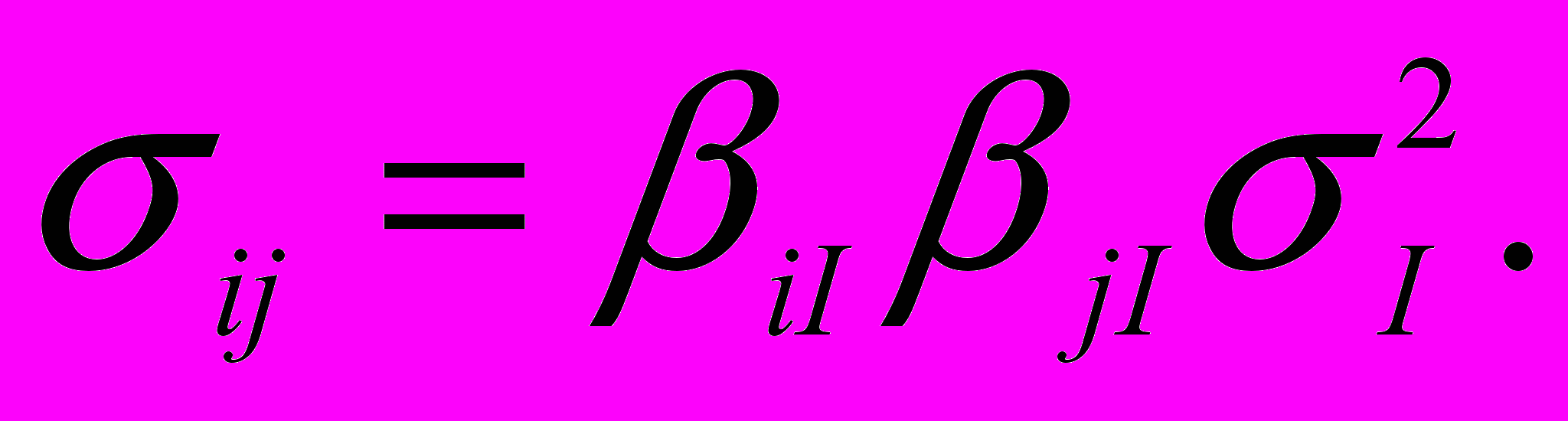
После этого оптимальный портфель проектов (портфель бизнес-единиц) подбирается с помощью определения точки касания кривых безразличия с эффективным множеством.

Важным положением теории портфеля проектов [2] является то, что совокупный риск портфеля можно разложить на две составные части: систематический риск (рыночный), который нельзя исключить, и которому подвержены все проекты в равной степени; и несистематический риск (собственный) для каждого конкретного проекта, который можно избежать, управляя портфелем проектов.

Достоинство: метод предполагает проведение анализа не всех портфелей, а лишь их эффективного множества.

Недостатки: не учитывается возможность переложения инвестиций; трудоемкость расчетов; специфичность к финансовому портфелю.

Модель любой задачи линейного программирования (ЗЛП) включает: целевую функцию (линейную форму), экстремум (оптимум) которой требуется найти по условию; ограничения в виде системы линейных уравнений (неравенств); требование неотрицательности переменных. ЗЛП сводится к следующему [4]. Найти максимум функции:



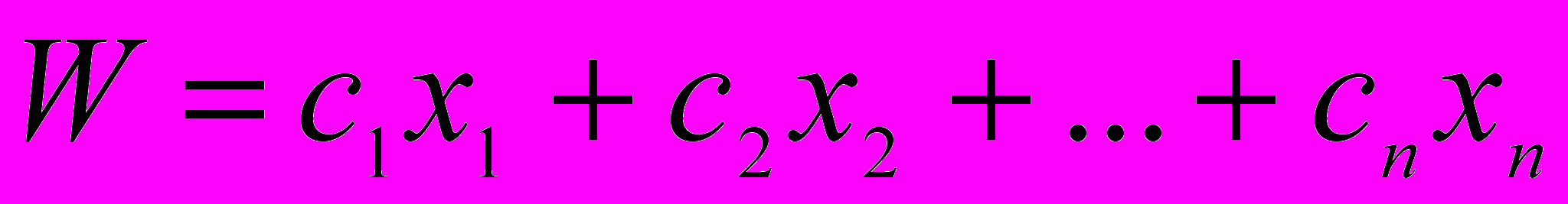
при выполнении ограничений:

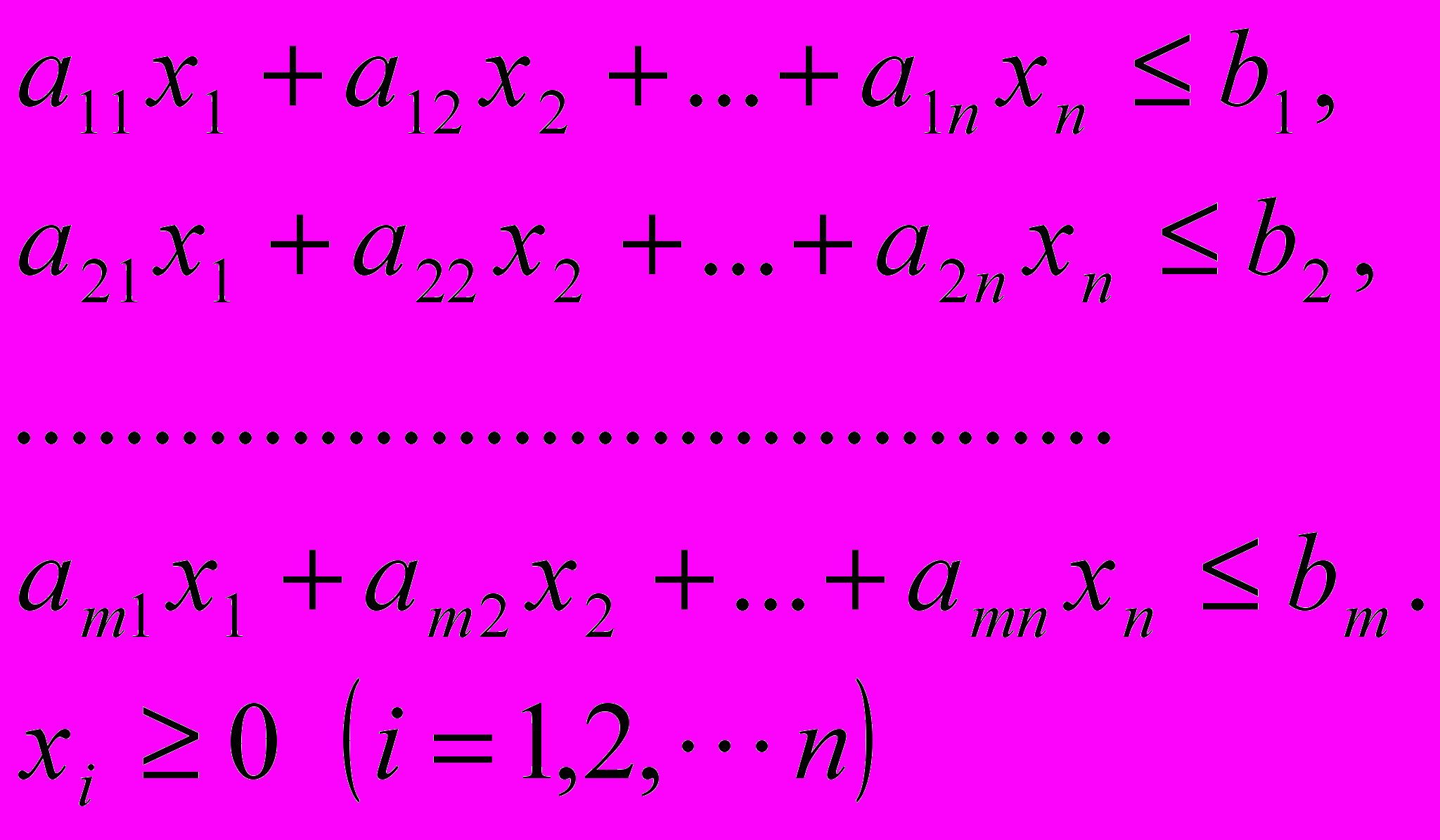(1.1)

В задачах линейного программирования число уравнений меньше числа переменных, т.е. 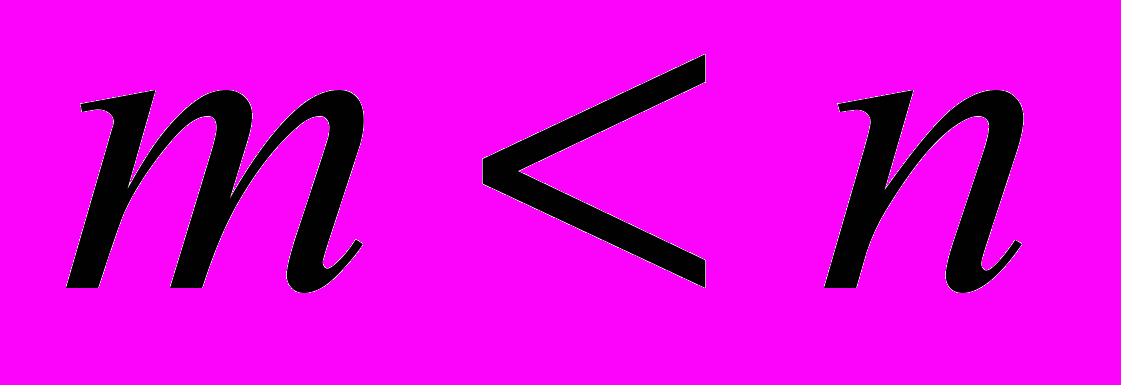. Вместо системы линейных уравнений (1.1) целесообразнее иногда иметь систему линейных неравенств. Для математического решения таких систем вводятся неотрицательные неизвестные, 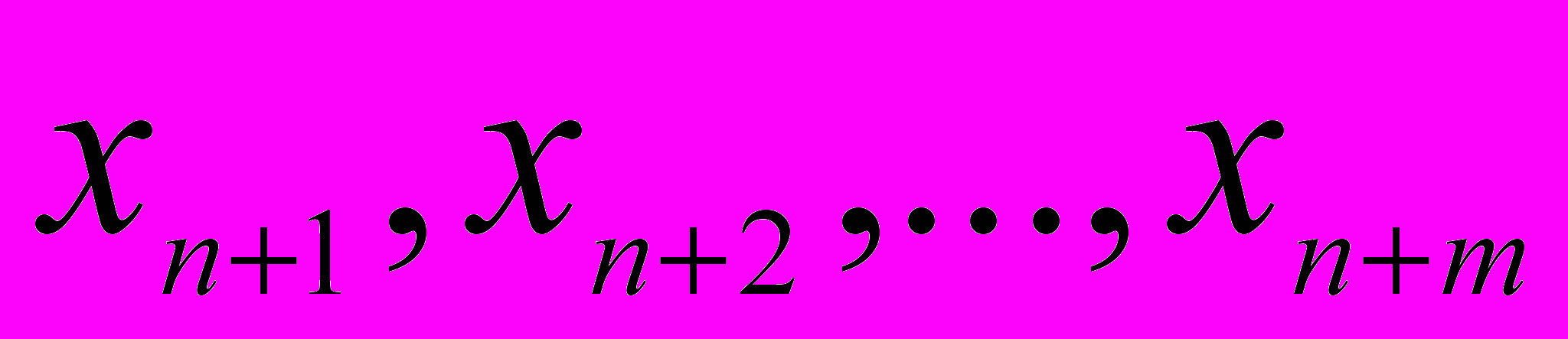, которые принято называть дополнительными [5]. С помощью этих неизвестных ограничения в виде неравенств переводятся в систему уравнений типа (1.1).

Решение , при котором функция W принимает оптимальное значение, называется оптимальным решением.

Для управления портфелем инновационных проектов постановка задачи линейного программирования может быть приведена к следующему виду. Необходимо определить такие ресурсы в 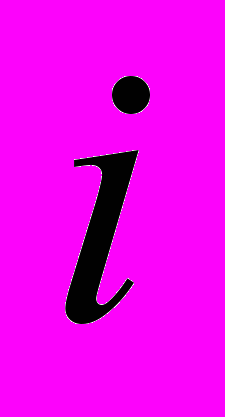-й проект (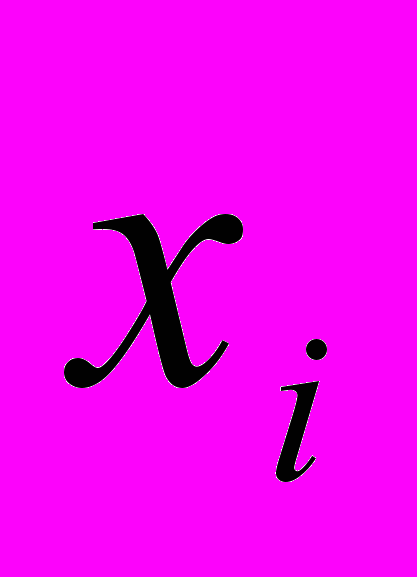), которые позволили бы достичь максимального значения показателя эффективности портфеля проектов. Константы 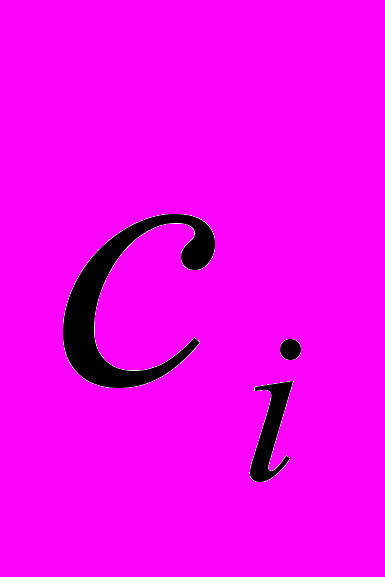и – входные параметры для данной задачи и определяются расчетным путем. Правая часть системы уравнений (1.1) - константы 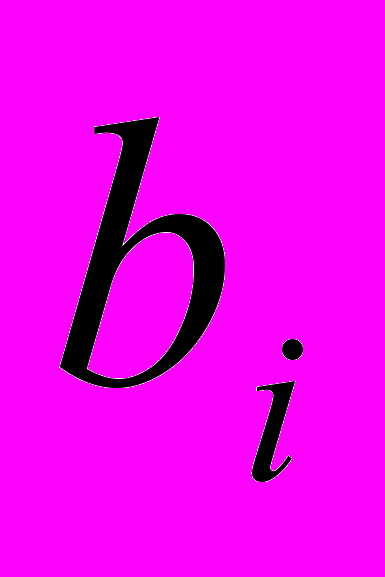может задаваться исходя из требований стратегии инвестора, либо как расчетная величина.

Достоинство: рассматриваемый метод позволяет не только выбрать оптимальный вариант решения, но и проводить анализ чувствительности результатов расчета варьированием исходных данных.

Недостаток: применение метода линейного программирования ограничивается использованием в целевой функции критерия риска, что обусловлено нелинейностью связи входных и выходных параметров, т.е. состав портфеля проектов, количество проектов в котором меняется.

Другим методом формирования оптимального портфеля проектов, в процессе планирования развития предприятий является метод динамического программирования (ДП). Сущность данного метода заключается в «многошаговом» оптимальном решении, каждый раз оптимизируется решение только на конкретном шаге процесса формирования оптимального инновационного портфеля. Эффективность операции на каждом шаге характеризуется показателем 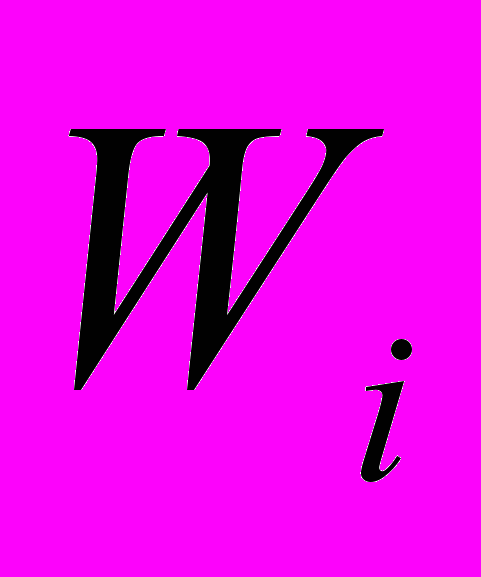(выигрышем). Эффективность всей операции складывается из показателей эффективности на отдельных шагах: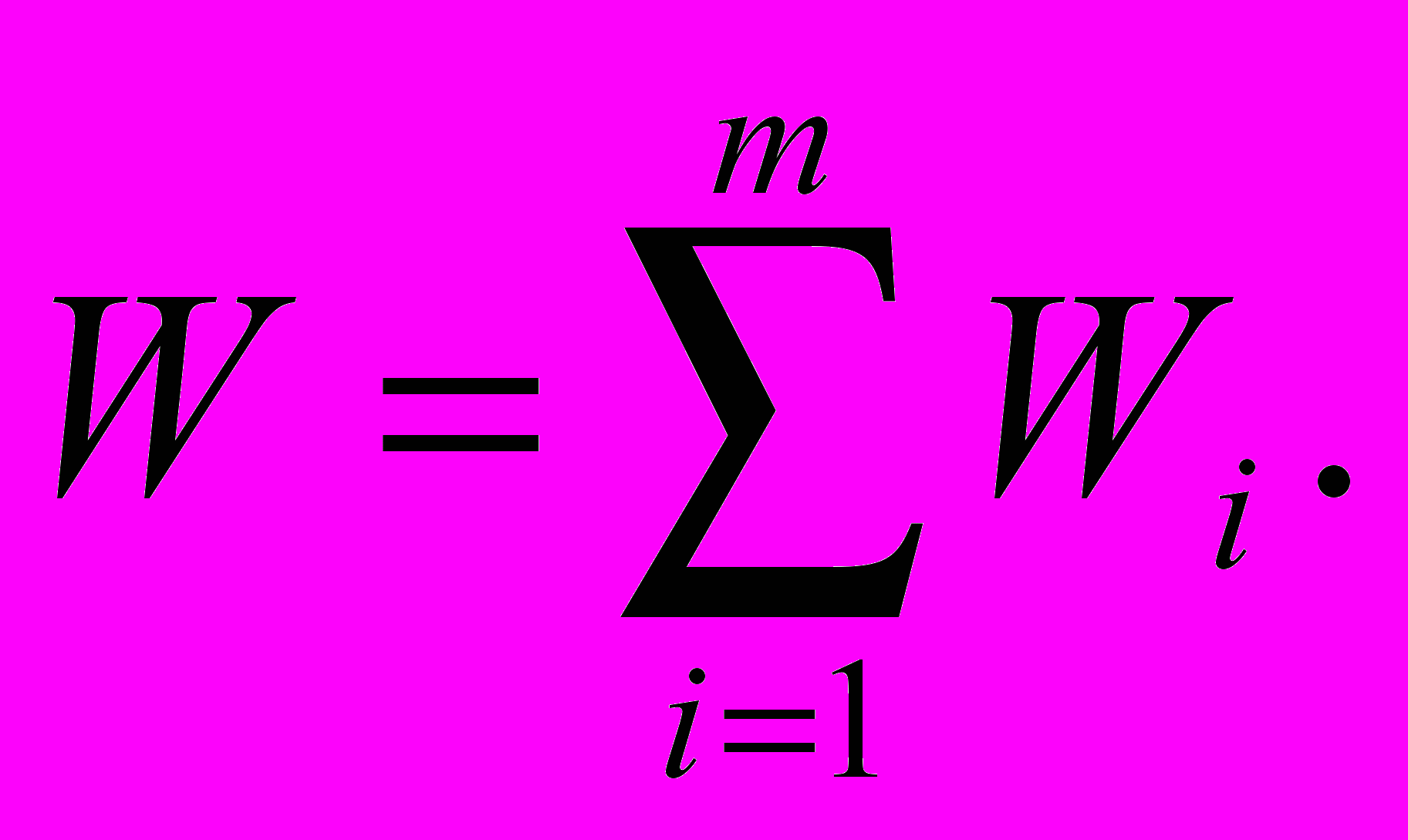

Постановка задачи ДП осуществляется в следующей последовательности [3; 5]:

1. Определяются параметры, характеризующие состояние системы перед каждым шагом.

2. Операция разбивается на шаги.

3. Определяется набор шаговых управлений для каждого шага и налагаемые на них ограничения.

4. Записывается «функция выигрыша» 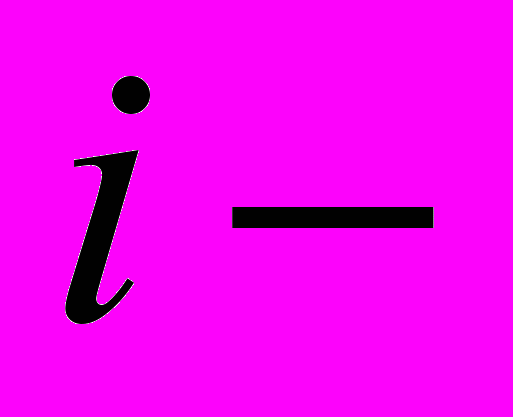го шага управления :



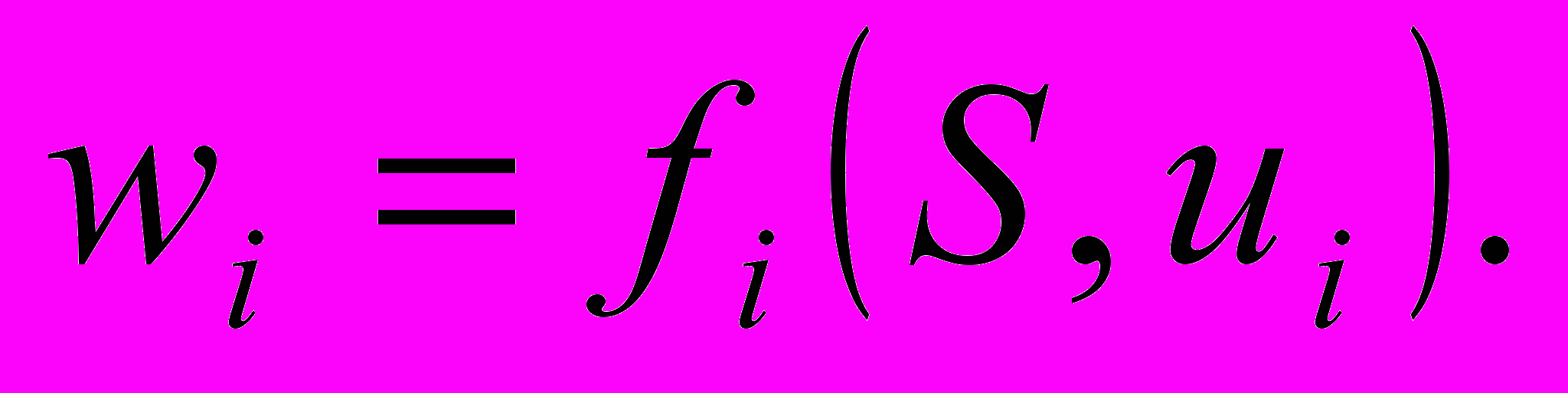
5. Определяется изменение состояния системы (переход в новое состояние - ) под влиянием управления на 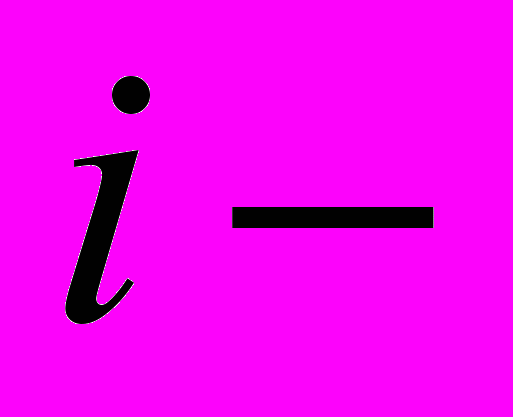ом шаге: .

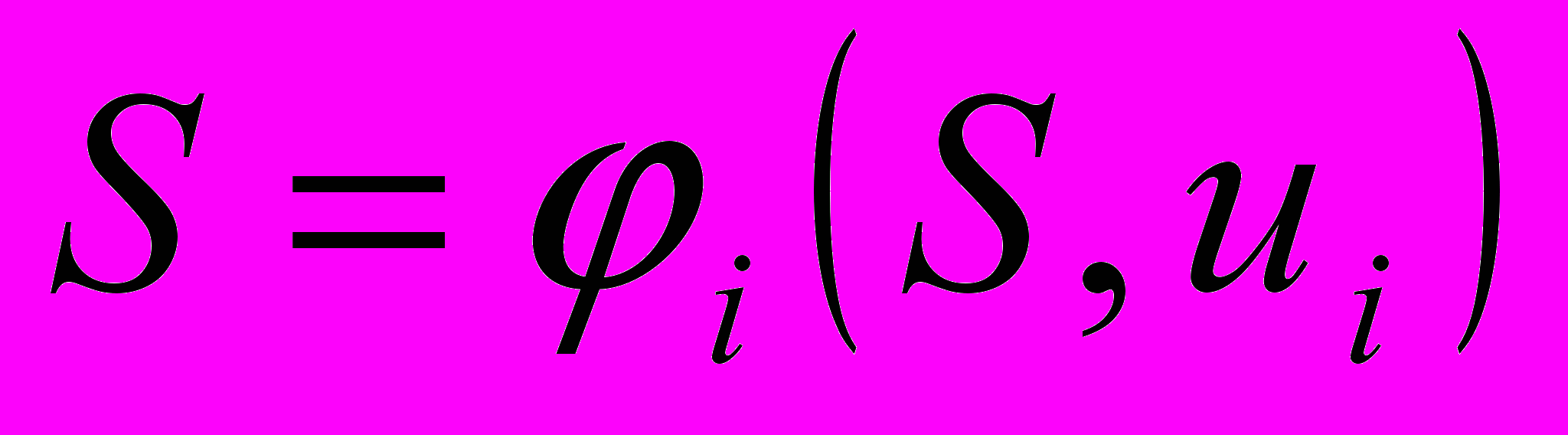6. Записывается рекуррентное уравнение, выражающее условный оптимальный выигрыш 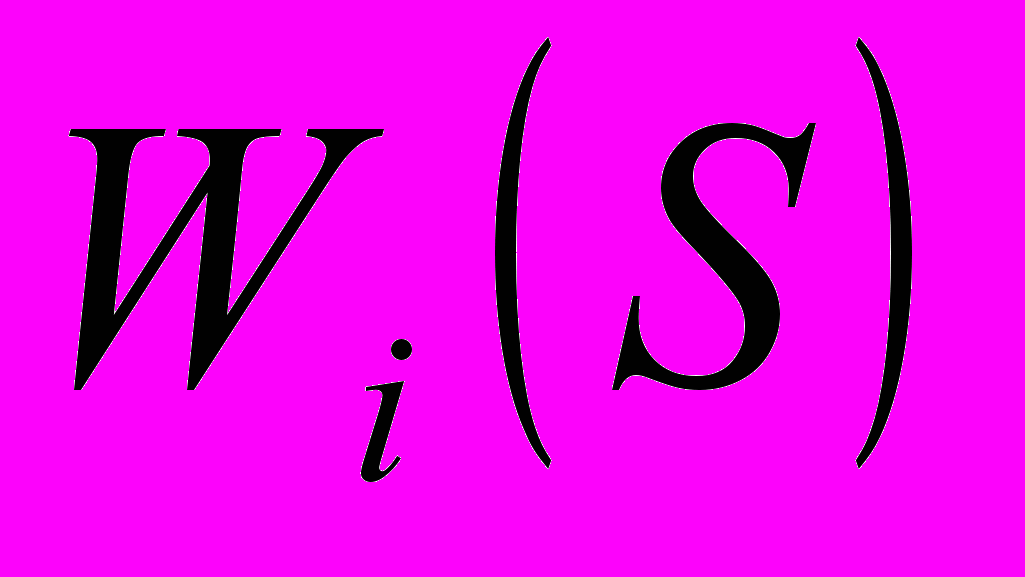(начиная с 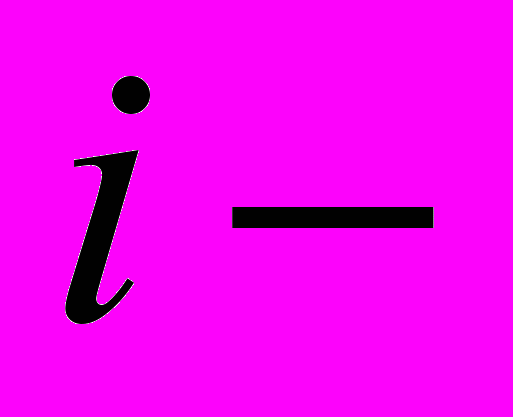го шага и до конца) через функцию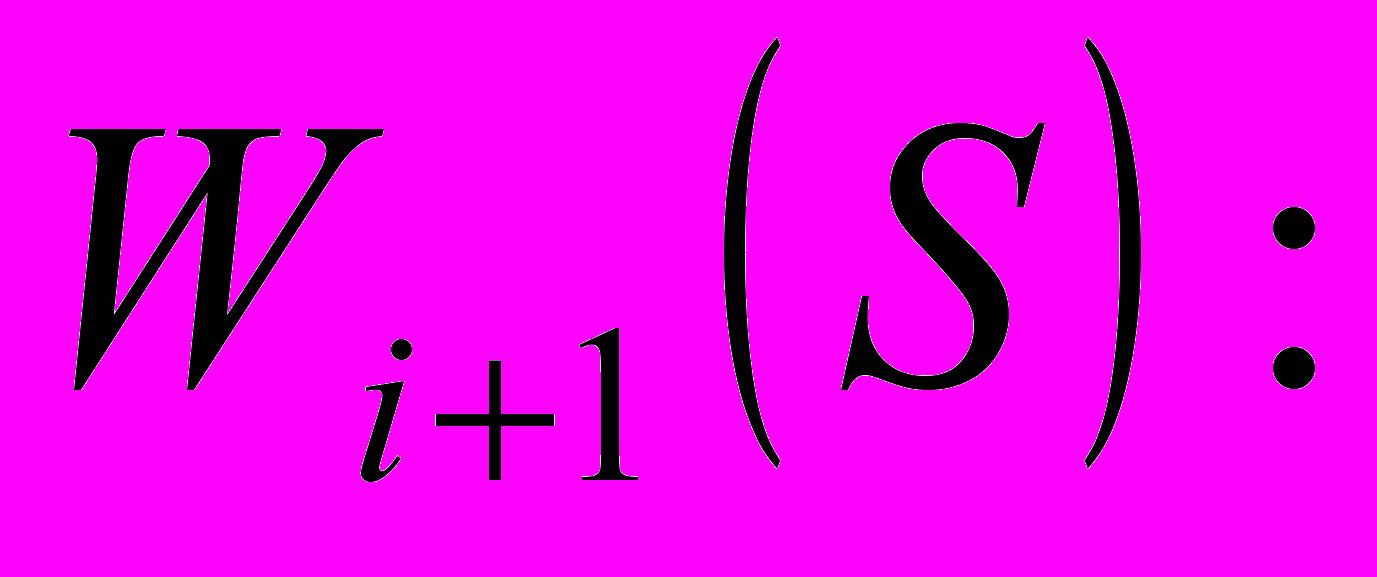

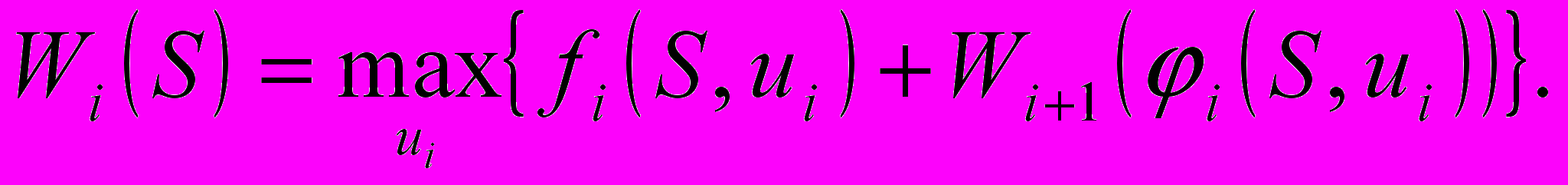
Использование метода ДП при формировании оптимального портфеля проектов имеет следующие достоинства:

- использование в целевой функции критерия максимизации экономического результата инновационной деятельности;

- позволяет учесть нелинейность связи входных и выходных параметров;

- позволяет учесть эффект диверсификации при формировании портфеля проектов.

Использование метода динамического программирования при планировании инновационного развития предполагает необходимость замены каждой целочисленной переменной булевыми переменными [4, 6] для снятия ограничений при построении портфеля инновационных проектов.

Среди приближенных методов наибольшее распространение получили вероятностные алгоритмы формирования оптимального портфеля, среди которых распространен метод поиска с запретами. Алгоритм поиска с запретами является разной реализацией одной и той же идеи: организации стохастического Марковского процесса. Каждый из этих алгоритмов устроен таким образом, чтобы соответствующая ему цепь Маркова была конечной, неразложимой и непериодической, что гарантирует получение требуемого результата построения инновационного портфеля [2].

Основоположником алгоритма поиска с запретами (Tabu search) является Ф. Гловер [1], который предложил принципиально новую схему локального поиска. В соответствии с данной схемой алгоритма поиска, лицо, принимающее решение (ЛПР) не останавливается в точке локального оптимума, а перемещается от одного локального оптимума к другому, в поисках между несколькими локальными оптимумами глобального оптимума. По данной схеме локального поиска, основным механизмом, позволяющим ЛПР отойти от локального оптимума, является список запретов Tabu (i_k). Список запретов формируется на основе обобщения нескольких предшествующих вариантов комбинации проектов i_k, i_k–1,…, i_k–l+11, и запрещает часть окрестности текущего решения N(i_k). То есть на каждом шаге алгоритма очередная точка i_k+1 является оптимальным решением подзадачи [7].

f(i_k+1) = max {f(j) | j Î N(i_k) \ Tabu_l (i_k)}.

Список запретов Tabu_l(i_k) Ì N (i_k) учитывает специфику задачи и, как правило, запрещает те решения, которые менялись на последних l шагах алгоритма. Константа l ³  0 задает длину списка запретов. При l = 0 получают стандартный локальный спуск (напр. полное использование инвестиционного потенциала предприятий).

Использование приближенных методов портфельного планирования позволяет решать задачу формирования оптимального инновационного портфеля уже на первых итерациях. Преимуществом метода поиска с запретами является высокая вероятность получения приемлемого решения за достаточно небольшое количество итераций.

Результаты анализа методов портфельного планирования показали, что распространенные на сегодняшний момент методы портфельного планирования имеют несомненный практический интерес. Вместе с тем, при выборе методов портфельного планирования, необходимо учитывать особенности инновационной деятельности предприятий АПК. А они таковы, что в силу дефицита собственных оборотных средств, низкого уровня инвестиционного потенциала, предприятия ограничены в инвестиционных ресурсах, поэтому вынуждены концентрировать свое внимание на разработке и реализации наиболее значимых инновационных проектов, число которых, как правило, невелико. На наш взгляд в этих условиях в наибольшей степени при построении оптимального инновационного портфеля подходит метод полного перебора проектов на основе решения задачи линейного программирования с использованием булевой переменной.

Таким образом, на сегодняшний день не существует полностью готовых методических решений по решению задачи формирования оптимального инновационного портфеля.

Литература

1. Управление инвестициями: В 2-х т. Т 1. // Под общ. ред. В.В. Шеремета.   М.: Высшая школа, 2002. – 416 с.

2. Охорзин В.А. Математическая экономика. – Красноярск: СибГАУ, 2006. – 232 с.

3. Первозванский А.А., Первозванская Т.Н. Финансовый рынок: расчет и риск. // -М.: ИНФРА-М, 2000. – 192 с.

4. Калашников В.В. Организация моделирования сложных систем// - М.: Знание, 1989. – 126 с.

5. Бурков В.Н., Ириков В.А. Модели и методы управления организационными системами. // - М.: Наука, 2004.   314 с.

6. Антамошкин А.Н. Регулярная оптимизация псевдобулевых переменных. Красноярск: Изд-во Краснояр. ун-та, 1989. – 160 с.

7. Сигал И.Х. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы / И.Х. Сигал, А.П. Иванова. – М.: ФИЗМАТЛИТ, 2002. – 240 с.