Асимптотически оптимальная плотность распределения случайных узлов в формулах Ньютона−Котеса

Вид материала

Доклад

Подобный материал:

• Функция распределения. Плотность распределения. Основные параметры непрерывных случайных, 7.05kb.
• Лабораторная работа №2 Тема: Формирование выборки случайных чисел, распределенных, 151.75kb.
• Основные виды случайных величин, 28.43kb.
• Вопросы к экзамену по дисциплине «теория массового обслуживания», 20.42kb.
• Задачи по теории вероятностей и математической статистике, 57.05kb.
• Характеристика специальности 210406 «сети связи и системы коммутации», 37.03kb.
• Числовые характеристики случайных величин, 50.29kb.
• К публикации ранней лингвистической работы Исаака Ньютона, 1152.48kb.
• Программа вступительных испытаний по предмету прикладная математика и информатика для, 16.87kb.
• Анализ проф. Ю. Н. Тюрин 1/2 год, 15kb.

Асимптотически оптимальная плотность распределения случайных узлов в формулах Ньютона−Котеса


Д.В. Бутенина


Северо-Западный государственный заочный технический университет

факультет информационных систем управления

кафедра информатики

Россия, 191186, г. С.-Петербург, ул. Миллионная, 6

тел.: (812) 3186340, e-mail: dvbu@mail.ru


Доклад посвящен адаптивной оптимизации квадратурных формул типа Ньютона-Котеса для вычисления одномерных интегралов на случайной сетке. При этом функционал погрешности оказывается зависящим от функции плотности распределения 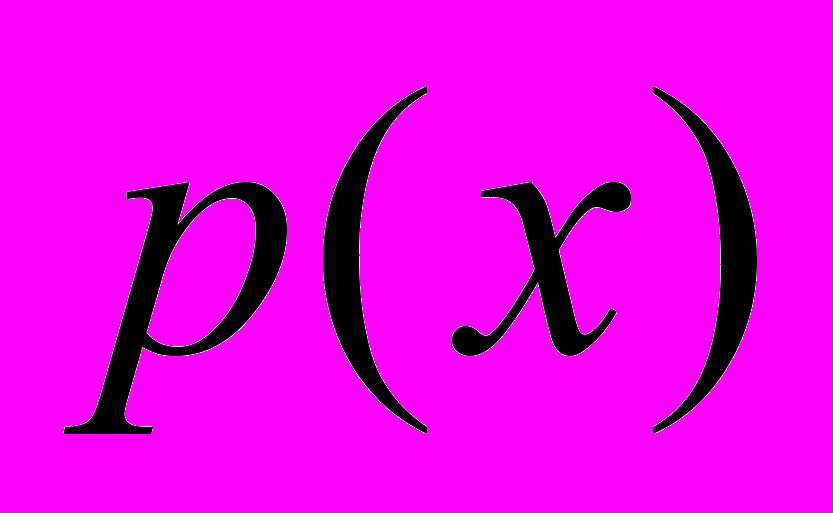случайных узлов, а также от параметров задачи (- интегрируемая на отрезке [a,b] функция, - максимальная степень многочленов, для которых точна соответствующая квадратурная формула).

Ниже приводится функционал для формулы трапеций:



где - функция распределения случайной величины .

Оптимизация функционала 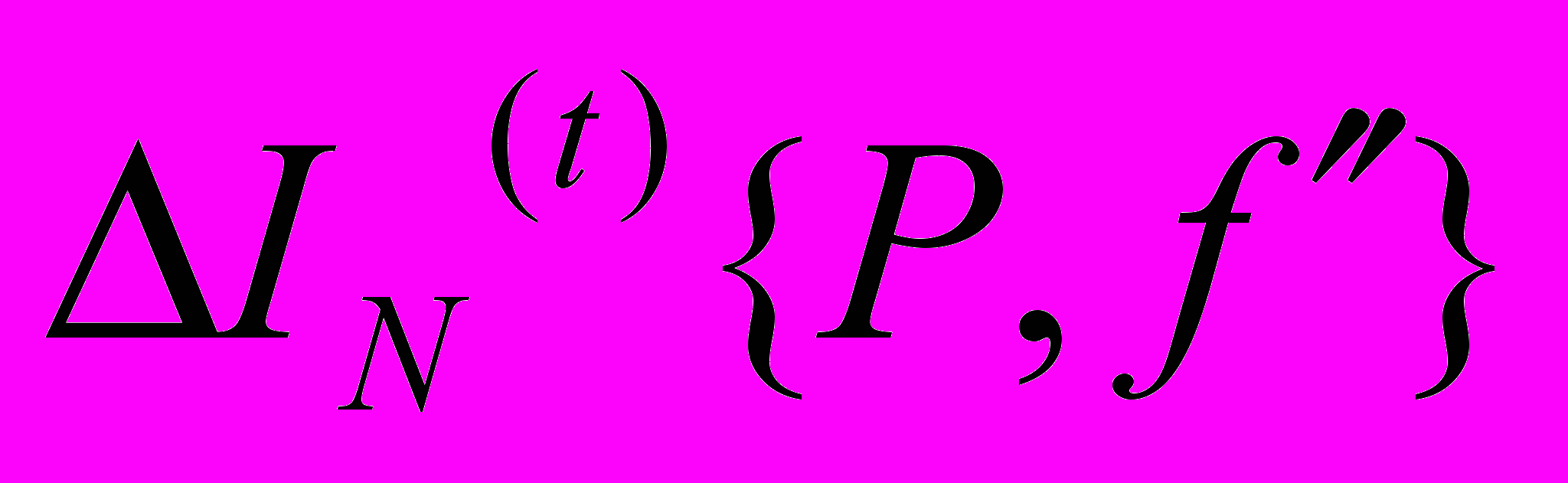при числе случайных узлов по функции плотности дает следующее выражение для асимптотической оптимальной плотности : , где − нормировочный коэффициент. В общем случае . Использование оказывается эффективным в случае резких изменений соответствующей производной на отрезке [a,b]. В противном случае близкой к оптимальной является равномерная плотность (детерминированный аналог − равноотстоящие узлы интегрирования). Адаптивность алгоритмов понимается как подстройка плотности к оптимальному значению в процессе вычислений.