Эволюция урока в общеобразовательных учебных заведениях России (на примере урока математики) 13. 00. 01 общая педагогика, история педагогики и образования
| Вид материала | Урок |
- Организация воспитательной работы в средних духовных учебных заведениях россии во второй, 384.13kb.
- Социально-педагогическая реабилитация несовершеннолетних в специализированных учреждениях, 451.01kb.
- Психолого-педагогическое сопровождение саморазвития старшеклассника в профильном обучении, 385.96kb.
- Эстетическое воспитание в системе частного образования XIX века (на примере симбирской, 1200.82kb.
- Логистика массовой оценки учебных достижений учащихся (на примере Единого государственного, 422.51kb.
- Педагогические условия подготовки студентов к межкультурной коммуникации (на примере, 306.64kb.
- Организация ПроФильного обучения на основе реализации сетевой модели в условиях локальной, 453.58kb.
- Методология, теория и практика социальной защиты детства в современной россии (в контексте, 1254.22kb.
- Гносеологические основы становления и развития педагогики семьи как самостоятельной, 995.95kb.
- Основные тенденции модернизации систем профессионального образования в китае и россии, 802.56kb.
На правах рукописи
Марушкина Ираида Алексеевна
Эволюция урока
в общеобразовательных учебных заведениях России (на примере урока математики)
13.00.01 – общая педагогика, история педагогики и образования
АВТОРЕФЕРАТ
диссертации на соискание учёной степени
кандидата педагогических наук
Калуга – 2010
Работа выполнена в государственном образовательном
учреждении высшего профессионального образования
«Елецкий государственный университет им. И.А. Бунина»
Научный руководитель: доктор педагогических наук, профессор
Саввина Ольга Алексеевна
Официальные оппоненты: академик РАО, заслуженный деятель науки РФ, заслуженный учитель РФ, доктор педагогических наук, профессор Колягин Юрий Михайлович;
доктор педагогических наук, доцент
Ромашина Екатерина Юрьевна
Ведущая организация: государственное образовательное учреждение высшего профессионального образования «Воронежский государственный университет»
Защита состоится «30» июня 2010 года в 13 часов на заседании диссертационного совета Д 212.085.01 по защите докторских и кандидатских диссертаций при ГОУ ВПО «Калужский государственный педагогический университет им. К.Э. Циолковского» по адресу: 248023, г. Калуга, ул. Ст. Разина, 26.
С диссертацией можно ознакомиться в библиотеке ГОУ ВПО «КГПУ им. К.Э. Циолковского».
Автореферат размещен на Интернет–сайте Калужского государственного педагогического университета имени К. Э. Циолковского: www.kspu.kaluga.ru
Автореферат разослан 29 мая 2010 года.
Ученый секретарь
диссертационного совета,
кандидат педагогических наук,
доцент Е.И. Малахова



ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность исследования. Стратегические задачи современной школы, намеченные в национальной образовательной инициативе «Наша новая школа», указывают на то, что от «подготовленности, целевых установок миллионов российских школьников зависит, насколько мы сможем выбрать и обеспечить инновационный путь развития страны». Ключевой характеристикой российского образования должны становиться как передача знаний и технологий, так и «формирование творческих компетентностей, готовности к переобучению», развитие личности. Эти задачи находятся в русле тенденций, сложившихся в истории отечественного образования на протяжении столетий, поэтому обращение сегодня к историческому опыту особенно важно.
Уже более 200-х лет, со дня принятия первого Устава народных училищ России (1786 г.), урок остается основной формой организации образовательного процесса в средней школе России. Предпринятые в России попытки заменить урок другими формами обучения (белл-ланкастерской системой в начале XIX века и бригадно-лабораторным методом в начале 1920-х гг.) оказались неудачными, приведшими к падению уровня математического образования. Урок снова и снова возвращался в школу, доказав свою жизнеспособность.
В течение всей школьной жизни учащийся посещает за 11 лет приблизительно 11 220 уроков (ежегодно 34 учебных недели по 30 уроков. И так в течение 11 лет). Это более 7480 часов человеческой жизни. Если к этому времени еще добавить часы, затраченные на подготовку к урокам (выполнение домашнего задания), то становится очевидным, что развитие личности ребенка происходит главным образом на уроках.
В силу своей специфики все математические дисциплины воспитывают и развивают учащихся. Нет, наверное, ни одного учебного предмета, выстроенного в такой логической последовательности, где выводимые истины сами становятся основой для следующих. Уроки математики учат детей не только строгим логическим доказательствам, но и воспитывают в них такие нравственные качества личности, как честность, «любовь к истине», настойчивость.
С 1990-х гг. Россия перешла к новой системе социально-политических и экономических отношений; общеобразовательные учреждения получили право самостоятельно выбирать как методы и средства, так и формы организации образовательного процесса, что способствовало процессу модернизации современного урока математики и, более того, поиску форм организации обучения, альтернативных уроку (в качестве примера можно привести увлечение методом Монтессори в Тульской, Московской и др. областях). Чтобы оценить их действенность, важно видеть не только результат, но и сравнить их с отечественным историческим опытом организации и проведения уроков математики.
Проблему организации и проведения уроков в дореволюционной России начали разрабатывать педагоги Н.А. Бобровников, Н.Ф. Бунаков, М.И. Демков, П.Ф. Каптерев, К.Д. Ушинский, Ф.И. Янкович де Мириево и др., методисты-математики Ф.И. Буссе, Д.Д. Галанин, П.С. Гурьев, В.Р. Мрочек, М.Г. Попруженко, А.Ф. Фролов, Ф.В. Филиппович и др. Организацию занятий в трудовой школе XX века рассматривали советские педагоги И.И. Векслер, А.М. Воронец, А.В. Ланков, А.Н. Шапошников и др. Вопросы о месте урока в учебно-воспитательном процессе, об организации урока, типологии уроков, методах обучения на уроке развивались в трудах советских педагогов М.А. Данилова, Б.П. Есипова, М.И. Махмутова, И.Т. Огородникова, М.Н. Скаткина и др., методистов-математиков Е.С. Березанской, Ф.Ф. Нагибина, В.В. Репьева и др.
Идеи реализации личностно-ориентированного обучения на уроках нашли отражение в исследованиях Г.Д. Кирилловой, Л.Г. Петерсон, И.С. Якиманской и др.
Особенности организации урока в современных условиях рассматриваются в диссертационных исследованиях С.Г. Манвелова (на примере урока математики) и С.Н. Ячиновой (на примере целеполагающего элемента уроков).
История классно-урочной системы в контексте становления и развития средней школы России затронута в работах С.Ф. Егорова, Ш.И. Ганелина, В.В. Королева, Т.Д. Корнейчик, З.И. Равкина, А.И. Пискунова и др.
Дидактика урока в советской школе рассмотрена в диссертациях Л.А. Степашко, С.А. Золотаревой, Т.А. Филатовой, Е.В. Елисеевой. В них подробно описано развитие урока в различных хронологических границах (середина 1950-х – середина 1960-х гг.; середина 1960-х – середина 1970-х гг.; середина 1970-х – середина 1980-х гг.), но без привлечения материалов, касающихся обучения математике.
Формы организации обучения математике рассмотрены в исследованиях по истории отечественного математического образования (монографиях Т.С. Авдеевой, И.К. Андронова, Ю.М. Колягина, Т.С. Поляковой, О.А. Саввиной, О.В. Тарасовой и др., а также в публикациях В.М. Бусева, Ю.А. Дробышева, Г.В. Кондратьевой, О.Н. Куприковой, В.Е. Пыркова, И.М. Смирновой, Р.С. Черкасова и др). Однако история урока математики затронута в этих исследованиях лишь попутно. Специально историческому контексту становления урока математики уделено внимание лишь в диссертационном исследовании В.Я. Саннинского, в котором была рассмотрена эволюция элементов урока математики, но в ограниченных хронологических рамках (до 1950-х гг.).
Между тем изучить феномен урока математики в контексте истории отечественного математического образования (начиная с XVIII в. до настоящего времени) необходимо еще и потому, что эффективность этой формы организации образовательного процесса проверена длительной и широкой практикой. Причем в отличие от индивидуальных форм обучения она требует гораздо меньших экономических затрат.
Поиск инноваций в конструировании урока требует выявления тенденций в развитии теории и практики урока, опоры на исторический опыт. Анализ исследований в этом направлении устанавливает их неполноту, что позволяет констатировать, что в настоящее время обострились противоречия между:
– процессами модернизации современного урока математики и необходимостью сохранения традиций его организации и проведения в теории и истории отечественного образования;
– историко-культурной и педагогической потребностью в осмыслении исторического опыта построения урока математики в общеобразовательных учреждениях России и отсутствием целостного взгляда на его эволюцию в отечественных исследованиях.
Необходимость разрешения названных противоречий обусловила выбор темы и послужила основанием для формулировки проблемы исследования: каковы особенности становления и развития урока математики как основной формы организации обучения в отечественной образовательной практике и педагогической теории?
Объект исследования – эволюция форм организации образовательного процесса в средней школе России с конца XVIII в. по настоящее время.
Предмет исследования – генезис урока математики в общеобразовательных учебных заведениях России.
Цель исследования – реконструировать историю эволюции урока математики в общеобразовательных учебных заведениях России с конца XVIII в. по настоящее время.
Хронологические рамки исследования: с момента принятия Устава народных училищ России 1786 г. по настоящее время. Выбор нижней границы обусловлен тем, что Уставом 1786 г. была узаконена классно-урочная система обучения. Выбор верхней границы – тем, что урок продолжает оставаться основной формой организации образовательного процесса в современной средней школе.
Задачи исследования:
- установить соотношение теории и практики организации урока математики на разных этапах развития отечественного образования (в т. ч. установить соотношение требований к уроку, регламентированных нормативными документами и сложившихся в практике организации урока математики на разных этапах развития отечественного образования);
- выявить особенности постановки целей урока математики в различные исторические периоды;
- показать динамику продолжительности урока в указанных хронологических границах;
- раскрыть тенденции в использовании методов обучения на уроках математики в отечественной образовательной практике с конца XVIII в. по настоящее время;
- обосновать эволюционный характер развития урока математики в общеобразовательных учебных заведениях России и разработать периодизацию его истории с конца XVIII в. по настоящее время.
Методологической основой исследования явились положения, раскрывающие закономерности общественно-исторического развития: положение о всеобщей связи и взаимной обусловленности явлений и процессов, о социальной деятельности человека, развитии социальных систем и роли системы образования в активном становлении личности. Исследование основывалось на диалектическом подходе к изучению исторических процессов, базирующемся на принципах научной объективности и историзма и позволяющем рассматривать обучение как изменяющийся и развивающийся во времени процесс с учетом конкретных социокультурных условий.
Для решения поставленных задач использовались следующие методы исследования:
- изучение, анализ, систематизация исторической литературы, педагогических первоисточников и периодики, архивных документов;
- аналитико-синтетический метод изучения фактов в единстве с историческим подходом к изучаемым явлениям;
- эмпирико-реалистический подход, суть которого заключается в сопоставлении официальных документов, событий и фактов, которые имели место в реальной практике конкретных учебных заведений;
- сравнительно-исторический метод (анализ и оценка опыта преподавания математики в дореволюционной средней школе России в ретроспективном плане);
- диахронный анализ и оценка выявленных тенденций в практике и методике обучения математике в дореволюционной России.
Источники исследования:
а) опубликованные:
- официальные материалы: циркуляры, уставы, учебные планы средних учебных заведений, постановления, распоряжения, приказы; декреты Советской власти, Постановления ЦК КПСС; справочно-статистические материалы о средней школе;
- труды, доклады съездов (I и II Всероссийских съездов преподавателей математики (1911–1912 гг. и 1913–1914 гг.), протоколы педагогических комитетов учебных заведений;
- периодическая печать (дореволюционные журналы, а также периодика советского и современного периодов);
- программы по математике средней школы (дореволюционной и советской);
- материалы совещаний, конференций.
б) материалы государственного архива Тульской области (Ф. 326, Ф. 616); материалы Российского государственного исторического архива (Ф. 732, Ф. 733, Ф. 736).
Основные этапы исследования. Исследование осуществлялось в несколько этапов.
Первый этап (2005–2006 гг.). Изучение историко-педагогической, историко-математической и учебно-методической литературы конца XVIII – начала XXI вв. Выявление степени разработанности темы, определение исходных параметров исследования (объекта, предмета, цели, задач).
Второй этап (2006–2008 гг.). Сравнительно-сопоставительный анализ документов, регламентирующих организацию урока в общеобразовательных учреждениях России, архивных материалов и свидетельств учителей разных поколений. Систематизация и обобщение материалов исследования, апробация и публикация его результатов.
Третий этап (2008–2010 гг.). Проверка и уточнение основных положений диссертации, оформление результатов исследования.
На протяжении всего исследования уточнялись разночтения и факты, связанные с историей урока математики, поэтому на всех этапах продолжалось изучение источников и архивных материалов.
Научная новизна: 1) на основе изучения обширного круга источников впервые дано целостное представление об эволюции урока математики в отечественных общеобразовательных учебных заведениях; 2) обоснована периодизация становления и развития урока математики; 3) установлен новый круг персоналий, оставивших заметный след в истории урока математики (Н.А. Бобровников, Н.В. Бугаев, П.С. Гурьев, Ф.В. Филиппович, А.Ф. Фролов и др.); 4) выявлен и введен в научный оборот ряд новых историко-педагогических фактов (применение П.С. Гурьевым на уроках математики разноуровневого раздаточного материала, постановка им вопроса о рациональном использовании времени на уроке математики; разработка методики организации объяснения на уроках алгебры у В. П. Ермакова, на уроках геометрии – у А.Н. Острогорского; разработка методики организации объяснения, закрепления, ведения опроса, проверки домашнего задания у А.Ф. Фролова, В. Омельянович-Павленко; разработка методики проведения самостоятельной работы на уроках математики у П.С. Гурьева).
Теоретическая значимость исследования заключается в том, что в нем: 1) дано комплексное представление об эволюции урока математики в отечественной средней школе; 2) установлен вклад отечественных педагогов-математиков в развитие дидактики урока математики; 3) показан эволюционный характер становления и развития урока в общеобразовательных учреждениях России; 4) раскрыты сущностные стороны урока математики в их историческом развитии; 5) установлена цикличность использования методов на уроках математики в общеобразовательных учебных заведениях России XVIII-XXI вв.
Практическая значимость исследования определяется тем, что его результаты: 1) могут быть применены при изучении и характеристике основных тенденций отечественного образования XVIII-XXI вв.; 2) позволят обогатить курс истории образования новыми сведениями; 3) могут быть востребованы в системе подготовки и повышения квалификации педагогических кадров; 4) ориентируют на возрождение традиций в области математического образования; 5) содержат факты и выводы, использование которых в процессе обучения в вузе будет способствовать повышению профессиональной культуры и укреплению патриотического сознания учителя математики.
Достоверность результатов исследования обеспечивается методологической обоснованностью исходных позиций, применением системы методов, адекватной его задачам, широтой источниковой базы, объективностью и достоверностью используемых архивных материалов и первоисточников.
На защиту выносятся следующие положения:
1. Соотношение теории и практики организации урока математики на разных этапах развития отечественного образования было неодинаково. Заложенные Уставами 1786 и 1804 гг. тенденции развития урока (требование следовать определенной организации ведения объяснения и опроса, достижение развивающей цели, использование наглядного метода) опережали их практическое внедрение.
В практике учителей XIX – начала XX вв. (Н.А. Бобровникова, П.С. Гурьева, М.Г. Попруженко и др.) появились новые идеи организации урока математики (различные виды опроса учащихся; устные упражнения; проверка домашнего задания; активизация знаний учащихся в начале урока; следование четкому плану урока и др.), но они не имели теоретического обоснования.
Начиная с 1932 г., наметились тенденции сближения теории и практики организации урока математики. В трудах педагогов (М.А. Данилова, Б.П. Есипова, И.Т. Огородникова, С.В. Иванова, М.И. Махмутова и др.) и методистов-математиков (В.В. Репьева, В.Я. Санинского и др.) были найдены пути усовершенствования урока, которые нашли отражение в массовом опыте советской школы.
В отечественной педагогике, начиная с 1990-х гг., теория вступает в противоречие с практикой работы учителей: с одной стороны, педагогами-теоретиками декларируются новые идеи в построении урока, с другой – в реальной практике учителя проявляют консервативность в организации урока.
2. Отсчет постановки вопроса о целеполагании урока следует начать с 1786 г. На ранних этапах развития урока ставились обучающие и развивающие цели. Под обучающими целями понимали накопление определенной суммы знаний. В нормативных документах указывалось на необходимость развития мышления, памяти и внимания учащихся. К концу XIX в. был поднят вопрос о воспитательной цели урока математики, под которой подразумевалось формирование нравственных качеств у учащихся. В начале XX в. была предложена классификация всех тех целей, которые характерны для современного урока математики (образовательная, воспитательная, практическая, причем развивающая цель не выделялась обособленно, а входила как составляющаяся в воспитательную цель). С 1990-х гг. и по настоящее время на уроках математики ставится триединая цель, включающая обучающую, воспитательную и развивающую составляющие.
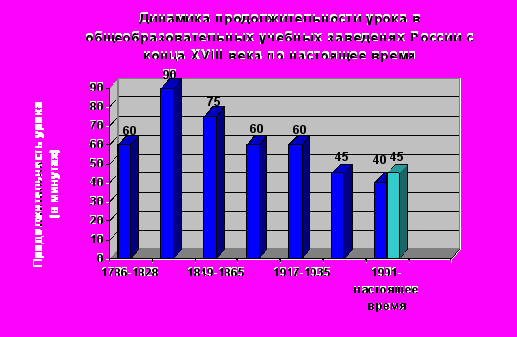
3. Продолжительность урока в общеобразовательных учебных заведениях России с конца XVIII по начало XXI вв. была нестабильной. Согласно Уставу 1786 г., урок длился 60 минут. Уставом 1828 г. его продолжительность изменилась и стала составлять 90 минут. Ко второй половине XIX в. она уменьшалась до 60 минут (с 1865 г.). Такой продолжительность урока оставалась и в XX в., до 1917 г. С 1935 г. по настоящее время урок длится 45 минут (в начальной школе – 30–35 мин.).
4. С конца XVIII в. на уроках математики преобладали словесные (объяснительно-иллюстративный, догматический) методы обучения. Уставом 1828 г. рекомендуются наглядный и вопросно-ответный методы обучения. В середине 1860-х гг. в школьной практике широко используется катехизический метод обучения. В конце XIX – начале XX вв. на уроках начинают внедряться специфические методы обучения математике: метод целесообразных задач (С.И. Шохор-Троцкий), практические методы (в арифметике – Д.Д. Галанин, в алгебре – Н.Г. Лексин, в геометрии – В.Р. Мрочек и Ф.В. Филиппович). С начала XX в. до 1917 г. широко используются на уроках математики лабораторные и практические работы. В трудовой школе (1917–1932 гг.) понимание сути урока изменилось: его стали рассматривать в статусе догматического метода обучения. Основными были бригадно-лабораторный, исследовательский и коллективно-трудовой методы обучения. После выхода Постановления 1932 г. вернулись к словесным и наглядным методам обучения. В 1950-х гг. в свете политехнизации обучения усилилось внимание к практическим методам (измерительные работы на местности). В конце 1970-х гг. получили распространение объяснительно-иллюстративные методы обучения с поддержкой ТСО, в начале XXI в. – с поддержкой цифровых образовательных ресурсов. Таким образом, в использовании методов обучения на уроках математики прослеживается определенная цикличность (например, приоритет отдается то объяснительно-иллюстративным методам, то практическим).
5. Становление и развитие урока математики в общеобразовательных учреждениях России проходило эволюционно. Для описания этого исторического процесса целесообразна многоуровневая периодизация (периоды и этапы). I период (1786 – 1917 гг.) – период становления урока как основной формы организации образовательного процесса – охватывает четыре этапа эволюции урока математики (см. с.21). II период (1917 – 1932 гг.) – отказ от урока как основной формы организации образовательного процесса. III период (с 1932 г. – по настоящее время) – период стабилизации урока – содержит три этапа эволюции урока математики (см. с. 21 – 22).
Апробация и внедрение результатов исследования осуществлялись по следующим основным направлениям:
– публикация материалов исследования в различных научных и научно-методических изданиях;
– обсуждение отдельных вопросов исследования на международных (Санкт-Петербург, 2007 г.; Тамбов, 2008 г.), межвузовских (Елец, 2006–2010 гг.; Саранск, 2007г.; Коломна, 2008г.) научно-практических конференциях.
Структура диссертации. Диссертация состоит из введения, двух глав, заключения, библиографического списка (234 наименования) и приложений.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснованы актуальность, проблема, объект, предмет, методы и задачи исследования, описаны его этапы, научная новизна, теоретическая и практическая значимость, сформулированы основные положения, выносимые на защиту.
В первой главе «Теория и практика урока математики в контексте развития отечественного дореволюционного математического образования» проанализирован исторический путь становления понятия «урок», структуры урока математики в России, прослежена динамика продолжительности урока, рассмотрена эволюция целей и методов обучения математике, установлены особенности видов уроков математики в различные исторические периоды.
В современной Российской педагогической энциклопедии приводится следующее определение: «…урок – это форма организации учебно-воспитательного процесса в учебных заведениях при классно-урочной системе обучения; составная часть процесса обучения, урок проводится с коллективом учащихся постоянного состава (класса) в течение определенного промежутка времени». Однако такое понимание урока сложилось не сразу.
Эволюция урока математики в общеобразовательных учебных заведениях России тесно связана с историей образования в Европе в целом. Так, на введение классно-урочной системы обучения в европейскую и российскую школы оказали влияние труды Я.А. Коменского. На установление жесткой последовательности этапов в структуре урока – «формальные ступени» И.Ф. Гербарта и др.
В России элементы этой системы, по сути, были узаконены Уставом народных училищ 1786 г. Согласно ему каждый учитель должен был вести «ежемесячный список ученического прилежания», в котором отмечал отсутствующих (можно сказать, это был прообраз современного классного журнала). В Уставе говорилось, что в учебном процессе должны использоваться классные доски и ученические тетради. Термин «урок» тогда еще не употреблялся, форма организации занятий с детьми называлась «учебным часом».
Следует заметить, что в русской лексике слово «урок» появилось еще в X веке. При этом оно употреблялось в различных значениях: запрет, наказание, задание, школьные и домашние экзерциции и пр. В таком размытом понимании термин «урок» впервые встречается в Уставе гимназий 1804 г.: «Учитель Математики и Физики преподает уроки в неделю по 18 часов: в первом классе обучает по шести часов в неделю, проходя по порядку части Чистой Математики: Алгебру, Геометрию и Плоскую Тригонометрию».
Однако в следующем гимназическом Уставе (1828 г.) урок уже выступает как завершенный отрезок учебного времени.
Согласно Уставам 1786 г. и 1804 г. продолжительность урока была 60 мин. Эти данные были получены в результате сопоставления времени, которое учащиеся тратили на учебную деятельность, и количеством уроков, проводимых в этот день. Начиная с Устава 1828 г., его продолжительность стала составлять 90 минут. С середины XIX в. она уменьшилась до 75 минут (изменения в учебном плане 1849 г.). В 1865 г. было принято Высочайшее повеление, согласно которому урок стал длиться 60 минут. Такая продолжительность урока сохранялась до Октябрьской революции 1917 г.
Анализ работ отечественных педагогов П. С. Гурьева, Ф.И. Буссе, Н.В. Бугаева, Н.А. Бобровникова, Н.Г. Лексина, С.И. Шохор-Троцкого и др. позволил проследить эволюцию целей урока математики с конца XVIII в. и до 1917 г.
В первых уставах и циркулярных письмах не было упоминания ни о целях обучения математике, ни о целях урока математики, но в них предъявлялись определенные требования к уроку и ставилась основная задача обучения: накопление определенной суммы знаний, т.е. Уставом 1786 г. ставились прежде всего обучающие цели: это объяснение нового материала (хором выучивали наизусть текст учебника), опрос учащихся и решение задач.
Устав 1804 г. и Циркулярное письмо 1810 г. ориентировали учителей не только на передачу определенной суммы знаний, но и на формирование у учащихся способности к логическому мышлению, интереса к предмету, умения самостоятельно выбирать решение, т. е. на развитие учащихся. В 1830-х гг. П.С. Гурьев добавил такую цель обучения математике, как развитие «самодеятельности» учащихся. В середине XIX века Ф.И. Буссе определял две главные цели обучения арифметике: развивающую и обучающую. В конце 1860-х гг. впервые встречается постановка конкретной дидактической цели на уроке математики (например, цель урока – привести не к доказательству, а только к уяснению признаков). В середине 1880-х гг. Н.В. Бугаев утверждал, что на уроках математики учащиеся, строя логические цепочки рассуждений, привыкают быть правдивыми. У них формируются лучшие моральные качества, такие как честность, правдивость, трудолюбие и т.п., т.е. происходит воспитание личности учащихся.
Идеи воспитательных целей на уроках математики находят отражение в трудах педагогов начала XX века. Н.А. Бобровников, Н.Г. Лексин предлагали формулировать обучающие и воспитательные цели уроков математики. С. И. Шохор-Троцкий обращал внимание на необходимость воспитания интереса, любви к математике и самостоятельности учащихся.
В начале XX в. критика формализма в обучении математике, осознание оторванности процесса и результатов обучения математике от жизни привели к появлению практической цели.
Анализ дореволюционных работ по проблеме целеполагания позволяет сделать вывод о том, что первая классификация целей обучения математике в отечественной методике математики представлена в книге В.Р. Мрочека и Ф.В. Филипповича «Педагогика математики» (1910 г.). Педагоги-математики считали, что необходимо выделить три группы целей обучения математике: практические, образовательные и воспитательные. При этом следует отметить, что, несмотря на то, что развивающая цель не выделялась в качестве самостоятельной, она латентно содержалась в составе воспитательной цели. Такая классификация целей имеет место и в современных исследованиях по методике обучения математике.
В рассматриваемый период (конец XVIII в. – 1917 г.) имел место и процесс определения структуры урока и методов обучения.
Начиная с первого Устава 1786 г., урок (в т.ч. урок математики) состоял из четырех этапов: организационный момент, объяснение, опрос, подведение итогов урока. В начале урока читалась молитва, и учитель отмечал отсутствующих в классе. По окончании урока ученик должен был поблагодарить учителя за труд и взять у него письменное свидетельство о своем поведении. На уроке преобладали словесные методы обучения (объяснительно-иллюстративный, догматический, лекционный).
Устав 1804 г. определял новую стратегию обучения. Учителя должны были заботиться об образовании и «изощрении рассудка» учащихся. Недостатки обучения вскрывало Циркулярное письмо 1810 г.: вместо постепенного развития учащихся в обучении остается «засилие трех китов: зубрения, повторения, долбления».
Согласно Уставу 1828 г., в структуру урока (в т. ч. урока математики) добавляется этап фронтального опроса учащихся с применением вопросно-ответного метода обучения. На уроках рекомендовалось применять метод наглядного обучения с опорой на возрастные особенности детей.
В 1830 г. П.С. Гурьев расширил структуру урока математики, добавив в нее этап закрепления изученного материала в виде самостоятельной работы учащихся.
В середине 1860-х гг. появляются такие этапы урока математики, как проверка и постановка домашней работы и специфический для урока математики этап решения устных задач в классе.
Этапы урока математики выстраивались уже в определенной последовательности. Так, у А.Ф. Фролова урок математики состоял из проверки домашней работы, опроса, закрепления изученного, постановки домашней работы.
В начале XX в. добавились такие этапы урока математики, как подведение к новой теме в виде устных упражнений, закрепление нового материала с опорой на предыдущий учебный материал, повторение. На уроках начали внедряться специфические методы обучения математике: метод целесообразных задач (С.И. Шохор-Троцкий), практические методы (в арифметике – Д.Д. Галанин, в алгебре – Н.Г. Лексин, в геометрии – В.Р. Мрочек и Ф.В. Филиппович). С начала XX в. до 1917 г. широко использовались на уроках математики активные методы обучения (лабораторные и практические работы).
С. И. Шохор-Троцкий предлагал схему объяснения учителя по методу целесообразных задач: 1) сначала надо предложить учащимся набор наглядных (простых) задач; 2) затем – задачи из обыденной жизни; 3) далее – отвлечённые задачи; 4) сделать логический вывод из всей работы; 5) закрепить вывод.
Н.А. Бобровников отмечал поэтапность построения урока математики: 1) подготовительный, «умственный счет». Несколько минут в начале урока посвящалось переходу от прежде изученного к теме урока на основе задач, решаемых в уме. 2) Изложение новой темы. 3) Закрепление нового материала. 4) Опрос учащихся.
В.Р. Мрочек и Ф.В. Филиппович одними из первых в отечественной методико-математической науке предложили классификацию методов обучения: 1) догматический: лекционное изложение (объяснение урока) и заучивание учеником по книге или запискам. 2) Катехизический: даются вопросы и готовые ответы. «Метода» основана на зубрении и спрашивании. 3) Эвристический: даются вопросы, наводящие на ответ (Сократ). «Метода» основана на подборе целесообразных задач. 4) Генетический: особый вид синтеза – генезис дает картину развития данной отрасли знания. Особенно ценная метода для прохождения начал математики. 5) Наглядный. 6) Лабораторный. 7) Комбинационный: индуктивно-эвристический и генетически-эвристический.
На рубеже XIX – XX вв. предпринимаются попытки предложить классификацию уроков (Н.А. Бобровников, М.И. Демков и др.). В начале ХХ века выделяются следующие виды уроков математики: уроки объяснения нового материала и уроки закрепления изученного (А.Ф. Фролов, В. Омельянович-Павленко, В.А. Евтушевский, А.Н. Острогорский, П. Христич); «вступительные уроки», которые можно трактовать как повторительные уроки в начале учебного года (М.Г. Попруженко, А.Ф. Фролов); уроки повторения в конце учебного года; уроки повторения в течение учебного года или обобщающие уроки (М.Г. Попруженко); «предметные» уроки (Н. А. Бобровников).
Таким образом, к 1917 г. в теории и практике дореволюционной школы урок математики сформировался как целостная форма организации образовательного процесса.
Во второй главе «Теория и практика организации образовательного процесса в советской и современной средней школе (на примере обучения математике)» сопоставлены различные точки зрения о понимании сущности урока в советской школе, рассмотрено дальнейшее развитие основных этапов урока математики, проанализированы цели и методы обучения на уроках математики.
В трудовой школе (1918–1932 гг.) понимание образовательной цели сузилось до необходимости дать каждому учащемуся ряд полезных сведений и навыков, требуемых в различных областях трудовой деятельности. В качестве воспитательной цели выступало требование воспитания подрастающего поколения, активного строителя будущего социалистического государства, в духе марксистко-ленинской идеологии. Под развивающей целью понимали развитие личностных качеств в детях, таких, как умение работать в коллективе, умение подчинять свои интересы интересам общества, развитие самостоятельности, инициативы и творческих способностей учащихся. Под практической целью понимали умение строить учащимися графики и диаграммы, умение пользоваться справочниками и таблицами. Общепринятые развивающие цели (развитие памяти, речи, логического мышления и т. д.) на занятиях фактически не ставились.
Опыт трудовой школы негативно сказался на математическом образовании в нашей стране. Пропагандировалась и идеализировалась лабораторная форма организации учебного процесса в трудовой школе вместе с исследовательским методом и комплексным построением содержания учебных программ. Данная система учебного процесса не дала желаемых результатов: ребенок не получал упорядоченных знаний, не видел результатов своего труда, имел абстрактное представление обо всем. Способным ученикам в дальнейшем для достижения своей цели приходилось много работать самостоятельно, заново постигать многие учебные предметы, которые изучались на недостаточном уровне для поступления в ВУЗы.
В педагогической литературе того времени существовала путаница в терминах и понятиях, которая была устранена только к началу 1930-х гг. Так, комплексный метод, метод проектов по своей сущности больше соответствовали не методам, а системе построения учебно-образовательного процесса. Лабораторный метод, бригадно-лабораторный метод, экскурсионный метод, Дальтон-план следует относить к формам организации учебного процесса в трудовой школе.
В конце 1920-х гг. педагоги И.И. Векслер и Р. Харитонова предложили свою классификацию методов обучения математике: 1) догматический; 2) эвристический; 3) наглядный; 4) исследовательский. В то же время методист-математик А.Н. Шапошников выделял другие методы: 1) лекционный; 2) «вопросный» (сократовский, или эвристический); 3) исследовательский метод; 4) коллективно-трудовой метод.
Выявленные и обозначенные в Постановлении ЦК ВКП(б) от 25 августа 1931 г. (опубликованном 5 сентября 1931 г.) недостатки обучения в трудовой школе обусловили пересмотр взгляда государства на организацию школьного обучения. Постановлением ЦК ВКП(б) от 25 августа 1932 г. «Об учебных программах и режиме в начальной и средней школе» утверждалось, что основной формой организации учебной работы в средней школе должен являться урок.
Согласно Постановлению СНК СССР и ЦК ВКП(б) 1935 г. «Об организации учебной работы и внутреннем распорядке в начальной, неполной средней и средней школе» продолжительность урока стала составлять 45 минут. Динамика продолжительности урока с конца XVIII в. по настоящее время представлена на диаграмме:
Критическое переосмысление не оправдавших себя методов обучения трудовой школы 1920-х гг. заставило в начале 1930-х гг. вернуться к традиционным словесным (рассказ, беседа, школьная лекция) и наглядным (демонстрация, иллюстрация) методам обучения.
Однозначно можно сказать, что уже в 1930-х гг. в структуру урока математики входили те же этапы, что и до Октябрьской революции 1917 г. Л.В. Федорович (1935) выделял шесть этапов в структуре урока математики: 1) подготовка класса к уроку; 2) начало урока: проверка домашних заданий; 3) объяснение нового материала; 4) самостоятельная работа учащихся; 5) подведение итогов урока; 6) конец урока.
Е.С. Березанская (1934) и Г. Машков (1937) придерживались структуры урока математики, включающей: 1) вводную часть (проверка домашней работы); 2) центральную часть (объяснение нового материала или закрепление изученного); 3) заключительную часть (постановка домашней работы).
У практикующих учителей конспект урока математики мог содержать четыре этапа: 1) повторение и устные упражнения (5-10 минут); 2) теоретический опрос по изученной теме; 3) сообщение нового материала с использованием вопросно-ответного метода; 4) задание на дом (М.И. Змиева и др.).
Вместе с вопросом о целостной структуре урока математики педагогов интересовала и организация отдельных этапов урока математики, таких как объяснение (Л.В. Федорович, М.И. Змиева), опрос (Г.А. Стальков, К.С. Богушевский и др.), устные упражнения (Ф.Ф. Нагибин, В.М. Розентуллер, В.А. Голубев, Е.Н. Филоматитская), домашнее задание (Л.В. Федорович, Г.А. Стальков, К.С. Богушевский) и повторение (Н.Т. Зерченинов, Г.А. Стальков).
Теоретическое осмысление целеполагающей части урока математики было сделано в конце 1940-х гг. М.Н. Покровской. Она впервые дифференцирует воспитательную цель урока математики через воспитательные задачи: 1) воспитание внимания на уроках математики; 2) воспитание умения сознательно переключать внимание с одного объекта на другой; 3) воспитание интереса и любви к математике. Что касается первой и второй задач, то их можно отнести и к развивающим целям урока математики. Следовательно, в теоретических исследованиях 1940-х гг. развивающая составляющая обучения математике рассматривалась в составе воспитательной цели так же, как и в дореволюционный период.
В программе средней школы за 1947/1948 учебный год речь идет о развивающих целях обучения математике: развивать умственные способности учащихся, формировать умение делать правильные умозаключения, устанавливать зависимости между величинами, вырабатывать марксистское мировоззрение.
В начале 1950-х гг. добавляется такая цель на уроках математики, как воспитание культуры математической речи учащихся (устной и письменной). Выдвигались требования к речи учителя и учащихся. В.М. Розентуллер предлагал учащимся вести специальный математический словарь терминов. Для обогащения речи учащиеся писали математические сочинения и рефераты по разным вопросам (доказательство теоремы, объяснение решения задачи, вывод формулы, а также составление письменного сочинения на основе самостоятельного изучения некоторого вопроса) (В.М. Розентуллер).
В директивах XIX съезда КПСС (1952 г.) указывалось на необходимость приступить к осуществлению в общеобразовательных школах политехнического обучения. В 1958 году был принят Закон «Об укреплении связи школы с жизнью и о дальнейшем развитии системы народного образования в СССР». В Программе, принятой XXII съездом КПСС 31 октября 1961 г., было сказано, что обучение и воспитание подрастающего поколения должны быть тесно связаны с жизнью и с производственным трудом. Предполагалось, что это позволит человеку после окончания школы сразу включиться в производство и сочетать работу с дальнейшим обучением и образованием в соответствии со своим призванием и потребностями общества. Таким образом, в учебную работу вводилась политехническая цель обучения, реализация которой на уроках математики выражалась в усилении практической направленности изучения дисциплины.
Программа средней школы за 1954/1955 учебный год декларирует следующие цели преподавания математики: сообщение учащимся основ знаний по арифметике, алгебре, геометрии, тригонометрии, привитие умений и навыков для применения сведений из математики при решении различных практических задач, содействие развитию логического мышления и пространственного воображения.
В свете задач политехнического обучения особое значение приобрело привитие учащимся счетно-конструктивных навыков, умения пользоваться таблицами, счетными приборами, измерительными и чертежными инструментами. В это время снова широко использовались активные методы обучения (лабораторные и практические работы по математике).
В 1959 г. вышла статья липецкого учителя К.А. Москаленко «Как должен строиться урок», в которой автор критиковал сложившуюся к тому времени структуру урока и предлагал «объединить процессы выявления знаний и обучения». Такой урок получил у него название «объединенный». На нем в один процесс объединялись такие этапы урока, как проверка домашнего задания, опроса и изучения нового материала.
Опыт липецких учителей характеризовался системными изменениями в организации урока и имел следующие особенности:
- отказ от традиционной формы комбинированного урока;
- активное начало урока (математический диктант, самостоятельная работа);
- взаимосвязь всех элементов урока, направленность их на достижение поставленных целей (организационный момент, устные упражнения, объяснение нового материала и т. д.);
- объединение работы по формированию новых знаний с повторением ранее изученного материала (изучение нового материала в течение всего урока идет небольшими порциями и тут же закрепляется, проверяется осмысленность и правильность его усвоения; эти этапы сливаются в один);
- появление в структуре урока математики игровых моментов (в качестве закрепления использовались различные математические викторины и игры (игра «Получи 5», игра «Кто быстрее?» и т. д.));
- использование комментированного решения примеров и задач как одного из эффективных приемов закрепления знаний и выработки практических навыков у учащихся;
- сокращение объема домашних заданий за счет увеличения практической работы на уроке;
- проверка домашнего задания в ходе урока без выделения для этого специального времени;
- оценивание работы учащихся в форме поурочных баллов. При выставлении поурочного балла учитывается степень активного отношения школьника к учебной деятельности на уроке: его вопросы, дополнения, ответы, суждения об ответах товарищей и, разумеется, качество ответов на вопросы учителя и товарищей. Учитель мог выставить за урок 10-15 отметок. Поурочный балл, по сути, снимал проблему дисциплины, поскольку все ученики с самого начала урока заняты интересной и оцениваемой работой;
- внедрение упреждающего изучения материала (задолго до начала изучения конкретной темы школьникам заранее мало-помалу давали некоторый фрагмент или представление о том материале, который в будущем обязательно встретится и будет изучаться в соответствии с программой);
- планирование творчески работающим учителем не конкретного урока, а блока уроков по каждой теме.
В 1960-х гг. советский педагог-математик А.Я. Хинчин доказывал, что на уроках математики у учащихся формируются моральные личные качества, такие, как честность, правдивость, настойчивость, мужество, трудолюбие. Это происходит, во-первых, тогда, когда учащиеся учатся полноценно аргументировать свое решение. Во-вторых, тогда, когда учащиеся строят логические схемы рассуждения («логический скелет»), т. е. воспитывается у них математический стиль мышления. В-третьих, тогда, когда учащиеся приучаются к точности символики. Идеи А.Я. Хинчина получили среди методистов всеобщее признание. Вместе с тем, нельзя не отметить, что они были не новы. А.Я. Хинчин почти через 90 лет повторил и развил мысли дореволюционного математика Н.В. Бугаева, высказанные им в работе «Математика как орудие научное и педагогическое».
Отечественные методисты С.Е. Ляпин (1965 г.), Ю.М. Колягин и др. (1975 г.), Н. В. Метельский (1982 г.) и др. дали классификацию целей урока математики, которая практически совпадала с классификацией В.Р. Мрочека и Ф.В. Филипповича (1910 г.) и остается неизменной по настоящее время. В данную классификацию входят образовательные, воспитательные и практические цели обучения. Воспитательная цель формировалась под влиянием марксистско-ленинской идеологии. Отдельно развивающая цель в классификации не упоминается (она смешивается с образовательной и воспитательной целью у С.Е. Ляпина; с воспитательной целью – у Ю.М. Колягина и др.; со специфической целью – у Н.В. Метельского).
В конце 1970-х – начале 1980-х гг. в школьную практику входит использование технических средств обучения (ТСО) (кодоскопы, диафильмы, магнитофоны, тетради с печатной основой), разрабатываются учебно-методические комплекты по работе с ТСО на каждом уроке, идет оснащение кабинета математики наглядными средствами обучения.
Новые элементы в объяснение, закрепление, опрос вносит учитель математики из г. Донецка В.Ф. Шаталов. Новые виды уроков практикует учитель из г. Белорецка Р.Г. Хазанкин.
Начиная с 1990-х гг., в отечественной педагогической науке и практике активизировались исследования проблем совершенствования урока. Происходящие общественно-политические процессы в стране и мире обозначили новые векторы поиска ответа на обозначенную проблему. В конце 1990-х гг. С.Г. Манвелов предлагает многоаспектную типологию уроков математики.
Среди факторов, оказывающих наиболее значительное влияние на поиск путей модернизации современного урока, можно выделить:
- гуманизацию образования (личностно-ориентированное обучение);
- интеграцию России в мировое образовательное пространство;
- модернизацию отечественного образования (профилизация старшей ступени обучения);
- информатизацию образования (в том числе возможность осуществления дистанционного образования).
Эти факторы обусловили появление уроков новых видов, таких как видеоурок, дистанционный, интегрированный и т.д.
В заключении подведены общие итоги исследования и сделаны следующие выводы.
История урока математики показывает, что изменения в нем происходили постепенно и непрерывно. Единственным исключением была трудовая школа. Но здесь не произошло кардинального изменения самого урока, от него просто отказались. В каждом историческом периоде урок математики совершенствовался, обогащался новыми этапами, методами обучения и т. д. В дореволюционное время сформировались основные этапы урока. Трудовая школа дала опыт в проведении лабораторных и практических работ. Все это позволяет говорить об эволюционном характере становления урока математики в отечественной общеобразовательной школе.
В указанных хронологических рамках следует выделить три периода в становлении и развитии урока математики. I период (1786 – 1917 гг.) – период становления урока как основной формы организации учебного процесса – охватывает четыре этапа эволюции урока математики. II период (1917– 1932 гг.) – отказ от урока как основной формы организации учебного процесса. III период (1932 г. – настоящее время) – период стабилизации урока – включает три этапа эволюции урока математики. В качестве основных параметров определения границ периодов и этапов рассмотрим изменение структуры урока, обогащение его структурных элементов новым содержанием, появление новых этапов урока.
I период (1786 – 1917 гг.).
Первый этап (1786 – 1828 гг.): структура урока математики включала четыре этапа: орг. момент, объяснение, опрос, подведение итогов урока; ставились обучающая и развивающая цели урока математики; применялись словесные методы обучения, что привело к господству догматического метода обучения.
Второй этап (1828 – 1864 гг.): Уставом 1828 г. вводится фронтальный опрос учащихся; впервые у педагога-математика П.С. Гурьева присутствует такой этап урока, как закрепление изученного материала (самостоятельная работа учащихся); поднимается проблема предварительной подготовки учителя к уроку; используются вопросно-ответный и наглядный методы обучения; на практике учителя используют раздаточный материал и индивидуальные доски для самостоятельной работы учащихся.
Третий этап (1864 – 1900 гг.): впервые появляются следующие этапы урока: проверка и постановка домашней работы, решение устных задач в классе; осуществляется смена школьных принадлежностей на уроке (использование индивидуальных досок для классной работы, тетрадей – для домашней); впервые формулируется воспитательная цель обучения математике; практически подтверждается, что на уроках использовались фронтальный опрос учащихся, катехизический и наглядный методы обучения; ставится конкретная цель урока.
Четвертый этап (1900 – 1917 гг.): добавляются такие этапы урока, как подведение к новой теме в виде устных упражнений, закрепление нового материала с опорой на предыдущий учебный материал, этап повторения; от учителей требуется написание плана урока; структура урока математики разделяется на законченные этапы, подчиненные единой теме и цели урока; осуществляется принцип связи обучения с жизнью: добавляется практическая цель урока и внедряются активные методы обучения (лабораторный, практический).
II период (1917 - 1932 гг.). Отказ от урока как основной формы организации обучения.
III период (1932 г. – по настоящее время).
Первый этап (1932 - середина 1950-х гг.): обращение к дореволюционному опыту организации урока, его фактическое копирование в советской средней школе. Складывается традиционная структура комбинированного урока, скованная жесткими рамками соблюдения последовательности его этапов: организационный момент (установление внешнего порядка, проверка наличия демонстрационного материала, отметка отсутствующих в классе, постановка целей), проверка домашнего задания, устные упражнения, опрос (устный и письменный), объяснение нового материала, закрепление изученного материала (работа у классной доски или самостоятельная работа), задание на дом, подведение итогов урока; не разработана четкая классификация целей урока математики (смешиваются понятия воспитательной и развивающей целей); осуществляется политехническая цель обучения (директивы XX съезда КПСС) – усиление практической направленности в преподавании математики (задачи с практическим содержанием, измерения на местности); на уроках используются различные виды опроса; отмечается формальное отношение к устным вычислениям.
Второй этап (середина 1950-х гг. – 1990-е гг.): разрабатывается и внедряется «объединенный» урок, в котором сливаются в единый процесс проверка знаний, объяснение и закрепление; использование методов и приемов, нацеленных на актуализацию знаний учащихся (математические диктанты, дидактические игры); реализация возможности варьировать этапами урока; смешение воспитательной и развивающей целей урока математики: выработка умения логической полноценной аргументации способствует воспитанию лучших моральных качеств и патриотизма; активное использование ТСО (кодоскопы, диафильмы, магнитофоны) на уроках математики, в практику вошли тетради с печатной основой.
Третий этап (1990-е гг. – настоящее время): намечается отказ от единой структуры урока, что повлияло на появление нестандартных уроков, которые не укладываются ни в одну из известных структур; четкость в трактовке целей урока математики (обучающая, воспитывающая, развивающая), в типологии уроков математики (С.Г. Манвелов); использование методов обучения с информационно-компьютерной поддержкой.
В результате исследования удалось установить, что формирование и развитие классно-урочной системы в России происходило эволюционным путем, без резких скачков, и состояло из постепенного развития всех ее элементов. Начиная с середины XIX, века наметилась явная тенденция к сокращению продолжительности урока.
Эволюция урока математики в отличие от развития классно-урочной системы в целом имела свою специфику (постановка на уроках практической цели, широкое использование устного счета и других специфических элементов урока).
Ретроспективный анализ теории и практики урока математики в общеобразовательных учебных заведениях России позволяет прогнозировать, что в ближайшие десятилетия урок математики не потеряет своей актуальности, и поиск иных форм, заменяющих урок, бесперспективен. В этой связи наше исследование требует продолжения по следующим направлениям: ретроспективный анализ особенностей организации и проведения уроков естественнонаучных и гуманитарных школьных предметов, сравнительно-сопоставительная характеристика форм организации обучения в России и странах Западной Европы.
Основное содержание и результаты исследования отражены в следующих публикациях.
Статьи в ведущих рецензируемых научных журналах и изданиях по перечню ВАК РФ:
1. Марушкина, И.А. Динамика продолжительности урока в уставах и учебных планах дореволюционной средней школы [Текст] / И.А. Марушкина // Вестник Тамбовского государственного университета им. Г.Р. Державина. Серия «Гуманитарные науки». – 2008. – №3(59). – С. 203–206. – 0,35 п.л.
2. Марушкина, И. А. Каким был урок математики в дореволюционной средней школе? [Текст] / И.А. Марушкина, О.А. Саввина // Педагогика. – 2010.– №3. – С. 70-78. – 0,62 п.л.
Другие публикации:
3. Марушкина, И.А. Об актуальности изучения истории развития урока математики в России [Текст] / И.А. Марушкина // Вестник Елецкого государственного университета им. И.А. Бунина. Серия: «Педагогика». – Вып. 11. – Елец: ЕГУ им. И.А. Бунина, 2006. – С.144–145. – 0,15 п.л.
4. Марушкина, И.А. Липецкий опыт в истории советской школы [Текст] / И.А. Марушкина // Методическая подготовка учителя математики в педвузе: методология, теория, практика: межвузовский сборник научно-методических работ / Под ред. Г.И. Саранцева. – Саранск: Мордовский гос. пед. ин-т, 2007. – С. 113-116. – 0,2 п.л.
5. Марушкина, И.А. Наглядность на уроках математики в средней школе России в XIX – начале XX века [Текст] / И.А. Марушкина // Проблемы теории и практики обучения математике: Сборник научных работ, представленных на Международную научную конференцию «LX Герценовские чтения», посвященную 210-летию РГПУ им. А.И.Герцена /Под ред. В.В. Орлова. – СПб.: Изд-во РГПУ им. А.И.Герцена, 2007. – С. 8–12.– 0,2 п.л.
6. Марушкина, И.А. О целях урока математики в XIX – начале XX века [Текст] / И.А. Марушкина // Современная математика и математическое образование, проблемы истории и философии математики: Международная конференция / Отв. ред. А.А. Артемов. – Тамбов: Изд-во Першино Р.В., 2008. – С.164–166. – 0,2 п.л.
7. Марушкина, И.А. Роль домашних заданий в преподавании математики [Текст] / И.А. Марушкина // Актуальные вопросы преподавания математики в школе и педагогическом вузе: Сборник материалов Московской областной научно-практической конференции / Отв. ред. М.П. Замаховский. – Коломна: Коломенский государственный педагогический институт, 2008. – С.80–82. – 0,2 п.л.
8. Марушкина, И.А. Организация образовательного процесса в единой трудовой школе в 1917-1931 гг. (на примере обучения математике) [Текст] / И.А. Марушкина // Вестник Елецкого государственного университета им. И.А. Бунина. Серия: «Педагогика». – Вып. 17. – Елец: ЕГУ им. И.А. Бунина, 2008. – С.97–110. – 0,8 п.л.
