Geum.ru

Вопросы к экзамену. Линейные и нелинейные функционалы, свойства линейных функционалов

Вид материалаВопросы к экзамену

Содержание


А. Теорема о единственности решения уравнения А
Вопросы к экзамену.
Подобный материал:
Вариационное исчисление, методы математической физики, методы оптимизации.

ВОПРОСЫ К ЭКЗАМЕНУ.


Линейные и нелинейные функционалы, свойства линейных функционалов.

Записать и пояснить вид функционала, позволяющего решать задачу о нахождении кривой минимальной длины между двумя точками.

Функционал, позволяющий решать задачу о нахождении поверхности минимальной площади, натянутой на замкнутую кривую. Задача о брахистохроне. Определение интегральных функционалов. Обобщения на многомерность, на учёт производных высших порядков. Понятие о приращении функционала. Непрерывность функционала. Определение вариации функционала, два подхода и их неравнозначность. Определение кривой, минимизирующей (максимизирующей) функционал. Теорема о необходимом признаке экстремума функционала, стационарные точки. Постановка задачи о минимуме функционала 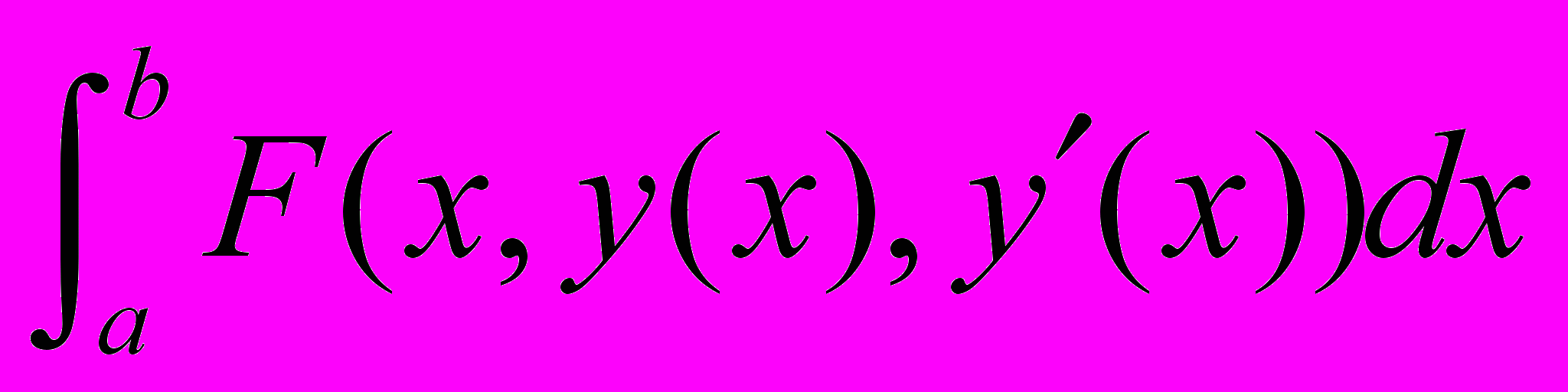, ограничения, граничные условия. Классы допустимых кривых, этапы минимизации функционала и окончательный вид вариации функционала. Уравнение Эйлера и лемма, необходимая для его получения. Обобщение: функционалы, содержащие несколько функций одного переменного и соответствующие уравнения Эйлера. Обобщение: функционалы, содержащие одну функцию одного переменного, несколько её высших производных и соответствующие уравнения Эйлера. Функционалы, зависящие от функций нескольких переменных, понятия вариации функции и вариации функционала. Вывод уравнения Эйлера в случае функционала, зависящего от функции двух переменных. Примеры: задача Дирихле для уравнения Лапласа и соответствующий функционал. Примеры: задача Дирихле для уравнения Пуассона и соответствующий функционал. Некоторые обобщения: Функционалы зависят от функций трёх переменных, или содержат производные более первого порядка. Вариационные задачи на условный экстремум. Голономные и неголономные связи. Теорема о экстремуме функционала при наличии голономных связей. Экстремумы функционалов при наличии неголономных связей. Понятие о изопериметрических задачах.

Линеал, определение, свойства.

Предгильбертово и гильбертово пространства. Скалярное произведение, норма, полнота, сепарабельность.

Симметричный оператор А. Теорема о единственности решения уравнения Аu=f для симметричного оператора А.Теорема о минимуме квадратичного функционала.Пример 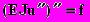.Положительность дифференциального оператора на линеале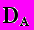(нулевые граничные условия). Вид соответствующего функционала. Классическое и обобщенное решения. Интуитивные соображения о сходстве и различии.

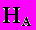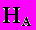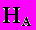Пространство (энергетическое прстранство).Схема его построения на основе гильбертова прстранства и оператора А Теорема о полноте пространства.Соотношения между нормами пространств и.Теорема о существовании минимума квадратичного функционала в пространстве 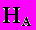. Определение обобщенного решения. Понятие непрерывной зависимости обобщенного решения от правой части уравнения.

Определение минимизирующей последовательности для квадратичного функционала.

Простейшие подходы к построению функционалов в случае неоднородных граничных условий.

Приближенная минимизация функционала. Метод ортогональных рядов.

Приближенная минимизация функционала. Метод Ритца. Получение системы алгебраических уравнений Ритца. Определитель Грамма. Доказательство теоремы о сходимости метода Ритца. Замечания. Нестрогие рассуждения о удачном или неудачном выборе базиса.

Метод Бубнова –Галёркина. Система алгебраических уравнений метода. Условия совпадения с системой метода Ритца. Теорема о сходимости метода в частном случае. Широта и области применения метода Бубнова –Галёркина. Замечания к методу.

Метод наименьших квадратов. Понятие А-базиса. Система алгебраических уравнений метода и теорема о сходимости. Замечания к методу. . Пример в Maple V. Кратко о методе Куранта.

Линейные ограниченные операторы. Метод наискорейшего спуска минимизации функционала, скорость сходимости. Решение интегрального уравнения в Maple V. Обоснование применимости метода. Сопоставление точного и приближённого решений. О других итерационных методах.

Основные проблемы, которые нужно решить при использовании метода квадратичного функционала для решения обыкновенных дифференциальных уравнений. Неравенство Фридрихса и его частные случаи. Частные случаи выбора констант. Неравенство Пуанкаре и его частные случаи.

Обыкновенные дифференциальные уравнения второго порядка в дивергентной форме. Ограничения на функции в уравнении. Общий вид граничных условий и их частные случаи. Краевая задача u(a)=u(b)=0. Доказательство возможности примения теории минимума квадратичного функционала.

Обыкновенное дифференциальное уравнение с краевыми условиями u`(a)=u`(b)=0. Доказательство возможности минимизации квадратичного функционала для получения приближенного решения в этом случае. Особый частный случай предыдущей задачи, уход от неединственности решения переходом к более узкому пространству.

Вариационное исчисление, методы математической физики, методы оптимизации.

ВОПРОСЫ К ЭКЗАМЕНУ.


Приближенная минимизация функционала. Метод ортогональных рядов.

Приближенная минимизация функционала. Метод Ритца.

Метод Галеркина решения операторных уравнений.

Сходство и различие методов Ритца и Галеркина( области пересечения).

Метод Куранта решения операторных уравнений

Решение операторных уравнений методом наискорейшего спуска.

Проблема выбора базиса.

Применение метода Ритца к обыкновенным дифференциальным уравнениям (пример).

Применение метода Галеркина к обыкновенным дифференциальным уравнениям (пример).

Примеры применения перечисленных методов для решения дифференциальных уравнений в частных производных.

Проблема выбора базиса при решении дифференциальных уравнений в частных производных

Пример на применение метода наискорейшего спуска.

11. Основы линейного программирования. Характерные постановки задач, математические и экономические трактовки.
12. Элементы выпуклого анализа. Выпуклые множества и функции.
13. Теоремы о представлении выпуклых множеств и их отделимости.
14. Понятие двойственности в линейном программировании и признак оптимальности решения.
15 Первая и вторая геометрические интерпретации задач линейного программирования. Теоремы о угловых точках
16. Теоретические основы симплекс метода и его вариантов

17. Линейное программирование и матричные игры.
18. Постановка задачи выпуклого программирования. Функция Лагранжа. Седловые точки и теорема о минимаксах.
19. Теорема Куна – Таккера.
20. Двойственность в выпуклом программировании. Методы решения задач.
21. Общая задача оптимального управления. Задача об оптимальном быстродействии.
22. Принцип максимума Понтрягина и классическое вариационное исчисление.

  1. Задача линейного программирования
  2. Определения: план, допустимый план, оптимальный план, решение задачи.
  3. Определение общей и канонической задачи линейного программирования.
  4. Методы приведения ОЗЛП к КЗЛП.
  5. Понятия: аффинное множество, гиперплоскость, базис.
  6. Определение выпуклого многогранника и выпуклого множеств. Отличия.
  7. Понятия линейная оболочка и выпуклая оболочка.
  8. Понятие о конусе.
  9. Понятие об угловой точке.
  10. Первая геометрическая интерпретация задачи линейного программирования.
  11. Базисный план.
  12. Связь базисного плана и угловой точки.
  13. Основные идеи симплекс –метода.
  14. Основные этапы в симлекс- методе.
  15. Критерии оптимальности, отсутствия решения, или неограниченности целевой функции.
  16. Вид симплекс- таблицы и этапы её преобразования.
  17. Понятие о двойственной задаче.
  18. Основные свойства пары двойственных задач.
  19. Характеристика оптимизационной нелинейной задачи.
  20. Основные трудности решения подобных задач.
  21. Понятие об условной оптимизации.
  22. Метод неопределённых множителей Лагранжа теорема для функции Лагранжа
  23. Понятие о стационарной точке.
  24. Основные этапы градиентных методов оптимизации.
  25. Метод дробления шага и метод наискорейшего спуска.
  26. Определение выпуклой и вогнутой функции.
  27. Достаточное условие выпуклости.
  28. Метод допустимых направлений, основные этапы.
  29. Понятие о прогрессивном направлении.
  30. Условие оптимальности текущей точки в методе допустимых направлений.
  31. Понятие о седловой точке.
  32. Теорема Куна- Таккера и её значение.
  33. Условие регулярности Слейтера.
  34. Правило дополняющей нежесткости.
  35. Двойственность в нелинейном программировании.
  36. Задачи оптимального управления и их классификация.
  37. Основные идеи вычислительного метода динамического программирования.
  38. Задача о покупке акций (задача об оптимальном вложении капитала.)

1

Элементы функционального анализа. Теоремы о минимуме квадратичного функционала. Пример (Балка, жестко заделанная по краям).


2

Условность теоремы о минимуме квадратичного функционала на линеале. О необходимости расширения линеала. Расширение линеала DA. Предгильбертово пространство SA и пространство HA.. Скалярное произведение в HA..


3

Связь норм гильбертовах пространств H и HA.. Существование минимума квадратичного функционала в HA.. Теорема о минимуме квадратичного функционала. Различные неравенства для норм H и HA.. Невязка и оценка погрешности приближённого решения.


4

Метод ортогональных рядов минимизации функционала. Теорема о представлении решения в методе ортогональных рядов. Недостатки метода. Пример в Maple V. График – поведение невязки.


5

Метод Ритца. Получение системы алгебраических уравнений Ритца. Определитель Грамма. Доказательство теоремы о сходимости метода Ритца. Замечания. Нестрогие рассуждения о удачном или неудачном выборе базиса. Пример в Maple V.


6

Метод Бубнова –Галёркина. Система алгебраических уравнений метода. Условия совпадения с системой метода Ритца. Теорема о сходимости метода в частном случае. Широта и области применения метода Бубнова –Галёркина. Замечания к методу. Пример в Maple V.


7

Метод наименьших квадратов. Понятие А-базиса. Система алгебраических уравнений метода и теорема о сходимости. Замечания к методу. . Пример в Maple V. Кратко о методе Куранта.


8

Линейные ограниченные операторы. Метод наискорейшего спуска минимизации функционала, скорость сходимости. Решение интегрального уравнения в Maple V. Обоснование применимости метода. Сопоставление точного и приближённого решений. О других итерационных методах.


9

Основные проблемы, которые нужно решить при использовании метода квадратичного функционала для решения обыкновенных дифференциальных уравнений. Неравенство Фридрихса и его частные случаи. Частные случаи выбора констант. Проверка неравенства Фридрихса в Maple V для частных функций.


10

Неравенство Пуанкаре и его частные случаи. Проверка неравенства Пуанкаре в Maple V для частных функций.


11

Обыкновенные дифференциальные уравнения второго порядка в дивергентной форме. Ограничения на функции в уравнении. Общий вид граничных условий и их частные случаи. Краевая задача u(a)=u(b)=0. Доказательство возможности примения теории минимума квадратичного функционала. Maple-пример.


12

Обыкновенное дифференциальное уравнение с краевыми условиями u`(a)=u`(b)=0. Доказательство возможности минимизации квадратичного функционала для получения приближенного решения в этом случае. Особый частный случай предыдущей задачи, уход от неединственности решения переходом к более узкому пространству.

13

Общий случай граничных условий для обыкновенного дифференциального уравнения второго порядка. Четыре частных случая граничных условий. Константы положительной определённости и вид функционалов. Проблема выбора базиса. Основные требования к базису.


14

Примеры базисов для обыкновенных дифференциальных уравнений. Базис из полиномов и способы обеспечения выполнения краевых условий. Базис из собственных функций операторов (или операторов близких в некотором смысле к исходному). Конкретные базисы для дифференциальных уравнений с различными краевыми условиями.


15

Решение в Maple V обыкновенных дифференциальных уравнений методами ортогональных рядов, Бубнова- Галёркина, Ритца, наименьших квадратов.


16

Краевые задачи для уравнений в частных производных. Однородная эллиптичность и дивергентная форма уравнений, производная по конормали. Типы краевых условий. Симметрия дифференциального оператора краевой задачи в частных производных. Положительная определённость опера торов в случае задачи Дирихле.


17

Положительная определённость операторов задач Ньютона и Неймана. Понятие о главных и естественных краевых условиях. Смешанные краевые условия. Неоднородные краевые условия.


18

Решение некоторых задач для уравнений с частными производными в среде пакета Maple V.