Разработка алгоритмов решения обратных задач промышленной диагностики аппроксимационным методом 05. 13. 01 «Системный анализ, управление и обработка информации (в промышленности)»
| Вид материала | Автореферат |
- Разработка моделей и алгоритмов оптимизации процедур диагностирования на граф-моделях, 272.8kb.
- Повышение эффективности функционирования транспортно-погрузочного комплекса предприятий, 243.9kb.
- Комплекс программных средств поддержки принятия решений при сетевой обработке информации, 192.61kb.
- Программа вступительного экзамена в аспирантуру по специальности 05. 13. 01 «системный, 49.66kb.
- Разработка нелинейных динамических систем для формирования хаотических колебаний, 219.26kb.
- Тестирование объектно-ориентированного программного обеспечения на основе моделирования, 214.61kb.
- Разработка и исследование метода одновременной оценки корней характеристического уравнения, 156.31kb.
- Методы поэтапной структурной отимизации магистральных корпоративных сетей 05. 13., 234.66kb.
- Метод и алгоритмы обработки информации в системе прогнозирования качества агломерата, 229.88kb.
- Системный анализ параметров сердечно-сосудистой системы учащихся югры 05. 13. 01 системный, 641.8kb.
На правах рукописи
Золин Алексей Георгиевич
Разработка алгоритмов решения обратных задач промышленной диагностики аппроксимационным методом
05.13.01 – «Системный анализ, управление и обработка информации
(в промышленности)»
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Самара– 2010
Работа выполнена в ГОУ ВПО «Самарский государственный технический университет».
Научный руководитель доктор технических наук, профессор Батищев Виталий Иванович
Официальные оппоненты: доктор технических наук, профессор Кузнецов Павел Константинович
кандидат технических наук Сергеев Антон Владимирович
Ведущая организация:
ГОУ ВПО «Пензенский государственный университет»
Защита состоится «_01_» июня 2010 г. в 11.00 час. на заседании совета
Д 212.217.03 при ГОУ ВПО ”Самарский государственный технический
университет” по адресу: г. Самара, ул. Галактионовская, 141, 6 корпус, ауд. 28.
С диссертацией можно ознакомиться в научной библиотеке
Самарского государственного технического университета
(г. Самара, ул. Первомайская, 18)
Автореферат разослан « 29» апреля 2010 года.
Ученый секретарь
диссертационного совета
кандидат технических наук,
доцент Н.Г. Губанов
Характеристика работы
Актуальность темы. В исследовании проблемы эффективного контроля и диагностики состояния технологических объектов, системный подход является актуальным на современном уровне развития техники, поскольку значительный рост сложности вновь создаваемого оборудования и эксплуатация его в условиях напряженного режима функционирования, выдвигают качественно новые требования к методам технического контроля и промышленной диагностики.
Получение информации в рабочих режимах функционирования оборудования, для оперативного технического контроля, порождает проблемы, обусловленные случайным характером диагностируемых процессов, некорректностью задач нахождения неизвестных характеристик по косвенным измерениям и необходимостью получения результатов обработки данных в минимальные сроки. Повышение быстродействия за счет увеличения производительности вычислительных средств ведет прогрессирующему удорожанию средств диагностики.
Решению таких проблем способствует применение аппроксимационного подхода, позволяющего использовать априорную информацию в форме аналитических моделей исследуемых зависимостей. Использование аппроксимационного подхода дает предпосылки системного объединения через математическую модель априорной информации, выражающей физическую сущность решаемой задачи, а также процедуры осуществления измерений и интерпретации их результатов.
Вопросы разработки аппроксимационных методов и алгоритмов в разное время исследовали В.Ф. Бахмутский, Дж. Бокс, И.И. Волков, В.И. Батищев, В.И. Глызин, Е.Д. Горбацевич, Ф.Ф. Дедус, А.Ф. Дедус, Г. Дженкинс, Л.А. Залманзон, А.Б. Изотин, Д. Лампард, С.А. Махортых, В.Н. Пойда, С.А. Прохоров, А.Ф. Романенко, В.П. Рыжов, Р.Х. Садыхов, Г.А. Сергеев, О.П. Ситников, А.М. Трахтман, М.П. Цапенко, П.М. Чеголин, В.М. Чернышов и другие ученые. Однако, в инженерной практике аппроксимационные методы промышленной диагностики не нашли должного распространения, в основном, по причине сложности и неустойчивости традиционных решений задач оценивания параметров нелинейных моделей и ограничений, накладываемых характером классических ортогональных базисов при построении моделей.
Учитывая это, следует признать актуальным дальнейшее развитие методов решения задач диагностики промышленного оборудования с использованием аппроксимационного подхода. Важным является построение новых, адекватных реальным техническим процессам базисных модельных систем и разработка устойчивых и простых в реализации алгоритмов оценивания характеристик диагностируемого оборудования.
Целью работы является разработка и исследование новых методов, алгоритмов и программных средств решения некорректных обратных задач в системах промышленного контроля и диагностики, основанных на принципах аппроксимации исследуемых зависимостей и их функциональных характеристик аналитическими моделями.
Для достижения указанной цели в работе поставлены и решены следующие задачи:
– обзор и системный анализ типовых методов технической диагностики промышленных объектов;
– обзор и анализ методов решения обратных задач являющихся базовыми при осуществлении технической диагностики объектов;
– анализ, классификация и группировка моделей функциональных характеристик промышленных объектов и процессов;
– разработка методик выбора и реализации методов оценивания параметров моделей;
– исследование методов построения оптимальных методов построения ортогональных базисных систем;
– разработка алгоритмов оценивания параметров моделей.
Научная новизна:
1. На основе системного анализа типовых методов промышленной диагностики предложена новая классификация моделей диагностируемых сигналов и процессов, ориентированная на эффективное применение аппроксимационного подхода при решении обратных задач технической диагностики промышленных объектов;
2. Исследован метод формирования ортогональных полиномов на базе ряда дробно-рациональных функций, позволяющий, в отличие от существующих, синтезировать ортогональные базисные системы адекватные классу корреляционных и импульсных переходных функций реально осуществимых процессов;
3. Разработаны не имеющие известных аналогов методы параметрической оптимизации ортогональных базисов, сформированных на базе ряда дробно-рациональных функций, обеспечивающие реализацию адекватного модельного представления функциональных характеристик экспериментальных зависимостей;
4. Разработаны и исследованы новые алгоритмы решения задач промышленной диагностики на основе метода моментов, которые, в отличие от существующих, позволяют получать простые, статистически устойчивые решения в случае некорректных задач с моделями с нелинейными параметрами.
Практическая значимость результатов исследований заключается в возможности применения полученных методов при решении задач промышленной диагностики с использованием аппроксимационного подхода. Отдельные результаты могут быть использованы при чтении специальных курсов и подготовке учебных пособий.
Апробация работы. Основные положения работы и результаты исследований обсуждались на различных конференциях, в том числе: конференция «Окружающая среда для нас и будущих поколений.» г. Самара 2004 год; конференция «Информационные, измерительные и управляющие системы» г.Самара 2005 год; конференция «Актуальные проблемы информационной безопасности при противодействии криминалу и терроризму. Теория и практика использования аппаратно-программных средств» г. Самара 2007 год; конференция «Нефтегазовые и химические технологии» г.Самара 2007 год; конференция «Перспективы развития информационных технологий» г.Новосибирск 2008 год; конференция «Математическое моделирование и краевые задачи» г.Самара 2004, 2007, 2008, 2009 годы; конференция «Компьютерные технологии в науке, практике и образовании» г.Самара 2006, 2009 годы.
Публикации по результатам исследований. Основное содержание диссертации изложено в 14 публикациях, в том числе в 2 статьях в журналах рекомендованных ВАК, материалах и тезисах докладов 12 конференций.
Реализация результатов работы. Результаты, выводы и рекомендации работы использованы в учебном процессе ГОУ ВПО «Самарский государственный технический университет», а также в ОАО «Автоваз» при разработке алгоритмического и программного обеспечения системы моделирования процессов смесеобразования и сгорания топлива в автомобильных двигателях.
На защиту выносятся:
– Классификация моделей, адекватных исследуемым процессам и явлениям при решении задач технической диагностики промышленных объектов.
– Метод формирования обобщенного класса ортогональных базисных систем на основе семейства дробно-рациональных параметрических функций.
– Методы и алгоритмы параметрической оптимизации базисных систем при аппроксимации сигналов и их функциональных характеристик ортогональными функциями и полиномами.
– Алгоритмы решения задачи оценки параметров распределения частиц в дисперсных средах на основе метода моментов на примере получения параметров распределения диаметров частиц в двухфазных дисперсных потоках.
Объем и структура работы. Диссертация состоит из введения, 5 глав, выводов, библиографического списка, включающего 118 наименований. Основная часть диссертации изложена на 155 с. машинописного текста, содержащего 21 рисунок, 15 таблиц.
Содержание работы
Во введении обоснована актуальность исследуемой проблемы, сформулирована цель и основные задачи работы, аргументирована научная новизна исследований, показана практическая значимость полученных результатов, представлены выносимые на защиту основные положения.
В первой главе рассматриваются методы промышленной диагностики и неразрушающего контроля в промышленности. По своей сути методы диагностики являются обратными задачами. Использование этих методов в производстве, т.е. в условиях устоявшихся технологических процессов, в рамках узкоспециализированных задач, с ограниченным диапазоном вариации параметров, позволяет накапливать экспериментальную информацию об исследуемых процессах и явлениях. Данная информация может быть использована как априорная при решении обратных задач диагностики.
В зависимости от типа диагностируемых объектов, характера протекаемых в них процессов и способа организации диагностических процедур существует два вида математической постановки задачи диагностики.
Первая характерна для задач тестовой диагностики, когда на объект подается специально сформированное воздействие, а отклики объекта в заданных контрольных точках позволяют делать заключение о его техническом состоянии. Она выражается следующей зависимостью:
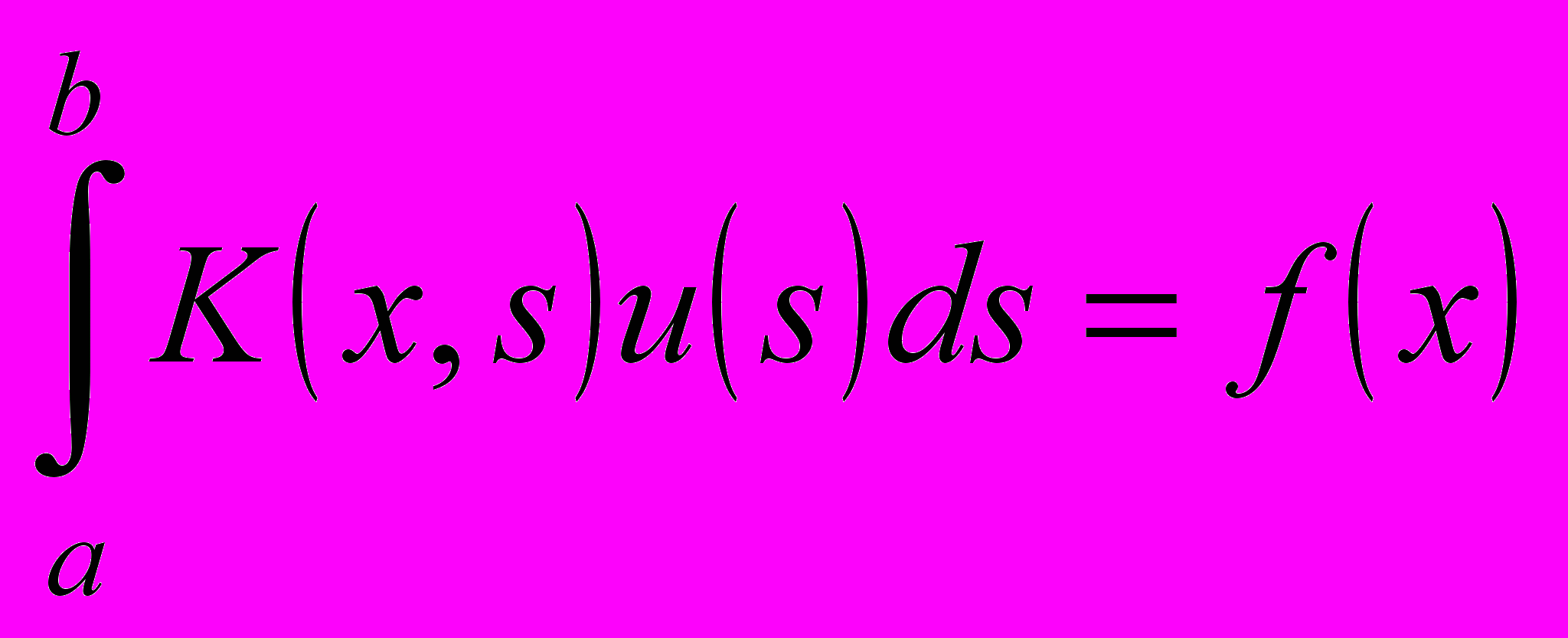 (1)
(1)где f(x) – результаты измерений, u(s) – искомая информативная функциональная характеристика объекта диагностики, K(x,s) – ядро уравнения (аппаратная функция).
Данное уравнение является интегральным уравнением Фредгольма I рода. Нахождение u(s) представляет собой некорректно поставленную обратную задачу, классические методы численного решения уравнения (1) неустойчивы. В случае, когда есть основания для априорного выбора аналитической модели u(s), можно применить аппроксимационный метод, используя модели заданного вида либо ортогональные функции или полиномы.
К таким задачам относятся обработка и интерпретация результатов косвенных измерений, задачи качественного и количественного анализа многокомпонентных систем в спектроскопии, хромоторграфии, рентгеноскопии, дифрактометрии, томографии, задача нахождения распределения параметров частиц в многофазных средах.
В случае диагностики оборудования в режимах его нормального функционирования исследуемые сигналы, как правило, имеют случайный характер. В этом случае используют уравнение Винера-Хопфа
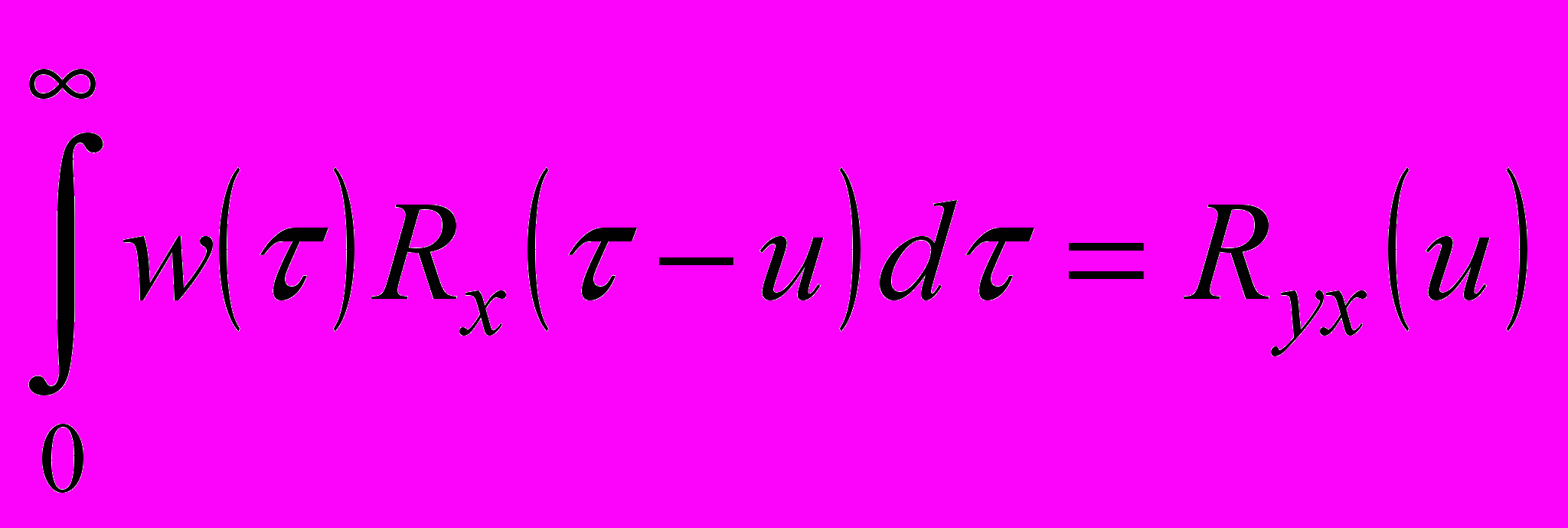 , (2)
, (2)где искомая информативная функциональная характеристика объекта диагностики w(τ) вычисляется по значениям автокорреляционной функции Rxx(t-τ) входного сигнала и взаимной корреляционной функции Rxy(t) входного и выходного сигналов объекта диагностики. При нестационарности процессов по математическому ожиданию вместо корреляционных функций в выражении (2) используют структурные функции.
Анализ эволюции и современного состояния рассматриваемого в работе технического и методико-алгоритмического обеспечения показывает, что в этой области накоплен значительный потенциал. Реализация возможностей и развитие методов и средств аппроксимационного подхода дает не только перспективные методы обработки, но и методологическую основу единого системного подхода – системное объединение всех этапов исследования: измерения, анализа и обработки данных, интерпретации результатов.
Во второй главе проводится обзор и анализ классических методов решения обратных задач технической диагностики.
В соответствии с типами введения априорной информации можно выделить три группы численных методов решения некорректных обратных задач: детерминистские, статистические, проекционные.
Важным частным случаем проекционных методов, является ситуация, когда аналитическая форма искомого решения известна, или решение с высокой степенью достоверности может быть аппроксимировано моделью, построенной либо на основе априорных сведений, либо путём обобщения результатов измерений числовых и функциональных характеристик объекта диагностирования и протекающих в нём процессов. В этом случае размерность задачи может быть существенно уменьшена и, как правило, соответствующая система уравнений для нахождения небольшого числа неизвестных параметров оказывается хорошо обусловленной. Важным преимуществом этого подхода является то, что практически никогда нельзя получить абсурдное решение, если аналитическая модель выбрана в соответствии с исследуемым процессом.
Эффективность методов решения обратных задач технической диагностики аппроксимационными методами, непосредственно связана с выбором модельного базиса. Системы базисных функций могут быть либо выбраны из множества известных, либо сформированы по определенной методике под решаемую задачу.
Для первого случая в работе дается обзор классических ортогональных полиномов, наиболее часто встречающихся на практике, сгруппированных по области определения аргумента: на конечном интервале, на положительной полуоси и на интервале [-∞, +∞].
Однако, рассмотренные полиномы, по сути, являются математическими абстракциями и построенные на их основе модели имеют спектральные плотности не соответствующие спектральным плотностям реальных технических процессов. Привлечение базисных систем, согласованных с априорной информацией и физической сущностью исследуемых явлений, позволит повысить точность и достоверность результатов диагностирования.
В третьей главе рассматривается аппроксимационный метод решения задач промышленной диагностики при исследовании сигналов, носящих случайный характер.
Приводятся типовые модели применяемые в задачах идентификации ЛДО: в работе собраны модели ИПФ, АКФ входного сигнала и ВКФ сигналов производственных объектов и объектов управления, наиболее часто встречающихся на практике.
Поскольку спектральные плотности реальных технических процессов и передаточные функции физически реализуемых линейных динамических систем имеют дробно-рациональную форму, предлагается способ формирования базисных систем на основе обобщенного семейства дробно-рациональных функций. Рассмотрим семейство дробно-рациональных функций
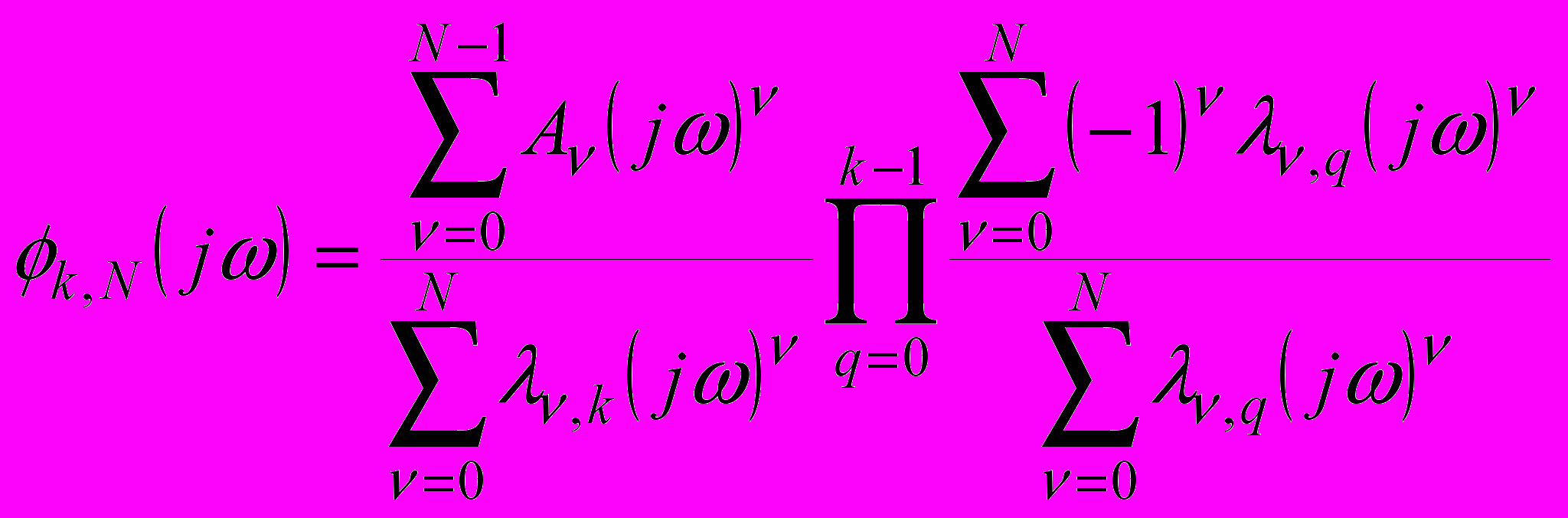 (3)
(3)В случае, если корни полинома
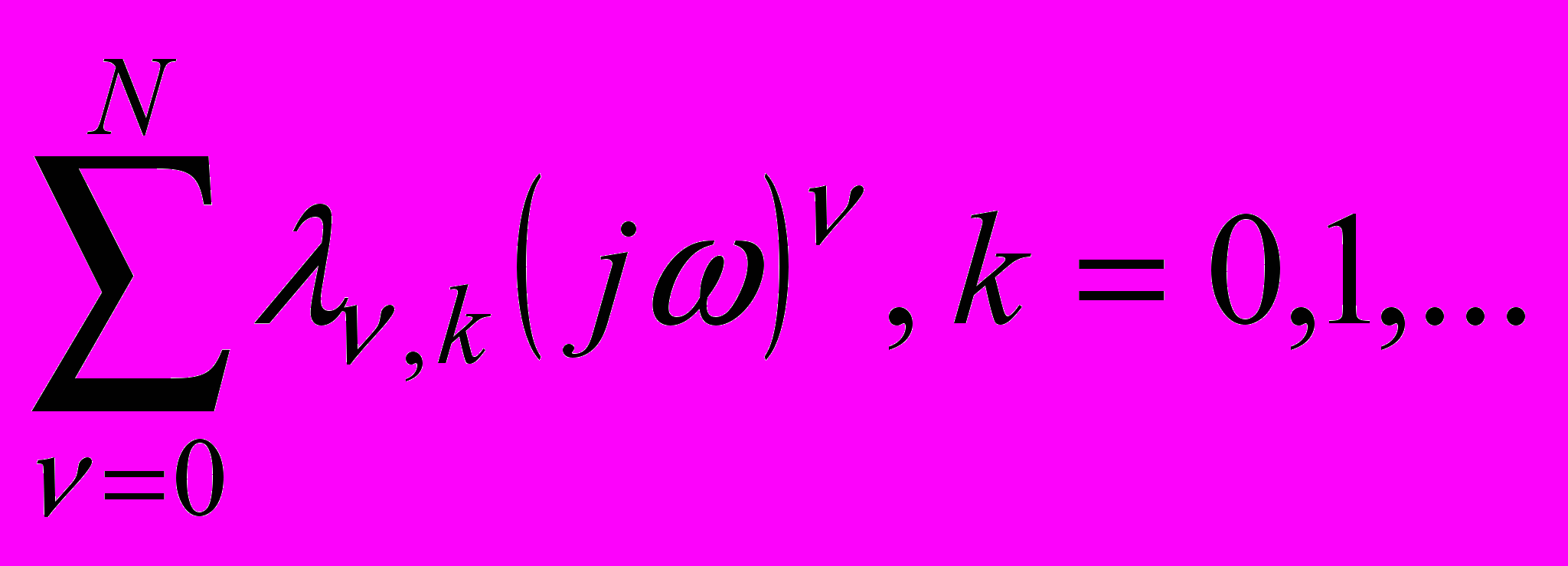 (4)
(4)имеют отрицательные вещественные части, то функции
 (5)
(5)ортогональны, т.е.
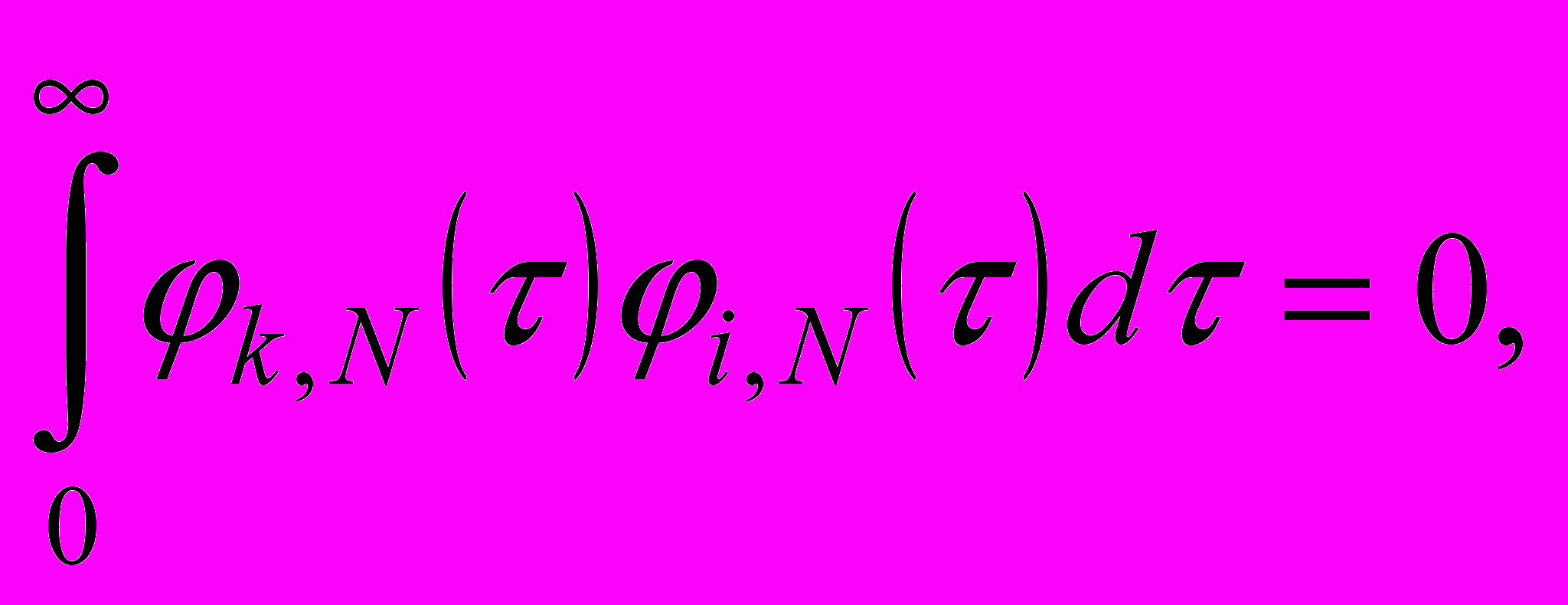 при
при 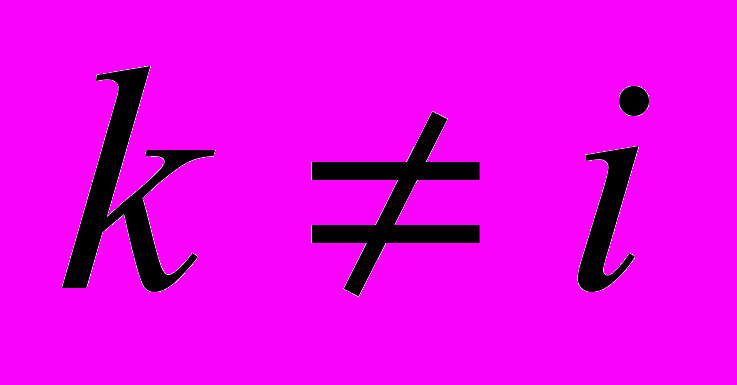 (6)
(6)В диссертации показано, что функции {φk,N(τ)} представляют ортогональный базис, k=0,1,…, причем их Фурье-преобразования – дробно-рациональные функции, что соответствует свойствам спектральной плотности мощности случайного процесса.
В случае N=1, базис {φk,N(τ)} представляет собой обобщенные функции Дирихле, а путем фиксации отдельных параметров можно получить частные случаи: ортогональные функции Дирихле и Лагерра.
При N=2 базис {φk,N(τ)} имеет вид:
 (7)
(7)Данный класс дробно-рациональных соотношений порождает большое множество базисных систем, получаемое соответствующим выбором параметров A0, A1, λ0,q, λ1,q. Эти функции относят к классу ортогонализированных экспоненциальных функций.
В случае N=2, A0=α1(1+α3), A1=1, αq=α1, ωq=α2, получаются ортогонализированные экспоненциальные функции, соответствующие обобщенному виду АКФ реально осуществимых процессов.
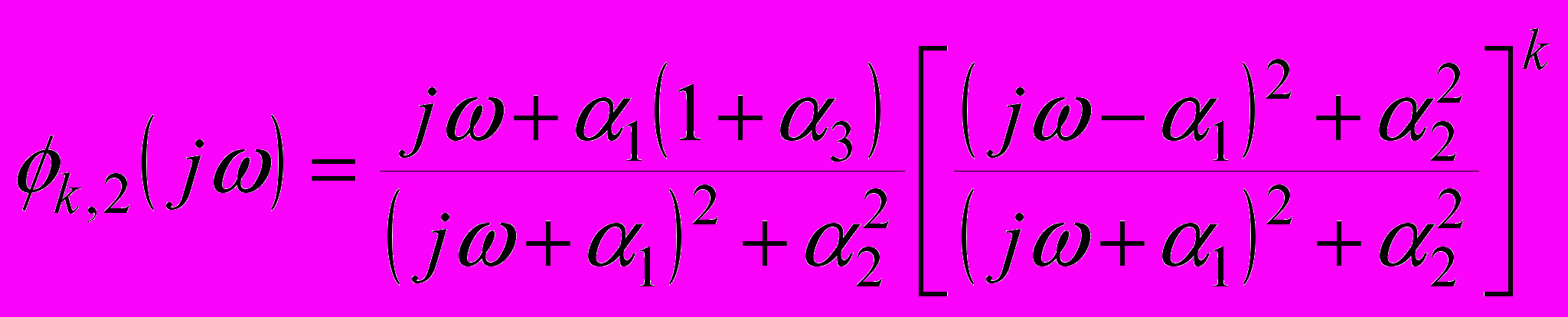 (8)
(8)Предложенный общий подход к построению базисных систем показывает широкие возможности использования дробно-рациональных функций при генерации классов ортогональных полиномов при решении обратных задач аппроксимационным методом. Однако для реализации этих возможностей необходимо решить задачи параметрической оптимизации базисных функций.
Критерий среднеквадратического приближения для модели в частотной области, построенной на базисе (7), имеет вид:
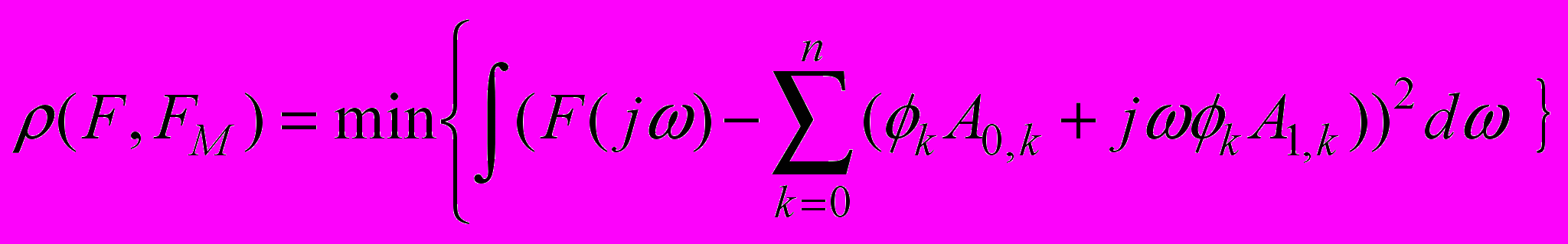 , (9)
, (9)где F(jω) – Фурье-образ аппроксимируемой функции, ϕk(jω) - полином вида
 (10)
(10)Представление функций базиса (7) во временной области для N=2 обозначим как
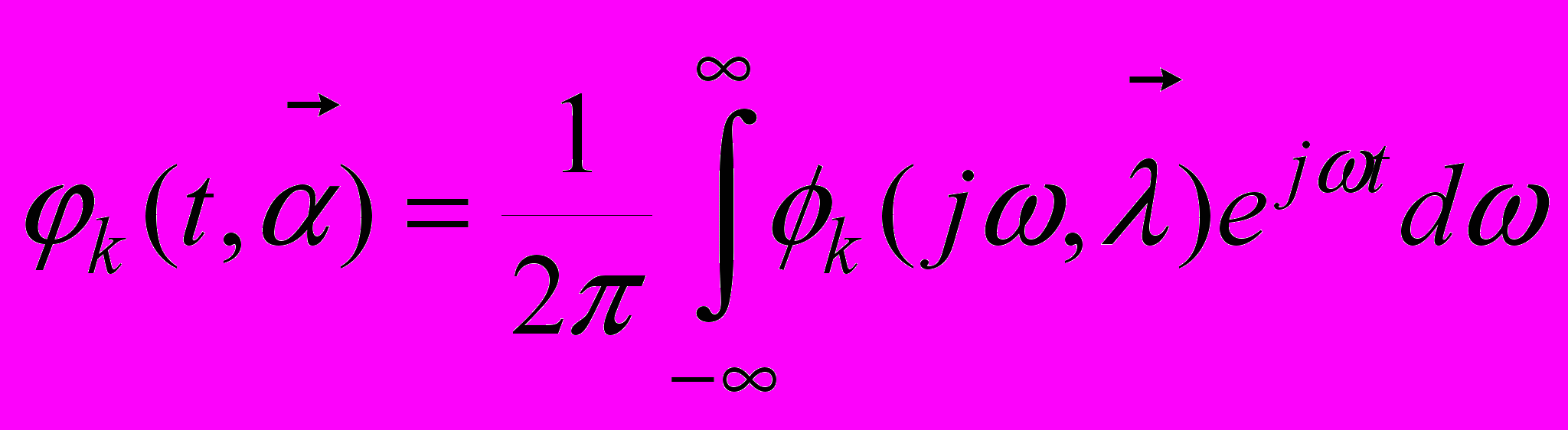 , (11)
, (11)Критерий среднеквадратического отклонения при аппроксимации функциями φk (t) описывается соотношением
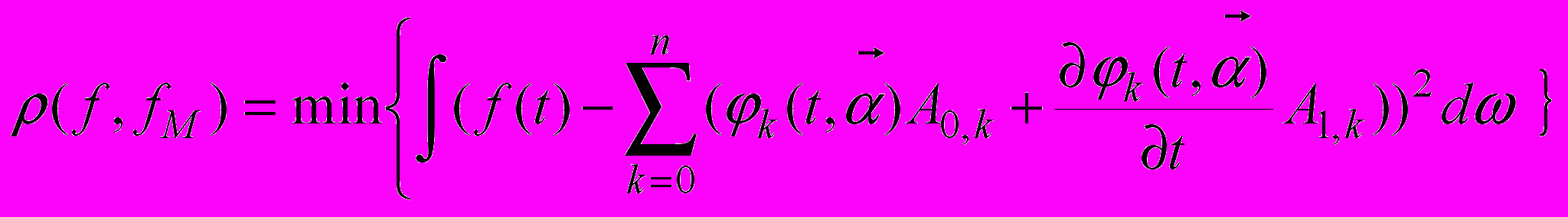 , (12)
, (12)Оптимальное значение параметров находится при решении системы уравнений, образуемой условиями равенства нулю частных производных ρ(F,FM) и ρ(f,fM) по параметрам.
В задачах идентификации ЛДО аппроксимируемыми функциями являются ИПФ и ВКФ.
Задача оценивания коэффициентов разложения корреляционных функций во временной области в ортогональном базисе с оптимальной подстройкой параметров базисных функций есть частный случай общей задачи аппроксимации. Комплексное решение задачи аппроксимации корреляционной функции моделями может быть обеспечено применением обобщающей зависимости, описывающей корреляционную функцию:
 (13)
(13)В качестве базиса целесообразно использовать базис (8), позволяющий получить ортогонализированные экспоненциальные функции, соответствующие обобщенному виду корреляционных функций реально осуществимых процессов.
Подставляя в выражение (12) вместо f(t) и fM(t) корреляционную функцию стационарного случайного процесса

где
 , и ее модель
, и ее модель  (14)
(14)получим систему уравнений, связывающих значения параметров A0,…,An и α1,…, αp модели корреляционной функции (14) со значениями реализации стационарного случайного процесса xº(t)
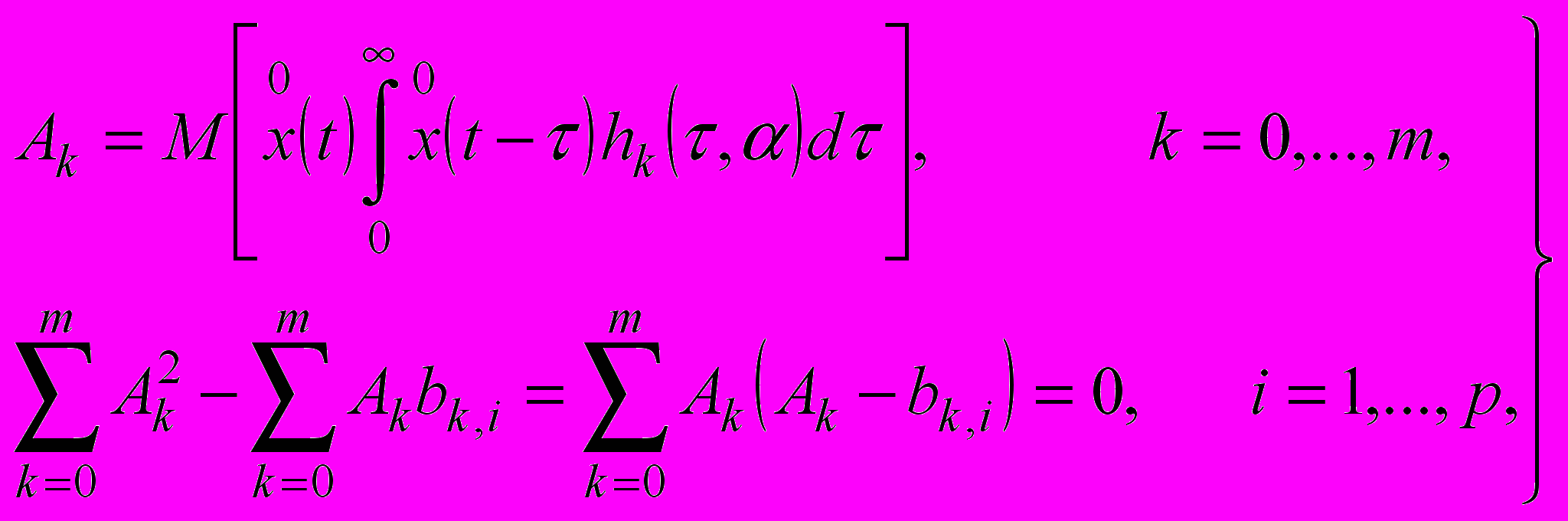 (15)
(15)где
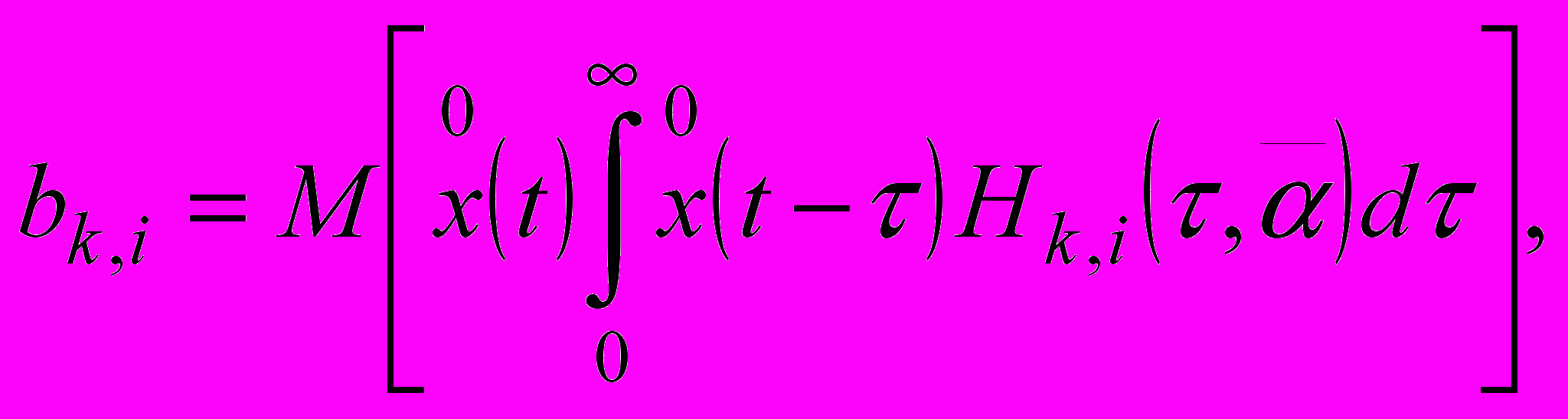 (16)
(16)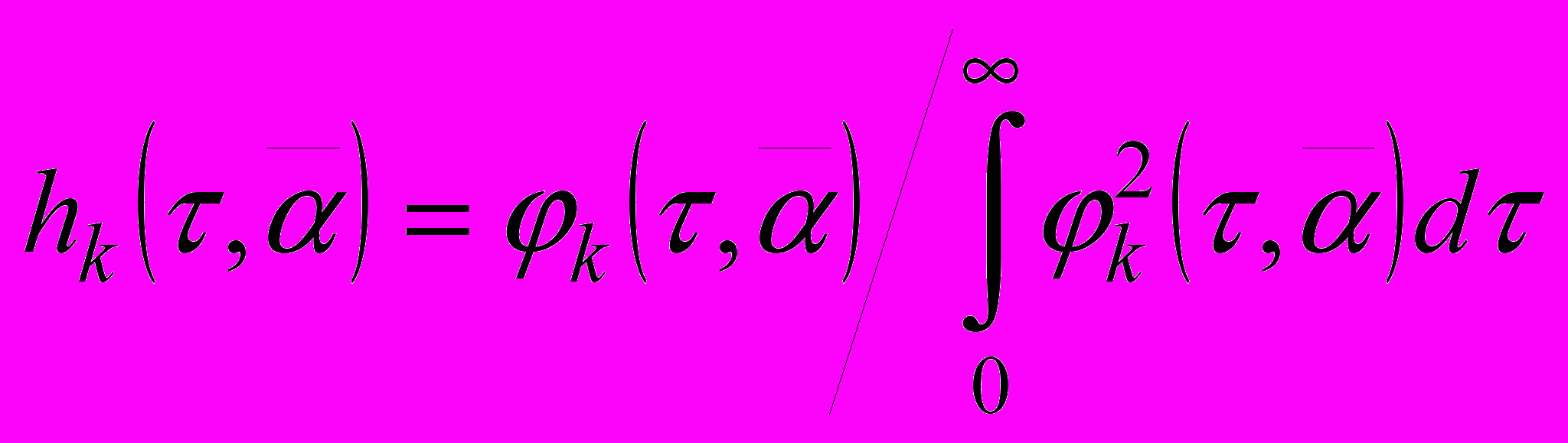 (17)
(17) (18)
(18)Таким образом, параметрическая оптимизация модели, построенной на основе рассмотренной системы ортогональных функций, может быть осуществлена в общем случае путем оценивания дополнительных коэффициентов bk,i, k=0,…,n; i=0, … ,p согласно (16) и выполнения условий, определяемых системой (15).
В четвертой главе рассматривается аппроксимационный метод решения задач промышленной диагностики с использованием параметрических моделей заданного вида.
В различных областях, таких как аналитическая химия, рентгеновская дифрактометрия, γ-спектроскопия, ультразвуковая дефектоскопия и других, известно большое количество работ, посвященных обоснованию аналитических математических моделей, свойственных и адекватных различным объектам, процессам и ситуациям.
В работе приводится библиотека наиболее характерных пиков сигналов используемых в дифрактометрии, хромотографии, аналитической химии, акустической диагностике.
Практическая реализация метода решения обратных задач технической диагностики, основанного на среднеквадратической аппроксимации экспериментальных зависимостей и искомых решений, может оказаться чрезвычайно затруднительной при использовании моделей с нелинейно входящими в них параметрами. В случае использования параметрических моделей заданного вида целесообразно разрабатывать и применять подходы, позволяющие получать простые и статистически устойчивые решения.
В работе предложен метод нахождения распределения диаметров частиц в двухфазном дисперсном потоке.
Непосредственно измерению подлежат значения функции скорости счета f(s), связанной с искомой плотностью распределения u(θ) диаметров θ капель интегральным уравнением Фредгольма I рода.
 . (19)
. (19)Ядро уравнения K(s, θ) в случае анализа распределения размеров капель электропроводящей жидкости в газо-жидкостном потоке, основанном на подсчете количества капель с диаметром, большим определенного числа, в некоторой области потока за единицу времени, вычисляется по формуле:
 , (20)
, (20)где Fc - площадь сечения сопла в месте измерения, P - общее число капель, проходящих в единицу времени в сечении Fc , s - параметр измерительного преобразователя, обеспечивающий формирование импульса при θ≥ s.
Для данной задачи известны четыре модели распределения диаметров частиц в двухфазных дисперсных потоках
 (21)
(21)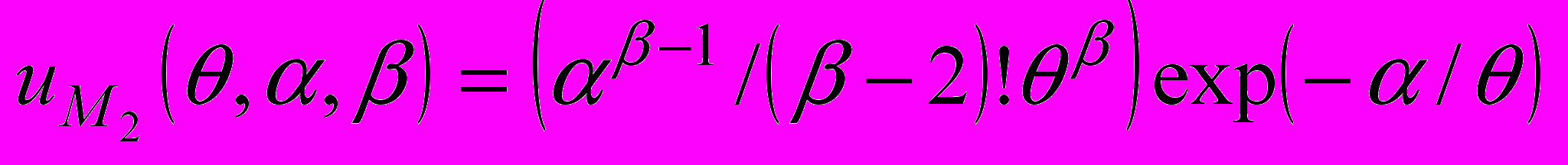 (22)
(22)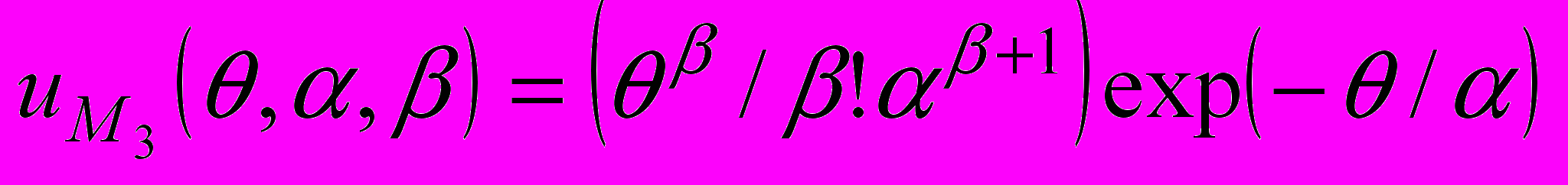 (23)
(23)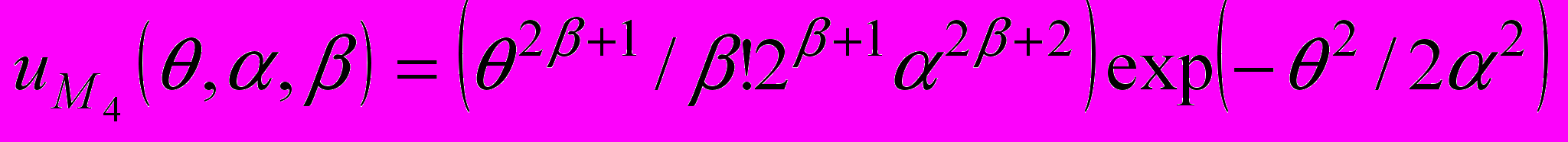 (24)
(24)Составим систему из (m+1) уравнений:
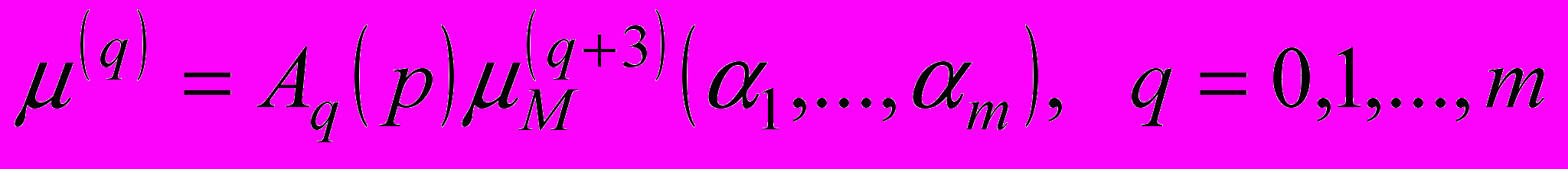 (25)
(25)где

начальный момент порядка (q+3) случайной величины θ с распределением uM(θ ,α),
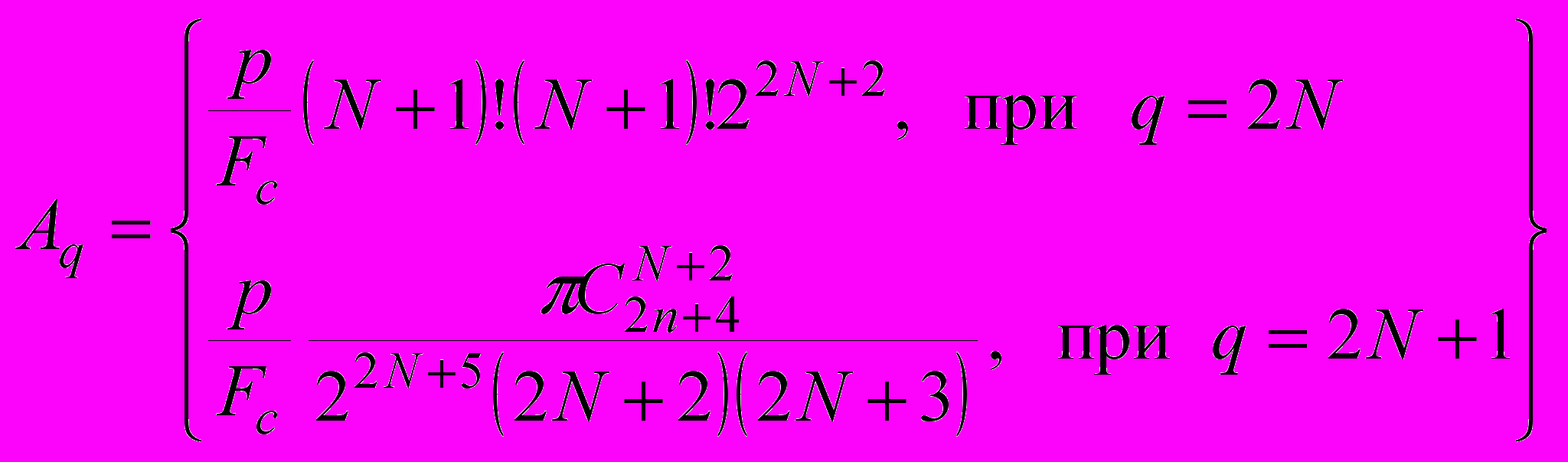 (26)
(26)Система должна быть решена относительно α1,…, αm и p.
Тогда, при использовании модели (21) система будет содержать два уравнения для моментов порядка 0 и 1.
Учитывая дискретный характер функций скорости счета f(s) и ограниченный диапазон изменения размеров частиц θmin ≤θ≤ θmax, получим алгоритм оценки значения параметра α.
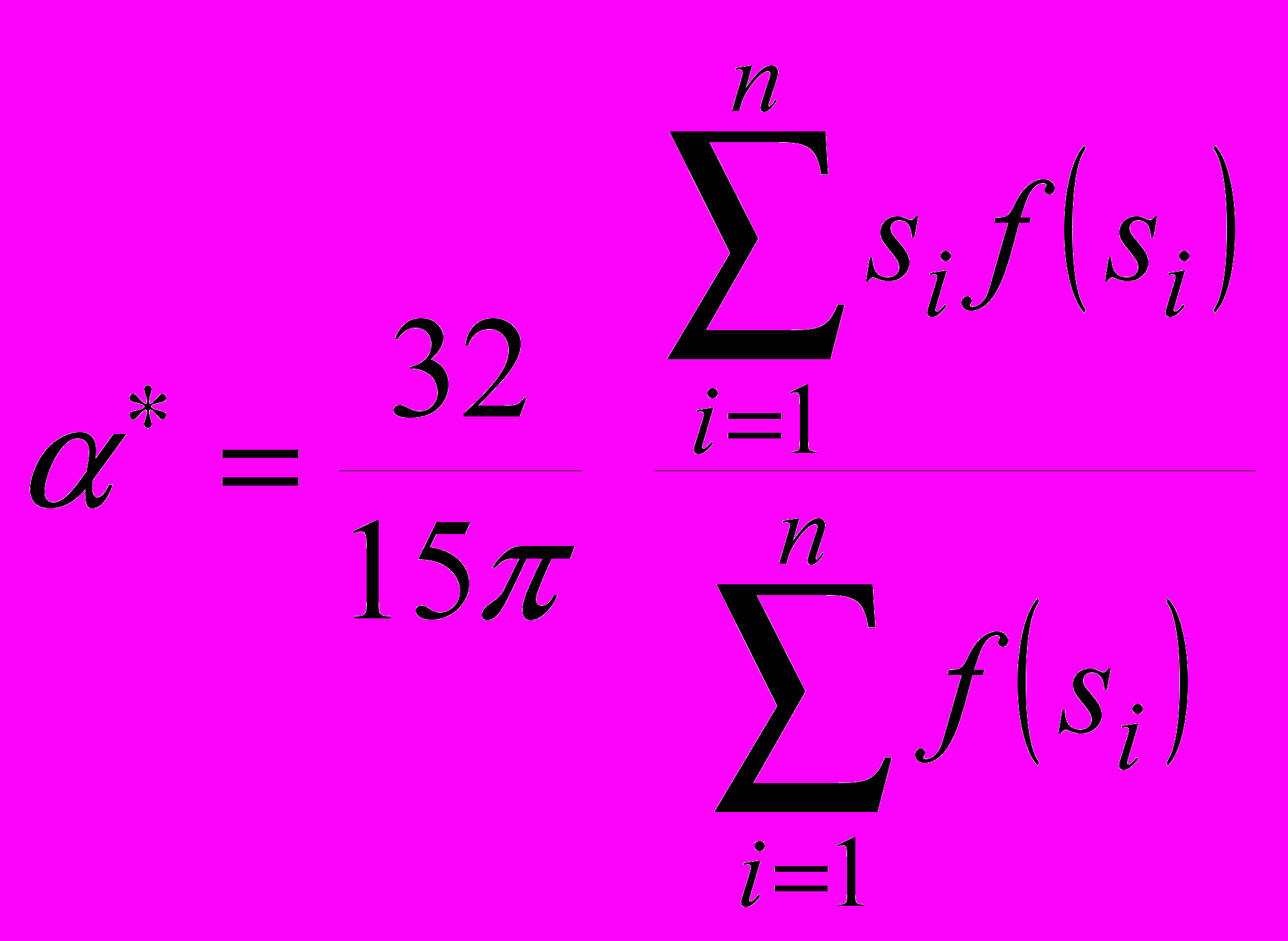 (27)
(27)Для модели (22) , система будет содержать три уравнения.
Решая ее, получим следующий алгоритм оценивания параметров α и β:
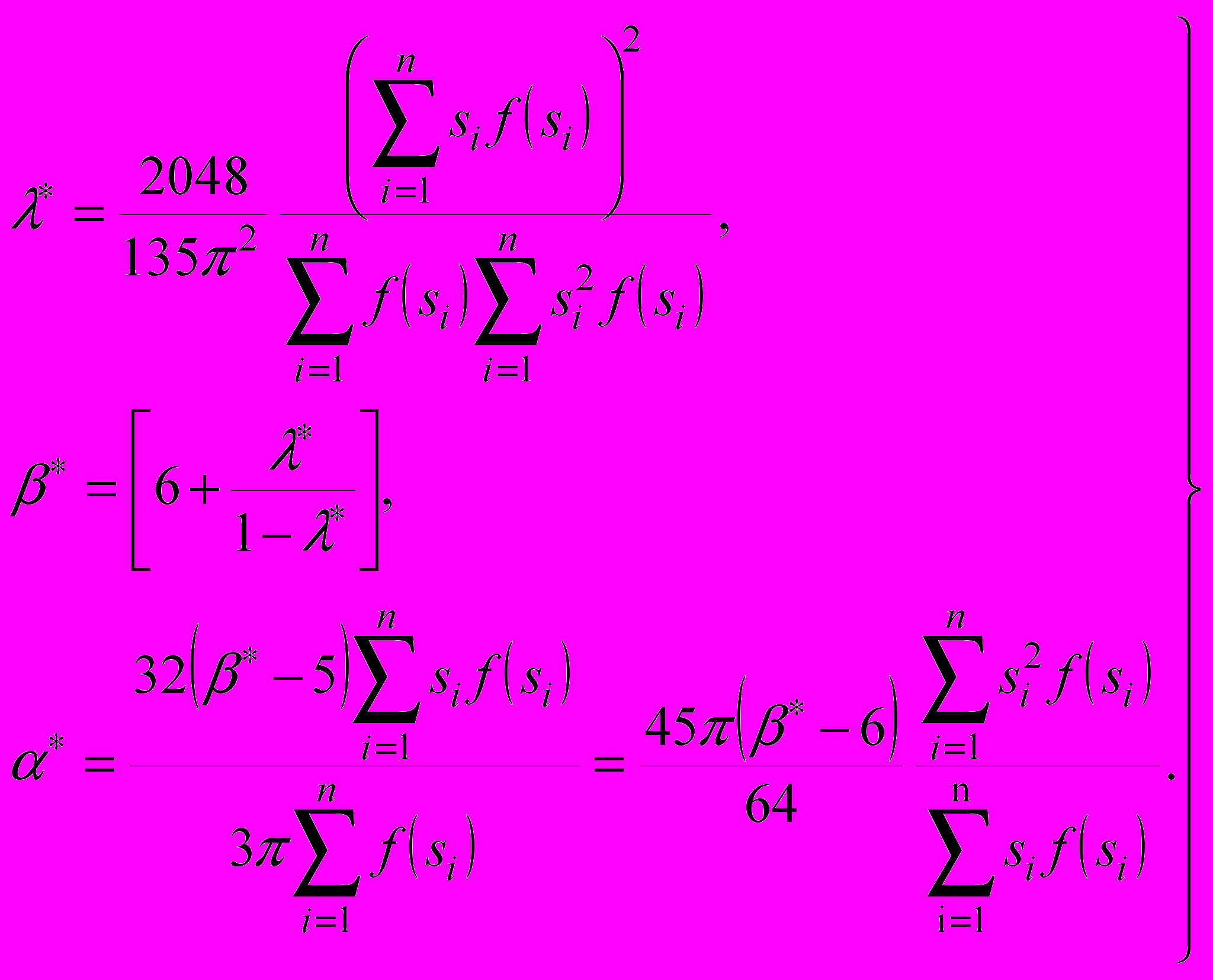 (28)
(28)Квадратные скобки в выражении β*=[.] означают оператор округления числа в скобках до ближайшего целого.
Для модели (23) алгоритмы вычисления оценок параметров α и β будут иметь следующий вид:
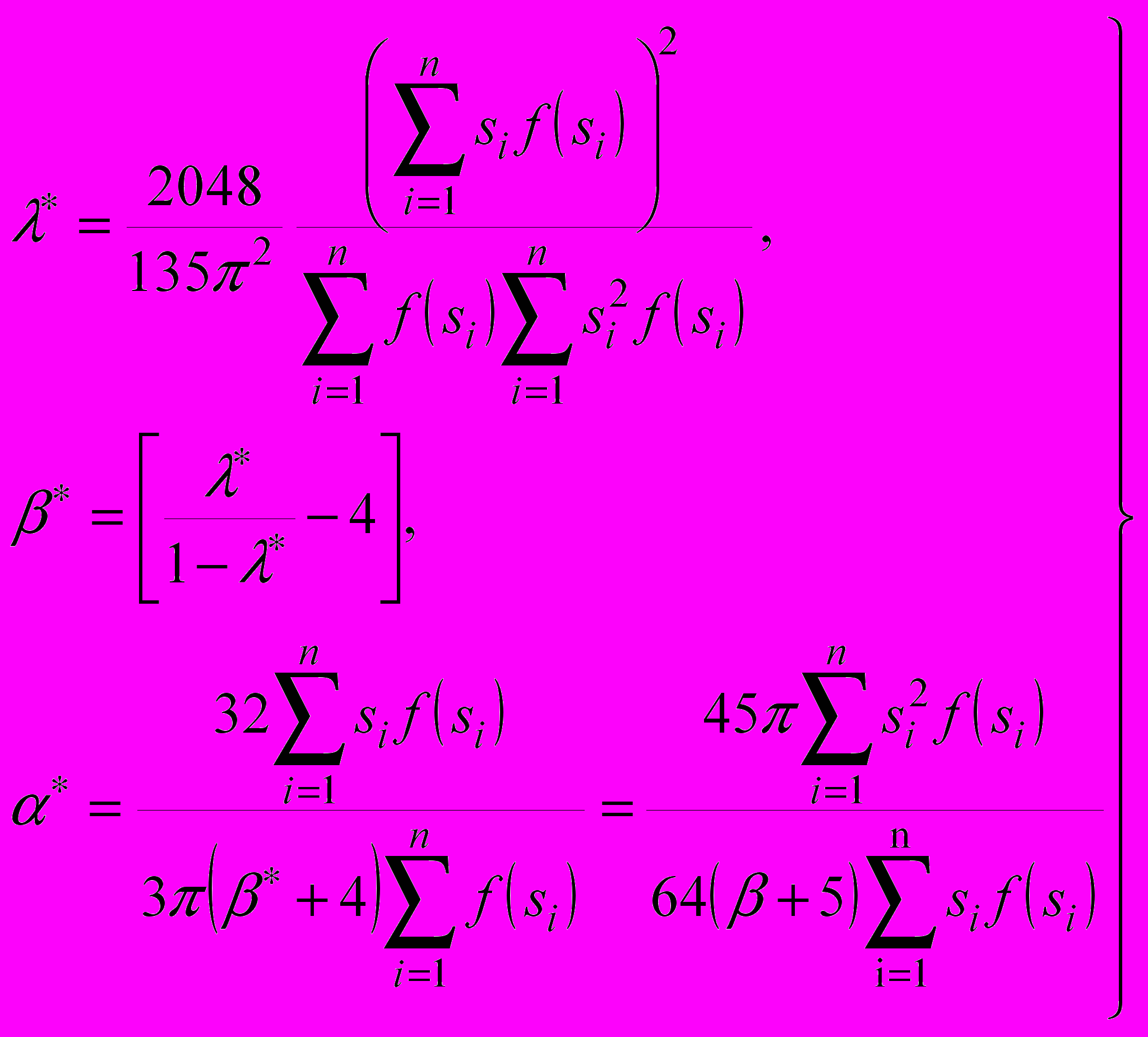 (29)
(29)Если число, заключенное в квадратных скобках выражения β*=[.], принадлежит интервалу [0,1] , то значение параметра β*=1, в остальных случаях β* округляется до ближайшего целого числа. Если 4/5<λ*<1, модель (23) следует считать непригодной для интерпретации результатов.
Наконец, для модели (24) получим систему:
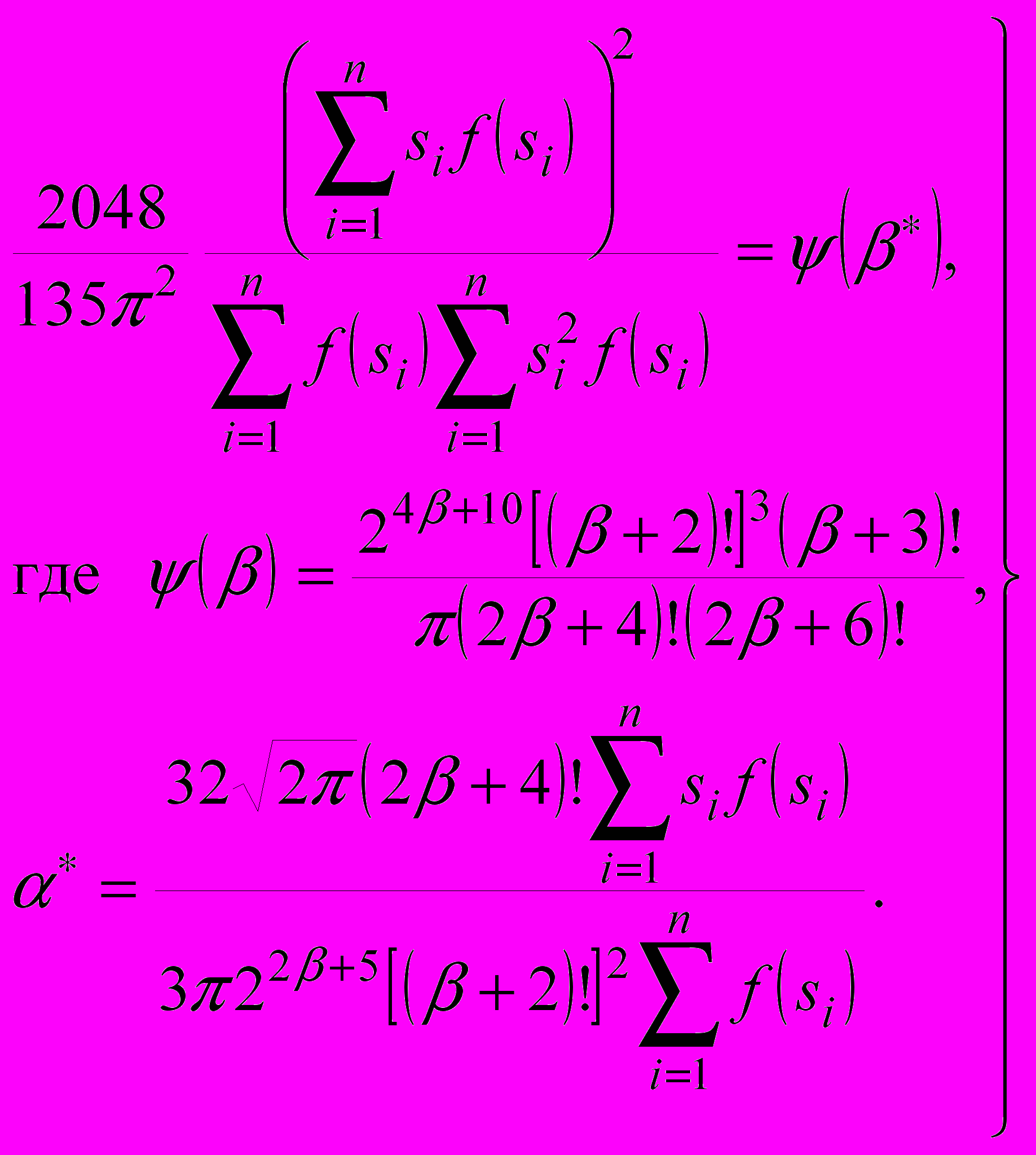 (30)
(30)Поскольку оценка параметра β не может быть получена в явном виде и должна принимать только целочисленные значения для решения первого уравнения в системе (30) может быть предложена следующая процедура. Функции ψ(β*) могут быть вычислены рекуррентно:
 (31)
(31)Вычислениями поочередно ψ(1), ψ(2),… проверяется соответствие ψ(β) левой части первого уравнения в системе (30). При обеспечении такого соответствия процесс подбора прекращается.
Использование критерия моментов в данном случае дает простые и статистически устойчивые решения.
В пятой главе рассматривается численное решение задачи оценки параметров распределения диаметров частиц в двухфазных потоках с использованием метода моментов.
Приводится сравнительный анализ полученных результатов для моделей (21)-(24). На рисунке 1 показана зависимость относительной среднеквадратической погрешности решения от величины шума. Зависимость дисперсии результата от величины погрешности показана на рисунке 2.
Лучшие результаты получились при использовании модели (21): при значительном увеличении помехи, погрешность результата не превысила 5%. Дисперсия полученных результатов также самая низкая из всех моделей. Вычисления с моделью (22) показали, что определение параметров модели сильнее зависят от уровня помех, однако, если величина шума не превышает 4%, погрешность решения также не выходит за рамки 5%. С другой стороны разброс значений полученных данных превышает аналогичный показатель у моделей (21) и (23) (рисунок 2), что говорит о большей неустойчивости решения.
Модель (21) является частным случаем (23) при β=1. Наличие дополнительного параметра в модели (23) ухудшает качество решения: относительная погрешность результата находится в районе 15-16%, однако при увеличении уровня помех, значительно не возрастает. Дисперсия полученных результатов также достаточно низкая.
Модель (24) в ходе экспериментов показала наихудший результат, что объясняется сложностью самой модели и большей нелинейностью входящих в нее параметров. Однако, при уровне помех до 5% погрешность результатов меньше чем у модели (23). Вычисления с моделью (24) имеют самую большую дисперсию, существенно превышающую дисперсию результатов с использованием моделей (21) и (22).
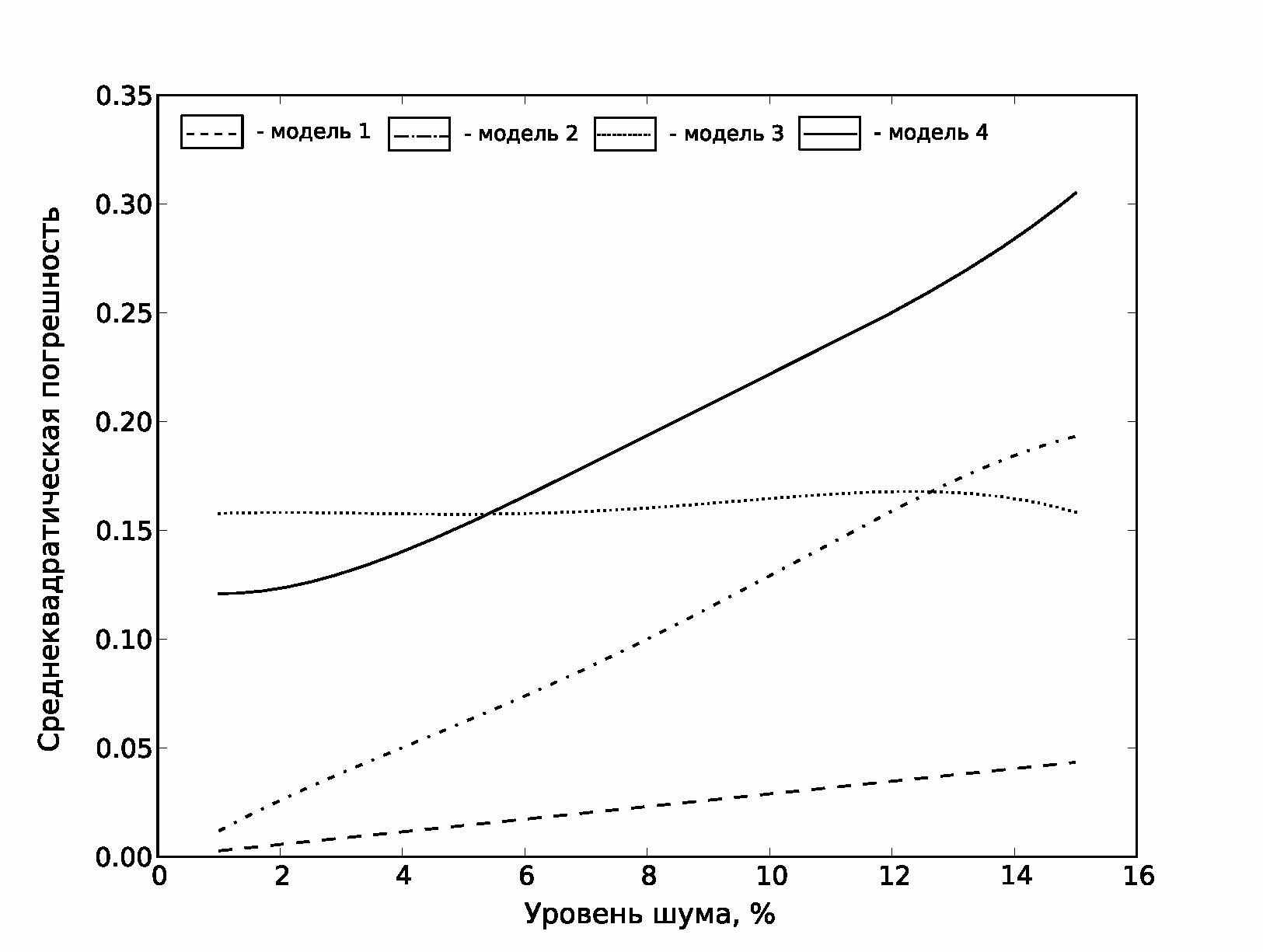
Рисунок 1. Зависимость относительной среднеквадратической погрешности решения от величины помехи.
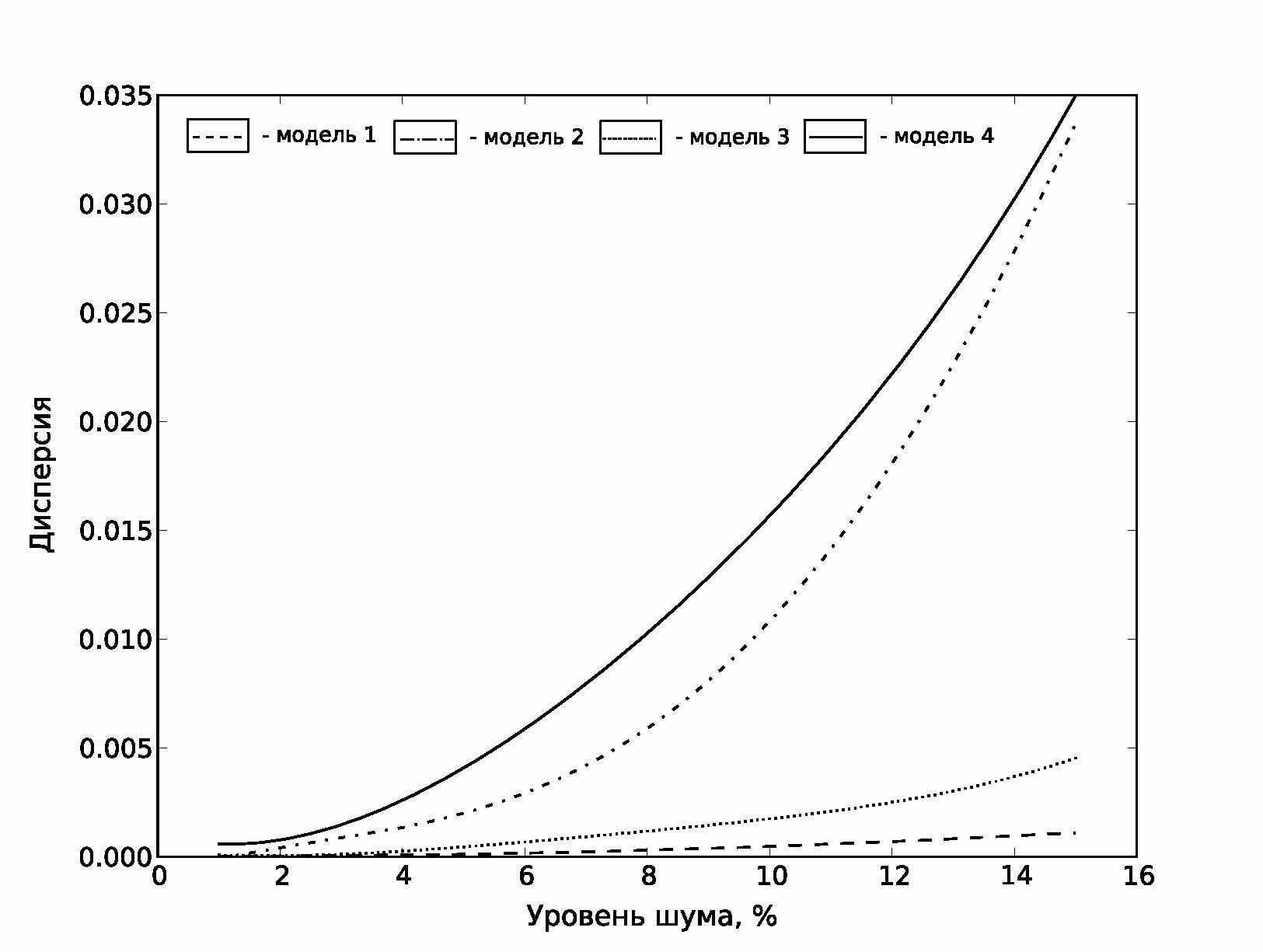
Рисунок 2. Зависимость дисперсии результата от величины помехи.
Использование аппроксимационного метода позволяет получать адекватные результаты, в случае неверного выбора модели результата при обработке экспериментальных данных. Для исследования была вычислена правая часть с использованием модели (21) и находились параметры по алгоритмам для модели (23). В результате при уровне шума до 15%, погрешность решения находилась в районе 5%, степень разброса полученных результатов оказалась самая низкая из всех проведенных опытов.
Во второй части главы проведены исследования аппроксимационных свойств ортогонального базиса (8), состоящего из ортогонализированных экспоненциальных функций, соответствующих обобщенному виду корреляционных функций реально осуществимых процессов. Показано, что при аппроксимации корреляционных и импульсных переходных функций использование данного базиса имеет ряд преимуществ по сравнению с ортогональными функциями Лагерра: уменьшается порядок модели: в большинстве случаев достаточно одного полинома со степенью 0; уменьшается погрешность аппроксимации: она зависит практически только от погрешности вычисления параметров полинома.
Аппроксимация аналитических сигналов, преобразование Фурье которых не является дробно-рациональными функциями, с использованием базиса (8) позволяет создавать более компактные модели по сравнению с функциями Лагерра, однако в данном случае преимущества не столь очевидны.
Основные результаты диссертационной работы
1. Проведен обзорный анализ методов промышленной диагностики и неразрушающего контроля. Дан обзор наиболее часто встречающихся задач промышленной диагностики, сформулированных как обратные и некорректные. Выделен классы задач, позволяющий применить детерминистский подход, класс задач со стационарными случайными процессами.
2. Проведен сравнительный анализ основных методов решения обратных некорректно поставленных задач и способов введения априорной информации. Дан обзор ортогональных базисов, наиболее часто используемых при решении задач аппроксимации.
3. Исследована задача идентификации ЛДО, относящаяся к классу задач со стационарными случайными процессами. Дано общее решение уравнения Винера-Хопфа аппроксимационным методом. Показано, что в случае, когда известно аналитическое выражение искомой функциональной зависимости, задача сводится к параметрической. Представлены типовые модели применяемые в задачах идентификации ЛДО. Предложено использовать критерий среднеквадратического приближения в качестве критерия соответствия модели оцениваемой функции с использованием ортогональных базисов.
4. Проведен сравнительный анализ основных методов оценивания параметров модели: совпадения значений модели в выбранных точках, равномерного приближения, среднеквадратического приближения, критерий моментов. Показано, что для линейных систем с аддитивным шумом наиболее подходящим является критерий среднеквадратического приближения и его модификации.
5. Исследован способ формирования ортогональных базисных систем на основе дробно-рациональных функций, соответствующих Фурье-преобразованию АКФ и ИПФ. Определены условия ортогональности полученных базисов во временной области.
6. Проведен обзорный анализ некоторых исследуемых ортогональных базисов, получаемых путем фиксации параметров полиномов, входящих в базис. Приведены варианты базисных систем со степенью полинома N=2 в частотной и временной областях. Рассмотрен частный случай, позволяющий получить ортогонализированные экспоненциальные функции , соответствующие обобщенному виду АКФ реально осуществимых процессов в задачах идентификации ЛДО.
7. Разработаны и исследованы алгоритмы оптимизации параметров модели и коэффициентов обобщенного базиса с полиномами степени N=2 в частотной и временной областях. Разработаны алгоритмы определения параметров модели и коэффициентов ортогональных функций при аппроксимации корреляционных функций.
8. Для класса задач, позволяющих применить детерминистский подход представлена библиотека элементарных математических моделей аналитических пиков, используемых в различных отраслях промышленности. Рассмотрена возможность описывать реальные аналитические сигналы. Использование таких моделей в качестве априорной информации, позволяет применять аппроксимационные подходы к решению некорректных задач промышленной диагностики.
9. Разработаны и исследованы алгоритмы оценки характеристик распределения размеров частиц в двухфазных дисперсных потоках. В качестве критерия соответствия модели оцениваемой функции выбран критерий моментов. Применение данного критерия позволило получить простые и статистически устойчивые методы для вычисления оценок нелинейных параметров моделей.
10. Проведена численная реализация решения задачи оценки характеристик распределения размеров частиц в двухфазных дисперсных потоках, подтвердившая эффективность аппроксимационного метода с использованием критерия моментов.
11. Проведен сравнительный анализ аппроксимационных свойств синтезированных базисных систем соответствующих обобщенному виду корреляционных функций реально осуществимых процессов, подтвердивший преимущества исследуемых ортогональных функций по сравнению с функциями Лагерра.
Основное содержание диссертации опубликовано в следующих работах:
1. Батищев В.И., Золин А.Г., Косарев Д.Н., Романеев А.Е. Аппроксимационный подход к решению обратных задач анализа и интерпретации экспериментальных данных. // Вестник Самарского государственного технического университета. – Серия технические науки. – 2006. – №40 – С.14-17
2. Батищев В.И., Волков И.И., Золин А.Г. Построение и оптимизация ортогональных базисных систем для аппроксимации спектрально-корреляционного анализа и идентификации линейных динамических объектов. // Вестник Самарского государственного технического университета. – Серия технические науки. – 2007. – №40 – С.47-52
3.Зубенко В.Л., Золин А.Г. Проектирование приводов станков с ЧПУ графо-блочно-матричным методом // Самарский техн. ун-т, Самара, ВИНИТИ, 1994. – №1032 – В94. – С. 34-42.
4. Батищев В.И., Золин А.Г., Кобзев Д.А., Романеев А.Е. Прогностическое моделирование влияния гидротехнических сооружений на окружающую среду. // Окружающая среда для нас и будущих поколений: Сборник тезисов IX Международной конференции. – Самара: СамГТУ, 2004. – С. 24-25.
5. Золин А.Г. Отображение математических формул в задачах моделирования процессов и систем. // Информационные, измерительные и управляющие системы: Материалы Международной научно-технической конференции. – Самара: СамГТУ, 2005. – С. 92-93.
6. Золин А.Г. Анализ применения критерия моментов при решении обратных некорректно поставленных задач. // Компьютерные технологии в науке, практике и образовании: Труды всероссийской межвузовской научно-практической конференции. – Самара: СамГТУ, 2006. – С. 14-17.
7. Золин А.Г. Влияние ядра интегрального уравнения на некорректность обратной задачи // Математическое моделирование и краевые задачи: Труды Всероссийской научной конференции. – Самара: СамГТУ, 2007г. – С. 48-50.
8. Золин А.Г., Михайлова Н.П. Решение обратных задач при моделировании систем безопасности. // Актуальные проблемы информационной безопасности при противодействии криминалу и терроризму. Теория и практика использования аппаратно-программных средств: Материалы Всероссийской научно-технической конференции. – Самара: СамГТУ, 2007. – С 78-84.
9. Золин А.Г. Решение некорректных задач аппроксимационным методом с использованием полиномов Лагерра // Нефтегазовые и химические технологии: Всероссийская научно-практическая конференция. – Самара: СамГТУ, 2007. – С. 38-41.
10. Золин А.Г. Исследование базисных систем на основе дробно-рациональных функций // Математическое моделирование и краевые задачи: Труды Всероссийской научной конференции. – г.Самара: СамГТУ, 2008г. – С. 55-58.
11. Золин А.Г. Использование критерия моментов при решении задачи распределения диаметров капель в газо-жидкостных потоках // Перспективы развития информационных технологий: Сборник материалов I Всероссийской научно-практической конференции. – Новосибирск: ЦРНС, 2008г. – С. 24-30.
12. Золин А.Г. Эхо-импульсный метод как обратная задача акустической диагностики // Математическое моделирование и краевые задачи: Труды Всероссийской научной конференции. – Самара: СамГТУ, 2009г. – С. 44-47.
13. Золин А.Г. Решение обратных задач с использованием критерия моментов. // Инновации и актуальные проблемы техники и технологий: Труды всероссийской научно-практической конференции молодых ученых. – г. Саратов: Сар.Гос.Тех.Университет, 2009. – С. 32-35.
14. Золин А.Г. Определение параметров дефектов в акустической диагностике. // Компьютерные технологии в науке, практике и образовании: Труды всероссийской межвузовской научно-практической конференции. – Самара: СамГТУ, 2009. – C. 36-39.
Подписано в печать 22.04.2010 г.
Бумага ксероксная. Печать оперативная.
Объём 1,12 усл. печ. лис. Формат 60х84/16
Тираж 100 экз. Заказ № 430
Отпечатано в типографии
Самарского государственного технического университета
443100, Самара, ул. Молодогвардейская, 244, корпус 8
