Программа дисциплины «Математические основы моделирования социально- политических процессов» для специальности 030201. 65 «Политология» подготовки специалиста Автор д ф. м н., профессор Самовол В. С

Вид материала

Программа дисциплины

Содержание МоскваТребования к студентам Тематический план учебной дисциплины. Дополнительные главы линейной алгебры Элеметы теории обыкновенных дифференциальных уравнений Методы социально-политического моделирования Модель войны (модель ланкастера) как пример простейшей модели социально-политического типа Использование логистических моделей в социальном моделировании Модель коллективного поведения Всего часов Содержание программы РАЗДЕЛ 1. Дополнительные главы линейной алгебры РАЗДЕЛ 2. Элементы теории обыкновенных дифференциальных уравнений Тема 3.1. Модель войны (модель Ланкастера) как пример простейшей модели социально-политического типа Тема 3.2. Использование логистических моделей в социальном моделировании Тема 3.3. Модель коллективного поведения Тематика контрольных работ Вопросы для оценки качества усвоения курса

Подобный материал:

• Программа дисциплины Социально-пcихологические основы, 147.32kb.
• Программа дисциплины Прикладной политический анализ для направления 030201. 65 «Политология», 573.34kb.
• Программа дисциплины «Английский язык для профессиональной коммуникации» для направления, 132.48kb.
• Программа дисциплины Политология для специальности 080102. 65 «Мировая экономика» подготовки, 320.74kb.
• Программа дисциплины исследование социально-экономических и политических процессов, 215.8kb.
• Программа дисциплины «Исследование социально-экономических и политических процессов», 221.09kb.
• Программа дисциплины «Гендерная политика и институциональное строительство» Для направления, 376.34kb.
• Программа дисциплины исторические основы современных политических конфликтов для направления, 312.29kb.
• Рабочая программа дисциплины «Муниципальная политика и управление» для студентов специальности, 162.15kb.
• Рабочая программа дисциплины «Политическая история России» для студентов специальности, 537.47kb.

Министерство экономического развития и торговли Российской Федерации


Государственный университет-Высшая школа экономики

Факультет Прикладной политологии


Программа дисциплины


«Математические основы моделирования

социально- политических процессов»

для специальности 030201.65 «Политология»

подготовки специалиста

Автор д.ф.м.н., профессор Самовол В.С.

Рекомендовано секцией УМС Одобрено на заседании кафедры

«математические и статистические Высшей математики

методы в экономике» Зав. кафедрой А.А. Макаров

Председатель А.С. Шведов ____________________________

_______________________ " " 2007 г

" " 2007 г.


Утверждена УС факультета

_________________________________

Ученый секретарь

_________________________________

« ____» ___________________200 г.


Москва


Требования к студентам: Учебная дисциплина «Математические основы моделирования социально-политических процессов» (4 курс факультета «Прикладная политология») предполагает предварительную подготовку студентов в объеме базового математического образования, включая такие разделы высшей математики, как основы линейной алгебры и математического анализа, а также теории вероятностей и математической статистики. Необходимый объем знаний студенты факультета прикладной политологии приобретают в процессе обучения на первом и втором курсах, что предусмотрено учебными планами факультета.

Аннотация: Курс «Математические основы моделирования социально-политических процессов» содержит избранные разделы математических знаний и элементы математических методов, необходимые современному специалисту-политологу для осмысления и формализации социально-политических явлений и процессов, выявления характеризующих их тенденций и анализа определяющих их взаимосвязей. Современный специалист должен обладать навыками математической формулировки сложнейших социально-политических задач современности, формирования баз статистических данных, необходимых для анализа изучаемых процессов и явлений, уметь применять необходимый математический инструментарий при выборе и обосновании решений, анализе их эффективности, а также возможных последствий принимаемых решений. Данный курс ставит целью обеспечение соответствующей специальной математической подготовки студентов факультета прикладной политологии. В результате курса студенты должны овладеть некоторыми дополнительными (по сравнению с полученным ранее базовым математическим образованием) методами линейной алгебры, а также основами анализа и решения дифференциальных уравнений, уметь их использовать при постановке прикладных задач, содержательно интерпретировать получаемые количественные результаты анализа.

Учебная задача курса: Материал курса ориентирован на приобретение и закрепление у слушателей навыков математической формализации задач современной политологии, моделирования сложных современных социально-политических процессов и явлений, использования математических методов в рамках современной теории принятия решений в социально-политической сфере. К особенностям курса можно отнести обучение специальным математическим методам на материале, включающем анализ количественных и качественных характеристик социально-политических процессов. В результате изучения курса студент должен уметь пользоваться основными математическими методами в прикладных областях политологии, знать основные направления приложений этих методов в современных областях социальных наук, иметь представление об основных достижениях в сфере приложения математики в социально-политическом моделировании.


Тематический план учебной дисциплины.

№	Название темы	Всего часов	Аудиторные часы		Самостоятельная работа
			Лекции	Семинары
1	ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ ЛИНЕЙНОЙ АЛГЕБРЫ	10	4		6
2	ЭЛЕМЕТЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ	10	4		6
3	МЕТОДЫ СОЦИАЛЬНО-ПОЛИТИЧЕСКОГО МОДЕЛИРОВАНИЯ	34	13		21
3.1	МОДЕЛЬ ВОЙНЫ (МОДЕЛЬ ЛАНКАСТЕРА) КАК ПРИМЕР ПРОСТЕЙШЕЙ МОДЕЛИ СОЦИАЛЬНО-ПОЛИТИЧЕСКОГО ТИПА	20	8		12
3.2	ИСПОЛЬЗОВАНИЕ ЛОГИСТИЧЕСКИХ МОДЕЛЕЙ В СОЦИАЛЬНОМ МОДЕЛИРОВАНИИ	9	3		6
3.3	МОДЕЛЬ КОЛЛЕКТИВНОГО ПОВЕДЕНИЯ	5	2		3
	Всего часов	54	21		33

Формы контроля. Формирование итоговой оценки.


Предусмотрена одна контрольная работа. Контрольная работа проводится в конце модуля, ее продолжительность не превышает 80 минут. Итоговая экзаменационная оценка в конце третьего модуля получается по следующей формуле: Z=0,5*K +0,5* I, где Z – итоговая оценка, K– оценка за контрольную работу, I–оценка за итоговую контрольную работу по курсу, проводимую в конце модуля (не превышает 80 минут).

По всем формам отчетности оценки ставятся по 10-бальной шкале. Перевод в 5-бальную шкалу осуществляется согласно следующему правилу


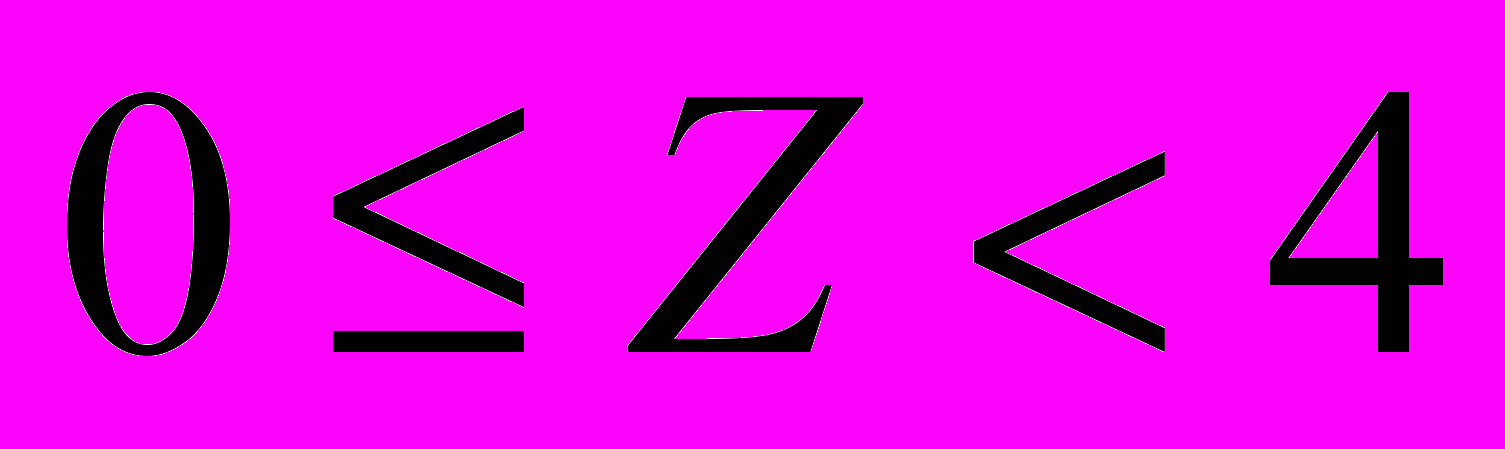неудовлетворительно

удовлетворительно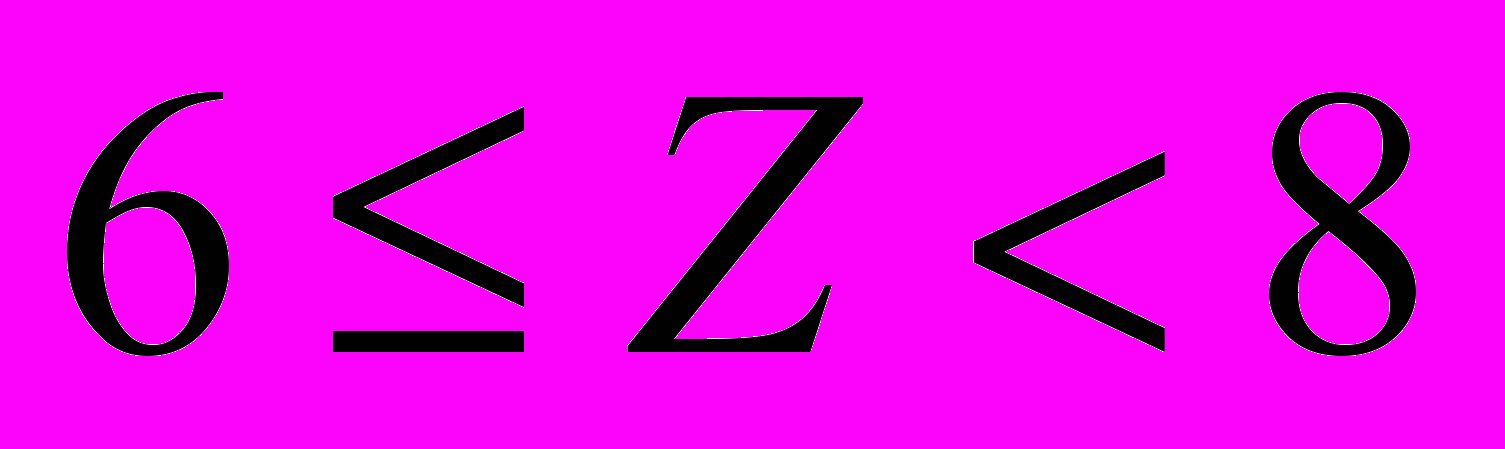

хорошо

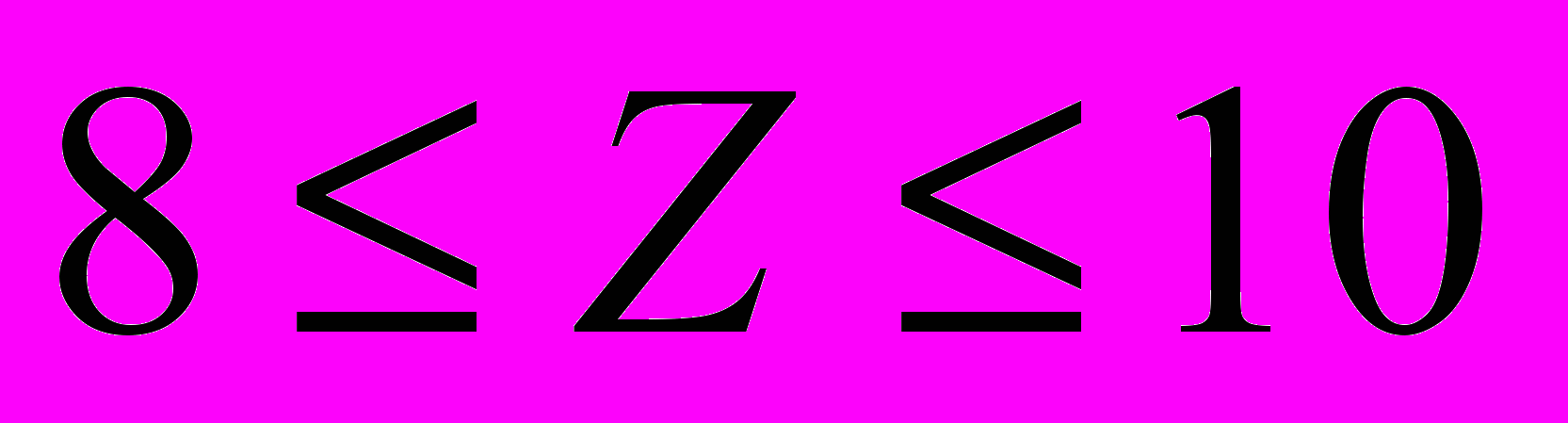отлично.

Базовые учебники:

1. Красс М. С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. М.: Дело, 2000.
   
2. Бурмистрова Е.Б., Лобанов С.Г. Линейная алгебра с элементами аналитической геометрии. – М. : Изд-во ГУ ВШЭ, 1998.
   

Основная литература

1. Мангейм Дж.Б., Рич Р.К. Политология. Методы исследования. М.: Весь Мир. 1999.
   

2. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – Ижевск.: Изд-
   

во НИЦ «Регулярная и хаотическая динамика», 2000.


Дополнительная литература


1. Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Наука, 1971.

2. Арнольд В.И. Теория катастроф. М.: Наука, 1990.
   
3. Арнольд В.И. «Жесткие» и «мягкие» математические модели. – М. МЦНМО, 2000.
   
4. Иванилов В.Ю., Огарышев В.Ф., Павловский Ю.Н. Имитация конфликтов. М.: Изд-во ВЦ РАН, 1993.
   
5. Капица С.П. Общая теория роста человечества. М.: Наука, 1999.
   
6. Краснощеков П.С., Петров А.А. Принципы построения моделей. Глава 12. М.: Фазис. 2000.
   
7. Павловский Ю.Н. Механизм ядерного сдерживания – математический и гуманитарный анализ. Вестник РАН, т. 70, № 3, 2000.
   
8. Постон Т., Стюарт И. Теория катастроф и ее приложения. М.: Мир, 1980.
   
9. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. М.: ИНФРА-М, 1998.
   
10. Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями. М. :Мир, 1986.
    

Содержание программы

РАЗДЕЛ 1. Дополнительные главы линейной алгебры

Совместность системы однородных уравнений. Линейное пространство решений системы однородных уравнений. Условие существования ненулевого решения системы.

Понятия собственного вектора и собственного числа матрицы. Способы их вычислений. Геометрическая интерпретация. Число собственных векторов, соответствующих одному собственному числу. Кратные собственные числа. Корневые векторы матрицы, отвечающие кратным собственным числам, их смысл и методы вычислений.

РАЗДЕЛ 2. Элементы теории обыкновенных дифференциальных уравнений

Понятие обыкновенного дифференциального уравнения. Порядок уравнения. Уравнения первого порядка, разрешенные относительно производной. Уравнения первого порядка с разделяющимися переменными и методы их решения. Линейные уравнения первого порядка.

Линейные уравнения первого порядка с постоянными коэффициентами. Системы линейных уравнений первого порядка с постоянными коэффициентами. Методы интегрирования систем линейных уравнений первого порядка с постоянными коэффициентами. Линейные уравнения с постоянными коэффициентами высших порядков. Методы сведения таких уравнений к системам линейных уравнений первого порядка.


РАЗДЕЛ 3. Методы социально-политического моделирования

Тема 3.1. Модель войны (модель Ланкастера) как пример простейшей модели социально-политического типа

Постановка задачи в модели Ланкастера. Математическая формализация с помощью системы двух линейных дифференциальных с постоянными коэффициентами. Решения системы. Содержательная интерпретация решений. Разбор конкретных моделей войны применительно к известным историческим ситуациям. Усложнение модели и анализ ее структурной устойчивости. Модель Ланкастера как пример «мягкого» математического моделирования.


Тема 3.2. Использование логистических моделей в социальном моделировании

Модель Мальтуса. Переход от «жесткой» модели Мальтуса к реалистичной «мягкой» модели логистического типа, построенной на основе дифференциального уравнения. Математический анализ решений полученного дифференциального уравнения. Содержательная интерпретация полученных математических результатов. Некоторые аспекты проблемы оптимизации в моделях социального типа.

Тема 3.3. Модель коллективного поведения

Простейшая модель коллективного поведения Краснощекова. Математическая формализация модели. Исследование аналитических результатов модели коллективного поведения в случае наличия единственного лидера в зависимом коллективе. Анализ поведения зависимого коллектива с двумя и тремя лидерами. Исследование поведения больших коллективов, члены которых не являются абсолютно зависимыми.

ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ

1. Построение и расчет модели войны или сражения.
   
2. Параметрический анализ эволюционной модели динамики численности населения.
   
3. Анализ устойчивости эволюционных моделей с обратной связью.
   
4. Количественный анализ моделей поведения коллектива с одним и несколькими лидерами.
   

ВОПРОСЫ ДЛЯ ОЦЕНКИ КАЧЕСТВА УСВОЕНИЯ КУРСА

1. Собственные числа и собственные векторы матриц.
   
2. Корневые векторы.
   
3. Приведение матрицы к жордановой нормальной форме
   
4. Основные виды обыкновенных дифференциальных уравнений
   
5. Системы линейных обыкновенных дифференциальных уравнений первого порядка (ОДУ) с постоянными коэффициентами и их свойства
   
6. Методы решений систем ОДУ
   
7. Модель Ланкастера и ее математическая формализация с помощью системы ОДУ.
   
8. Содержательная интерпретация решений модели Ланкастера
   
9. Модель Мальтуса
   
10. Анализ решений дифференциального уравнения в модели Мальтуса
    
11. Содержательная интерпретация модели Мальтуса
    
12. Модель коллективного поведения Краснощекова
    
13. Исследование аналитических результатов модели коллективного поведения
    

Автор программы В.С. Самовол