Правила взвешивания: Определяют нулевую точку весов n 0

Вид материала

Лабораторная работа

Содержание Правила взвешивания Определение линейных размеров тела Порядок обработки результатов прямых измерений

Подобный материал:

• Правила определяют общие требования к организации учета электрической энергии и взаимосвязь, 88.38kb.
• Правила проведения торгов в форме открытого конкурса общие положения, 847.22kb.
• Необходимостью создания наиболее совершенных орудий производства и приёмов их производства,, 1170.34kb.
• Правила проведения валютных операций, 248.58kb.
• Постановление министерства транспорта и коммуникаций республики беларусь, 130.52kb.
• Домашнее задание Подведение итогов урока Оценивание своей работы и работы одноклассников, 45.45kb.
• Правила пожарной безопасности при эксплуатации предприятий нефтепродуктообеспечения, 1174.83kb.
• Правила оказания услуг по реализации туристского продукта I. Общие положения Настоящие, 164.72kb.
• Инкотермс это международные правила толкования торговых терминов, которые определяют, 784.15kb.
• Задачи : развивать языковую интуицию учащихся; уметь аргументировано излагать свою, 92.24kb.

Лабораторная работа 1.1

ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ТВЁРДОГО ТЕЛА МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИЗМЕРЕНИЯ ЛИНЕЙНЫХ РАЗМЕРОВ И ВЗВЕШИВАНИЯ

Цель работы – освоение метода расчёта погрешностей прямых и косвенных измерений по Стьюденту на примере расчёта плотности твёрдого тела правильной геометрической формы.


Плотностью тела называется физическая величина, равная отношению массы тела (m) к его объему (V)



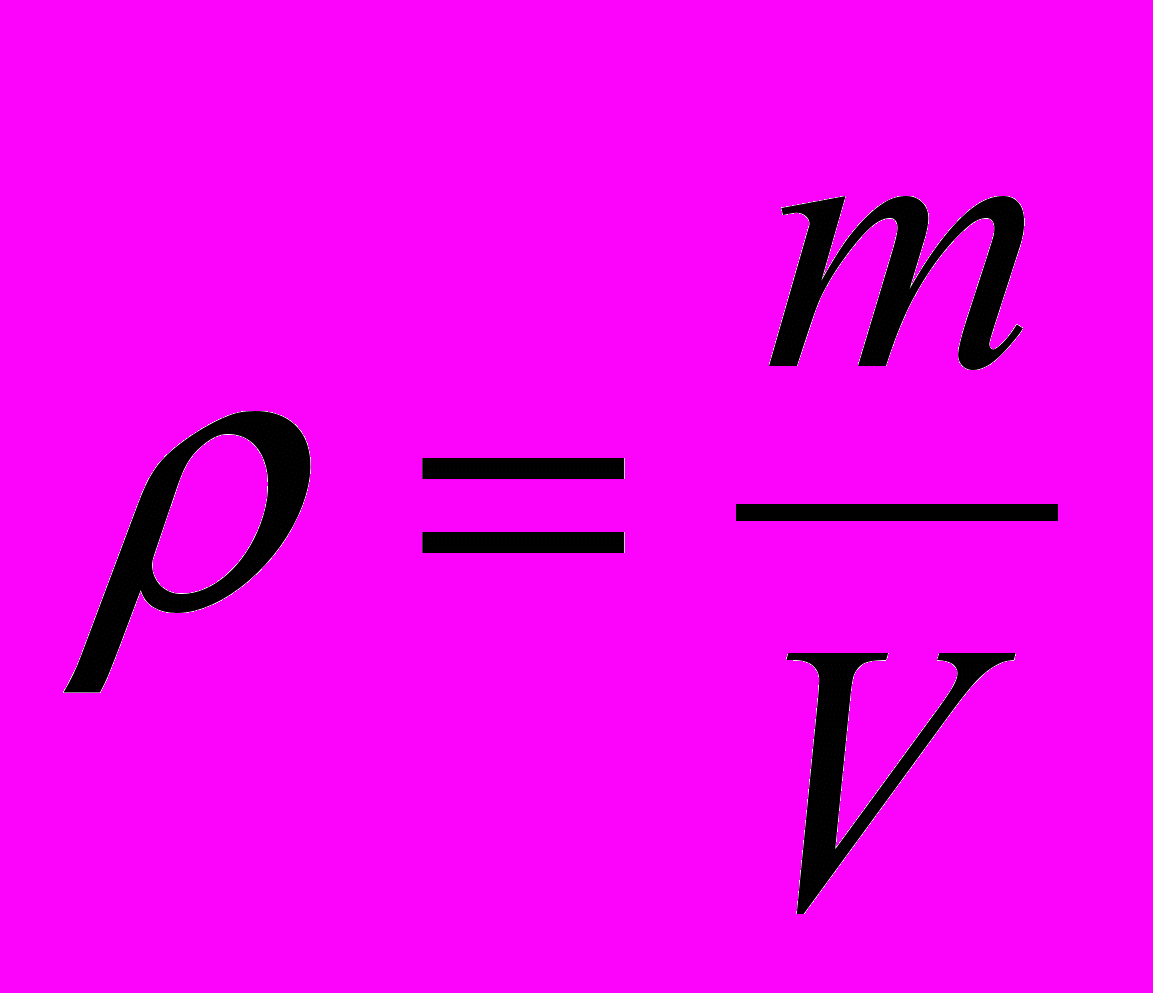
Массу тела измеряют с помощью рычажных лабораторных весов.

Правила взвешивания:

1. Определяют нулевую точку весов n₀ – положение стрелки ненагруженных весов.
   
2. Определяют цену деления весов. Кладут тело на левую чашку весов и уравновешивают его гирями. Определяют нулевую точку 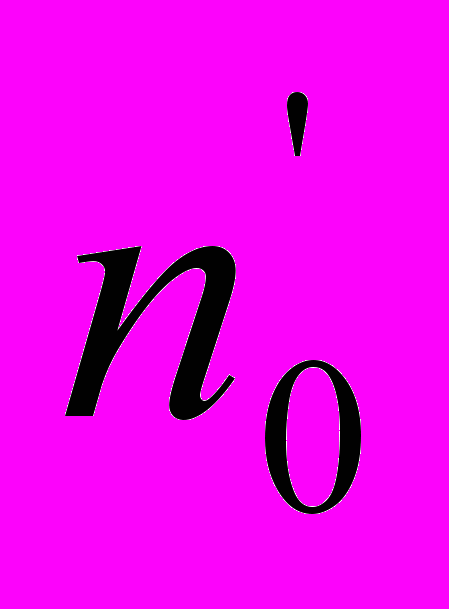нагруженных весов. Добавляют малый перегрузок P (порядка 20 мг) и вновь определяют нулевую точку .
   

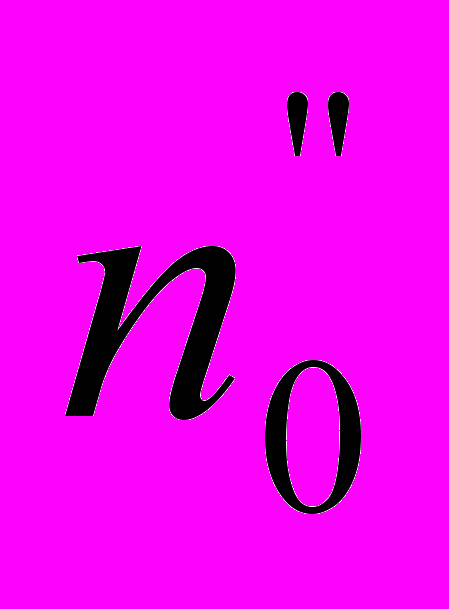Цена деления весов

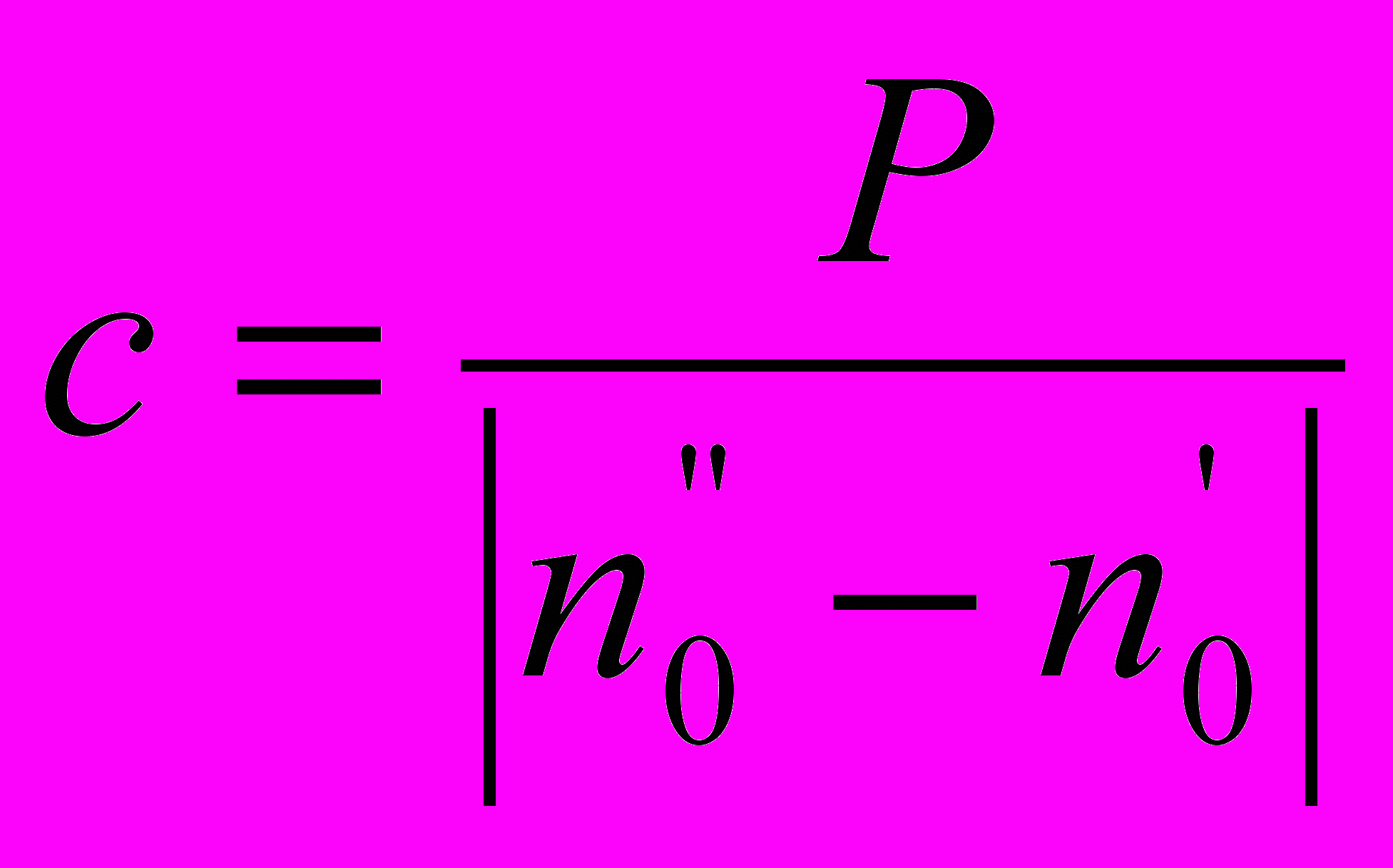
3. Положить тело на левую чашку весов и уравновесить его гирями. Если нулевая точка нагруженных весов 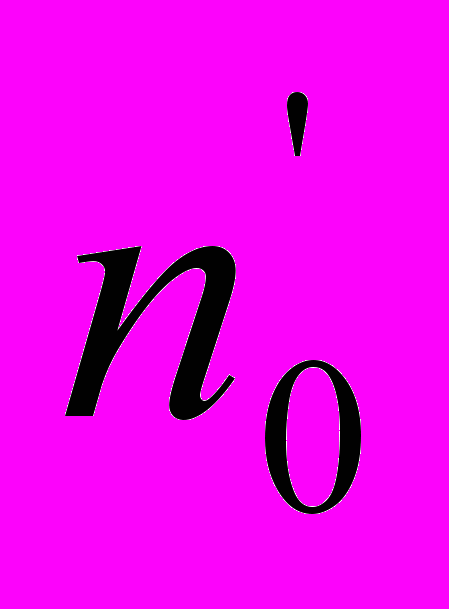совпадает с нулевой точкой ненагруженных весов, то масса тела m равна массе гирь М₁. Рассмотрим более общий случай: 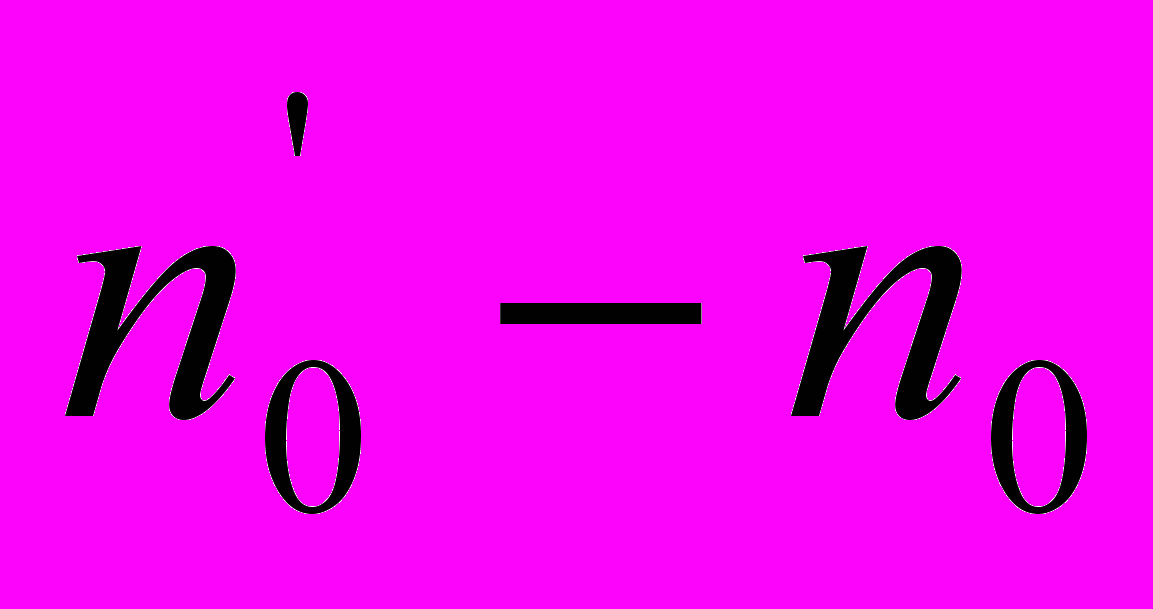. Это означает, что масса гирь не равна массе тела.
   

Очевидно, в этом случае

,

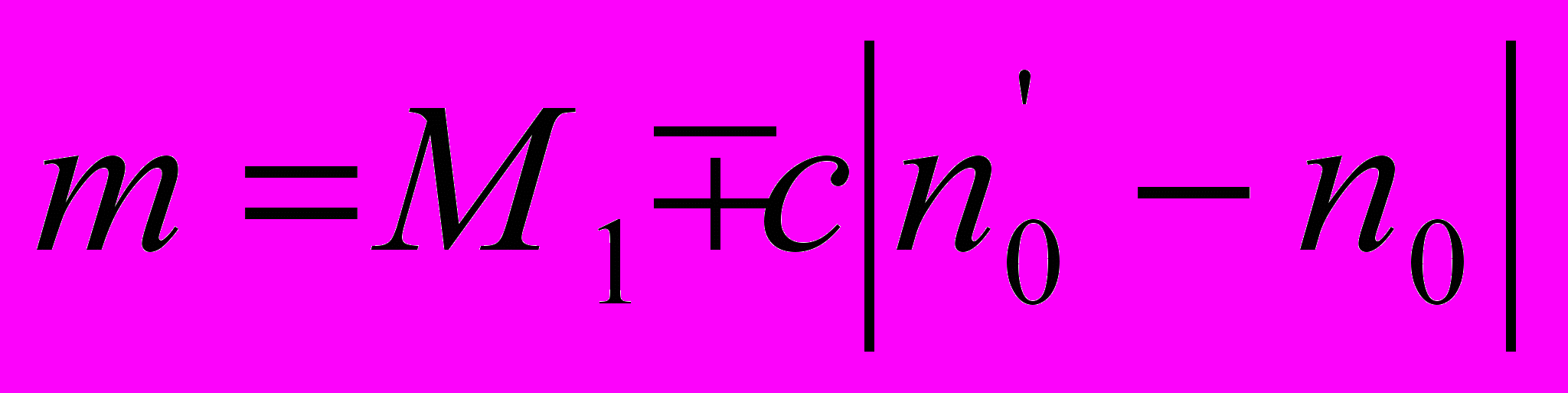где с — цена деления весов.

Знаки выбирают следующим образом: если перевешивает тело, берут знак «+», если перевешивают гири – знак «-».

Объем тел правильной геометрической формы можно рассчитать по линейным размерам тела, измеренным штангенциркулем.

Штангенциркуль

Штангенциркуль предназначен для измерения наружных и внутренних линейных размеров тел, внешних и внутренних диаметров цилиндров с величинами отсчёта 0,1; 0,05 или 0,02мм. Его внешний вид показан на рисунке 1.

Он состоит из штанги и подвижной части (ползунка). Штанга и подвижная часть изготавливаются из высококачественной инструментальной стали и имеют специальные выступы («губки») для фиксации их у начала и конца измеряемого тела. На штанге нанесена миллиметровая шкала, штрихи которой имеют строго одинаковую толщину и составляют 0,05 мм. На подвижной части штангенциркуля нанесена вспомогательная шкала (нониус), позволяющая определять размер с соответствующей точностью. Вспомогательная шкала имеет десять делений, каждое из которых на 0,1 мм меньше 2 мм. Если толщина предмета равна нулю, то начала основной и вспомогательной шкал, а также 10-е деление вспомогательной и 19-е деление основной шкалы совпадают.

Сдвиг подвижной части на 0,1 мм обеспечивает совпадение первого деления вспомогательной шкалы со вторым делением основной, сдвиг на 0,2 мм – совпадение второго деления вспомогательной шкалы с четвёртым делением основной и т. д. Таким образом, измеряемая величина равна целому числу миллиметров основной шкалы, расположенных слева от нулевого деления вспомогательной шкалы, плюс число десятых, равное номеру совпадающего деления вспомогательной шкалы с делением основной шкалы.





Рис. 1. Штангенциркуль


Погрешность при измерении штангенциркулем принимают равной половине цены деления по нониусу. Например, при цене деления по нониусу 0,1мм погрешность составляет 0,05 мм.

На рисунке 2 приведены примеры расположения шкал на штангенциркуле при различных значениях измеряемых величин. Стрелками указаны совпадающие штрихи основной и вспомогательной шкал.






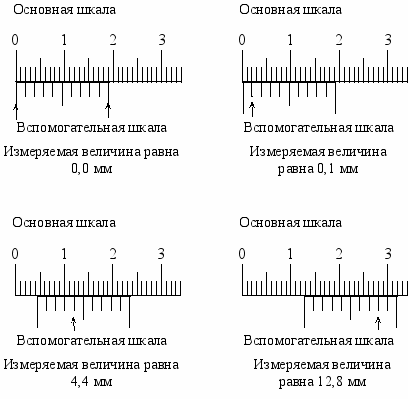
Рис. 2. Примеры измерения штангенциркулем

Определение линейных размеров тела

В соответствии с формой тела записать формулу для вычисления объема, установить, какие линейные размеры необходимо непосредственно измерить и составить таблицы измеряемых величин. В качестве примера приведена таблица для линейных размеров цилиндра.


Таблица 1

№ опыта	di (см)	Δdi	(Δdi)2	№ опыта	hi (см)	Δhi	(Δhi)2
1				1
2				2
3				3
4				4
5				5

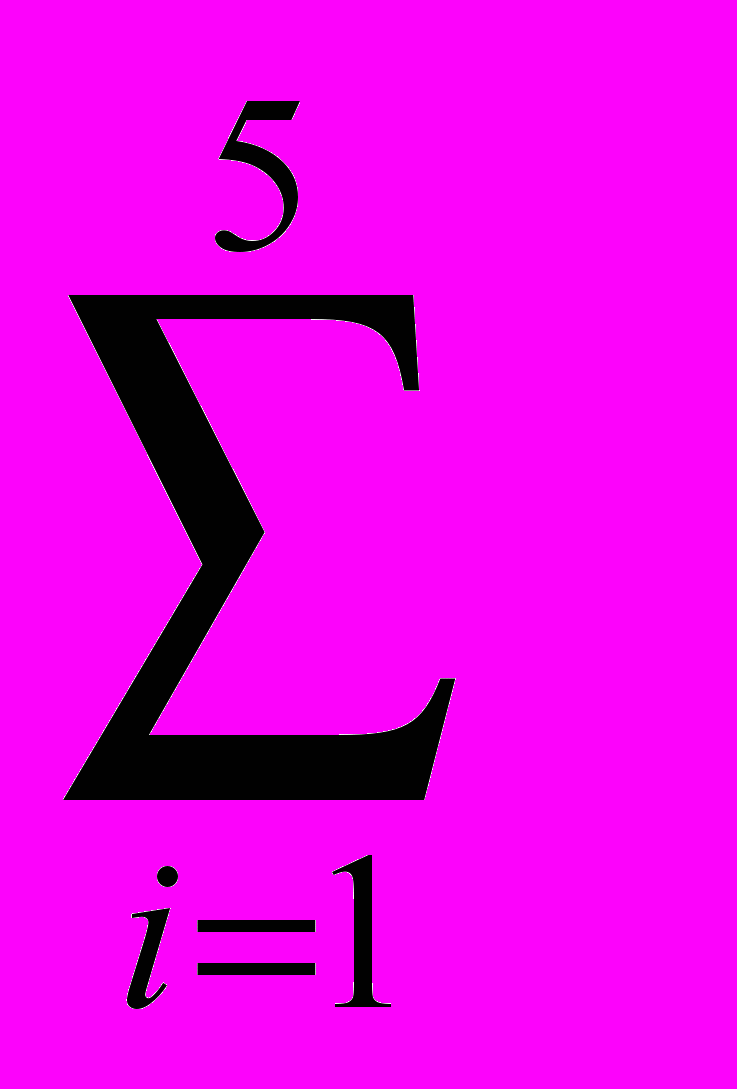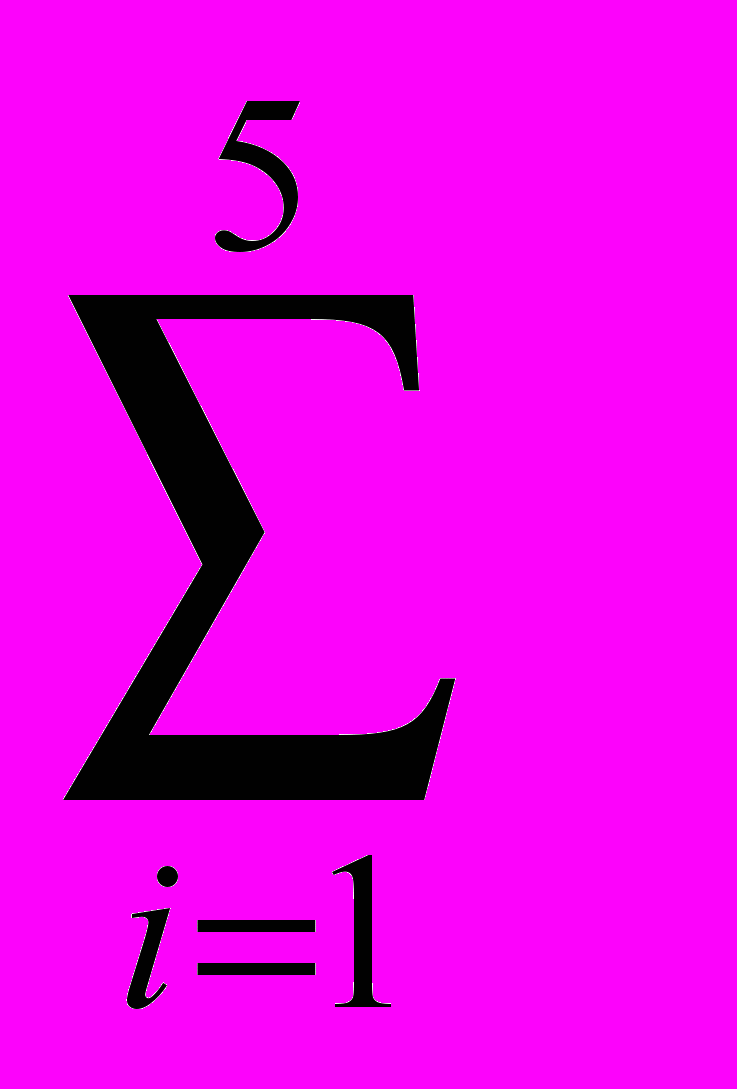Измерение каждой величины провести не менее пяти раз и результаты измерений занести в таблицу.

Порядок обработки результатов прямых измерений

1. Рассчитать среднее арифметическое значение измеренной величины
   

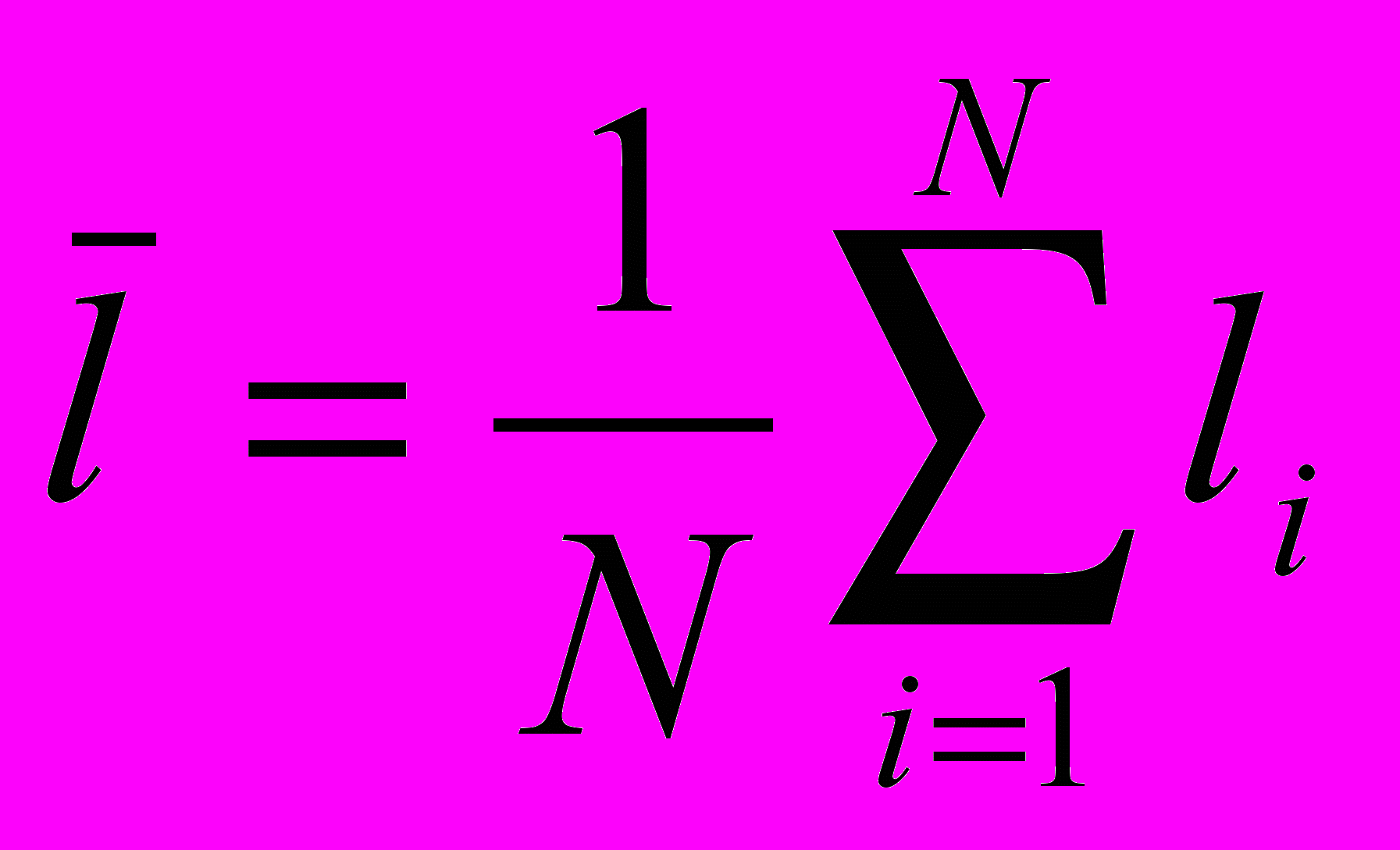
2. Определить погрешность отдельных измерений Δl_i=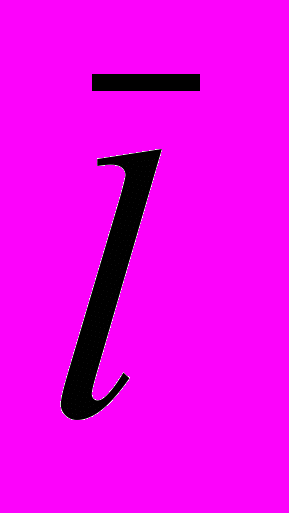-l_i и записать в таблицу.
   
3. Вычислить квадраты погрешностей отдельных измерений (Δl_i)² и записать в таблицу.
   
4. Определить среднюю квадратичную погрешность среднего арифметического значения измеренной величины
   

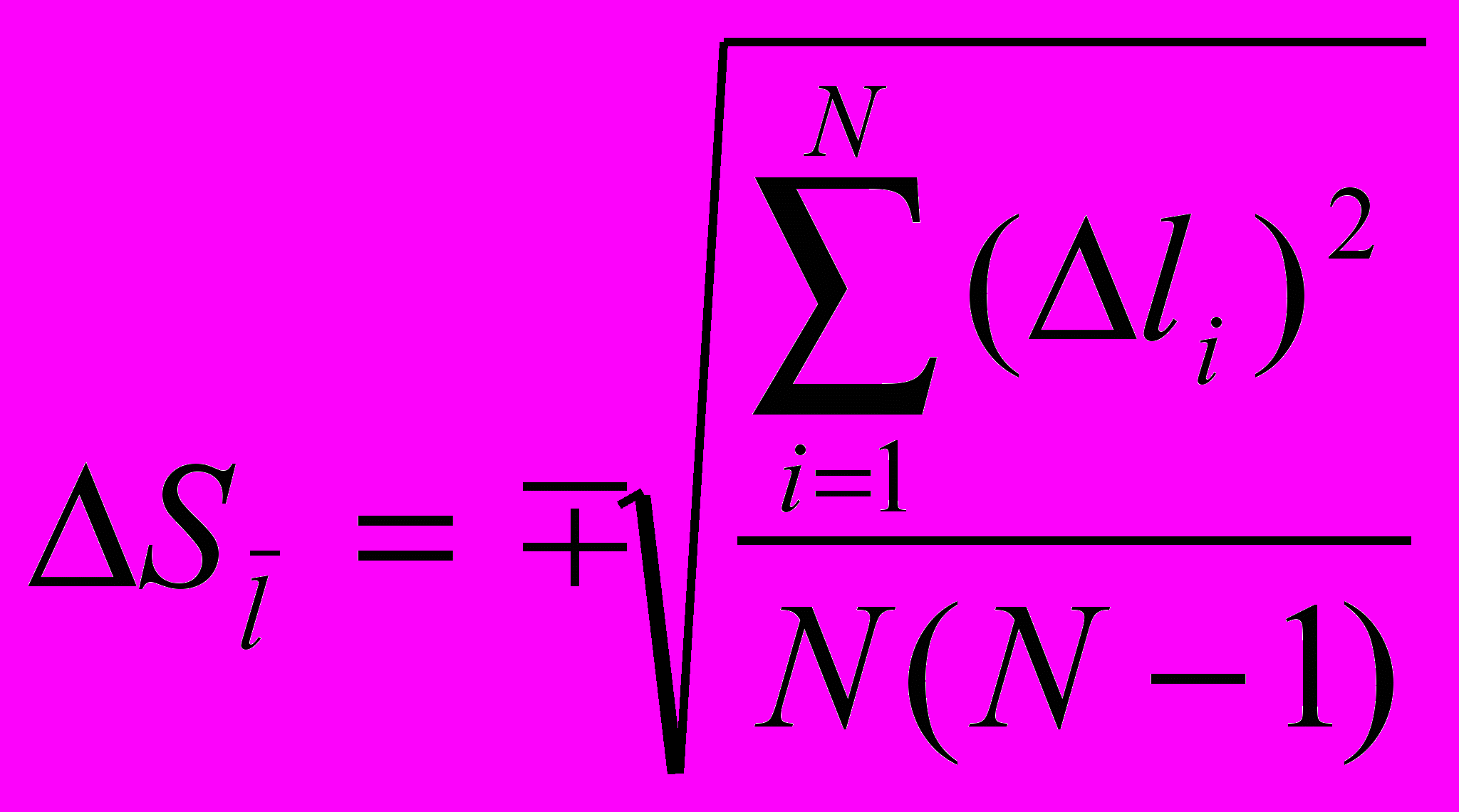
5. По заданной преподавателем доверительной вероятности (надежности) α и числу проведенных измерений N определить коэффициент Стьюдента t(α, N). В инженерной практике принято проводить измерения с надежностью α = 0,9. Поэтому, если преподавателем специально не оговаривается значение доверительной вероятности, примите ее равной 0,9.
   
6. Определить величину экспериментальной погрешности
   

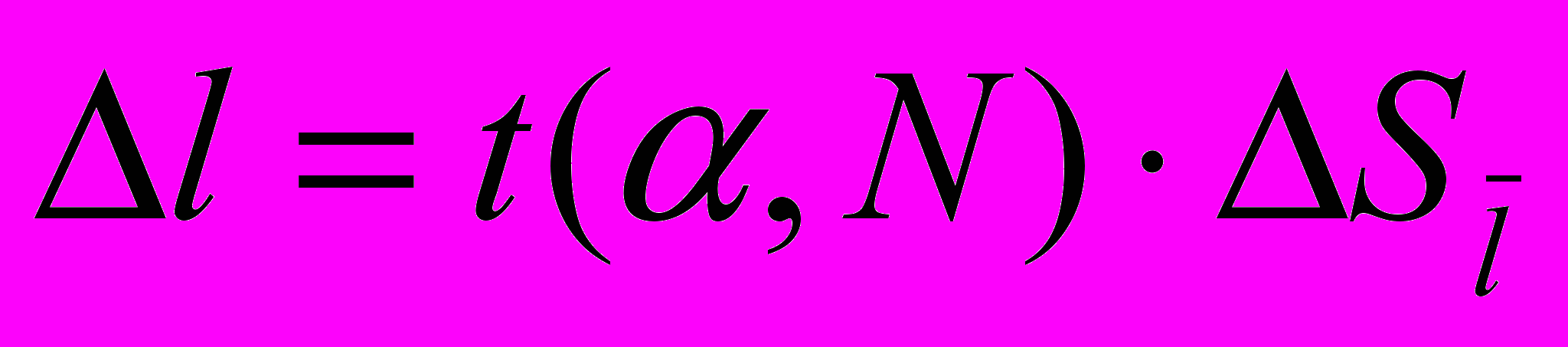
и записать результат прямых измерений в виде



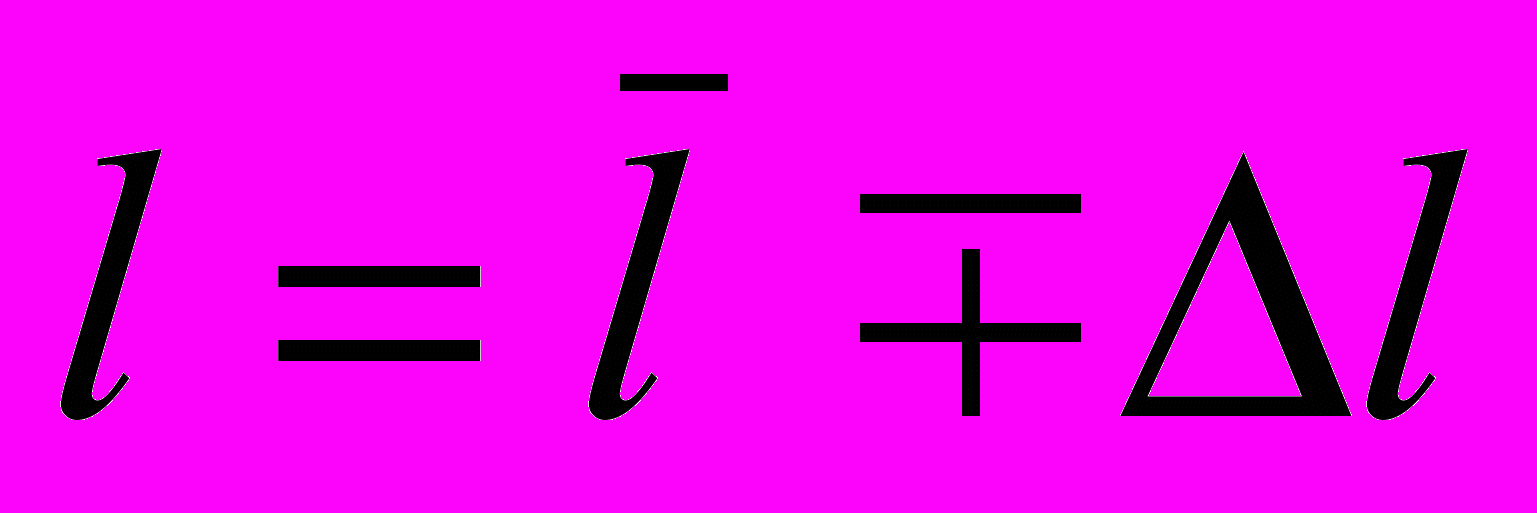
с обязательным указанием размерности. При записи результата значение погрешности округлить до первой значащей цифры. После этого округлить значение результата до цифры того же арифметического разряда, что и в погрешности.

7. Определить точность измерения, характеризуемую относительной погрешностью
   

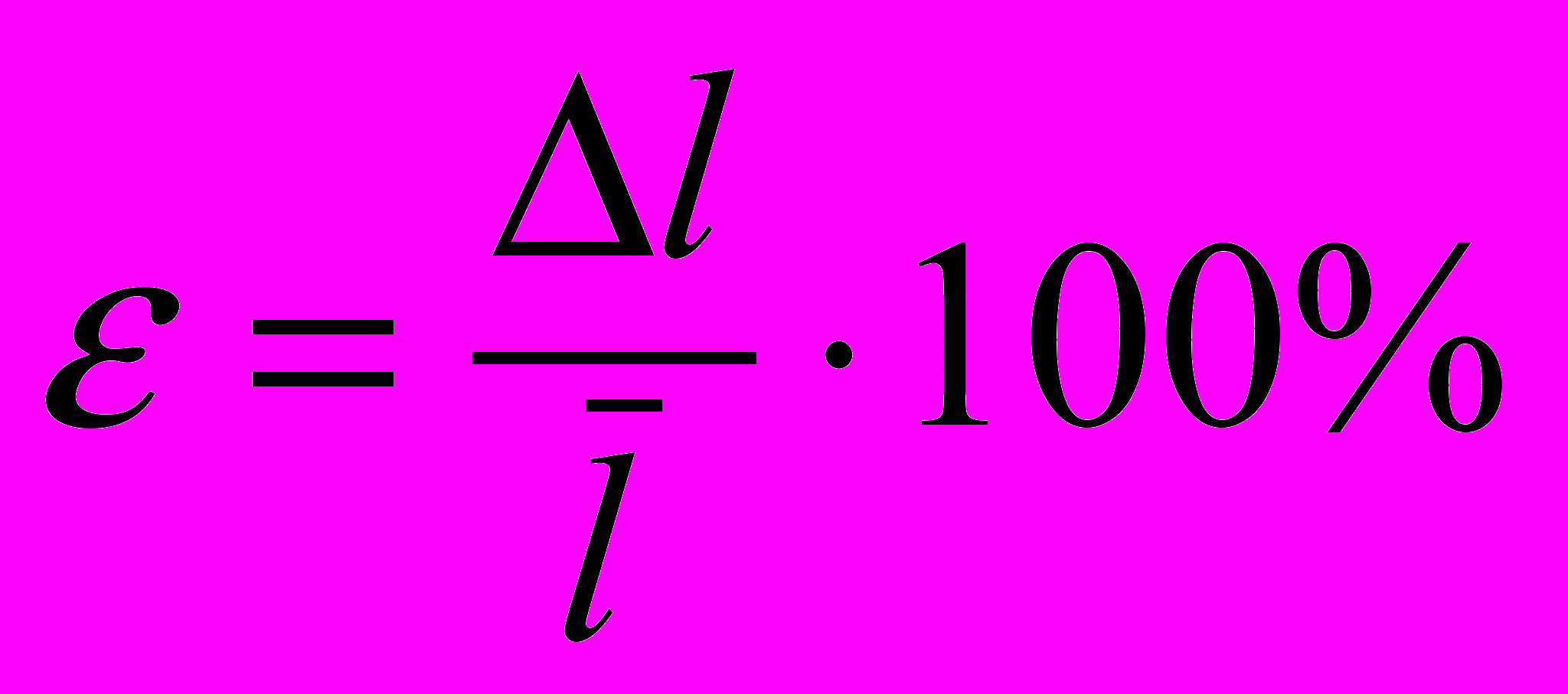
По расчетной формуле найти среднее значение плотности тела. Величину объема тела рассчитать по средним значениям измеренных линейных размеров. В соответствие с теорией обработки результатов экспериментальных измерений относительная погрешность при косвенных измерениях определяется через относительные погрешности прямых измерений по формуле



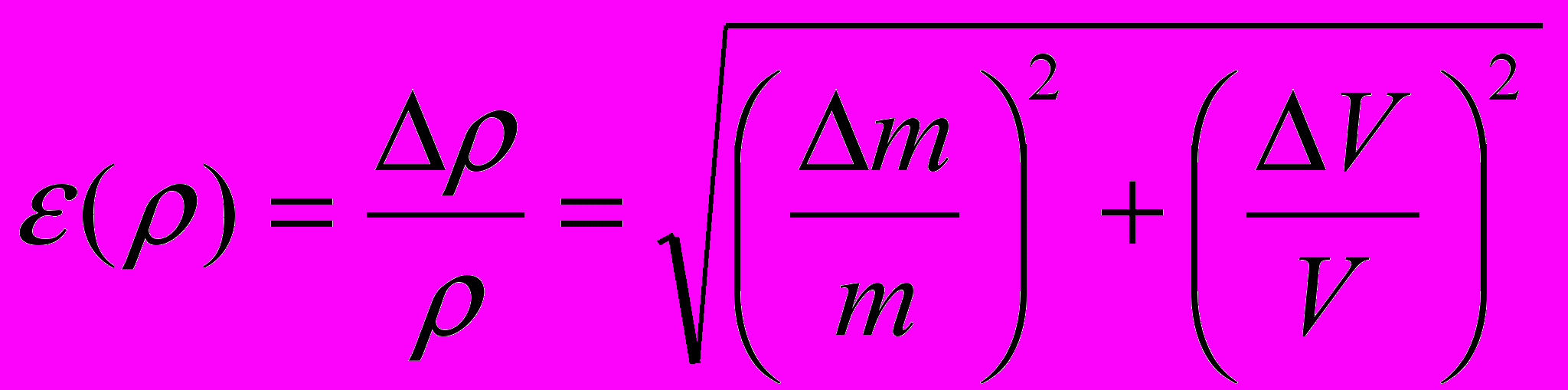
В частности, для цилиндра, у которого ,



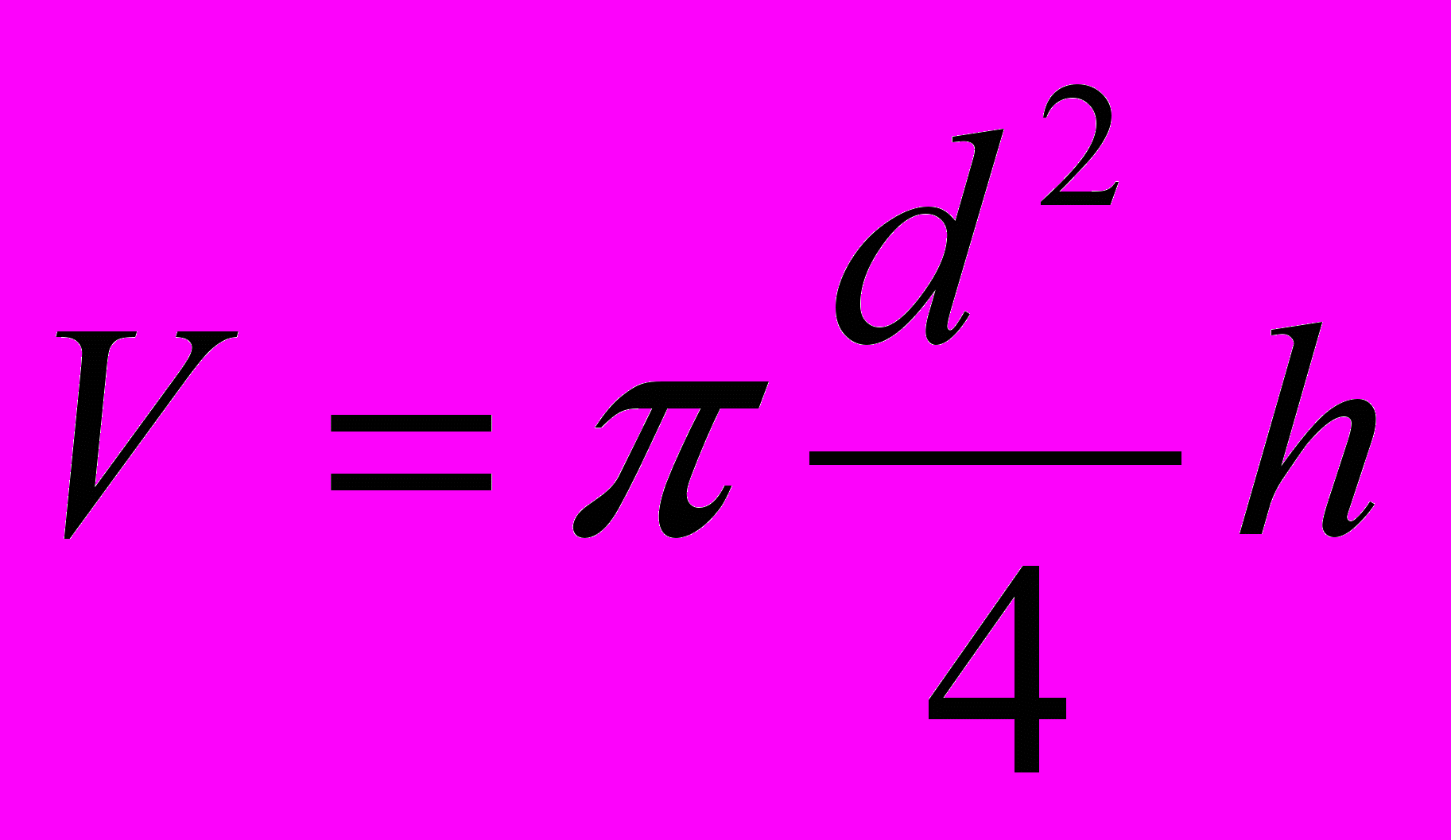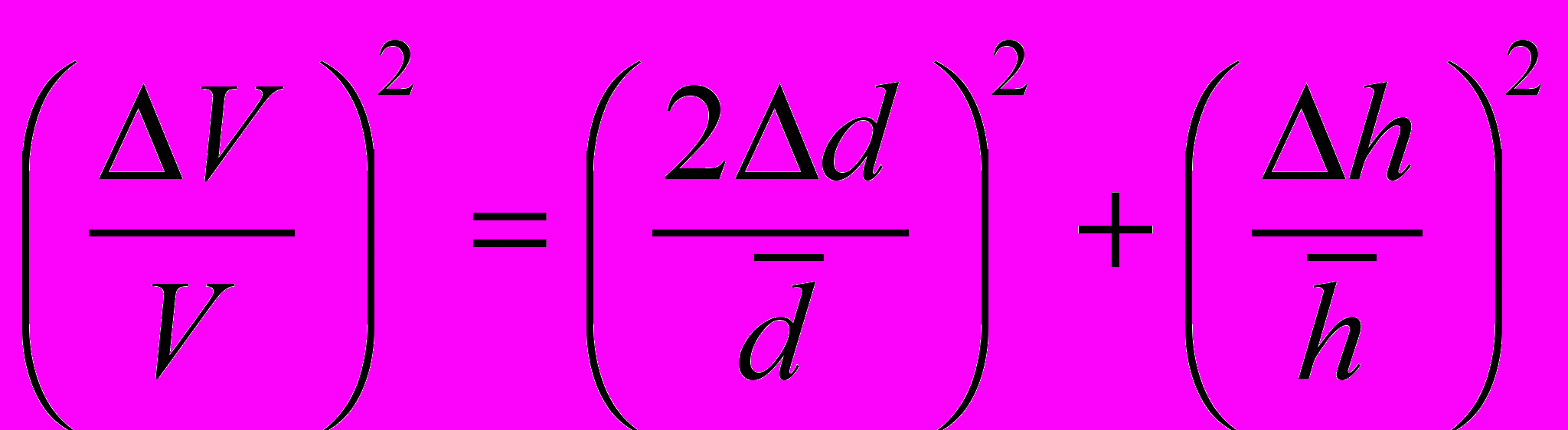
По относительной погрешности 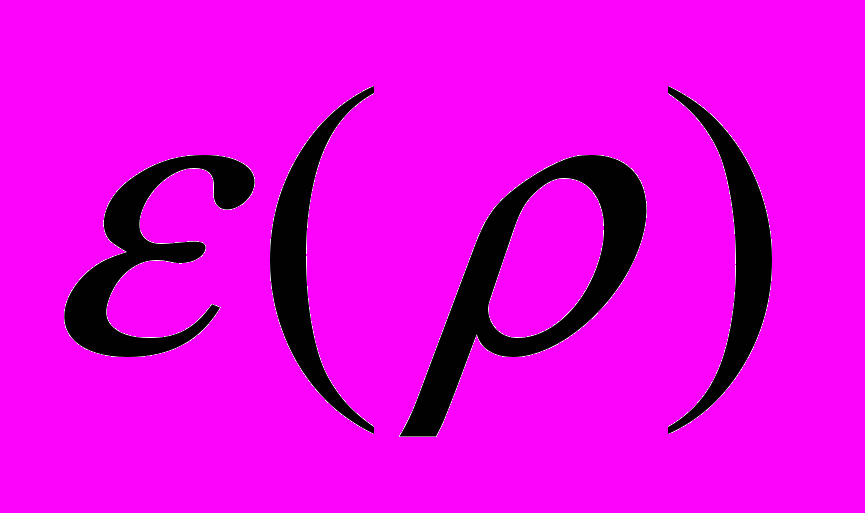и среднему значению 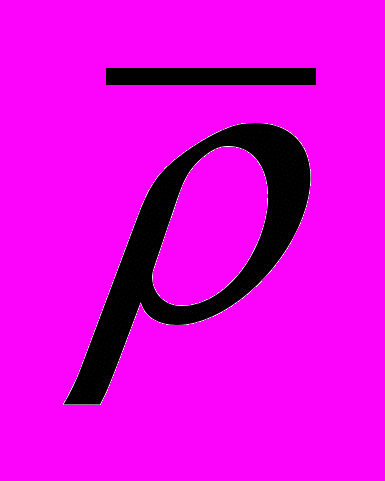найти погрешность измерения плотности .

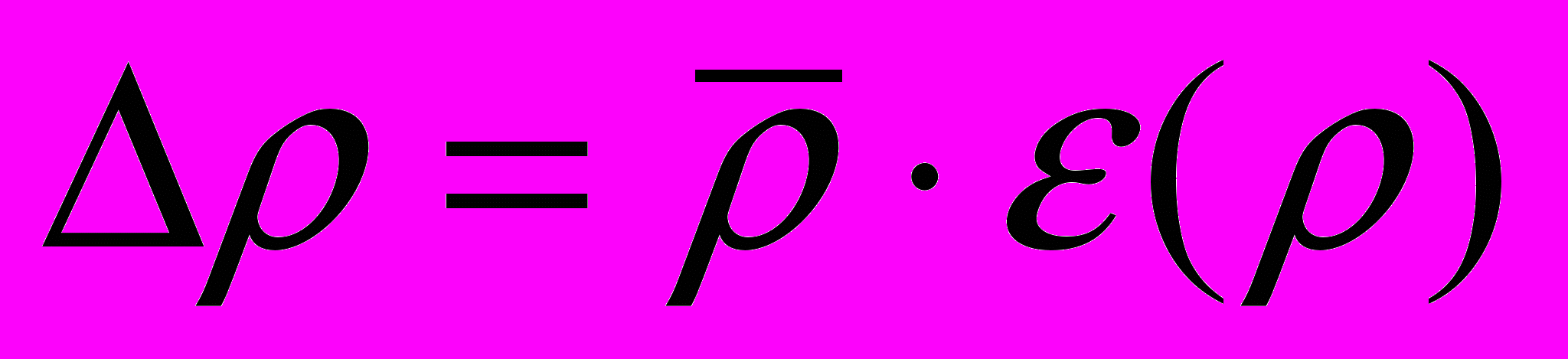Окончательный результат записать в виде



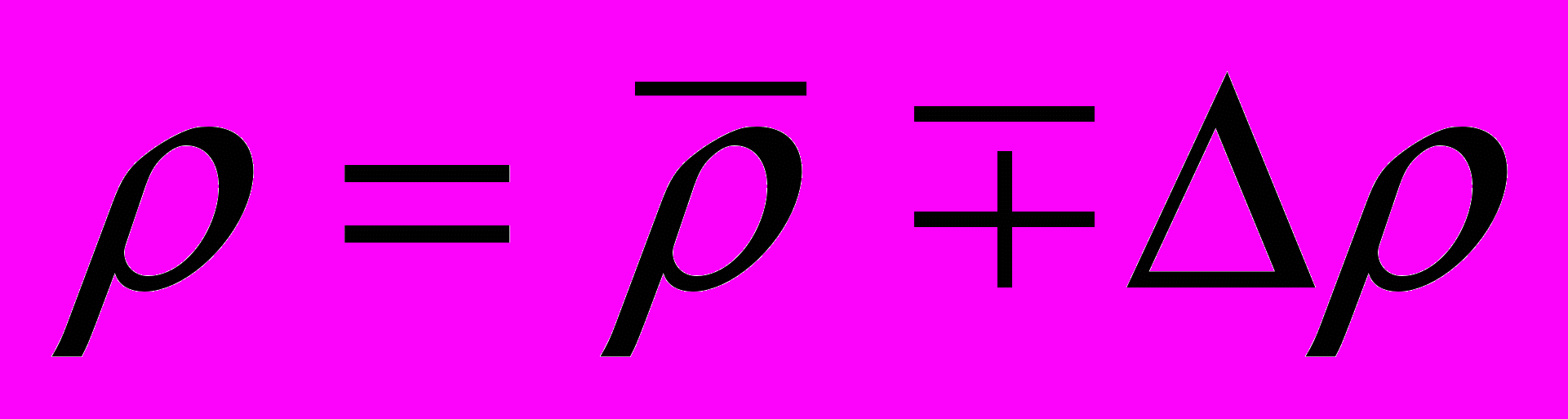
с указанием размерности и учётом указанных ранее округлений.


Контрольные вопросы:

1. Что значит «измерить» физическую величину и «записать» результат измерений?
   
2. Что такое «прямые измерения» физической величины? Каков порядок обработки результатов при прямых измерениях физической величины?
   
3. Что такое «косвенные измерения» физической величины? Каков порядок обработки результатов при косвенных измерениях физической величины?
   
4. Что такое «систематические погрешности? Как их можно устранить?
   
5. Что такое «случайные погрешности»? »? Как можно уменьшить их влияние?
   
6. Что такое «промахи»? Как их можно устранить?
   
7. Чем систематические погрешности отличаются от случайных?
   
8. Что такое «коэффициент Стьюдента»?
   
9. Как выявляются промахи при ограниченном числе измерений?
   
10. Как учитывается погрешность измерительного прибора?