Методы, модели и алгоритмы интеллектуального анализа данных при создании обучающих систем в текстильной и легкой промышленности 05. 13. 01 Системный анализ, управление и обработка информации (промышленность)
| Вид материала | Автореферат |
| V = – объем пространства признаков, t Таблица 1. Экстраполирующие свойства простейших решающих правил Третья глава В четвертой главе В пятой главе В приложении |
- Эволюционный метод синтеза непрерывно дискретных систем управления, 288.26kb.
- Метод и алгоритмы обработки информации в системе прогнозирования качества агломерата, 229.88kb.
- Комплекс программных средств поддержки принятия решений при сетевой обработке информации, 192.61kb.
- Разработка моделей и алгоритмов оптимизации процедур диагностирования на граф-моделях, 272.8kb.
- Повышение эффективности функционирования транспортно-погрузочного комплекса предприятий, 243.9kb.
- Методы поэтапной структурной отимизации магистральных корпоративных сетей 05. 13., 234.66kb.
- Агрегирование моделей анализа надежности и безопасности технических систем сложной, 509.58kb.
- Модели и алгоритмы периоперационной лучевой визуализации желчевыводящих протоков, 426.55kb.
- Тестирование объектно-ориентированного программного обеспечения на основе моделирования, 214.61kb.
- Разработка нелинейных динамических систем для формирования хаотических колебаний, 219.26kb.
Утверждение 1. Если в Nр-мерном пространстве многоградационных признаков логическое РП безошибочно разделяет обучающую последовательность длины n на M классов, то с вероятностью 1– можно утверждать, что вероятность ошибочного распознавания Pош с помощью этого РП будет меньше:
=
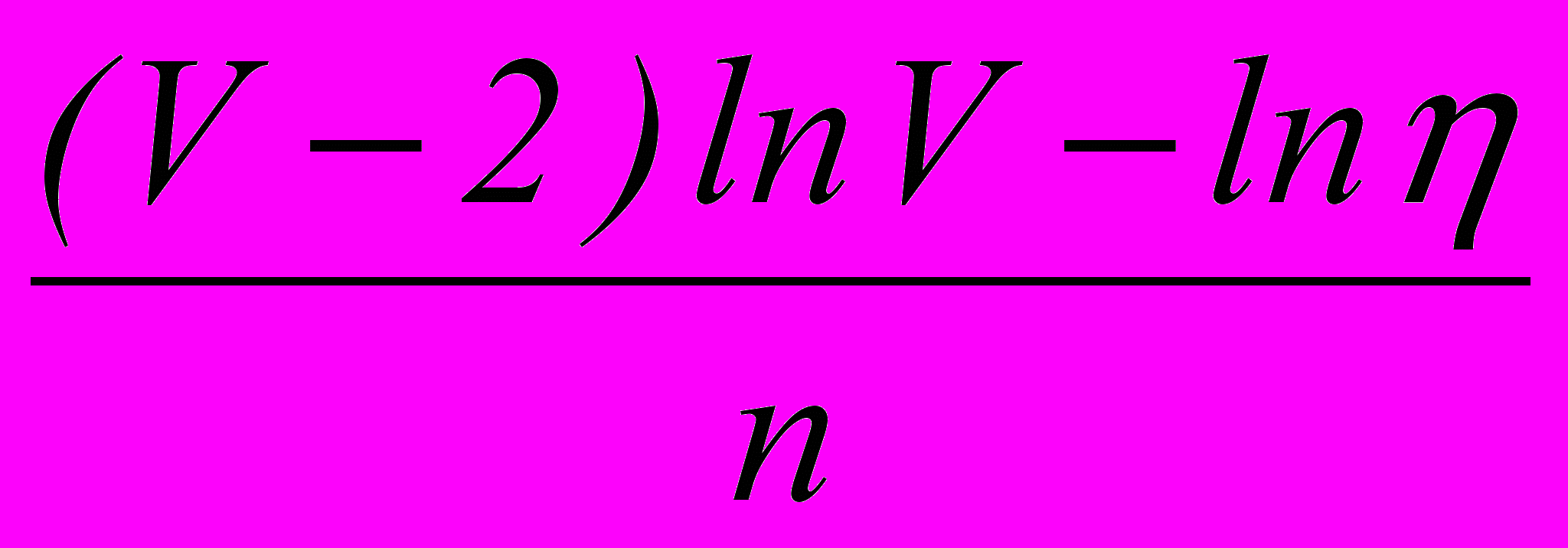 , (1)
, (1)где V =
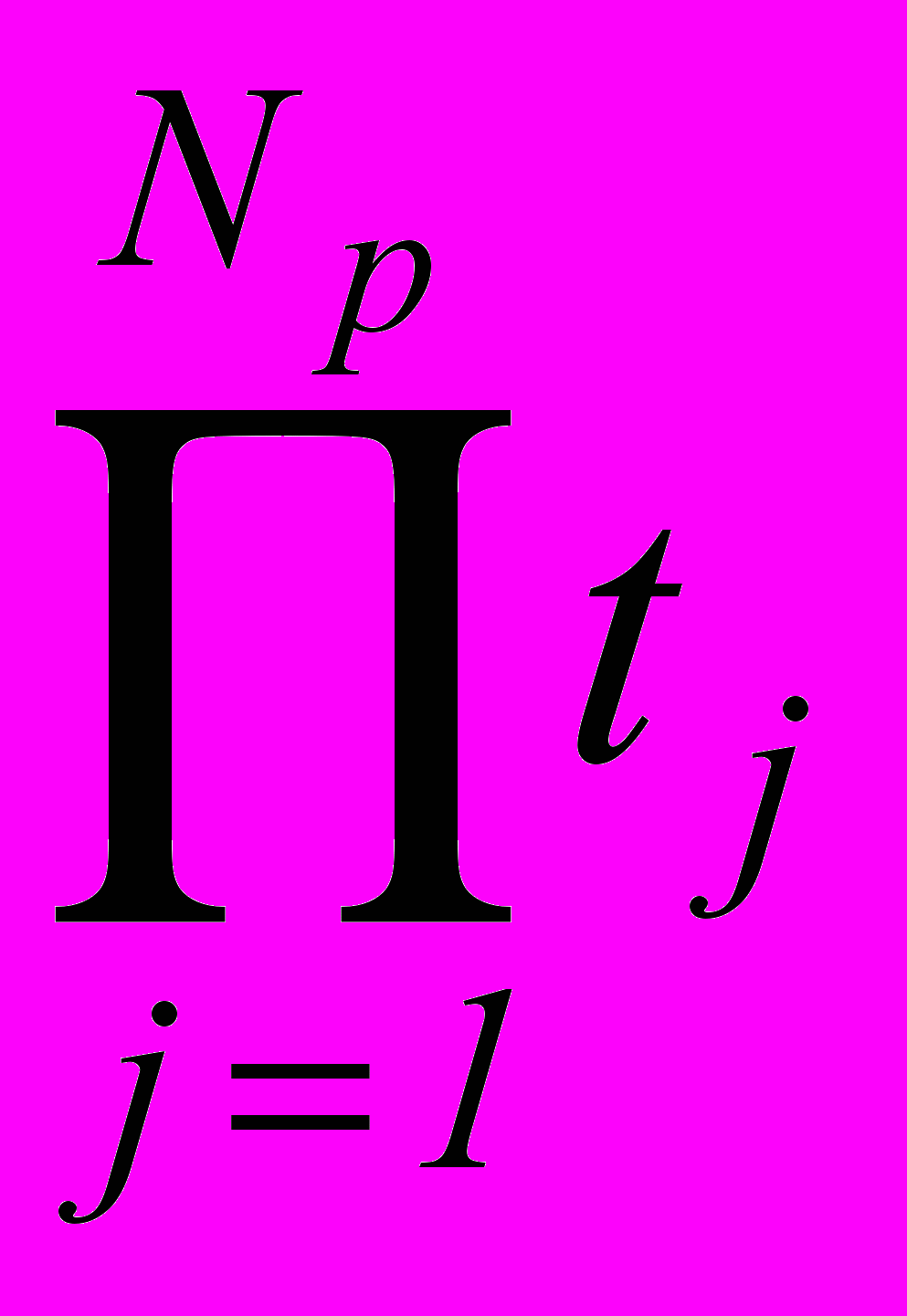 – объем пространства признаков, tj – количество интервалов кодирования признака Xj , j =
– объем пространства признаков, tj – количество интервалов кодирования признака Xj , j = 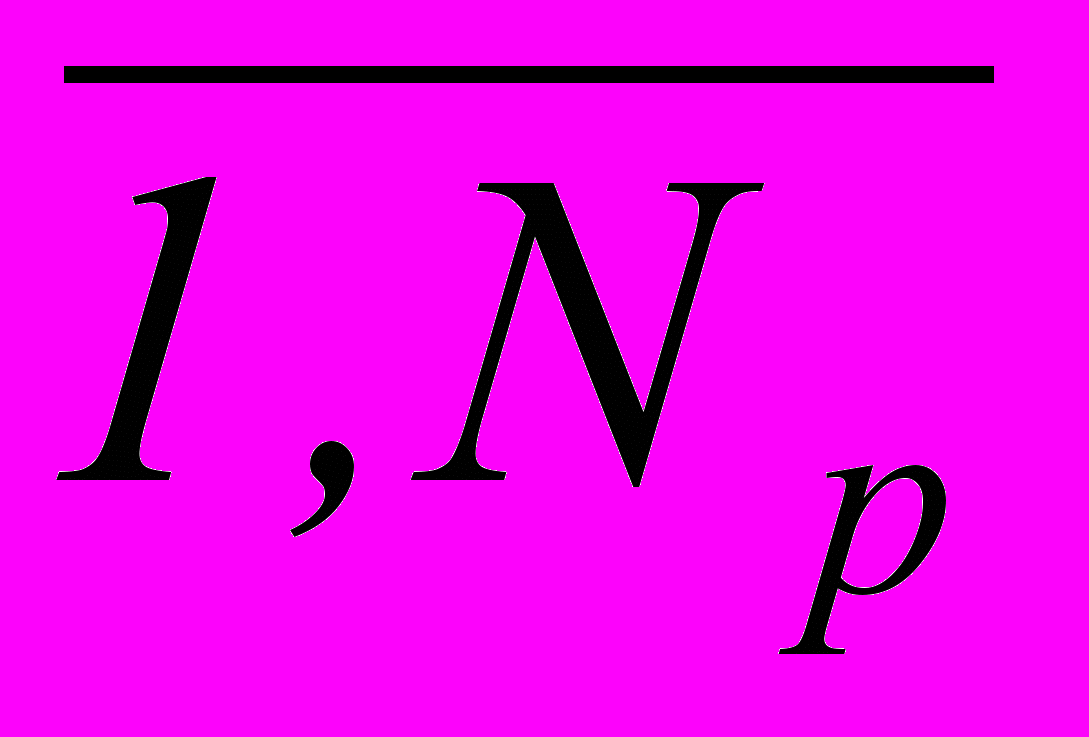 .
.Утверждение 2. В случае 0 с вероятностью 1– можно утверждать, что вероятность ошибочного распознавания с помощью логического РП будет меньше + , где
=
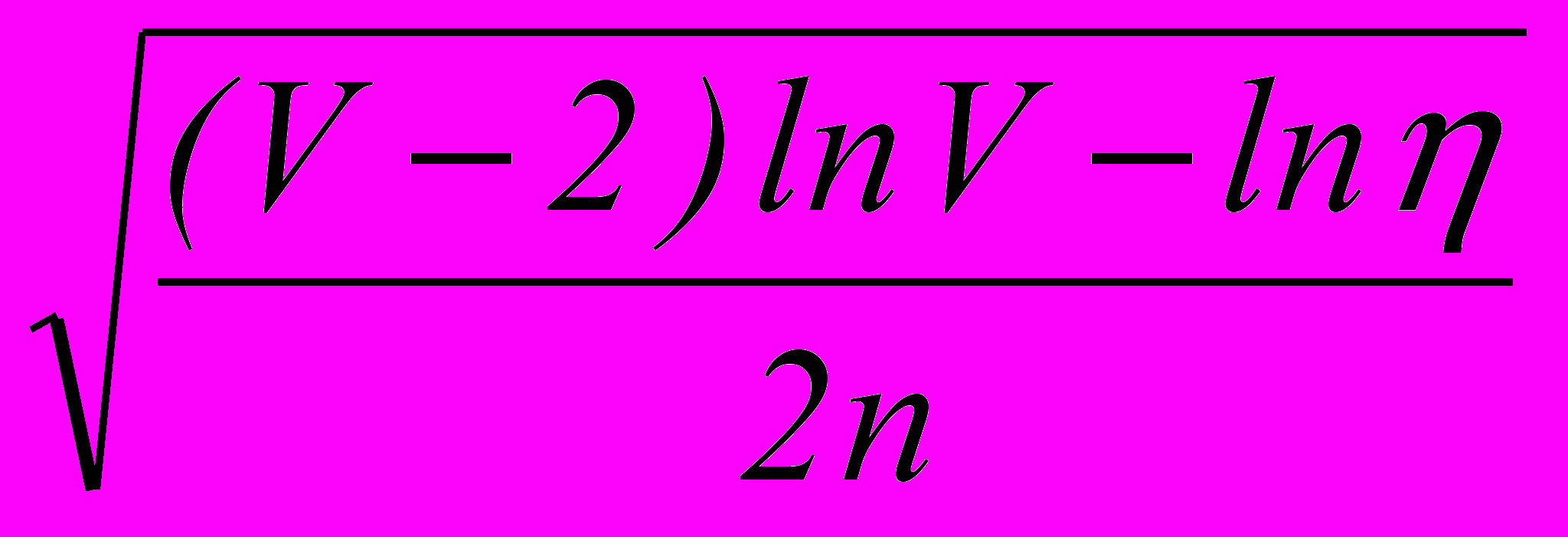 . (2)
. (2)Таким образом, минимизация объема V пространства признаков за счет оптимального кодирования и сокращения числа признаков позволяет повысить точность и надежность распознающей БЗ, основанной на логических правилах.
Если при сохранении разделяющей силы рабочего словаря устраняются “дублирующие” пороги, а логическое РП осуществляет покрытие каждого из классов одним гиперпараллелепипедом (Sm = 1) с гранями, параллельными осям координат-признаков, то V M и
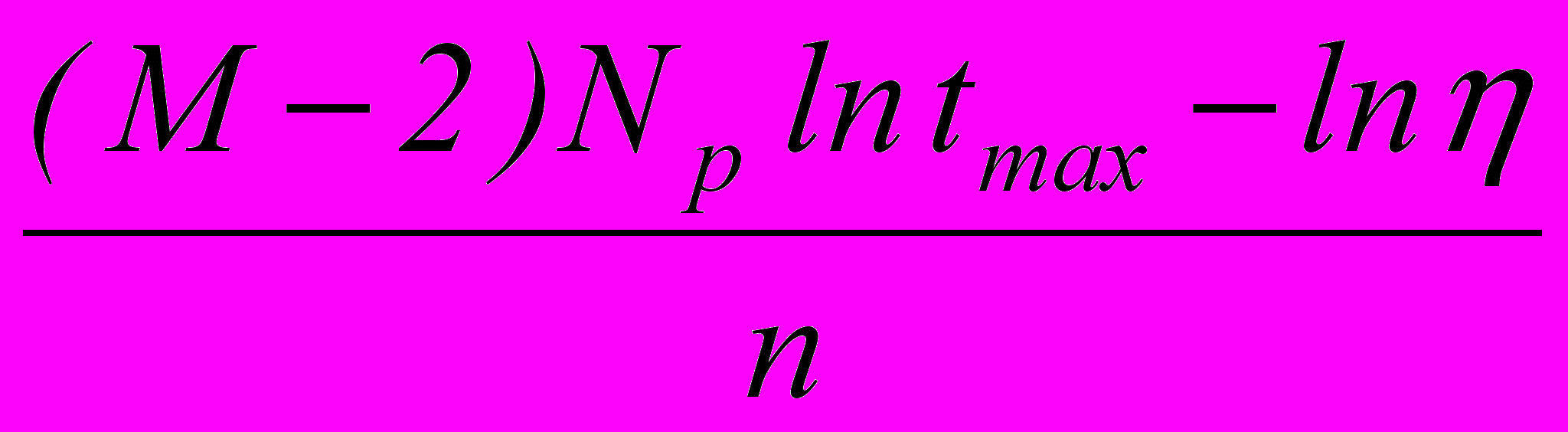 при = 0,
при = 0,где tmax =
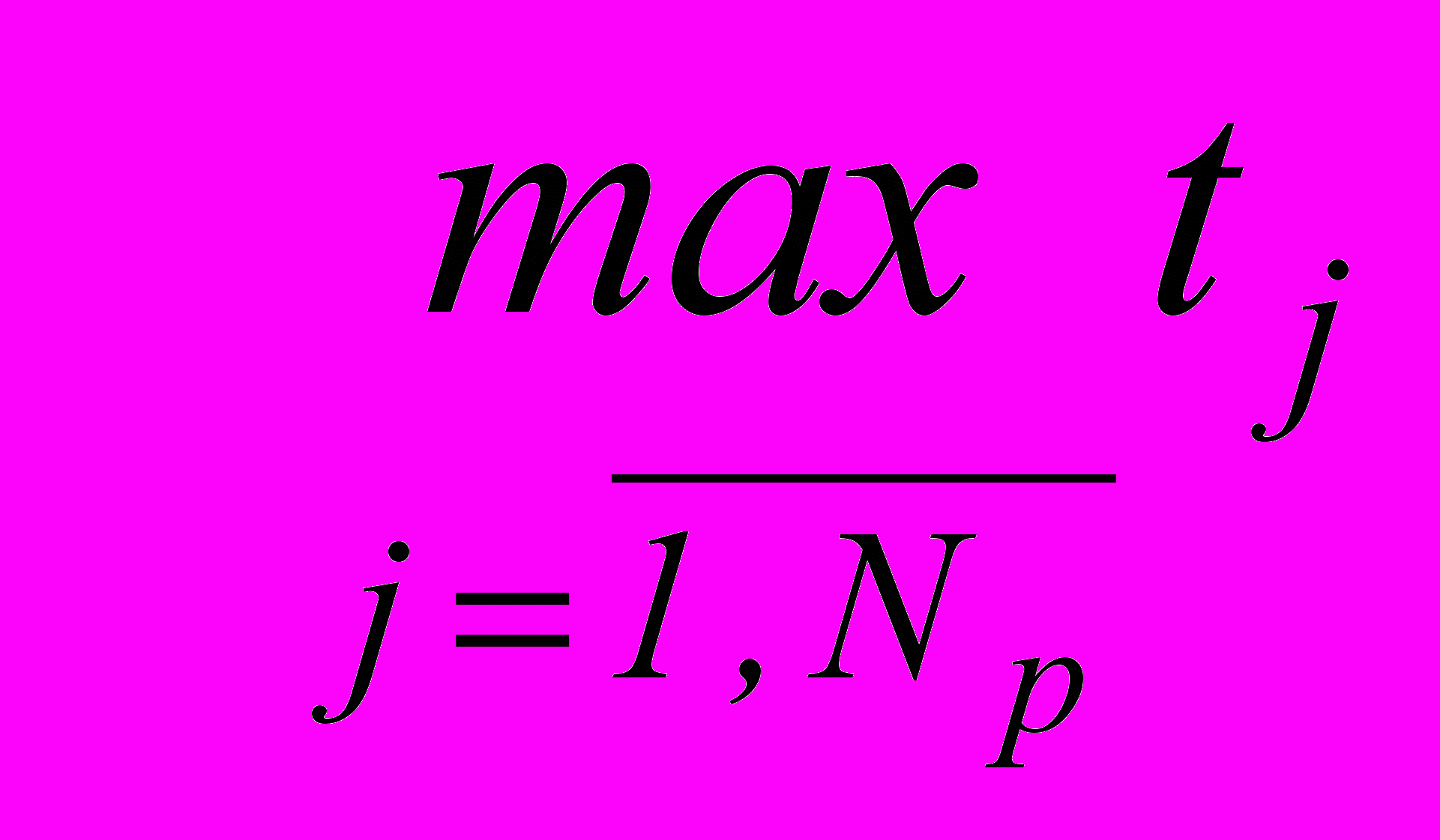 , и
, и
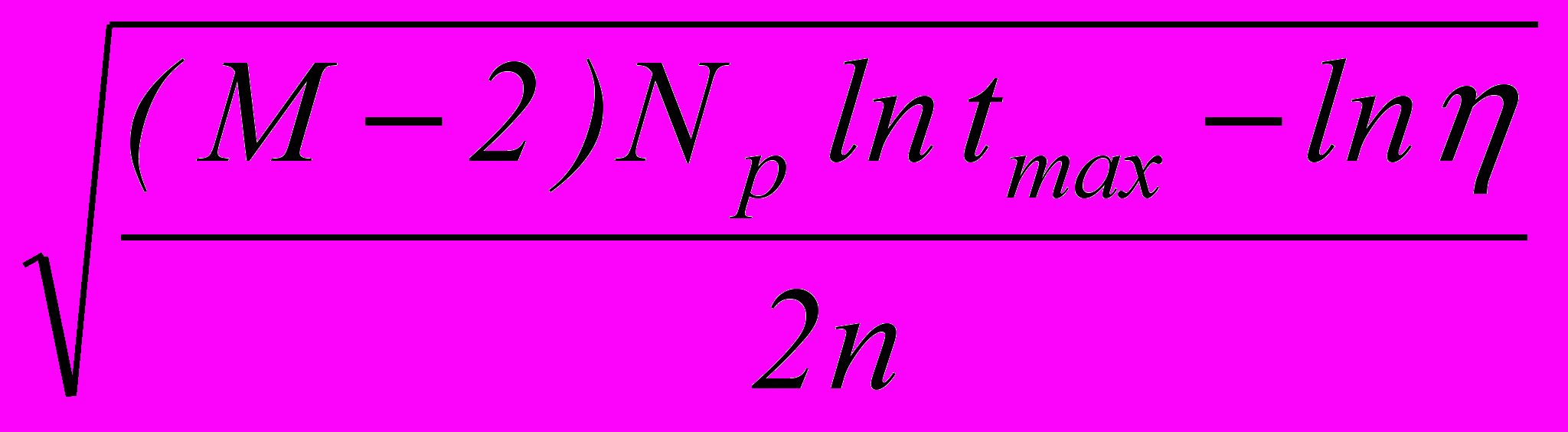 при 0.
при 0.Также получены оценки качества для линейных и кусочно-линейных РП. Их описание сведено в табл. 1, где МЛК – многогранные логические классификаторы; k = k – Nр, k – число гиперплоскостей, составляющих РП.
Таблица 1. Экстраполирующие свойства простейших
решающих правил
| Эмпирический риск | Гарантированное уклонение среднего риска от эмпирического, | ||
| Логическое РП (Sm = 1) | Линейные РП | МЛК | |
| = 0 | MNр | M 2Nр | M 2(Nр + k )(Nр +1) |
| 0 | 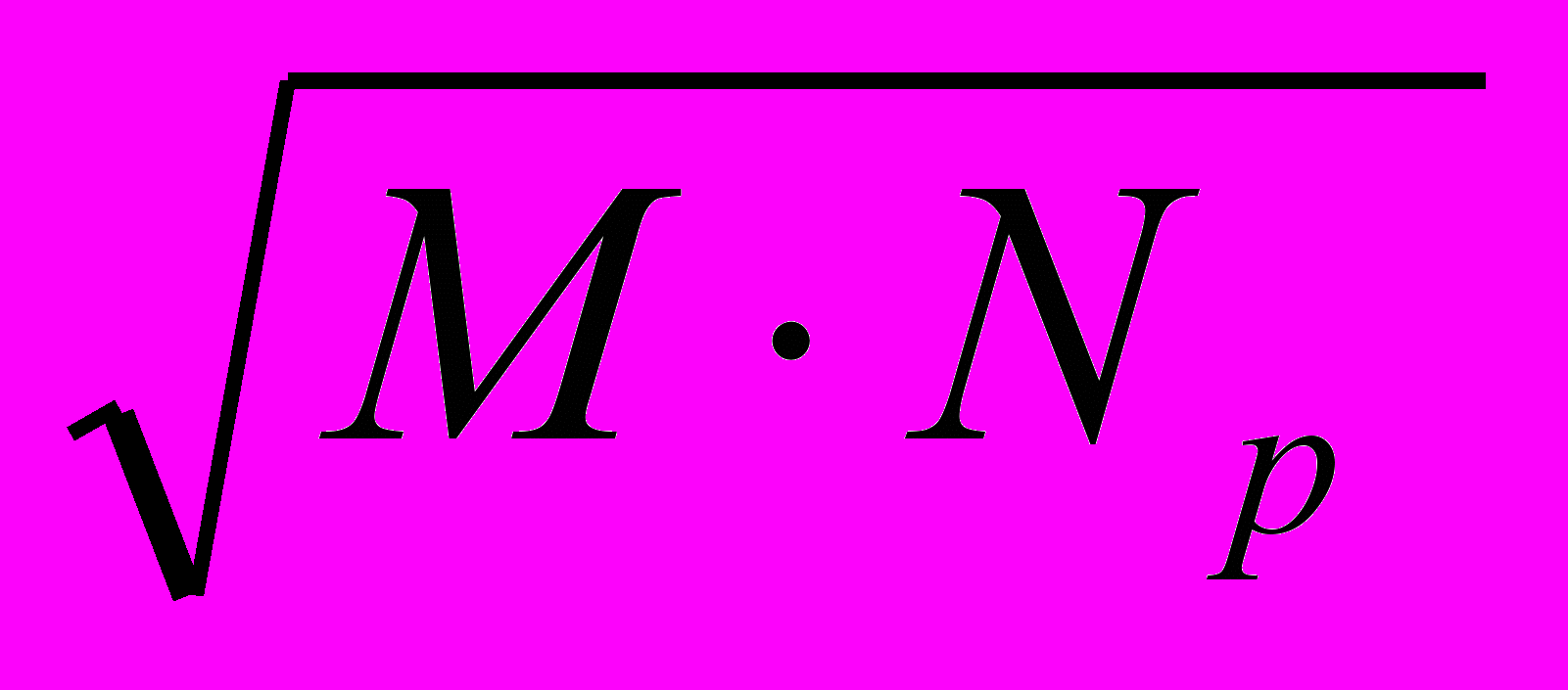 | M 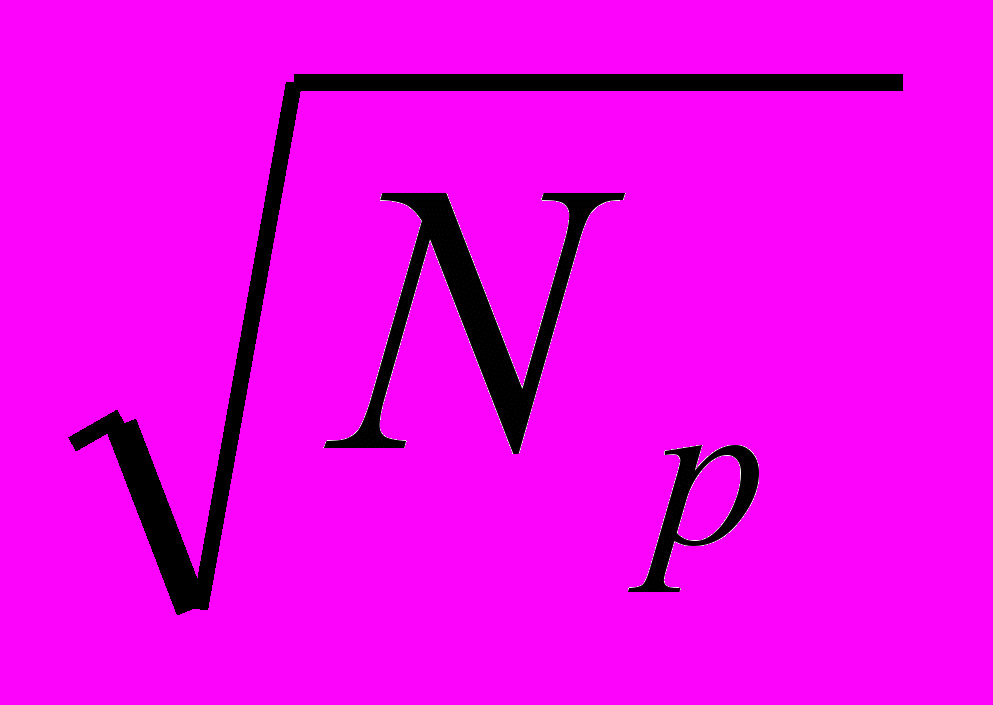 | M 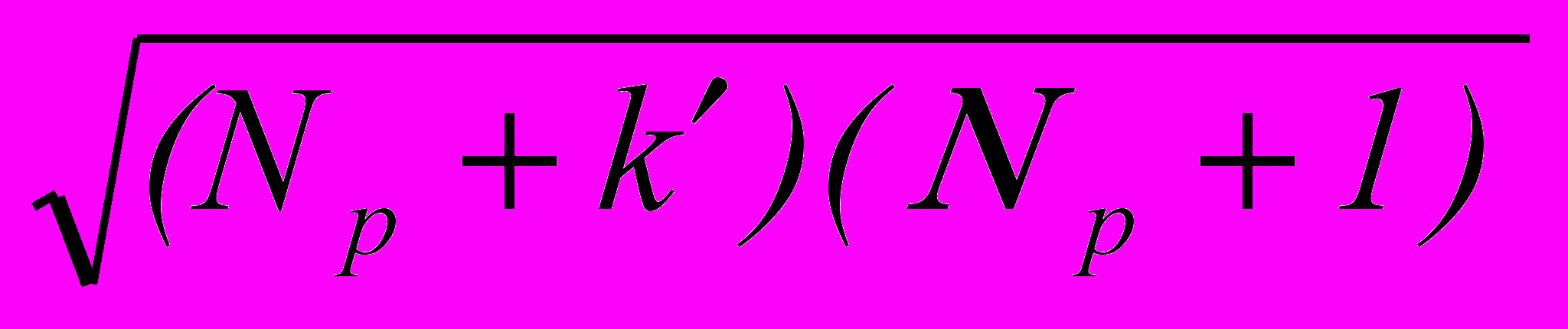 |
На основе анализа теоретических и экспериментальных результатов выработаны практические рекомендации по использованию основных алгоритмов ОРО в условиях ограниченных ОВ. В задачах обучения, априорный алфавит которых представлен значительным числом классов (M 5), с точки зрения обеспечения надежности распознающей БЗ наиболее целесообразно применение простейших РП типа прямоугольных логических классификаторов, решающих деревьев, при Nр 5 – линейных РП. При построении системы искусственного интеллекта, реализующей стратегию прямого вывода, более сложные РП (включая вероятностные методы, учитывающие распределение объектов по классам) предпочтительно использовать на начальных шагах, когда осуществляется разбиение на небольшое число промежуточных образов. На последних шагах, характеризующихся сильным ветвлением, возникает необходимость применения простейших логических РП, усложнение РП необходимо использовать лишь локально для разделения “трудных” классов или для уточнения описания класса в случае достаточного числа его прецедентов.
Найденные при формировании свойств материалов и при проектировании объектов легкой промышленности адекватные нелинейные модели регрессии или детерминированные зависимости для выходных переменных отдельных звеньев ТП, используются для уточнения описаний классов объектов за счет добавления к системе РП соответствующих нелинейных неравенств. Поскольку при обучении распознающей БЗ описания классов формируются в терминах выходных признаков, например показателей качества готовой продукции, то в первую очередь рассматриваются зависимости для конечных этапов технологического процесса.
Первоначально формируются описания классов с помощью построения кусочно-линейных РП. Знание статистической структуры описаний классов, особенно важное при M > 2, добавляется заменой соответствующих гиперпараллелепипедов и многогранников на гипертрубы, описываемые системой неравенств – доверительных границ для прогнозов значений зависимых признаков.
В пределе, при наличии строгих функциональных детерминированных зависимостей для всех звеньев технологической цепочки, описания классов сжимаются до минимальных размеров, гарантированное уклонение среднего риска от эмпирического стремится к нулю, а экстраполирующая сила системы РП – к единице.
При выявлении материалов с новыми свойствами, заданными через интервалы значений соответствующих выходных переменных, с помощью адекватных статистических моделей определяется область в пространстве признаков рабочего словаря, которая проверяется на технологическую реализуемость.
Исследованы вопросы повышения точности описания классов при формировании распознающей БЗ в условиях мультиколлинеарности системы признаков. На этапе выбора рабочего словаря при комплексном применении множества дискриминантных алгоритмов влияние мультиколлинеарности устраняется за счет ликвидации дублирующих признаков. Сужение, уточнение многогранных Nр-мерных областей класса может осуществляться не только аналитически по уравнениям регрессии через заданные в каждом классе интервалы выходных признаков, но и последовательным расширением центроидов классов в процессе применения методов автоматической классификации (таксономии).
Третья глава посвящена решению задачи оптимизации систем описания правил вывода на знаниях.
Описания технологических объектов, выбираемых из БД, по виду шкалы принимаемых значений содержат признаки различного типа – количественные, порядковые и классификационные.
При оценке в рамках комплексного подхода качества логических решающих правил требуется минимизировать пространство признаков, снижая тем самым величину Pош .
Задача оптимизации объема пространства признаков может быть представлена как бинарная задача минимизации нелинейной целевой функции
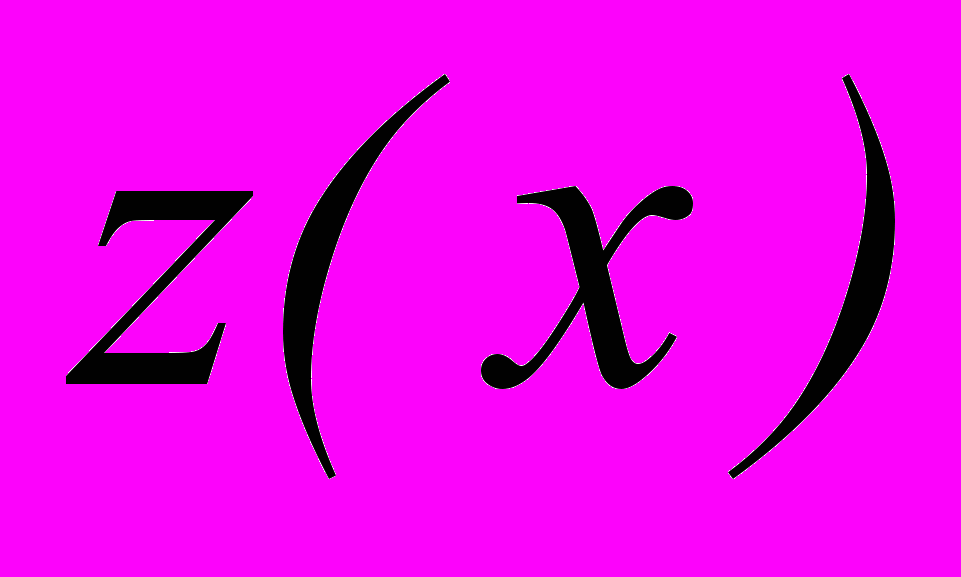 =
= 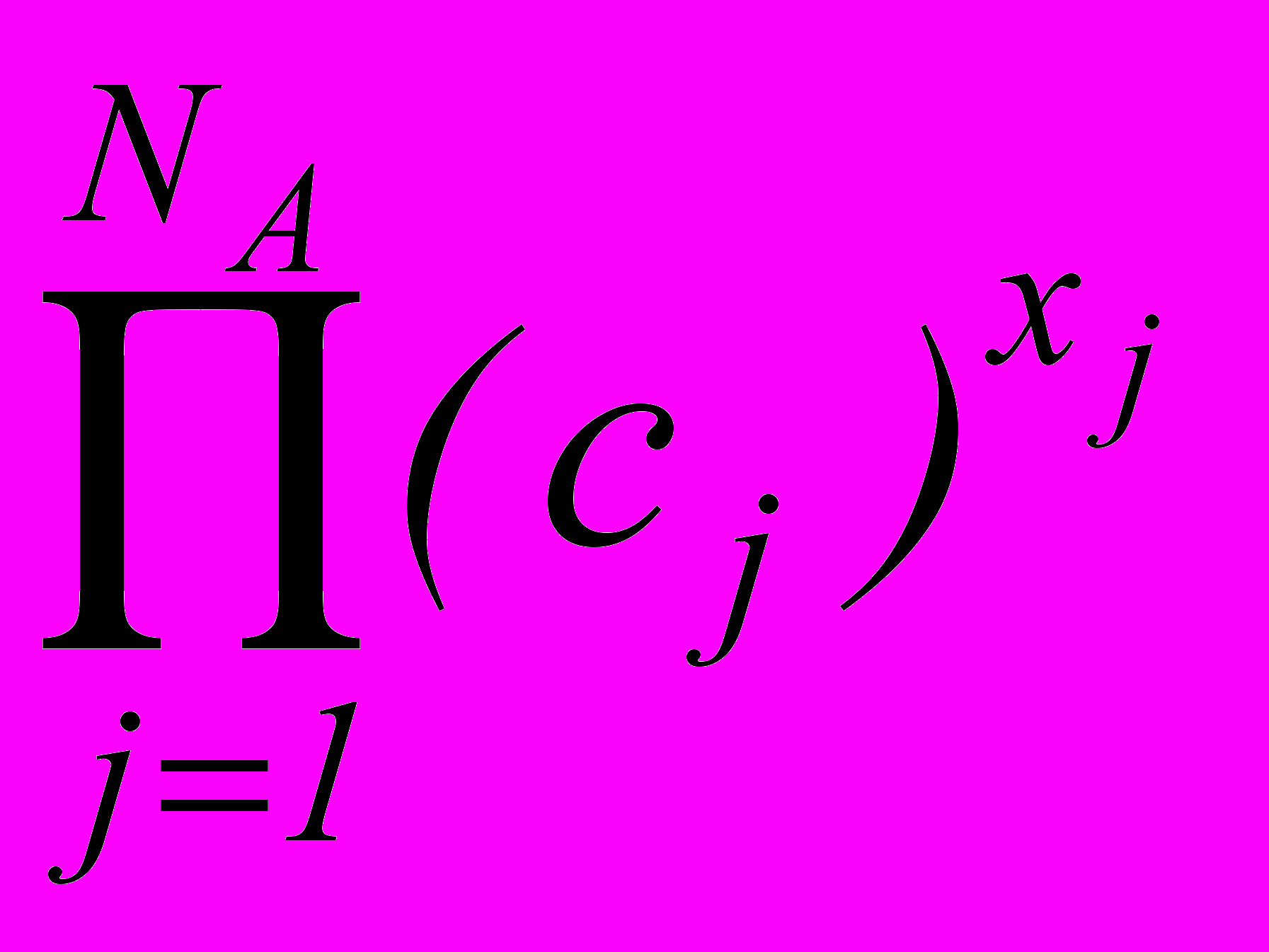 , (3.1)
, (3.1)где cj = tj, при условии сохранения достаточности рабочего словаря, имеющем вид линейных ограничений
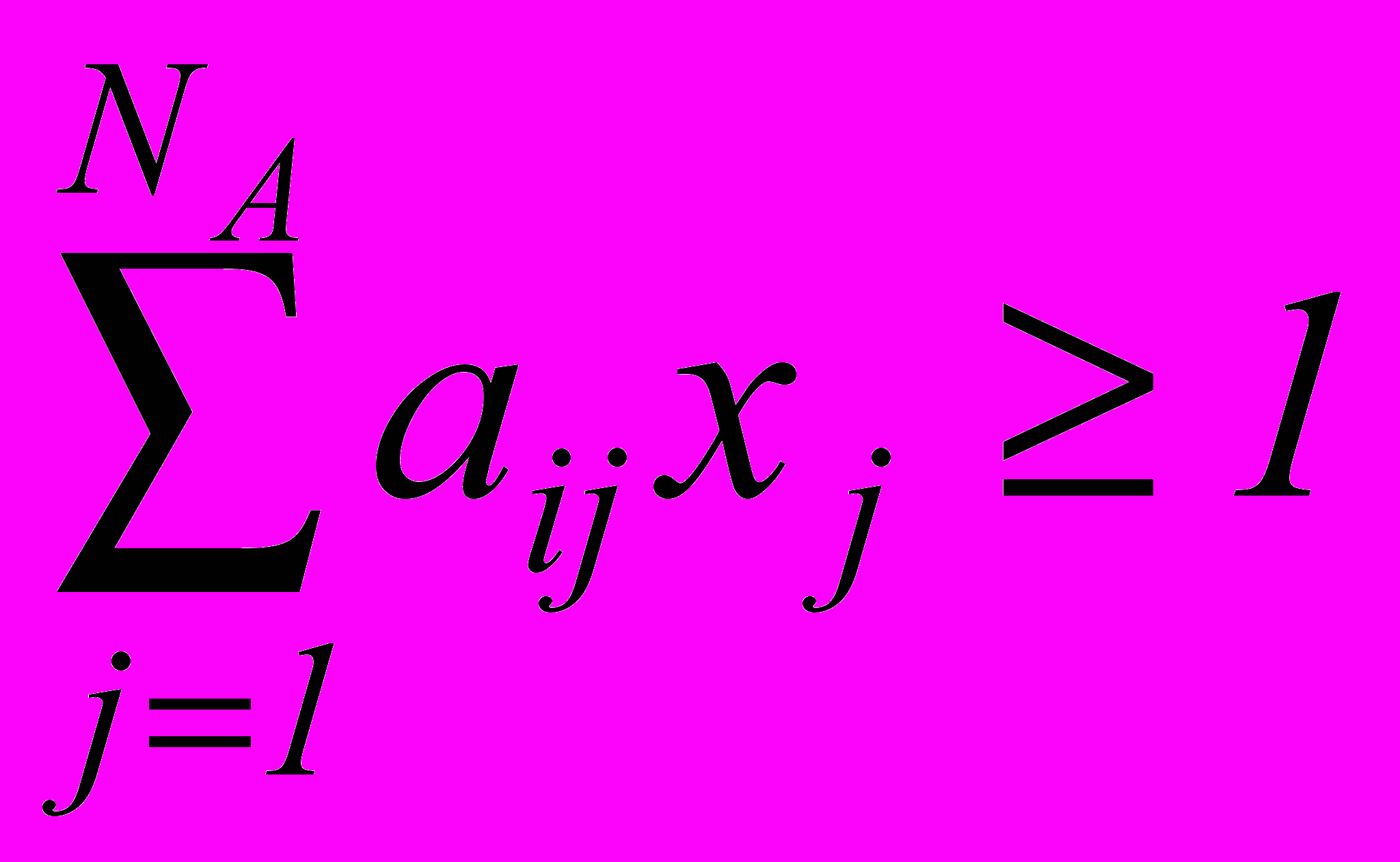 , (3.2)
, (3.2)где aij = 01, xj = 01, i =
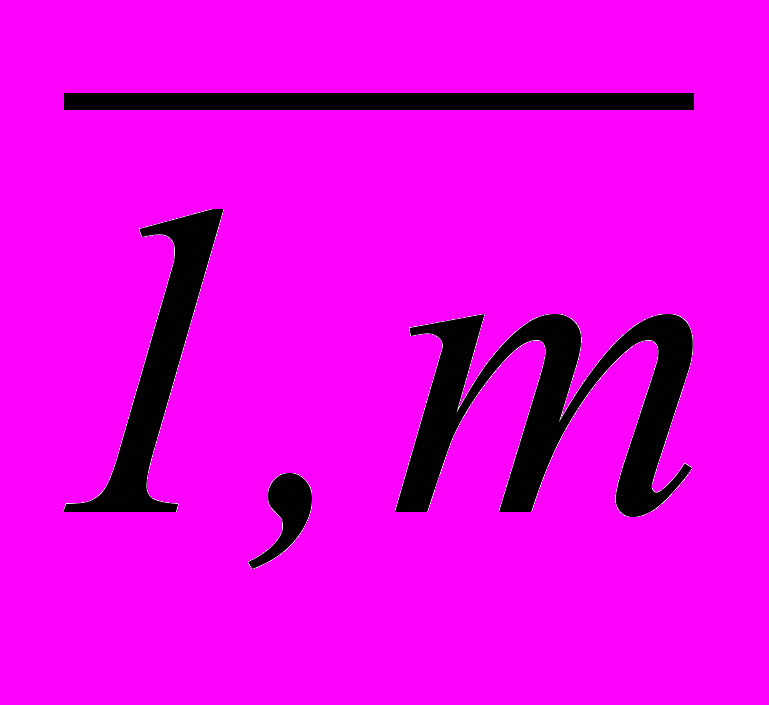 , j =
, j = 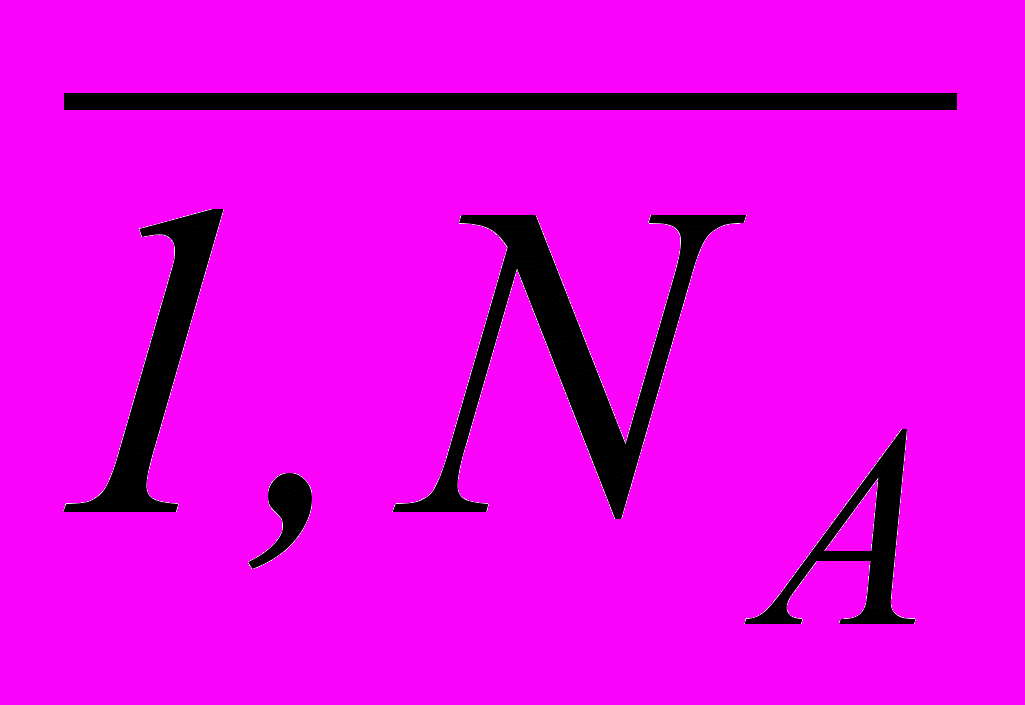 , m = M(M – 1)/2.
, m = M(M – 1)/2.Если xj = 0, то j-й признак входит в состав рабочего словаря, в противном случае – нет. Единичное значение коэффициента aij матрицы ограничений указывает на способность j-го признака априорного словаря разделить i-ю пару классов.
Дискретизация признакового пространства сводится к определению числа градаций признаков, мест расположения порогов и должна осуществляться совместно с выбором рабочего словаря признаков. Перебор колоссального числа вариантов при значительном числе классов продукции (M > 10) и размерности априорного словаря признаков (NA > 50) делает затруднительным решение данной задачи на компьютере за приемлемое время. Поиск близких к оптимальным систем описания звеньев технологической цепочки производится путем последовательного кодирования отдельных признаков, выбора рабочего словаря, минимизирующего объем пространства признаков, и устранения “дублирующих порогов” (повторного кодирования) для признаков, разделяющих одинаковые пары классов.
При формировании РП, осуществляющих покрытие каждого класса объектов ОВ гиперпараллелепипедами с гранями, ортогональными координатным осям, предложен алгоритм кодирования независимых признаков, который обеспечивает разделение всех непересекающихся по данному признаку классов, используя минимальное число порогов. Если априорный словарь признаков достаточен для распознавания M типов продукции в классе логических РП, то кодирование по методу МЧП является оптимальным в смысле минимизации объема пространства признаков без учета зависимости их реальных разделяющих сил от подсистемы совместно используемых признаков.
Реальная разделяющая сила признака Xj
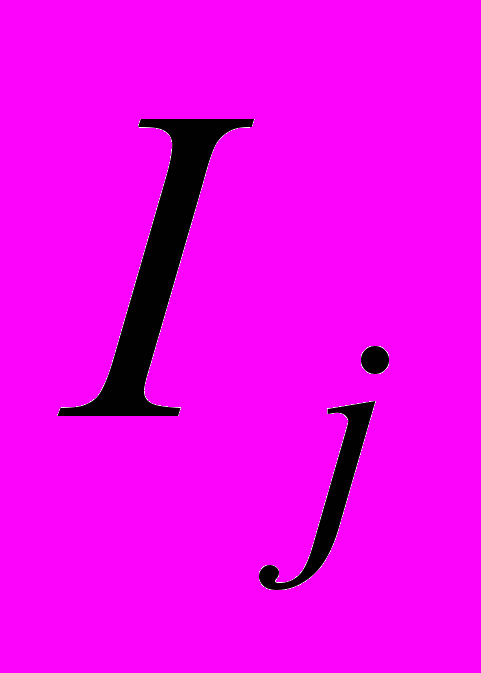 =
= 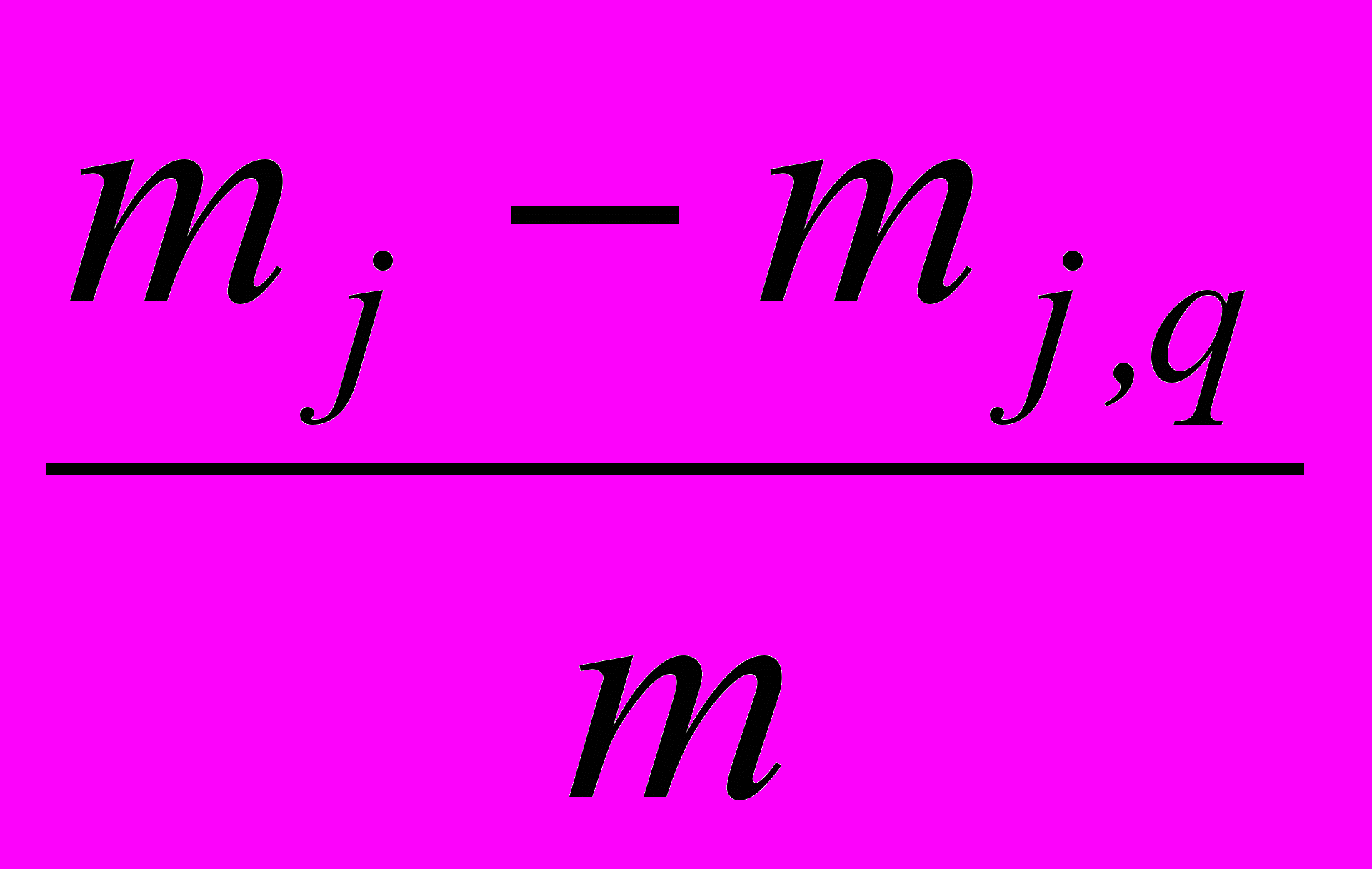 ,
,где mj – мощность множества Rj пар классов, полностью разделимых признаком Xj; mj,q – коэффициент ослабления разделяющей силы признака Xj; mj,q = RjRq; Rq – множество пар классов, полностью разделимых подсистемой Xq совместно используемых признаков, Xq = Xр\Xj, m = M(M–1)/2. Зависимость Ij от совместно используемой подсистемы ухудшает экстраполирующие свойства распознающей БЗ.
С целью уменьшения гарантированной оценки риска в процессе логического вывода на новых данных исследованы возможности поиска оптимального объема пространства признаков после их кодирования методом МЧП.
Показано, что уменьшение суммарного числа градаций, то есть минимизация числа взвешенных признаков
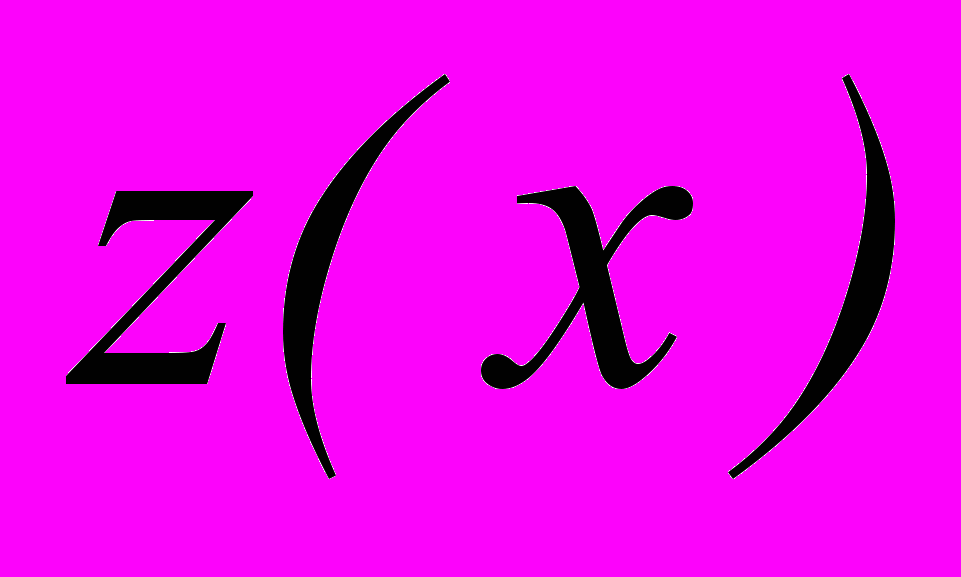 =
= 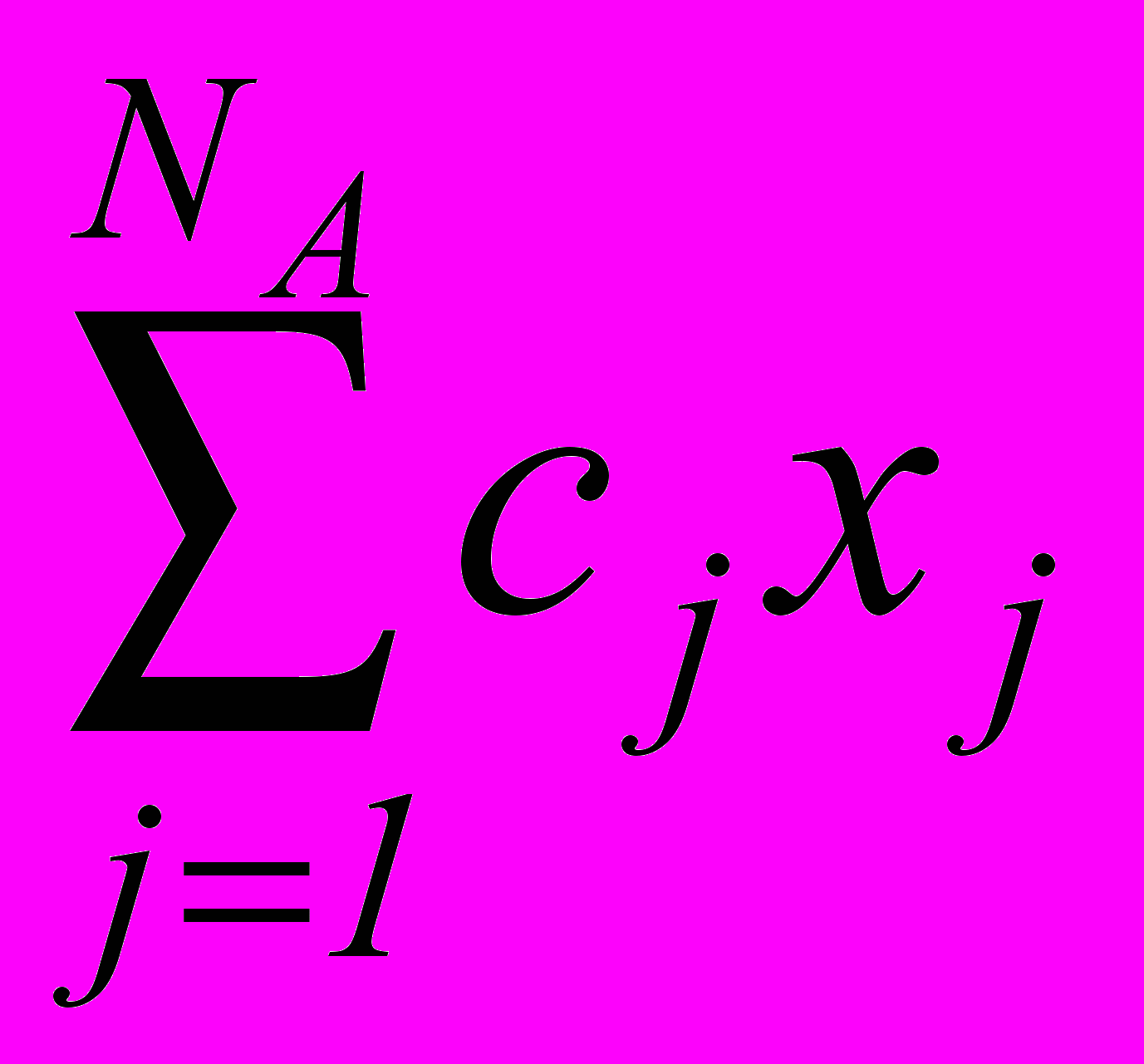 , (3.3)
, (3.3)с весовыми коэффициентами
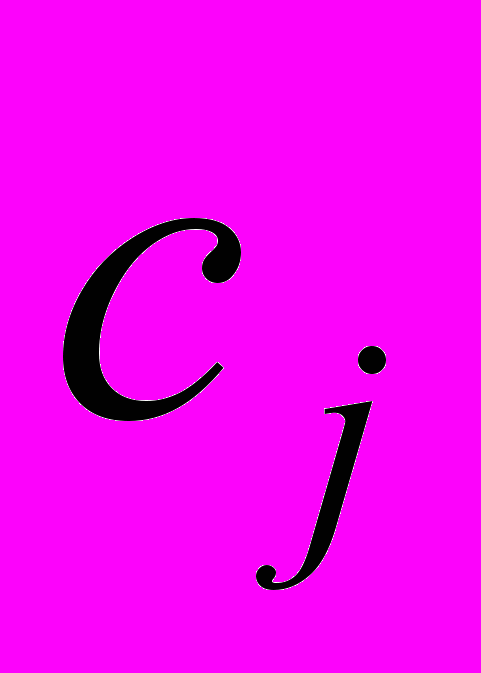 =
= 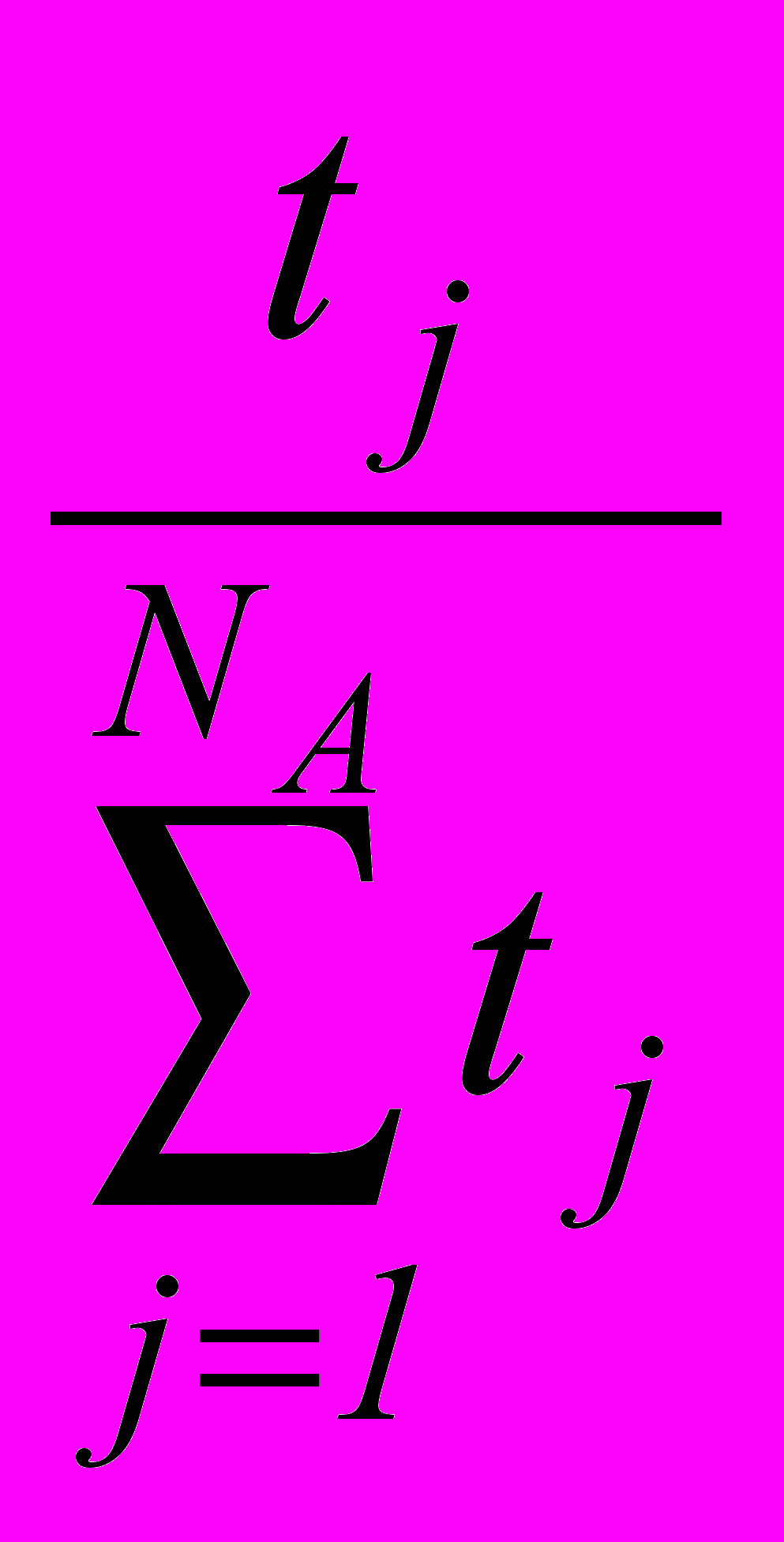
при ограничениях (3.2) позволяет эффективно решать задачу оптимизации объема пространства признаков в общем случае зависимых разделяющих сил. Если число градаций имеет незначительный разброс, либо один из признаков имеет число градаций, близкое числу классов M, то поставленная задача эффективно решается путем сокращения количества признаков без учета числа их градаций (при cj = 1).
Поскольку “сильная” зависимость реальных разделяющих сил, когда каждый признак делит только одну-две пары классов по сравнению с подсистемой используемых совместно с ним признаков, встречается редко, то в практических приложениях повышение экстраполирующей силы РБЗ достигается за счет минимизации числа признаков рабочего словаря.
Для решения задачи минимизации числа взвешенных признаков с большим объемом входных данных (M 10, NA 50) предложено использовать -оптимизацию и точный алгоритм ветвей и границ. Метод ветвей и границ для решения бинарных линейных задач имеет ряд особенностей, позволяющих учитывать специфику задачи и требования к программной реализации алгоритмов. В вычислительном отношении чрезвычайно просты стратегия одностороннего обхода (используются логические операции) и операция сложения, определение целевой функции при нулевых значениях незафиксированных переменных и организация информации о дереве вариантов с помощью целочисленного вектора.
Разработан и реализован аддитивный алгоритм ветвей и границ для выбора рабочего словаря многоградационных признаков. Время решения задач размерностью до 20 переменных (признаков) и 45 ограничений (10 классов) на современных компьютерах не превосходит 1 мин и в среднем занимает около 15 с. Алгоритм работает лучше на матрицах высокой плотности, равной 0,6–0,9, то есть при наличии информативных признаков, число градаций которых стремится к M (при кодировании методом МЧП). В особо трудных случаях используется -оптимальное решение z(x) z*(x)[1+] ( 0,01) или последнее допустимое решение по достижении предельного времени.
Оставшееся подмножество признаков XA\ Xр используется только при формировании концептуальной составляющей поля знаний. После принятия решения о классе производимой продукции эти признаки позволяют дать полное заключение о характеристиках исходных ингредиентов и диапазонах параметров ТП.
Если приходится оценивать наличие свойства в рассматриваемом изделии, когда исследуемый объект в той или иной степени может принадлежать двум или нескольким нечетким классам и требуется сравнить степень принадлежности или вероятность истинности при сопоставлении различных вариантов решений, то используется подход на основе нечеткой логики с привлечением знаний и опыта экспертов. Оценки специалистов позволяют существенно сократить затрачиваемые время и средства на моделирование сложных объектов, а трудноформируемые связи для выходных показателей – представить интеллектуальной системой в виде словесных описаний, например, сообщить о зависимостях потребительских свойств наборов различных нитей от параметров формования в терминах надмолекулярных структур волокнообразующих полимеров.
Выполнена формализация нечетких классов, их степеней разделимости и процесса кодирования признаков. Выставление порогов осуществляется по следующему алгоритму. В случае, если унарные ортогональные проекции нечетких классов на ось Xj находятся в отношении нечеткого порядка, то пороги выставляются в точках значений признаков, соответствующих максимальному показателю пересечения проекций размытых множеств (пары классов). В случае четкого отношения порядка пороги выставляются посередине между носителями пары проекций размытых классов; если несколько пар классов могут быть разделены одним порогом, то он выставляется посередине между носителями, ближайшими друг к другу, обеспечивая тем самым минимальное число порогов кодирования признака Xj.
Несмотря на недостаток исходных данных, при обучении приходится решать задачу минимизации числа признаков (3.3) для определения тех параметров, без которых информативность оставшейся подгруппы сохраняет значение, близкое к исходному – при ограничениях
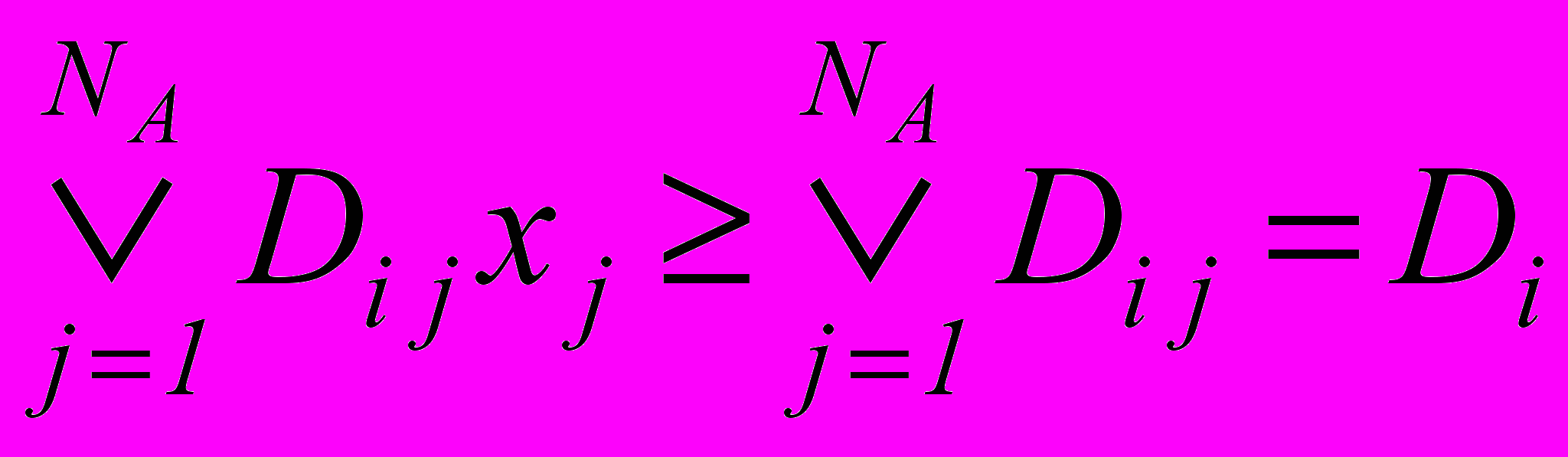 ,
,где cj – затраты на вычисление признака Xj; степень разделимости Dij(m1, m2) определяется, например, через максимальный показатель пересечения размытых множеств:
Dij(m1, m2) = 1 –
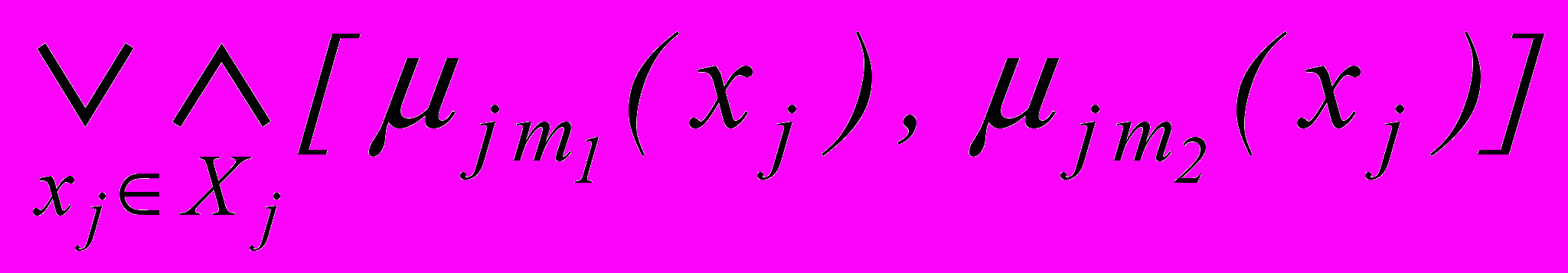 ,
,функция jm(xj ) определяет унарную ортогональную тень на ось Xj :
jm(xj ) =
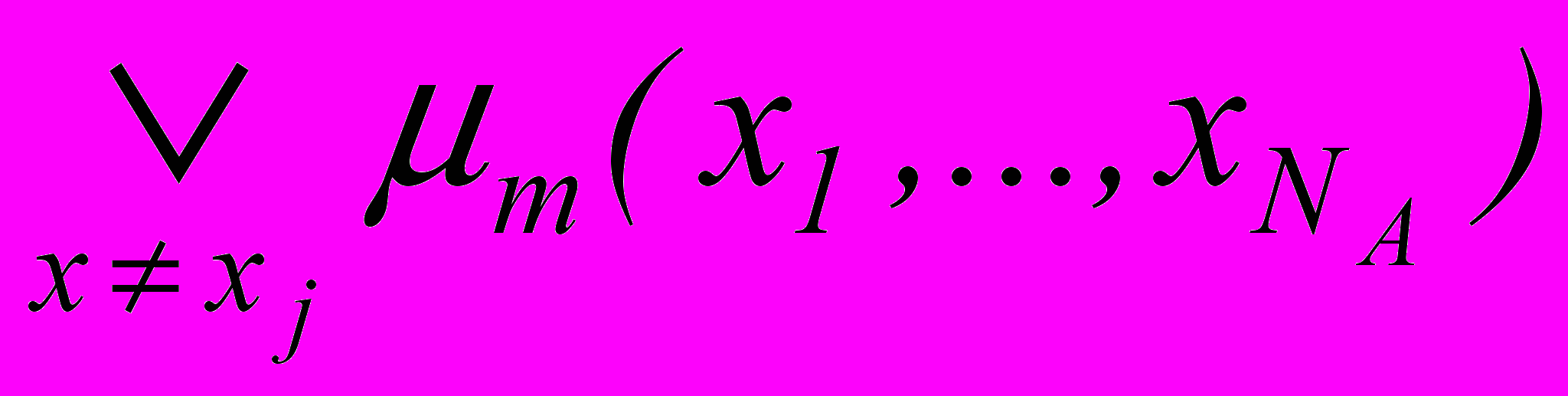 ,
,i =
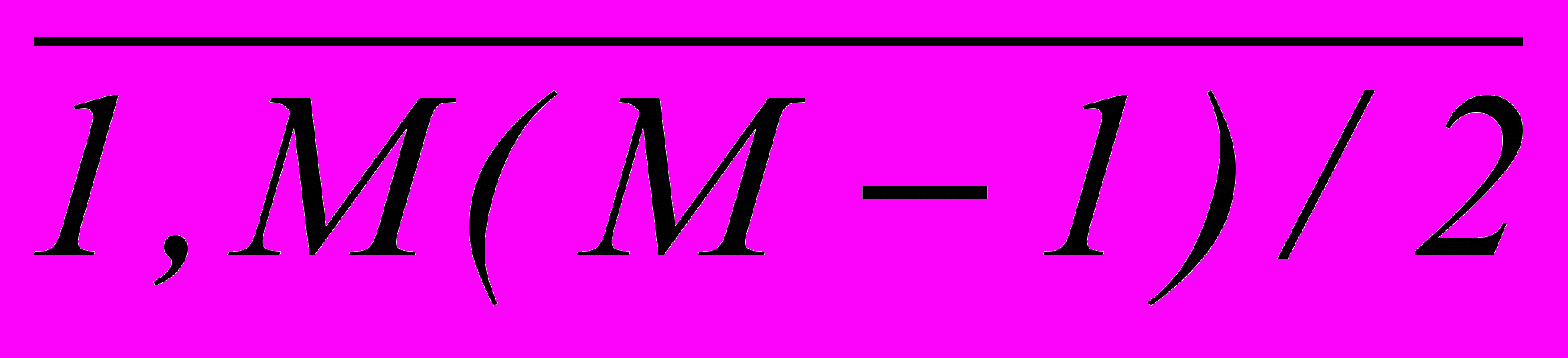 , j =
, j = 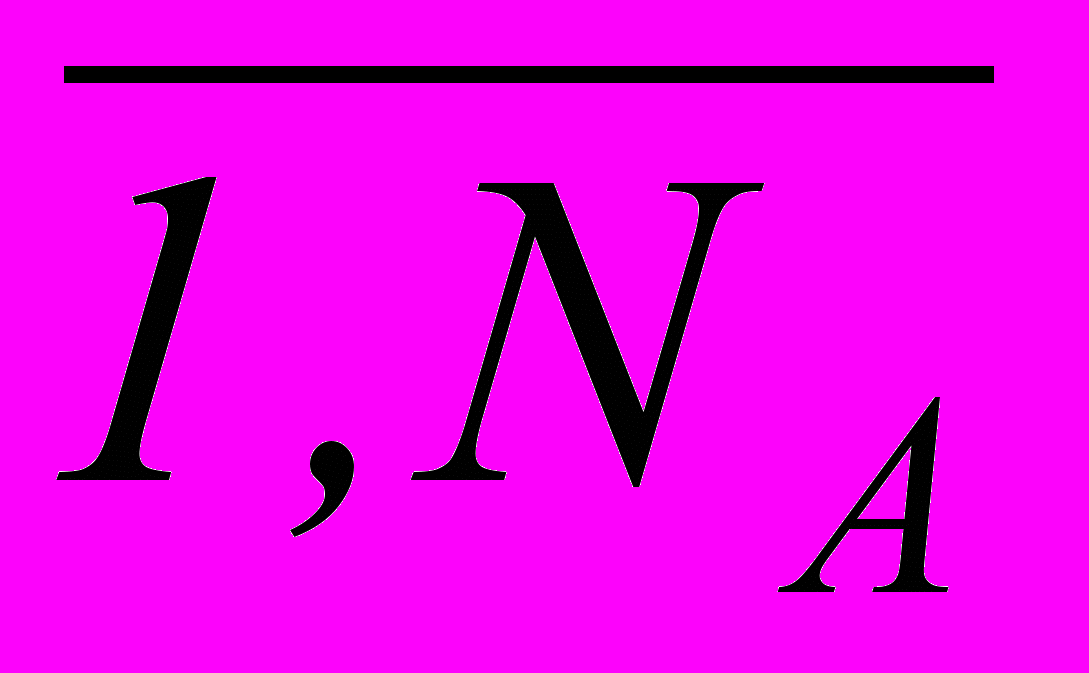 .
.Эта задача решается с помощью аддитивного алгоритма ветвей и границ как бинарная линейная задача о покрытии множества.
В четвертой главе осуществлена разработка методологии обработки баз данных при построении модели знаний на основе решающих правил. Модель знаний о ТП представляется как совокупность статической и динамической составляющих. Статическая модель отражает понятийную, концептуальную структуру предметной области. Иерархичность понятийной структуры может трактоваться как предметная онтологическая модель, узлами которой являются концепты, а отношениями – переходы между узлами. Динамическая модель описывает функциональные связи между понятиями, на основе которых принимаются решения.
Ключевым процессом при построении обучающей информационной системы является получение исходных материалов и знаний от специалистов. Понятийная структура обучающей системы: сведения о классах , их интервальные описания и макроструктура специальных текстов воссоздается коммуникативными методами.
Модели, построенные методами обучения распознаванию образов, при заданной онтологии знаний обучающей системы позволяют находить систему решающих правил, описывающих порядок изготовления продукции заданных классов, и формировать динамическую модель. В конечном итоге выявляются имплицитные структуры знаний, не поддающиеся определению текстологическими и психосемантическими методами.
Поскольку обучающая система по промышленным технологиям должна охватывать широкий спектр объектов: сырья, оборудования, производств и наполняться по принципу “от ингредиентов до изделия”, основными задачами автора-предметника являются: эксплицирование иерархии понятий с использованием отношений типа “часть – целое” для уровней сырья, материалов, деталей и продукта; описание значений и ограничений на свойства понятий для различных экземпляров классов; построение структуры технологического процесса или сценария из фрагментов, представляющих оборудование и связанных пространственными и функциональными отношениями.
Формально онтология определяется как упорядоченная тройка вида <P, R, F>, где P – конечное множество понятий предметной области; R – конечное множество отношений между понятиями; F – конечное множество функций интерпретации. Множества понятий и отношений образуют концептуальный граф, фрагмент которого представлен на рис. 2.
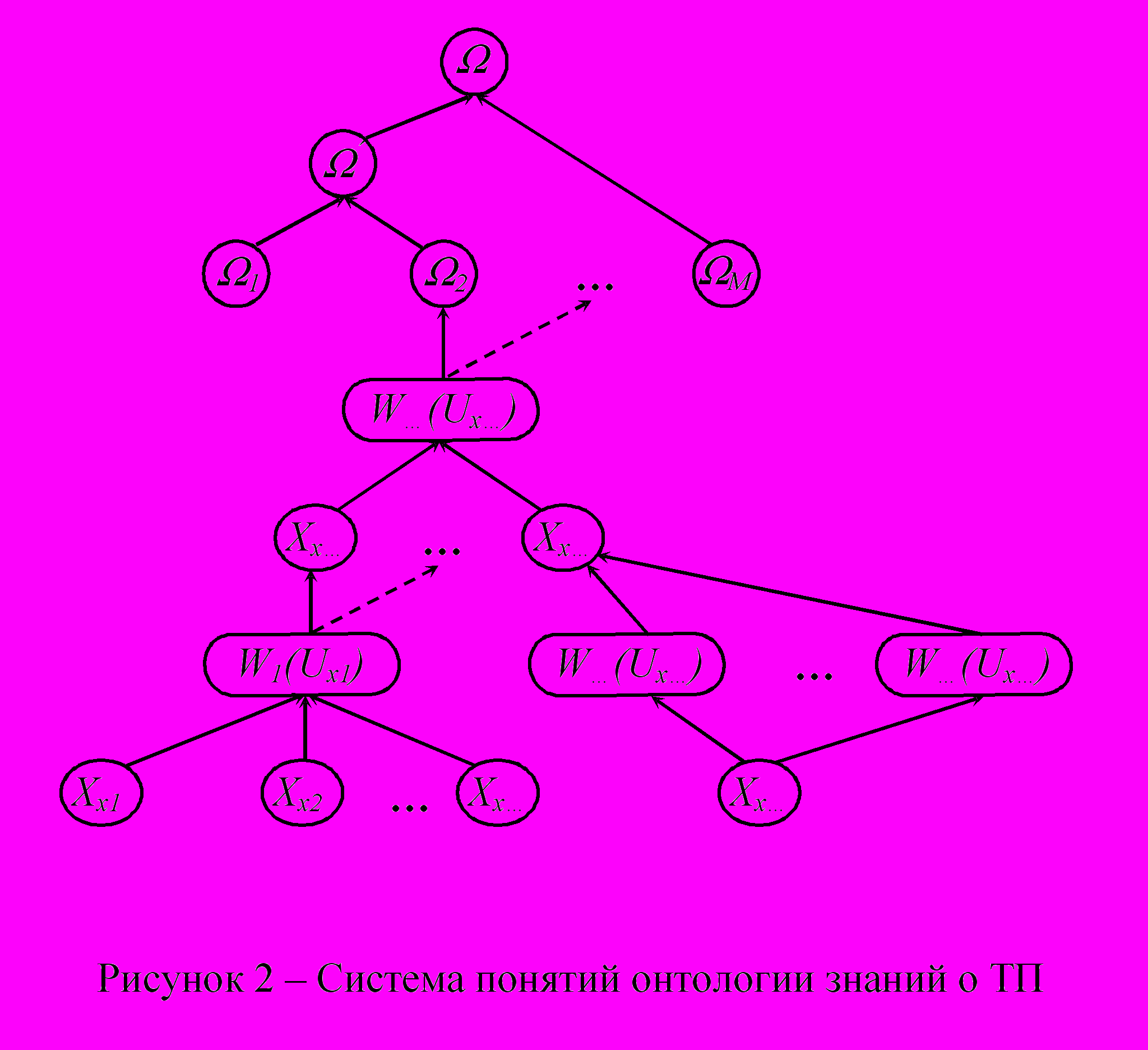
Понятие (сырье, материалы, детали, изделия) раскрывается через соответствующие атрибуты Xx, представляющие набор признаков, определяемый булевым вектором x, Xx X Y. Отношения между понятиями устанавливаются через функцию преобразования W(Ux ), выполняемую на определенном этапе ТП, Ux U. Одно и то же понятие может быть воспроизведено разными ТП, а одна технология при разных режимах может дать различные понятия. Готовые изделия образуют понятия-классы m, которые в свою очередь могут образовывать семантические подмножества . Объект i отображается на графе в одну непрерывную цепь.
Наличие описаний объектов-прецедентов, известных принадлежностью одному из описываемых классов, в единой базе данных позволяет сформулировать следующие основные этапы построения базы знаний о ТП.
1. Объединение всего набора входных параметров ТП в единое глобальное пространство XA = X U – априорный словарь признаков.
2. Конструирование запроса для извлечения из реляционной базы данных записей типа “объект – описание – решение (заключение эксперта) о принадлежности объекта”.
3. Анализ достаточности данных для формирования базы знаний.
4. Обучение распознаванию образов на основе комплексного применения дискриминантных алгоритмов, построение динамической модели как системы решающих правил.
5. Представление решающих правил в базе знаний.
Совокупность задач, которые необходимо решить в процессе формирования базы знаний, зависит от метода формирования набора решающих правил (метода обучения), объема исходной априорной информации и критерия оптимизации сформированного поля знаний.
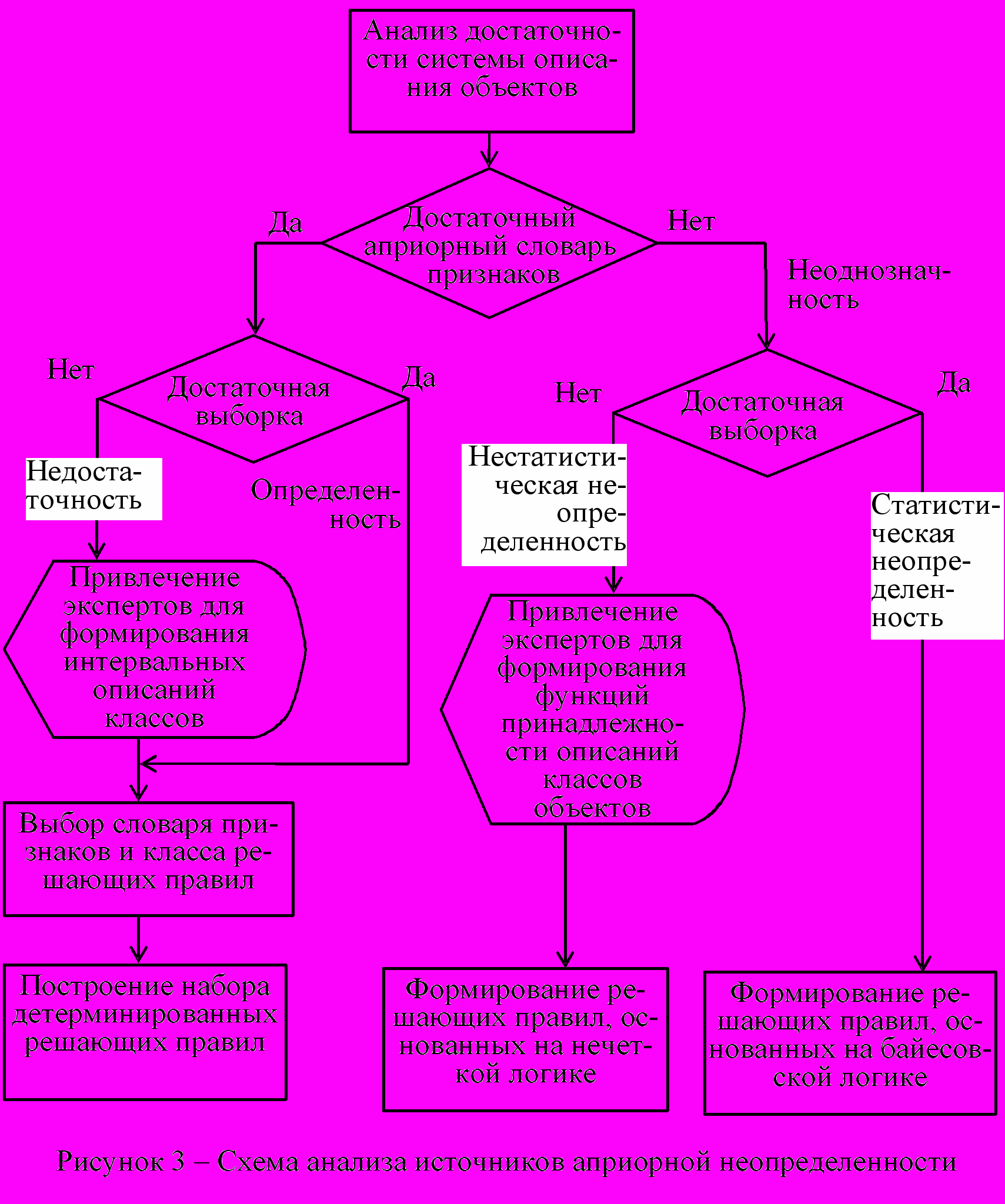
Выбор метода формирования набора решающих правил на начальном этапе создания базы знаний предложено осуществлять на основе анализа источников априорной неопределенности (рис. 3). Определяющими ограничениями при формировании базы знаний могут быть ограниченный объем обучающей выборки и / или недостаточный априорный словарь признаков XA (мала размерность NA пространства признаков).
Достаточность ОВ определяется условием n(2)/h 10…30, где n(2)=
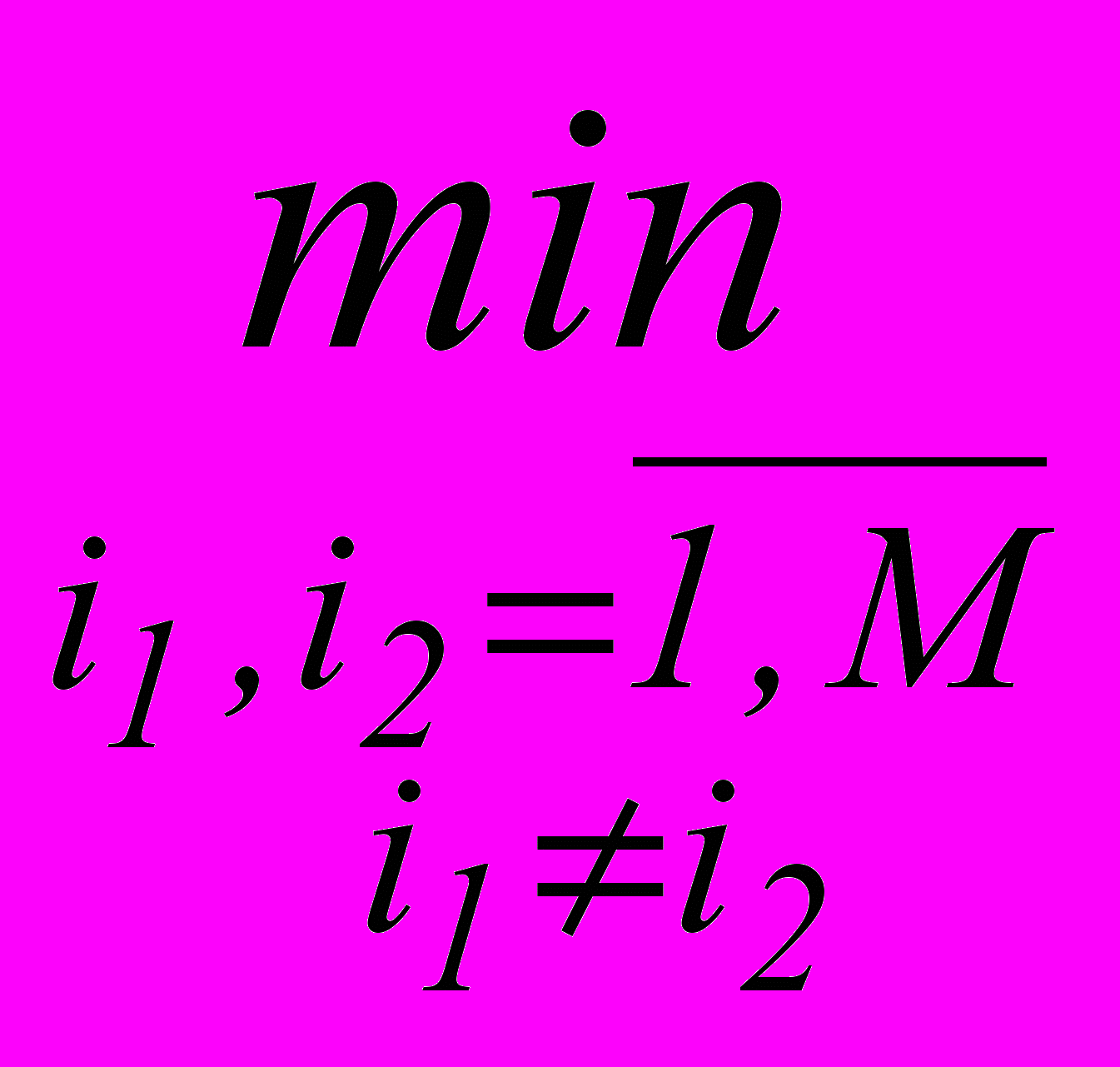 n(i1, i2), n(i1, i2) число объектов ОВ, принадлежащих паре классов i1 и i2, h = h(K, NР) емкость класса РП.
n(i1, i2), n(i1, i2) число объектов ОВ, принадлежащих паре классов i1 и i2, h = h(K, NР) емкость класса РП.В этом случае используются алгоритмы обучения детерминированного типа, минимизирующие величину эмпирического риска. Выбор РП минимальной емкости, производимый за счет снижения размерности рабочего словаря признаков Xр и использования простого класса K, осуществляется в данном случае в целях упрощения интерпретируемости сформированного правила k. При формировании знаний, основанных на легко интерпретируемых логических РП, основная задача заключается в поиске оптимального рабочего словаря признаков.
Для случая большого числа классов и ситуации недостоверности предложен новый алгоритм обучения, формирующий бинарную решающую матрицу (БРМ). Логическое решающее правило отличается высокой экстраполирующей силой. Заполнение БРМ происходит по следующему правилу:
xi j(m) =
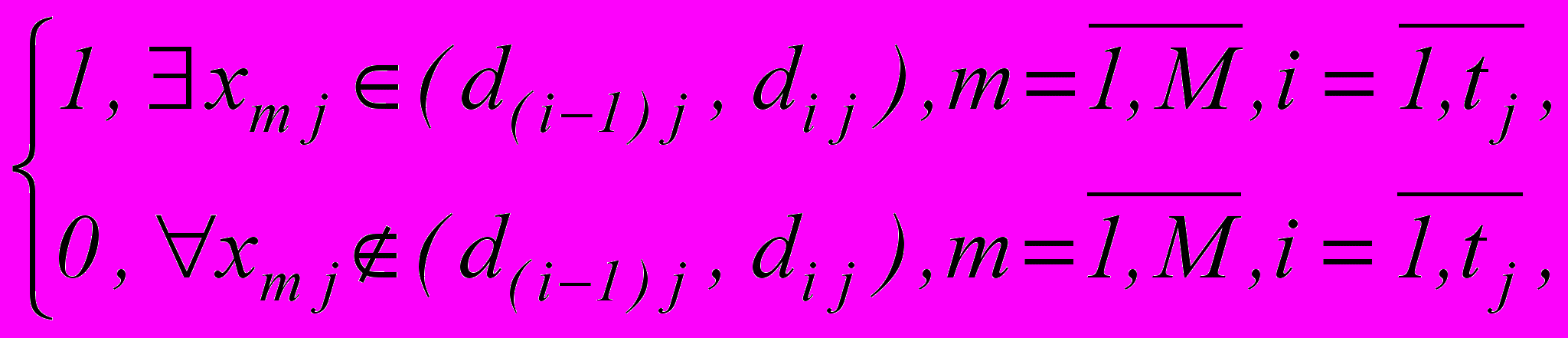
где xi j(m) – значение элемента БРМ, характеризующего принадлежность значений признака X j класса объектов Ωm i-му интервалу кодирования xi j . Исследуемый объект распознается в пространстве “своих” градаций. Распознавание осуществляется посредством поэлементной конъюнкции ячеек матрицы, на которые указывают значения признаков распознаваемого объекта, и выделения единичной ячейки, соответствующей коду класса.
При выявлении внутри m-го класса регрессионных зависимостей
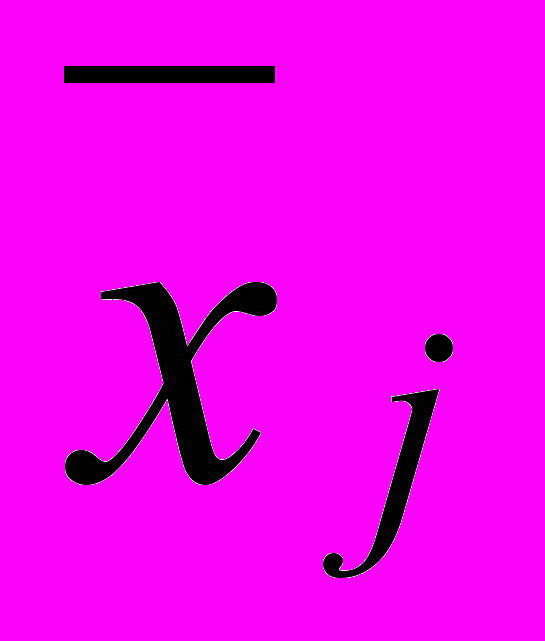 = f(xj 1 , xj 2 , …), в качестве порогов используются доверительные границы для прогнозов значений признака xj по входным переменным xj-1 , xj-2 последних звеньев технологической цепочки:
= f(xj 1 , xj 2 , …), в качестве порогов используются доверительные границы для прогнозов значений признака xj по входным переменным xj-1 , xj-2 последних звеньев технологической цепочки: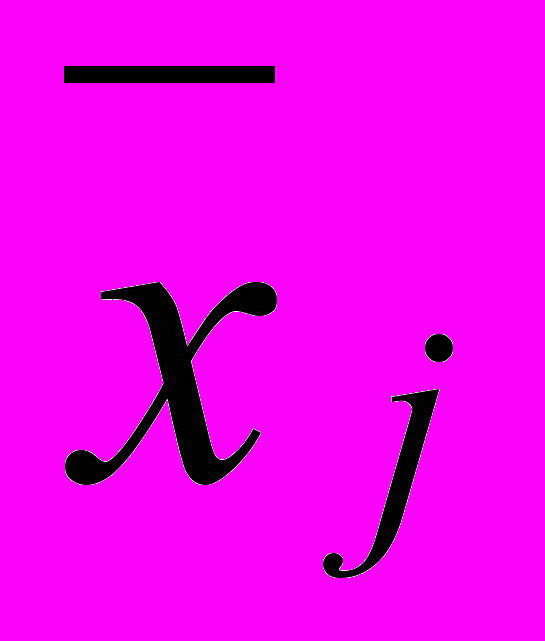 (xj 1 , xj 2 , …) – t1-Sxj (xj 1 , xj 2 , …) d(i-1) j ,
(xj 1 , xj 2 , …) – t1-Sxj (xj 1 , xj 2 , …) d(i-1) j ,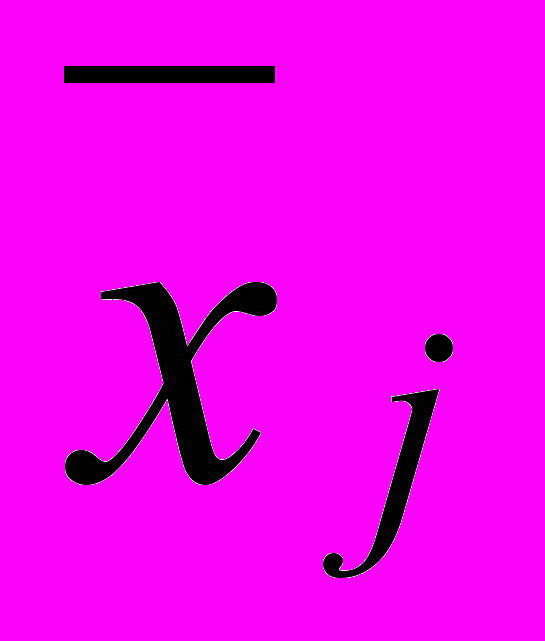 (xj 1 , xj 2 , …) + t1-Sxj (xj 1 , xj 2 , …) d(i-1) j ,
(xj 1 , xj 2 , …) + t1-Sxj (xj 1 , xj 2 , …) d(i-1) j ,где t1– – квантиль распределения Стьюдента с числом степеней свободы nm 1, nm =
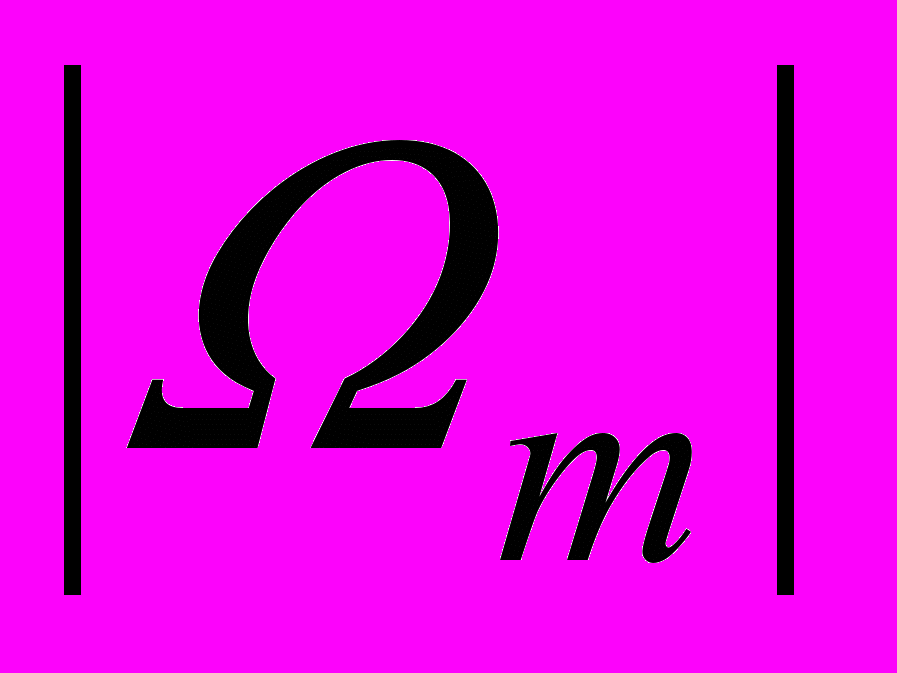 ;
;1 – – доверительная вероятность;
Sxj (xj 1 , xj 2 , …) – оценка стандартного отклонения признака xj.
Простота процедуры обучения (установка интервальных порогов) и распознавания (логические операции и операции сравнения) позволяет легко реализовать семантическую интерпретацию БРМ.
Использование алгоритмов распознавания нечетких (размытых) образов позволяет учесть сложность структуры классов объектов для полиробастных технологических процессов, а также нестатистическую неопределенность принадлежности объектов к некоторым классам, связанную с недостаточностью описаний объектов и малым размером обучающей выборки. Предложен новый алгоритм обучения, формирующий многоградационную матрицу степеней принадлежности
 , i j m =
, i j m = 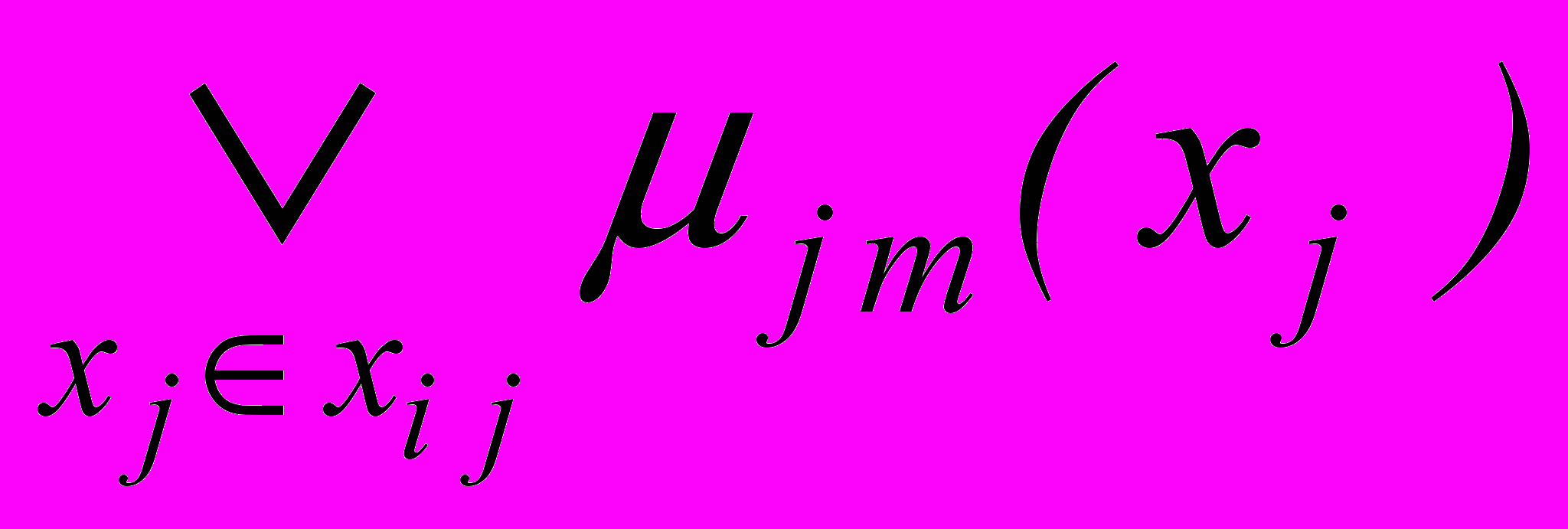 , m =
, m = 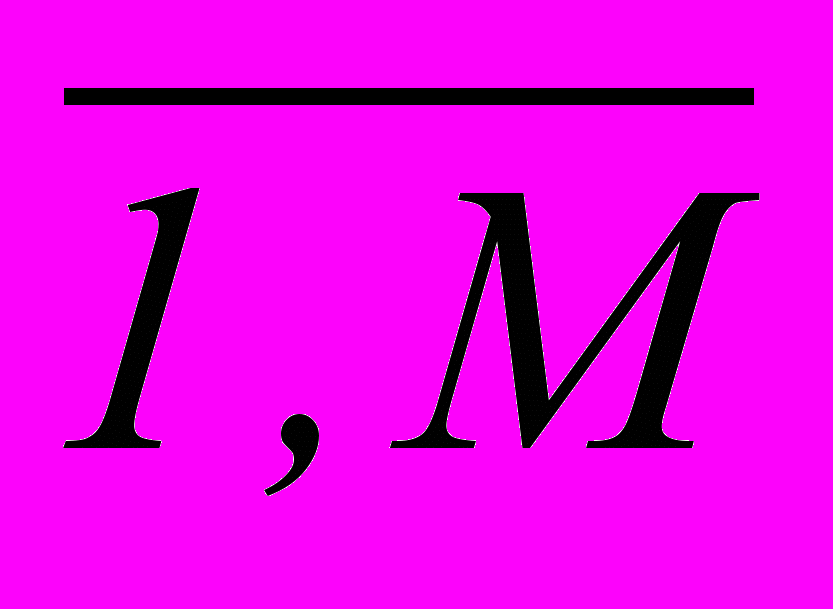 , i =
, i = 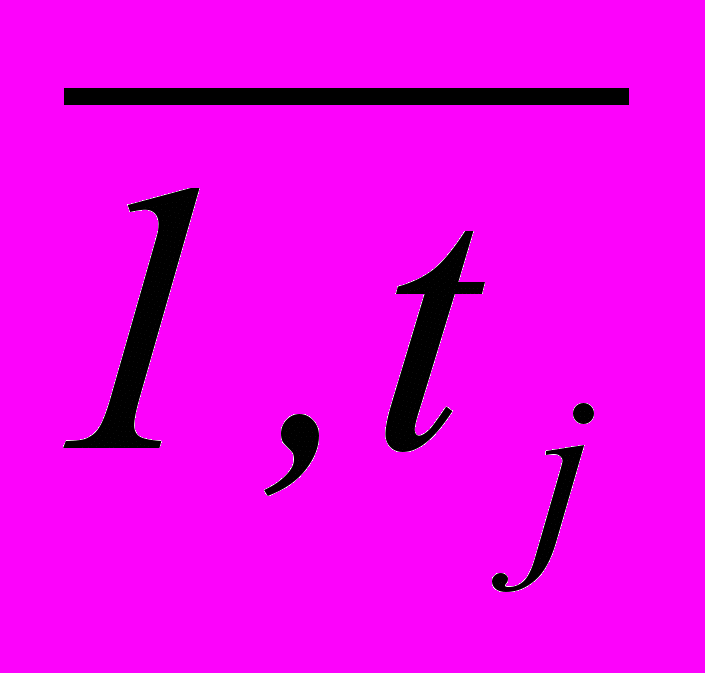 .
.Решение о классе объекта выносится в четкой или размытой форме. Лингвистическое значение нечеткого класса имеет вид
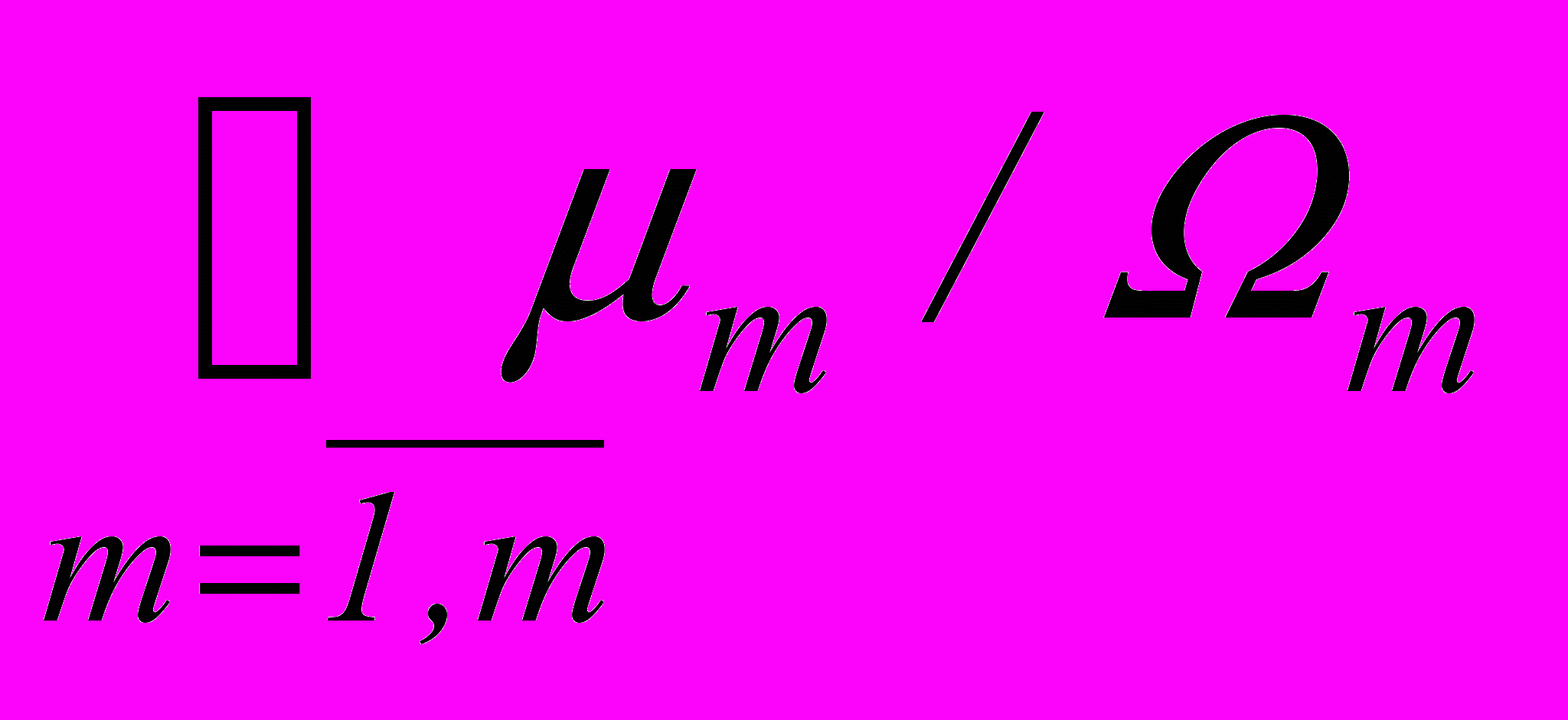 , где m =
, где m = 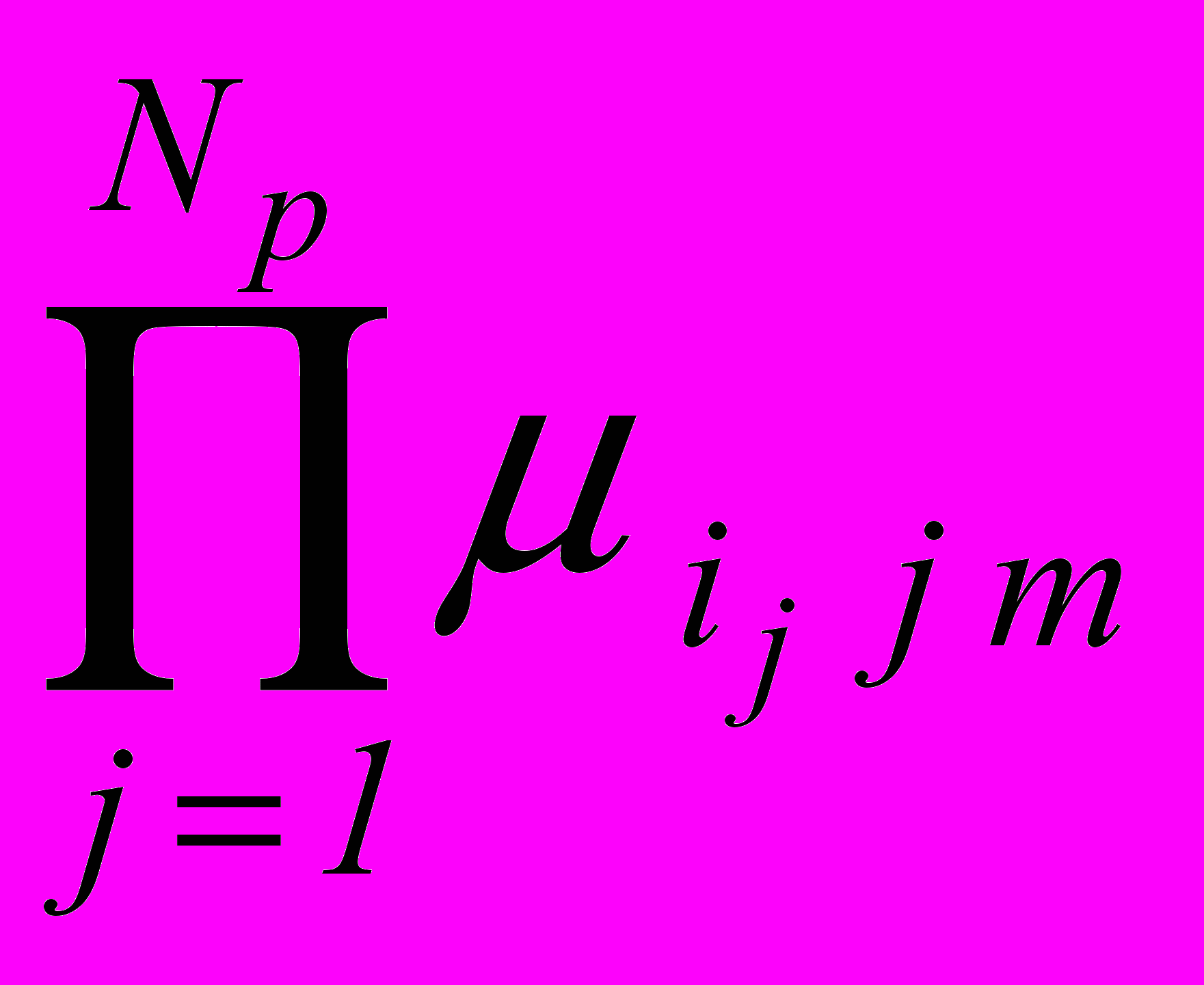 , m =
, m = 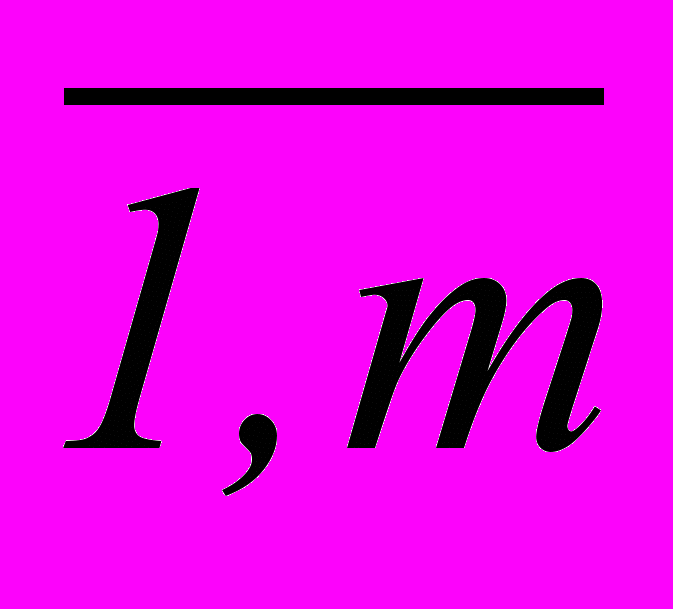 . Четкое наименование класса обеспечивается выбором терма с индексом
. Четкое наименование класса обеспечивается выбором терма с индексомm* =
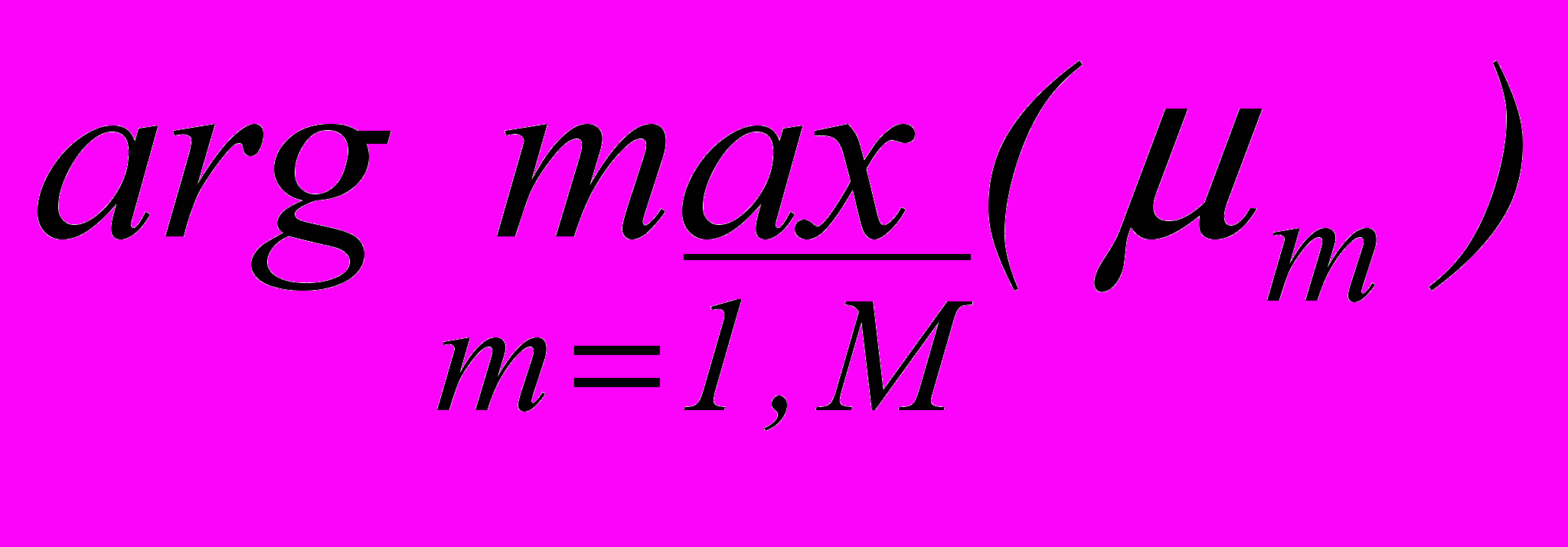 , m* .
, m* .Нечеткое РП помимо учета опыта эксперта позволяет эффективно организовать процесс распознавания с использованием простых логических операций и операций умножения.
В ситуациях статистической неопределенности, для задач выявления новых свойств на фоне большого числа случайных, неучтенных факторов, воздействующих на условия протекания технологического процесса, предлагается упрощенный последовательный критерий отношения вероятностей (ПКОВ), который на n-м шаге измерения признака X имеет вид
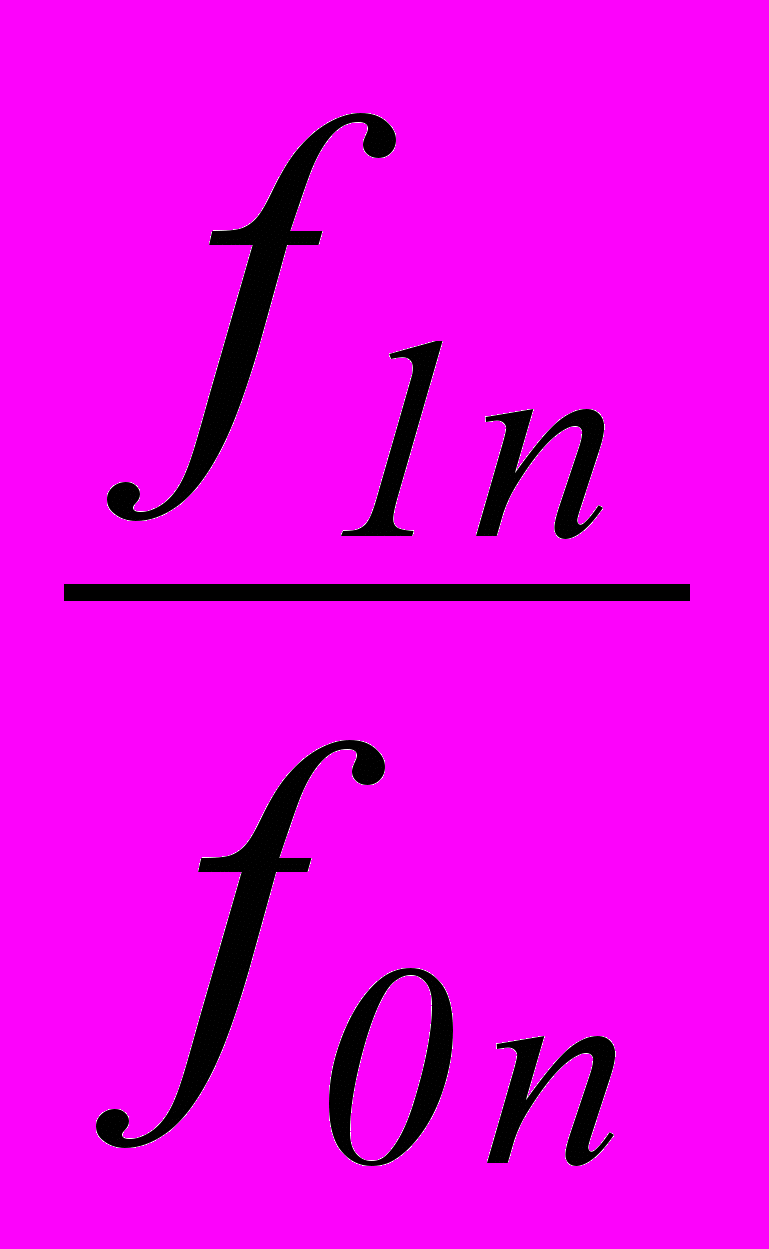 =
= 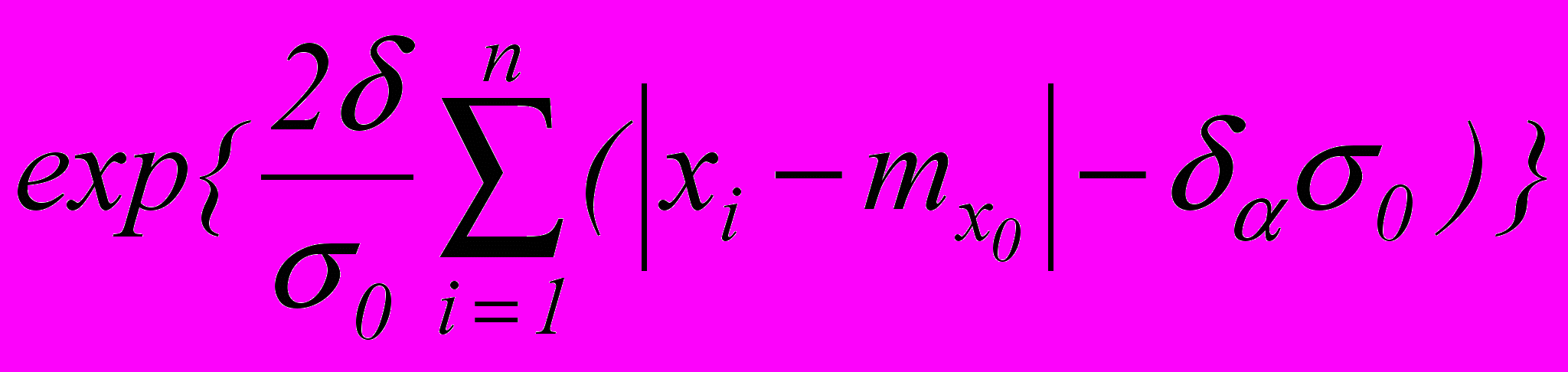 ,
,где – граница критической области теста
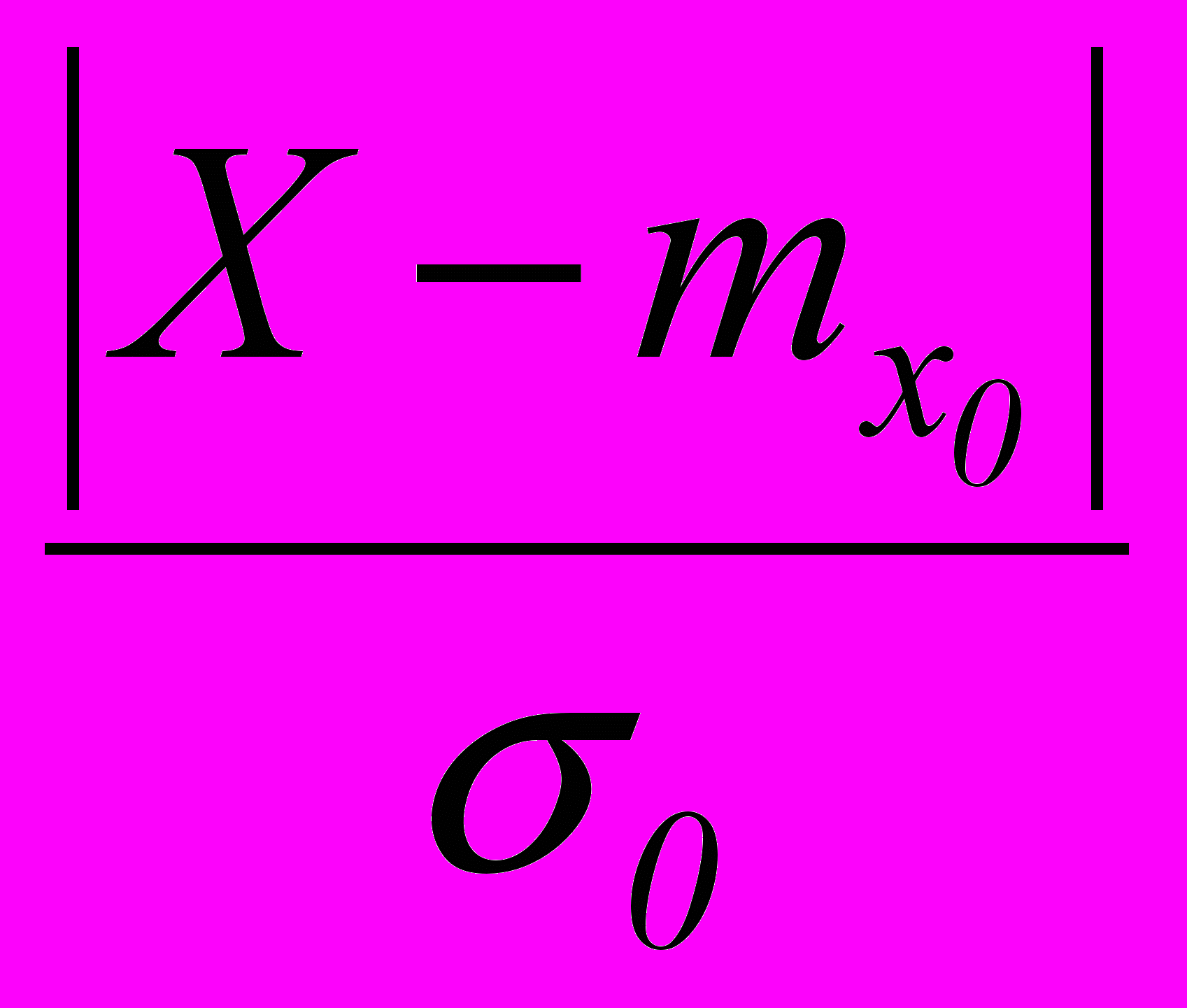 для заданного уровня значимости , 2 – ширина области безразличия, 0 выбирается исходя из заданной точности измерения признака X. Последовательное РП позволяет накапливать информацию о значениях признака X объекта на этапе логического вывода.
для заданного уровня значимости , 2 – ширина области безразличия, 0 выбирается исходя из заданной точности измерения признака X. Последовательное РП позволяет накапливать информацию о значениях признака X объекта на этапе логического вывода.В случае неравноценности ошибок первого и второго родов определены параметры усеченного ПКОВ, позволяющие повысить эффективность последовательного метода при выявлении интересующего свойства.
При большом числе классов объектов, подлежащих распознаванию, усеченный ПКОВ удобно применять совместно с простейшими логическими РП для разделения пар пересекающихся классов. Если логическое РП разделяет классы, интервалы значений признаков которых не пересекаются, с помощью установленных при обучении порогов, то в случае трудноразделимых классов используются пороги, зависящие от состава и объема выборки измеренных значений признака.
Разработано и реализовано алгоритмическое обеспечение инструментального комплекс для автоматизации проектирования динамической модели знаний интеллектуальных обучающих систем технологической направленности. Динамическая модель строится как система решающих правил, оперирующих признаками рабочего словаря XР XA , на основе знаний как эксплицированных специалистом, так и полученных методами обучения распознаванию образов.
Исходными данными являются описания XA производимых объектов с указанием их принадлежности соответствующему классу. Список признаков, входящих в априорный словарь, специалист формирует исходя из заданного алфавита классов объектов, в частном случае – при составлении онтологии знаний об описываемых ТП. Основное внимание при наполнении комплекса уделяется алгоритмам ОРО, обеспечивающим высокую экстраполирующую силу найденных правил при ограниченном обучающем материале, – алгоритмам, основанным на логических и линейно-логических решающих правилах.
Решающие правила, построенные как простой набор дискриминантных функций линейного и более сложного вида, даже в случае полного разделения классов не содержат знаний о диапазонах изменения значений параметров ТП и их взаимодействий для получения готового изделия заданного класса. Их анализ позволяет указать лишь состав наиболее важных технологических параметров и их весовые коэффициенты для попарной различимости технологических процессов.
Логические правила в форме бинарной решающей матрицы и нечеткой решающей матрицы легко поддаются семантической интерпретации и соответствующей реализации в базе знаний. В общем виде семантика логического правила выглядит следующим образом: “продукция класса m может производиться последовательно на оборудовании … при значениях параметров … , равных …, из деталей … со свойствами …, лежащими в диапазонах …., которые изготовлены из материалов с параметрами, лежащими в диапазонах …, которые изготовлены из сырья …, имеющего свойства … “.
Выбор среди множества альтернативных логических РП в условиях недостаточной ОВ осуществляется на основе рассмотрения сформированных систем описания, так как в этом классе алгоритм распознавания синтезируется непосредственно в процессе кодирования и поиска рабочего словаря признаков, а лучшее качество имеет алгоритм, для которого минимальной является величина объема пространств признаков V.
Комплекс использовался при создании базы знаний для распознавания деталей сложной формы на ряде многономенклатурных конвейерных производств. Экспериментальные исследования показали, что программа распознавания, реализующая БРМ, помимо экономии объема требуемой памяти обеспечивает более высокое быстродействие по сравнению с остальными реализованными алгоритмами логического распознавания.
Показано, что способ кодирования признаков должен соответствовать введенному критерию информативности группы признаков, который, в свою очередь, должен быть согласован со сложностью решающего правила. Для дискретных линейных решающих функций предложен интервальный критерий информативности группы признаков, позволяющий увеличить их экстраполирующую силу.
Учет взаимосвязи основных этапов обучения на основе комплексного применения дискриминантных алгоритмов в условиях ограниченной априорной информации позволяет создавать динамическую модель знаний с обеспечением высокой точности при принятии решения по новым данным.
В пятой главе рассмотрена методика использования разработанных методов и алгоритмов интеллектуального анализа данных при создании обучающих систем в области технологии и дизайна.
Проблема выделения информационных блоков и установления логических связей между сотнями, а иногда тысячами учебных элементов решается на примере формирования логической схемы обучающей системы при ее реализации в гипермедиа технологии, когда учебный материал кроме гипертекста включает графическую информацию, анимационные, аудио- и видео фрагменты, а также интерактивные виртуальные сцены.
Интервальные описания позволяют построить соответствующую бинарную решающую матрицу и сформировать систему решающих правил в терминах рассматриваемой предметной области. Описан процесс разбиения учебного материала с выделением на основе решающей матрицы декларативных, отличительных, повторяющихся и дополнительных информационных фрагментов. Он позволяет сократить объем мультимедийных и текстовых данных за счет устранения дублирующих сведений, встречающихся при описании порядка создания продукции различного типа. Этот эффект также будет наблюдаться для текстового и графического материала при полиграфическом представлении обучающего средства, если его разделы сформированы на основе множества выделенных классов .
Размещение информационных блоков для некоторых гипертекстовых учебников осуществлено в разработанной с участием автора информационно-образовательной среде Санкт-Петербургского университета технологии и дизайна, функционирующей в глобальной сети Интернет.
Формирование проектно-художественной концепции сложного системного объекта – ассортимента производственной одежды – выполняется с помощью разработанной системы дизайн-программирования (рис. 4).
| Рисунок 4 – Формирование ассортимента производственной одежды |

В основу поля знаний системы положена функциональная структура ассортимента ПО, раскрываемая в признаковом пространстве объективных функционально-эргономических характеристик изделий. Отработка концепции корпоративного дизайна в соответствии с выявленной видовой номенклатурой выполняется с помощью графической подсистемы. База данных для ассортиментных групп структурирована в соответствии с онтологической схемой по группам, видам, подвидам и типам изделий производственной одежды. Каждая признаковая категория представлена в базе графическим изображением соответствующего уровня детализации: от базовых силуэтных форм до функциональных и функционально-декоративных элементов. База знаний реализует решающие правила, сформулированные специалистом-дизайнером, и подпрограммы для управления сценарием, заложенным в процесс проектирования. Пользователю предлагаются такие решения, которые отвечают эстетическим и эргономическим требованиям, обеспечивают безопасность проектируемой одежды в зависимости от сферы ее будущего использования.
Конструктивность принципов комплексного применения множества дискриминантных алгоритмов проверена при построении поля знаний ряда обучающих систем.
Обучающая система "Текстильные технологии" предназначена для формирования знаний по широкому спектру текстильных объектов: сырья, оборудования, производств текстильной промышленности. Изучение технологических процессов и оборудования, структуры и свойств продуктов и полупродуктов текстильных производств осуществляется по принципу “от волокна до изделия”. Для построения разделов выделены следующие классы знаний: "Волокна", "Пряжа", "Трикотаж", "Ткань", "Нетканые материалы", "Одежда", "Отделка", "Контроль качества". Фрагмент онтологии и динамической структуры обучающей системы приведен на рис. 5. Процедурные информационные блоки в основном представляют аудиовизуальную информацию (рис. 6): обычную и анимированную графику, демонстрирующую особенно важные технологические операции и труднодоступные для фотосъемки узлы; звуковые сообщения и видеофрагменты для пояснений при освоении учебного материала.
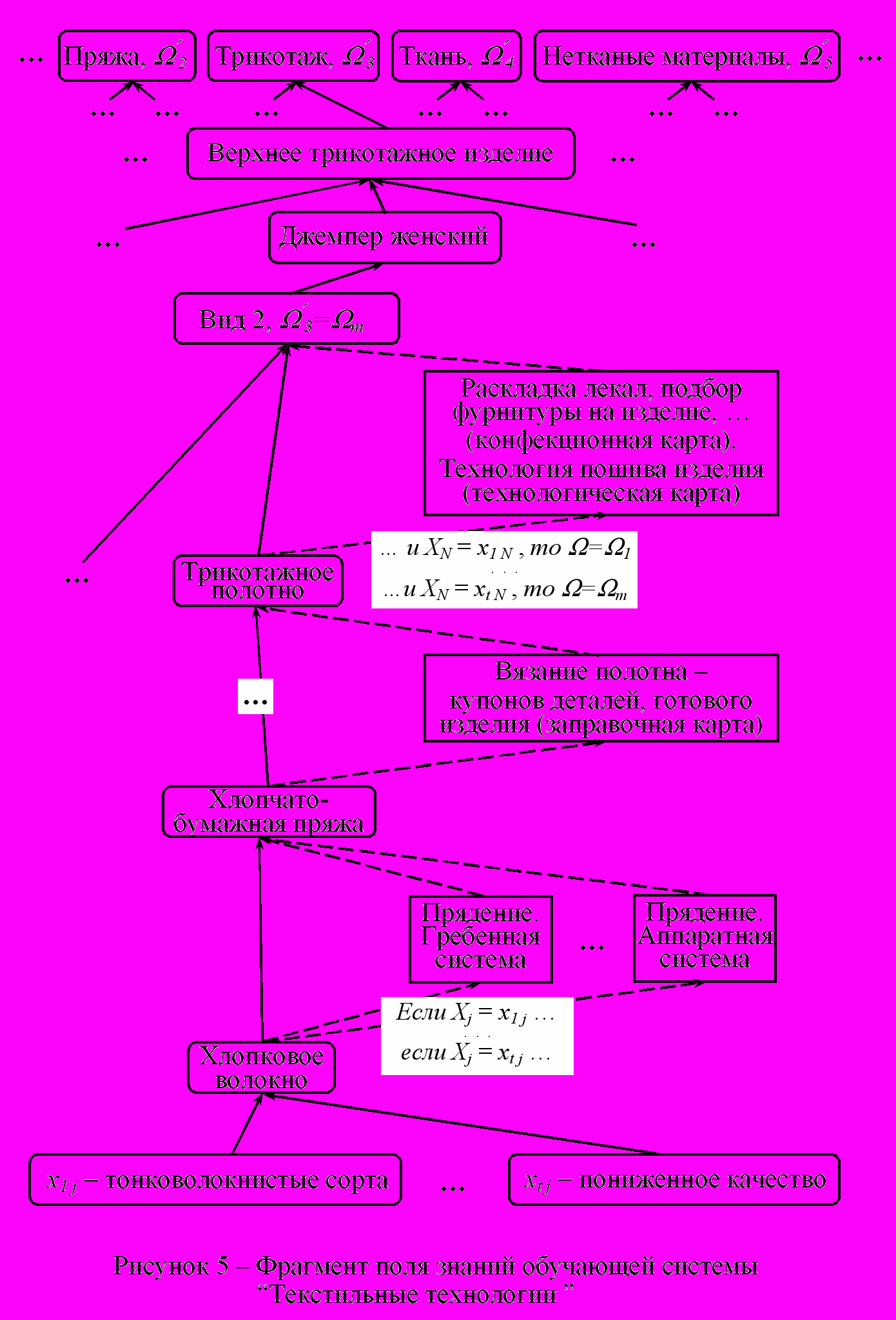
| Рисунок 6 – Обучающая система "Текстильные технологии" |

Приведены примеры использования решающих правил при выделении различных классов для построения моделей процесса обучения, описывающих этапность решения учебных задач и освоения учебных элементов.
В обучающей системе “Анализ данных” множество представляет собой классы задач, для решения которых требуется поиск статистических зависимостей различного вида. Сквозные типовые задачи, относящиеся к различным классам, основаны на этапности выполнения процедур анализа данных с применением информационных технологий. При построении модели мультимедийного учебника была сформирована бинарная матрица использования процедур анализа данных для различных классов технологических задач. На ее основе составлена схема логических связей учебных элементов.
Весь учебный материал по уровням освоения учебного материала и способу представления разделов курса разбит на три категории:
иерархическая схема этапов анализа ( =0);
теоретические сведения ( =1);
примеры решения задач в соответствующем специализированном пакете ( =2…3).
Информационные блоки каждого класса делятся на три типа: декларативный блок с теоретическими сведениями – описаниями базовых понятий, методов и моделей и процедурные блоки с алгоритмом анализа или пошаговым выполнением метода в специализированном пакете. Система использует анимацию графики, демонстрирующей ход решения примеров и задач; звуковые сообщения для пояснений по использованию курса, перевода английских терминов и предложений в области статистики.
В основу методического построения комплекса учебно-методических материалов (КУММ) “Разработка экспертных систем” положена информационная модель обучения. В ходе работы по отбору и структурированию учебных элементов была составлена модель содержания учебного материала и бинарная матрица освоения учебных элементов для различных целевых групп. В результате преобразования набора БРМ сформирована как логическая структура поля знаний, так и процедурный компонент в виде набора правил.
КУММ предусматривает возможность реализации различных траекторий обучения, выбор которых зависит как от целей, поставленных перед обучаемым, так и от начального состояния обучаемого. Реализация этих возможностей обусловлена составом КУММ (учебное пособие, мультимедийный курс, содержащий справочник, систему тестирования, тренажер) и применяемыми методическими приемами. В состав тренажера включена инструментальная среда для разработки прикладных экспертных систем. Она способствует развитию и закреплению навыков создания практических приложений. Среда дополнена средствами для получения консультаций и контроля знаний, введения лексики по выбранной предметной области.
Методика построения обучающих систем технологической направленности на основе методов обучения распознаванию образов применима при реализации моделей процесса обучения, в которые заложены различные уровни усвоения учебного материала (рис. 7).
Логическое РП в форме БРМ позволяет разбить учебно-методический материал на декларативные и процедурные информационные блоки и установить связи между ними, обеспечивая первый уровень освоения учебного материала. Использование заданных моделью обучения тестов на основе процедурных блоков и наложение обратных связей на гипертекстовое представление позволяет перейти на уровень автоматизированной обучающей системы ( = 2). Внедрение интеллектуальной составляющей – базы знаний о ТП и механизма объяснений позволяет подключить уровень причинно-следственных связей, описывающих переходы типа “процедурный блок–информационный фрагмент” ( = 3...4). Записанная в виде продукций базы знаний система РП составляет основу экспертной обучающей системы, функционирующей в режиме тренажера или консультанта. Подключение инструмента разработчика или исследовательского пакета прикладных программ дает обучаемому возможность выйти на уровень манипулирования профессиональными знаниями. Реализация переходов между уровнями освоения учебного материала при смене целей обучения и адаптации процесса обучения к текущему профилю пользователя возможна в рамках многоагентного подхода как управление разнотипными знаниями.
Новизна разработанных обучающих программ подтверждена выдачей свидетельств об официальной регистрации программы для ЭВМ.
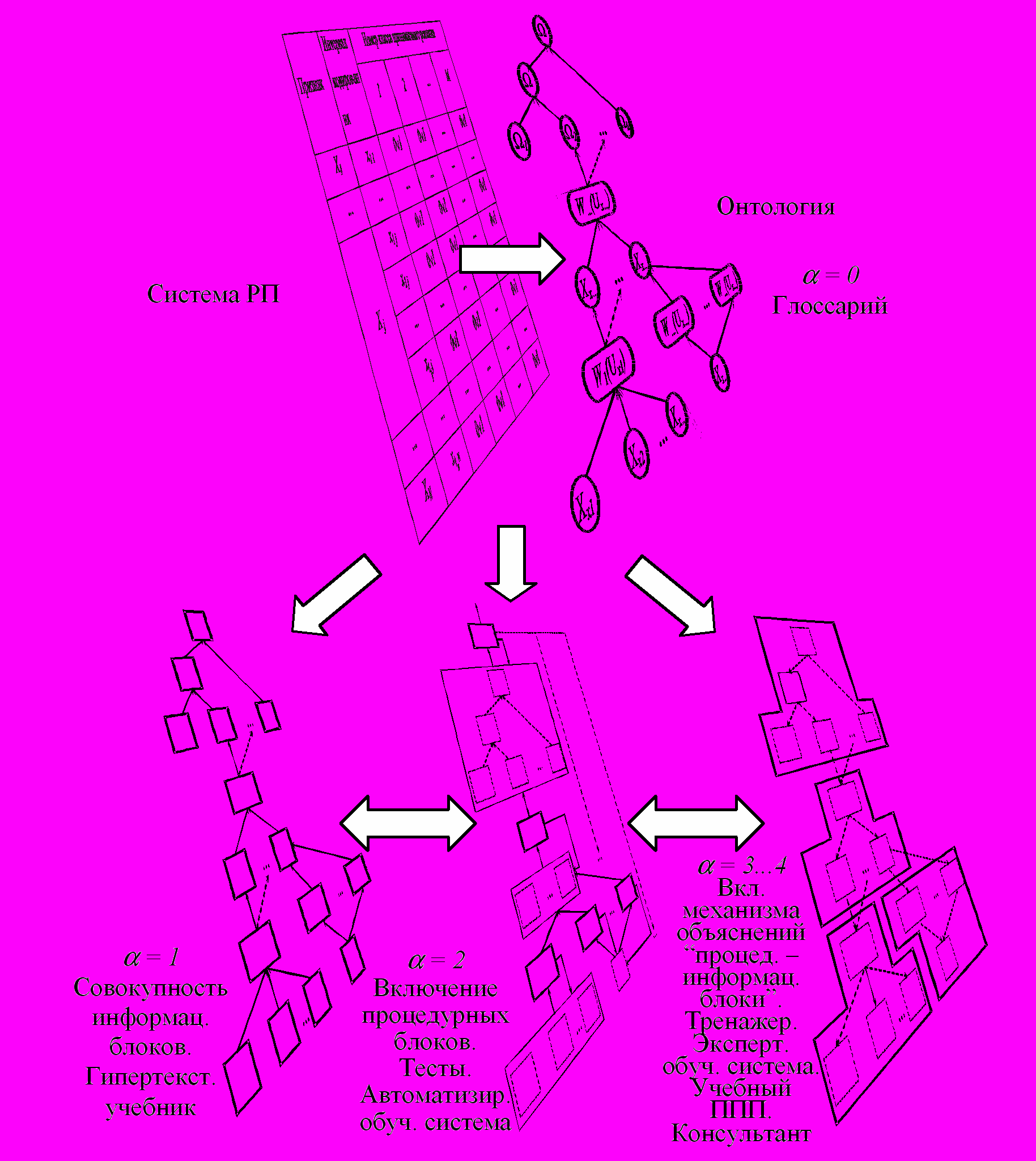
Рисунок 7 – Уровни усвоения учебного материала
В приложении дан вывод гарантированных оценок риска для простейших классов решающих правил и основных соотношений последовательного метода выделения класса с новыми потребительскими свойствами, приведено краткое описание способов снижения вычислительных затрат при минимизации набора признаков, представлены фрагменты экранных изображений разработанных обучающих программ и акты внедрения результатов диссертационной работы.
