Методы, модели и алгоритмы интеллектуального анализа данных при создании обучающих систем в текстильной и легкой промышленности 05. 13. 01 Системный анализ, управление и обработка информации (промышленность)

Вид материала

Подобный материал:

1 2 3 4 5

Содержание работы

Во введении изложены основные положения диссертационной работы, обоснована актуальность темы, определена цель исследований и решаемые задачи, дана характеристика научной новизны и практической значимости работы. Представлены данные об апробации работы и публикациях.

В первой главе проведен анализ современного состояния проблемы создания обучающих систем и синтеза образовательных ресурсов. Выявлены тенденции перехода к новым моделям организации учебного материала и технических средств обучения.

Рассмотрены этапы развития и технологии реализации компьютерных обучающих систем, методы выделения учебных элементов, принципы сборки конечных модулей и курсов. Совершенствованию методов создания систем учебного назначения в значительной степени способствовали труды российских ученых: А. И. Башмакова (МГЭИ (ТУ)), В. П. Беспалько (МГОУ), И. Л. Братчикова (СПбГУ), А. Ю. Деревниной (ТюмГУ), Дозорцева В.М. (РГУ нефти и газа им. И. М. Губкина), З. О. Джалиашвили (СПбГИТМО (ТУ)), В. И. Солдаткина (РГИОО), А. В. Соловова (Самарский ГАУ), Д. В. Сошникова (МАИ (ГТУ)), В. П. Тихомирова (МЭСИ), Т. Б. Чистяковой (СПбГТИ (ТУ)), работы, выполняемые в рамках ряда федеральных программ: “Электронная Россия на 2002–2010 годы”, “Развитие единой образовательной информационной среды на 2001–2005 годы”, “Создание системы открытого образования”, при разработке федерального портала “Российское образование” www.edu.ru, Федерального центра информационно-образовательных ресурсов eor.edu.ru, информационной системы “Единое окно доступа к образовательным ресурсам” window.edu.ru, распределенного Российского портала открытого образования www.openet.ru и др. Из зарубежных работ в этой области исследований отмечены работы Б. Скиннера, Н. Краудера, У. К. Ричмонда, А. Пателя, Кинчука, К. Лемона, В. Люка.

Расширение функциональных возможностей средств электронного обучения, интеллектуализация обучающей системы возможны после построения ряда информационных моделей, основными из которых являются модели обучаемого, процесса обучения и предметной области (рис. 1). Одной из основных характеристик обучаемого является показатель уровня усвоения учебного материала , который может меняться от осмысленного понимание новой информации до уровня творческой деятельности и создания новых знаний. На основе оценки уровня усвоения студентами учебных элементов выполняется коррекция учебного материала в процессе обучения. Модели процесса обучения и предметной области определяют набор логических связей и декомпозицию учебного материала. Его структуризация обычно выполняется на основе дидактических рекомендаций, зависит от педагогического мастерства и слабо поддерживается рабочими методиками. Повышение эффективности гипертекстовой обучающей системы в области технологии и дизайна, способной формировать гибкую, индивидуальную цепочку учебных элементов, опирается на объектное хранение учебных модулей и устранение дублирующих мультимедийных и текстовых данных, описывающих, например, повторяющиеся для различных технологических процессов операции.

Компонентами, которые необходимо формализовать при построении модели предметной области, описывающей технологические процессы и конструкторские решения, являются вербальная модель (снабженная иллюстрациями, формулами, таблицами и т. п.), а также большое количество экспериментальных данных. Целый ряд конструкторско-технологических задач в текстильной и легкой промышленности являются слабоформализованными. Для принятия конкретных решений в сфере дизайна, конструирования одежды и обуви необходим значительный предшествующий опыт специалиста, снижающий неопределенность проектной задачи. В таких условиях обучающая система должна быть основана на знаниях.

Развитию методологических основ системного подхода к исследованиям в области текстильной и легкой промышленности способствовали труды российских и зарубежных ученых: В. Е. Романова, К. Е. Перепелкина, А. Г. Севостьянова, А. М. Сталевич, Н. Н. Труевцева, Б. Н. Гусева, Е. Я. Сурженко, Е. Б. Кобляковой, А. С. Далидович и др. Знания о ТП позволяют воссоздать в пространстве и времени последовательность технологических переходов, указав все причинно-следственные связи (отношения), возможные альтернативные последовательности, диапазоны значений технологических параметров, обеспечивающие получение готового продукта требуемого качества. Выделены особенности задач, возникающих при концептуализации текстильных объектов и объектов легкой промышленности. Показано, что с точки зрения описания понятий и их свойств вопросы описания и формализации исходных ингредиентов и готового продукта могут решаться одинаково.

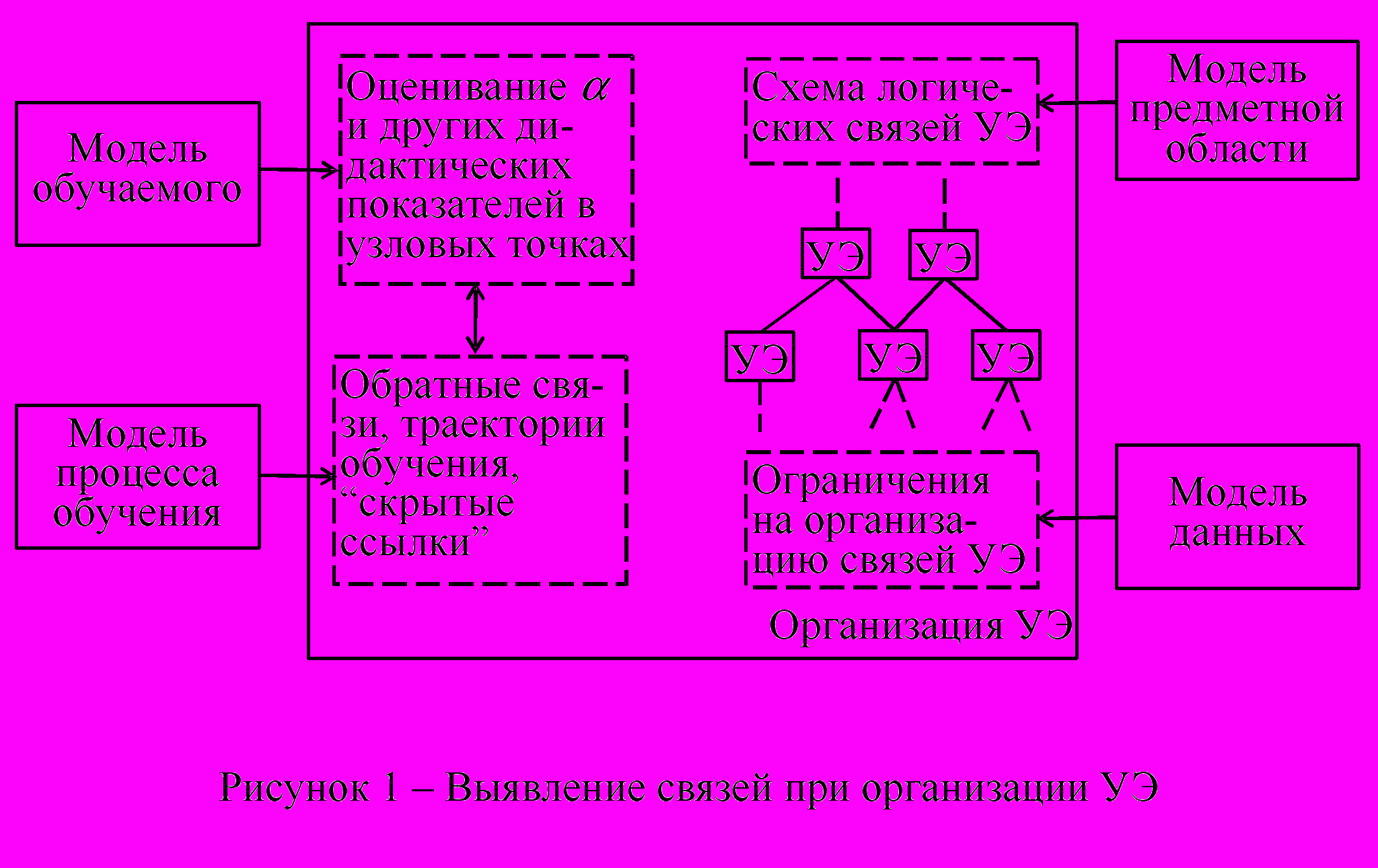
Современный рыночный принцип создания новых текстильных, швейных и других изделий базируется на следующей “цепочке заказа”: изделие определенного функционального назначения → текстильный материал заданной структуры → волокна заданного состава. Многоуровневое представление технологических процессов и оборудования, структуры и свойств продуктов и полупродуктов текстильных производств осуществляется по принципу “от волокна до изделия”. Отмечено, что этапность выполнения технологических операций, выделение классов готовой продукции, разработка для каждой конкретной области применения текстильных материалов их специальных видов с оптимизированными свойствами свидетельствуют в пользу построения дискретных моделей знаний о технологических процессах.

Рассматривается проблема выявления знаний при разработке интеллектуальных обучающих систем. Выделение категорий технологических объектов выполняется специалистом в предметной области по сочетаниям свойств всех или отобранных выходных признаков, например, потребительских свойств изделия либо методами автоматической классификации. Число атрибутов, идентифицирующих технологические и текстильные объекты в базе знаний (БЗ) технологических процессов, исчисляется сотнями. В подобных условиях представление поля знаний вручную чрезвычайно затруднено: консеквенты большинства правил указывают на абстрактные категории, а увеличенное число условий в антецеденте трудно сформировать умозрительно. Для представления знаний, эксплицированных специалистами, и извлечения знаний из массива данных, образованных триадами “объект–атрибуты–значение”, предложено использовать методологию обучения распознаванию образов для автоматического построения обобщающих правил, описывающих принадлежность ситуаций к классам. В случаях, когда объем обучающих данных ограничен, в особенности при наличии большого числа классов, определена необходимость рассмотрения прогностических свойств построенной системы решающих правил.

Решающие правила, построенные в процессе обучения распознаванию образов, используются для представления динамических знаний о ТП в виде набора продукций. Причинно-следственные связи между классами объектов и их признаками, отражающие закономерности в обучающих последовательностях, чаще всего устанавливаются с помощью логических РП. Эти правила при малой мере сложности являются универсальными для эффективного решения прикладных задач. Они легко поддаются семантической интерпретации и позволять автоматически формировать сообщения типа “на заданном оборудовании, в заданной последовательности, с заданными режимами подвергнуть исходные элементы определенному воздействию”.

Дополнительные требования к представлению знаний, которые нельзя формализовать символьным представлением – использование обычной и анимированной графики, видео, 3D-моделей, демонстрирующих особенно важные технологические операции и труднодоступные для фотосъемки узлы.

На основании проведенного анализа современного состояния проблемы создания обучающих систем делается вывод о том, что знания, эксплицированные специалистом и извлеченные методами ОРО в результате научных исследований, при эксплуатации технологического оборудования, могут переноситься в сферу учебного процесса в виде многофункциональной обучающей системы, охватывающей различные уровни усвоения учебного материала и предоставляющей возможность гибкого использования учебных элементов в процессе обучения, благодаря достоинствам моделей данных, основанных на гипертексте, объектном подходе и методе экспертных систем. В завершении главы выявлены основные направления научного исследования, выбраны соответствующие методы и поставлены задачи диссертационной работы.

Вторая глава посвящена развитию теоретических основ формализации знаний о технологических процессах на основе дискриминантных методов распознавания образов.

Формально технологический оператор можно описать математической моделью

Y(t) = W(t, U) X(t),

где X(t) – свойства сырья или материалов, участвующих в преобразовании в выходной продукт; t – время; U – конструкционные и режимные параметры оборудования, а также параметры входных и выходных технологических потоков; W(t, U) – оператор преобразования, отображающий пространства X и U в пространство значений выходных переменных Y; Y(t) – потребительские свойства готового продукта. Часто перечисление заданных свойств Y является вербально формулируемой целью ТП.

На практике любой ТП представляет последовательность ряда частных технологических подпроцессов (этапов). Пример – последовательное изготовление пряжи, нитей, тканей, одежды. Такая технологическая цепочка может реализовываться последовательно или параллельно. Параметрами, характеризующими все этапы технологической цепочки, являются:

X = X_С X_М X_Д – характеристики исходных компонентов, где

X_С = X_С1 X_С2… – характеристики используемого сырья,

X_М = X_М1 X_М2… – характеристики материалов,

X_Д = X_Д1 X_Д2… – параметры деталей;

U = { U_C₁, U_С2, … , U_М1, _…,U_Д_К} – параметры оборудования и технологических потоков на этапах обработки сырья, материалов, деталей;

Y = Y_П  Y_Э – потребительские свойства продукции, где Y_П = Y_П1 Y_П2… – показатели качества произведенной продукции, Y_Э – показатели работоспособности изделия после его эксплуатации.

Сложные многоконтурные технологические системы могут быть представлены эквивалентной разомкнутой схемой путем выделения отдельных подсистем.

Возможные наименования продукции, сортность, уровни потребительских и эксплуатационных показателей качества при одной и той же структуре технологической цепочки представляет собой множество классов , содержащее M элементов. Классификация выполняется специалистом-экспертом или автоматически по сочетанию потребительских свойств продукции Y. В трудноформализуемых ситуациях – с использованием весовых коэффициентов и функций принадлежности нечетких переменных размытым множествам-классам.

Составление алгоритма управления, описывающего, при необходимости, применение оборудования в режимах пуска, останова и нормальной эксплуатации, выполняется отдельно для каждого класса продукции.

Выделен ряд базовых задач, в которых конкретная технология определяется по сочетанию диапазонов изменения параметров X, U и Y. Большинство из них могут решаться на основе построения схем формализации ТП в рамках выявления логических и статистических закономерностей по эмпирическим данным, а при нехватке последних – с привлечением знаний экспертов и аппарата нечеткой логики. Исходные данные представляются матрицей

,

содержащей векторы значений входных X и выходных Y показателей звеньев технологической цепочки, условий U протекания ТП для n прецедентов _i , i =

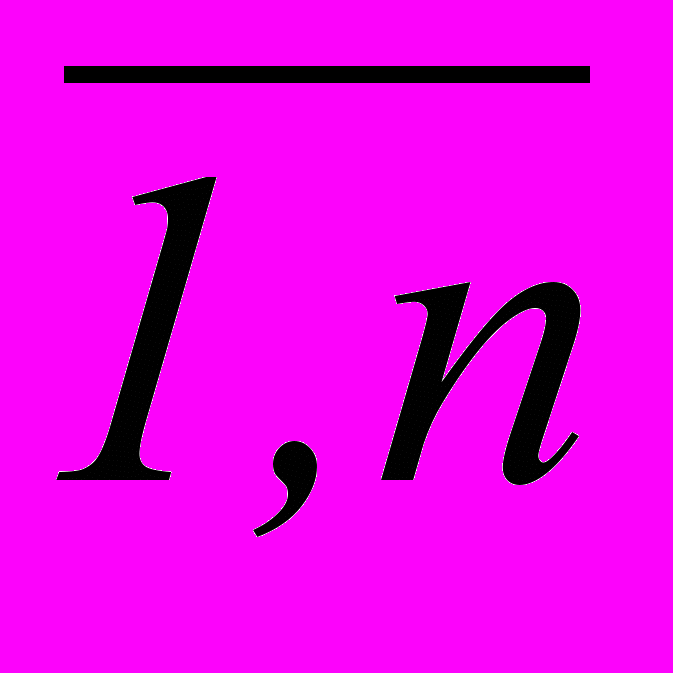, с известными решениями (заключениями эксперта).

Модель ТП в форме “объект–атрибуты–значения” при наличии реальных связей содержит их в неявной форме. Весь набор входных параметров для дальнейших исследований можно объединить в единое глобальное пространство X_A = X  U – априорный словарь признаков с описаниями свойств ТП:

.

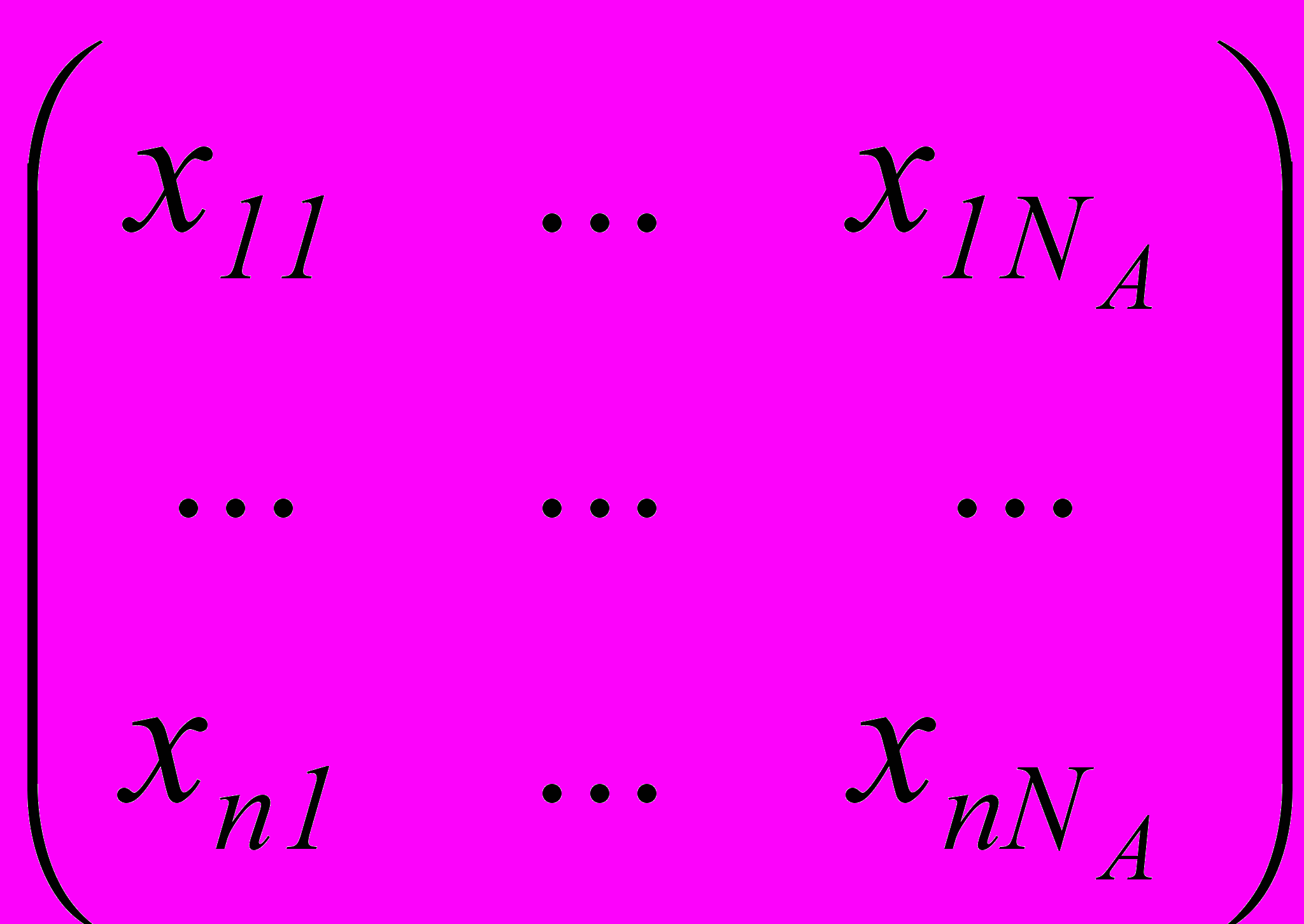Каждый объект описывается вектором (x₁, …, x_NА) в N_А-мерном пространстве признаков априорного словаря X_А = {X_j  j =

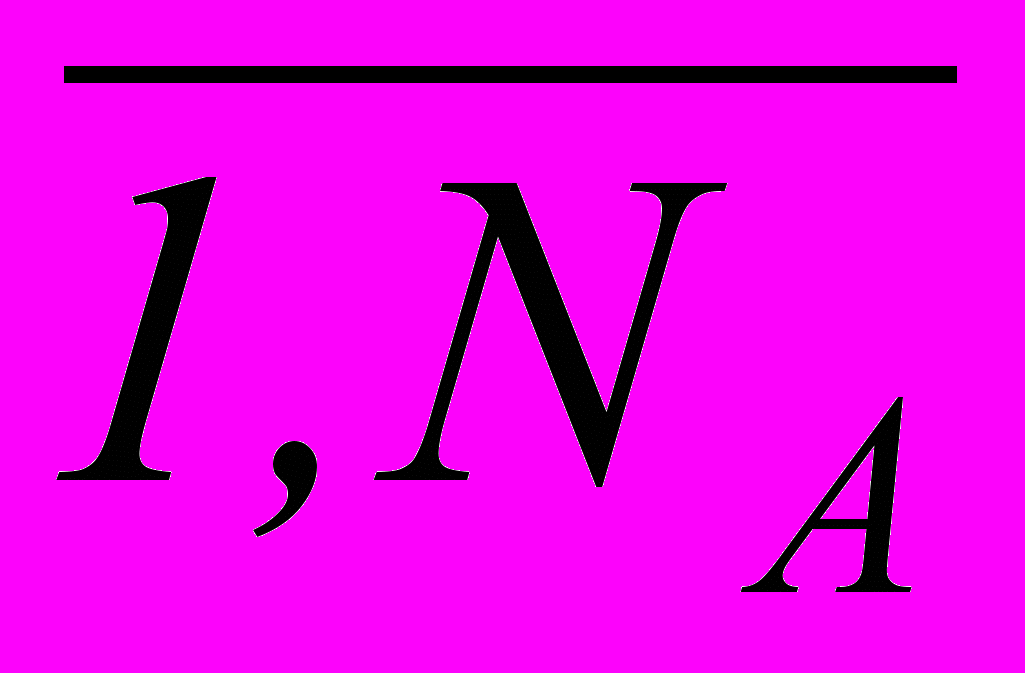}. Для описания классов объектов используется обучающая выборка ₁, …, _i, …, _n, где _i – объект-прецедент, известный принадлежностью одному из распознаваемых (описываемых) классов, i =

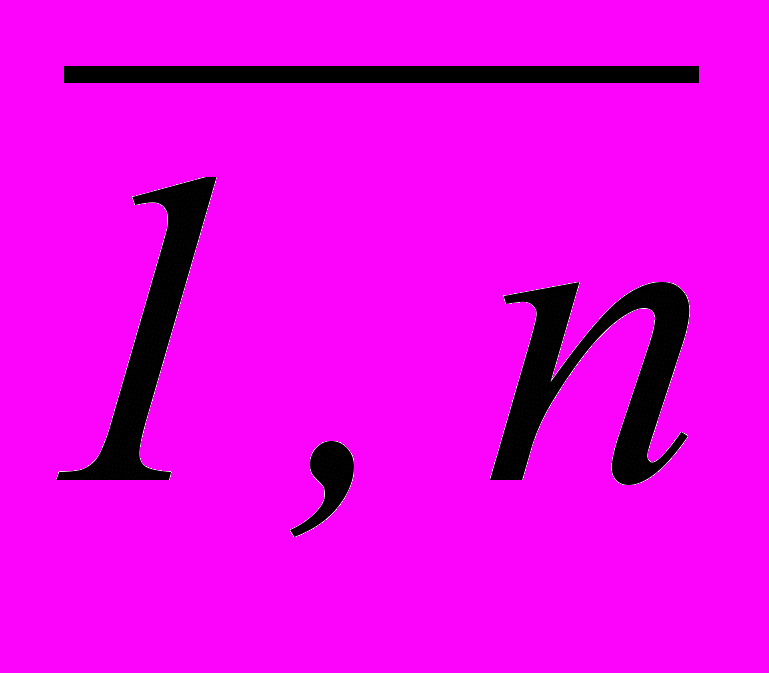, n – длина (объем) ОВ.

Для формирования поля знаний в виде системы продукционных правил требуется построить соответствующие решающие правила (дискриминантный алгоритм распознавания). Это можно сделать, решив четыре взаимосвязанные задачи:

1) пороговое кодирование признаков;

2) выбор оптимального рабочего словаря признаков X_Р = {X_j  j =

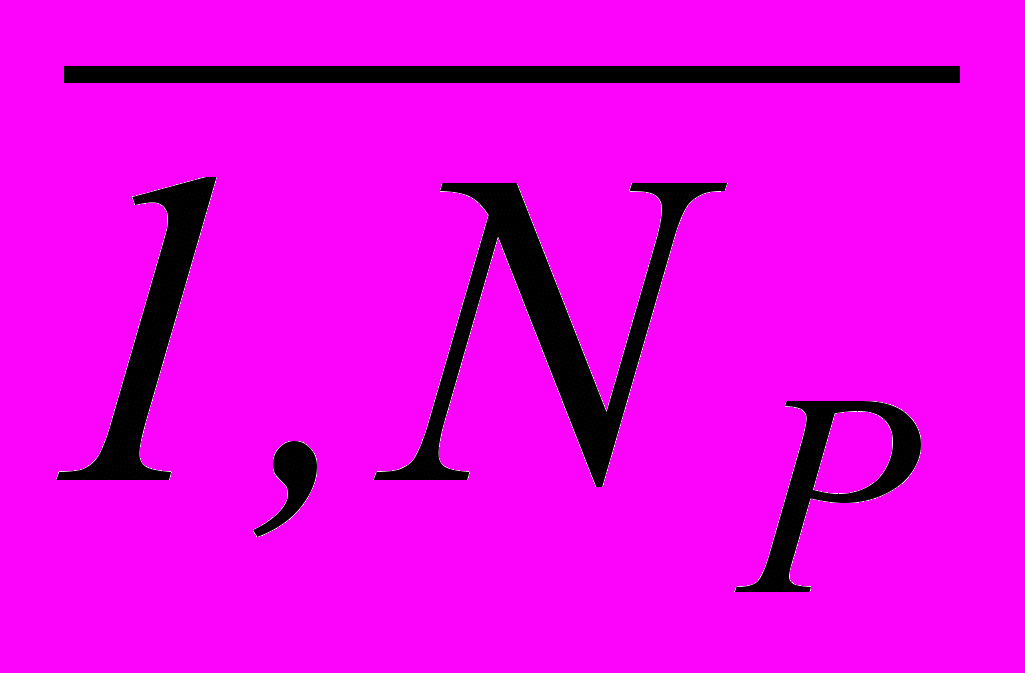}, X_Р X_А (структурная идентификация РП);

3) выбор класса решающих правил: логического, линейно-логического, линейного, кусочно-линейного, квадратичного или более сложного и соответствующего типа алгоритма распознавания;

4) определение параметров выбранного алгоритма (параметрическая идентификация РП).

Выбрать тот или иной метод конструирования набора решающих правил на начальном этапе формирования поля знаний позволяет анализ причин и видов априорной неопределенности. В случае недостаточности глобального множества признаков, характеризующих ТП, при отсутствии возможности его пополнения для повышения точности РП целесообразно использовать дополнительные источники информации: последовательное (неоднократное) измерение признака(ов) в процессе наблюдения за изготовлением готового продукта или учет опыта эксперта при построении решающего правила. Последовательный алгоритм выделения класса с новыми потребительскими свойствами применяется при статистической неопределенности задачи ОРО, по запросу на дополнительные измерения, до достижения заданной точности распознавания. В ситуации нестатистической неопределенности используется нечеткое РП, позволяющее учесть субъективную информацию эксперта.

Ситуация описанная В. А Дюком, когда объекты различных классов перемешаны в признаковом пространстве, приводит к тому, что дискриминантные правила отказываются от распознавания или в лучшем случае “цепляют” только кусочки настоящих логических закономерностей в данных. Чтобы избежать нарушения гипотезы компактности, следует перед обучением соответствующие “трудные” классы разбить на подклассы или, если выполняется поиск неочевидных, скрытых регулярностей, предварительно выделить подгруппы объектов ОВ методами таксономического анализа.

Среди подходов к формированию систем РП выделяются два направления. Первое связано с оптимизацией критерия качества сформированного РП при заданной системе описания объектов. Решение последней задачи (обучение в узком смысле) обычно представляется с помощью алгоритма ОРО, причем существенное значение для эффективности сформированного РП имеет объем n ОВ. В этой группе подходов различные методы отличаются друг от друга сложностью аппроксимирующих решающих функций, формируемых алгоритмом ОРО, видом показателя качества и способом оптимизации этого показателя. Обычно минимизируется риск в известном классе РП. Второе направление сводится к формированию систем описания объектов, в пространстве которых оптимизируется критерий качества РП заданного класса либо разделение классов становится чрезвычайно простым.

Существующие подходы обеспечивают выбор системы описания объектов и построение алгоритма распознавания лишь в узком классе РП. Влияние решения каждой из взаимосвязанных задач на эффективность создаваемой базы знаний приводит к необходимости совместного решения задач обучения при ограниченных ОВ. Предлагается использовать комплексное применение множества дискриминантных алгоритмов. В рамках данного подхода РП классифицируются по типу разделяющих поверхностей. Обучение осуществляется в широком смысле (вводится дополнительный этап – выбор класса РП), что позволяет добиться более глубокого минимума эмпирического риска по сравнению с известными методами обучения.

Методология совместного выбора класса РП, соответствующего алгоритма обучения и системы описания объектов предназначена для формирования динамической модели знаний в условиях ограниченной ОВ. Процесс обучения распознающей БЗ представляется как двухпараметрическая дискретная экстремальная задача, решение которой дает возможность учесть структуру взаимосвязи основных этапов обучения.

Поиск РП при достаточном словаре X_А и ограниченной ОВ осуществляется после определения экстраполирующих свойств решающих правил различной сложности. С этой целью множество классов РП {K} = K упорядочивается по критерию минимума гарантированной оценки риска (вероятности ошибки распознавания) P_ош, определяемой с заданной мерой надежности 1–. Оценки P_ош для различных классов РП вычисляются через меры сложности на основе неравенств Вапника-Червоненкиса, как

P_ош = _min(K, X_р) + (n, , M, h),

где _min – величина минимума эмпирического риска в классе K,  – гарантированное уклонение среднего риска от эмпирического, h = h(K, X_р) – емкость класса РП K, равная в общем случае числу настраиваемых при обучении параметров. Тогда искомый класс РП K^* определяется как

K^* = arg

[

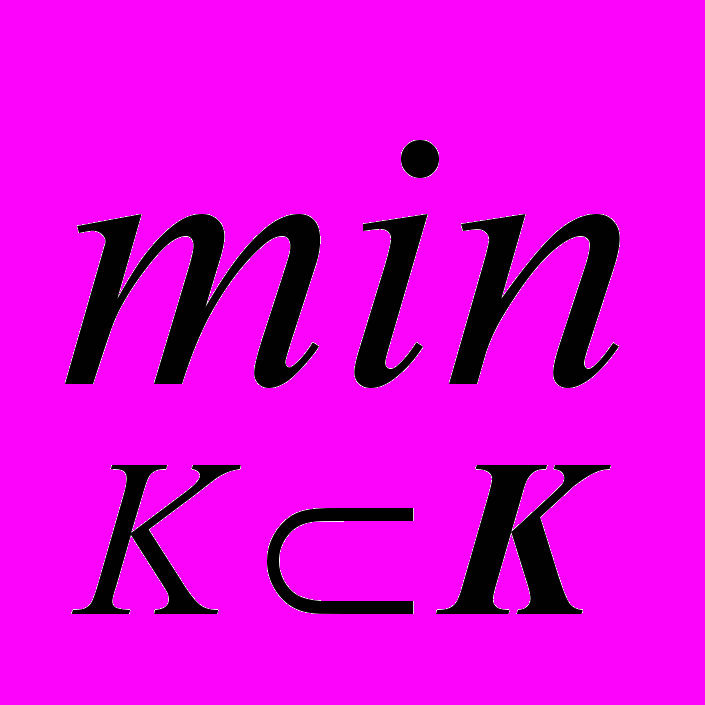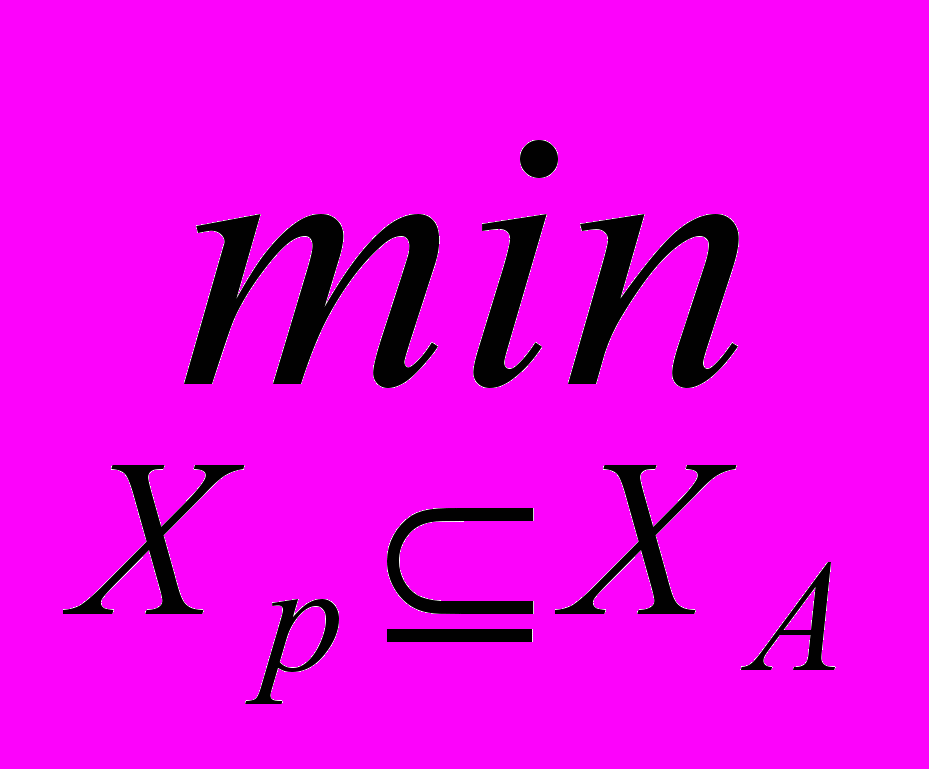P_ош(n, , M, K, X_р)].

Для определения величины минимума эмпирического риска в классе K _min(K, X_р), входящей в выражение для P_ош, используется один из таких алгоритмов обучения при заданном рабочем словаре X_р, которые строят РП в данном классе K. При этом предполагается, что в классе K различные алгоритмы обучения дают на одной и той же ОВ близкие значения минимума эмпирического риска _min. Допустимость этого предположения обусловлена тем обстоятельством, что при ограниченной ОВ и рабочем словаре, информативность которого I(X_р)  1, выполняется соотношение _min << , причем диапазон изменений минимума эмпирического риска для различных алгоритмов обучения распознающей БЗ в каждом фиксированном классе РП _min(K, X_р) значительно меньше изменения величины _min при переходе от одного класса к другому.

Выбор X_р в классе K осуществляется путем сокращения размерности признакового пространства, при котором _min сохраняется на нулевом уровне. При этом, если ОВ ограничена, P_ош(K) 

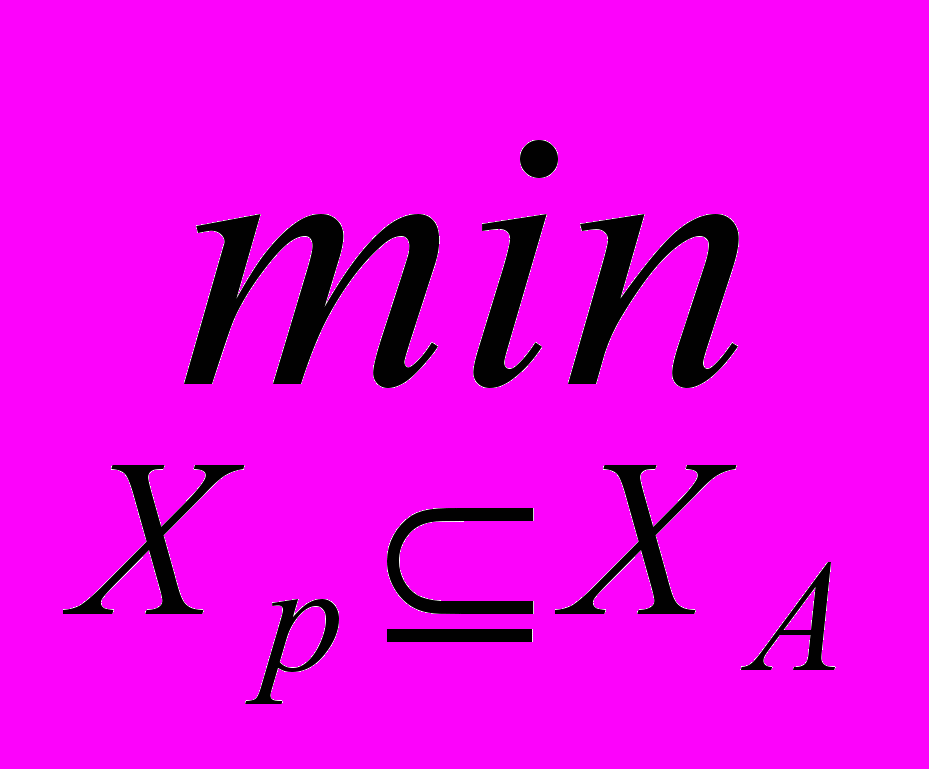P_ош(K, X_р). Формирование системы описания для логических РП осуществляется за счет сокращения объема пространства признаков V при _min  0, где V =

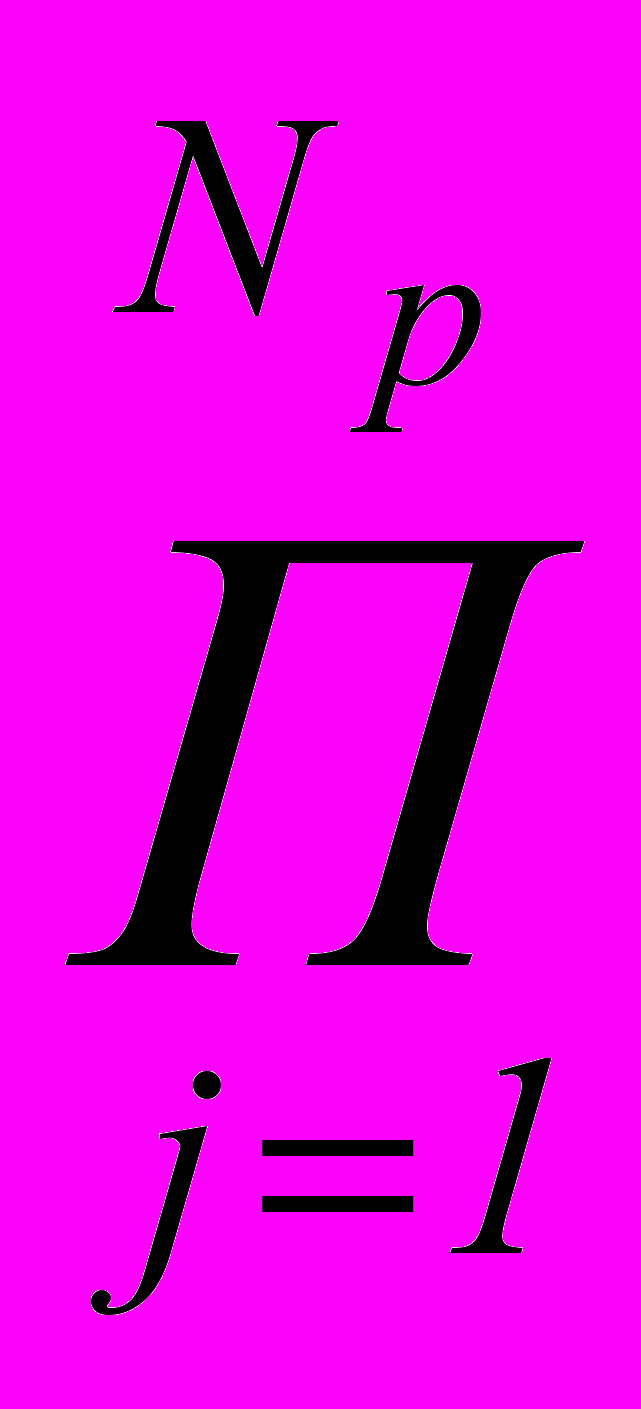t_j, j =

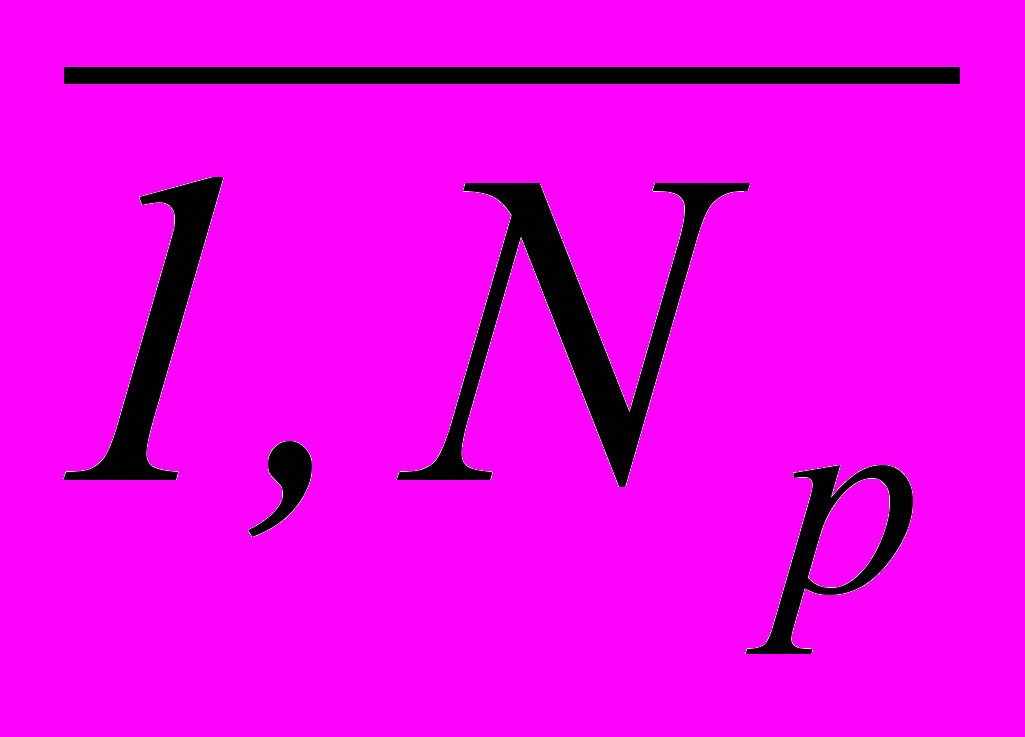, t_j – число градаций j-го признака. Кодирование признаков для логических РП и поиск рабочего словаря осуществляются без непосредственного определения величин минимума эмпирического риска _min и гарантированной вероятности ошибки распознавания P_ош, а с использованием критерия информативности группы признаков – их разделяющей силы I. Способ определения информативности зависит от класса используемых РП. При равномерном распределении числа объектов ОВ по множеству  минимум эмпирического риска оценивается соотношением _min  1 – I, причем при _min  0 всегда I  1.

Уменьшение избыточности кода и объема признакового пространства может осуществляться устранением “дублирующих” порогов для отдельных признаков при сохранении разделяющей силы их группы. В общем случае требуется разработка специальных методов кодирования.

Отбор входных и выходных отличительных признаков при обучении в глобальном пространстве описания технологического процесса упрощает семантическую интерпретацию системы построенных РП.

В диссертационной работе процесс обучения трактуется как совместный поиск такого класса РП, а также необходимого и достаточного пространства признаков, при которых объекты ОВ становятся легкоразделимыми на классы с помощью несложных поверхностей. Стремление к простоте, положенное в основу закона предсказания, позволяет успешно решать задачу ОРО. Определены экстраполирующие свойства простейших классов решающих правил, обладающих минимальной емкостью: логических, линейно-логических, линейных и кусочно-линейных.

Blog

Содержание работы