Информатика Ответы на вопросы 3
| Вид материала | Документы |
- Ответы на вопросы, 90.99kb.
- Дополнение к Приложению к Сказке. Ответы на вопросы, 274.58kb.
- Масюченко Светлана Дмитриевна Ответы на вопросы Интернет конкурс, 43.06kb.
- Ответы на экзаменационные вопросы по истории России 11 класс, 4049.18kb.
- Крайон. Действовать или ждать? Вопросы и ответы, 13038.17kb.
- План урока Организационный момент. Объяснение нового материала. Лекция. Тест и ответы, 67.88kb.
- Тесты Вопросы и задания для самопроверки Ответы на тесты Ответы и задания для самопроверки, 429.4kb.
- Елина Елена Валентиновна, гбоу нпо «Профессиональный лицей №12» Элементы проникающей, 62.09kb.
- Задание объектом нашего исследования являются современные системы безопасности: охранная, 300.74kb.
- Экзаменационные вопросы. Учкекен 2005 Составитель к э. н. Кумыкова А. М. Настоящее, 1733.51kb.
23 Алгоритмы поиска и выборки элементов из массивов данных.
Двоичный (бинарный) поиск элемента в массиве
Если у нас есть массив, содержащий упорядоченную последовательность данных, то очень эффективен двоичный поиск.
Переменные Lb и Ub содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Мы начинаем всегда с исследования среднего элемента отрезка. Если искомое значение меньше среднего элемента, мы переходим к поиску в верхней половине отрезка, где все элементы меньше только что проверенного. Другими словами, значением Ub становится (M – 1) и на следующей итерации мы работаем с половиной массива. Таким образом, в результате каждой проверки мы вдвое сужаем область поиска. Так, в нашем примере, после первой итерации область поиска – всего лишь три элемента, после второй остается всего лишь один элемент. Таким образом, если длина массива равна 6, нам достаточно трех итераций, чтобы найти нужное число.
Двоичный поиск - очень мощный метод. Если, например, длина массива равна 1023, после первого сравнения область сужается до 511 элементов, а после второй - до 255. Легко посчитать, что для поиска в массиве из 1023 элементов достаточно 10 сравнений.
Function BinSearch (a:array;Lb,Ub:integer;Key:integer);
Var done:Boolean;
M:integer;
Begin
While not done do
Begin
M:= round((Lb + Ub)/2);
If (key
Ub:=m-1
Else if (key>a[m]) then
Lb:=m+1
Else BinSearch:=m;
If (Lb>Ub) then done:=true;
end;
End;
Интерполяционный поиск элемента в массиве
Представьте себе, что Вы ищете слово в словаре. Маловероятно, что Вы сначала загляните в середину словаря, затем отступите от начала на 1/4 или 3/4 и т.д, как в бинарном поиске.
Если нужное слово начинается с буквы 'А', вы наверное начнете поиск где-то в начале словаря. Когда найдена отправная точка для поиска, ваши дальнейшие действия мало похожи на рассмотренные выше методы.
Если Вы заметите, что искомое слово должно находиться гораздо дальше открытой страницы, вы пропустите порядочное их количество, прежде чем сделать новую попытку. Это в корне отличается от предыдущих алгоритмов, не делающих разницы между 'много больше' и 'чуть больше'.
Мы приходим к алгоритму, называемому интерполяционным поиском: Если известно, что К лежит между Kl и Ku, то следующую пробу делаем на расстоянии (u-l)(K-Kl)/(Ku-Kl) от l, предполагая, что ключи являются числами, возрастающими приблизительно в арифметической прогрессии.
Интерполяционный поиск работает за log log N операций, если данные распределены равномерно. Как правило, он используется лишь на очень больших таблицах, причем делается несколько шагов интерполяционного поиска, а затем на малом подмассиве используется бинарный или последовательный варианты.
// Поиск в массиве K[1..N] числа X интерполяционным поиском
find:=false;
FindPos:=-1;
L:=1; u:=N;
while(u>=l)
begin
i=L+(u-L)*(X-K[l])/(K[u]-K[L]);
if(X
else if(X>K[i]) then l=i+1
else begin
find:=true;
FindPos:=I;
End;
24 Алгоритмы сортировки данных. Критерии эффективности работы алгоритма .Сортировка выбором. Сортировка пузырьком. Сортировка простыми вставками. Сортировка Шелла. Сортировка пирамидальная. Сортировка быстрая. Сортировка поразрядная.
Алгоритм сортировки — это алгоритм для упорядочения элементов в списке. В случае, когда элемент списка имеет несколько полей, поле, служащее критерием порядка, называется ключом сортировки. На практике, в качестве ключа часто выступает число, а в остальных полях хранятся какие-либо данные, никак не влияющие на работу алгоритма.
Критерии Эффективности
Единственного эффективнейшего алгоритма сортировки нет, ввиду множества параметров оценки эффективности:
Время — основной параметр, характеризующий быстродействие алгоритма. Называется также вычислительной сложностью. Для упорядочения важны худшее, среднее и лучшее поведение алгоритма в терминах размера списка (n). Для типичного алгоритма хорошее поведение — это O(n log n) и плохое поведение — это O(n²). Идеальное поведение для упорядочения — O(n). Алгоритмы сортировки, использующие только абстрактную операцию сравнения ключей всегда нуждаются по меньшей мере в O(n log n) сравнениях в среднем;
Память — ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. При оценке используемой памяти не будет учитываться место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы.
Устойчивость (stability) — устойчивая сортировка не меняет взаимного расположения равных элементов.
Естественность поведения — эффективность метода при обработке уже упорядоченных, или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.
Данные нам методы сортировки удобно поместить в сводную таблицу
(Warning! Таблица не проверена. Там где стоят знаки вопроса, значение под сомнением!)
(BrutalScorp-respect for the table)
| Вид сортировки | Быстродействие | Память | Устойчивось | Естественность | Краткое описание |
| Быстрая | O(n*log(n)) | требует | неустойчив | естественный | выбираем опорный элемент Ак. Затем эл-ты меньше Ак переносим влево, большие вправо. Затем обе части обрабатываем аналогично |
| Выбором | O(n2) | не требует | неустойчив | неестественный | строим массив из "правильных эл-тов" слева-направо. после каждого прохода неотсортированный участок уменьшается |
| Пузырьком | O(n2) | не требует | устойчив | Неестественный, (естественный только у модифицир.) | С каждым перебором массива “легкий” эл-т поднимается выше. Производится до тех пор пока не всплывут все |
| Слиянием | O(n*log(n)) | требует | устойчив | Естественный | Разбивка и сортировка сначала по 2 эл-та, затем 4, 8, 16… |
| Вставками | O(n2) | не требует | устойчив | Естественный | “просеивание” элемента в отсортированный участок |
| Шелла | O(n*log(n)) или n12 | ?не требует? | неустойчив | ?Естественный? | Сортируется сначала каждый 8, затем каждый 4, 2. (разбиваются на пары через 8,4,2) |
| Поразрядная | O(n*log(n)) | требует(?) | устойчив | неестественный | Выстраивание эл-тов по карманам старших разрядов, затем младших |
Теперь можно заняться подробным описанием алгоритмов с примерами.
Сортировка выбором
Сортировка выбором (англ. selection sort) — алгоритм сортировки, относящийся к неустойчивым алгоритмам сортировки. На массиве из n элементов имеет время выполнения в худшем, среднем и лучшем случае Θ(n2), предполагая что сравнения делаются за постоянное время.
Шаги алгоритма:
- находим минимальное значение в текущем списке
- производим обмен этого значения со значением на первой позиции
- теперь сортируем хвост списка, исключив из рассмотрения уже отсортированный первый элемент
for i := 1 to n - 1 do
begin
min := i;
for j := i + 1 to n do
if a[min] > a[j] then
min := j;
t := a[i];
a[i] := a[min];
a[min] := t
end;
Сортировка пузырьком
Сортировка пузырьком (англ. bubble sort) — простой алгоритм сортировки. Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: O(n2).
Алгоритм
Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При проходе алгоритма, элемент, стоящий не на своём месте, «всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма.
for i := n - 1 downto 1 do
for j := 1 to i do
if a[j] > a[j+1] then
begin
t := a[j];
a[j] := a[j+1];
a[j+1] := t;
end;
Сортировка простыми вставками
Сортировка вставками (англ. insertion sort) — простой алгоритм сортировки. Хотя этот метод сортировки намного менее эффективен, чем более сложные алгоритмы (такие как быстрая сортировка), у него есть ряд преимуществ:
- прост в реализации
- эффективен на небольших наборах данных
- эффективен на наборах данных, которые уже частично отсортированы
- это устойчивый алгоритм сортировки (не меняет порядок элементов, которые уже отсортированы)
- может сортировать список по мере его получения
На каждом шаге алгоритма, мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированном списке, до тех пор пока набор входных данных не будет исчерпан. Выбор очередного элемента, выбираемого из исходного массива — произволен, может использоваться практически любой алгоритм выбора.
На рис (a) мы вынимаем элемент 3. Затем элементы, расположенные выше, сдвигаем вниз - до тех пор, пока не найдем место, куда нужно вставить 3. Это процесс продолжается на рис(b) для числа 1. Наконец, на рис (c) мы завершаем сортировку, поместив 2 на нужное место.
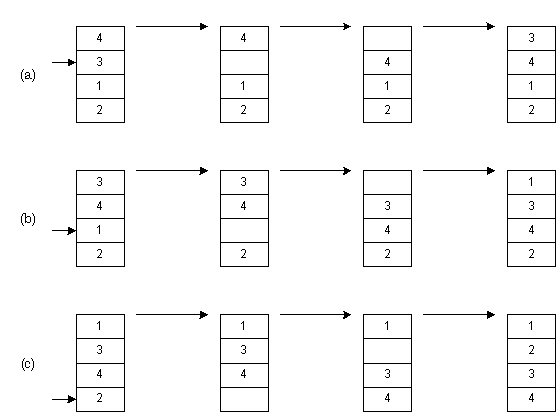
For i:=2 to Сount do
Begin
Tmp:=Arr[i];
j:=i-1;
While (Arr[j]>Tmp) and (j>0) do
Begin
Arr[j+1]:=Arr[j];
j:=j-1;
End;
Arr[j+1]:=Tmp;
End;
Сортировка Шелла (Ох и презабавная вещь).
Вариант описания №1 (длинный)
Сортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками.
Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].

1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).

В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.
3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

4. В конце сортируем вставками все 16 элементов.

Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные ?
Hа самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.
Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности.
Вариант описания №2 (короткий)
Шаг 1. Упорядочиваемое множество разбивается на несколько непересекающихся подмножеств по следующему правилу:
берутся элементы неупорядоченного множества, расположенные на одинаковом расстоянии (дистанции) друг от друга. Полученные множества сортируются методом простых вставок, что позволяет уменьшить общую неупорядоченность множества.
Шаг 2. Алгоритм завершает работу, когда дистанция равна 1, иначе уменьшается дистанция между элементами и повторяется шаг 1.
Примечание:
Выбор последовательности дистанций между элементами в сортировке методом Шелла является отдельной проблемой, которая подробно рассматривается Д.Кнутом в монографии “Искусство программирования для ЭВМ. Т.3: Сортировка и поиск”.
Пример:
const N=10; {Количество элементов массива}
var a: array[1..N] of integer; {массив}
p: boolean; {флаг наличия перестановки}
l,d,i,j: integer; {служебные переменные}
...........
d:=N div 2; {Расстояние между обрабатываемыми элементами массива,
на каждом этапе алгоритма уменьшается в 2 раза вплоть до 0,
когда происходит останов алгоритма}
while d>0 do
begin
for j:=1 to N-d do {Перебор всех пар элементов массива,
расстояние между которыми равно d}
begin
l:=j {запоминаем индекс текущего элемента}
repeat
p:=false; {пока элементы не переставлялись}
if a[l]
c:=a[l];a[l]:=a[l+d];a[l+d]:=c; {меняем местами элементы массива}
l:=l-d; {перейдём к той паре, в которую
входит меньший из переставленных элементов}
p:=true; {запомним, что была перестановка}
end;
until (l<=1) and p; {продолжаем, пока идут перестановки и
не произошёл выход за пределы массива}
end;
d:=d div 2; {Уменьшим расстояние между сравниваемыми элементами
в 2 раза}
end;
Пирамидальная сортировка (Эх, мать…)
Вариант №1 (Вики):
Пирамидальная сортировка — алгоритм сортировки, работающий в худшем, в среднем и в лучшем случае (т.е. гарантированно) за О(n log n) операций при сортировке n элементов.
Может рассматриватъся как усовершенствованная пузырьковая сортировка, в которой элемент всплывает (min-heap) / тонет (max-heap) по многим путям.
Алгоритм:
Сортировка пирамидой использует сортирующее дерево. Сортирующее дерево – это такое двоичное дерево, у которого выполнены условия:
1. Каждый лист имеет глубину либо d либо d-1
2. Значение в любой вершине больше, чем значения ее потомков.
Пример сортирующего дерева
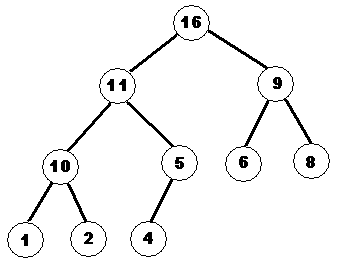
Удобная структура данных для сортирующего дерева – такой массив Array, что Array[1] – элемент в корне, а потомки элемента Array[i] - Array[2i] и Array[2i+1].

Алгоритм сортировки будет состоять из двух основных шагов:
1. Выстраиваем элементы массива в виде сортирующего дерева:
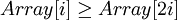
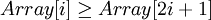
п
 ри
ри Этот шаг требует О(n) операций.
2. Будем удалять элементы из корня по одному за раз и перестраивать дерево. Т.е. на первом шаге обмениваем Array[1] и Array[n], преобразовываем Array[1], Array[2], ... , Array[n-1] в сортирующее дерево. Затем переставляем Array[1] и Array[n-1], преобразовываем Array[1], Array[2], ... , Array[n-2] в сортирующее дерево. Процесс продолжается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда Array[1], Array[2], ... , Array[n] - упорядоченная последовательность.
Этот шаг требует О(n log n) операций.
Вариант №2 (Алголист)
Итак, мы постепенно переходим от более-менее простых к сложным, но эффективным методам. Пирамидальная сортировка является первым из рассматриваемых методов, быстродействие которых оценивается как O(n log n).
В качестве некоторой прелюдии к основному методу, рассмотрим перевернутую сортировку выбором. Во время прохода, вместо вставки наименьшего элемента в левый конец массива, будем выбирать наибольший элемент, а готовую последовательность строить в правом конце.
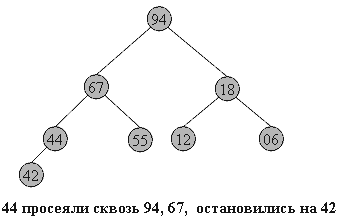
Пример действий для массива a[0]... a[7]:
44 55 12 42 94 18 06 67 исходный массив
44 55 12 42 67 18 06 |94 94 <-> 67
44 55 12 42 06 18 |67 94 67 <-> 06
44 18 12 42 06 |55 67 94 55 <-> 18
06 18 12 42 |44 55 67 94 44 <-> 06
06 18 12 |42 44 55 67 94 42 <-> 42
06 12 |18 42 44 55 67 94 18 <-> 12
06 |12 18 42 44 55 67 94 12 <-> 12
Вертикальной чертой отмечена левая граница уже отсортированной(правой) части массива.
Рассмотрим оценку количества операций подробнее.
Всего выполняется n шагов, каждый из которых состоит в выборе наибольшего элемента из последовательности a[0]..a[i] и последующем обмене. Выбор происходит последовательным перебором элементов последовательности, поэтому необходимое на него время: O(n). Итак, n шагов по O(n) каждый - это O(n2).
Произведем усовершенствование: построим структуру данных, позволяющую выбирать максимальный элемент последовательности не за O(n), а за O(logn) времени. Тогда общее быстродействие сортировки будет n*O(logn) = O(n log n).
Эта структура также должна позволять быстро вставлять новые элементы (чтобы быстро ее построить из исходного массива) и удалять максимальный элемент (он будет помещаться в уже отсортированную часть массива - его правый конец).
Итак, назовем пирамидой(Heap) бинарное дерево высоты k, в котором
- все узлы имеют глубину k или k-1 - дерево сбалансированное.
- при этом уровень k-1 полностью заполнен, а уровень k заполнен слева направо, т.е форма пирамиды имеет приблизительно такой вид:
- выполняется "свойство пирамиды": каждый элемент меньше, либо равен родителю.
Как хранить пирамиду? Наименее хлопотно - поместить ее в массив.
Соответствие между геометрической структурой пирамиды как дерева и массивом устанавливается по следующей схеме:
- в a[0] хранится корень дерева
- левый и правый сыновья элемента a[i] хранятся, соответственнно, в a[2i+1] и a[2i+2]
Таким образом, для массива, хранящего в себе пирамиду, выполняется следующее характеристическое свойство: a[i] >= a[2i+1] и a[i] >= a[2i+2].
Плюсы такого хранения пирамиды очевидны:
никаких дополнительных переменных, нужно лишь понимать схему.
узлы хранятся от вершины и далее вниз, уровень за уровнем.
узлы одного уровня хранятся в массиве слева направо.
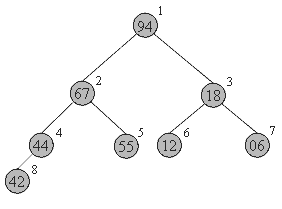
Запишем в виде массива пирамиду, изображенную выше.. Слева-направо, сверху-вниз: 94 67 18 44 55 12 06 42. На рисунке место элемента пирамиды в массиве обозначено цифрой справа-вверху от него.
Восстановить пирамиду из массива как геометрический объект легко - достаточно вспомнить схему хранения и нарисовать, начиная от корня.
Фаза 1 сортировки: построение пирамиды
Hачать построение пирамиды можно с a[k]...a[n], k = [size/2]. Эта часть массива удовлетворяет свойству пирамиды, так как не существует индексов i,j: i = 2i+1 ( или j = 2i+2 )... Просто потому, что такие i,j находятся за границей массива.
Следует заметить, что неправильно говорить о том, что a[k]..a[n] является пирамидой как самостоятельный массив. Это, вообще говоря, не верно: его элементы могут быть любыми. Свойство пирамиды сохраняется лишь в рамках исходного, основного массива a[0]...a[n].
Далее будем расширять часть массива, обладающую столь полезным свойством, добавляя по одному элементу за шаг. Следующий элемент на каждом шаге добавления - тот, который стоит перед уже готовой частью.
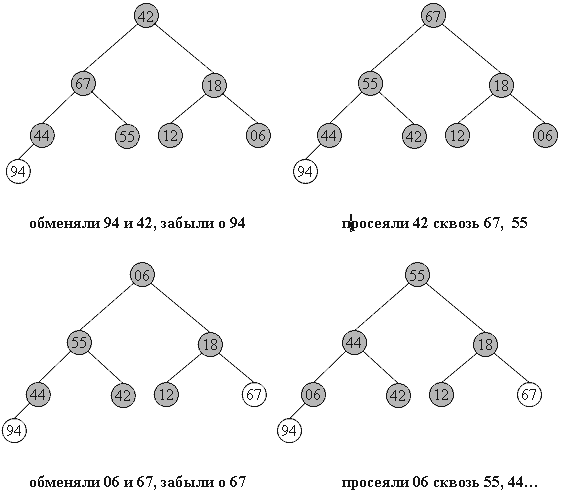
Чтобы при добавлении элемента сохранялась пирамидальность, будем использовать следующую процедуру расширения пирамиды a[i+1]..a[n] на элемент a[i] влево:
Смотрим на сыновей слева и справа - в массиве это a[2i+1] и a[2i+2] и выбираем наибольшего из них.
Если этот элемент больше a[i] - меняем его с a[i] местами и идем к шагу 2, имея в виду новое положение a[i] в массиве. Иначе конец процедуры.
Новый элемент "просеивается" сквозь пирамиду.
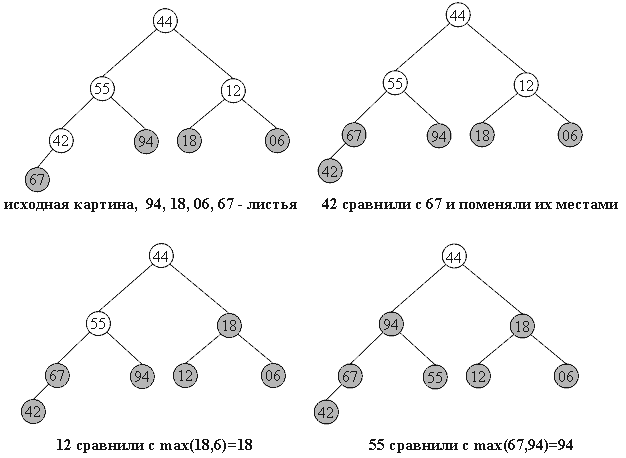
Ниже дана иллюстрация процесса для пирамиды из 8-и элементов:
44 55 12 42 // 94 18 06 67 Справа - часть массива, удовлетворяющая
44 55 12 // 67 94 18 06 42 свойству пирамиды,
44 55 // 18 67 94 12 06 42
44 // 94 18 67 55 12 06 42 остальные элементы добавляются
// 94 67 18 44 55 12 06 42 один за другим, справа налево.
В геометрической интерпретации ключи из начального отрезка a[size/2]...a[n] является листьями в бинарном дереве, как изображено ниже. Один за другим остальные элементы продвигаются на свои места, и так - пока не будет построена вся пирамида.
На рисунках ниже изображен процесс построения. Неготовая часть пирамиды (начало массива) окрашена в белый цвет, удовлетворяющий свойству пирамиды конец массива - в темный.
Фаза 2: собственно сортировка
Итак, задача построения пирамиды из массива успешно решена. Как видно из свойств пирамиды, в корне всегда находится максимальный элемент. Отсюда вытекает алгоритм фазы 2:
- Берем верхний элемент пирамиды a[0]...a[n] (первый в массиве) и меняем с последним местами. Теперь "забываем" об этом элементе и далее рассматриваем массив a[0]...a[n-1]. Для превращения его в пирамиду достаточно просеять лишь новый первый элемент.
- Повторяем шаг 1, пока обрабатываемая часть массива не уменьшится до одного элемента.
Очевидно, в конец массива каждый раз попадает максимальный элемент из текущей пирамиды, поэтому в правой части постепенно возникает упорядоченная последовательность.
94 67 18 44 55 12 06 42 // иллюстрация 2-й фазы сортировки
67 55 44 06 42 18 12 // 94 во внутреннем представлении пирамиды
55 42 44 06 12 18 // 67 94
44 42 18 06 12 // 55 67 94
42 12 18 06 // 44 55 67 94
18 12 06 // 42 44 55 67 94
12 06 // 18 42 44 55 67 94
06 // 12 18 42 44 55 67 94
Каково быстродействие получившегося алгоритма ?
Построение пирамиды занимает O(n log n) операций, причем более точная оценка дает даже O(n) за счет того, что реальное время выполнения downheap зависит от высоты уже созданной части пирамиды.
Вторая фаза занимает O(n log n) времени: O(n) раз берется максимум и происходит просеивание бывшего последнего элемента. Плюсом является стабильность метода: среднее число пересылок (n log n)/2, и отклонения от этого значения сравнительно малы.
Пирамидальная сортировка не использует дополнительной памяти.
Метод не является устойчивым: по ходу работы массив так "перетряхивается", что исходный порядок элементов может измениться случайным образом.
Поведение неестественно: частичная упорядоченность массива никак не учитывается.
Пример:
Type
arrType = Array[1 .. n] Of Integer;
{ первый вариант : }
Procedure HoarFirst(Var ar: arrType; n: integer);
Procedure sort(m, l: Integer);
Var i, j, x, w: Integer;
Begin
i := m; j := l;
x := ar[(m+l) div 2];
Repeat
While ar[i] < x Do Inc(i);
While ar[j] > x Do Dec(j);
If i <= j Then Begin
w := ar[i]; ar[i] := ar[j]; ar[j] := w;
Inc(i); Dec(j)
End
Until i > j;
If m < j Then Sort(m, j);
If i < l Then Sort(i, l)
End;
Begin
sort(1, n)
End;
Type
arrType = Array[1 .. n] Of Integer;
{ второй вариант : }
Procedure HoarSecond(Var ar: arrType; n: Integer);
Procedure Sort(m, l: Integer);
Var i, j, x, w: Integer;
Begin
If m >= l Then Exit;
i := m; j := l;
x := ar[(m+l) div 2];
While i < j Do
If ar[i] < x Then Inc(i)
Else If ar[j] > x Then Dec(j)
Else Begin
w := ar[i]; ar[i] := ar[j]; ar[j] := w;
End;
Sort(m, Pred(j));
Sort(Succ(i),l);
End;
Begin
Sort(1, n)
End
Сортировка быстрая («Чем дальше в лес, тем злее дятлы…»)
Вариант №1 (Вики):
Алгоритм
Быстрая сортировка использует стратегию «разделяй и властвуй». Шаги алгоритма таковы:
- Выбираем в массиве некоторый элемент, который будем называть опорным элементом.
- Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него.
- Рекурсивно упорядочиваем подсписки, лежащие слева и справа от опорного элемента.
Базой рекурсии являются списки, состоящие из одного или двух элементов, которые уже упорядочены. Алгоритм всегда завершается, поскольку за каждую итерацию он ставит по крайней мере один элемент на его окончательное место.
Улучшения
При выборе опорного элемента из данного диапазона случайным образом, худший случай становится очень маловероятным и ожидаемое время выполнения алгоритма сортировки - O(n log n).
Вариант №2 (Forum.pascal.net):
Быстрая сортировка Хоара
Это улучшенный метод, основанный на обмене. При "пузырьковой" сортировке производятся обмены элементов в соседних позициях. При пирамидальной сортировке такой обмен совершается между элементами в позициях, жестко связанных друг с другом бинарным деревом. Ниже будет рассмотрен алгоритм сортировки К. Хоара, использующий несколько иной механизм выбора значений для обменов. Этот алгоритм называется сортировкой с разделением или быстрой сортировкой. Она основана на том факте, что для достижения наибольшей эффективности желательно производить обмены элементов на больших расстояниях.
Предположим, что даны N элементов массива, расположенные в обратном порядке. Их можно рассортировать, выполнив всего N/2 обменов, если сначала поменять местами самый левый и самый правый элементы и так далее, постепенно продвигаясь с двух сторон к середине. Это возможно только, если мы знаем, что элементы расположены строго в обратном порядке.
Рассмотрим следующий алгоритм: выберем случайным образом какой-то элемент массива (назовем его X). Просмотрим массив, двигаясь слева направо, пока не найдем элемент a[ i ]>X (сортируем по возрастанию), а затем просмотрим массив справа налево, пока не найдем элемент a[ j ]
После такого просмотра массив разделится на две части: левую с элементами меньшими (или равными) X, и правую с элементами большими (или равными) X. Итак, пусть a[k] (k=1,...,N) - одномерный массив, и X - какой-либо элемент из a. Надо разбить "a" на две непустые непересекающиеся части а1 и а2 так, чтобы в a1 оказались элементы, не превосходящие X, а в а2 - не меньшие X.
Рассмотрим пример. Пусть в массиве a: <6, 23, 17, 8, 14, 25, 6, 3, 30, 7> зафиксирован элемент x=14. Просматриваем массив a слева направо, пока не найдем a[ i ]>x. Получаем a[2]=23. Далее, просматриваем a справа налево, пока не найдем a[ j ]
Описанный алгоритм прост и эффективен, так как сравниваемые переменные i, j и x можно хранить во время просмотра в быстрых регистрах процессора. Наша конечная цель - не только провести разделение на указанные части исходного массива элементов, но и отсортировать его. Для этого нужно применить процесс разделения к получившимся двум частям, затем к частям частей, и так далее до тех пор, пока каждая из частей не будет состоять из одного единственного элемента. Эти действия описываются следующей программой. Процедура Sort реализует разделение массива на две части, и рекурсивно обращается сама к себе...
Сложность O(n*logn), на некоторых тестах работает быстрее сортировки слияниями, но на некоторых специально подобранных - работает за O(n2).
Примеры:
Type
arrType = Array[1 .. n] Of Integer;
{ первый вариант : }
Procedure HoarFirst(Var ar: arrType; n: integer);
Procedure sort(m, l: Integer);
Var i, j, x, w: Integer;
Begin
i := m; j := l;
x := ar[(m+l) div 2];
Repeat
While ar[i] < x Do Inc(i);
While ar[j] > x Do Dec(j);
If i <= j Then Begin
w := ar[i]; ar[i] := ar[j]; ar[j] := w;
Inc(i); Dec(j)
End
Until i > j;
If m < j Then Sort(m, j);
If i < l Then Sort(i, l)
End;
Begin
sort(1, n)
Type
arrType = Array[1 .. n] Of Integer;
{ второй вариант : }
Procedure HoarSecond(Var ar: arrType; n: Integer);
Procedure Sort(m, l: Integer);
Var i, j, x, w: Integer;
Begin
If m >= l Then Exit;
i := m; j := l;
x := ar[(m+l) div 2];
While i < j Do
If ar[i] < x Then Inc(i)
Else If ar[j] > x Then Dec(j)
Else Begin
w := ar[i]; ar[i] := ar[j]; ar[j] := w;
End;
Sort(m, Pred(j));
Sort(Succ(i),l);
End;
Begin
Sort(1, n)
End;
End;
Сортировка поразрядная
Пусть имеем максимум по k байт в каждом ключе (хотя за элемент сортировки вполне можно принять и что-либо другое, например слово - двойной байт, или буквы, если сортируются строки). k должно быть известно заранее, до сортировки.
Разрядность данных (количество возможных значений элементов) - m - также должна быть известна заранее и постоянна. Если мы сортируем слова, то элемент сортировки - буква, m = 33. Если в самом длинном слове 10 букв, k = 10. Обычно мы будем сортировать данные по ключам из k байт, m=256.
Пусть у нас есть массив source из n элементов по одному байту в каждом.
Для примера можете выписать на листочек массив source = <7, 9, 8, 5, 4, 7, 7>, и проделать с ним все операции, имея в виду m=9.
- Составим таблицу распределения. В ней будет m (256) значений и заполняться она будет так:
for i := 0 to Pred(255) Do distr[i]:=0;
for i := 0 to Pred(n) Do distr[source[i]] := distr[[i]] + 1;
Для нашего примера будем иметь distr = <0, 0, 0, 0, 1, 1, 0, 3, 1, 1>, то есть i-ый элемент distr[] - количество ключей со значением i.
- Заполним таблицу индексов:
index: array[0 .. 255] of integer;
index[0]:=0;
for i := 1 to Pred(255) Do index[i]=index[i-1]+distr[i-1];
В index[ i ] мы поместили информацию о будущем количестве символов в отсортированном массиве до символа с ключом i.
Hапример, index[8] = 5 : имеем <4, 5, 7, 7, 7, 8>.
- А теперь заполняем новосозданный массив sorted размера n:
for i := 0 to Pred(n) Do Begin
sorted[ index[ source[i] ] ]:=source[i];
{
попутно изменяем index уже вставленных символов, чтобы
одинаковые ключи шли один за другим:
}
index[ source[i] ] := index[ source[i] ] +1;
End;
Итак, мы научились за O(n) сортировать байты. А от байтов до строк и чисел - 1 шаг. Пусть у нас в каждом числе - k байт.
Будем действовать в десятичной системе и сортировать обычные числа ( m = 10 ).
сначала они в сортируем по младшему на один беспорядке: разряду: выше: и еще раз:
523 523 523 088
153 153 235 153
088 554 153 235
554 235 554 523
235 088 088 554
Hу вот мы и отсортировали за O(k*n) шагов. Если количество возможных различных ключей ненамного превышает общее их число, то 'поразрядная сортировка' оказывается гораздо быстрее даже 'быстрой сортировки'!
Пример:
Const
n = 8;
Type
arrType = Array[0 .. Pred(n)] Of Byte;
Const
m = 256;
a: arrType =
(44, 55, 12, 42, 94, 18, 6, 67);
Procedure RadixSort(Var source, sorted: arrType);
Type
indexType = Array[0 .. Pred(m)] Of Byte;
Var
distr, index: indexType;
i: integer;
begin
fillchar(distr, sizeof(distr), 0);
for i := 0 to Pred(n) do
inc(distr[source[i]]);
index[0] := 0;
for i := 1 to Pred(m) do
index[i] := index[Pred(i)] + distr[Pred(i)];
for i := 0 to Pred(n) do
begin
sorted[ index[source[i]] ] := source[i];
index[source[i]] := index[source[i]]+1;
end;
end;
var
b: arrType;
begin
RadixSort(a, b);
end.
