Чулюков Владимир Алексеевич, профессор, к ф. м н., доцент Одобрен на заседании кафедры 200 г протокол № Воронеж 2009 структура конспект
| Вид материала | Конспект |
| Краткое содержание лекционного материала Анализ сортировки Шелла. WHILE r > 1 DO Анализ HeapSort While a[i].key Анализ сортировки слиянием |
- Программа одобрена на заседании кафедры коррекционной педагогики и специальных методик, 662.03kb.
- Методические материалы к дисциплине «античная художественная историография», 118.47kb.
- План научной деятельности наименование филиала Краснодарского университета мвд россии, 792.09kb.
- Учебный план одобрен Ученым советом ночу впо «мнюи» от «25» ноября 2010 г. Протокол, 2956.82kb.
- Программа рассмотрена и одобрена на заседании кафедры экономики таможенного дела Российской, 164.95kb.
- Программа обсуждена на заседании кафедры нгиг " 31 " августа 2009 года, протокол, 88.19kb.
- Утверждено на заседании кафедры, 51.88kb.
- А. М. Горького Институт по переподготовке и повышению квалификации программа курса, 53.14kb.
- Учебно-методический комплекс для студентов специальности 010400 «Физика «подготовлено, 160.07kb.
- М. К. Аммосова программа курса физика для государственных университетов Специальность, 247.34kb.
Краткое содержание лекционного материала
Сортировка с помощью включений с убывающим приращением
В 1959 г. Д.Шеллом было предложено усовершенствование сортировки с помощью прямого включения. Метод демонстрируется в таблице 2.1.Сначала отдельно группируются и сортируются элементы, отстоящие друг от друга на расстоянии 4 позиции. Такой процесс называется 4-сортировкой. Рассмотрим пример из 8 элементов, где каждая группа состоит точно из двух элементов. После первого прохода элементы перегруппировываются - теперь каждый элемент группы отстоит от другого на две позиции - и вновь сортируются. Это называется 2-сортировкой. И, наконец, на третьем проходе идет обычная или 1-сортировка.
На первый взгляд можно засомневаться: если необходимо несколько проходов сортировки, причем в каждый включаются все элементы, то не добавят ли они больше работы, чем сэкономят? Однако на каждом этапе либо сортируется относительно мало элементов, либо элементы уже довольно хорошо упорядочены и требуется сравнительно немного перестановок.
Ясно, что такой метод в результате дает упорядоченный массив, и, конечно же, сразу видно, что каждый проход от предыдущего только выигрывает (так как каждая i-сортировка объединяет две группы, уже отсортированные 2i-сортировкой). Так же очевидно, что расстояния в группах можно уменьшать по-разному, лишь бы последнее было единичным, ведь в самом плохом случае последний проход и сделает последнюю работу. Однако совсем не очевидно, что такой прием «уменьшающихся расстояний» может дать лучшие результаты, если расстояния не будут степенями двойки. Поэтому приводимая программа не ориентирована на некую определенную последовательность расстояний.
Т
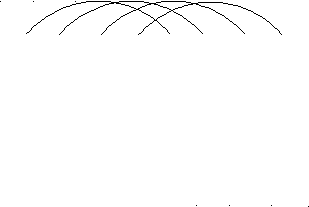 аблица 2.1.Сортировка с помощью включений с убывающими приращениями
аблица 2.1.Сортировка с помощью включений с убывающими приращениями| 44 | 55 | 12 | 42 | 94 | 18 | 06 | 67 |
4
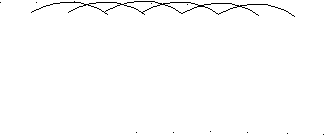 -сортировка:
-сортировка:| 44 | 18 | 06 | 42 | 94 | 55 | 12 | 67 |
2
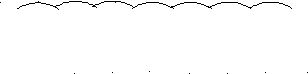 -сортировка:
-сортировка:| 06 | 18 | 12 | 42 | 44 | 55 | 94 | 67 |
1-сортировка:
| 06 | 12 | 18 | 42 | 44 | 55 | 67 | 94 |
Все t приращений обозначаются соответственно h1,…,ht, для них выполняются условия:
ht = 1, hi+1
Каждая h-сортировка программируется как сортировка с помощью прямого включения. Причем простота условия окончания поиска места для включения обеспечивается методом барьеров. Ясно, что каждая из сортировок нуждается в постановке своего собственного барьера и программу для определения его местоположения необходимо делать насколько возможно простой. Поэтому приходится расширять массив не только на одну-единственную компоненту a[0], а на h1 компонент. Его описание теперь выглядит так:
a: ARRAY[-h1..n] OF item
Сам алгоритм для t = 4 описывается процедурой Shellsort в программе 2.1.
PROCEDURE ShellSort;
CONST t = 4;
VAR i, j, k, s: index; x: item; m:1..t;
h: ARRAY[1..t] OF INTEGER;
BEGIN h[1]:=9; h[2]:=5; h[3]:=3; h[4]:=1;
FOR m:=1 TO t DO
BEGIN k:=h[m]; s:= -k; {место барьера}
FOR i: = k+1 TO n DO
BEGIN x:=a[i] ; j:=i-k;
IF s=0 THEN s: = -k; s:=s+1; a[s]:=x;
WHILE x.key
BEGIN a [j +k]:=a[j]; j: =j-k
END;
a[j +k]:=x
END
END
END;
Программа 2.1. Сортировка Шелла
Анализ сортировки Шелла. Анализ этого алгоритма поставил несколько весьма трудных математических проблем, многие из которых так еще и не решены. В частности, не известно, какие приращения дают наилучшие результаты. Но вот удивительный факт: они не должны быть кратны друг другу. Это позволяет избежать явления уже очевидного из приведенного выше примера, когда при каждом проходе взаимодействуют две цепочки, которые до этого нигде еще не пересекались. И действительно, желательно, чтобы взаимодействие различных цепочек проходило как можно чаще. Справедлива такая теорема: если k - рассортированная последовательность i-сортируется, то она остается k - рассортированной. В своей работе Кнут показывает, что имеет смысл использовать такую последовательность (она записана в обратном порядке):1, 4, 13, 40, 121,…, где hk-1= 3hk+1, ht= 1 и t=[log3 n]-1. Он рекомендует и другую последовательность: 1, 3, 7, 15, 31, …, где hk-1= 2hk+1, ht= 1 и t=[log2 n]-1.Математический анализ показывает, что в последнем случае для сортировки n элементов методом Шелла затраты пропорциональны n. Хотя это число значительно лучше n2, тем не менее, мы не ориентируемся в дальнейшем на этот метод, поскольку существуют еще лучшие алгоритмы.
Пирамидальная сортировка
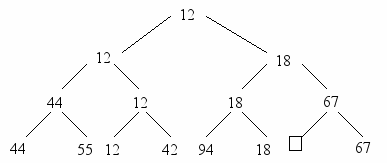
Метод сортировки с помощью прямого выбора основан на повторяющихся поисках наименьшего ключа среди n элементов, среди оставшихся n - 1 элементов и так далее. Обнаружение наименьшего среди n элементов требует — это очевидно — n - 1 сравнения, среди n - 1 уже нужно n - 2 сравнений и так далее. Как же в таком случае можно усовершенствовать упомянутый метод сортировки? Этого можно добиться, только оставляя после каждого прохода больше информации, чем просто идентификация единственного минимального элемента. Например, сделав n/2 сравнений, можно определить в каждой паре ключей меньший. С помощью n/4 сравнений — меньший из пары уже выбранных меньших и т. д. Проделав n - 1 сравнений, мы можем построить дерево выбора, вроде представленного на рис. 2.2 и идентифицировать его корень как нужный нам наименьший ключ.
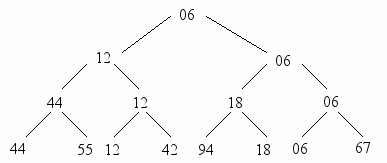
Рис. 2.2. Повторяющиеся выборы среди двух ключей
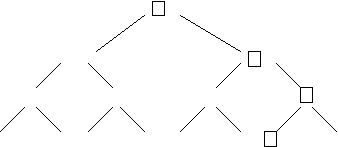
Второй этап сортировки — спуск вдоль пути, отмеченного наименьшим элементом, и исключение его из дерева путем замены на пустой элемент (дырку) (рис. 2.3). Элемент, передвинувшийся в корень дерева (рис.2.4.), вновь будет наименьшим (теперь уже вторым) ключом, и его можно исключить. После n таких шагов дерево станет пустым (т. е. в нем останутся только дырки), и процесс сортировки заканчивается. Обратите внимание — на каждом из n шагов выбора требуется только log n сравнений. Поэтому на весь процесс понадобится порядка n * log n элементарных операций плюс еще n шагов на построение дерева. Это весьма существенное улучшение не только прямого метода, требующего n2 шагов, но и даже метода Шелла, где нужно 1.2n шагов. Естественно, сохранение дополнительной информации делает задачу более изощренной, поэтому в сортировке по дереву каждый отдельный шаг усложняется. Ведь, в конце концов, для сохранения избыточной информации, получаемой при начальном проходе, создается некоторая древообразная структура. Наша следующая задача — найти приемы эффективной организации этой информации.
12
44 12 18
44 55 12 42 94 18 67
Р
 ис. 2.3. Выбор наименьшего ключа.
ис. 2.3. Выбор наименьшего ключа.Рис.2.4.Заполнение дырок.
Конечно, хотелось бы, в частности, избавиться от дырок, которыми в конечном итоге будет заполнено все дерево, и которые порождают много ненужных сравнений. Кроме того, надо было бы поискать такое представление дерева из n элементов, которое требует лишь n единиц памяти, а не 2n - 1, как это было раньше. Этих целей действительно удалось добиться в методе пирамидальная сортировка, изобретенном Д.Уилльямсом, где было получено, очевидно, существенное улучшение традиционных сортировок с помощью деревьев. Пирамида определяется как последовательность ключей hl, hl+1,...,hr, такая, что
hi <= h2i и hi< =h2i+1, для i = l,..., r/2.
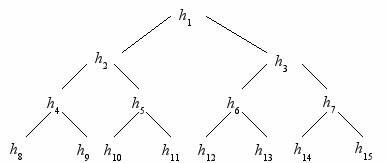
Если любое двоичное дерево рассматривать как массив по схеме на рис. 2.6, то можно говорить, что деревья сортировок на рис. 2.7 и 2.8 суть пирамиды, а элемент h1, в частности, их наименьший элемент: h1 = min(h1,h2,…, hn).
Р
 ис. 2.6. Массив h, представленный в виде двоичного дерева
ис. 2.6. Массив h, представленный в виде двоичного дереваР
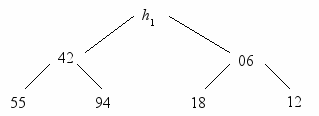
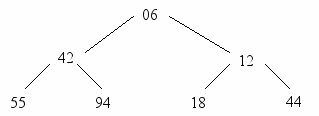 ис. 2.7. Пирамида из семи элементов.
ис. 2.7. Пирамида из семи элементов.Рис. 2.8.Просеивание ключа 44 через пирамиду.
П
 редположим, есть некоторая пирамида с заданными элементами hl+1,.., hr для некоторых значений l и r и нужно добавить новый элемент x, образуя расширенную пирамиду hl ,..., hr. Возьмем, например, в качестве исходной пирамиду h1, ...,h7, ( показанную на рис. 2.7) и добавим к ней слева элемент h1 = 44. Новая пирамида получается так: сначала x ставится наверх древовидной структуры, а затем он постепенно опускается вниз, каждый раз по направлению наименьшего из двух примыкающих к нему элементов, а сам этот элемент передвигается вверх. В приведенном примере значение 44 сначала меняется местами с 06, затем с 12, и в результате образуется дерево, представленное на рис. 2.8. Теперь мы сформулируем тот сдвигающий алгоритм так: i, j — пара индексов, фиксирующих элементы, меняющиеся на каждом шаге местами. Остается лишь убедиться самому, что предложенный метод сдвигов действительно сохраняет неизменными условия, определяющие пирамиду.
редположим, есть некоторая пирамида с заданными элементами hl+1,.., hr для некоторых значений l и r и нужно добавить новый элемент x, образуя расширенную пирамиду hl ,..., hr. Возьмем, например, в качестве исходной пирамиду h1, ...,h7, ( показанную на рис. 2.7) и добавим к ней слева элемент h1 = 44. Новая пирамида получается так: сначала x ставится наверх древовидной структуры, а затем он постепенно опускается вниз, каждый раз по направлению наименьшего из двух примыкающих к нему элементов, а сам этот элемент передвигается вверх. В приведенном примере значение 44 сначала меняется местами с 06, затем с 12, и в результате образуется дерево, представленное на рис. 2.8. Теперь мы сформулируем тот сдвигающий алгоритм так: i, j — пара индексов, фиксирующих элементы, меняющиеся на каждом шаге местами. Остается лишь убедиться самому, что предложенный метод сдвигов действительно сохраняет неизменными условия, определяющие пирамиду.Р.Флойдом был предложен некий "лаконичный" способ по строения пирамиды «на том же месте». Его процедура сдвига представлена как программа 2.2. Здесь h1…hn — некий массив, причем hn/2+1 ... hn уже образуют пирамиду, поскольку индексов i, j, удовлетворяющих отношениям j = 2i (или j = 2i + 1), просто не существует. Эти элементы образуют как бы нижний слой соответствующего двоичного дерева (рис. 2.6), для них никакой упорядоченности не требуется. Теперь пирамида расширяется влево: каждый раз добавляется и сдвигами ставится в надлежащую позицию новый элемент. Табл. 2.2 иллюстрирует весь тот процесс, а получающаяся пирамида была показана на рис.2.5
PROCEDURE sift(l,r: index);
LABEL 13;
VAR i, j: index; x:item;
BEGIN i := l; j := 2*i; x := a[i];
WHILE (j<=r) do
BEGIN IF j < r THEN
IF a[j].key > a[j+1].key then j := j+1;
IF x.key <= a[j].key then goto 13;
a[i]:=a[j]; i:=j; j:=2*j;
END;
13: a[i]:=x
END;
Программа 2.2. Sift
Следовательно, процесс формирования пирамиды из n элементов h1,..., hn на том же самом месте описывается так:
l := (n DIV 2) + 1;
WHILE l > 1 DO
BEGIN l := l-1; sift(l, n) END
Таблица 2.2.Построение пирамиды.
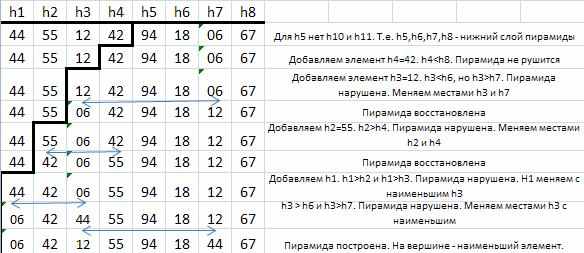
Для того чтобы получить не только частичную, но и полную упорядоченность среди элементов, нужно проделать n сдвигающих шагов, причем после каждого шага на вершину дерева выталкивается очередной (наименьший) элемент. И вновь возникает вопрос: где хранить "всплывающие" верхние элементы и можно или нельзя проводить обращение на том же месте? Существует, конечно, такой выход: каждый раз брать последнюю компоненту пирамиды (скажем, это будет x), прятать верхний элемент пирамиды в освободившемся теперь месте, а x сдвигать в нужное место. В табл. 2.3 приведены необходимые в этом случае n - 1 шагов.
Сам процесс описывается с помощью процедуры sift (программа 2.2) таким образом:
r := n;
WHILE r > 1 DO
BEGIN x :=a[1]; a[1]:=a[r]; a[r]:=x;
r: = r- 1; sift (1,r)
END
Пример из табл. 2.3 показывает, что получающийся порядок фактически является обратным. Однако это можно легко исправить, изменив направление "упорядочивающего отношения" в процедуре sift. В конце концов, получаем процедуру HeapSort (программа 2.3).
Таблица 2.3. Пример процесса сортировки с помощью Heapsort.
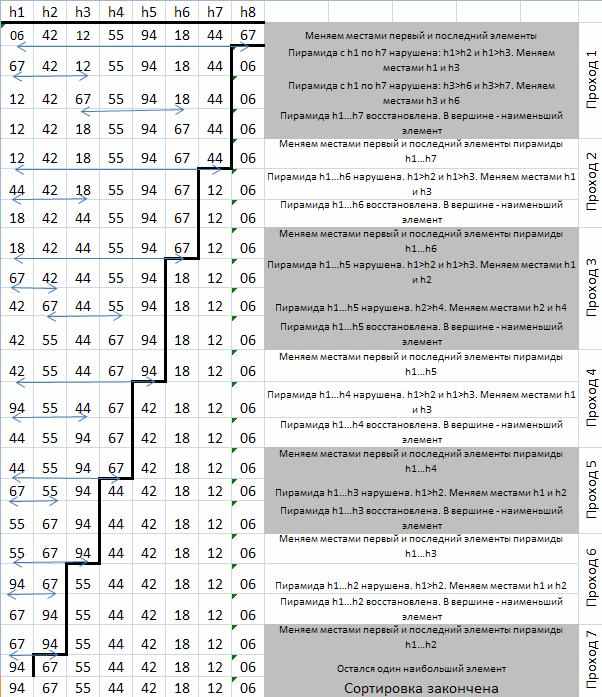
procedure HeapSort;
var l,r:index; x:item;
procedure sift;
label 13;
var i,j: index;
begin i:=l; j:=2*i; x:=a[i];
while j<=r do
begin if j
if a[j].key
if x.key>=a[j].key then goto 13;
a[i]:=a[j];
i:=j;
j:=2*i
end;
13: a[i]:=x
end;
begin l:=(n div 2)+1; r:=n;
while l>1 do
begin l:=l-1; sift
end;
while r>1 do
begin x:=a[1]; a[1]:=a[r]; a[r]:=x;
r:=r-1; sift
end
end;
Программа 2.3. HeapSort
Анализ HeapSort. На первый взгляд вовсе не очевидно, что такой метод сортировки дает хорошие результаты. Ведь, в конце концов, большие элементы, прежде чем попадут на свое место в правой части, сначала сдвигаются влево. И действительно, процедуру не рекомендуется применять для небольшого, вроде нашего примера, числа элементов. Для больших же n HeapSort очень эффективна; чем больше n, тем лучше она работает. Она даже становится сравнимой с сортировкой Шелла.
В худшем случае нужно n/2 сдвигающих шагов, они сдвигают элементы на log(n/2),log(n/2 -1),…, log(n-1) позиций (целая часть логарифма по основанию 2) Следовательно, фаза сортировки требует n - 1 сдвигов с самое большое log(n - 1), log(n - 2),..., 1 перемещениями. Кроме того, нужно еще n – 1 перемещений для просачивания сдвинутого элемента на некоторое расстояние вправо. Эти соображения показывают, что даже в самом плохом из возможных случаев HeapSort потребует n * log n шагов. Великолепная производительность в таких плохих случаях — одно из привлекательных свойств HeapSort.
Совсем не ясно, когда следует ожидать наихудшей (или наилучшей) производительности. Но вообще-то кажется, что HeapSort "любит" начальные последовательности, в которых элементы более или менее отсортированы в обратном порядке. Поэтому ее поведение несколько неестественно. Если мы имеем дело с обратным порядком, то фаза порождения пирамиды не требует каких-либо перемещений. Среднее число перемещений приблизительно равно n/2 * log(n), причем отклонения от этого значения относительно невелики.
Сортировка с помощью разделения
Разобравшись в двух усовершенствованных методах сортировки, построенных на принципах включения и выбора, мы теперь коснемся третьего улучшенного метода, основанного на обмене. Если учесть, что пузырьковая сортировка в среднем была самой неэффективной из всех трех алгоритмов прямой (строгой) сортировки, то следует ожидать относительно существенного улучшения. И все же это выглядит как некий сюрприз: улучшение метода, основанного на обмене, о котором мы будем сейчас говорить, оказывается, приводит к самому лучшему из известных в данный момент методу сортировки для массивов. Его производительность столь впечатляюща, что изобретатель Ч. Хоар даже назвал метод быстрой сортировкой (Quicksort).
В Quicksort исходят из того соображения, что для достижения наилучшей эффективности сначала лучше производить перестановки на большие расстояния. Предположим, у нас есть n элементов, расположенных по ключам в обратном порядке. Их можно отсортировать за n/2 обменов, сначала поменять местами самый левый с самым правым, а затем последовательно двигаться с двух сторон. Конечно, это возможно только в том случае, когда мы знаем, что порядок действительно обратный. Но из этого примера можно извлечь и нечто действительно поучительное.
Давайте попытаемся воспользоваться таким алгоритмом: выберем наугад какой-либо элемент (назовем его x) и будем просматривать слева направо массив до тех пор, пока не обнаружим элемент ai > x, затем просмотрим его справа налево, пока не найдем элемент aj < x. Теперь поменяем местами эти два элемента и продолжим процесс «просмотра с обменом», пока два просмотра не встретятся где-то в середине массива. В результате массив разделится на две части: левую – с ключами, меньшими, чем x, и правую – с ключами большими х. Теперь этот процесс разделения представим в виде процедуры (программа 2.4).
Procedure partition;
Var w,x: item;
Begin i:=1; j:=n;
Случайно выбрать x;
Repeat
While a[i].key < x.key do i:=i + 1;
While x.key < a[j].key do j:=j - 1;
If i <= j then
Begin w:=a[i]; a[i]:=a[j]; a[j]:=w;
i:=i+1; j:=j-1
end
until i > j
end;
Программа 2.4. Сортировка с помощью разделения.
Обратите внимание, что вместо отношений > и < используются ≥ и ≤, а в заголовке цикла с WHILE — их отрицания < и >. При таких изменениях x выступает в роли барьера для того и другого просмотра. Если взять в качестве x для сравнения средний ключ 42, то в массиве ключей
44 55 12 42 94 06 18 67
для разделения понадобятся два обмена: 18 44 и 6 55
18 06 12 42 94 55 44 67
Последние значения индексов таковы: i = 5, a j = 3. Ключи a1...ai-1 меньше или равны ключу х = 42, а ключи aj+1 ... аn больше или равны х. Следовательно, существует две части, а именно:
ak.key<=x.key для: k = 1, …, i-1,
(*)
ak.key>=x.key для: k = j+1, …, n.
И, следовательно,
ak.key = x.key k = j+1, …, I -1
Описанный алгоритм очень прост и эффективен, поскольку главные сравниваемые величины i, j и x можно хранить во время просмотра в быстрых регистрах машины. Однако он может оказаться и неудачным, что, например, происходит в случае n идентичных ключей: для разделения нужно n/2 обменов. Этих вовсе необязательных обменов можно избежать, если операторы просмотра заменить на такие:
While a[i].key <= x.key do i: = i+1;
While x.key <= a[j].key do j: = j -1
Однако в этом случае выбранный элемент x, находящийся среди компонент массива, уже не работает как барьер для двух разнонаправленных просмотров. В результате просмотры массива со всеми идентичными ключами приведут, если только не использовать более сложные условия их окончания, к переходу через границы массива. Простота условий, употребленных в программе 2.4, вполне оправдывает те дополнительные обмены, которые происходят в среднем относительно редко. Можно еще немного сэкономить, если изменить заголовок, управляющий самим обменом: от i <= j перейти к i < j. Однако это изменение не должно касаться двух операторов:
i: = i + 1; j: = j - 1.
Поэтому для них потребуется отдельный условный оператор. Необходимость условия i <= j можно проиллюстрировать следующим примером при x = 2:
1 1 1 2 1 1 1
Первый просмотр и обмен дают
1 1 1 1 1 1 2,
причем i = 5, j = 6. Второй просмотр не изменяет массив и заканчивается с i = 7 и j = 6. Если бы обмен не подчинялся условию i <= j, то произошел бы ошибочный обмен a6 и a7.
Убедиться в правильности алгоритма разделения можно, удостоверившись, что отношения (*) представляют собой инварианты оператора цикла с Repeat. Вначале при i = 1 и j = n их истинность тривиальна, а при выходе с i > j они дают как раз желаемый результат.
Теперь напомним, что наша цель — не только провести разделение на части исходного массива элементов, но и отсортировать его. Сортировку от разделения отделяет, однако, лишь небольшой шаг: нужно применить этот процесс к получившимся двум частям, затем — к частям частей, и так до тех пор, пока каждая из частей не будет состоять из одного-единственного элемента. Эти действия описываются листингом программы 2.5.
procedure QuickSort;
procedure sort(l,r:index);
var i,j:index; x,w:item;
begin
i:=l; j:=r;
x:=a[(l+r) div 2];
repeat
while a[i].key
while x.key
if i<=j then
begin w:=a[i]; a[i]:=a[j]; a[j]:=w;
i:=i+1; j:=j-1
end
until i>j;
if l
if l
end;
begin
sort(1,n)
end;
Программа 2.5. Быстрая сортировка (Quicksort)
Анализ Quicksort. В благоприятных ситуациях каждый процесс разделения расщепляет массив на две половины и для сортировки требуется всего log n проходов. В результате общее число сравнений равно n*log n, а общее число обменов n* log(n)/6. Удивительный, однако, факт: средняя производительность Quicksort при случайном выборе границы отличается от упомянутого оптимального варианта лишь коэффициентом 2*ln (2).
Как бы то ни было, но Quicksort присущи и некоторые недостатки. Главный из них — недостаточно высокая производительность при небольших n, впрочем, этим грешат все усовершенствованные методы. Однако данный метод имеет то преимущество, что для обработки небольших частей в него можно легко включить какой-либо из прямых методов сортировки. Это особенно удобно делать в случае рекурсивной версии программы.
Остается все еще вопрос о самом плохом случае. Как тогда будет работать Quicksort? К несчастью, ответ неутешителен
 и демонстрирует одно неприятное свойство Quicksort. Разберем, скажем, тот несчастный случай, когда каждый раз для сравнения выбирается наибольшее из всех значений в указанной части. Тогда на каждом этапе сегмент из n элементов будет расщепляться на левую часть, состоящую из n-1 элементов, и правую, состоящую из одного-единственного элемента. В результате потребуется n (а не log n) разделений и наихудшая производительность метода будет порядка n2.
и демонстрирует одно неприятное свойство Quicksort. Разберем, скажем, тот несчастный случай, когда каждый раз для сравнения выбирается наибольшее из всех значений в указанной части. Тогда на каждом этапе сегмент из n элементов будет расщепляться на левую часть, состоящую из n-1 элементов, и правую, состоящую из одного-единственного элемента. В результате потребуется n (а не log n) разделений и наихудшая производительность метода будет порядка n2.Явно видно, что главное заключается в выборе элемента для сравнения - х. В нашей редакции им становится средний элемент. Заметим, однако, что почти с тем же успехом можно выбирать первый или последний. В этих случаях хуже всего будет, если массив окажется первоначально, уже упорядочен, ведь Quicksort определенно "не любит" такую тривиальную работу и предпочитает иметь дело с неупорядоченными массивами. Выбирая средний элемент, мы как бы затушевываем эту странную особенность Quicksort, поскольку в этом случае первоначально упорядоченный массив будет уже оптимальным вариантом. Таким образом, фактически средняя производительность при выборе среднего элемента чуточку улучшается. Сам Хоар предполагает, что x надо выбирать случайно. Такой разумный выбор мало влияет на среднюю производительность Quicksort, но зато значительно ее улучшает (в наихудших случаях). В некотором смысле быстрая сортировка напоминает азартную игру: всегда следует учитывать, сколько можно проиграть в случае невезения.
Заканчивая наш обзор усовершенствованных методов сортировки, мы попытаемся сравнить их эффективность. Как и раньше, n — число сортируемых элементов, а С и М — соответственно число необходимых сравнений ключей и число обменов. Для всех прямых методов сортировки можно дать точные аналитические формулы. Для усовершенствованных методов нет сколько-либо осмысленных, простых и точных формул. Существенно, однако, что в случае сортировки Шелла вычислительные затраты составляют с*n1.2, а для HeapSort и Quicksort — с* n* log n, где с — соответствующие коэффициенты.
Эти формулы просто вводят грубую меру для производительности как функции n и позволяют разбить алгоритмы сортировки на примитивные, прямые методы (n2) и на усложненные или "логарифмические" методы (n * log(n)).
Рассмотрев, несколько различных усложненных методов сортировки массивов нетрудно заметить главный недостаток – недостаточно высокая производительность при небольших n. Действительно эти сортировки не рекомендуется применять для небольшого числа элементов (для этого существуют простые методы сортировки). Хотя и это можно исправить, путем включения простых методов сортировки для небольших n.
Итак, сделаем вывод: выбор определенного метода сортировки зависит от структуры обрабатываемых данных, а также от количества элементов. При решении определенной задачи, выбранный метод сортировки должен быть наиболее эффективным.
Лекция № 3.
Тема: Сортировка последовательных файлов
Основные вопросы, рассматриваемые на лекции:
- Особенности сортировки последовательных файлов.
- Прямое слияние.
К сожалению, алгоритмы сортировки, рассмотренные в предыдущих лекциях, неприменимы, если сортируемые данные не помещаются в оперативной памяти, а, например, расположены на внешнем запоминающем устройстве с последовательным доступом, таком, как магнитная лента. В этом случае мы описываем данные как (последовательный) файл, который характеризуется тем, что в каждый момент имеется непосредственный доступ к одному и только одному элементу. Это — строгое ограничение по сравнению с возможностями, которые дает массив, и поэтому здесь приходится применять другие методы сортировки. Основной метод — это сортировка слиянием. Слияние означает объединение двух (или более) упорядоченных последовательностей в одну упорядоченную последовательность при помощи циклического выбора элементов, доступных в данный момент. Слияние — намного более простая операция, чем сортировка; она используется в качестве вспомогательной в более сложном процессе последовательной сортировки. Один из методов сортировки слиянием называется простым слиянием и состоит в следующем:
- Последовательность а разбивается на две половины b и с.
- Последовательности b и c сливаются при помощи объединения отдельных элементов в упорядоченные пары.
- Полученной последовательности присваивается имя a, и повторяются шаги 1 и 2; на этот раз упорядоченные пары сливаются в упорядоченные четверки.
- Предыдущие шаги повторяются; четверки сливаются в восьмерки, и весь процесс продолжается до тех пор, пока не будет упорядочена вся последовательность, ведь длины сливаемых последовательностей каждый раз удваиваются.
В качестве примера рассмотрим последовательность
44 55 12 42 94 18 06 67
На первом шаге разбиение дает последовательности
44 55 12 42
94 18 06 67
Слияние отдельных компонент (которые являются упорядоченными последовательностями длины 1) в упорядоченные пары дает
44 94 ' 18 55 ' 06 12 ' 42 67
Повое разбиение пополам и слияние упорядоченных пар дают
06 12 44 94 ' 18 42 55 67
Третье разбиение и слияние приводят, наконец, к нужному результату:
06 12 18 42 44 55 67 94
Операция, которая однократно обрабатывает все множество данных, называется фазой, а наименьший подпроцесс, который, повторяясь, образует процесс сортировки, называется проходом или этапом. В приведенном выше примере сортировка производится за три прохода, каждый проход состоит из фазы разбиения и фазы слияния. Для выполнения сортировки требуются три магнитные ленты, поэтому процесс называется трехленточным слиянием.
Собственно говоря, фазы разбиения не относятся к сортировке, поскольку они никак не переставляют элементы; в каком-то смысле они непродуктивны, хотя и составляют половину всех операций переписи. Их можно удалить, объединив фазы разбиения и слияния. Вместо того чтобы сливать элементы в одну последовательность, результат слияния сразу распределяют на две ленты, которые на следующем проходе будут входными. В отличие от двухфазного слияния этот метод называется однофазным или сбалансированным слиянием. Оно имеет явные преимущества, так как требует вдвое меньше операций переписи, но это достигается ценой использования четвертой ленты.
Разберем программу слияния подробно; предположим сначала, что данные расположены в виде массива, который, однако, можно просматривать только строго последовательно.
Вместо двух файлов можно легко использовать один массив, если рассматривать его как последовательность с двумя концами. Вместо того чтобы сливать элементы из двух исходных файлов, мы можем брать их с двух концов массива. Таким образом, общий вид объединенной фазы слияния-разбиения можно изобразить, как показано на рис. 3.1.
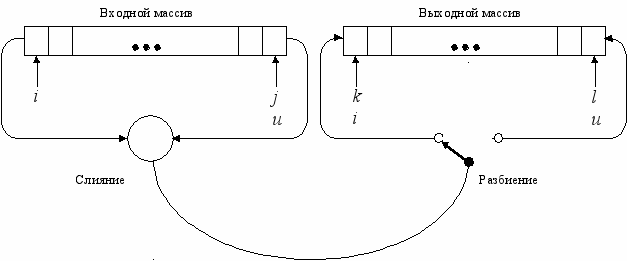
Рис. 3.1. Сортировка двух массивов методом слияния
Направление пересылки сливаемых элементов меняется (переключается) после каждой упорядоченной пары на первом проходе, после каждой упорядоченной четверки на втором проходе и т. д.; таким образом равномерно заполняются две выходные последовательности, представленные двумя концами одного массива (выходного). После каждого прохода два массива меняются ролями: входной становится выходным и наоборот. Программу можно еще больше упростить, объединив два концептуально различных массива в один массив двойной длины. Итак, данные будут представлены следующим образом:
a: array[l. .2*n] of item
Пусть индексы i и j указывают два исходных элемента, тогда как k и l обозначают два места пересылки (см. рис. 3.1). Исходные данные — это, разумеется, элементы а1, ..., аn. Очевидно, что нужна булевская переменная up для указания направления пересылки данных; up = true будет означать, что на текущем проходе компоненты а1, ..., аn будут пересылаться «вверх» — в переменные аn+1, ..., а2n, тогда как up — false будет указывать, что аn+1, ..., а2n должны переписываться «вниз» —в а1, ..., аn. Значение up строго чередуется между двумя последовательными проходами. И наконец, вводится переменная р для обозначения длины сливаемых подпоследовательностей (р-наборов). Ее начальное значение равно 1, и оно удваивается перед каждым очередным проходом. Для простоты мы будем считать, что n — всегда степень двойки. Итак, первая версия программы простого слияния имеет такой вид:
procedure mergesort;
var i,j,k,l: index;
up: Boolean; p: integer;
begin up :== true; p := 1;
repeat {инициация индексов}
if up then
begin i := 1; j:= n; k := n + 1; l := 2*n
end else
begin k :=1; l:=n; i := n+1; j := 2*n end;
«слияние р-наборов последовательностей i и j
в последовательности k и l»;
uр := - up; p := 2*р
until р = п
end
На следующем этапе мы уточняем действие, описанное на естественном языке (внутри кавычек). Ясно, что этот проход, обрабатывающий n элементов, состоит из последовательных слияний р-наборов. После каждого отдельного слияния направление пересылки переключается из нижнего в верхний конец выходного массива или наоборот, чтобы обеспечить одинаковое распределение в обоих направлениях. Если сливаемые элементы посылаются в нижний конец массива, то индексом пересылки служит k и k увеличивается на 1 после каждой пересылки элемента. Если же они пересылаются в верхний конец массива, то индексом пересылки является l и l после каждой пересылки уменьшается на 1. Чтобы упростить операцию слияния, мы будем считать, что место пересылки всегда обозначается через k, и будем менять местами значения k и l после слияния каждого р-набора, а приращение индекса обозначим через h, где h равно либо 1, либо -1. Уточнив таким образом «конструкцию», мы получаем
h := 1; m := n; {m-номера сливаемых элементов }
repeat q : = р; r : = р; т:= т-2*р;
«слияние q элементов из i и r элементов из j,
индекс засылки есть k с приращением h»;
h := -h;
обмен значениями k и l
until m = 0
На следующем этапе уточнения нужно сформулировать саму операцию слияния. Здесь следует учесть, что остаток подпоследовательности, которая остается непустой после слияния, добавляется к выходной последовательности при помощи простого копирования.
while (q<>0) and (r<>0) do
begin {выбор элемента из i uли j}
if a[i] .key < a[j] .key then
begin «пересылка элемента из i в k,
увеличение i и k»; q := q-1
end else
begin «пересылка элемента из j в k,
увеличение j и k» ; r :=r - 1
end
end;
«копирование остатка последовательности i»;
«копирование остатка последовательности j»
После уточнения операций копирования остатков программа будет ясна во всех деталях. Перед тем как записать ее полностью, мы хотим устранить ограничение, в соответствии с которым n должно быть степенью двойки. На какую часть алгоритма это повлияет? Легко убедиться в том, что в более общей ситуации лучше всего использовать прежний метод до тех пор, пока это возможно. В данном случае это означает, что мы продолжаем слияние р-наборов, пока длина остатков входных последовательностей не станет меньше p. Это влияет только на ту часть, где определяются значения q и r — длины последовательностей, которые предстоит слить. Вместо трех операторов
q := р; r:= p; m:= m - 2*р
используются следующие четыре оператора, и, как может убедиться читатель, здесь эффективно применяется описанная выше стратегия; заметим, что m обозначает общее число элементов в двух входных последовательностях, которые осталось слить:
if т >= р then q := p else q := m; m := m - q;
if т >= р then r := p else r := m; m := m - r;
И наконец, чтобы обеспечить окончание работы программы, нужно заменить условие р = n, управляющее внешним циклом, на р >= n. После этих модификаций мы можем попытаться описать весь алгоритм в виде законченной программы (см. программу 3.1).
procedure mergesort;
var i,j,k,l,t: index;
h,m,p,q,r:integer; up:boolean;
begin up:=true; p:=1;
repeat h:=1; m:=n;
if up then
begin i:=1; j:=n; k:=n+1; l:=2*n;
end else
begin k:=1; l:=n; i:=n+1; j:=2*n
end;
repeat
if m>=p then q:=p else q:=m; m:=m-q;
if m>=p then r:=p else r:=m; m:=m-r;
while (q<>0) and (r<>0) do
begin
if a[i].key < a[j] . key then
begin a[k]:=a[i]; k:=k+h; i:=i+1; q:=q-1;
end else
begin a[k]:=a[j]; k:=k+h; j:=j-1; r:=r-1
end
end;
while r<>0 do
begin a[k]:=a[j]; k:=k+h; j:=j-1; r:=r-1
end;
while q<>0 do
begin a[k]:=a[i]; k:=k+h; i:=i+1; q:=q-1
end;
h:=-h; t:=k; k:=l; l:=t
until m=0;
up:= not up; p:=2*p
until p>=n;
if not up then
for i:=1 to n do a[i]:=a[i+n]
end;
Программа 3.1.
Анализ сортировки слиянием. Поскольку на каждом проходе р удваивается и сортировка заканчивается, как только р>=n, она требует [log2n] проходов. По определению при каждом проходе все множество из n элементов копируется ровно один раз. Следовательно, общее число пересылок равно
М = п [log2 n]
Число С сравнений по ключу еще меньше, чем М, так как при копировании остатка последовательности сравнения не производятся. Но, поскольку сортировка слиянием обычно применяется при работе с внешними запоминающими устройствами, стоимость операций пересылки часто на несколько порядков превышает стоимость сравнений. Поэтому подробный анализ числа сравнений не представляет особого практического интереса.
Алгоритм сортировки слиянием выдерживает сравнение даже с усовершенствованными методами сортировки, которые обсуждались в предыдущей лекции. Но затраты на управление индексами довольно высоки, кроме того, существенным недостатком является использование памяти размером 2n элементов. Поэтому сортировка слиянием редко применяется при работе с массивами, т. е. данными, расположенными в оперативной памяти.
Лекция № 4.
Тема: Введение в рекурсию. Когда не нужно использовать рекурсию.
Основные вопросы, рассматриваемые на лекции:
- Рекурсия, терминология.
- Примеры задач, когда не нужно использовать рекурсию.
