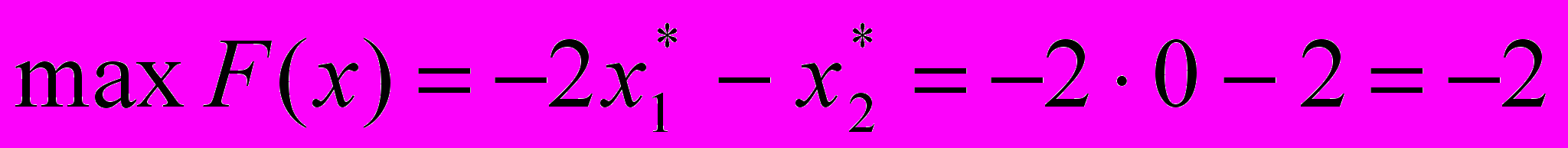Задание: Найти, при заданных ограничениях

Вид материала

Документы

Подобный материал:

• Задание по начертательной геометрии для студентов 1 курса   Задание №1 Задача №1 , 909.02kb.
• Расчетно-графическое задание №5. Колебания, 246.73kb.
• Задача линейного программирования состоит в том, что необходимо максимизировать или, 24.8kb.
• Программирование в ограничениях и недоопределенные модели а. С. Нариньяни, В. В. Телерман,, 419.59kb.
• Домашнее задание. Сумма баллов за урок Задание, 45.93kb.
• Задание объектом нашего исследования являются современные системы безопасности: охранная, 300.74kb.
• Задания для контрольной работы по bdc задание, 155.48kb.
• Ю. Е., Эф, гр. 826 Оптимизация структуры капитала, 71.71kb.
• Урока Глава Тема Домашнее задание, 10.37kb.
• Первое задание 7 Второе задание 10 Третье задание 24 Четвертое задание 30 Вопросы, 344.04kb.

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ПО ИССЛЕДОВАНИЮ ОПЕРАЦИЙ (СИМПЛЕКС-МЕТОД) (ВАРИАНТ №4)


Задание: Найти 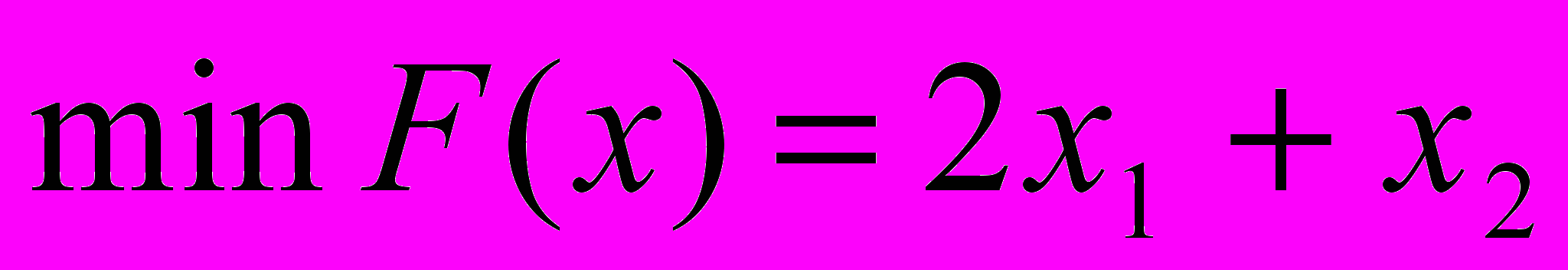, при заданных ограничениях: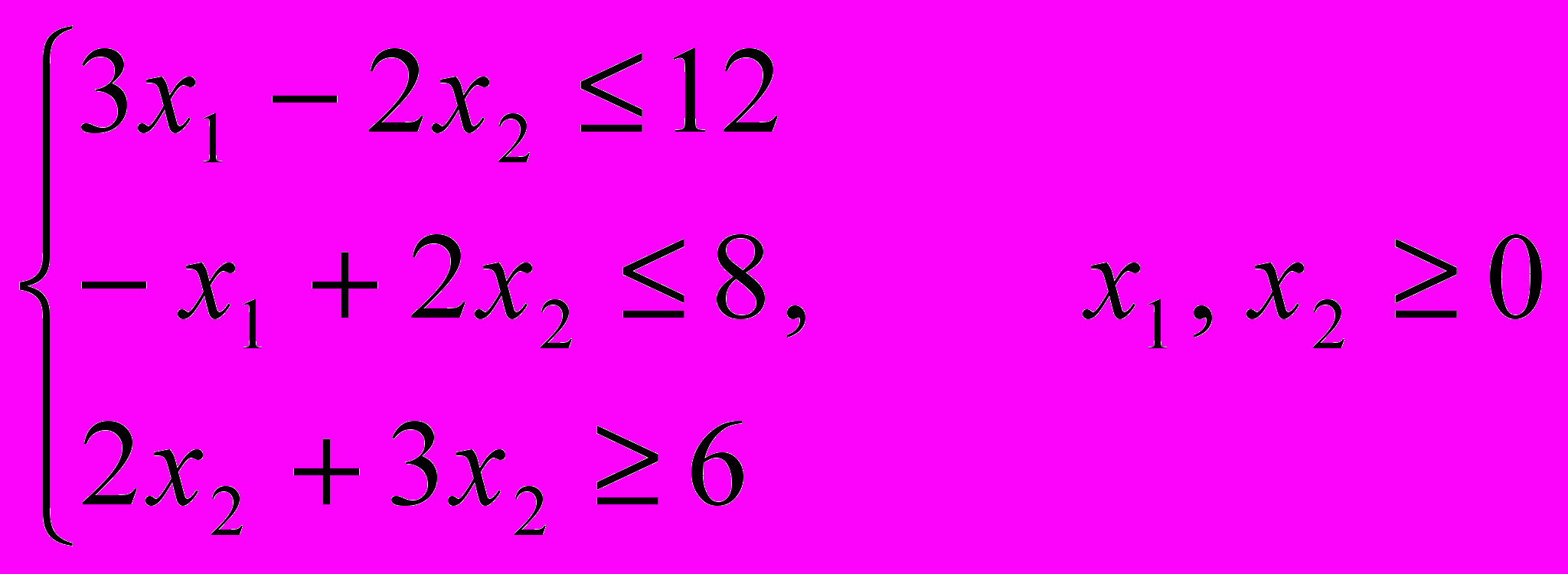



Т.к. в третьем уравнении имеется знак 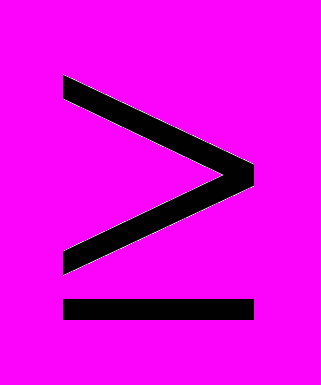, то введем искусственную переменную х₆ и перейдём к задаче максимизации (поменяем знак целевой функции), при этом в целевую ф-цию войдёт искусственная переменная х₆ с отрицательным знаком и коэффициентом М (М >>1).

.

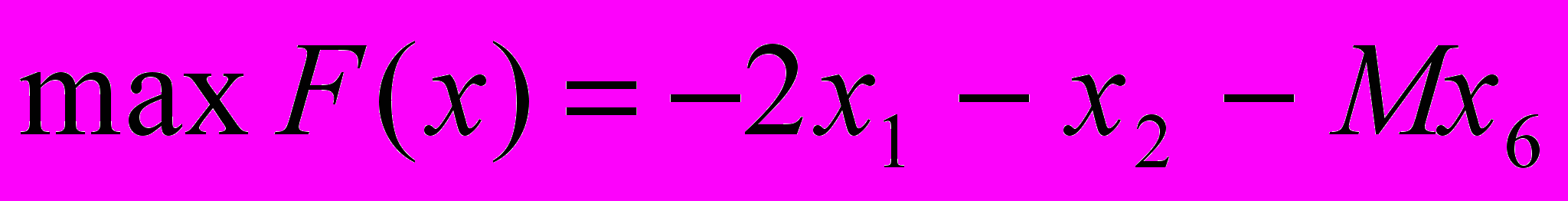Приведём ограничения к расширенной форме:



Из системы ограничений выберем базис, который составят переменные х₃, х₄, х₆, т.к. они образуют единичную матрицу:



Базис:

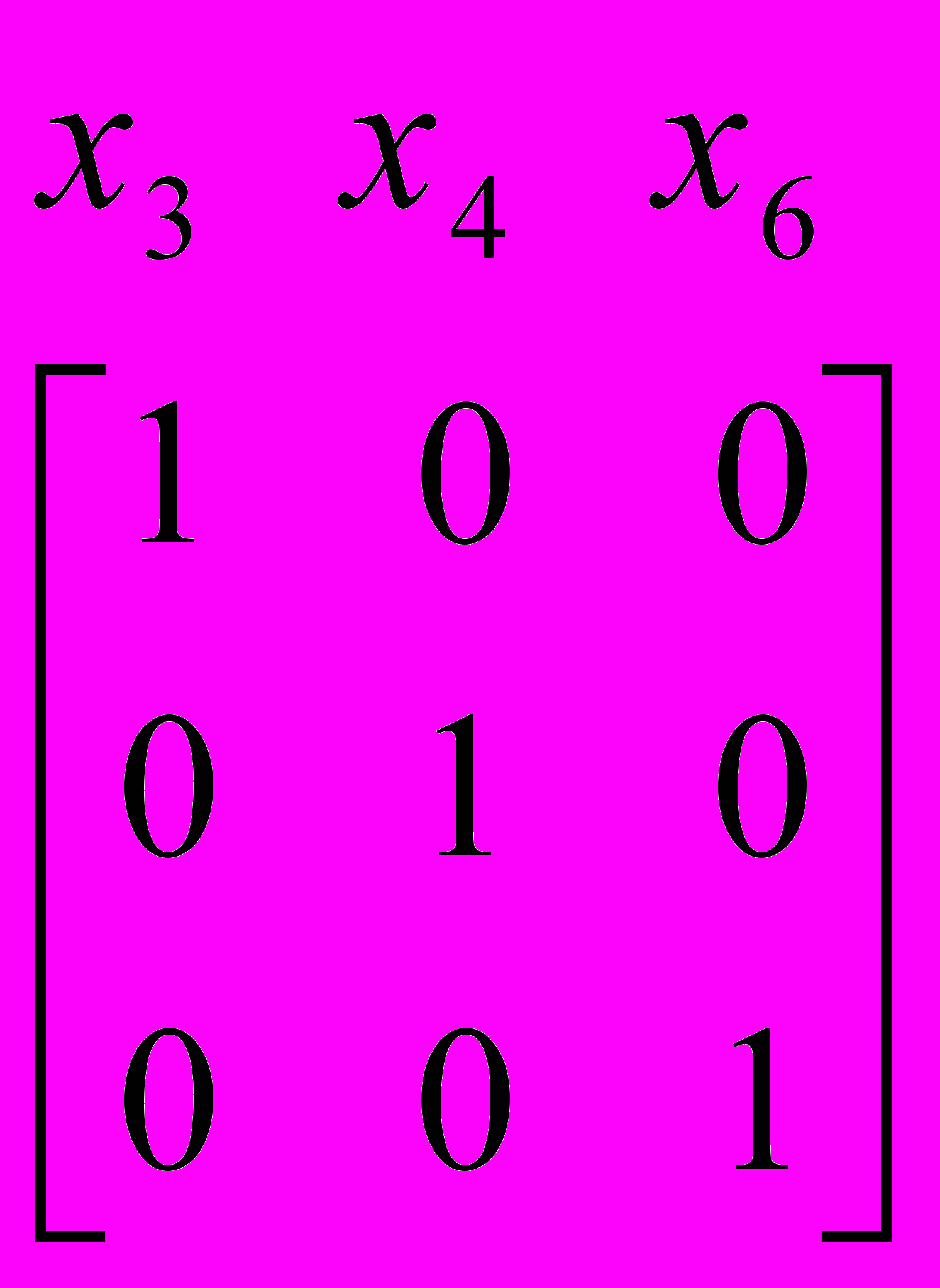
Составим симплекс-таблицу:

С			с1 = -2	с2 = -1	с3 = 0	с4 = 0	с5 = 0	с6 = -М
	ХР	В	А1	А2	А3	А4	А5	А6
с3 = 0	х3	12	3	-2	1	0	0	0
с4 = 0	х4	8	-1	2	0	1	0	0
с6 = -М	х6	6	2	3	0	0	-1	1
S				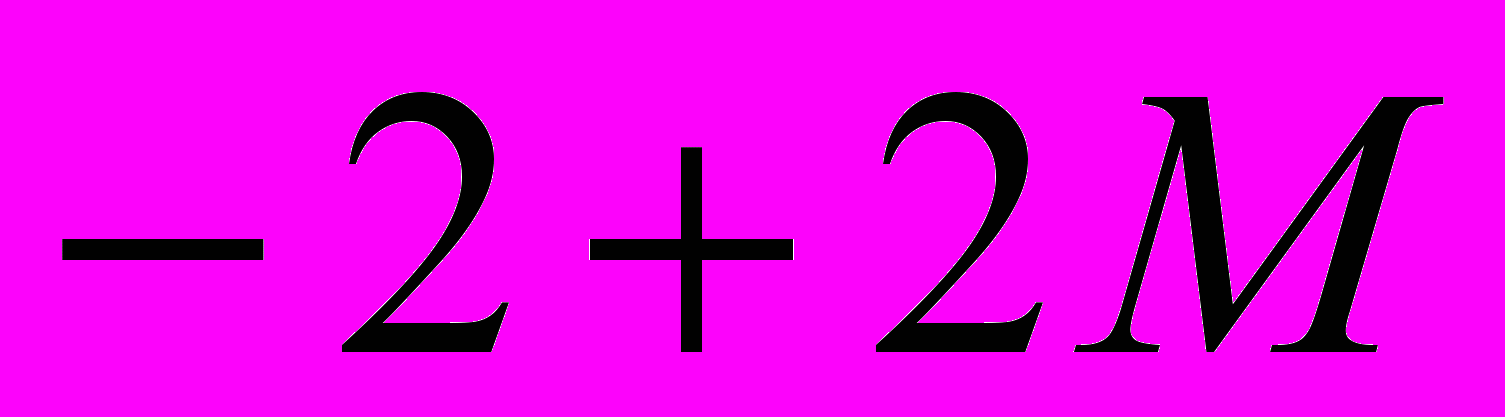	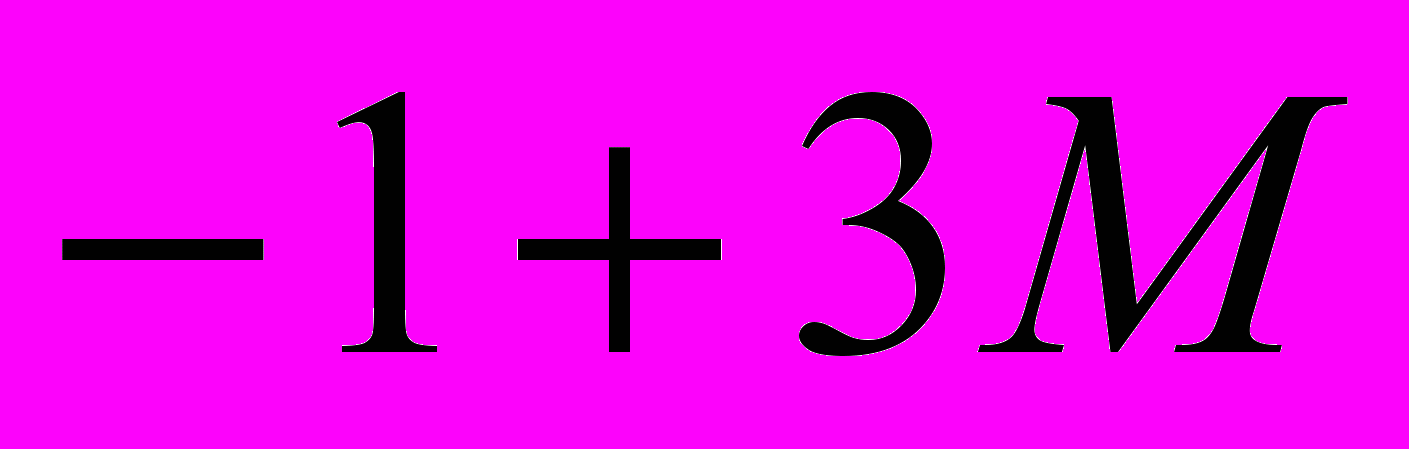0	0	-М	0

Определим симплекс-разности:













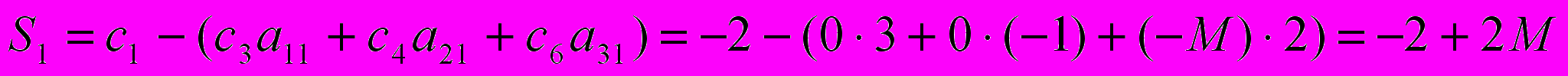
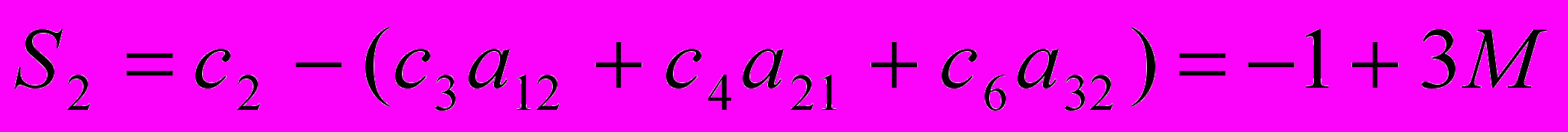
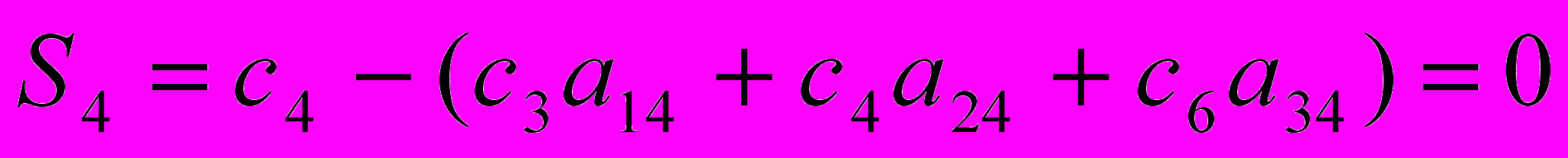
Т.к. М довольно большое число, то максимальной положительной симплекс-разностью будет являться S₂ = -1 + 3М. Столбец, в котором эта разность находится назовем направляющим. Для того чтобы определить направляющую строку найдём:

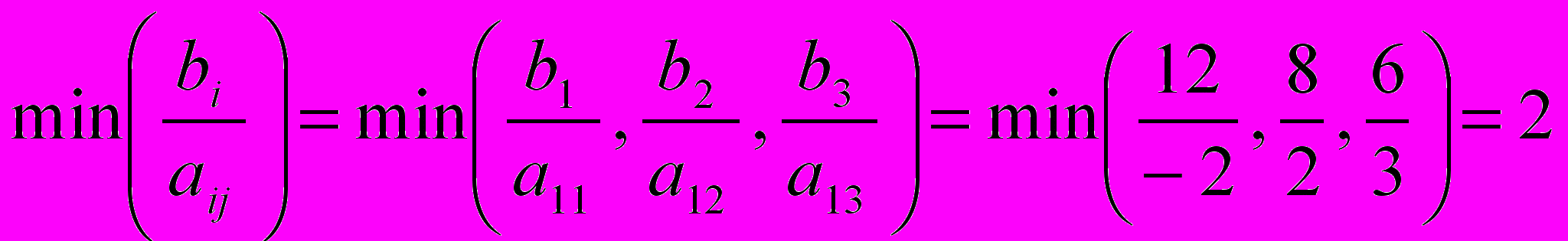(т.к. 6/3=2 - минимальное положительное число)

Следовательно, 3-я строка будет направляющей. Направляющий элемент 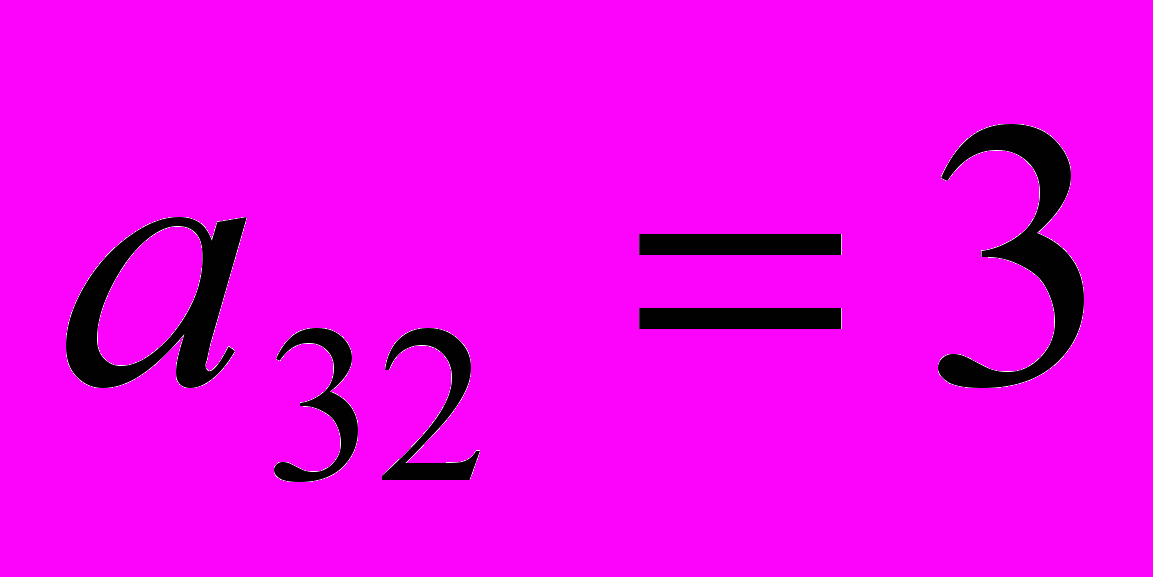будет направляющим, так как он находится на пересечении направляющей строки и направляющего столбца.

Теперь удаляем из базиса переменную х₆ (соответственно направляющей строке) и вводим переменную х₂ (соответственно направляющему столбцу).

Заполним новую таблицу, соответствующую новому базисному решению. Для этого в начале все элементы направляющей строки делим на направляющий элемент:





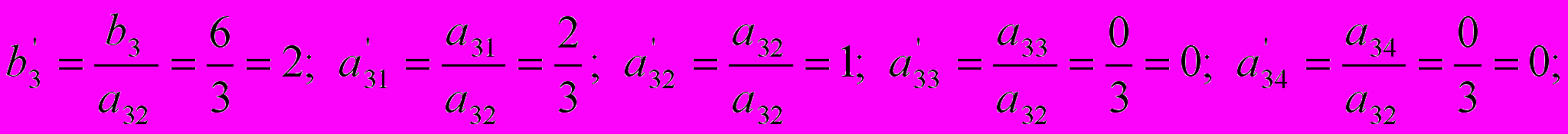
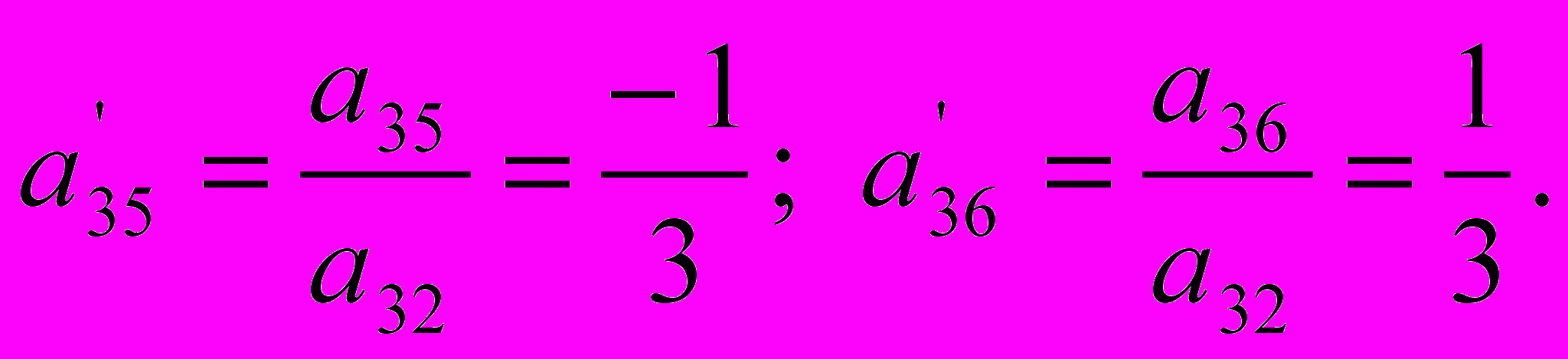
Элементы направляющего столбца (кроме направляющего элемента) будут равны нулю:

.

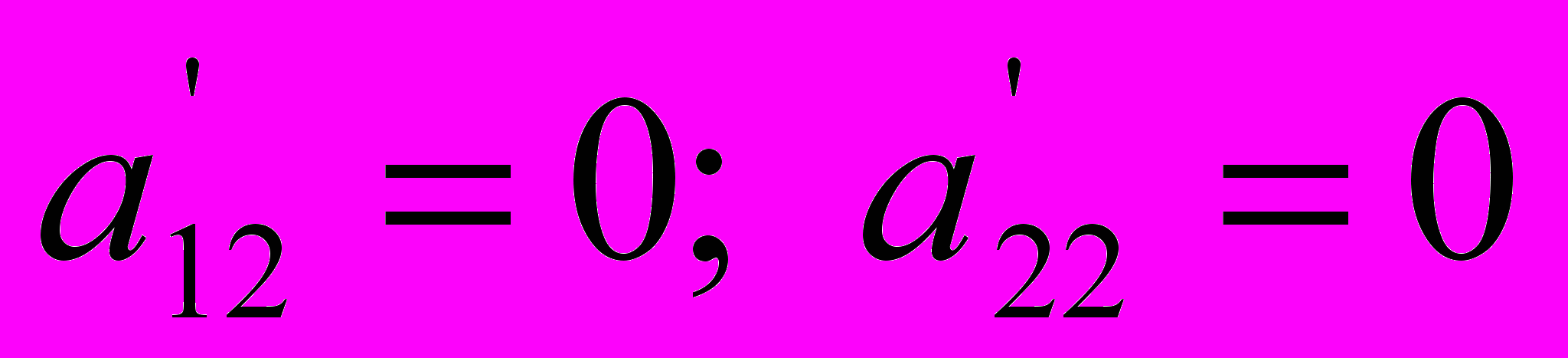Остальные элементы рассчитываются согласно мнемоническому правилу:

Пусть направляющий элемент 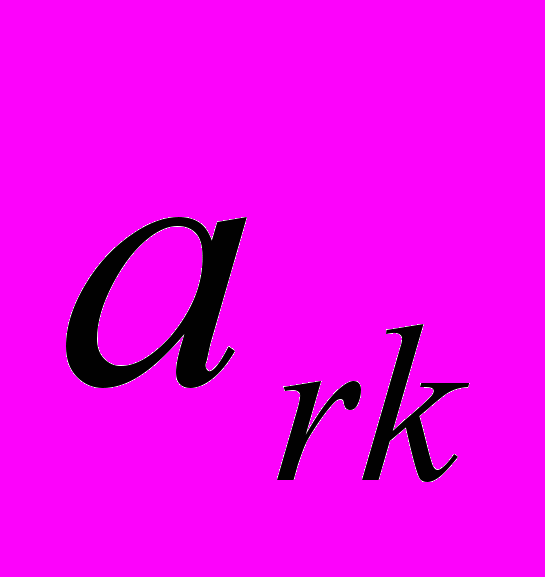, тогда:

;

.

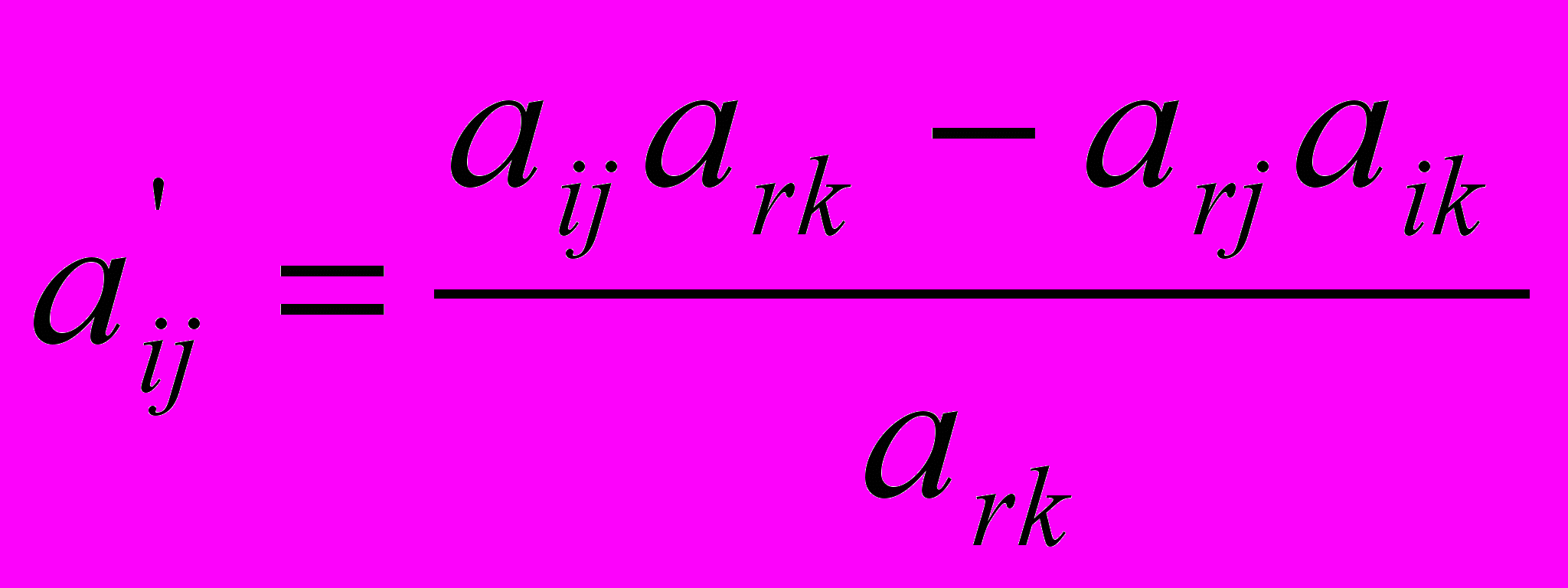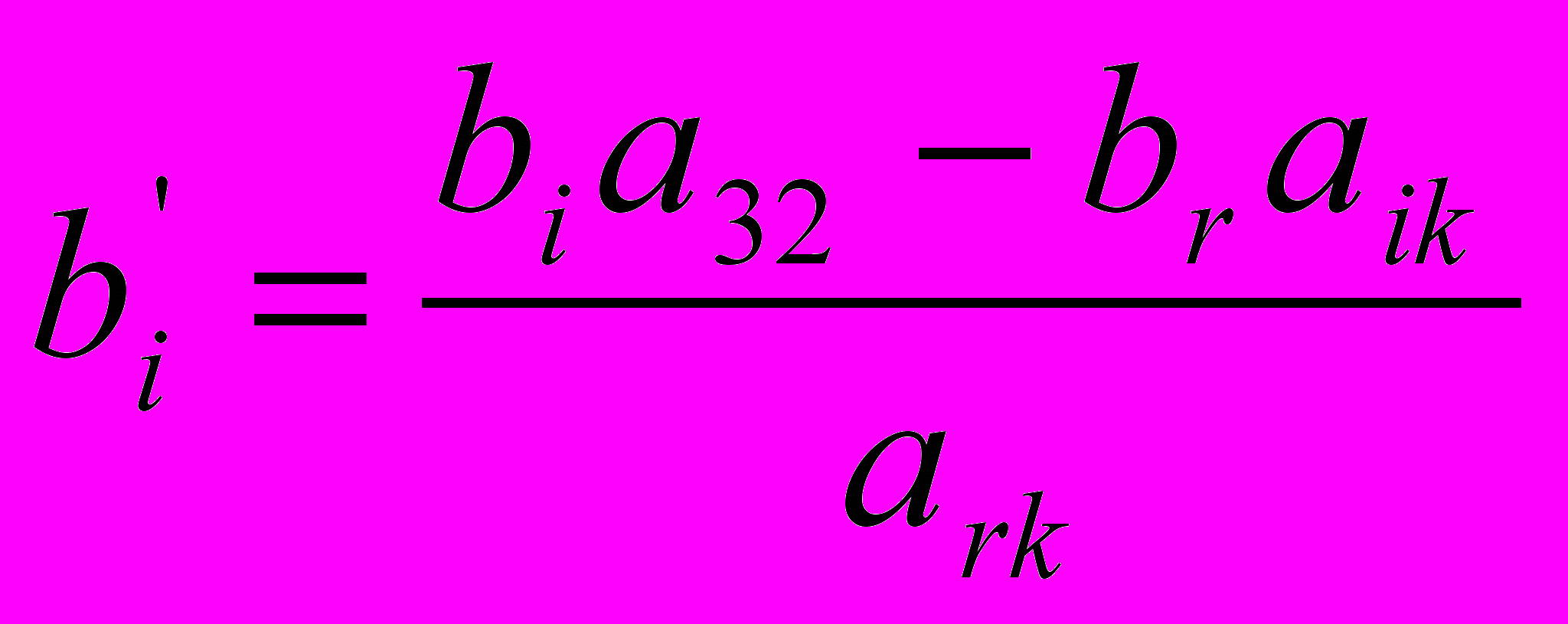Т.е. из произведения элементов, стоящих по одной диагонали прямоугольника (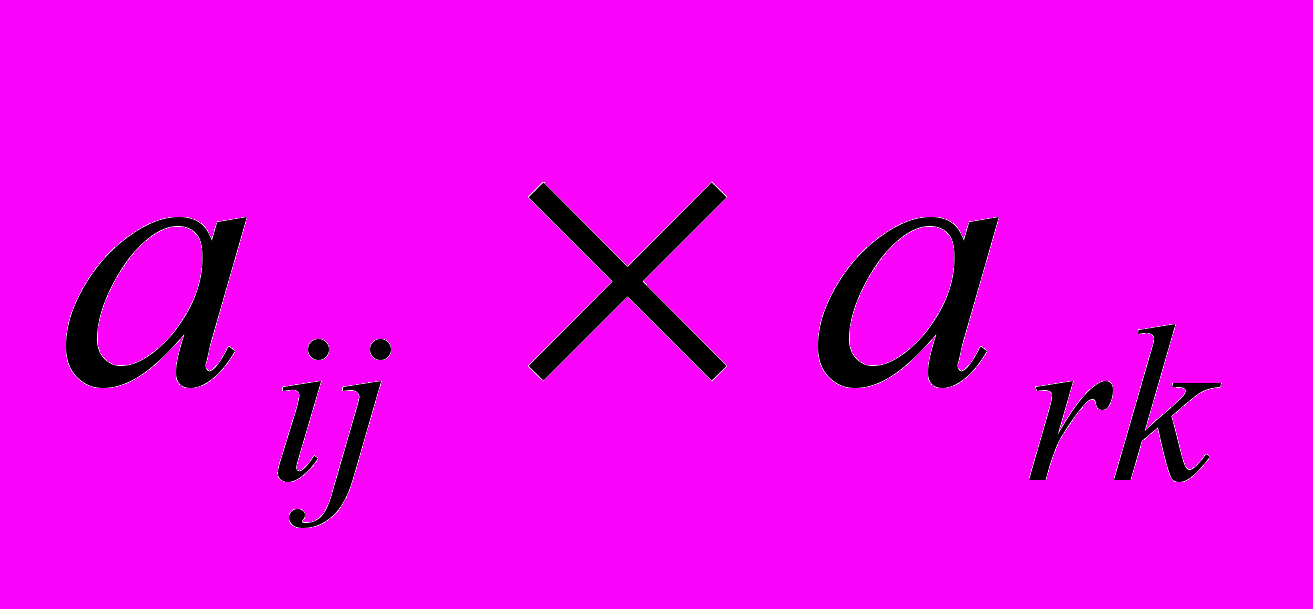), вычесть произведение элементов, стоящих по другую диагональ (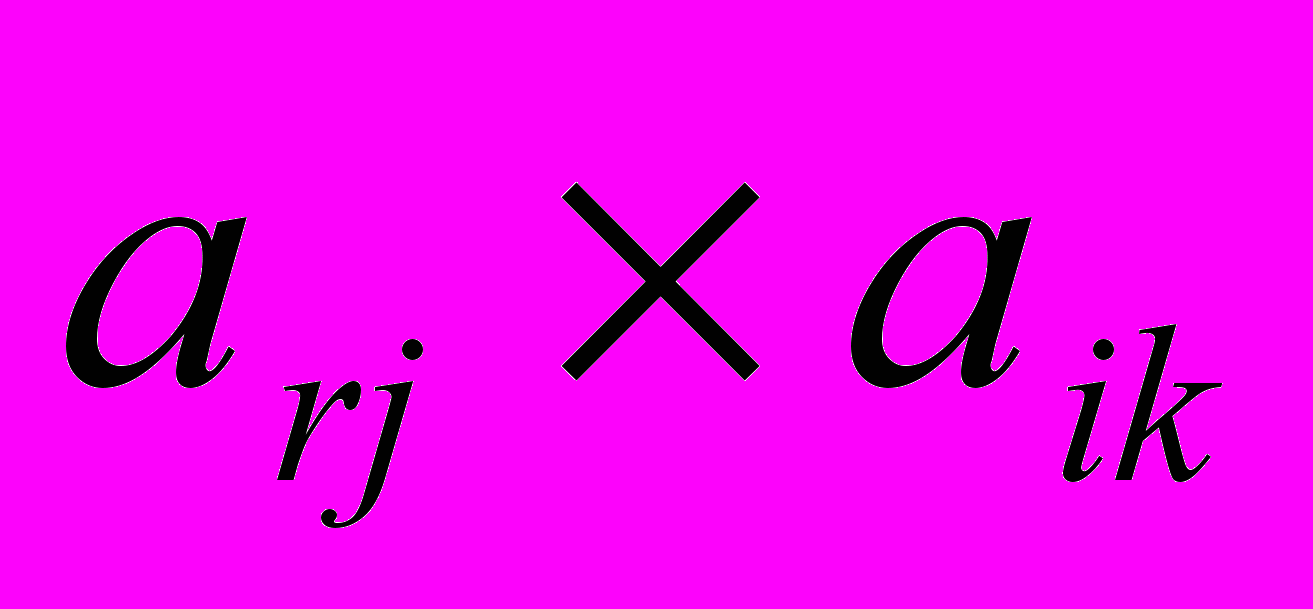), и полученную разность разделить на направляющий элемент.


Согласно вышеуказанной формуле получим:

;

;

;

;

;

;

;

;

;

;

;

.

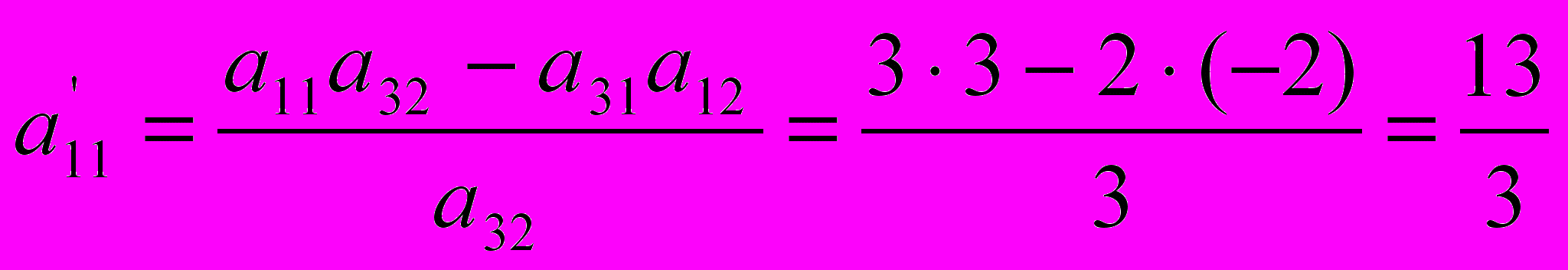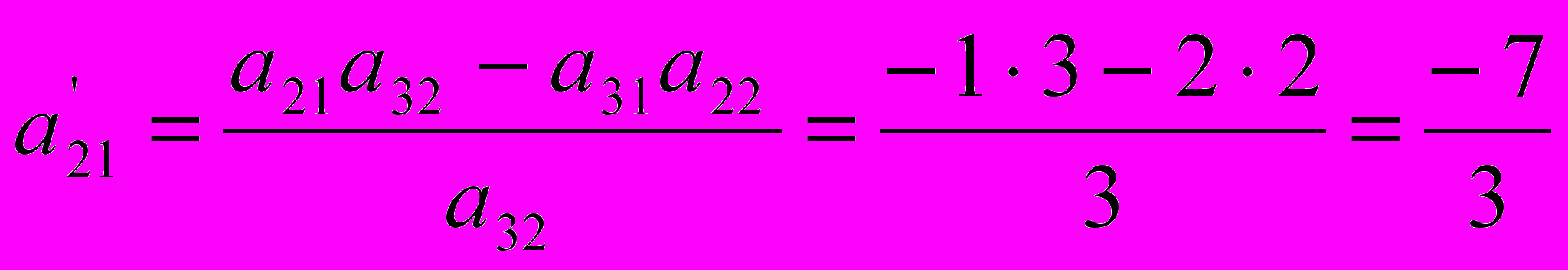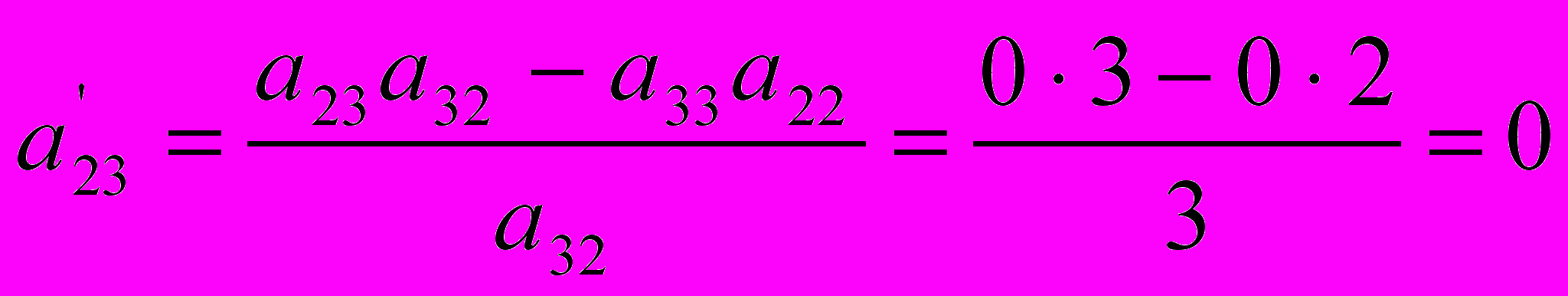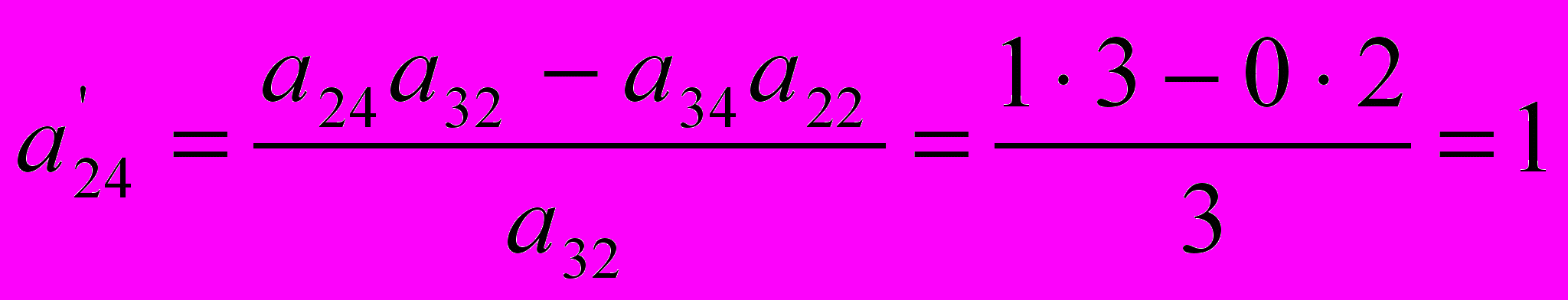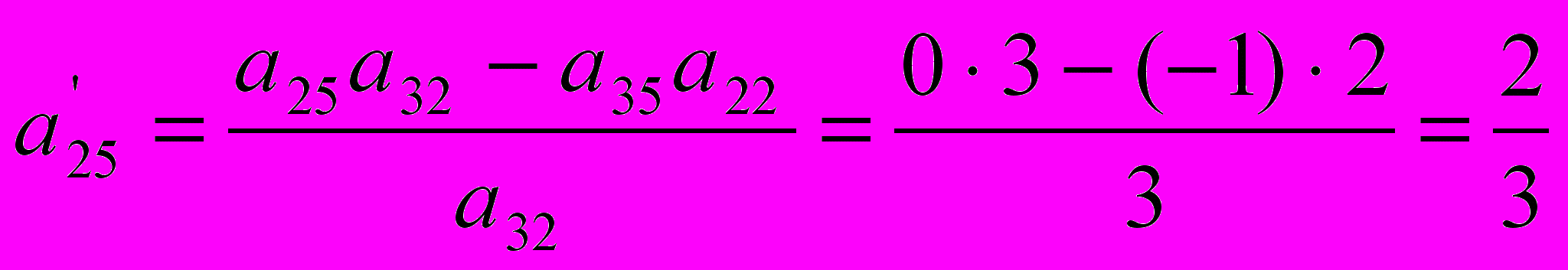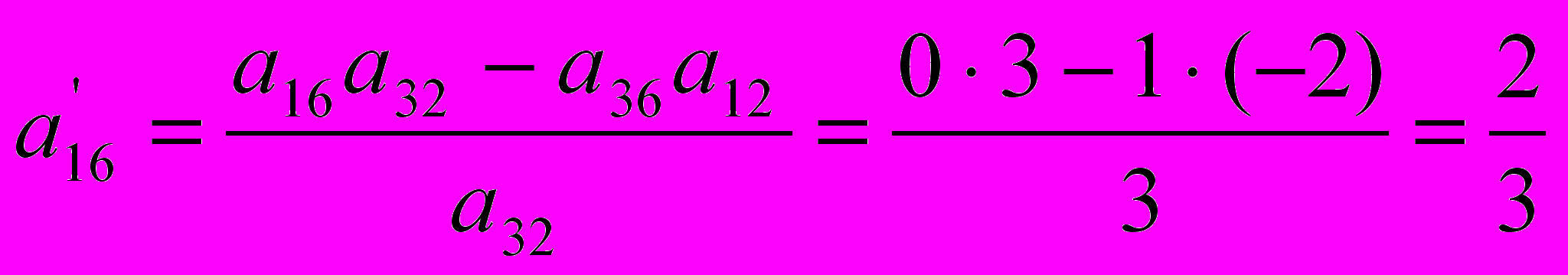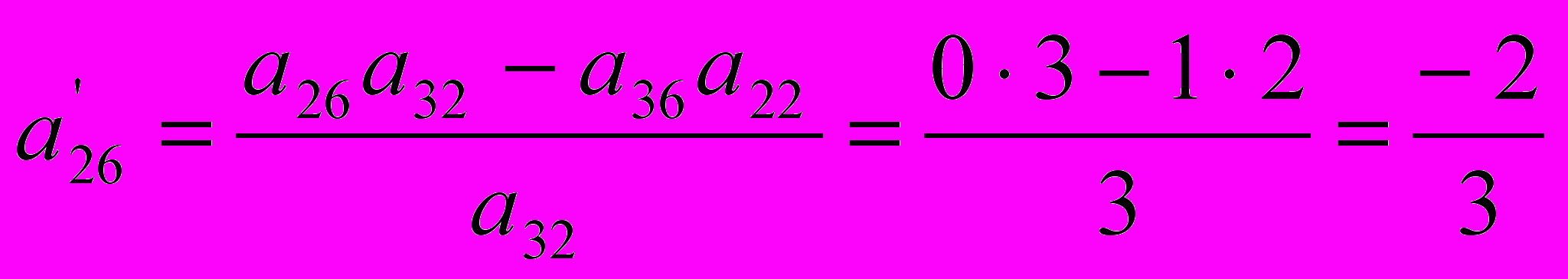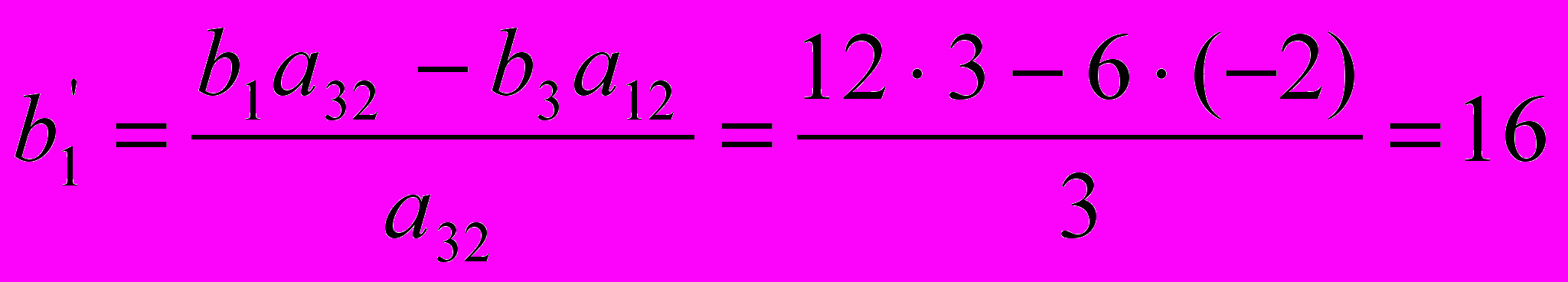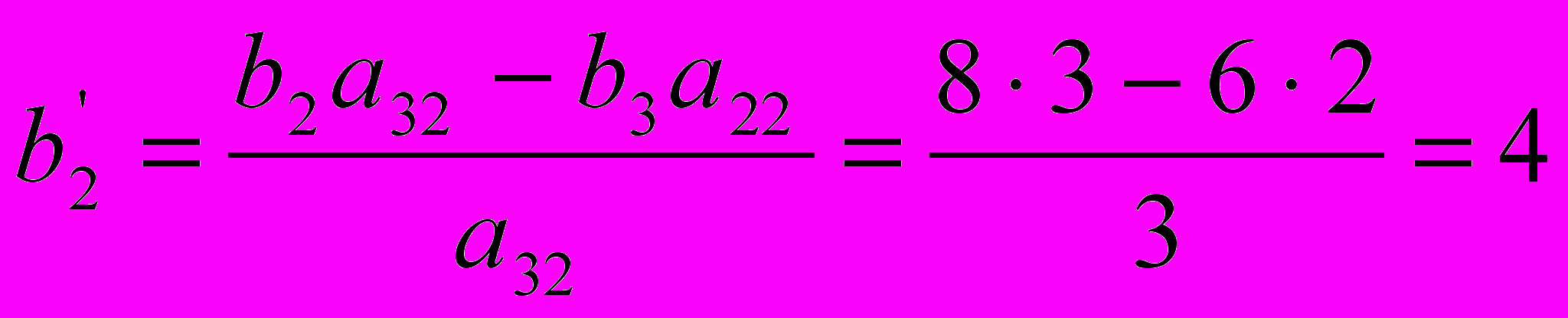Получим новую таблицу:

С			с1 = -2	с2 = -1	с3 = 0	с4 = 0	с5 = 0	с6 = -М
	ХР	В	А1	А2	А3	А4	А5	А6
с3 = 0	х3	16	13/3	0	1	0	-2/3	2/3
с4 = 0	х4	4	-7/3	0	0	1	2/3	-2/3
с2 = -1	х2	2	2/3	1	0	0	-1/3	1/3
S				0	0	0	-1/3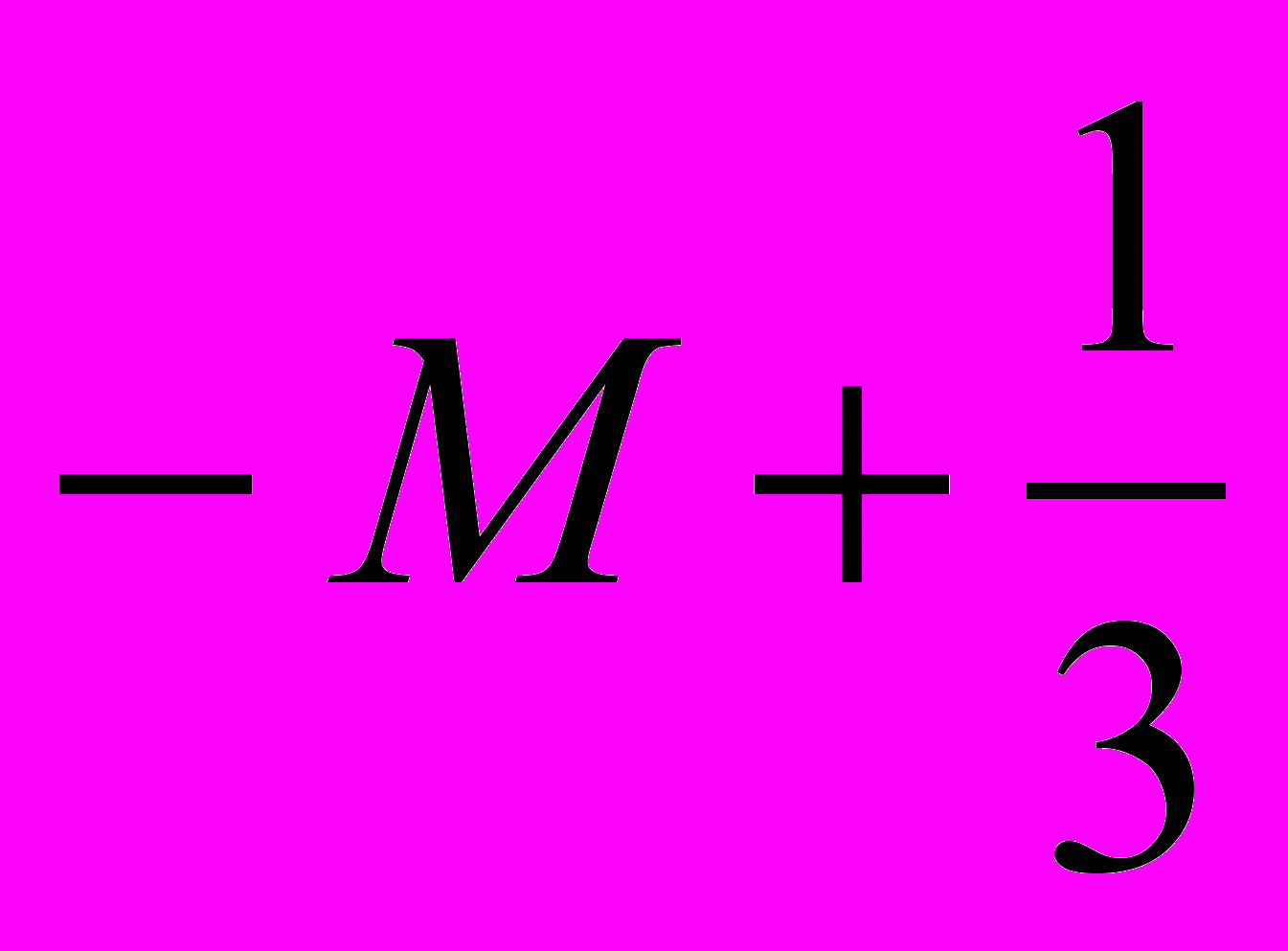

Определим симплекс-разности:













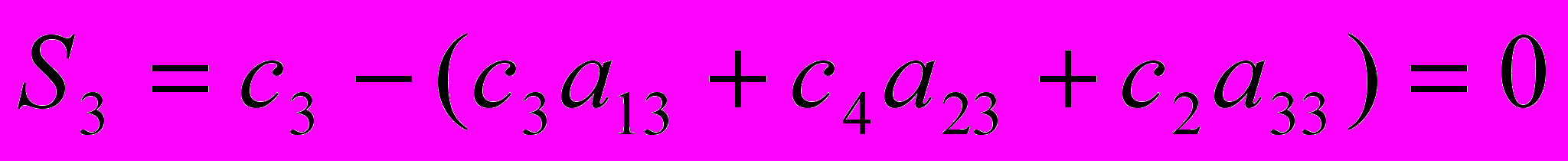
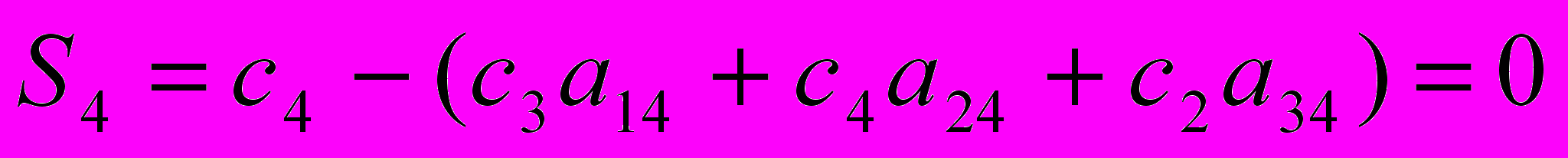
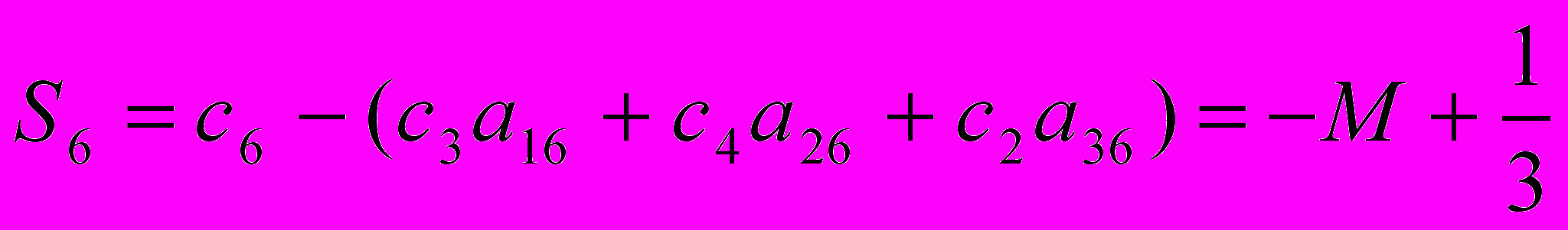
Все симплекс-разности отрицательны, следовательно, найденное решение является оптимальным.


Оптимальное решение: .

.
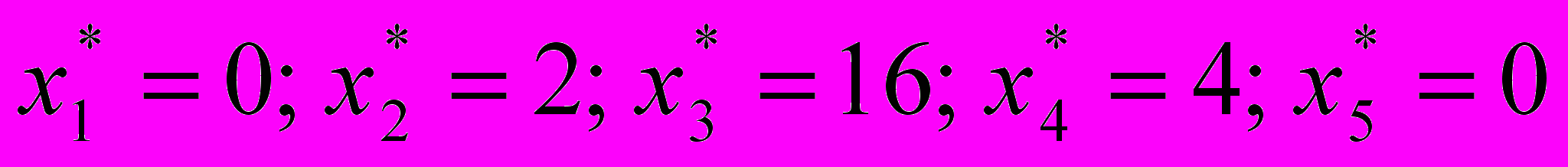