Урок на тему: «Признаки и свойства параллельных прямых»
| Вид материала | Урок |
- Урок по геометрии. 7 класс. Тема: параллельные прямые, 77.92kb.
- А. С. Пушкина р п. Колышлей Пензенской области Геометрия и сказки А. С. Пушкина Повторительно, 36.32kb.
- "Признаки параллельности прямых". Цель урока, 41.08kb.
- Курс, 1 и 2 потоки, 7-й семестр лекции (34 часа), зачет Кафедра, отвечающая за курс, 32.2kb.
- Урок химии в 9 классе. Тема: «Оксиды азота», 68.76kb.
- Урок по геометрии в 7 классе по теме: «Признаки равенства треугольников», 60.74kb.
- Рабочая программа: Примерная тематика рефератов, творческих и научно-исследовательских, 51.5kb.
- Вопросы по курсу начертательной геометрии, 203.17kb.
- Измерение отрезков. Единица измерения, 124.29kb.
- Лекция теоретический анализ литературы по теме исследования, 65.16kb.
Открытый урок
на тему:
«Признаки и свойства параллельных прямых».
Учитель Никитич Т.Н.
МОУ гимназия № 41
Научный руководитель:
кандидат психологических наук, доцент
Мельникова Е.Л.
г. Люберцы
2007/2008 учебный год.
Тема: признаки и свойства параллельных прямых
(По учебнику Атанасян и др., Геометрия 7 класс).
Оборудование: коробка, лимон.
Цель урока: 1) установить взаимосвязь между признаками и свойствами предметов;
2) рассмотреть свойства параллельных прямых, опираясь на их признаки;
3) показать учащимся применение свойств параллельных прямых.
Ход урока.
Актуализация знаний.
Блиц – опрос (ребенок должен ответить на вопросы в течение минуты).
- Какие геометрические фигуры мы сейчас изучаем? (Параллельные прямые).
- Параллельными называются прямые……...
- Два отрезка называются параллельными, если…
- Если прямая пересекает одну из параллельных прямых, то она …
- Если две прямые параллельны третьей, то…
- Через любую точку, не лежащую на данной прямой можно провести…
- Если две прямые перпендикулярны третьей, то …
Блиц – опрос (ребенок должен ответить на вопросы в течение минуты).
- Прямая х называется секущей по отношению к a и b, если …
- При пересечении a и b секущей m, углы 1и 5, 2 и 6 называются …
углы 3 и 6, 4 и 5 называются …
a 1 2 углы 6 и 4, 5и 3 называются …Д
оска 3 4 b 5 6
7 8
Если при пересечении двух прямых третьей секущей …
Если при пересечении двух прямых третьей секущей …
Если при пересечении двух прямых третьей секущей …
Мы повторили многое из того, что успели узнать о параллельных прямых, но ведь в науке, в том числе и в школьной, все взаимосвязано.
В изучении следующей нашей темы нам могут помочь знания биологии и русского языка.
Постановка проблемы 1 .
(Определение различий между свойствами и признаками предметов).
| Учитель | Дети |
| - У меня в коробке предмет. Догадайтесь какой. Я точно знаю, что это: 1) фрукт 2) ярко – желтый 3) имеет кожицу и мякоть 4) очень ароматный 5) цитрусовый 6) кислый на вкус |  Это лимон |
| - Что я сейчас назвала? | - Признаки лимона. |
| - Составьте предложение, которое начинается со слова «Если…» с использованием этих признаков. | - Если предмет фрукт, ярко- желтого цвета, имеет кожицу и мякоть, очень ароматный, цитрусовый, кислый на вкус, то это лимон» (Предложение записывается на доске). |
| - А что мы называем лимоном?. Запишем предложение на доске. | - Лимон – это фрукт, ярко – желтого цвета, имеет кожицу и мякоть, очень ароматный, цитрусовый, кислый на вкус. |
| «Открытие» знания 1. | |
| - Прочитайте предложение еще раз и сравните их. Что можно сказать? | - Предложения взаимообратные, то есть их можно считать задом наперед. |
| - Какое предложение характеризует свойства предмета? | - Прямое. |
| - А признаки? | - Обратное. |
| - Мы можем узнать с каким предметом имеем дело, если перечислим его … | - …признаки. |
| -А если мы видим предмет, хотим его описать, то говорим о … | - … свойствах. |
| - Значит, как связаны признаки и свойства предметов? | - Они взаимообратны, зная признаки, иы илжем догадаться, что это за предмет. Видя его, говарим о том какой он. |
| - На прошлом уроке мы говорим о параллельных прямых, сегодня о свойствах и признаках предметов. Попробуйте догадаться, какова будет тема сегодняшнего урока. | - Признаки и свойства параллельных прямых. |
Проблема 2.
(Опираясь на знание признаков, попробуем получить свойства параллельных прямых).
| Рассмотрим задачу 1 (устно). Задача 1.  А Е В Дано: AB, CD  30° EK - секущаяДоказать: ABIICD  30°С DК | Решение: ABIICD, ч.т.д. |
| - Пожалуйста, ответьте на вопрос Задачи 2. Задача 2. А Е В Дано: AB, CD 30° ABIICDEK - секущая Найти ?С DК - В чем затруднение? - Чем она отличается от предыдущей и в чем их сходство? | - Мы не можем решить эту задачу. - Известно, что прямые параллельны, углы EKC и CKE накрестлежащие. Однако мы не знаем следует ли из параллельности прямых равенство накрестлежащих углов при пересечении их третьей секущей. |
| - Какие это задания по смыслу? | - Взаимообратные. |
| - Первую мы решили, опираясь на признаки параллельности. Раз задачи взаимообратные, значит о чем пойдет речь? | - О свойствах параллельных прямых. |
Заполните таблицу, представленную на доске.
| Название теоремы | Признак параллельности прямых | Свойства параллельности прямых |
| 1.Формулировка 2. Условие (дано). 3. Заключение (доказательство) | Если при пересечении двух прямых секущей накрестлежащие углы равны, то прямые параллельны. a  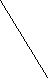 1 b 2 c Дано: a, b- прямые, c – секущая <1,<2 – накрестлежащие углы <1=<2 aIIb | Если две параллельные прямые пересечены секущей, то накрестлежащие углы равны. a 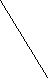1 b 2 c Дано: a, b- параллельные прямые, c – секущая <1,<2 – накрестлежащие углы <1=<2 |
| Учитель | Дети |
| - Из каких частей состоит любая теорема? | - Условие и заключение. Условие – то, что дано, заключение – то, что нужно доказать. |
| - Заполните графу, касающуюся признаков параллельности прямых | (1 ребенок работает у доски). |
| - Как связаны между собой признаки и свойства предметов. | - Они взаимообратные. |
| - Основываясь на первом признаке параллельности прямых попробуйте сформулировать первое свойство параллельности. | - Различные варианты, верный: «Если две параллельные прямые пересечены секущей, то накрестлежащие углы равны». |
| - Прочитайте условия теоремы, запишите, опираясь на него, что дано. - Исходя из заключения, что нужно доказать? | - (Дети заполняют соответствующую графу таблицы) |
| - Докажем полученную теорему (доказательство в соответствии с учебником Атанасян и др., Геометрия, 7 кл.) | |
| - Сравните условия и заключения первой и второй теории. Что вы можете о них сказать? | Условия первой – это заключения второй, условие второй – заключение первой. |
| - Как бы вы назвали такие теоремы? | - Различные варианты, верный: Обратные. |
| - Дайте определение теоремы, обратной данной. | - Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – ее условие. |
| - Вернемся к Задаче 2. | - Решение: ABIICD по условию, |
Закрепление пройденного материала.
Решение задач по готовым чертежам.
1
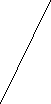. a 4 Дано: aIIb2 3 <1=75°
Найти: <2, <3, <4.
b 1c
Дано: aIIb
2
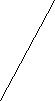. a 2 <1+<2=160°4 3 Найти: <3, <4, <5, <6.
b 5 1c 6
3
. Дано: aIIbc 1 2 <1 в 4 раза меньше <2.
3 Найти: <3.a b
Итог урока.
- Какую тему мы сегодня рассмотрели?
-Придумайте по 3 вопроса, касающиеся темы сегодняшнего урока (дети задают вопросы друг другу, получая отметки за самые интересные из них).
- В следующий раз мы докажем второй и третье свойство параллельности прямых, начиная решать задачи с применением этих свойств.
Список литературы.
1. Л.С. Атанасян и др. Геометрия, 7 класс – М.: Просвещение.
2. Н.Ф. Гаврилова «Поурочные разработки по геометрии: 7 класс – М.: ВАКО,2007.
3. Е.М. Рабинович «Задачи и упражнения на готовых чертежах.7-9 классы. Геометрия. – М.: Илекса, 2001.
4. Е.Л. Мельникова «Проблемный урок или как открывать знания вместе с детьми»- Москва, 2002.