Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний

Вид материала

Таблица 2. Матрица уровней принадлежности показателей нечетким подмножествам
Результат классификации по подмножествам
Ожидаемая доходность вложений в акции  Надежность эмитента  Текущая эффективность работы эмитента.
P/E  Cap  Liquidity  P/S  P/B  ROA  ROE  ROIC.
Х3 - оборачиваемость активов
Х4 - рентабельность затрат
Х5 - рентабельность активов
Ликвидность  Финансовая устойчивость  Эффективность бизнеса эмитента.
С. Определение состава бумаг, наполняющих каждый из выбранных модельных классов. D.

Подобный материал:

1 2 3

Исследование возможностей теории нечетких множеств позволяет провести ассоциацию между отдельными формализмами теории и теми областями финансового менеджмента и экономической теории в целом, где эти формализмы могут быть успешно применены (табл. 1).

Нечетко-множественные модели и методы корпоративного финансового менеджмента

Во диссертации рассматриваются модели и методы корпоративного финансового менеджмента на основе нечетко-множественных описаний. Разработанный матричный метод агрегирования данных на основе нечеткого классификатора позволяет переходить от количественных и качественных значений отдельных финансовых показателей деятельности корпорации к комплексному финансовому показателю и соответствующей степени риска банкротства. Метод может быть настроен на любые особенности корпорации, в том числе на учет значимости тех или иных отдельных факторов в комплексной оценке.

Рассматривается набор из N финансовых показателей, которые с высокой степенью относимости характеризуют степень риска банкроства предприятия. Это показатели ликвидности, финансовой автономии, оборачиваемости активов, соотношения кредиторской и дебиторской задолженностей в компании и другие показатели. При этом экспертным путем определяется система предпочтения одних показателей другим для комплексной оценки. В качестве степеней сравнения используются степени «строгого предпочтения», «нестрогого предпочтения», «безразличия».

Если экспертное сообщество располагает квазистатистикой по каждому выбранному показателю, собранной за ряд лет для предприятий данной отрасли, то можно, осуществив лингвистический анализ соответствующих гистограмм, восстановить серую шкалу Поспелова и набор ассоциированных с ней функций принадлежности. В работе результат лингвистической классификации уровней факторов приводит к идентификации вектора уровней принадлежности по каждому качественному уровню шкалы, причем сумма компонент вектора равна единице (по смыслу серой шкалы). Таким образом, предлагается свести совокупность указанных числовых векторов в матрицу (табл. 2), которая является основой для комплексной оценки финансового состояния предприятия.

Таблица 2. Матрица уровней принадлежности показателей нечетким подмножествам

Наименование показателя	Результат классификации по подмножествам
Наименование показателя	В_i1	В_i2	В_i3	В_i4	В_i5
Х₁	₁₁	₁₂	₁₃	₁₄	₁₅
…	…	…	…	…	…
Х_i	_i1	_i2	_i3	_i4	_i5
…	…	…	…	…	…
Х_N	_N1	_N2	_N3	_N4	_N5

Для получения такой комплексной оценки разработаны две системы весов для свертки отдельных элементов матрицы в единый комплексный показатель. Первая система – это система ранжирования отдельных факторов в оценке. В качестве этой системы наилучшим образом подходит система весов Фишберна. Если система показателей проранжирована в порядке убывания их значимости, то значимость i-го показателя r_i следует определять по правилу Фишберна:

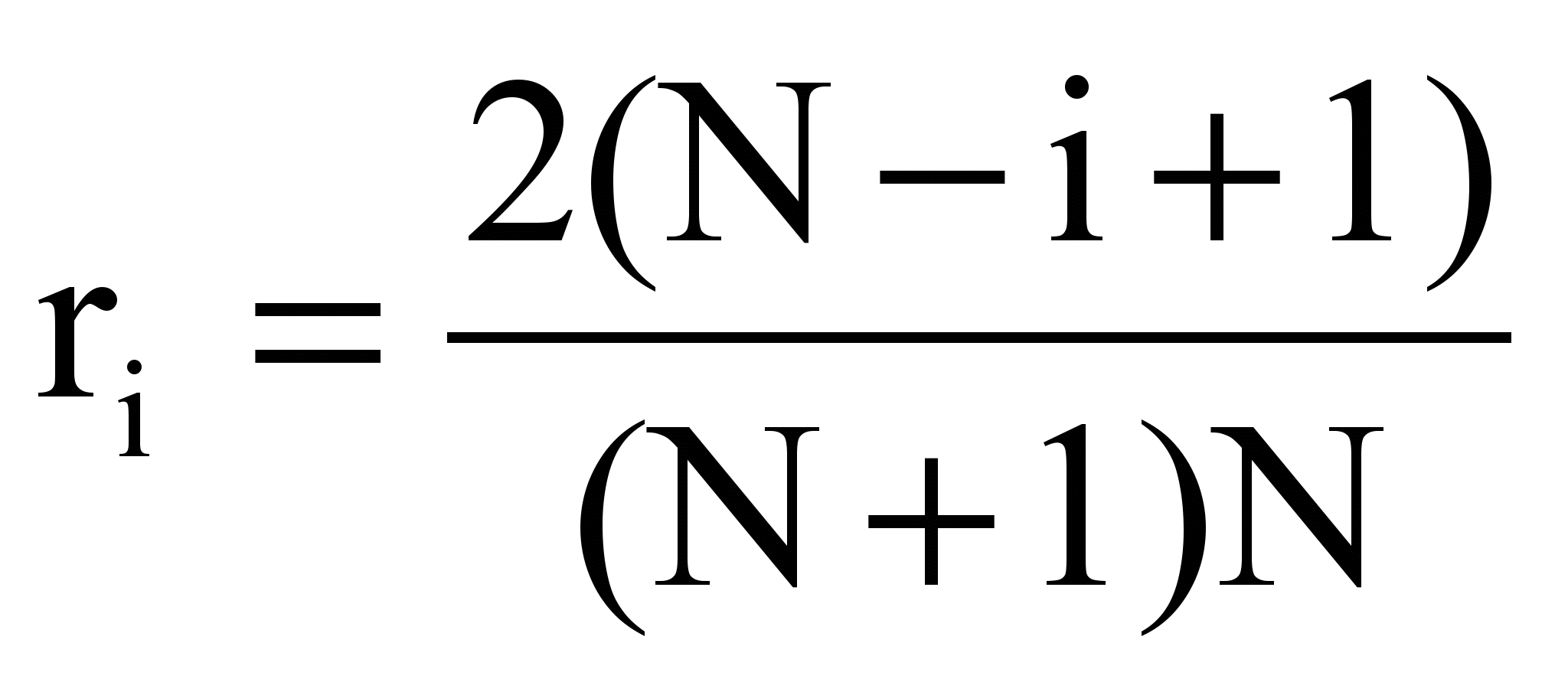. (1)

Правило Фишберна отражает тот факт, что об уровне значимости показателей неизвестно ничего кроме порядка убывания значимости. Тогда оценка (1) отвечает максиму энтропии наличной информационной неопределенности об объекте исследования, т.е. позволяет принимать наилучшие оценочные решения в наихудшей информационной обстановке. Если же все показатели обладают равной значимостью (равнопредпочтительны или системы предпочтений нет), тогда

r_i = 1/N. (2)

В случае смешанных систем предпочтений применяется специальное правило построения весов.

Вторая система весов g_j базируется на симметрично расположенных узловых точках серой шкалы Поспелова, определенной на стандартном 01-носителе: (0.1, 0.3, 0.5, 0.7, 0.9). Введение этой системы весов в комплексную оценку позволяет спроецировать значение комплексного показателя на 01-носитель и в последующем классифицировать его на основе симметричной серой шкалы Поспелова.

В итоге, матричная оценка финансового состояния корпорации состоит в двойной свертке данных таблицы 2. Уровень эффективности предприятия g оценивается по формуле:

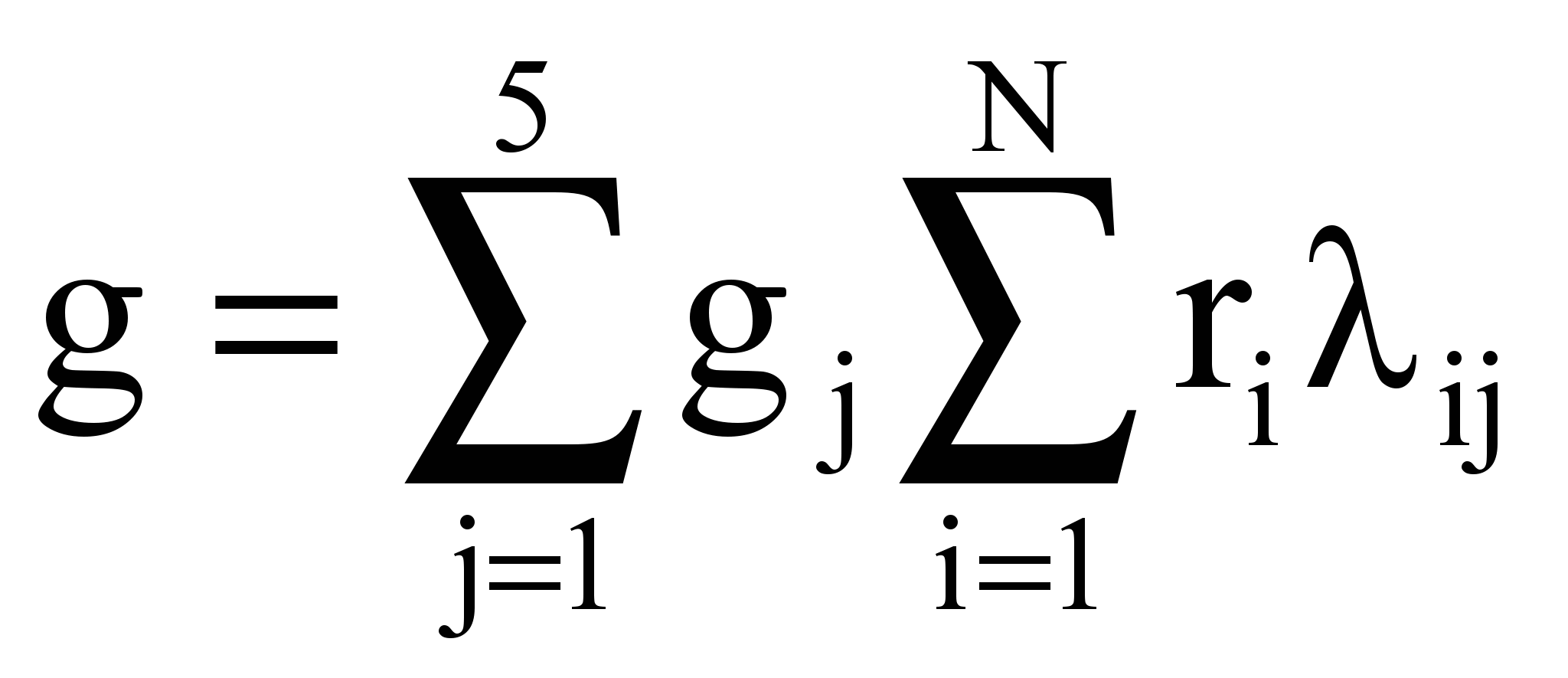, (3)

где

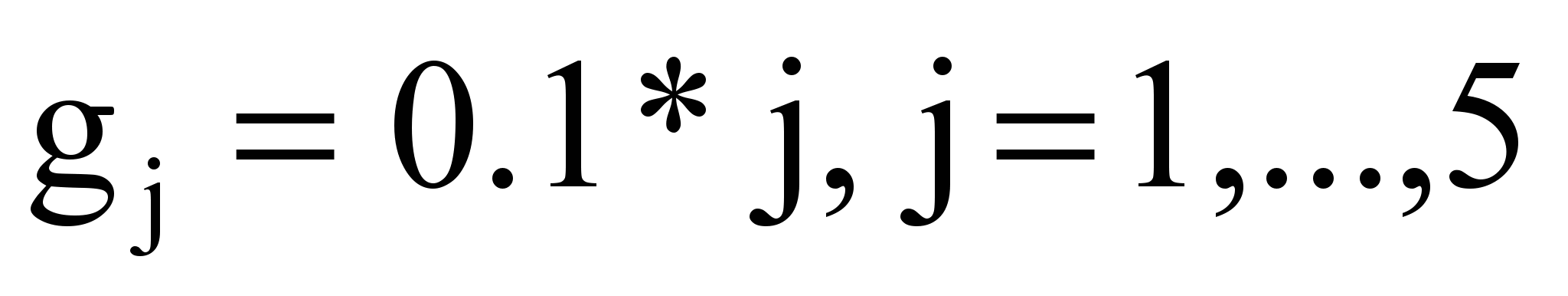, (4)

_i_j определяется по таблице 2, а r_i – по формуле (1) или (2).

Далее уровень полученного комплексного показателя проходит распознавание по простому правилу или на основе системы трапециевидных функций принадлежности. В частности, простое правило:

g[0, 0.2] – очень низкий уровень финансового состояния;
g[0.21, 0.4] –низкий уровень финансового состояния;
g[0.41, 0.6] – средний уровень финансового состояния;
g[0.61, 0.8] – высокий уровень финансового состояния;
g[0.81, 1] – очень высокий уровень финансового состояния.

Построенный метод комплексного анализа финансового состояния корпорации может быть с успехом применен в бизнес-процессе ежеквартального мониторинга состояния корпорации по данным ее финансовой отчетности

Также важной составляющей финансового менеждмента в корпорации является оценка эффективности и риска инвестиционных проектов. В работе рассматривается модель инвестиционого проекта и метод оценки риска инвестиций. При этом все параметры проекта представлены в виде треугольных нечетких чисел и их последовательностей. В этом случае результирующие показатели проекта имеют так называемый LR-вид.

Чтобы оценить риск инвестиций проекта по выбранному критерию, нужно оценить интегральную возможность того, что уровень NPV проекта окажется ниже требуемого порогового значения. В простейшем случае, когда NPV проекта является симметричным треугольным нечетким числом (т.е. может быть представлен в виде AA), тогда степень риска такого проекта оцениватеся по формуле:

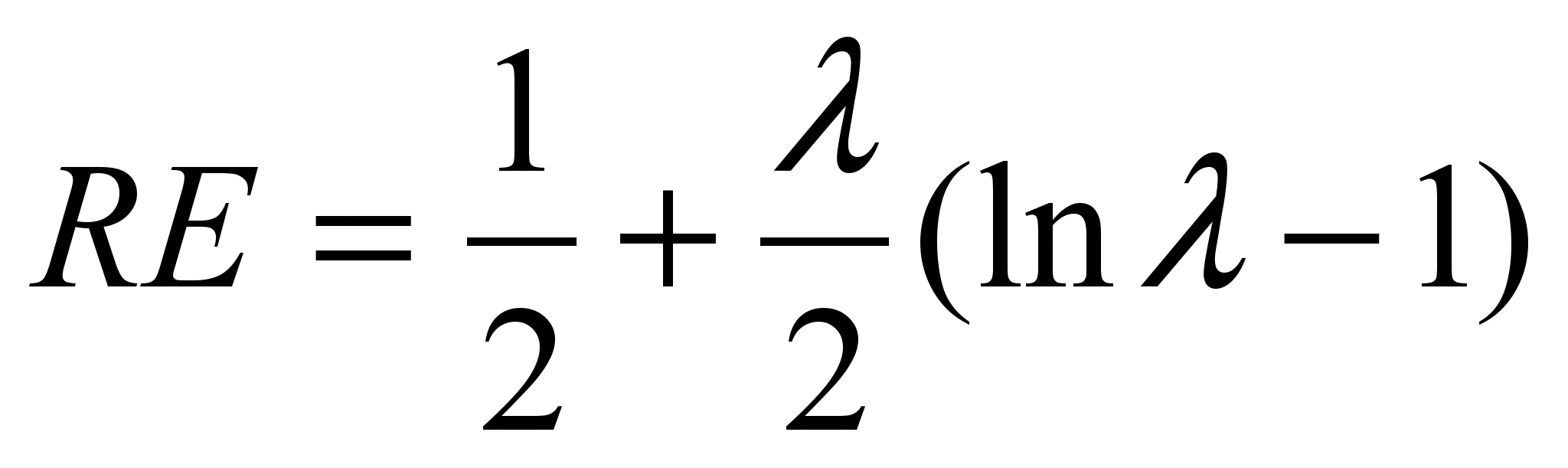, (5)

где 0 <  = А/A < 1. При  = 0 (ожидаемый эффект близок к нулю) RE=0.5, а при  = 1 (ожидаемое значение показателя совпадает с разбросом) RE=0 (риск проекта отсутствует).

В работе также показано, что возможна двусторонняя оценка степени риска проекта на основе формулы (5), без применения наукоемких вычислительных алгоритмов. При этом задача оценки риска инвестиционного проекта разрешена для произвольно-нечеткого вида критериального показателя инвестиционного проекта (предложен приближенный метод оценки риска для показателей произвольно-нечеткого вида).

Введен формализм риск-функции инвестиционного проекта. Пусть пороговый критерий эффективности проекта растет. Тогда растет и риск проекта как функция порогового критерия.

На основе лингвистического анализа риск-функции проекта устанавливается ряд пороговых уровней нормирующего фактора, по которым отслеживается чувствительность риска проекта к колебаниям значения норматива. Например, в большинстве случаев, допустимый риск проекта находится в диапазоне от 0 до 10%. Значение 10-20% является пограничным, а проект со степенью риска свыше 20% обладает недопустимым риском. Эти наблюдения сделаны на основе анализа формы риск-функций проектов.

Построенные методы оценки риска инвестиционного проекта представляют собой удобный инструмент для риск-менеджмента этих проектов. Своевременная идентификация пограничных уровней рисков проектов позволяет произвести в проекте своевременные корректировки, связанные с увеличением выручки и/или снижением затрат. Возможным оптимальным результатом управления проектом является выход из проекта с отсечением убытков.

При разработке модели стратегического планирования деятельности корпорации в работе рассматриваются два интегральных измерителя бизнеса: конкурентоспособность бизнеса и его перспективность. Проводится анализ в рамках стандартной модели Shell/DPM 3х3, имеющей высокое практическое значение для стратегического планирования (см. рисунок в материалах к диссертационному докладу). Главный вывод, который сделан на основе анализа модели – это позиция рассматриваемого бизнеса и его место и роль в совокупном портфеле бизнесов Компании.

Конкурентоспособность (А) измеряется на основе следующих базовых факторов:

соотношение доли бизнеса и доли основного конкурента – a₁;

распознаваемость имени Компании – a₂;
сила бренда бизнеса/Компании – a₃;
развитость дистрибьюторской сети – a₄;
технологические позиции бизнеса – a₅.

Перспективность бизнеса (B) измеряется на основе следующих базовых факторов:

доля бизнеса в структуре департамента Компании – b₁;
темпы роста бизнеса – b₂;
интенсивность конкуренции с бизнесом на открытом рынке – b₃;
прибыльность бизнеса – b₄;
чувствительность бизнеса к бизнес-циклам – b₅.

Всем перечисленным базовым факторам a_i, b_jсопоставляется 01-носитель. Если исторически эти факторы измеряются на основе другой количественной шкалы (например, от 1 до 5), то производится переход от существующей шкалы к 01-носителю на основе простого линейного преобразования.

Количественная оценка интегральных факторов A и B проводится в рамках стандартной матричной схемы оценки, но для распознавания уровня этих факторов применяется не стандартная пятиуровневая 01-классификация, а трехуровневуя 01-классификация, с подмножествами «Низкий уровень, Средний уровень, Высокий уровень» лингвистической переменной «Уровень фактора». Переход от пяти уровней к трем обусловлен тем, что модель Shell/DDM имеет размерность 3х3 (всего 9 позиций бизнеса).

Веса базовых факторов в интегральной оценке выбираются на основе дополнительных соображений. Одним из таких соображений выступает принцип Фишберна, используемый в матричной оценке комплексного финансового состояния корпорации.

В результате двумерного позиционирования бизнеса делается вывод о том, как в дальнейшем целесообразно управлять этим бизнесом (оставить как есть, дать дополнительные инвестиции, реорганизовать, сворачивать).Также в рамках процедуры стратегического планирования (в качестве отдельных процессов) использованы изложенные ранее методы оценки риска банкротства корпорации, оценки риска инвестиционного проекта, с внедрением процесса финансового планирования на основе нечетких чисел.

Методы оценки инвестиционной привлекательности российских ценных бумаг

В работе рассматриваются методы оценки инвестиционной привлекательности российских ценных бумаг различных типов. При этом в основе методов оценки лежит матричный подход. Исследован обширный контент рыночных исходных данных, построены и проанализированы гистограммы различных факторов оценки.

Адекватность разработанных методов оценки подтверждается, с одной стороны, их согласованностью с экспертным методом оценки долговых обязательств субъектов РФ, разработанным в агентстве AK&M, а, с другой стороны, результатами торгов российскими ценными бумагами в 2002 году (все акции, получившие положительную торговую рекомендацию в феврале 2002 года, в последующие несколько месяцев существенно выросли в цене).

Применительно к каждому типу ценных бумаг выбрана своя система показателей и своя система весов, которая зависит, в том числе, от страны, где осуществляется эмиссия ценных бумаг. Например, для облигаций субъектов РФ выбрана следующая система показателей:

X1 - отношение государственного долга к доходам бюджета;
X2 - отношение объема заемных средств к доходам бюджета;
X3 - доля собственных доходов в общем объеме доходов;
X4 - объем собственных доходов бюджета;
X5 - отношение профицита (дефицита) бюджета к доходам бюджета;
X6 - доля средств, направляемых в бюджеты других уровней в расходах;
X7 - доля выделяемых кредитов и бюджетных ссуд в расходах;
X8 - отношение задолженности по налогам к объему налоговых платежей;
X9 - доля прибыльных предприятий в общем количестве зарегистрированных на территории региона;
X10 - сальдо прибылей и убытков предприятий;
X11 - денежные доходы населения в расчете на одного жителя.

Выбранные показатели группируются в 2 блока: X1-X7, X8 – X11, а затем, в пределах каждого блока, осуществляется ранжирование показателей по невозрастанию предпочтений для оценки:

Х1  Х2  Х3  Х4  Х5  Х6  Х7, (6)

Х8  Х9  Х10  Х11, (7)

где «» означает отношение безразличия, а «» - отношение строгого предпочтения. Сами же блоки факторов упорядочиваются по весовой оценке в отношении 2:1. Это выражает предпочтение финансового блока для оценки кредитного риска облигаций субъектов РФ над показателями общеэкономического характера.

Из систем предпочтений (6) и (7) прямо вытекают определенные значения весов Фишберна для соответствующих показателей. Гистограммы распределения уровней факторов X1–X11 и их лингвистическая классификация позволяют осуществить нечеткое распознавание уровней этих факторов. В итоге, применяется матричный метод для комплексной оценки кредитного рейтинга облигаций субъектов РФ.

Модель скоринга акций РФ разработана с учетом опыта проектирования аналогичной модели, ориентированной на условия США. Ключевым фундаментальным индикатором оцененности акции выступает отношение цены акции к доходам по ней в годовом выражении (P/E), в долях. При этом, для повышения надежности оценки, в модели использованы интегральные средневзвешенные оценки факторов (ТТМ).

Были рассмотрены факторы, свидетельствующие о риске дефолта эмитента. В качестве последних выступают два фактора: капитализация эмитента (Cap) в миллионах долларах США и обеспеченность оборотных активов собственными средствами предприятия (Liquidity), в долях. Именно чистый оборотный капитал (ЧОК), участвующий в расчетах коэффициента обеспеченности, представляется наиболее представительным фактором для анализа. Отрицательное значение ЧОК свидетельствует о повышенном риске эмитента по отношению к его текушим финансовым обязательствам.

Далее были рассмотрены факторы, соотносящие цену акций и продажи, а также собственный капитал, в расчете на одну акцию (факторы P/S и P/B соответственно, в долях). Эти факторы, хорошо известные в мировой практике финансового анализа, оценивают, насколько эффективно работает предприятие, с одной стороны, и насколько «раздут» его капитал по отношению к стоимости собственных средств предприятия, с другой стороны. Также были рассмотрены факторы рентабельности предприятия – рентабельность активов, собственного капитала и инвестированного капитала (факторы ROA, ROE и ROIC соответственно, в процентах годовых).

Далее была разработана система предпочтения одних факторов другим. Показано, что шкала предпочтений факторов должна иметь следующий вид:

Ожидаемая доходность вложений в акции  Надежность эмитента  Текущая эффективность работы эмитента.

(8)

В такой системе предпочтений учтено то, что вложения в российские акции с мировой точки зрения – это заведомо рискованные вложения, и риск дефолта (фактор надежности) большей частью учтен инвесторами уже на страновом уровне (на шаге выбора страны для инвестиций) и волнует инвесторов во вторую очередь. Прежде всего инвестор рассчитывает на спекулятивный рост курсовой цены акций, на их перманентную недооцененность. И с этой точки зрения фактор P/E является главным в анализе. Далее, переходя от странового риска к частному риску дефолта эмитента, инвестор предпочтет иметь дело с компаниями, которые находятся на подъеме и занимают ощутимую долю на рынке. Отсюда роль капитализации и ликвидности в оценке.

Инвестор также понимает, что в долгосрочной перспективе курсовой рост может быть обеспечен только успешной устойчивой работой предприятия. И с этой точки зрения факторы эффективности занимают в анализе третье место.

С точки зрения факторов оценки система предпочтений (8) приобретает вид:

P/E  Cap  Liquidity  P/S  P/B  ROA  ROE  ROIC. (9)

Информации, заключенной в (9), достаточно для того, чтобы перейти непосредственно к скорингу акций. Из (9) вытекает система весов Фишберна, а гистограммы распределения оцениваемых факторов дают основания для нечеткого распознавания уровней этих факторов. Таким образом, и в данном случае уместно применение матричного метода для комплексной оценки скоринга акций.

Кредитный рейтинг облигаций РФ осуществляется в диссертационной работе по аналогии с рейтингом облигаций субъектов РФ и со скорингом акций РФ. Выстраивается система показателей и системы их предпочтения для оценки, анализируются гистограммы этих показателей и проводится комплексное оценивание уровней факторов матричным методом.

Фактор ликвидности (Х2) эмитента для оценки полагается основным. Ликвидность может быть оценена по-разному, но по укрупненному балансу предприятия возможен лишь анализ общей ликвидности как обеспеченности краткосрочных обязательств оборотными активами.

Далее рассматриваются факторы, характеризующие финансовую устойчивость. Соотношение собственных и заемных средств в структуре пассивов предприятия (коэффициент автономии Х1) является ключевым фактором для анализа. Существуют определенные проблемы в использовании этого показателя в финансовом анализе. Они связаны с тем, что очень часто ликвидность собственных средств предприятия низка (из-за необоснованных переоценок стоимости основных средств, например). Тем не менее в передовых компаниях ведется активная работа по техническому перевооружению производства, со списанием устаревших фондов, и при таком подходе коэффициент автономии является действительно содержательной характеристикой финансовой устойчивости эмитента.

Наконец, были рассмотрены факторы эффективности работы эмитента. Это:

Х3 - оборачиваемость активов. Чем быстрее оборачиваются активы, тем меньше дефолтный риск, связанный с неэффективным использованием основных средств (эффективное управление активами предполагает отсечение неэффективных затрат на использование инвестированного капитала);
Х4 - рентабельность затрат. Чем больше маржинальная прибыль, тем устойчивее бизнес, и тем меньше риск текущих убытков из-за оперативного изменения конъюнктуры продаж;
Х5 - рентабельность активов. Характеризует эффективность инвестиций, сделанных в активы предприятия.

Далее выстраивается система предпочтений одних факторов другим. Показано, что шкала предпочтений факторов должна иметь следующий вид:

Ликвидность  Финансовая устойчивость  Эффективность бизнеса эмитента. (10)

С точки зрения факторов оценки система предпочтений (10) приобретает вид:

Х2  Х1  Х3  Х4  Х5 . (11)

Применение нечетко-множественных описаний для моделирования решений на фондовом рынке

Проблема научного управления портфельными инвестициями включает в себя:

А. Выбор перечня модельных классов, в рамках которых будет проводиться инвестирование, и их конструктивное описание. Под модельными классами или модельными активами (model assets) здесь понимается совокупность ценных бумаг, сгруппированных по определенному классификационному признаку (функциональному, отраслевому, региональному и т.п.). Примеры модельных классов: бумаги с фиксированным доходом, акции иностранных государств, акции российских нефтяных компаний, облигации зарубежных корпораций и т.п.

В. Определение оптимальной долевой пропорции между модельными классами в структуре модельного портфеля (asset allocation). Под модельным портфелем мы понимаем совокупность модельных классов, суммарная доля которых в портфеле составляет 100%.

С. Определение состава бумаг, наполняющих каждый из выбранных модельных классов.

D. Определение стратегии и тактики хеджирования портфеля.

Для целей оптимизации портфеля каждому модельному классу необходимо сопоставить фондовый индекс (уже практикуемый специалистами фондового рынка или вновь созданный), на основании которого производить анализ поведения модельного класса во времени.

В работе применяется модель финальной доходности фондового индекса:

S(t) = S(t₀)  (1+r(t)(t-t₀)), (12)

где t – текущее время, t₀ – начальный отсчет времени, S(t) - прогнозный уровень индекса – треугольная нечеткая функция, r(t) – расчетный коридор доходности индекса - треугольная нечеткая функция. В каждый момент t случайная величина r(t) имеет нормальное распределение (r,,) с треугольно-нечеткими параметрами ,. Модель (12) адекватна, если утверждается квазистационарность случайного процесса.

Если известны параметры распределения финальной доходности (r,,) по каждому модельному активу, а также изестна корреляционная матрица индексов как матрица треугольно-нечетких чисел , то можно записать классическую задачу Марковица в нечеткой постановке.Пусть долевое распределение N активов в портфеле описывается вектором x. Тогда ожидаемая доходность портфеля r находится по формуле

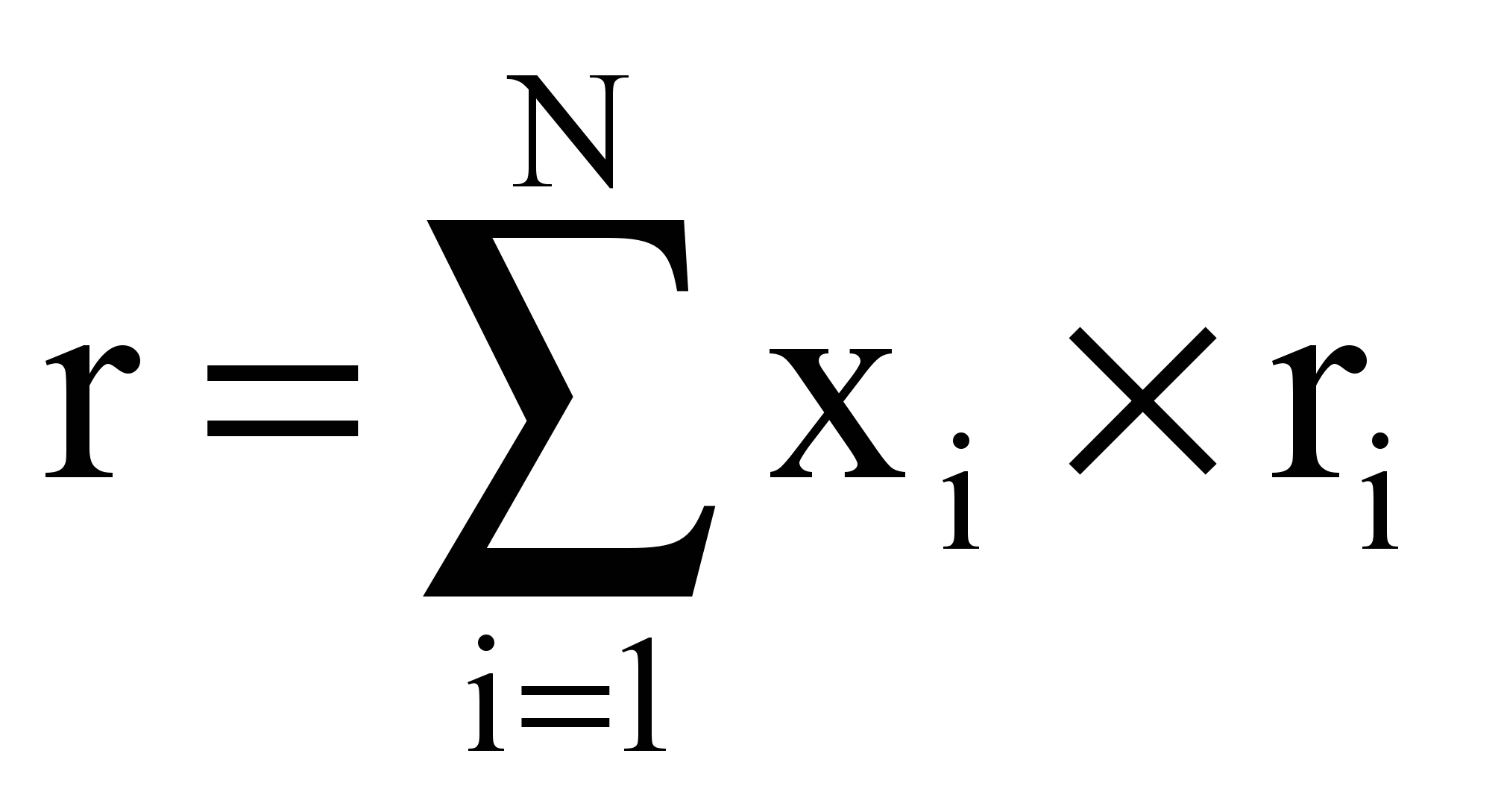, (13)

а стандартное отклонение портфеля -

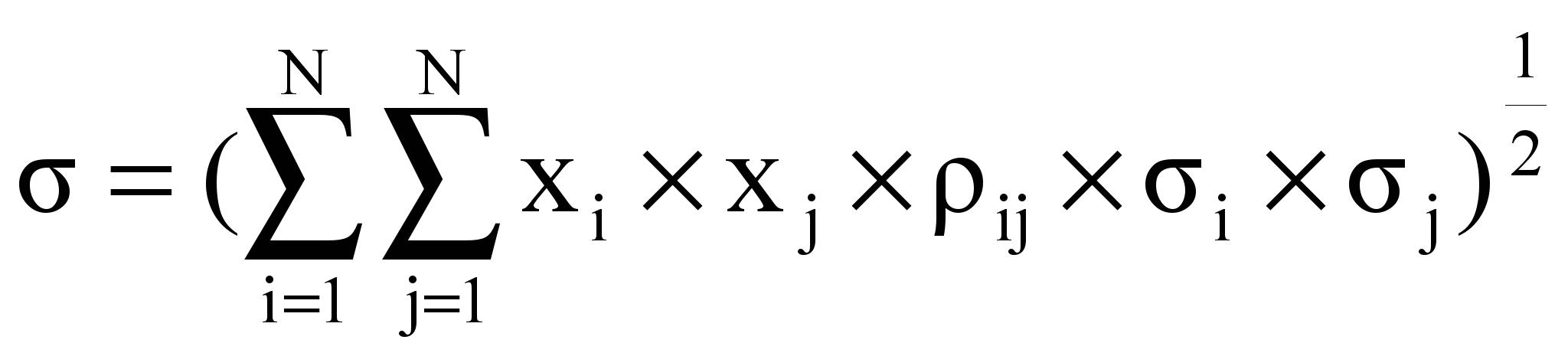. (14)

Задача управления таким портфелем имеет следующее описание: определить вектор {x_i}, максимизирующий целевую функцию r вида (13) при заданном ограничении на уровень риска , оцениваемый (14):

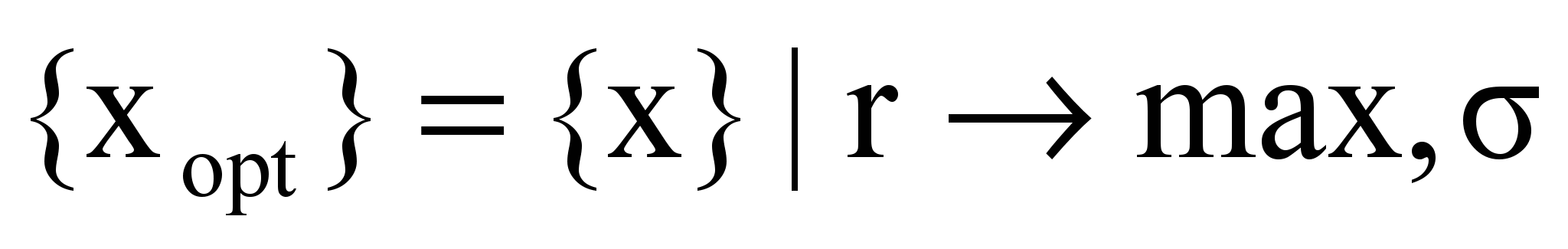=const  _M, (15)

где _M– риск бумаги с максимальной среднеожидаемой доходностью. Запись (15) есть не что иное, как классическая задача квадратичной оптимизации, не ее параметры являются треугольными нечеткими числами, а вычисления с этими числами проводятся по правилам мягкой арифметики Дюбуа-Прада.

Если задаваться различным уровнем ограничений по ,решая задачу (15), то можно получить зависимость макимальной доходности от вида

r_max = r_max(). (16)

Blog

Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний