Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний
| Вид материала | Автореферат |
- Рекомендуемый перечень тем выпускных квалификационных работ по направлению 010500., 30.79kb.
- Лабскер Л. Г. Вероятное моделирование в финансово-экономической области, 15.66kb.
- 1. теоретические и методологические основы анализа финансовой устойчивости предприятий, 9.61kb.
- Лекция. Обзор стандарта ibis. Создание и использование ibis моделей, 112.42kb.
- Темы курсовых работ по дисциплине «маркетинг» Теоретические и методологические основы, 33.15kb.
- Аннотация дисциплины «основы математического моделирования», 29.01kb.
- Курса «Методологические основы психологии». Курс реализуется в рамках специальности, 79.51kb.
- Теоретико-методологические основы деятельности учреждений культуры и образования, 874kb.
- О Конкурса асов компьютерного 3D-моделирования среди предприятий, использующих в проектных, 9.87kb.
- Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
На правах рукописи
НЕДОСЕКИН АЛЕКСЕЙ ОЛЕГОВИЧ
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ ФИНАНСОВОЙ ДЕЯТЕЛЬНОСТИ С ИСПОЛЬЗОВАНИЕМ НЕЧЕТКО-МНОЖЕСТВЕННЫХ ОПИСАНИЙ
Специальность 08.00.13 – «Математические и инструментальные методы экономики»
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
доктора экономических наук
Санкт-Петербург
2003
Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Санкт-Петербургский государственный университет экономики и финансов»
Научный консультант: Доктор экономических наук, профессор
Соколов Дмитрий Викторович
Официальные оппоненты: Доктор экономических наук, профессор
Ватник Павел Абрамович
Доктор экономических наук, профессор
Давнис Валерий Владимирович
Доктор экономических наук, профессор
Селищев Александр Сергеевич
Ведущая организация: Санкт-Петербургский государственный унивеситет
Защита диссертации состоится «___»________________2004 года в _____ часов на заседании диссертационного совета Д212.237.03 при Государственном образовательном учреждении высшего профессионального образования «Санкт-Петербургский государственный университет экономики и финансов» по адресу:
191023, Санкт-Петербург, ул. Садовая, д. 21, ауд. _____
С диссертацией можно ознакомиться в библиотеке Государственного образовательного учреждения высшего профессионального образования «Санкт-Петербургский государственный университет экономики и финансов».
Автореферат разослан «_____»___________________2004 г.
Ученый секретарь
диссертационного совета Завгородняя А.В.
I. ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы исследования определяется необходимостью внедрения в финансовый менеджмент корпораций принципиально новых идей и методов управления финансами, основанных на полномасштабном, научно обоснованном учете всей наличной информационной неопределенности относительно объекта управления. Создание таких методов требует проведения самостоятельного нового научного исследования.
В традиционном финансовом менеджменте корпораций и агентов фондового рынка еще не получила достаточного развития та мысль, что финансовые системы должны сделаться объектом пристального научного исследования и специального экономико-математического моделирования. Зачастую финансовые менеджеры предприятий практически не используют в своей работе компьютерные финансовые модели, ограничиваясь простейшим учетом финансовых потоков в приспособленных таблицах Excel (да и сами таблицы эти употребляются в российской практике не более 5-7 лет). В то же время для исследования финансовых систем недостаточно простейших моделей бухгалтерского учета, потому что систему образуют не только денежные потоки, но и лица, этими потоками управляющие. На систему оказывает влияние внешняя рыночная среда, со своими конъюнктурными возмущениями. Действие внешней среды, ограниченная способность финансового менеджера распознавать текущие состояния финансовой системы и прогнозировать будущие денежные потоки порождает фактор неустранимой неопределенности. При этом рыночная неопределенность не обладает классически понимаемой статистической природой. Соответственно, применимость к анализу финансовых систем классических вероятностей и вероятностных случайных процессов требует дополнительного специального обоснования.
Если, к примеру, взять хорошо известный метод Альтмана для оценки риска банкротства корпорации, то окажется, что коэффициенты в формуле Альтмана меняются от года к году и от страны к стране, т.е. метод Альтмана не обладает устойчивостью к колебаниям исходных данных. Недостаток метода состоит в том, что в нем делаются выводы относительно одной частной корпорации на основе комплекса данных о множестве корпораций, причем этот комплекс данных рассматривается как классическая статистика. Таким образом, индивидуальные отличия предприятия в ходе анализа по методу Альтмана не берутся в расчет, нивелируются, при этом выводы о вероятности банкротства предприятия делаются на весьма ненадежной основе.
В итоге, исследователь финансовых систем, отказываясь от классического вероятностного подхода, вынужден использовать в анализе экспертные, минимаксные и другие детерминистские подходы, которые не в состоянии учитывать неопределенность поведения финансовых систем надлежащим образом. Иногда в ходе моделирования финансовые аналитики используют субъективные вероятности, однако обоснованность введения точечных вероятностных оценок и субъективных вероятностных распределений в ряде используемых моделей недостаточна.
Аналогичные проблемы возникают и перед исследователями фондового рынка, где неопределенность носит генетический характер. Прокатившиеся по всему миру рыночные кризисы 1997 – 1998 и 2000 – 2001 года, принесшие только американским инвесторам убытки в 10 триллионов долларов, показали, что существующие теории оптимизации фондовых портфелей и прогнозирования фондовых индексов себя исчерпали, и необходима существенная ревизия методов фондового менеджмента. Можно говорить и о том, что прокатившиеся по миру экономические кризисы привели к формированию новой экономической парадигмы, в рамках которой не имеют научной силы статитстческие результаты и измерения, полученные на предшествующих этапах развития мировой экономики. Поэтому могут быть оспорены и традиционные способы прогнозирования фондовых индексов и макроэкономической динамики, а также научные результаты, полученные с применением этих методов. К примеру, обучая нейронную сеть на исторических данных растущего рынка акций, аналитик в качестве прогноза с помощью этой сети не получит ничего, кроме повышательного тренда. И этот вполне ожидаемый результат обусловлен прежде всего однобокостью такого механистического подхода к прогнозированию, не учитывающего развитие макроэкономических тенденций, оказывающих непосредственное влияние на поведение объекта прогнозирования (в данном случае, фондового рынка).
Таким образом, в свете явной недостаточности имеющихся научных методов для управления финансовыми активами, исследователи настроены на разработку принципиально новой теории управления финансовыми системами, функционирующими в условиях существенной неопределенности. Большое содействие этой теории может оказать и уже оказывает теория нечетких множеств, заложенная около полувека назад в фундаментальных работах профессора униферситета Беркли Лотфи А. Заде.
Все вышесказанное особенно справедливо в отношении экономической специфики постперестроечной России, где капиталистические отношения существуют не более 15 лет, что не позволяет анализировать ряды статистических данных традиционными способами, в силу существенной нестационарности соответствующих случайных процессов. Поэтому в этих информационных условиях считается наиболее целесообразным шире вовлекать в научный оборот методы анализа, базирующиеся на получении качественных оценок данных и приближенных рассуждений на этой основе. Отсюда вытекает необходимость и обоснованность разработки специальных методов исследования финансовых систем, которые, с одной стороны, в полной степени учитывали российские реалии организации и ведения бизнеса, а, с другой стороны, основывались на современных мировых направлениях экономической науки, одним из которых по праву считается направление нечетких множеств, мягких вычислений и приближенных рассуждений. Таким образом, диссертационное исследование является актуальным.
Цели и задачи исследования. Целью данной диссертационной работы является разработка экономико-математических моделей и методов исследования финансовых систем с применением результатов теории нечетких множеств. В соответствии с поставленной целью, в работе поставлены и решены следующие задачи:
- изучить методологические основы применения результатов теории нечетких множеств в экономических исследованиях;
- обосновать применимость нечетко-множественных описаний для решения задач финансового и инвестиционного анализа, фондового менеджмента, актуарных расчетов в пенсионных системах;
- разработать модель комплексного финансового анализа корпорации и матричного метода оценки риска банкротства корпорации;
- разработать модель инвестиционного процесса и группу методов оценки риска инвестиционного проекта, в зависимости от способа задания критерия эффективности инвестиционного проекта;
- создать нечетко-множественные методы для оценки сильных и слабых сторон бизнеса корпорации и для двумерной оценки бизнеса в координатах «конкурентоспособность – перспективность» в ходе стратегического планирования деятельности корпорации;
- разработать группу методов для оценки инвестиционной привлекательности ценных бумаг вида долговых обязательств субъектов Российской Федерации, акций и корпоративных облигаций;
- создать нечетко-множественную модель фондового портфеля и метод нечетко-множественной оптимизации фондового протфеля на основе классического метода оптимизации по Марковицу;
- разработать модель рациональной динамики фондовых инвестиций и метод прогнозирования фондовых индексов;
- разработать актуарную модель накопительной пенсионной системы и метод оптимизации потоков накопительной пенсионной системы по критерию минимума риска срыва плановых заданий по формированию пенсионных резервов;
- разработать ряд программных средств для финансового и фондового менеджмента, в основе которых лежат модели и методы настоящей диссертационной работы.
Обозначенные в работе цели из задачи диссертационного исследования ставились и решались с применением классических экономико-математических моделей и методов исследования финансовых систем, сформулированных в нечетко-множественной постановке задачи. В ряде случаев традиционные вероятностные модели и нечетко-множественные описания интегрировались в единую сводную синтетическую модель. В качестве базовых нечетко-множественных формализмов выступали: носитель, лингвистическая переменная, нечеткое число, нечеткая случайная величина, функция принадлежности.
Теоретической и методологической базой исследования послужили работы:
- зарубежных ученых: Э.Альтмана, Д.Бакли, А.Борисова, Г.Бояджиева, П.Друкера, Л.Дымовой, Д.Дюбуа, Л.Заде, К.Запоунидиса, А.Коффмана, Х. Лафуэнте, Г.Марковица, Д.Ралески, Х.Прада, П.Севастьянова, Р.Словински, Т.Куна, Б.Флое, Ж. Хил Алухи, В. Шарпа, Х.-Ю. Циммермана и других;
- российских ученых: А.Аверкина, А.Алехиной, В.Аркина, И.Батыршина, П.Виленского, К.Воронова, О.Ефимовой, С.Капицы, Р.Качалова, Г.Клейнера, В.Ковалева, Н.Кондратьева, А.Кравца, В.Лифшица, О.Максимова, Я.Миркина, Д.Поспелова, А.Рыжова, С.Смоляка, Е.Чижовой, А.Шоломицкого, А.Язенина и других.
Состояние вопроса. Несмотря на значительное количество серьезных научных исследований, теоретических работ и многочисленных публикаций, проблема эффективного применения нечетко-множественных описаний для финансового менеджмента освещена в науке явно недостаточно. В ряде работ предлагаются модели финансового менеджмента, содержащие нечетко-множественные описания, однако этим работам недостает качественной интерпретации результатов, полученных на основе предлагаемой модели. Так, например, в работах Бакли впервые получена чистая современная ценность инвестиционного проекта как треугольное число, однако не сделаны выводы об уровне риска такого проекта. В работах Алехиной приводится нечетко-множественная интерпретация ряда известных показателей финансового анализа предприятия, однако не сделан вывод о комплексном финансовом состоянии предприятия в такой постановке задачи.
Та же недостаточность наблюдается и в плане специализированных программных средств финансового менеджмента, основанных на начетких моделях. Такие программы в России полностью отсутствуют. За рубежом, в то же время, начинают постепенно появляться программные решения и информационные технологии, решающие экономические задачи с применением нечетко-множественных и родственных им описаний. Так, под руководством Зопоунидиса в Техническом университете на острове Крит была разработана экспертная система FINEVA для детального финансового анализа корпораций, содержащая в своем составе описания так называемых «грубых множеств» (rough sets) и базы знаний на этой основе. Чуть раньше в Германии, в конце 80-х годов, группой Циммермана была разработана система стратегического планирования ESP, в которой реализуется позиционирование бизнеса корпорации на основе нечетких описаний конкурентноспособности и привлекательности бизнеса. Таким образом, налицо серьезное отставание российской науки и практики по направлению диссертационной работы от зарубежного уровня исследований и прикладных результатов.
Информационной базой исследования послужили информационные источники Госкомстата, Центробанка, Минфина РФ, финансовая отчетность корпораций, данные российских и зарубежных финансовых порталов, монографии, статьи и материалы научно-практических конференций, публикации в периодических изданиях.
В качестве объекта исследования в работе выступают финансовые системы корпораций и фондового рынка.
Предметом исследования избраны методологические, теоретические, методические и практические проблемы математического моделирования финансовых систем, функционирующих в условиях существенной информационной неопределенности.
Структура работы. Диссертация состоит из введения, пяти глав, заключения, перечня цитируемых источников и приложений к работе.
II. ОСНОВНЫЕ ИДЕИ И ВЫВОДЫ ДИССЕРТАЦИИ
Обоснование применимости нечетко-множественных описаний в моделях и методах финансового менеджмента
Обзор существующих моделей и методов финансового менеджмента показаывает, что в большинстве случаев эти модели неадекватно описывают наличный уровень информационной неопределенности, а методы, использующие необоснованные формализмы, приводят к ошибочным или неверифицируемым оценкам.
В то же время применение результатов теории нечетких множеств к анализу финансовых систем позволяет получить принципиально новые модели и методы анализа этих систем. При этом оказывается возможным осуществить обоснованный переход от классических вероятностных моделей и экспертных оценок к нечетко-множественным описаниям. Так, классическое вероятностное распределение в модели может быть замещено вероятностным распределением с нечеткими параметрами, а совокупность экспертных оценок может быть интерпретирована набором функций принадлежности, образующим нечеткий классификатор.
Исследование состояния теории нечетких множеств применительно к экономике и финансам показывает, что уже созданы все необходимые формализмы для моделирования финансовых систем, однако нынешний уровень модельных представлений отстает от запросов практики финансового менеджмента. Нечеткие множества практически не применялись до настоящего времени для финансового анализа и планирования корпораций, оценки инвестиционной привлекательности ценных бумаг, для оптимизации фондового портфеля и прогнозирования фондовых индексов. В то же время для такого применения созрели все необходимые предпосылки, в том числе и идеологические, связанные со сменой научной парадигмы в экономических исследованиях.
Отдельно в диссертации рассматривается вопрос о моделировании активности лиц, принимающих решения в финансовой системе. Показано, что в подавляющем большинстве случаев финансовые решения основаны на невербализованной интуиции эксперта, которая должна выступать в качестве объекта научного исследования и получить формализованное описание в качественных и количественных терминах. При этом эвристический характер используемых приемов моделирования экспертной активности не свидетельствует против этих приемов, но устанавливает границу научного исследования, которая может отодвигаться по мере получения новой рыночной информации, а сама модель – уточняться.
В работе предлагается, для описания совокупности ограниченного количества данных, не обладающих свойством статистической однородности, использовать термин «квазистатистика». Квазистатистика – эта выборка наблюдений из их генеральной совокупности, которая считается недостаточной для идентификации вероятностного закона распределения с точно определенными параметрами, но признается достаточной для того, чтобы с той или иной субъективной степенью достоверности обосновать закон наблюдений в вероятностной или любой иной форме, причем параметры этого закона будут заданы по специальным правилам, чтобы удовлетворить требуемой достоверности идентификации закона наблюдений.
Такое определение квазистатистики дает расширительное понимание вероятностного закона, когда он имеет не только частотный, но и субъективно-аксиологический смысл. Здесь намечены контуры синтеза вероятности в классическом смысле - и вероятности, понимаемой как структурная характеристика познавательной активности эксперта-исследователя. Также это определение намечает широкое поле для компромисса в том, что считать достаточным объемом выборки, а что – нет.
Понятие квазистатистики дает широкий простор для применения нечетких описаний для моделирования законов, по которым проявляется та или иная совокупность наблюдений. Строго говоря, не постулируя квазистатистики, нельзя вполне обоснованно с научной точки зрения моделировать неоднородные и ограниченные по объему наблюдения процессы, протекающие на фондовом рынке и в целом в экономике, невозможно учитывать неопределенность, сопровождающую процесс принятия финансовых решений.
Рассматривая роль нечетко-множественных описаний для финансового моделирования, в работе отмечается, что такие модели и методы на их основе являются законными правоприемниками вероятностных моделей и методов, с одной стороны, и экспертных методов, с другой стороны (рис. 1).
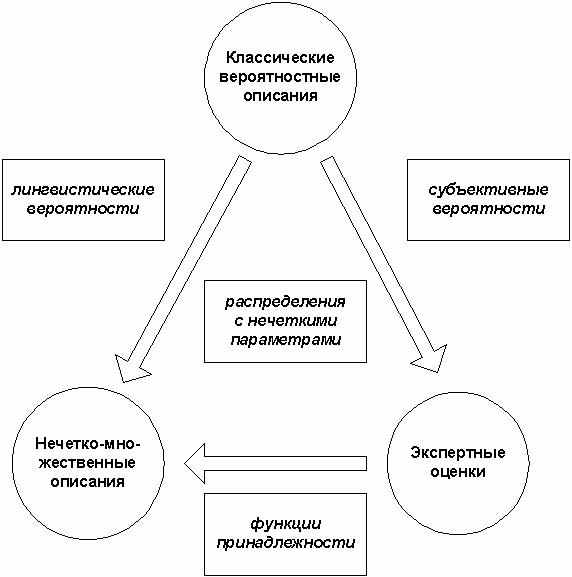
Рис. 1. Соотношение классических вероятностных, экспертных и нечетко-множественных описаний
Еще в 80-е годы прошлого века А.Борисовым и учеными его научной школы показано, что существуют эффективные методы согласования экспертных оценок на нечетко-множественной платформе, методы перехода от совокупности точечных и интервальных экспертных оценок к виду трапециевидной (или иной) функции принадлежности. Разумеется, этот вывод справедлив и для качественной интерпретации экономических данных произвольного вида. В работе, на основании результатов экспертных опросов, строятся классификаторы качественных уровней факторов в виде так называемой серой шкалы Поспелова и семейства функций принадлежности, ассоциированных с этой шкалой. Таким образом, в работе предложен конструктивный метод лингвистического раскознования количественных исходных данных о состоянии финансовой системы.
Аналогично, в работе обосновывается переход от классических случайных величин (основанных на классической генеральной совокупности статистически однородных данных) к нечетким случайным величинам (в аксиоматику которых входит, наряду с вероятностным, еще и возможностное пространство). Впервые нечеткая случайная величина была постулирована Д.Ралески. В работе предложена схема перехода от классического вероятностного распределения к вероятностному распределению с нечеткими параметрами, чем снимается жесткое допущение статистической однородности данных по выборке.
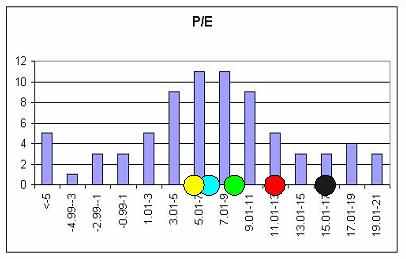
Рис. 2. Гистограмма фактора P/E и соответствующие узловые точки
В работе обосновывается высокое информативное значение гистограмм квазистатистики, которые оказывают неоценимое содействие экспертам в ходе лингвистической классификации уровня финансовых показателей. Оценивая гистограмму, эксперт (или экспертное сообщество) всегда может расставить на оси абсцисс гистограммы узловые точки (рис. 2), которые со 100%-ой уверенностью могут быть охарактеризованы экспертным сообществом как обладающие определенной качественной оценкой лингвистической шкалы (например, низкий уровень – средний уровень – высокий уровень). В работе предлагается формальный метод перехода от набора узловых точек к набору трапециевидных функций принадлежности, что позволяет завершить создание лингвистического классификатора, основанного на серой шкале Поспелова.
Таблица 1. Нечетко множественные описания
| № | Название формализма | Области применения |
| 1 | Функция принадлежности | Базовый формализм теории нечетких множеств. Применение повсеместно |
| 2 | Лингвистическая переменная | Базовый формализм теории нечетких множеств. Применение повсеместно |
| 3 | Треугольные нечеткие числа | Задание количественных параметров любой финансовой модели, в том числе при бизнес-планировании |
| 4 | Трапециевидные нечеткие числа | Классификация уровней факторов, в том числе при анализе риска банкротства, при оценке инвестиционной привлекательности ценных бумаг, в стратегическом планировании |
| 5 | Нечеткие последовательности и матрицы | Моделирование экономических процессов, макроэкономическое моделирование, прогнозирование |
| 6 | Нечеткие функции | Моделирование экономических процессов, макроэкономическое моделирование, прогнозирование, портфельная оптимизация |
| 7 | Вероятностные распределения | Портфельная оптимизация, актуарное моделирование |
| 8 | Нечеткие знания | Используются при разработке экспертных моделей в составе модели финансовой системы |
| 9 | Нечеткие классификаторы | Классификация уровней факторов, в том числе при анализе риска банкротства, при оценке инвестиционной привлекательности ценных бумаг, в стратегическом планировании |
