Литература: [1-7, 14, 15, 18]

Вид материала

Литература

Содержание Задача оптимального раскроя материала Транспортная задача. Задача о назначениях на работу. Задача о смесях (о рационе). Задача о рюкзаке. Задача о коммивояжере. Задача о станках. Задача о распределении капиталовложений Задача о размещении производства. Принцип свертки критериев. Принцип лексикографического предпочтения. Принцип минимакса. Принцип равновесия. Принцип оптимальности по Парето. Принцип недоминируемых исходов Принципы устойчивости (угрозы и контругрозы). Принцип пессимизма - оптимизма (критерии Гурвица). Концепция динамической устойчивости.

Подобный материал:

• Класс: 12 Зачёт №2 «Русская литература 1917-1941», 186.43kb.
• Литература 7 класс Зачетная работа№2 Содержание, 40.79kb.
• Литература Форш О. «Одеты  камнем», 38.6kb.
• Литература английского декаданса: истоки, становление, саморефлексия, 636.47kb.
• Тема: «Библейские мотивы в творчестве Б. Пастернака», 211.88kb.
• Литература 11 класс Программы общеобразовательных учреждений. Литература, 331.28kb.
• Учебника. Учитель Кулябина Зинаида Григорьевна. Выступление на Краевой научно-практической, 48.58kb.
• Жиркова Р. Р. Жондорова Г. Е. Мартыненко Н. Г. Образовательный модуль Языки и культура, 815.79kb.
• Английская литература. , 57.37kb.
• Планирование курса литературы 8 класса по программе, 14.4kb.

Раздел I. МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ

В данном разделе изложены общие (методологические) аспекты исследования операций, подробно раскрыты вопросы математического моделирования, рассматривается много примеров, аналогичных первому заданию контрольной работы. .

Литература: [1-7, 14, 15, 18].


§1. Этапы исследования операций.


Человек сталкивается с необходимостью принятия решения, как в бытовой, так и служебной областях своей деятельности. Принимаемые решения отличаются как по степени ответственности, так и по степени значимости последствий - от личных, до государственных масштабов. Различными аспектами проблем, связанных с выработкой управленческих решений, с "оптимальным" поведением людей» с пересечением интересов нескольких сторон, занимаются многие науки: экономика, социология, право и др.

В отличие от других подходов ИО анализирует эти проблемы с помощью математического аппарата (см. определение ИО во введении). Это означает, что хотя бы некоторые данные, фигурирующие в формулировке задачи, должны иметь количественные выражения. Качественные данные (условия) проблемы учитываются дополнительно и являются своеобразным фоном для использования математических моделей.

Принятие решения всегда предполагает наличие лица или лиц, принимающих решение (ЛПР), цели, вариантов выбора решения (множество допустимых решений). Решения принимаются с учетом определенной обстановки, сопутствующих условий, предпосылок. Это те главные факторы, присущие любой задаче принятия решения, и которые обязательно должны быть отражены в математической модели.

Цель ЛПР - с учетом существующих условий принять то решение из множества допустимых в данной ситуации решений, которое наилучшим образом способствует достижению преследуемой им цели (оптимальное решение).

Неотъемлемой частью методологии ИО является всесторонний качественный и, количественный анализ проблемы, предшествующий ее математическому моделированию. Поэтому. говорят о системном анализе проблемы, предполагающем выполнение следующих компонент:

- доматематический (гуманитарный) анализ проблемы;

- математический анализ проблемы;

- применение результатов исследования на практике. Проведение такого системного анализа каждой конкретной задачи должно осуществляться операционной группой, включающей: специалистов данной области (постановщиков проблем, заказчиков), математиков, экономистов, юристов, социологов, психологов и др.

Как не существует универсальных методов построения математических моделей, так и не существует универсальных методик и руководящих принципов ИО. Каждое отдельное исследование имеет свои особенности. Поэтому можно рекомендовать лишь некоторые, достаточно общие принципы и этапы исследования операций. Эти этапы включают:

1. Определение цели исследования,

2. Составление плана разработки проекта.

3. Формулировку проблемы.

4. Сбор данных (статистических, экспертных и прочих).

5. Построение математической модели.

6. Разработку вычислительного метода.

7. Разработку технического задания на программирование, программирование и отладку программ.

8. Проверку математической модели и оценку решения.

9. Реализацию результатов на практике.

Этапы 1-4 относятся к доматематической части исследования и выполняются специалистами той области, к которой принадлежит исследуемая задача или проблема (т.е. заказчиком или предо и кителем заказчика). Очень важно, чтобы перед математическим моделированием объект исследования (предметная область) был досконально изучен самими постановщиками (заказчиками). В частности; исследователям должны быть предоставлены все необходимые документальные и статистические данные в исчерпывающем объеме. Сбор статистических данных или иной информации - не дело математиков, их дело - организация хранения, анализ и обработка данных, предоставленных им заказчиками в удобной форме (в дискетах).

Этапы 5-8 относятся к математической части исследований. Это самые ключевые и сложные этапы исследования операций. Этап 9 - заключительная часть исследований проводится совместными усилиями заказчиков и математиков-разработчиков модели.

Достаточно полное описание содержания перечисленных этапов можно найти в книгах [1, 2] (см. список литературы во введении). Это надо знать экономистам - как будущим постановщикам задач, заказчикам научных исследований, руководителям отделов маркетинга и т.д.


§ 2. Математическое моделирование. Общая структура


При определении элементов математической модели и этапов формализации (определение этих понятий см. во введении) мы будем исходить из того, что в ИО и МП изучаются задачи принятия решения и, как частный случай, задачи оптимизации (определение см. во введении).

Одним из основных требований к составлению математических моделей является учет основных факторов проблемы. Для выявления основных элементов моделей задач, принятия решения требуется ответить на следующие вопросы:

- Кто принимает решение ?

- Каковы цели принятия решения для каждого ЛПР ?

- В чем состоит принятие решения ?

- Каковы возможности ЛПР (с точки зрения принятия решений)?

- При каких условиях происходит принятие решения?

Формализуя (описывая математически) ответы на эти вопросы мы получим требуемую модель задачи.

Пример 1. (планирование суточного выпуска продукции). Процесс изготовления изделий двух видов состоит в последовательной обработка каждого из них на трех станках. Известны: время эксплуатации каждого станка в сутки, обработки единицы каждого изделия на каждом станке, стоимость реализации единицы каждого изделия.

Требуется составить для фирмы план суточного выпуска изделий так, чтобы доход от их продажи был максимальным.

При анализе упомянутых важнейших факторов будем исходить только из условия задачи. Здесь:

ЛПР - планирующий орган (фирма);

Цель - максимизация дохода от продажи выпущенных за сутки изделий двух видов;

принятие решения для ЛПР состоит в определении суточных объемов выпуска каждого из двух видов изделий;

возможности ЛПР ограничены временными ресурсами эксплуатации станков трех видов - о других ограничениях или условиях в задаче ничего не говорится.

После выявления важнейших факторов нужно анализировать все параметры задачи: значение каких параметров известно (задано), какие параметры являются неизвестными (искомыми) величинами; какими из параметров мы можем управлять (управляемые переменные), а какими нет (неуправляемые параметры).

В нашем примере известными являются следующие параметры:

• суточная норма b₁ эксплуатации станка 1;
  
• - суточная норма b₂эксплуатации станка 2;
  
• суточная норма b₃ эксплуатации станка 3;
  
• время a_ij обработки единицы изделия вида i (i=l,2) на станке типа j (j=1,2,3);
  
• стоимость с₁ (продажи) единицы изделия вида 1;
  
• стоимость c₂ (продажи) единицы изделия вида 2;
  

Все эти параметры являются неуправляемыми, т.к. они заданы (их значения можно найти в справочниках, нормативах или определить из прошлого опыта). Неизвестными или искомыми являются следующие величины:

- объем суточного выпуска изделия вида 1;

- объем суточного выпуски изделия вида 2.

Эти два параметра можно считать управляемыми, т.к. фирма сама определяет их величину (исходя из реальных условий).

Далее для составления математической модели задачи нужно ввести систему обозначений неизвестных параметров задачи.

В нашем примере обозначим:

x₁ - объем суточного выпуска изделия вида 1,

x₂ - объем суточного выпуска изделия вида 2.

Тогда доход от продажи x₁ и x₂ есть:

c₁ x₁ + c₂ x₂,

а время, необходимое для обработки x₁, x₂ единиц изделий на станке j, есть

a_ij x₁ + a_2j x₁ (j=l,2,3).

Теперь первоначальную задачу можно сформулировать математически:

максимизировать c₁ x₁ + c₂ x₂,

выбирая x₁ и x₂ из условия

a₁₁ x₁ + a₂₁ x₂ b₁,

a₁₂ x₁ + a₂₂ x₂ b₁,

a₁₃ x₁ + a₂₃ x₂ b₁,

x₁0, x₂0.

Условия неотрицательности переменных следует из смысла величин x₁и x₂ - это дополнение модели недостающими сведениями. Полученную задачу запишем более компактно:

max c₁ x₁ + c₂ x₂,

при ограничениях

a₁₁ x₁ + a₂₁ x₂ b₁,

a₁₂ x₁ + a₂₂ x₂ b₁,

a₁₃ x₁ + a₂₃ x₂ b₁,

x₁0, x₂0.


Это есть задача математического программирования (см. определение во введении) с целевой функцией c₁ x₁ + c₂ x₂ и множеством допустимых решений X, которое описывается пятью неравенствами (на плоскости это есть многогранник, образованный пересечением пяти полуплоскостей).

Мы рассмотрели модель одной частной задачи принятия решения. Для выяснения общей структуры таких задач введем общие обозначения.

Обозначим через N множество сторон, принимающих участие в данной конкретной задаче принятия решения:

N={1,2,...,n},

где каждый элемент i множества N называется лицом, принимающим решение (ЛПР), например, отдельная личность, фирма, плановый орган большого концерна, правительства и др. Каждый элемент iN характеризуется своими возможностями. Обозначим через Х_i множество всех его допустимых решений (стратегий, альтернатив). Предположим, что такие множества математически описаны для всех участников:

X₁, X₂,..., X_n.

После этого процесс принятия решения всеми ЛПР сводится к следующему формальному акту: каждое ЛПР выбирает конкретный элемент x₁X₁, x₂X₂,…, x_nX_n из своего допустимого множества решений. В результате получается набор х = (x₁,...,x_n) выбранных решений, который мы называем ситуацией.

Формализация целей принятия решения осуществляется по следующей схеме. Тем или иным способом строятся аналитические законы (функции) f₁,....,f_n, ставящие в соответствие каждой ситуации x набор из n чисел

f₁(x), f₂(x),...,f_n(x).

Функция f_i(x) == f_i(x₁,...,x_n) называется критерием качества i-го ЛПР. Число f_i(x) является количественной оценкой ситуации x для i-гo ЛПР с точки зрения преследуемой им цели. Поэтому в модели цель i-ro участника формализуется так: выбрать такое свое решение x_iX_i, чтобы добиться возможно большего значения функции f_i. Однако достижение этой цели полностью от него не зависит в виду наличия других сторон, влияющих на общую ситуацию x с целью достижения своих собственных целей. Этот факт пересечения интересов (конфликтность) отражается в том, что функция f_i помимо x_i зависит и от остальных переменных x_j (ij). Поэтому в моделях принятия решения со многими участниками применяются более сложные принципы оптимального поведения, чем прямая максимизация или минимизация критерия качества.

Наконец, пусть каким-то образом (математически) описаны все те условия, при которых происходит принятие решения. Совокупность всех этих условий, выступающих в модели в виде некоторых уравнений связи, обозначим одним символом Σ Математически система Σ содержит описание связей между управляемыми и неуправляемыми переменными, описание влияния случайных факторов, учет динамических характеристик и др.

Таким образом, общая структура задачи принятия решения со многими участниками выглядит так:

1....,Xn;f₁....fn; Σ > (1)

Цель математического моделирования - для поставленной специалистами конкретной задачи получить конкретное описание элементов структуры (1). Надо заметить, что математическое моделирование - эта весьма сложная задача, требует от разработчиков больших трудозатрат, навыков, знаний и может быть выполнена лишь при наличии необходимого объема предварительной содержательной информации.

Резюмируя, можем сказать, что основными элементами математической модели любой задачи принятия решения являются:

1. Множество ЛПР (N).

2. Критерии качества (f₁,...,fn).

3. Множества допустимых решений (X₁,...,Xn).

4. Ограничения на параметры задачи, предпосылки, уравнения связи (Σ).

Конкретизируя эти элементы, их характеристики и свойства, мы получаем тот или иной конкретный класс задач (класс моделей) принятия решения. Так, если N состоит только из одного элемента (n=1), а все условия и предпосылки исходной реальной задачи можно описать в виде множества допустимых решений этого единственного ЛПР, то из (1) получаем структуру задач оптимизации (экстремальных задач):

<Х,f> (2)

В схеме (2) ЛПР может рассматриваться как планирующий орган, множество допустимых решении Х задается при помощи ограничений на возможности ЛПР, а критерий качества f называется целевой функцией. Задача оптимизации ставится так:

max f(x) (f(x)→max) (3)

^{xX xX}

min f(x) (f(x)→min) (4)

^{xX xX}

Это различная форма записи одной и той же задачи: (3) - задача на максимум, в которой требуется найти точку максимума x* функции f на множестве X; (4) -задача на минимум, в которой требуется найти точку минимума x** функции f на множестве X. Решениями (оптимальными) этих задач называются пары x* ,f(x*) и x** , f(x**) соответственно.


§ 3. Этапы математического моделирования.

Примеры.


Для построения математической модели конкретной задачи рекомендуется выполнить следующую последовательность работ:

1. Изучение условия задачи (предметной области).

2. Определение важнейших факторов (см. §2).

3. Выделение известных и неизвестных параметров.

4. Выявление управляемых и неуправляемых параметров.

5. Дополнение условия задачи недостающими сведениями.

6. Введение системы обозначений.

7. Составление математической модели задачи (математическое выражение важнейших факторов, соотношений и связей между параметрами).

В приведенных ниже примерах составления моделей проследите эти этапы, которые мы выполним без комментариев (см. по этому поводу Пример 1.).

Пример 2. (Размещение заказов). Фирма получила заказ ни несколько тысяч новых изделий, собирающихся из отдельных блоков. Руководство фирмы приняло решение разместить заказы на изготовление n блоков и выбрало n фирм-поставщиков. Каждый заказ настолько велик, что фирма-поставщик не может выполнить более одного заказа. Каждому поставщику предложено определить стоимость выполнения заказа, т.е. цену, по которой он готов поставить фирме различные блоки. Фирма должна заключить n контрактов на поставку ей n видов блоков, минимизировав при этом свои общие затраты на приобретение комплектующих узлов со стороны.

Обозначим: i - номер (название) блока, i = 1,....n; j - номер (название) фирмы-поставщика, j= 1,...,n; с_ij - стоимость выполнения i-ro блока j-ой фирмой (заданное число). Кроме того, введем для каждого i и j число.



Целевая функция, имеющая смысл общих затрат на покупку комплек­тующих блоков, запишется так



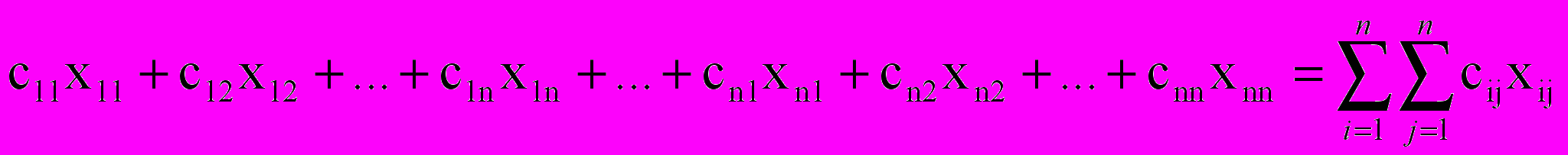
Ограничения задачи (на переменные х_ij) имеют следующий смысл:

1) каждый i-й блок должен быть выполнен (каким-либо поставщиком);

2) каждая фирма-поставщик j должна выполнить один (какой-либо) блок .

Математически эти условия запишутся соответственно:

x_i1+x_i2 +…+ x_in = 1,

x_ij+x_2j +…+ x_nj = 1.

Таким образом, приходим к следующей оптимизационной задаче (модели):



при ограничениях





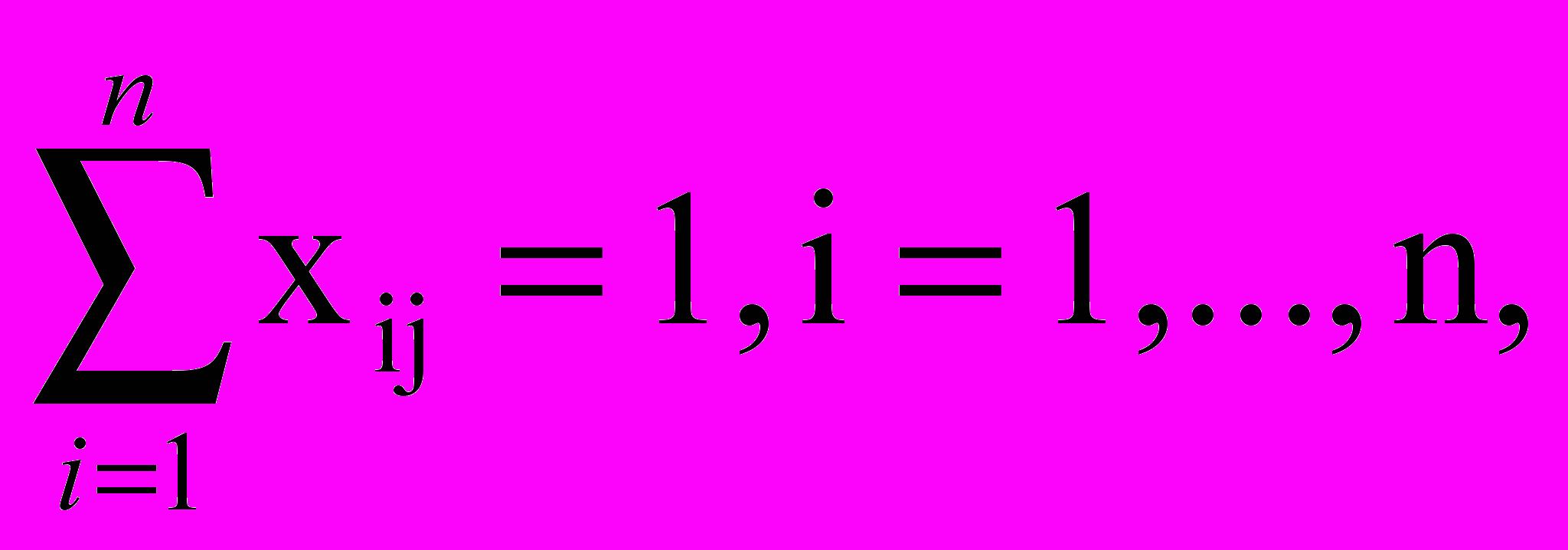
x_ij = 0 или 1 для всех i,j.

Пример 3 (Выбор портфеля ценных бумаг). Специалисту по финансовому анализу, работающему в банке (или в страховой компании) требуется определить наилучший набор акций, облигации и других ценных бумаг на выделенную сумму с целью минимизации риска, связанного с приобретением набора ценных бумаг.

Прибыль к концу планового периода на каждый доллар, вложенный в бумагу j-го вида, характеризуется двумя показателями: аj - фактическая прибыль (случайное число), j - ожидаемая прибыль. Требуется, чтобы ожидаемая прибыль на доллар инвестиций была для всего набора ценных бумаг не ниже заданной величины b.

Для получения модели примем все средства, выделенные на покупку ценных бумаг, равными единице и обозначим через x_j - долю от всех средств, выделяемую для приобретения ценных бумаг вида j.

Риск учитывается при помощи ковариации (см. теорию вероятностей)

_ij = М (а_i, - _i) (а_j - _j)

прибыли для ценных бумаг вида i и вида j.

Математическая модель имеет вид:



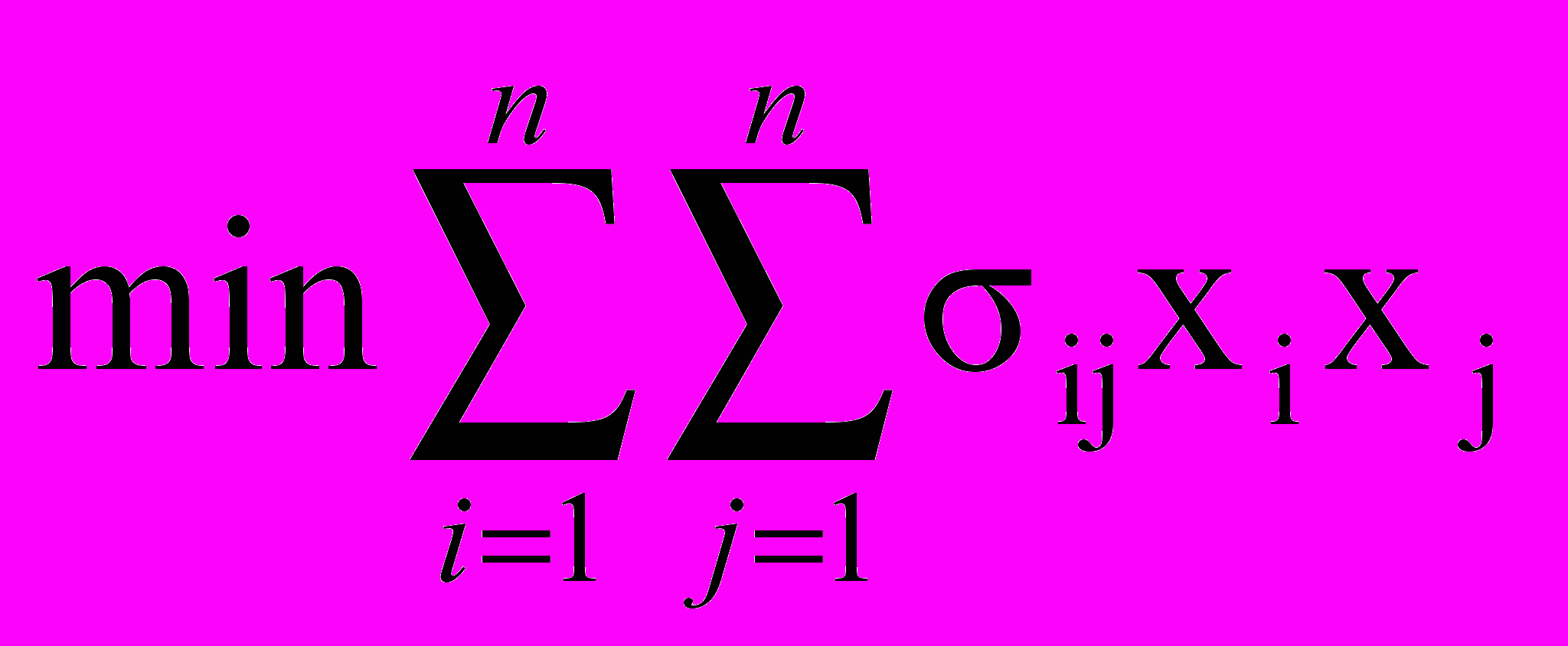
при ограничениях





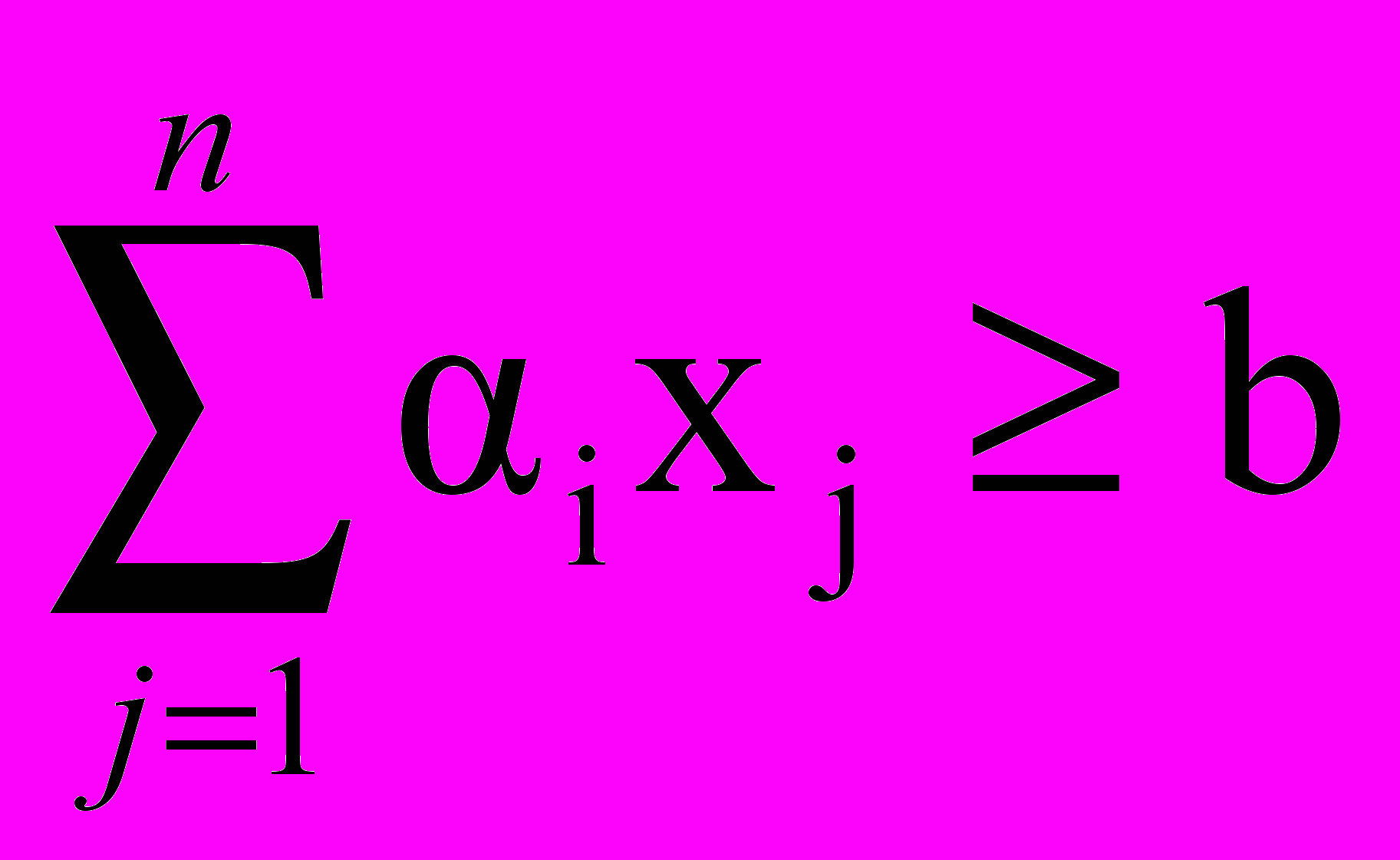
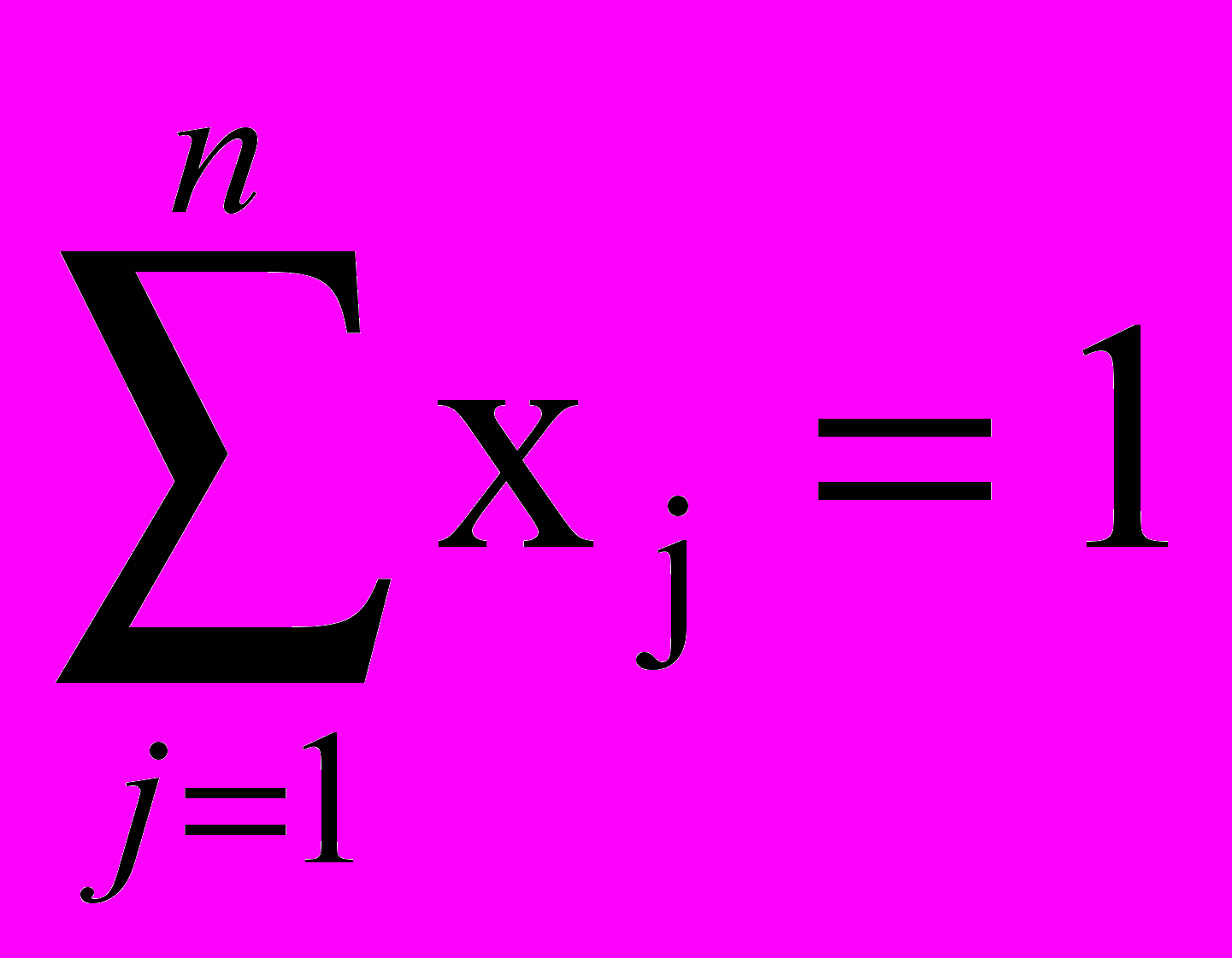
x_j  0, j=1,…,n

Здесь n - число разновидностей ценных бумаг. Целевая функция имеет смысл дисперсии фактической прибыли (рассеивание фактической прибыли от ожидаемой), первое ограничение есть условие на ожидаемую прибыль, а последнее - непревышение средств, выделенных на покупку ценных бумаг.

Пример 4 (Задача о рекламе). Фирма планирует проведение радиорекламной кампании по сбыту автомобилей в одном из регионов, где расположено s радиостанций, в течение двух недель. Фирма оценила предварительно, что если радиостанции j выделить у_j долларов, то чистый доход от увеличения сбыта равен R_j(y_j) (R_j - функция реализации дохода от объема финансирования рекламы). На рекламу выделена общая сумма, равная N долларам. Число рекламных объявлений в день не должно превышать M. Если фирма выделила j-й радиостанции у_j долларов, то число рекламных объявлений будет K_j(y_j) (K_j - функция, которая каждой выделенной сумме ставит в соответствие количество рекламных объявлений в день, считается известной). Как нужно финансировать s радиостанций, чтобы получить суммарную максимальную прибыль от реакции сбыта на рекламу ?

Очевидно, что математическая модель имеет вид:



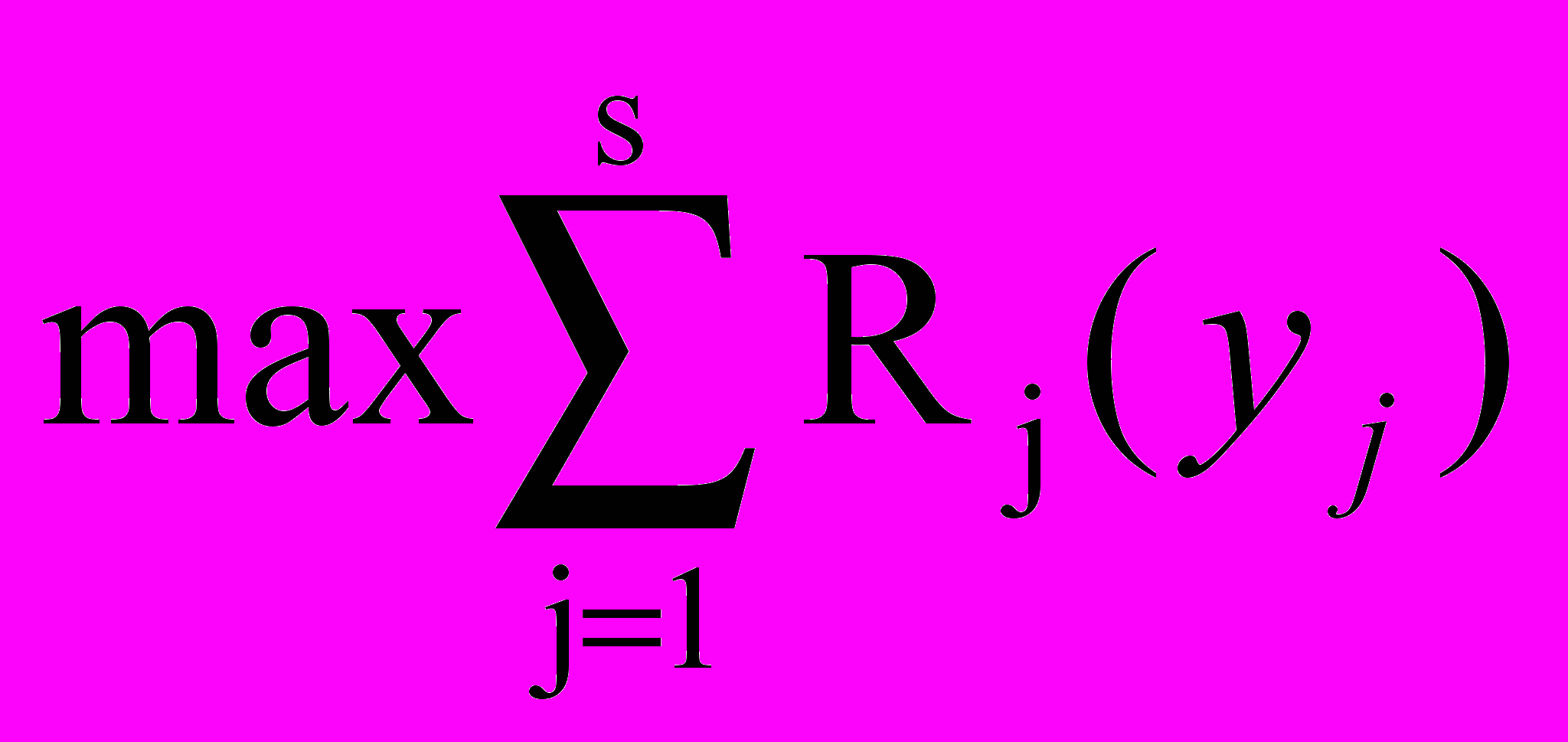
при ограничениях





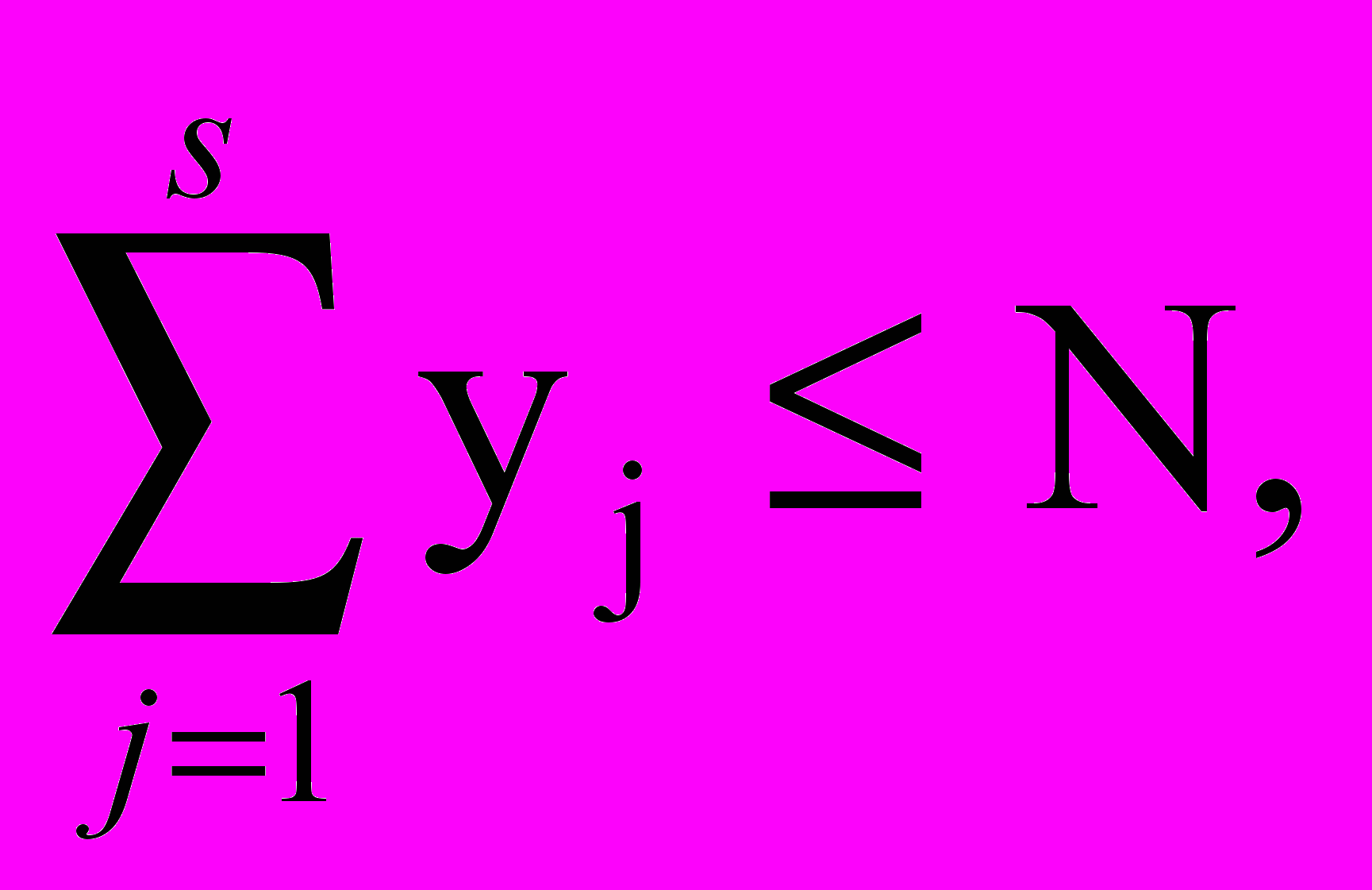
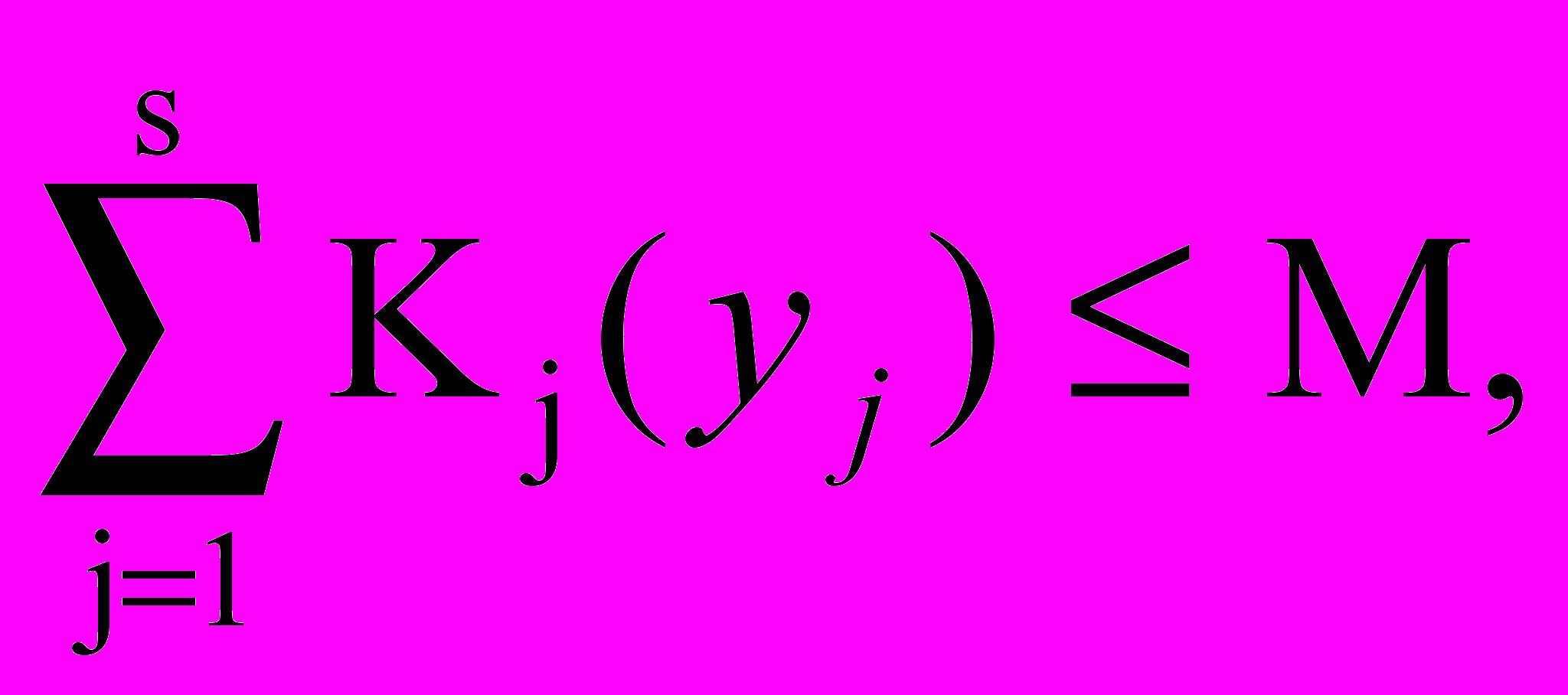
y_j  0, j = 1,…,s.

Пример 5 (Задача управления производством). Фирма должна разработать календарную программу выпуска некоторого вида изделий на плановый период, состоящий из Т отрезков (недель, месяцев, кварталов, лет). Предполагается, что для каждого из этих отрезков имеется точный прогноз спроса на выпускаемую продукцию. Время изготовления партии изделий настолько мало, что им можно пренебречь. Для разных отрезков спрос неодинаков; кроме того, на экономические показатели производства влияют размеры изготовляемых партий. Хранение возникающих при этом запасов (превышение выпуска над спросом на некоторых отрезках) связано с определенными затратами.

Требуется разработать такую программу, при которой общая сумма затрат на производство и содержание запасов минимальна при условии полного удовлетворения спроса на продукцию.

Обозначим:

x_t - выпуск продукции в течение некоторого отрезка t;

y_t - уровень запасов на конец отрезка t;

D_t - спрос на продукцию для отрезка t;

Затраты на отрезке t (обозначим их С_t) зависят от выпуска x_t и уровня запасов y_t, т.е. являются функцией от этих неизвестных величин: c_t = c_t (x_t, y_t).

Требование удовлетворения спроса в пределах каждого временного отрезка означает, что уровень запасов на конец отрезка t (т.е. yt) должен равняться сумме - уровня запасов и начало отрезка t (т.е. yt-1) и выпуска продукция на отрезке t (т.е. xt) минус спрос на отрезке t (т.е. Dt).

Отсюда получаем следующую модель:



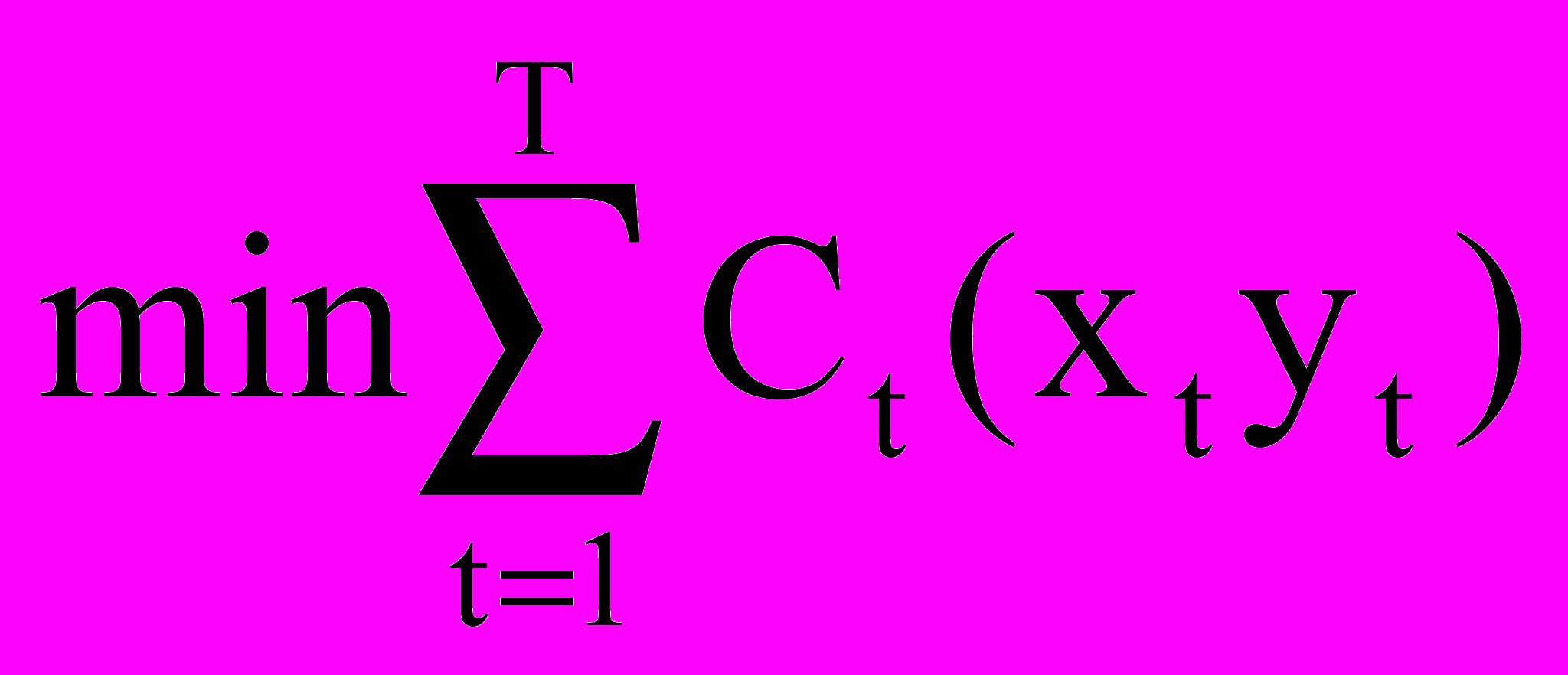
при ограничениях

уt-1 + xt - yt = Dt, t==1,2,…T;

yT = 0, xt, yt  0 для всех t.

Здесь y₀ - заданный уровень запасов на начало планового периода, а y_T -уровень запаса на конец периода. -

Пример 6 (Оптимизация схемы обслуживания). Система обслуживания состоит из n типов различных приборов (напр. кассы в магазинах, телефонные линии, автозаправочные колонки и пр.). Каждый прибор в любой момент времени обслуживает не более одной заявки (напр. покупателя, телефонного разговора, автомобиля и пр.). Известно количество приборов j-го типа и число заявок i-го типа, прибывших в систему в момент времени t. Известна также эффективность j-го прибора при обслуживании заявки i-го вида.

Требуется распределить свободные приборы по заявкам так, чтобы суммарная эффективность была наибольшей.

Для составления модели сначала введем обозначения свободных величин:

N_j - количество приборов j-го типа,

d_i^t - число заявок i-го типа в момент времени t.

μ_ij - эффективность j-го прибора при обслуживании заявки i-го вида. Обозначим искомую величину:

x_ij - число приборов j-го вида, отведенных для обслуживания заявок i-го типа.

Этих данных достаточно для составления математической модели задачи:



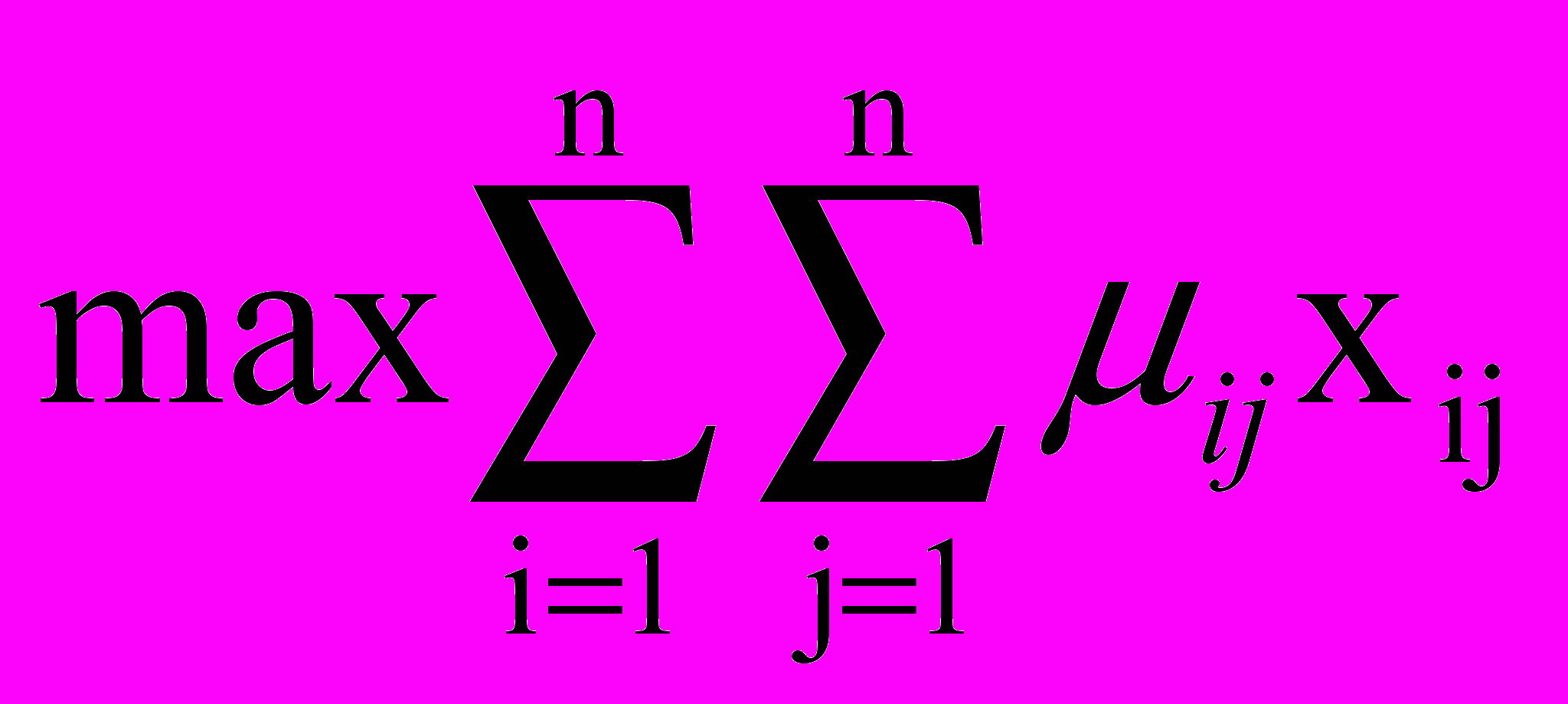
при ограничениях





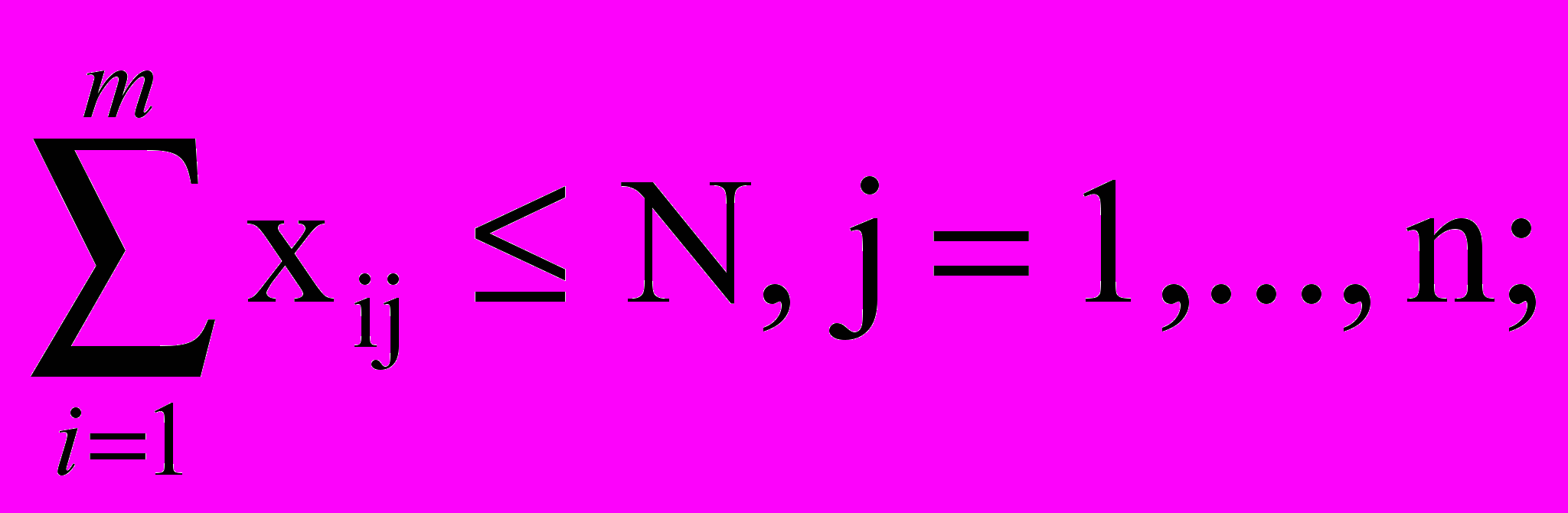
x_ij - целые неотрицательные числа для всех i, j, здесь m и n заданные числа видов заявок и приборов.

Пример 7 (Выбор оптимального вида посевной культуры). Фермер может посеять одну из трех культур: A₁, А₂ или А₃. Урожаи этих культур во многом зависят от погоды. Требуется установить, какую из этих культур сеять, чтобы обеспечить наибольший доход, если известны цена а_i одного центнера культуры A_i, i = 1,2,3, и средняя урожайность каждой культуры в зависимости от погоды (будет ли лето засушливым нормальным или дождливым). Достоверный прогноз погоды отсутствует.

Обозначим через h_ij - урожайность i-й культуры при погодных условиях j (здесь j=1 - обозначение засушливого лета, j=2 - нормального лета, j=3 – дождливого лета). Числа h_ij, как и числа a_i, заданы (известны). Реально может иметь место только одна из ситуаций (i,j), i = l, 2, 3; j = l, 2, 3. Причем (i,j) означает, что посеяна культура A_j, а погода находится в состоянии j. Всего таких ситуаций девять. JIПР (фермер) может выбрать только вид культуры, состояние погоды от него не зависит.

Если фермер засеял культуру A₁, то он может получить (в зависимости от состояния погоды) один из следующих доходов:

a₁h₁₁, a₁h₁₂, a₁h₁₃

соответственно для культуры A₂ :

a₂h₂₁, a₂h₂₂, a₂h₂₃

и для культуры А₃:

a₃h₃₁, a₃h₃₂, a₃h₃₃

Напишем все эти исходы в одну таблицу (матрицу):



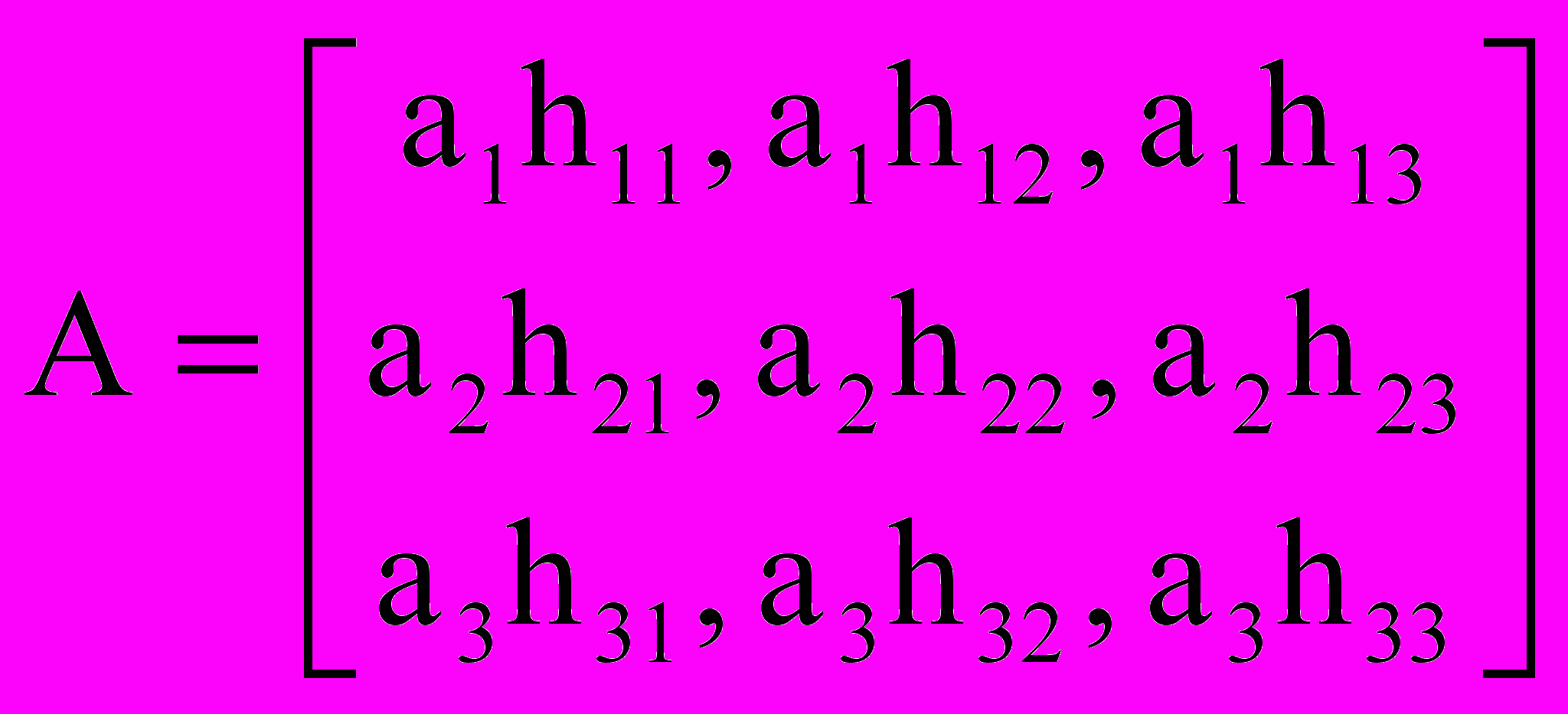
Эта матрица и есть математическая модель исходной задачи. В ней действие фермера сводится к выбору одной из строк матрицы (одной из трех стратегий). Его доход зависит от "выбора" природой одного из своих состояний (одного яд трех столбцов матрицы). Например, если фермер посеял культуру A₂, а лето получилось дождливым, то доход фермера равен a₂h₂₃.

Пример 8 (Выбор ассортимента товаров). На базе торговой организации имеется n типов одного из товаров ассортиментного минимума. В магазин должен быть завезен только один из типов данного товара. Требуется выбрать тот тип товара, который целесообразно завести в магазин. Если товар типа j будет пользоваться спросом, то магазин от его реализации получит прибыль p_j, если же он не будет пользоваться спросом - убыток q_j.

Составить математическую модель этой задачи в условиях неопределенного покупательского спроса.

Руководствуясь формализацией задачи примера 7, обоснуйте, что искомая модель имеет вид:



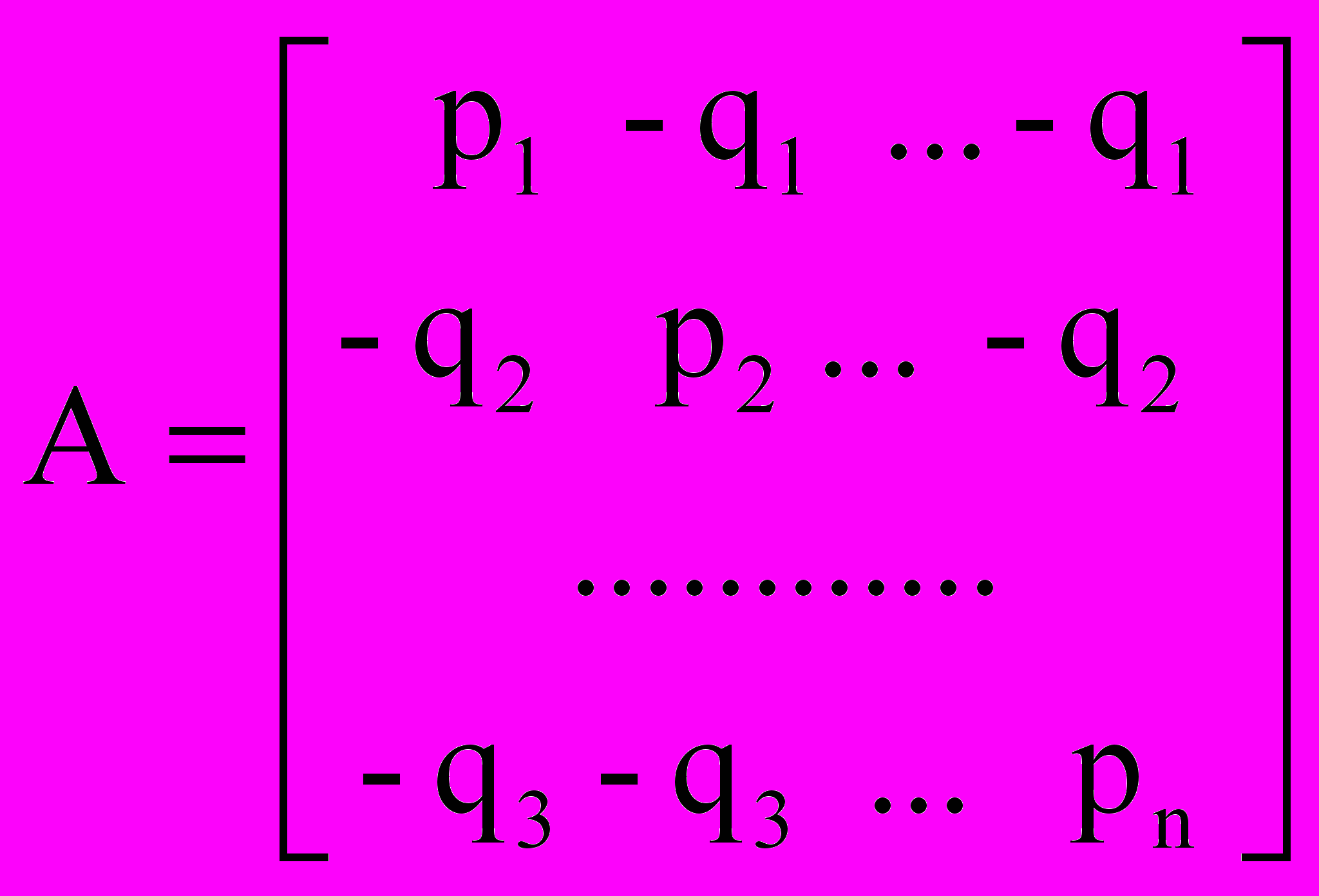
Объясните задачу магазина на этой модели.

Пример 9. (Планирование оптимального срока окончания проекта). Компания должна реализовать проект строительства объекта, состоящий из n операций (работ). Руководители комплекса оценили продолжительность выполнения каждой операции и установили последовательность операций, т.е. точно определили, какие операции обязательно должны быть закончены, чтобы могла начаться любая из операций, входящих в комплекс.

Руководству компании нужно выяснить, какова наименьшая возможная продолжительность реализации всего проекта, т.е. наиболее ранний из всех возможных сроков его завершения.

При составлении математической модели предположим (для простоты), что проект состоит из пяти операция А,В,С,Д,Е. По условию задачи известны последовательность операций и их продолжительность. Пусть эти данные для наших пяти операций таковы:

операции	непосредственно предшествующие операции	продолжительности операций
А	-	tA
В	-	tB
С	А	tC
D	А	tD
Е	B,D	tE
F	С,Е	-

Фиктивная операция F, начинающаяся в момент завершения проекта, вводится для удобства (см. ниже). Второй столбик таблицы означает, что операцию С нельзя начать, прежде чем незакончена операция А и т.д.

Примем, что переменными являются сроки начала операции (введем лишь те из них, которые нужны для решения задачи):

y_CD - момент начала операций С и Д;

y_E - момент начала операции Е;

y_F - момент начала операции F.

Здесь, y_F на самом деле есть момент завершения всего комплекса. Моменты y_A и y_B - это моменты 0 начала операций, т.к. операции А и В не имеют предшествующих. Модель имеет вид:

min y_F

при ограничениях

y_CD ≥ t_A

y_E ≥ t_B

y_E ≥ t_D + y_CD

y_F ≥ t_C + y_CD

y_F ≥ t_E + y_E


§ 4. Разделы и классы задач исследования операций.


Разделы и задачи исследования операций можно классифицировать, исходя из элементов общей структуры (1), подходя к их характеристикам с разных точек зрения. Поэтому одно только перечисление названий заняло бы несколько страниц. Мы определим здесь только наиболее крупные классы задач.

Начнем с характеристики среды (∑) принятия решения.

Если элементы модели (1) не зависят от времени, т.е. процесс принятия решения сводится к мгновенному акту выбора точки из заданного множества, то задача ИО называется статической. В противном случае, т.е. когда принятие решения представляет собой многоэтапный (дискретный) или непрерывный (во времени) процесс, задача ИО называется динамической. Примеры 1-4, 7 и 8 относятся к статическим, а примеры 5-6 и 9 - к динамическим задачам. Задачи ИО, не содержащие случайных величин и вероятностных явлений, называются детерминированными (см. примеры 1,2,4,5.9). Задачи со случайными факторами с вероятностной оценкой - стохастическими (пример 3,4,6), а задачи принятия решения в условиях неопределенности - конфликтными (примеры 7,8).

В зависимости от количества ЛПР в (1) различают задачи оптимизации (2) и игровые задачи (n ≥ 2, где n - число элементов во множестве N).

Игровая задача (или игра) - это математическая модель задачи принятия решения в условиях конфликта, т.е. в тех ситуациях, когда имеет место пересечение интересов двух или более сторон.

В зависимости от характера конфликта различают, антагонистические (примеры 7,8), неантагонистические (бескоалиционные) и кооперативные игры.

Если в задаче оптимизации все элементы линейны (целевая функция и ограничения), то получаем задачу линейного программирования (примеры 1,2), в противном случае - задачу нелинейного программирования (пример З и пример 4, если функции R_j, и K_j нелинейные). Если в задаче оптимизации присутствует фактор времени, то она называется задачей оптимального управления (пример 5). Иногда такие задачи называют задачами динамического программирования. Однако это неточное название, так как динамическое программирование - это название метода решения задач оптимального управления.

Часто у ЛПР имеется не одна , а несколько целей. Математическая модель

1,…,f_n;Σ> (5)

такой задачи называется задачей многокритериальной (или векторной) оптимизации. В модели (5) ЛПР выбирает решение х  Х так, чтобы получить как можно большие значения f₁(x),...,f_n(x) критериев.

Есть классы задач ИО, получивших свое название, исходя из их назначения: системы массового обслуживания (пример 6), задачи управления запасами (пример 3), задачи сетевого и календарного планирования (пример 9).

Перечисленные классы задач изучаются в разделах ИО с соответствующими названиями.

Для полноты восприятия ниже мы приведем те «классические» задачи ИО, которые, благодаря их типичности, встречаются во многих учебниках по математическому программированию. Некоторые из них относятся к начальному периоду возникновения теории оптимизации. Примеры служат для иллюстрации некоторых видов задач принятия решения и не претендуют на реалистичность в последней инстанции. Это «учебные задачи». Естественно, задачи и модели, представляющие непосредственный практический интерес, будут более подробными, глубокими и сложными. Учебные задачи - это первое приближение к реальным (практическим) задачам, их упрощенный аналог. Руководствуясь материалами предыдущих двух параграфов, читатель может самостоятельно получить математические модели этих задач в качестве упражнений.

Задача оптимального раскроя материала. Фирма изготовляет изделие, состоящее из р деталей (например комплект постельного белья). Причем в одно изделие эти детали входят в количествах k₁,…,k_r .С этой целью производится раскрой m партий материала. В i-й партии имеется b_i единиц материала. Каждую единицу материала можно раскроить на детали n способами. При раскрое единицы i-й партии j-м способом получается а_ijr деталей r-го вида.

Требуется составить такой план раскроя материалов, чтобы из них получить максимальное число изделий.

Транспортная задача. Имеется n поставщиков и m потребителей одного и того же продукта. Известны выпуск продукции у каждого поставщика и потребности в ней каждого потребителя, затраты на перевозки продукции от поставщиков к потребителям.

Построить план транспортных перевозок с минимальными транспортными расходами с учетом предложений поставщиков и спроса потребителей.

Задача о назначениях на работу. Имеется n работ и n исполнителей. Стоимость выполнения работы i исполнителем j равна c_ij. Нужно распределить исполнителей на работы так, чтобы минимизировать затраты (ФЗП).

Задача о смесях (о рационе). Из m видов исходных материалов, каждый из которых состоит из n компонент, составить смесь, в которой содержание компонент должно быть не меньше b₁,...,b_n. Известны цены единицы материалов: c₁...c_m и удельный вес j-гo компонента в единице i- гo материала.

Составить смесь, в которой затраты должны быть минимальны.

Задача о рюкзаке. Имеется n предметов. Вес предмета i равен p₁, ценность c₁ (i=l,…,n). Требуется при заданной ценности груза выбрать совокупность предметов минимального веса.

Задача о коммивояжере. Имеется n городов и задано расстояние c_ij между ними (i,j=l....,n). Выезжая из одного (исходного) города, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в исходный город.

Определить, в каком порядке следует объезжать города, чтобы суммарное пройденное расстояние было наименьшим.

Задача о станках. На универсальном станке обрабатываются одинаковые партии из n деталей. Переход от обработки детали i к обработке детали j требует переналадки станка, которая занимает c_ij времени.

Требуется определить последовательность обработки деталей, при которой общее время переналадок станка при обработке партии деталей минимально.

Задача о распределении капиталовложений. Имеется n проектов, причем для каждого проекта i известны ожидаемый эффект γ_j от его реализации и необходимая величина капиталовложений g_j. Общий объем капиталовложений не может превышать заданной величины b.

Требуется определить, какие проекты необходимо реализовать, чтобы суммарный эффект был наибольшим.

Задача о размещении производства. Планируется выпуск m видов продукции, которые могли бы производиться на n предприятиях (n>m). Издержки производства и сбыта единицы продукции, плановый объем годового производства продукции и плановая стоимость единицы продукции каждого вида известны.

Требуется из n предприятий выбрать такие m, каждое из которых будет производить один вид продукции.


§ 5. Основные требования к математическим моделям и их свойства.


Правильное построение математической модели исследуемой задачи - основное условие успешной разработки проекта. Неверно построенная модель может привести к ошибочным выводам или оказаться неэкономичной в эксплуатации. Правильно разработанная модель может существенно улучшить экономические результаты деятельности фирмы или эффективность функционирования организации. Разработка модели для анализа изучаемого вида деятельности требует творческого подхода. Кроме того, чтобы правильно понять сущность исследуемой проблемы, необходимо собрать и тщательно проанализировать большой объем данных. Практическое значение модель приобретает при условии, что ее изучение имеющимися средствами более доступно, чем изучение самого объекта. Из всего сказанного вытекают следующие требования к модели:

1) адекватность (соответствие модели своему оригиналу),

2) простота (незасоренность второстепенными факторами),

3) объективность (соответствие научных выводов реальным условиям),

4) чувствительность (способность модели реагировать изменению начальных параметров),

5) устойчивость (малому возмущению исходных параметров должно соответствовать малое изменение решения задачи (модели)).

6) универсальность (широта области применения).

В теории оптимизации в настоящее время разработано болбшое число моделей и методов решения различных классов задач (см. §4). Поэтому при составлении математической модели любой задачи возникают проблемы идентификации:

- можно ли использовать известную модель для формализации данной задачи?

- если нет, то в какой мере требуется переработка (подгонка) соответствующей модели ?

Идентификация модели и метода решения задачи показана на следующей схеме:


Идентификация модели


Подходит ли задача к моделям известных классов задач

Удается ли подгонка известной модели?

Составление новой модели

Выбор модели

Идентификация метода решения

Можно ли решить задачу с помощью известных методов?

Удается ли модифицировать известный метод

Разработка нового метода

Выбор метода

Решение задачи



Пример 10 (Задача размещения предприятий). С целью расширения сферы деятельности фирма планирует открыть несколько новых филиалов. Пункт i представляет собой одно и возможных точек размещения нового филиала с мощностью S_i, а постоянные затраты связанные с его эксплуатацией, равны F_i ≥ 0 (независимо от фактического объема выпуска). Существует всего m возможных пунктов (i=1,2,…,m) размещения, но открывать филиалы во всех этих пунктах нерационально. Для каждого пункта i изготовления и пункта j сбыта известны:

c_ij ≥ 0 - совокупные производственные и транспортные затраты, F_ij ≥ 0 -некоторые постоянные затраты (Пусть F_ij не зависит от объема перевозок x_ij > 0, но при x_ij=0 F_ij также равна нулю).

Требуется выбрать такие пункты размещения новых предприятий, чтобы суммарные затраты были минимальны.

Для построения математической модели этой задачи полезно ориентироваться на модель классической транспортной , задачи, сформулированной в §4 (исходя из схожести условий), которая имеет вид:

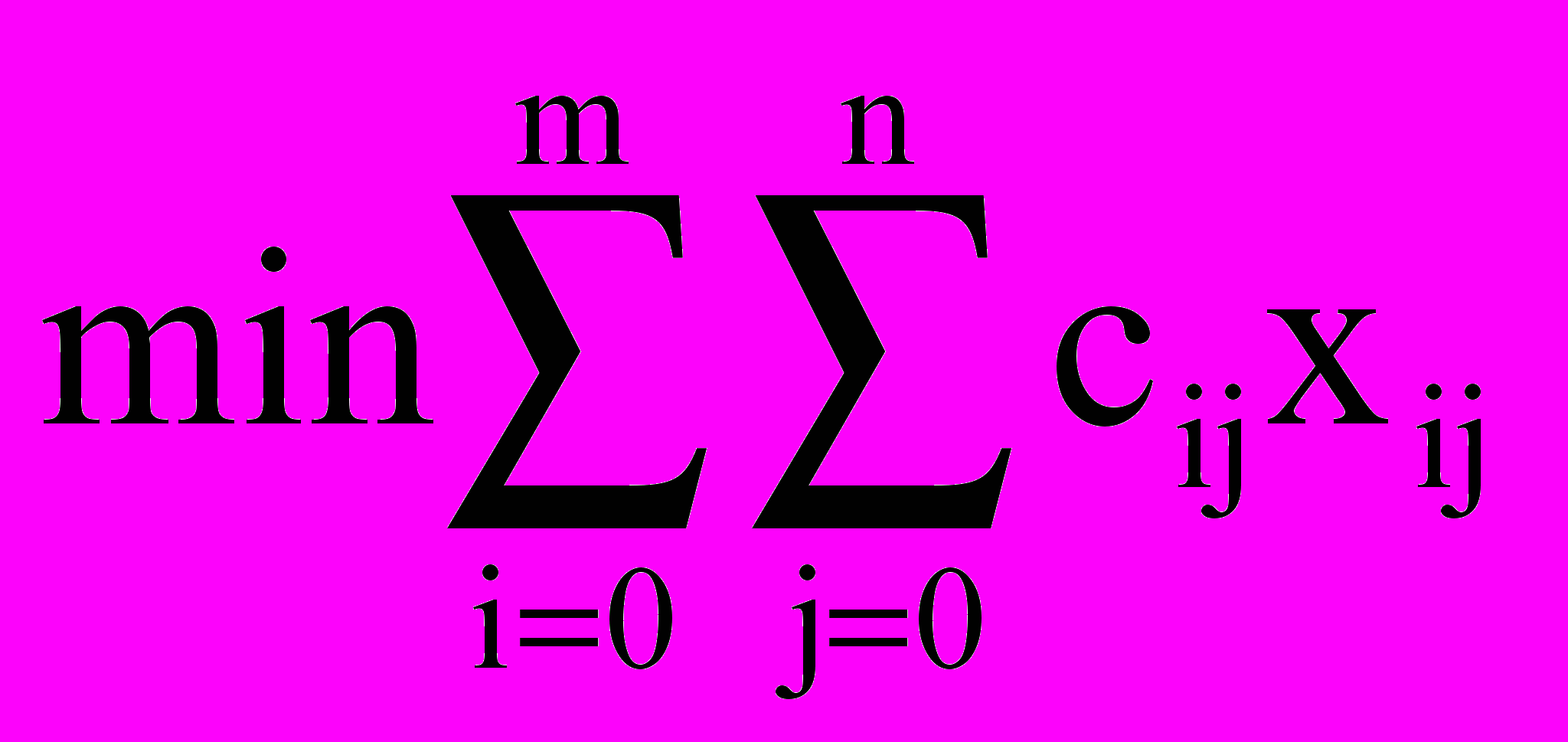(суммарные транспортные расходы) (5)

при ограничениях

(предложение) (6)

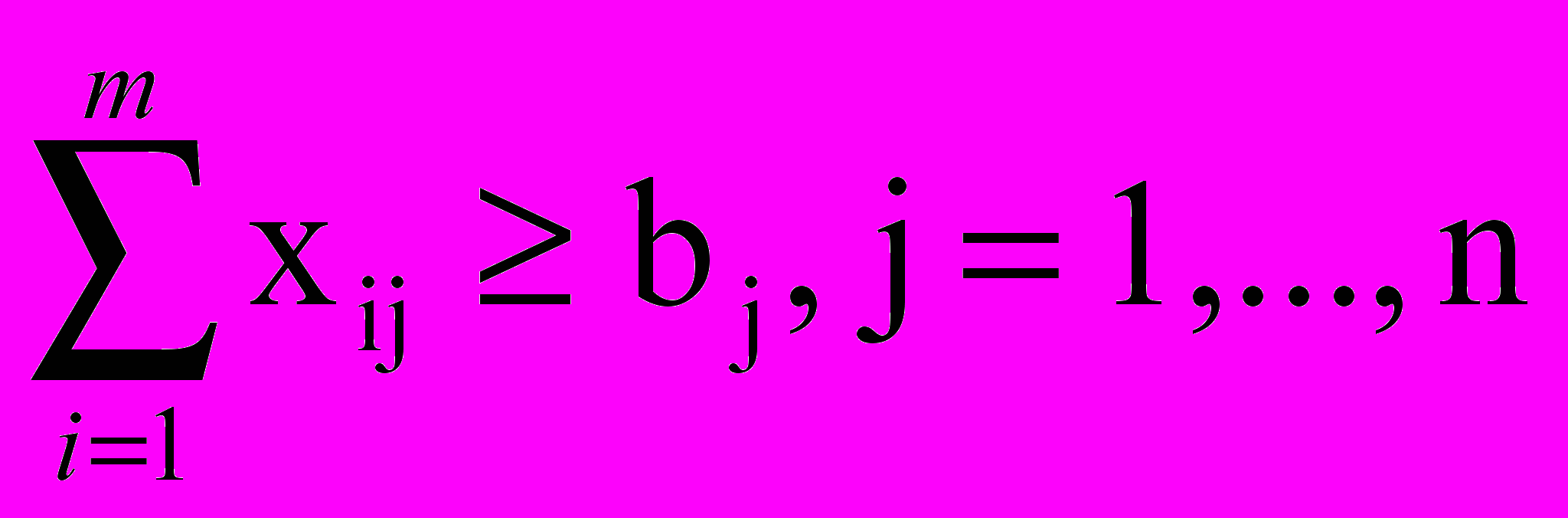(спрос) (7)

x_ij ≥ 0 (объем перевозок) (8)

В нашем примере введем обозначения:





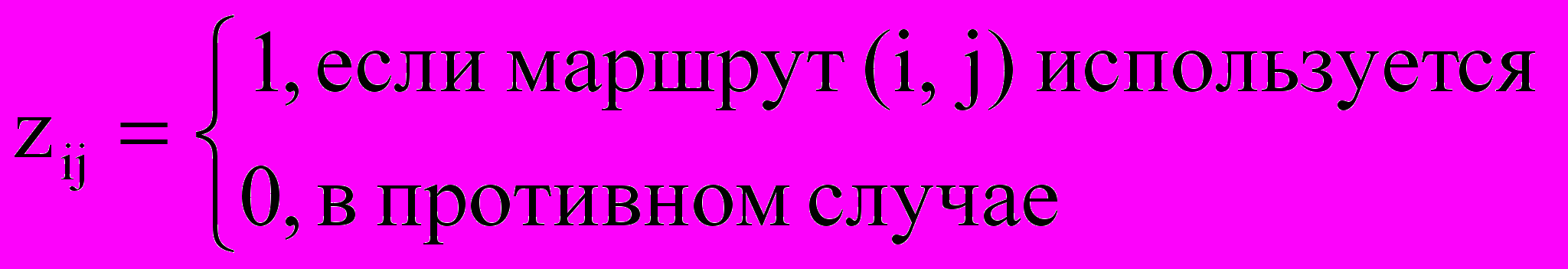
U_ij = min (а_i,b_j).

Тогда вместо целевой функции (5) получаем суммарные расходы в виде:

(9)

Вместо ограничения (6) на мощности поставщиков вводим ограничения на пропускные способности маршрутов:

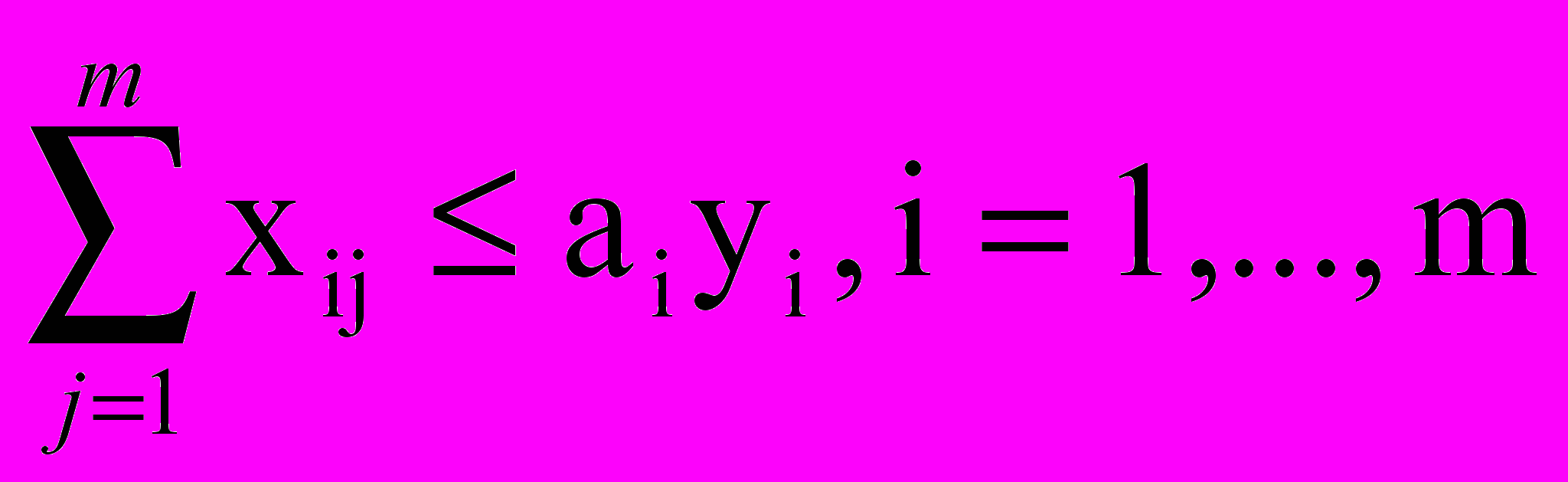(10)

Ограничение (7) по спросу потребителей остается без изменения:

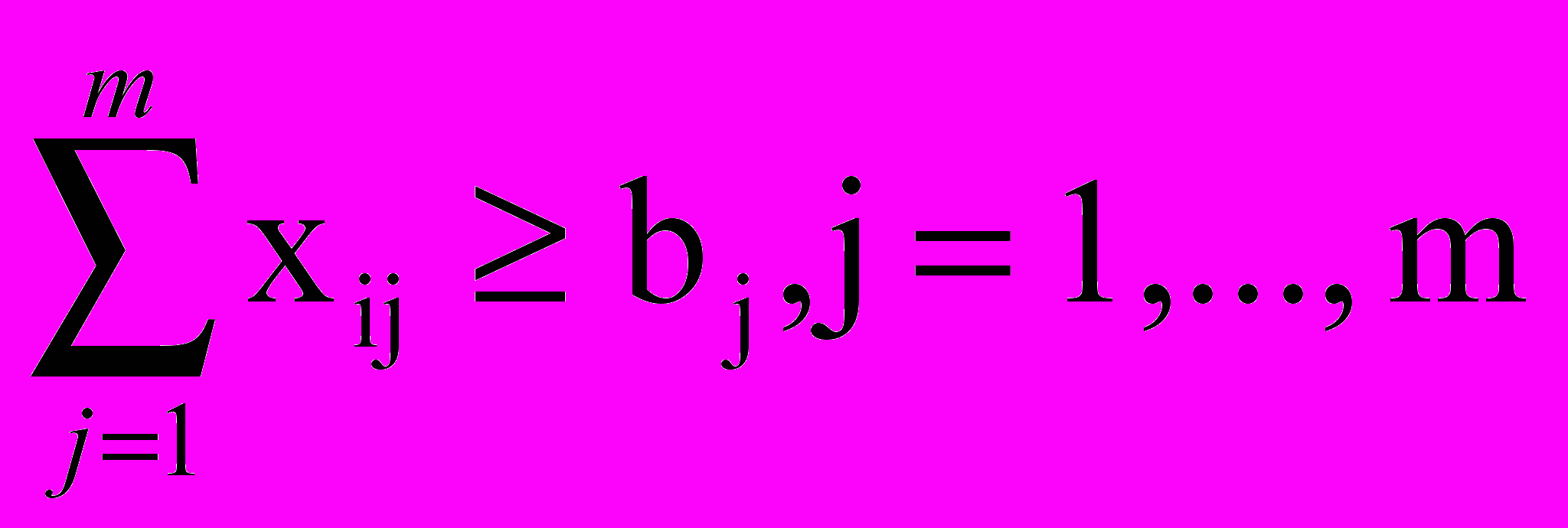(11)

Построение модели еще не закончено. Нужно добиться того, чтобы условие x_ij>0 выполнялось только в случае, когда z_ij = 1. Это достигается с помощью линейных ограничений:

x_ij ≤ U_ij z_ij при любых i,j= 1,...,m (12)

Кроме того,

х_ij ≥ 0, i,j = 1,...,m (13)

Теперь мы сможем сказать, что модель (9)-(13) задачи примера 10 получена в результате модификация модели (5) - (8) классической транспортной задачи.


§ 6. Формализация принципов оптимального поведения в моделях принятия решения.


Под принципом оптимальности понимается та совокупность правил, при помощи которых ЛПР определяет свое действие (решение, альтернативу, стратегию, управленческое решение), наилучшим образом способствующее достижению поставленной им цели. Принцип оптимальности выбирается исходя из учета конкретных условий принятия решения: количества участников, их возможностей и целей, характера столкновения интересов (антагонизм, неантагонизм, кооперация и т.п.).

В моделях принятия решения, особенно в теории игр, разработано большое число формальных принципов оптимального поведения. Мы здесь остановимся лишь на некоторых из них.

Принцип максимизации (минимизации). Такой принцип применяется, в основном, в задачах математического программирования (см. (2) - (4)).

Принцип свертки критериев. Применяется при "оптимизации"' многих критериев одним координирующим центром (задача многокритериальной оптимизации (5)). Для каждого из критериев (целевых функций)

f₁(u),...,f_n(u)

экспертным путем назначаются "веса" (числа)



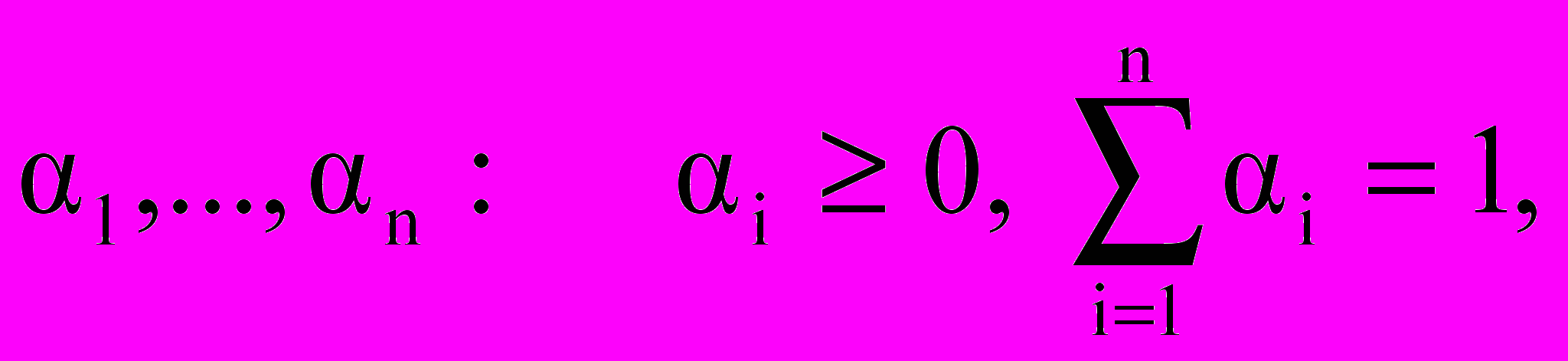
причем α_i показывает "важность или значимость" критерия f. Далее решение x* из множества допустимых решений Х выбирается так, чтобы максимизировать (или минимизировать) свертку критериев:



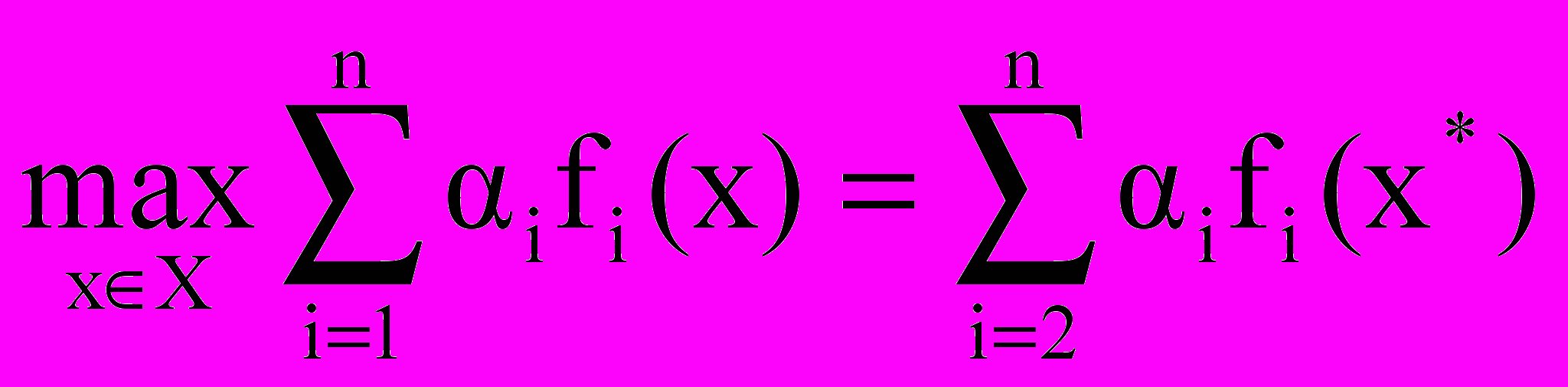
Принцип лексикографического предпочтения. Это еще один принцип оптимальности в задачах многокритериальной оптимизации. Сначала критерии ранжируются по "важности". Пусть такая ранжировка составлена:

f₁(x), f₂(x),...,f_n(x)

Решение х*Х "лучше" решения хХ в смысле лексикографического предпочтения, если выполнено одно из n+1 условий:

1. f₁(x*)>f₁(x);
   
2. f₁(x*)=f₁(x), f₂(x*)>f₂(x);
   
3. f₁(x*)=f₁(x), f₂(x*)=f₂(x), f₃(x*)>f₃(x);
   

………………

14. f_i(x*)=f_i(x) для i=1,…,n-1, f_n(x*)>f_n(x);
    

n+1) f_i(x*)=f_i(x) для i=1,…,n.

Принцип минимакса. Применяется при столкновении интересов двух противоборствующих сторон (антагонистический конфликт). Каждое ЛПР сначала для каждой своей стратегии (альтернативы) вычисляет "гарантированный" результат, затем окончательно выбирает ту стратегию, для которой этот результат наибольший по сравнению с другими его стратегиями. Такое действие не дает ЛПР "максимальный выигрыш", однако является единственным разумным принципом оптимальности в условиях антагонистического конфликта. В частности, исключен всякий риск.

Принцип равновесия. Это обобщение принципа минимакса, когда во взаимодействии участвуют много сторон, преследующих каждый свою цель (прямого противостояния нет). Пусть число ЛПР (участников неантагонистического конфликта) есть n. Набор выбранных стратегий (ситуация) x₁*, x₂*,…, x_n* называется равновесным, если одностороннее отклонение любого ЛПР от этой ситуации может привести разве лишь к уменьшению его же "выигрыша". В ситуации равновесия участники не получают «максимального» выигрыша, но они вынуждены придерживаться ее.

Принцип оптимальности по Парето. Данный принцип предполагает в качестве оптимальных те ситуации (наборы стратегий х₁,…,x_n), в которых улучшение «выигрыша» отдельного участника невозможно без ухудшения «выигрышей» остальных участников. Этот принцип предъявляет слабые требования к понятию оптимальности, чем принцип равновесия. Поэтому Парето-оптимальные ситуации существуют почти всегда.

Принцип недоминируемых исходов. Этот принцип является представителем многих принципов оптимальности в кооперативных играх (коллективное принятие решений) и приводит к понятию "ядра" решений. Все участники объединяются и совместными согласованными действиями максимизируют «общий выигрыш». Принцип недоминируемости - один из принципов ''справедливого'' дележа между участниками. Это та ситуация, когда ни один из участников не может аргументировано возразить против предлагаемого дележа (элемента "ядра"). Существуют и другие принципы «оптимального» дележа общего суммарного выигрыша.

Принципы устойчивости (угрозы и контругрозы). Идея всех принципов устойчивости на основе угроз и контругроз заключается в следующем. Каждая коалиция участников выдвигает свое предложение, сопровождая его реальной угрозой: если предложение не будет принято остальными участниками, то будут предприняты такие действия, которые ухудшают положение остальных участни­ков и не ухудшают (возможно улучшают) положение угрожающей коалиции. Оптимальным считается то решение, в условиях которого против всякой угрозы любой коалиции найдется контругроза со стороны какой-то коалиции.

Арбитражные схемы. Экономические конфликты наводят на мысль об "общественном арбитре". Нежелательно, чтобы столкновения интересов переходили, например, в открытые угрозы и контругрозы. Должны существовать социальные механизмы, которые позволяли бы учитывать предпочтения и стратегические возможности каждого участника и обеспечили бы "справедливое" решение конфликта. Такой предварительный механизм, будь то отдельное лицо или система голосования, называется арбитром. В теории игр оптимальное, в смысле арбитражной схемы, решение строится при помощи системы аксиом, включающих такие понятия, как статус-кво, оптимальность по Парето, линейность альтернатив, независимость от "рангов" и т.д.

Рассмотрим далее вопросы оптимального принятия решения в условиях неопределенности. Для выработки оптимального поведения ЛПР такую ситуацию полезно моделировать, как антагонистическую игру двух лиц, где в качестве противника ЛПР рассматривается природа. Последняя наделяется всеми мыслимыми в данных условиях возможностями.

В "играх с природой" существуют свои специфические (хотя и напоминающие принцип минимакса) принципы оптимального выбора решения.

Принцип крайнего пессимизма (критерий Вальда). Согласно этому принципу игра с природой (принятие решения в условиях неопределенности) ведется как игра с разумным, агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оптимальной считается стратегия ЛПР, при которой гарантируется выигрыш, не меньший, чем "разрешенный природой".

Принцип минимаксного риска (критерий Сэвиджа). Этот принцип также пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на "выигрыш", а на риск. Риск определяется как разность между максимальным выигрышем ЛПР (при условии полной информации о состоянии природы) и реальным выигрышем (при незнании состояния природы). В качестве оптимальной выбирается та стратегия, при которой величина риска минимальна.

Принцип пессимизма - оптимизма (критерии Гурвица). Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом («всегда рассчитывай на худшее!»), ни крайним оптимизмом ("авось кривая вывезет!"). Согласно этому критерию максимизируется взвешенное среднее между выигрышами крайнего пессимизма и крайнего оптимизма. Причем «вес» выбирается из субъективных соображений об опасности ситуаций.

Концепция динамической устойчивости. Все изложенные выше принципы оптимальности сформулированы относительно статических задач принятия решения. Попытка применения их в динамических задачах может сопровождаться всевозможными осложнениями.

Главное - это особенности динамических процессов. Нужно, чтобы тот или иной принцип оптимальности, выбранный в начальном состоянии процесса (в начальный момент времени), оставался оптимальным в любом текущем состоянии (в любой момент времени) до конца динамического процесса. Этот принцип называется динамической устойчивостью.