Geum.ru

Миклюшова Раиса Николаевна, учитель математики г. Горно-Алтайск 2008 год пояснительная записка

Вид материалаПояснительная записка

Содержание


Цель курса
Задачи курса
Ожидаемые результаты
Рациональные выражения
Ключевые понятия
Подобный материал:

Муниципальное образовательное учреждение

«Средняя общеобразовательная школа №8 г. Горно–Алтайска»


Решение

задач повышенной трудности


элективный курс

9 класс


Составила

Миклюшова Раиса Николаевна, учитель математики


г.Горно–Алтайск

2008 год


Пояснительная записка


Каждое занятие, а также все они в целом направлены на то, чтобы развить интерес школьников к предмету, познакомить их с новыми идеями и методами, расширить представление об изучаемом в основном курсе материале, а главное, порешать интересные задачи.

Этот курс предлагает учащимся знакомство с математикой как с общекультурной ценностью, выработкой понимания ими того, что математика является инструментом познания окружающего мира и самого себя.

Предлагаемый элективный курс своим содержанием сможет привлечь внимание обучающихся 9 классов, которым интересна математика. Данный элективный курс направлен на расширение знаний обучающихся, повышение уровня математической подготовки через решение большого класса задач. Наряду с основной задачей обучения математике — обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.


Цель курса:

углубить и расширить знания по алгебре за курс основной школы; создать в совокупности с основными разделами курса базу для развития способностей учащихся; помочь осознать степень своего интереса к предмету и оценить возможности овладения имb с точки зрения дальнейшей перспективы.

Задачи курса:

научить учащихся применять аппарат алгебры к решению сложных задач; помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их пользования; научить учащихся решать нестандартные задачи, которые относятся к более сложным в курсе алгебры, выполнять преобразования графиков на хорошем уровне, решать уравнения с параметрами.


Ожидаемые результаты

В объёме данного курса учащиеся должны научиться решать нестандартные задачи с параметрами, выполнять преобразования графиков функций вида 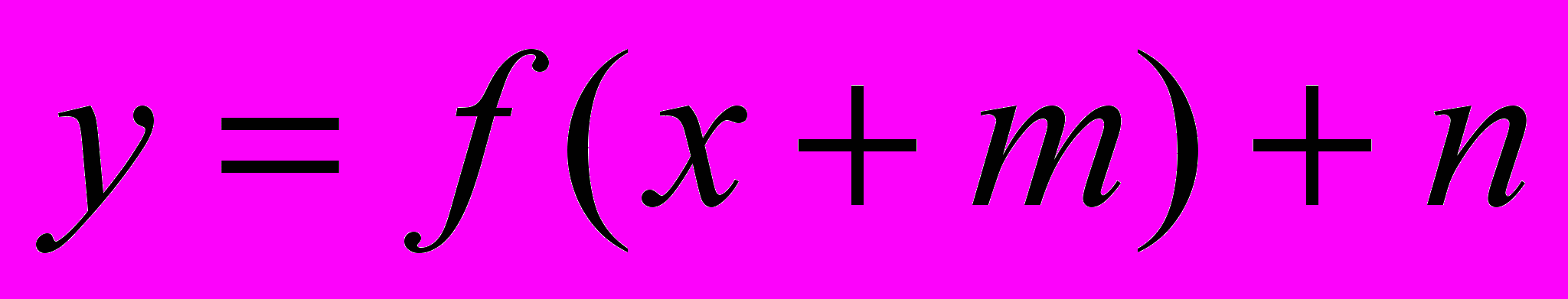, решать простейшие задачи с элементами комбинаторики и теории вероятности, решать уравнения содержащие переменную под знаком модуля, текстовые задачи.


Содержание программы

1.Рациональные выражения.

Учащиеся в этой части программы углубляют свои знания о рациональных выражениях, закрепляют основные способы преобразования выражений.


2. Рациональные неравенства и их системы

В этом разделе учащиеся вырабатывают навыки и умения решения более сложных неравенств и их систем.


3. Функции и их графики.

Учащиеся вырабатывают навыки чтения и построения графиков.


4. Уравнения с параметрами.

Учащиеся знакомятся с уравнениями с параметрами и основными способами их решения.


5. Элементы комбинаторики, статистики и теории вероятностей.

Этот раздел раскрывает начальные понятия, идеи и методы комбинаторики, теории вероятностей и статистики.


Изучение курса заканчивается зачётной работой в форме теста.


Тематическое планирование

№ п∕п
тема
Всего
Лекция
Практика
Форма контроля

I
Рациональные выражения
4
1
3



1
Преобразование целого выражения в многочлен






1



2
Разложение на множители






1



3
Преобразование дробных выражений



1
1
Самостоятельная работа

II
Рациональные неравенства и их системы
3
1
2



1
Линейные и квадратные неравенства



1






2
Рациональные неравенства






1



3
Решение задач. Системы неравенств






1
Самостоятельная работа

III
Функции и их графики
3
1
2



1
Функции. Способы задания функции



1






2
Простейшие преобразования графиков функций






1



3
Решение задач






1
Работа в группах

IV
Уравнения с параметрами
3
1
2



1
Линейные и квадратные уравнения спараметрами



1
1



2
Дробно-рациональные уравнения с параметрами






1



V
Элементы комбинаторик, статистики и теории вероятностей
3
1
2



1
Комбинаторные задачи



1
1



2
Простейшие вероятностные задачи






1



VI
Зачётное занятие






1
тест



Ключевые понятия

Выражение

Дробные выражения

Комбинаторика

Многочлен

Неравенства

Параметр

Рациональные неравенства

Системы уравнений

Статистика

Теория вероятностей

Уравнения с параметрами


Литература для учащихся: 1. А.Г.Мордкович. Учебник алгебры, 9 кл.

2. А.Г. Мордкович. Задачник, 9 кл.

3. Сборник заданий для подготовки к итоговой аттестации в 9 кл. Москва. Просвещение, 2008г.


Литература для учителя:

1. А.Г.Мордкович. Учебник алгебры, 9 кл.

2. А.Г. Мордкович. Задачник, 9 кл.

3. Сборник заданий для подготовки к итоговой аттестации в 9 кл. Москва. Просвещение, 2008г.

4. М.Е.Едеев, С.П.Соловьёв, Л.А.Соловьёва. Комбинаторика и начала теории вероятностей

5. А.Г.Мордкович, П.В.Семёнов. События. Вероятности. Статистическая обработка данных 7-9 классы