Деформационная точность механической обработки сложных криволинейных поверхностей изделий корабельного машиностроения кремлева Л. В., Худяков М. П

Вид материала

Документы

Содержание W>0, то элемент может резать. Если W

Подобный материал:

• «Технология машиностроения» Специализация «Дизелестроение», 37.35kb.
• Кафедра технологии машиностроения и методики профессионального обучения курсовой проект, 88.72kb.
• Кафедра технологии машиностроения и методики профессионального обучения курсовой проект, 81.68kb.
• Кафедра технологии машиностроения и методики профессионального обучения курсовой проект, 89.23kb.
• «Технология машиностроения», 442.34kb.
• Применение компьютерных технологий при изготовлении выплавлямых моделей рабочих колес, 30.82kb.
• 05. 02. 07 Технология и оборудование механической и физико-технической обработки, 24.16kb.
• А. И. Скворцов основы механической обработки заготовок, 1088.78kb.
• Программа-минимум кандидатского экзамена по специальности 05. 02. 07 «Технология, 256.06kb.
• Т. А. Дуюн моделирование тепловых деформаций с целью обеспечения точности механической, 116.36kb.

ДЕФОРМАЦИОННАЯ ТОЧНОСТЬ МЕХАНИЧЕСКОЙ ОБРАБОТКИ СЛОЖНЫХ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ ИЗДЕЛИЙ КОРАБЕЛЬНОГО МАШИНОСТРОЕНИЯ


Кремлева Л.В., Худяков М.П. (МГТУ "Станкин", Москва, РФ)


The methods and the some results of studying of deformation accuracy of machining of the high stressness large dimensional hull constructions are

stated in the given paper.


Существенная нестабильность резания, чувствительность технологической системы к изменению параметров в процессе рассматриваемой обработки приводит к тому, что получение требуемой точности связано главным образом с деформационной точностью и устойчивостью при обработке.

Предлагается методика расчета мгновенных усилий и деформаций при обработке многозубым инструментом произвольного профиля, позволяющая оптимизировать точностные характеристики процесса обработки и устойчивость технологической системы в условиях нестационарного резания.

Методика использует геометрическую модель формообразования и время как одну из обобщенных координат. При этом кинематическая цепь технологической системы замыкается силовой временной зависимостью, определяемой в целом через геометрический анализ мгновенных сечений срезаемого слоя. Модель дискретна, что позволяет, в частности, сохранить ее общность при изменениях условий контакта инструмента и изделия.

Дифференциальные уравнения, составляющие модель решаются численно, используется аппарат быстрого преобразования Фурье. В процессе решения могут быть получены как силовые, так и кинематические динамические образы процесса резания, что позволяет прогнозировать его деформационную точность. Соответствующие характеристики, взятые интегрально, дают усредненные значения сил и скоростей резания, используемые в технологических расчетах.


Порядок составления модели:

1. Определение геометрии i-й криволинейной режущей кромки в СКИ, — системе координат инструмента, — в матричном виде в однородных координатах:
   

r_i (u)=[f(u)cos((u+f(u)tg_ii_i)/(f(u)tg_i)); f(u)sin((u+f(u)tg_ii_i)/(f(u)tg_i)); u; 1]; (1)

где u — параметр высоты профиля: u[0, H], мм;

 — круговая частота вращения инструмента, с^-1;

f(u) — функция формы профиля.

2. Определение положения i-й режущей кромки в момент времени t в СКС — системе координат станка через покоординатные связи СКИ и СКС:
   

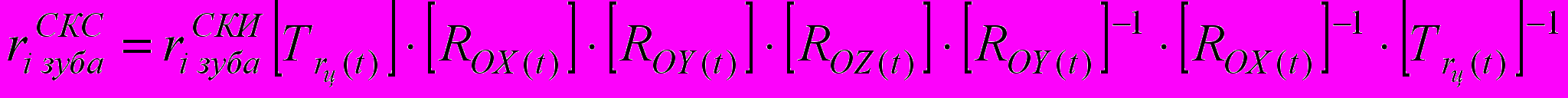; (2)

где 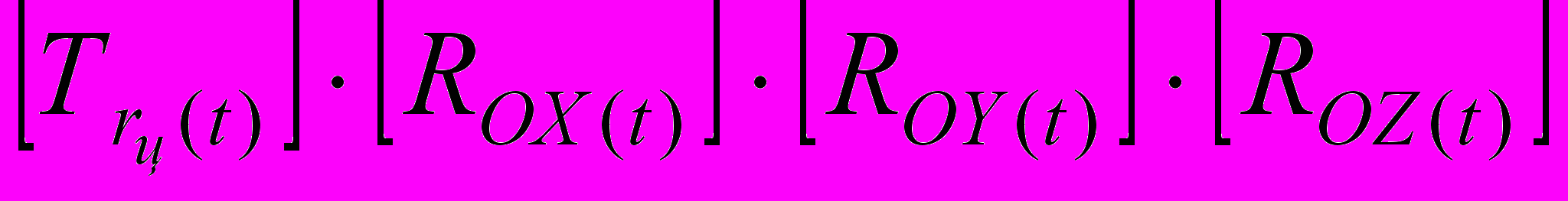=[A] — матрица связи СКС и СКИ;

3. Определение участков режущих кромок, участвующих в резании:
   

а) Разбиение режущей кромки на отдельные элементы равномерно вдоль оси вращения инструмента с шагом =H/n, где n — количество элементов.

б) В каждый момент времени t_i (от t₀=0 до t_{конечное}=L/S, L — длина траектории) определим положение элемента в пространстве в СКС по уравнению (2), т.е. координаты X, Y, Z для i-го из n элемента на N-ом зубе.

в) Мгновенное сечение срезаемого слоя на элементе с координатами (X, Y, Z):

,

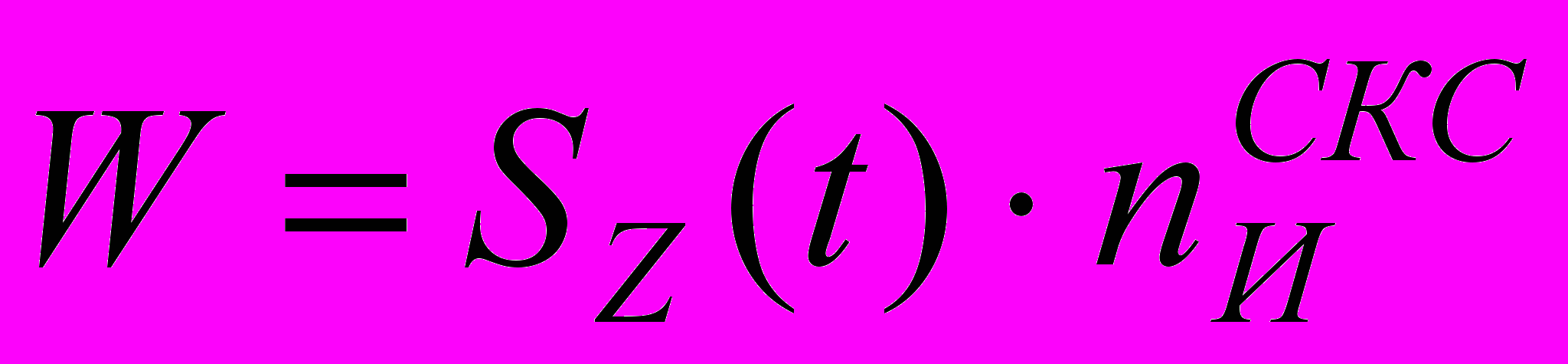где 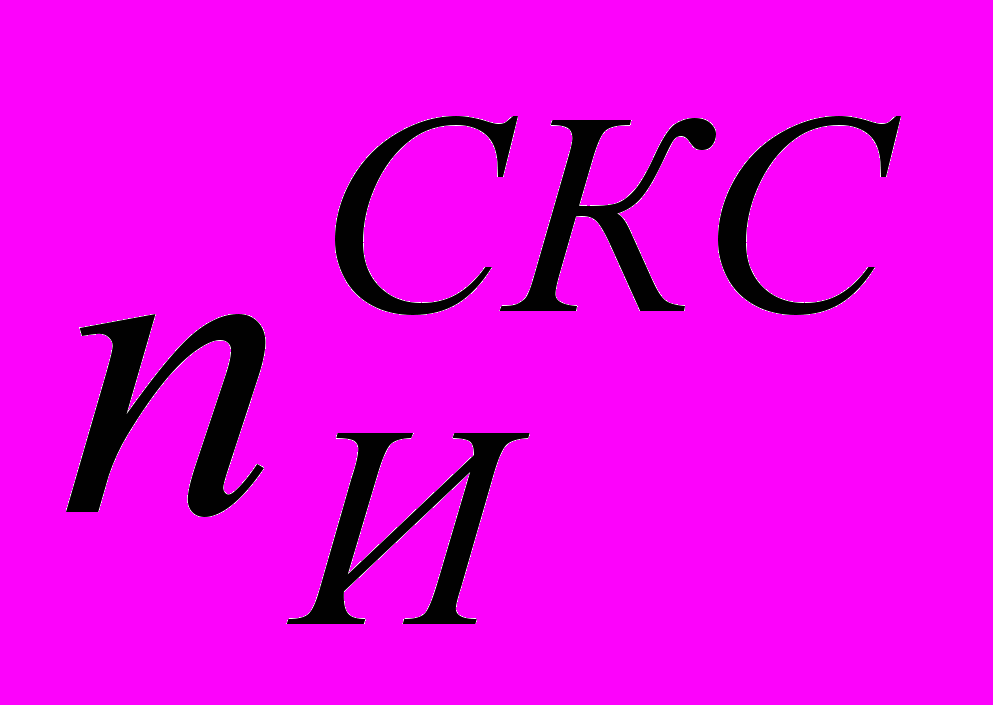— нормаль к образующей поверхности инструмента в точке с координатами (X, Y, Z) в СКС:

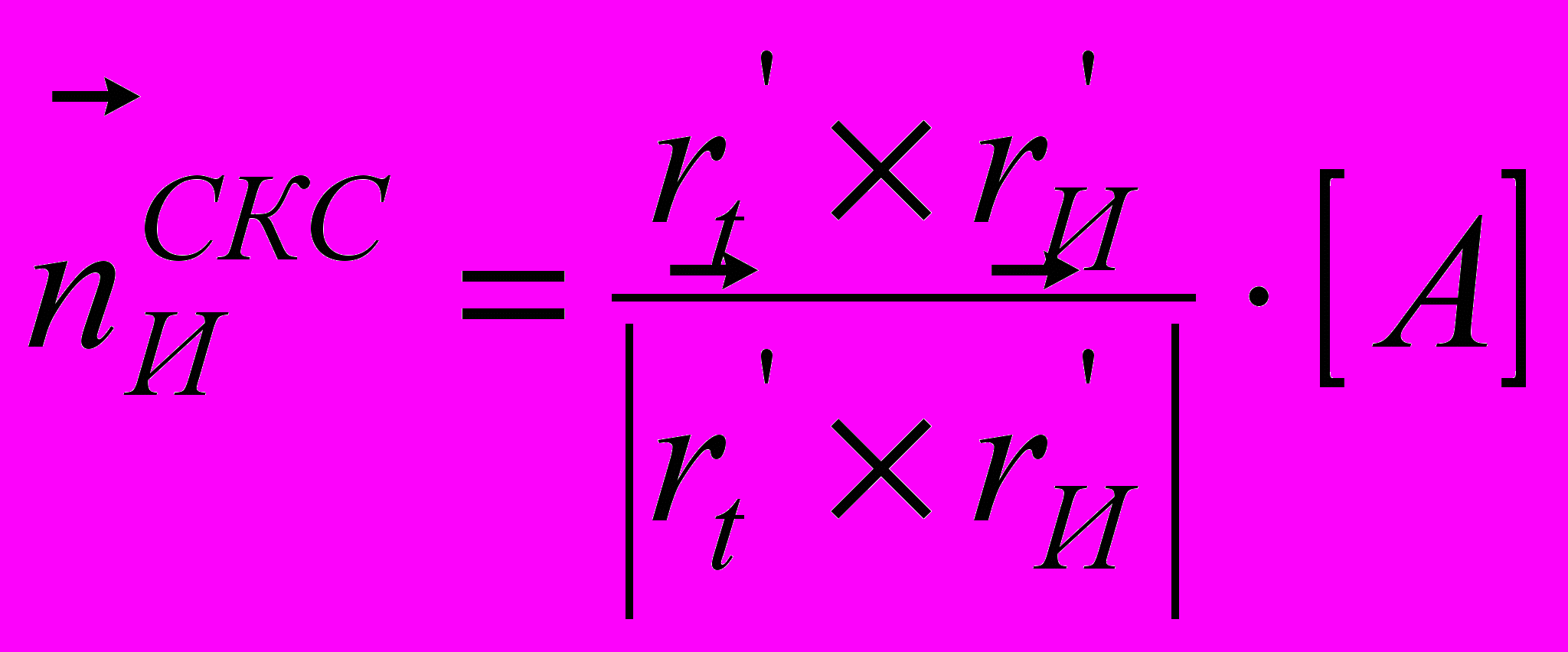; (3)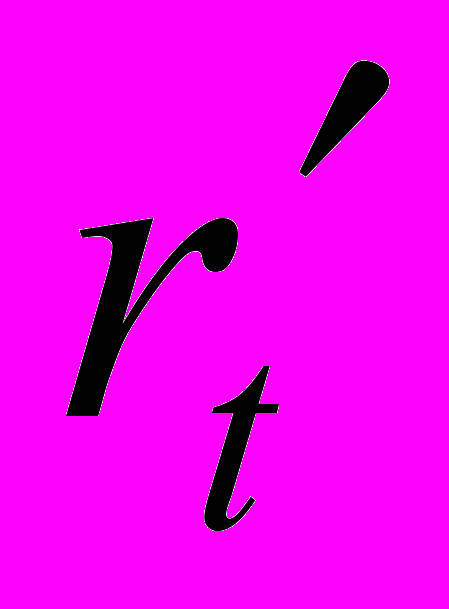

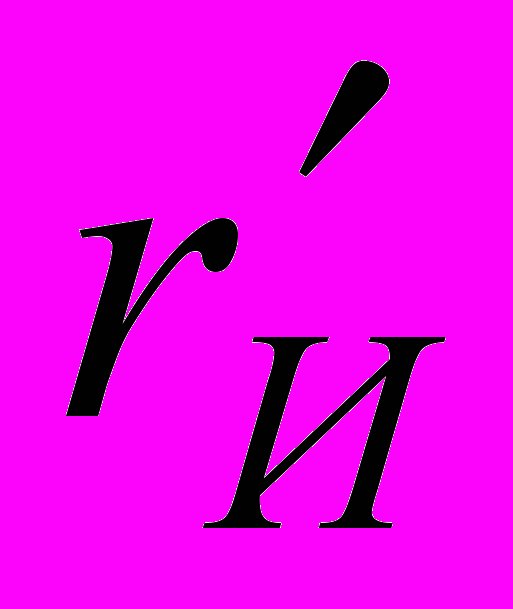; — касательные вдоль координатной линии образующей поверхности инструмента в СКИ;

Если W>0, то элемент может резать.

Если W0, то элемент не режет и элементарная толщина среза а_ЭЛ =0.

Если W>0, то проверяем положение режущего элемента по отношению к ориентированному объему заготовки (внутри-снаружи). Если при этом точка режущей кромки находится внутри заготовки, то элементарная толщина среза:

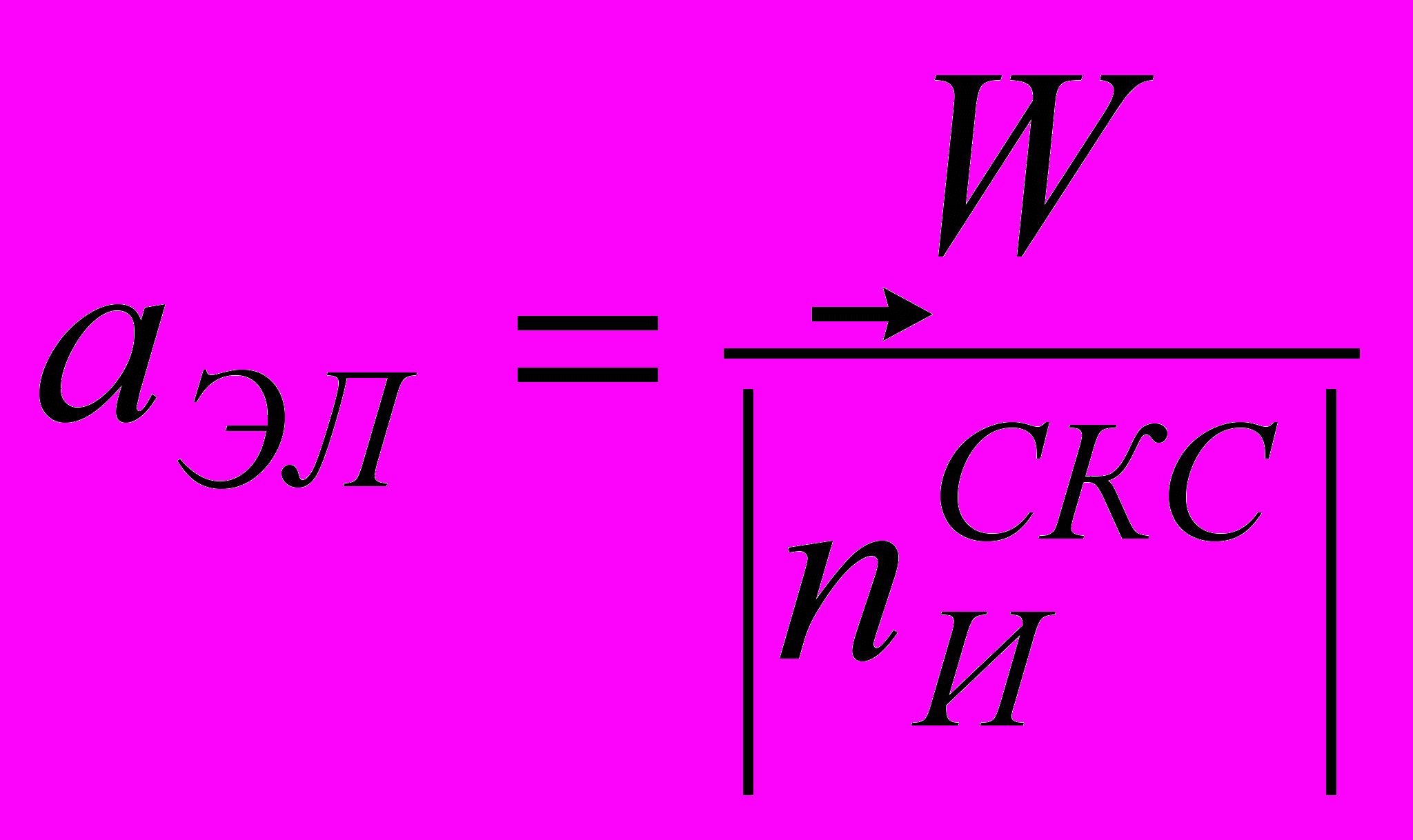; (4)

элементарные ширина среза в_ЭЛ=, площадь среза S_ЭЛ= а_ЭЛ  в_ЭЛ .

Если точка режущего элемента снаружи заготовки, то в_ЭЛ=0 и S_ЭЛ=0.

4. Определение суммарной нагрузки резания:
   

Для элементарных тангенциальной p_T*, радиальной p_R* и осевой p_A* составляющих силы резания, действующих на режущий элемент:

p_T* = p_удS_ЭЛ; p_R* = k_R p_T*; p_A* = k_A p_T* (5)

где p_уд – удельная сила резания; k_R ,k_A – коэффициенты.

При участии в резании u режущих элементов k зубьев суммируем:

p_T(t) =   p_T*u, k; p_R(t) =   p_R*u, k; p_A(t) =   p_A*u, k; (6)

Преобразуем далее (5) в частотную область посредством БПФ.

5. Определение деформаций и границ устойчивости ТС при резании:
   

представим динамическую модель ТС как эквивалентную, приведенную к зоне резания двухмассовую упругую систему, линейную относительно коэффициентов жесткости и демпфирования. Как показал анализ, подобное представление вполне адекватно для рассматриваемого случая обработки. Система является замкнутой, многоконтурность системы обусловлена участием в работе нескольких зубьев фрезы. Ограничивались низшими собственными частотами. Полученная система дифференциальных уравнений решалась численно методом Рунге-Кутта.

В качестве апробации разработанных моделей было проведено моделирование процесса фрезерования призматических заготовок с прямолинейной подачей, некоторые результаты которого приведены на рис. 1–3. Результаты стендовых испытаний показали хорошее соответствие полученных решений.

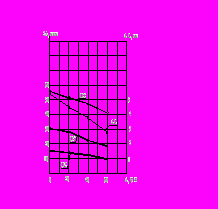Рис. 1. Влияние угла наклона режущей кромки  на размах колебаний инструмента и приращение длины траектории L за счет вибраций. Торцовое симметричное фрезерование: D=125 мм, z=8, шаг расположения зубьев - равномерный, угол в плане =900, величина биений на режущих кромках - 0, n=200 об/мин, ширина заготовки B=60 мм, припуск t=5 мм, Sz=0,1 мм/зуб. Обрабатываемый материал - сталь 20ХСНД

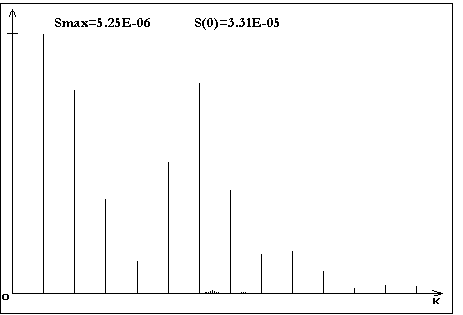
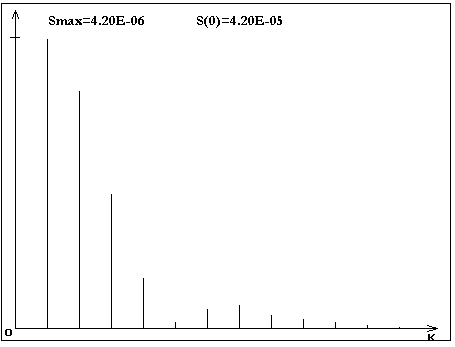
а) б)

Рис. 2. Расчетные спектры колебаний для различной величины угла наклона линии зуба . Условия расчета как на рис. 1: а) =0⁰, б) =30⁰

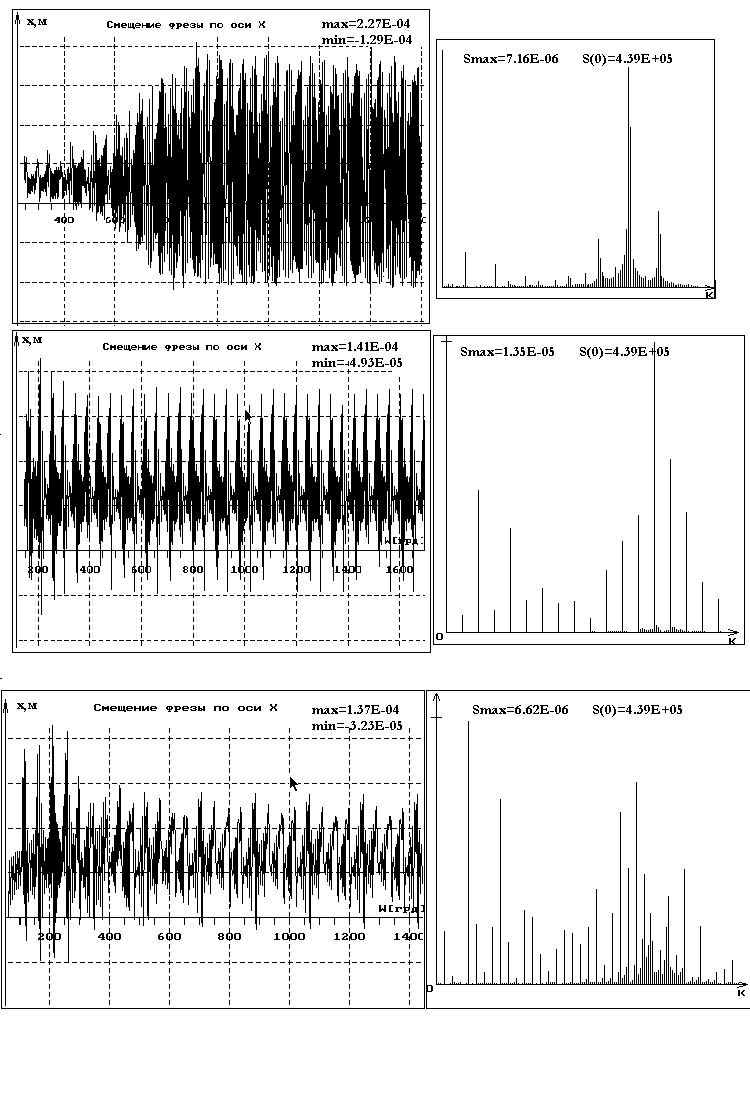Рис. 3. Расчетные колебательные процессы и амплитудные спектры для различных вариантов расположения зубьев по торцу окружности. Торцовое симметричное фрезерование. D=125 мм, z=8,  =80, =900, n=200 об/мин, B=60 мм, t=3 мм, Sz=0,1 мм/зуб. Обрабатываемый материал - сталь 20Х13: а) равномерный угловой шаг (неустойчивый процесс); б) переменный угловой шаг 4 (максимум устойчивости), в) переменный угловой шаг 3 (минимум деформаций)

Вывод:

Предложена математическая модель и методика расчета мгновенных усилий и деформаций при обработке многозубым инструментом произвольного профиля, позволяющая оптимизировать точностные характеристики процесса обработки и устойчивость технологической системы в условиях нестационарного резания за счет параметров инструмента и режимов резания.