Конкурс научных молодежных работ «Молодежь Белгородской области»
| Вид материала | Конкурс |
| 5. Разработка метода предварительных экспертных оценок глубины затопления в нижнем бьефе низконапорных гидроузлов в случае проры |
- Конкурс научных молодежных работ «Молодежь Белгородской области», 732.53kb.
- Конкурс научных молодежных работ «Молодежь Белгородской области», 674.28kb.
- Конкурс проводится с целью стимулирования интереса школьников к изучению истории родного, 50.93kb.
- Первый международный конкурс научных работ молодых ученых в области нанотехнологий, 29.76kb.
- Е. И. Хузин Положение о конкурсе среди молодежных объединений и организаций города, 76.85kb.
- Первый международный конкурс научных работ молодых ученых в области нанотехнологий, 47.1kb.
- Первый международный конкурс научных работ молодых ученых в области нанотехнологий, 45.14kb.
- На конкурс представляются следующие документы: На конкурс представляются следующие, 163.58kb.
- Открытый Конкурс работ проводится в научных областях: юриспруденция, политология, культурология,, 34.95kb.
- Конкурс научных работ аспирантов, соискателей, научных сотрудников "Экономический рост, 22.12kb.
5. Разработка метода предварительных экспертных оценок глубины затопления в нижнем бьефе низконапорных гидроузлов в случае прорыва их напорного фронта
Анализ результатов расчетов параметров волны прорыва, определенных с помощью различных методик расчета показал, что методика Историка обладает достаточной степенью достоверности и значительной простотой в использовании по сравнению с более точными численными методами с точки зрения ее использования для прогнозирования последствий прорыва многочисленных низконапорных гидроузлов.
В соответствии с [6] при определении размеров ущерба от аварий гидроузлов используются три основных параметра волны прорыва: максимальная глубина затопления (наносимая также на топографическую основу при: определении границ зоны затопления, площади земель, перечня населенных пунктов и объектов народного хозяйства, подвергшихся воздействию воды); максимальная скорость движения волны прорыва и продолжительность затопления. Далее, в соответствии со значениями найденных параметров, зона затопления разбивается на три зоны воздействия: сильного, среднего и слабого разрушения, в соответствии с которыми принимаются коэффициенты расчета.
Изучение прогнозируемых параметров волны прорыва, используемых при расчетах ущерба от наводнения в случае аварии ряда средне- и низконапорных гидроузлов позволило сделать вывод о том, что чаще всего основным параметром волны прорыва, определяющим значения коэффициентов зон воздействия является максимальная глубина затопления (hmax), так как:
а) максимальные скорости движения волны прорыва наблюдаются, в основном, в русле реки, а на пойме и выше, где и располагаются объекты народного хозяйства, их значения, в основном соответствуют средней и слабой зонам разрушения (в то время как значения глубин соответствуют сильной зоне разрушения);
б) продолжительность затопления земель должна достигать не менее 48 часов (даже для самых неустойчивых зданий и сооружений; для более устойчивых – до 240 часов), чтобы определить зону воздействия как сильную, что встречается крайне редко при расчете параметров волны прорыва низконапорных гидроузлов в случае отсутствия подпора со стороны расположенных в нижнем бьефе ГТС (область применения методики Историка).
Несмотря на то, что упрощенная графоаналитическая методика Историка, является достаточно недорогой и доступной в использовании, работа с безразмерными графиками и определение осредненного поперечного сечения рассматриваемого створа является сравнительно сложным и трудоемким процессом. Поэтому в работе была поставлена задача, взяв за основу методику Историка, разработать методику предварительных экспертных оценок глубины затопления в нижнем бьефе низконапорных гидроузлов в случае прорыва их напорного фронта, путем использования основных принципов метода планирования эксперимента [7].
В процессе предварительных расчетных исследований установлено, что наиболее существенно на значения hmax влияют следующие параметры гидроузла и условия распространения волны прорыва в нижнем бьефе: объем водохранилища до начала аварии (Wвод), длина водохранилища до начала аварии (Lвод), глубина водохранилища у плотины до начала аварии (Н0), шероховатость русла верхнего бьефа (n0), величина раскрытия прорана (Впр), расход воды в нижнем бьефе гидроузла до начала аварии (Q0), расстояние от створа плотины до створа наблюдения (х). Предложены некоторые приближенные зависимости максимальной глубины затопления от основных параметров гидроузла и условий распространения волны прорыва в нижнем бьефе. Эти зависимости имеют вид: hmax = f1(Wвод); hmax = f2(Lвод); hmax = f3(H0); hmax = f4(n0); hmax = f5(Bпр); hmax = f6(Q0); hmax = f7(x).
Каждая из зависимостей, являясь функцией одной переменной, получена при определенных условиях распространения волны прорыва и фиксации на принятых уровнях всех влияющих факторов, кроме одного. При других значениях влияющих факторов эти зависимости получаются иными.
Приняты следующие допущения:
1. Не рассматривалась зависимость глубины затопления от величины раскрытия прорана (расчеты проводились с некоторым запасом – при условии максимально возможного разрушения плотины).
2. Анализ результатов инвентаризации низконапорных гидроузлов Московской области показал, что длина водохранилищ таких объектов колеблется в интервале примерно от 0,8 до 2 км (что справедливо и для других низконапорных гидроузлов, расположенных в различных регионах Российской Федерации). Варьирование длины водохранилища в данной области не повлияет существенным образом на результаты расчетов глубины затопления в нижнем бьефе, в связи с чем, для всех расчетных случаев было принято Lвод ≈ 1,5 км.
3. Расчеты проводились в предположении, что в нижнем бьефе гидроузлов отсутствует подпор от нижележащих водохранилищ (в соответствии с областью применения графоаналитической методики Историка Б. Л.).
Таким образом, зависимость максимальной глубины затопления от основных влияющих факторов можно представить в общей форме выражением:
hmax = f1(Wвод, H0, n0, Q0, x) (9);
Предположим, что зависимость (9) можно с достаточной точностью аппроксимировать уравнением регрессии степенного вида:
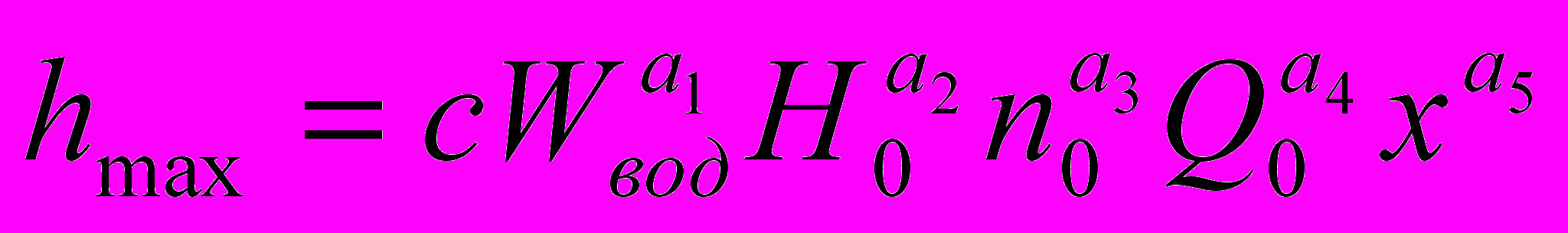 (10);
(10); После логарифмирования уравнение (10) линеаризуется:
lghmax = lgc + a1lgWвод + a2lgН0 + a3lgno + a4lgQo + a5lgx (11).
Возможность аппроксимации зависимости (9), уравнением вида (11) устанавливается проверкой гипотезы адекватности линейной модели при выражении результата эксперимента полиномом [7]:
y = b0 + b1x1 + b2x2 + b3x3 + b4x4 + b5x5+ b12x1 x2+b13x1 x3 + b14x1 x4+
+ b15x1 x5+ b23x2 x3+ b24x2 x4+ b25x2 x5+ b34x3 x4 + b35x3 x5+ b45x4 x5 (12)
где y – это lghmax; x1,…, x5 – кодированные значения факторов.
Для оценки коэффициентов полинома, используя полуреплику от полного факторного эксперимента 25, рассмотрено 16 расчетных случаев. Принятые уровни факторов приведены в табл. 7.
Кодированные значения факторов определялись по выражению:
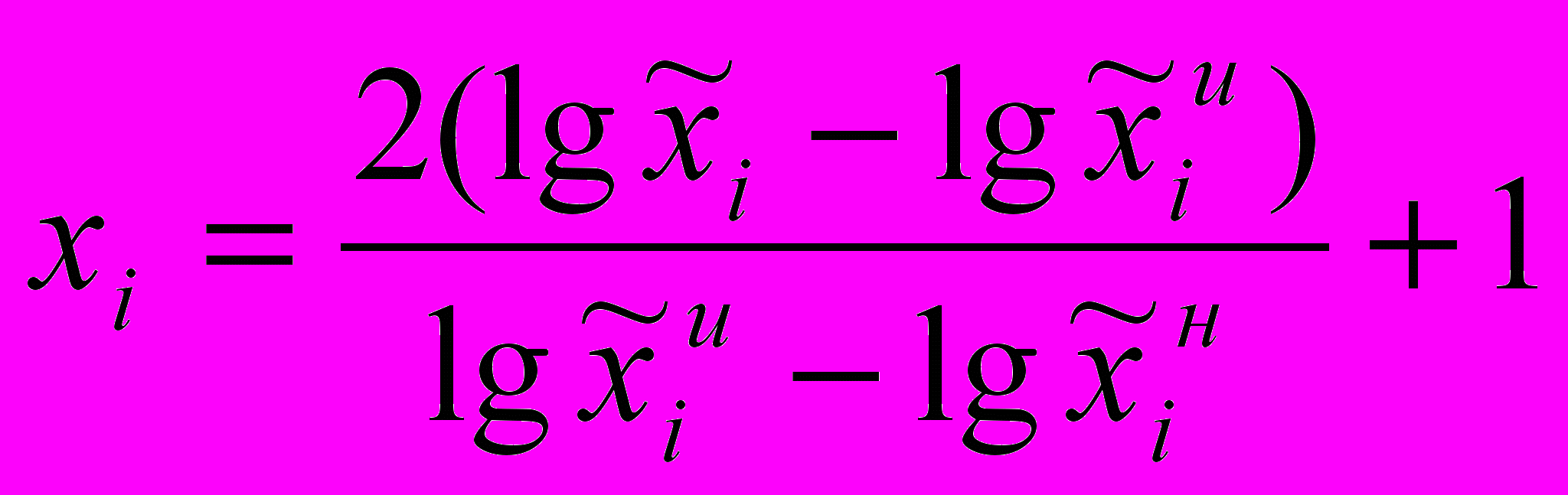 , (13)
, (13)где xi – кодированное значение i – го фактора;
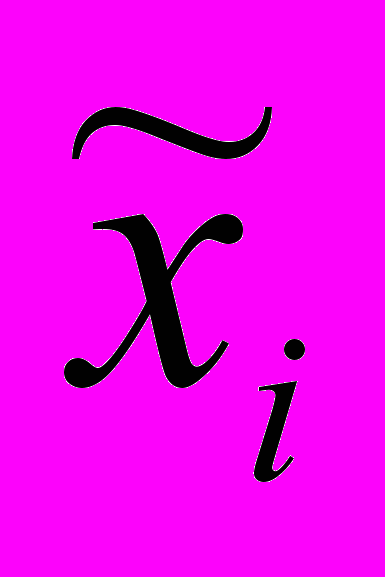 - натуральное значение i – го фактора;
- натуральное значение i – го фактора; 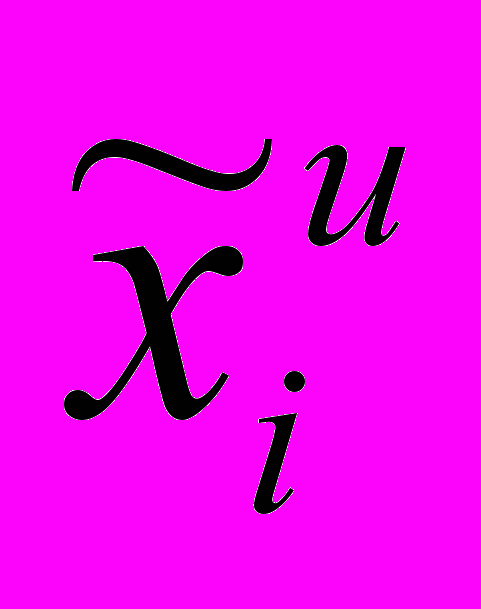 - натуральное значение верхнего уровня i – го фактора;
- натуральное значение верхнего уровня i – го фактора; 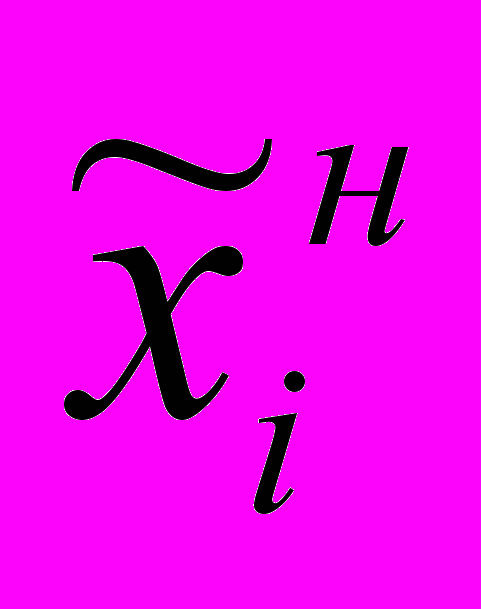 - натуральное значение нижнего уровня i – го фактора.
- натуральное значение нижнего уровня i – го фактора.Выполнено исследование, заключающееся в поиске значений глубин затоплений в нижнем бьефе при различном сочетании влияющих факторов. Условия выполнения каждого из 16 предусмотренных планом расчетных случаев определялись матрицей планирования (табл. 8).
Таблица 7
Факторы и их уровни
| Факторы | Кодовое обозначение факторов | Уровни факторов | ||
| Верхний +1 | Основной 0 | Нижний -1 | ||
| Wвод, м3 | x1 | 5000000 | 2525000 | 50000 |
| H0, м | х2 | 20 | 10,5 | 1 |
| Q0, м3/с | х3 | 100 | 50,5 | 1 |
| n0 | х4 | 0,2 | 0,11 | 0,02 |
| х, м | x5 | 50000 | 25250 | 500 |
После математической обработки экспериментальных данных получено уравнения регрессии для yhmax, имеющее вид:
yhmax = 5,03 – 0,32x1 + 4,07x2 + 0,32x3 +0,051x4 – 1,4x5 - 0,23x1 x2 –
- 0,12x1 x3 + 0,31x1 x4 - 0,4x1 x5 + 0,23x2 x3+ 0,001x2 x4 – 1,14x2 x5 – 0,31x3 x4 +
+ 0,4x3 x5 – 0,1x4 x5 (14)
Таблица 8
Матрица планирования
| Номер опыта | xo | х1 | х2 | х3 | х4 | х5 | х1 x2 | х1 x3 | х1 x4 | х1 x5 | х2 x3 | х2 x4 | х2 x5 | х3х4 | х3х5 | х4х5 | yhmax |
| 1 | + | - | - | - | - | + | + | + | + | - | + | + | - | + | - | - | 0,63 |
| 2 | + | + | - | - | - | - | - | - | - | - | + | + | + | + | + | + | 1,17 |
| 3 | + | - | + | - | - | - | - | + | + | + | - | - | - | + | + | + | 11,36 |
| 4 | + | + | + | - | - | + | + | - | - | + | - | - | + | + | - | - | 4,22 |
| 5 | + | - | - | + | - | - | + | - | + | + | - | + | + | - | - | + | 1,17 |
| 6 | + | + | - | + | - | + | - | + | - | + | - | + | - | - | + | - | 0,63 |
| 7 | + | - | + | + | - | + | - | - | + | - | + | - | + | - | + | - | 9,22 |
| 8 | + | + | + | + | - | - | + | + | - | - | + | - | - | - | - | + | 11,36 |
| 9 | + | - | - | - | + | - | + | + | - | + | + | - | + | - | + | - | 1,26 |
| 10 | + | + | - | - | + | + | - | - | + | + | + | - | - | - | - | + | 0,40 |
| 11 | + | - | + | - | + | + | - | + | - | - | - | + | + | - | - | + | 6,40 |
| 12 | + | + | + | - | + | - | + | - | + | - | - | + | - | - | + | - | 12,23 |
| 13 | + | - | - | + | + | + | + | - | - | - | - | - | - | + | + | + | 1,13 |
| 14 | + | + | - | + | + | - | - | + | + | - | - | - | + | + | - | - | 1,26 |
| 15 | + | - | + | + | + | - | - | - | - | + | + | + | - | + | - | - | 11,60 |
| 16 | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | 6,40 |
Проверка значимости коэффициентов полинома произведена при помощи t-критерия Стьюдента по зависимости:
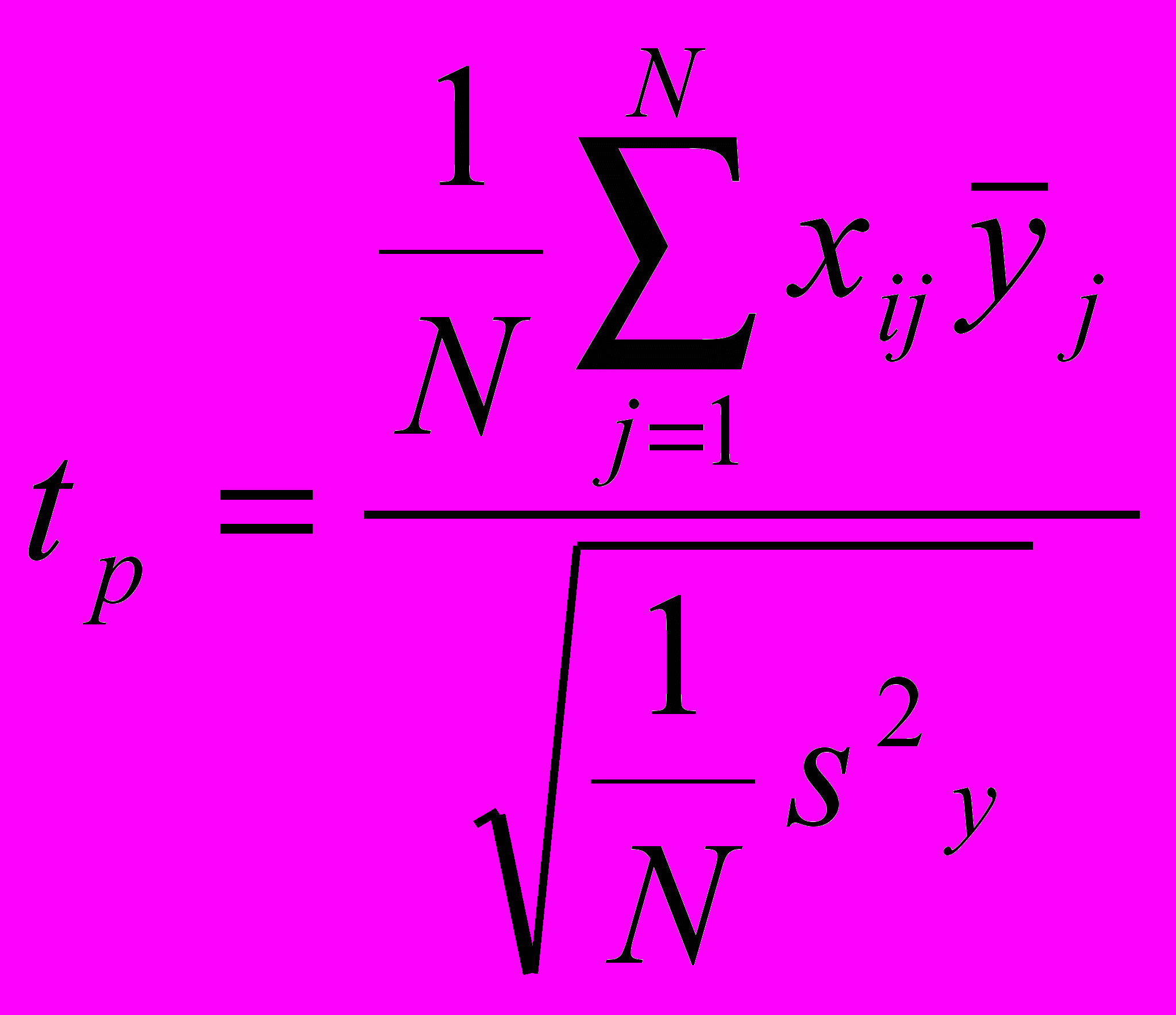 >
> 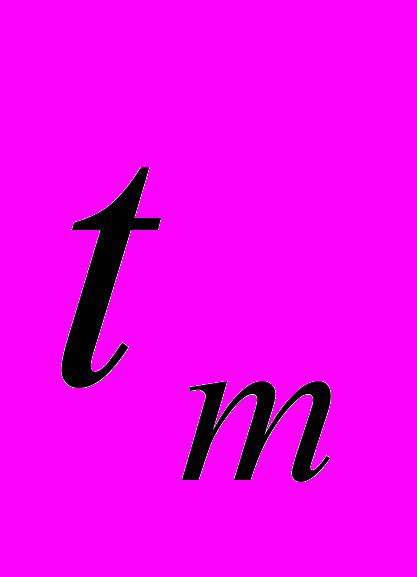 , (15)
, (15)где tm – табличное значение t-критерия Стьюдента [7];
N – число опытов (16);
хij – кодированные значения фактов (i – номера факторов; j – номера опытов);
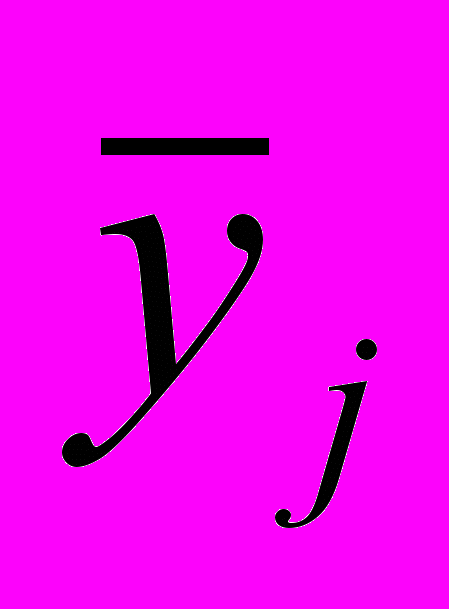 - среднее арифметическое значение параметра оптимизации;
- среднее арифметическое значение параметра оптимизации;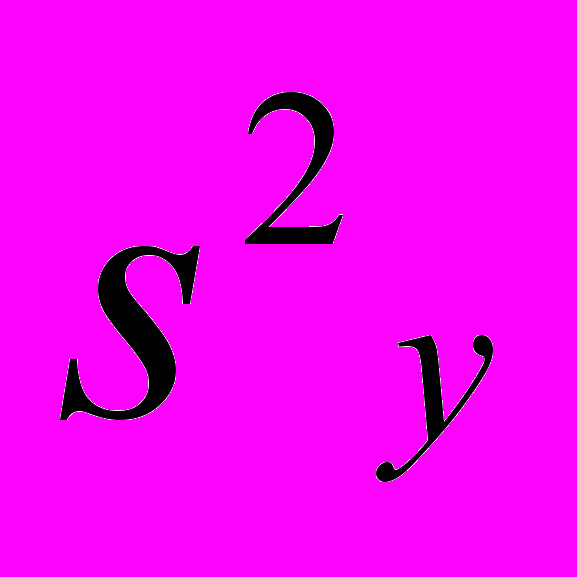 - дисперсия коэффициентов регрессии.
- дисперсия коэффициентов регрессии.В том случае, когда условие (15) выполняется, коэффициенты регрессии значимы; в противном случае – не значимы. В табл. 9 приведены расчетные и табличные значения t-критерия Стьюдента.
Таблица 9
t-критерии Стьюдента
| Коэффициент | 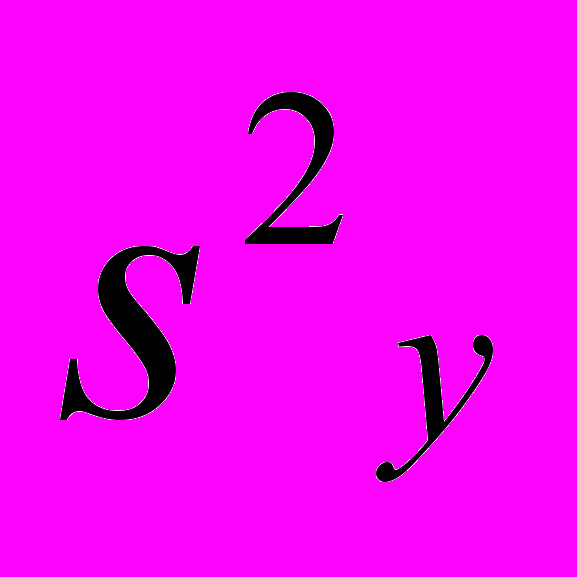 | b | tp | tm [7] |
| х4х5 | 47,58 | 0,100 | 0,0140 | 2,12 |
| х3х5 | 47,43 | 0,400 | 0,0580 | 2,12 |
| х3х4 | 46,88 | 0,310 | 0,0450 | 2,12 |
| х2х5 | 46,29 | 1,140 | 0,1670 | 2,12 |
| х2х4 | 47,59 | 0,001 | 0,0001 | 2,12 |
| х2х3 | 47,54 | 0,230 | 0,0333 | 2,12 |
| х1х5 | 47,43 | 0,400 | 0,0581 | 2,12 |
| х1х4 | 47,49 | 0,310 | 0,0450 | 2,12 |
| х1х3 | 47,58 | 0,120 | 0,0173 | 2,12 |
| х1х2 | 47,54 | 0,230 | 0,0334 | 2,12 |
Осуществлен переход от кодированных значений факторов к натуральным с помощью зависимостей вида:
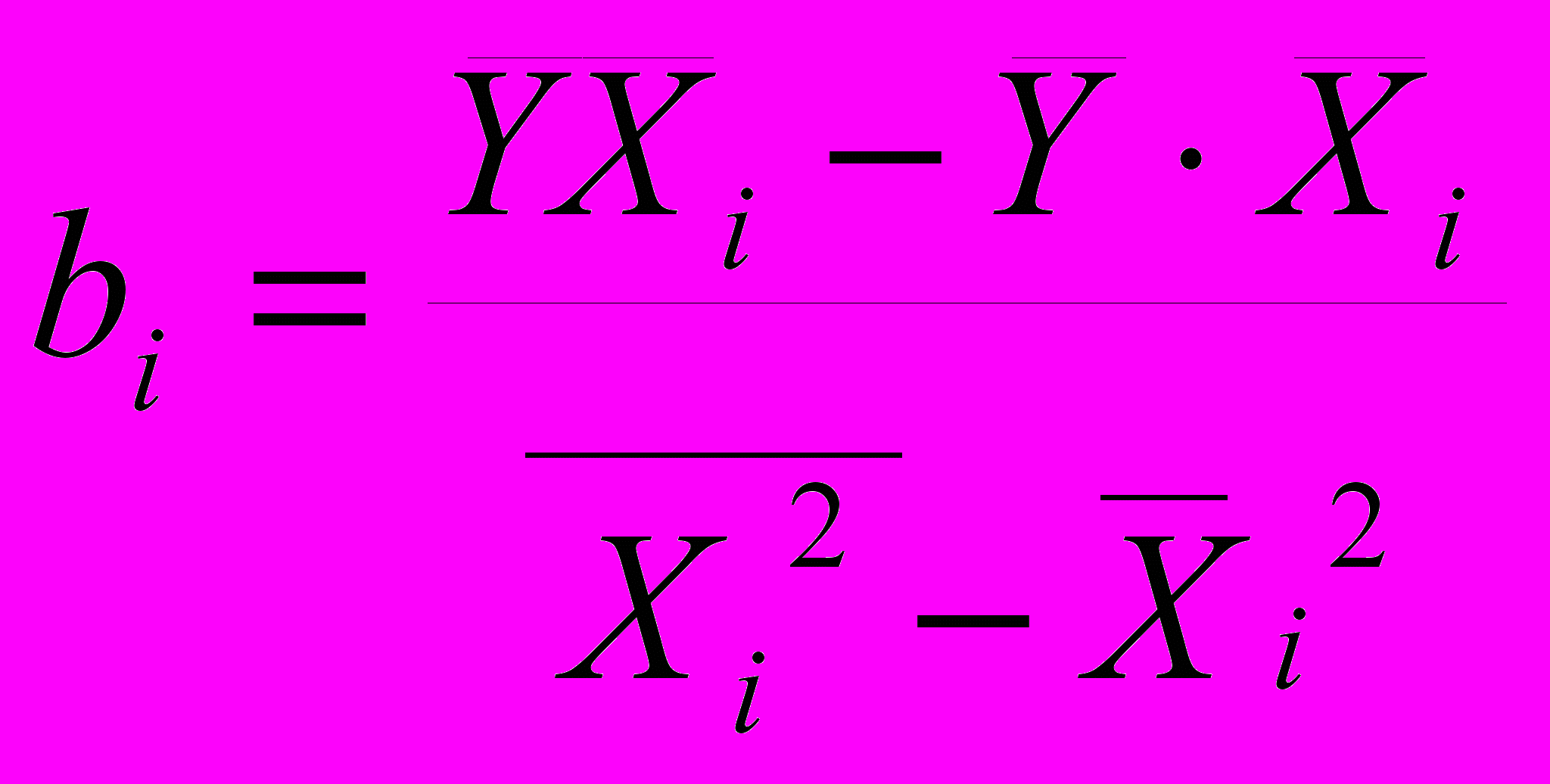 , где
, где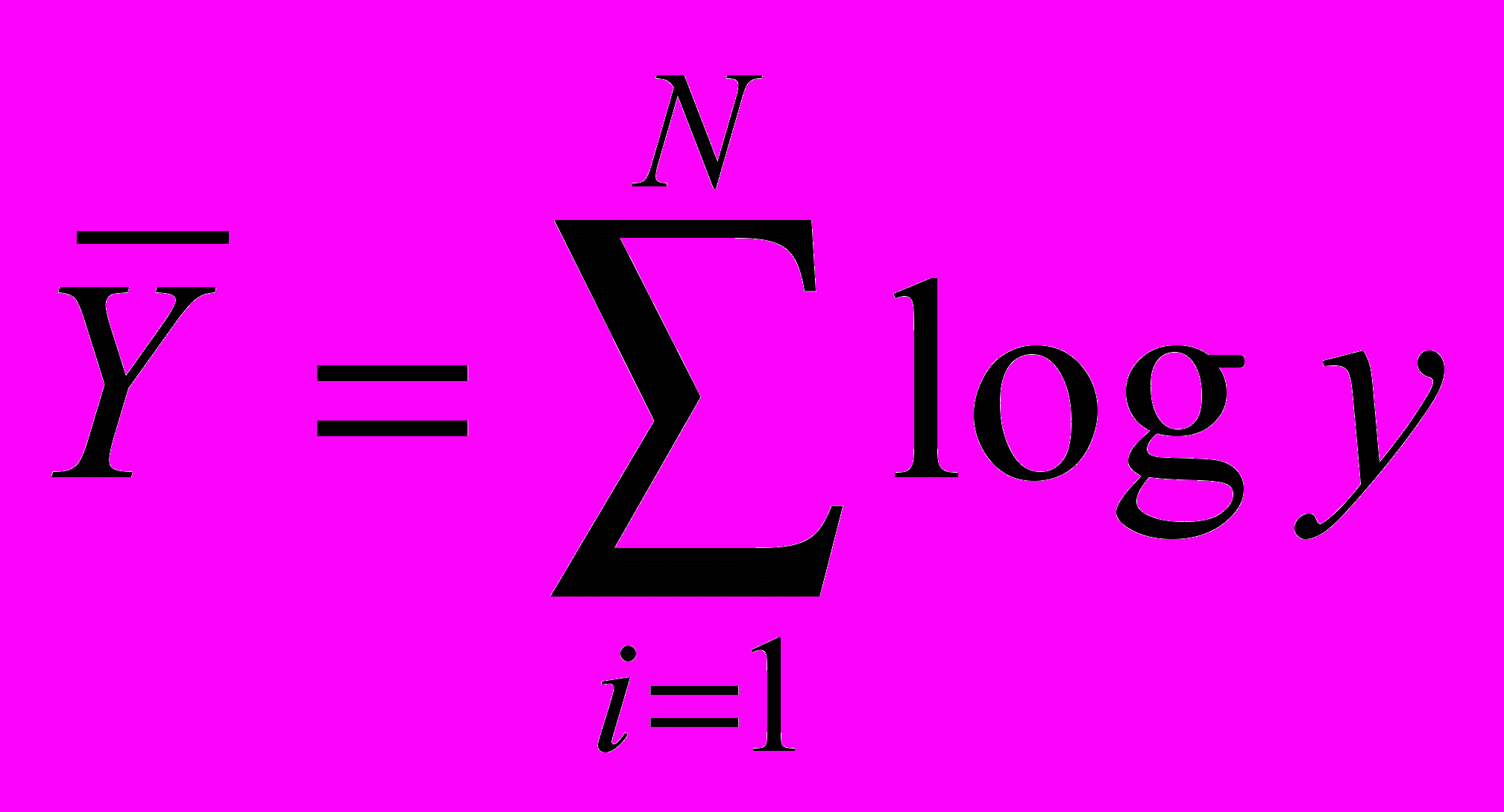 ;
; 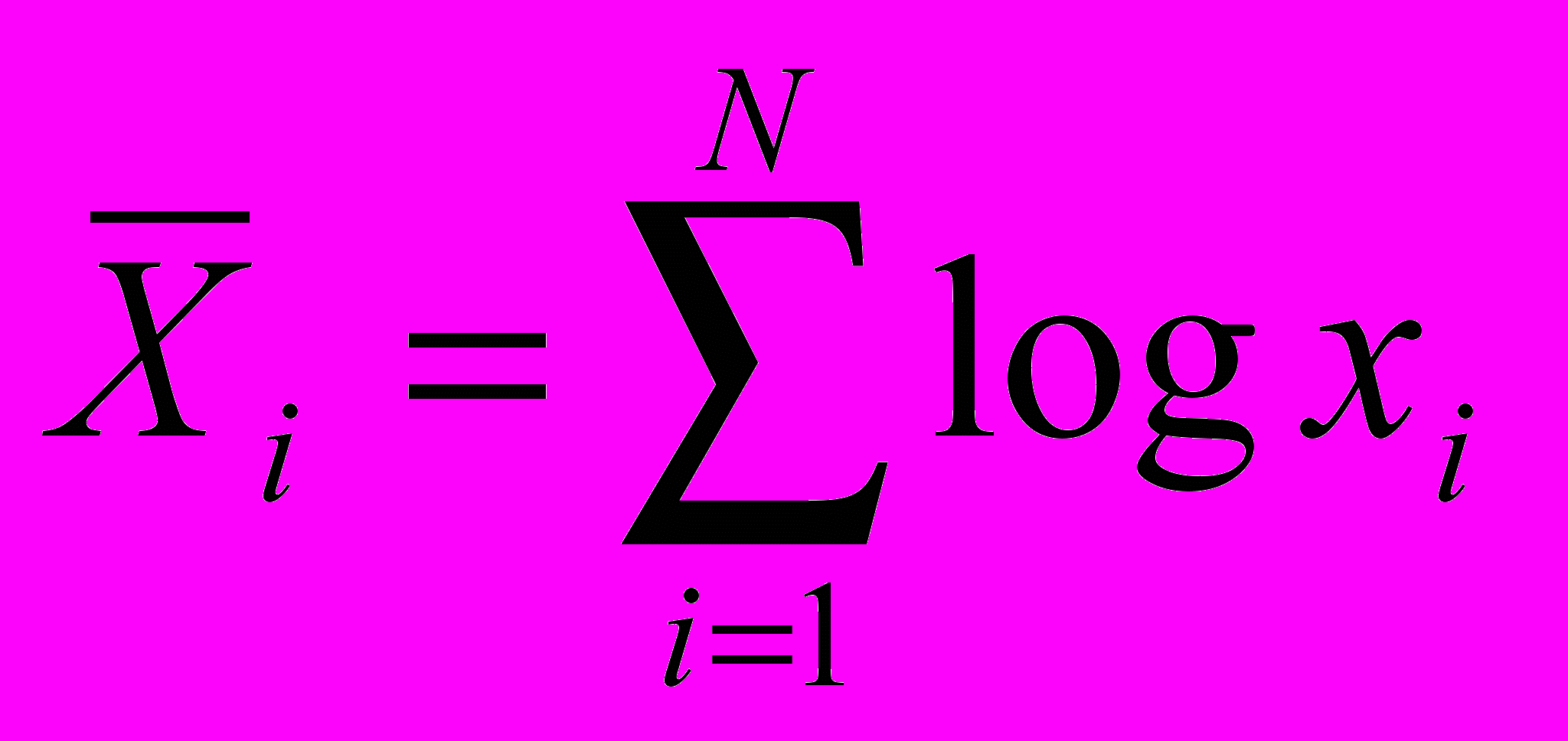 ;
; 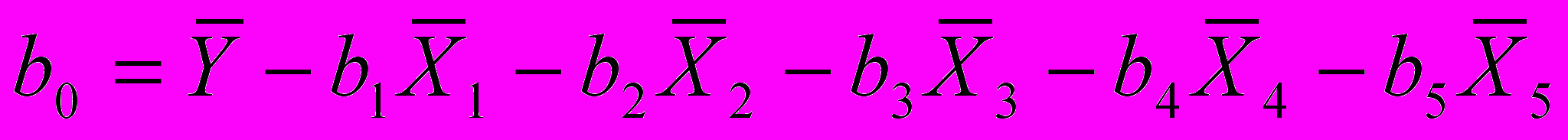 .
.В результате перехода от кодированных значений факторов к натуральным получили:
lghmax = 0,4 – 0,05lgWвод + 0,98lgН0 +0,05lgQo+ 0,02lgno - 0,13lgx
После потенцирования имеем степенное уравнение вида:
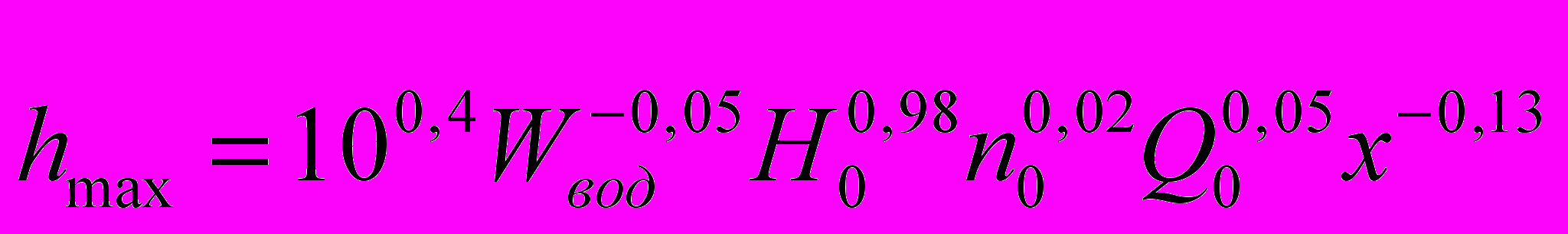 или
или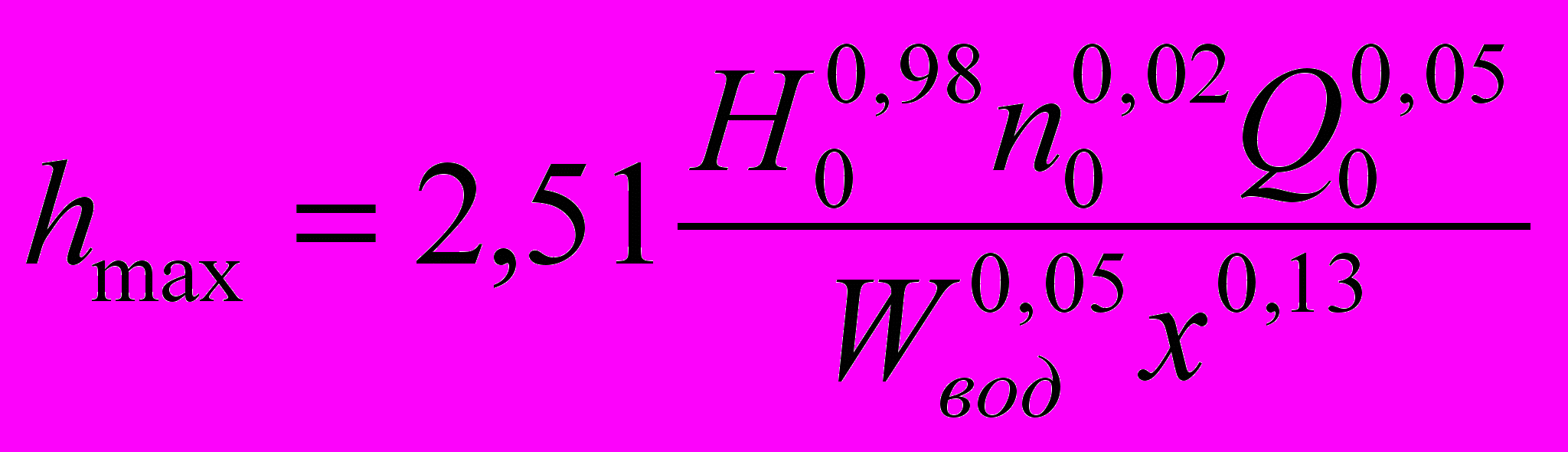 (16)
(16)С помощью табл. 10 определен коэффициент детерминации и критерий Фишера для полученного уравнения (16).
Таблица 10
Таблица к расчету коэффициента детерминации и критерия Фишера
| № | y | 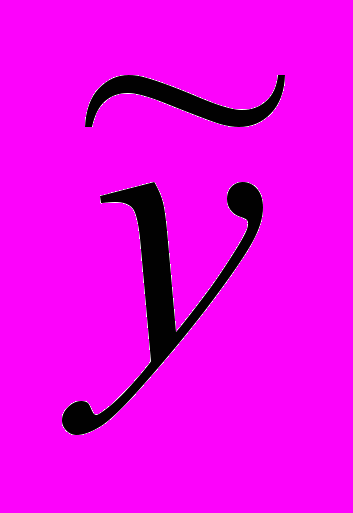 | y- 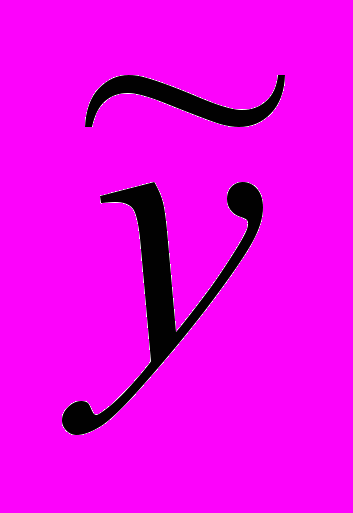 | y- 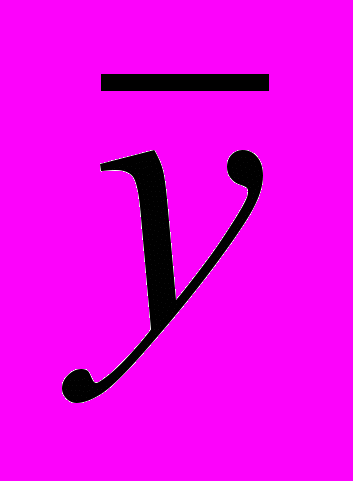 | (y- 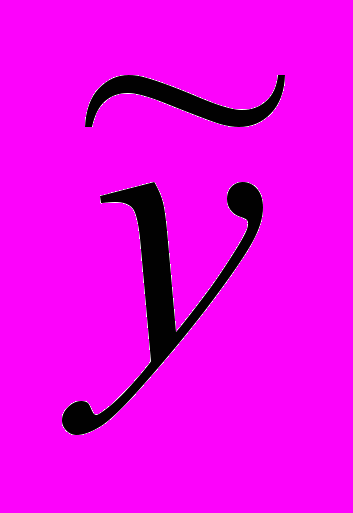 )2 )2 | (y- 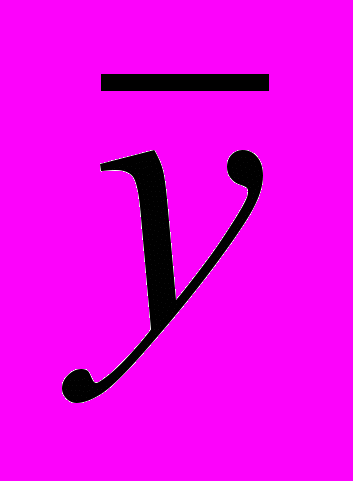 )2 )2 |
| 1 | 0,63 | 0,65 | -0,02 | -4,39 | 0,0005 | 19,27 |
| 2 | 1,17 | 0,94 | 0,23 | -3,85 | 0,0512 | 14,82 |
| 3 | 11,36 | 11,35 | 0,01 | 6,34 | 0,0002 | 40,20 |
| 4 | 4,22 | 4,95 | -0,73 | -0,80 | 0,5376 | 0,64 |
| 5 | 1,17 | 1,50 | -0,33 | -3,85 | 0,1062 | 14,82 |
| 6 | 0,63 | 0,65 | -0,02 | -4,39 | 0,0005 | 19,27 |
| 7 | 9,22 | 7,85 | 1,37 | 4,20 | 1,8759 | 17,64 |
| 8 | 11,36 | 11,35 | 0,01 | 6,34 | 0,0002 | 40,20 |
| 9 | 1,26 | 1,24 | 0,02 | -3,76 | 0,0002 | 14,14 |
| 10 | 0,40 | 0,54 | -0,14 | -4,62 | 0,0205 | 21,34 |
| 11 | 6,40 | 6,53 | -0,13 | 1,38 | 0,0168 | 1,90 |
| 12 | 12,23 | 9,44 | 2,79 | 7,21 | 7,7942 | 51,98 |
| 13 | 1,13 | 0,86 | 0,27 | -3,89 | 0,0725 | 15,13 |
| 14 | 1,26 | 1,24 | 0,02 | -3,76 | 0,0002 | 14,14 |
| 15 | 11,60 | 14,96 | -3,36 | 6,58 | 11,2798 | 43,30 |
| 16 | 6,40 | 6,53 | -0,13 | 1,38 | 0,0168 | 1,90 |
| | | | | 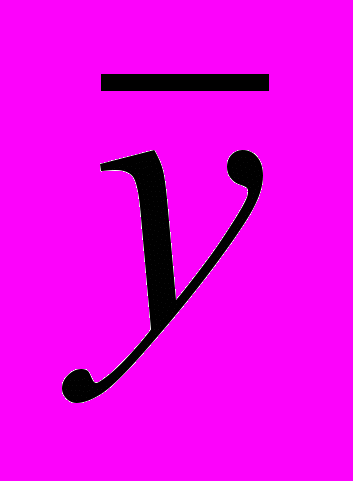 = 5,03 = 5,03 | 1,36 | 20,67 |
Примечание: y – значения, полученные в результате расчета по формуле Историка,
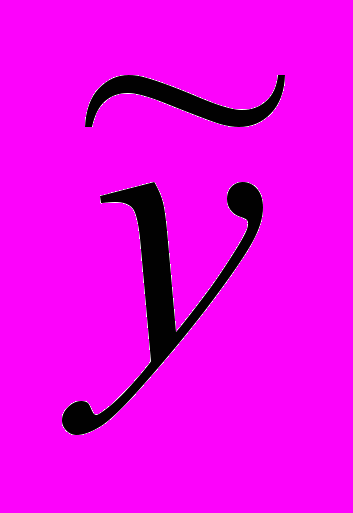 - значения, рассчитанные по формуле (15),
- значения, рассчитанные по формуле (15), 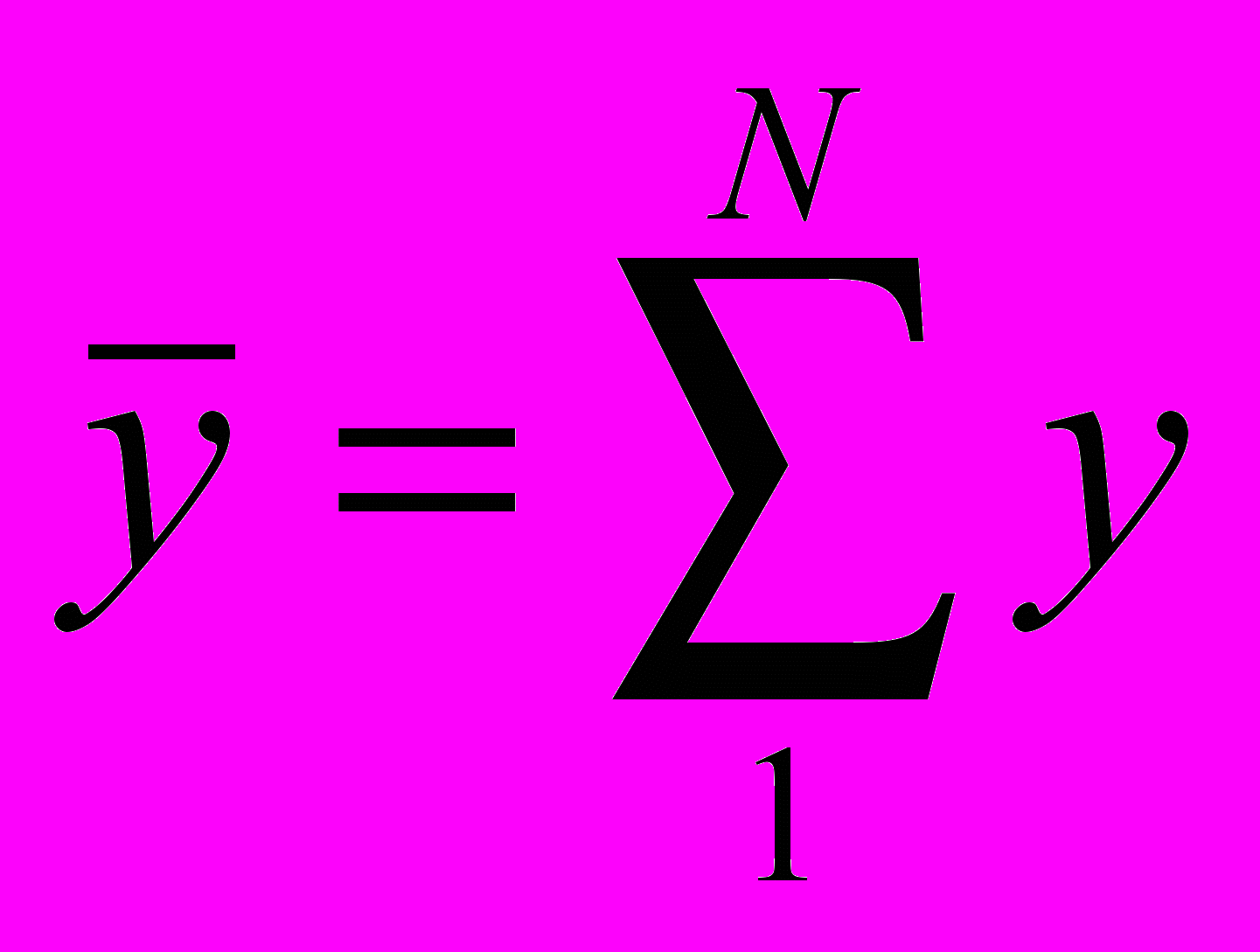 .
.Определен индекс корелляции:
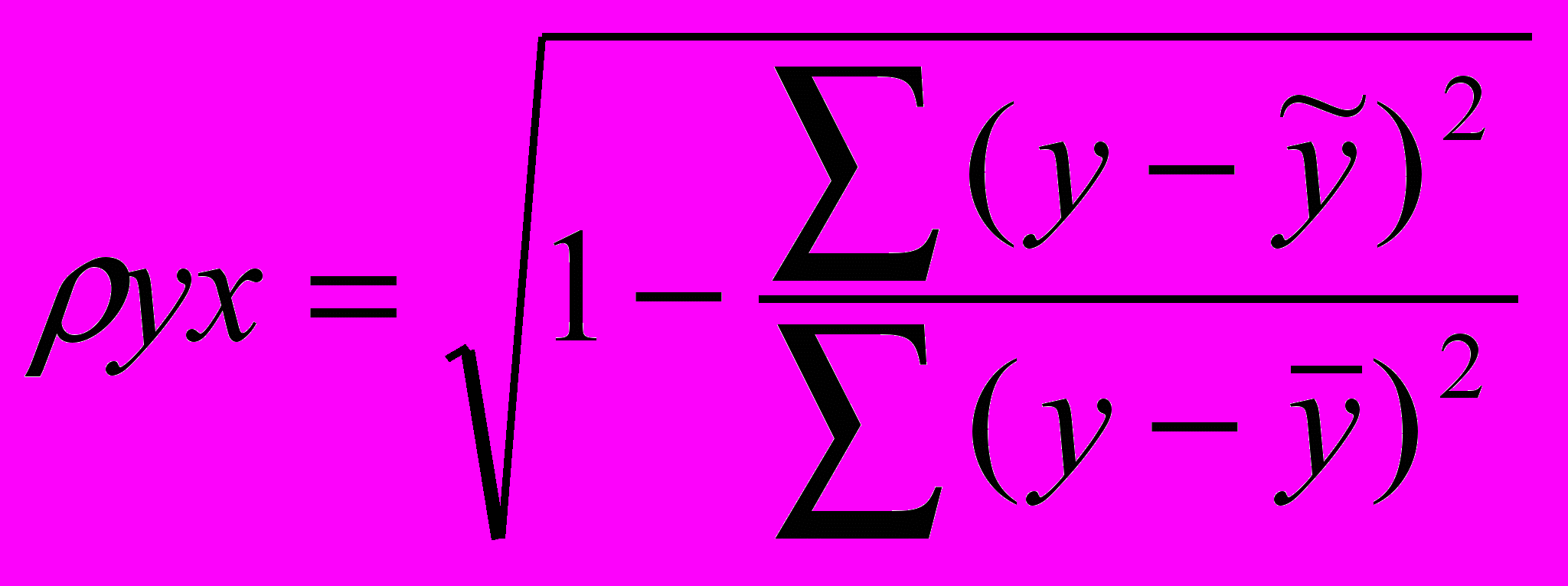 = 0,9644
= 0,9644Связь между показателем y и факторами x1, x2, x3, x4, x5 можно считать достаточно сильной.
Коэффициент детерминации:
R2 = ρyx2 = 0,93
Вариация результата y на 93,0 % объясняется вариацией факторов x1, x2, x3, x4, x5.
Рассчитан критерий Фишера:
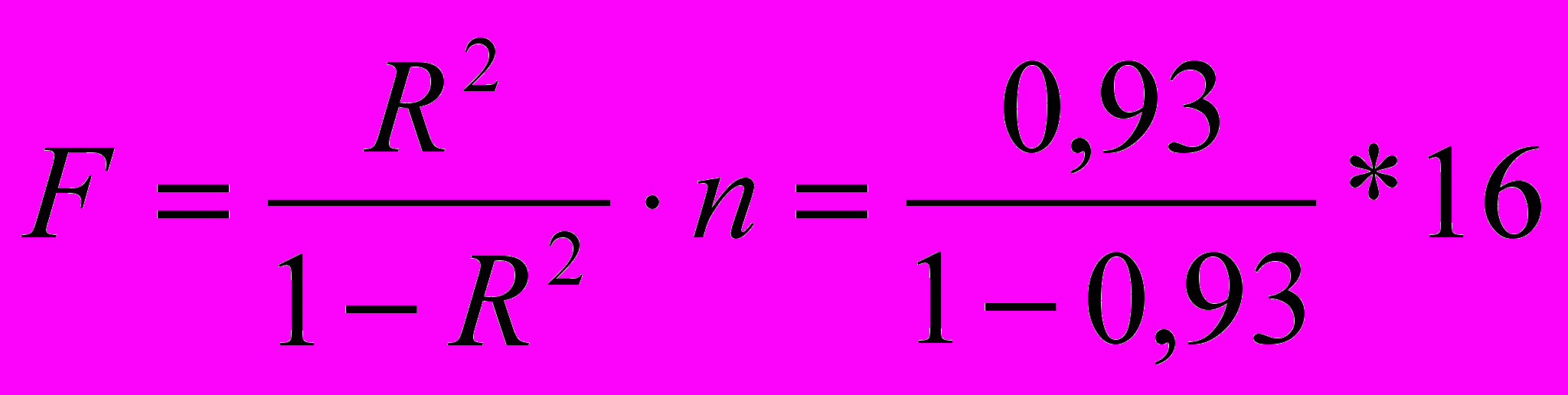 = 212,54, где
= 212,54, гдеn – число единиц совокупности.
F > Fтабл = 2,4 для α = 0,05
Уравнение в целом статистически значимое с вероятностью 0,95, т.к. F > Fтабл.
Средняя относительная ошибка аппроксимации:
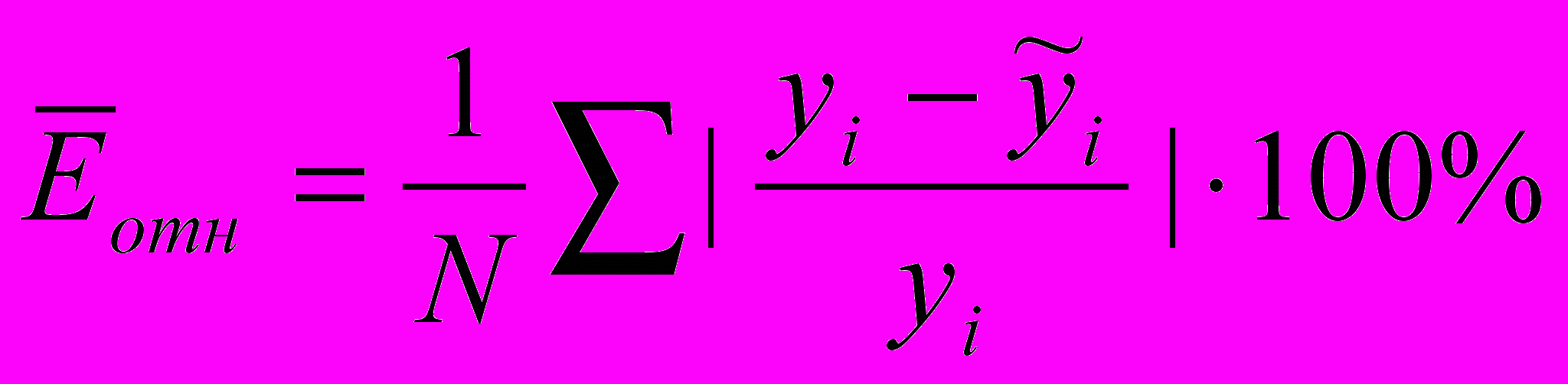
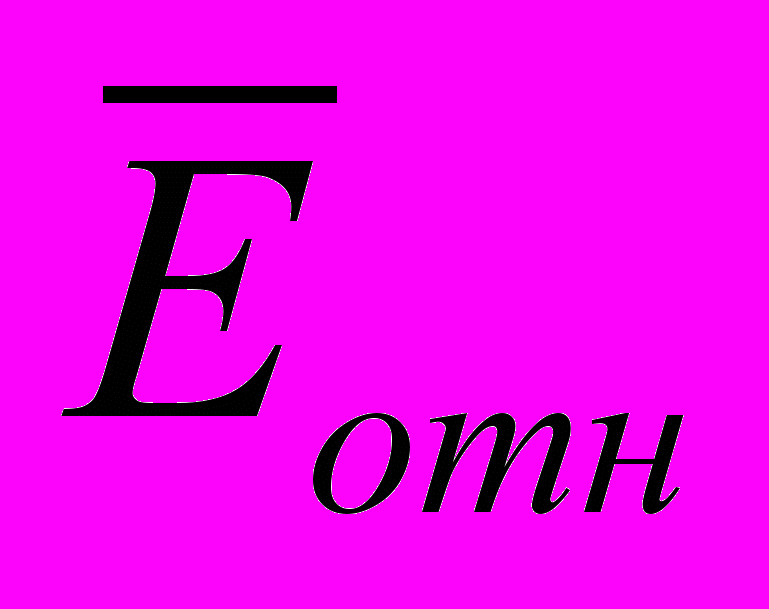 = 12,8 %.
= 12,8 %.