Конкурс научных молодежных работ «Молодежь Белгородской области»

Вид материала

Конкурс

Содержание 4. Сравнение параметров волны прорыва, определенных различными методами в случае призматического русла треугольного поперечного Н – глубина водохранилища до начала аварии; L V – средняя по сечению скорость течения; g – ускорение силы тяжести; λ – коэффициент гидравлического трения; Q=ωV I) 0,0001 – 0,0005; Х2 – шероховатость русла (n

Подобный материал:

• Конкурс научных молодежных работ «Молодежь Белгородской области», 732.53kb.
• Конкурс научных молодежных работ «Молодежь Белгородской области», 674.28kb.
• Конкурс проводится с целью стимулирования интереса школьников к изучению истории родного, 50.93kb.
• Первый международный конкурс научных работ молодых ученых в области нанотехнологий, 29.76kb.
• Е. И. Хузин Положение о конкурсе среди молодежных объединений и организаций города, 76.85kb.
• Первый международный конкурс научных работ молодых ученых в области нанотехнологий, 47.1kb.
• Первый международный конкурс научных работ молодых ученых в области нанотехнологий, 45.14kb.
• На конкурс представляются следующие документы: На конкурс представляются следующие, 163.58kb.
• Открытый Конкурс работ проводится в научных областях: юриспруденция, политология, культурология,, 34.95kb.
• Конкурс научных работ аспирантов, соискателей, научных сотрудников "Экономический рост, 22.12kb.

4. Сравнение параметров волны прорыва, определенных различными методами в случае призматического русла треугольного поперечного сечения

В настоящем разделе представлены материалы сравнения результатов расчета по программе «SV_1», реализующей одномерные уравнения Сен-Венана, разработанной С. Я. Школьниковым с графоаналитической методикой Б. Л. Историка и методикой ВНИИГОЧС.

Автор обратилась с просьбой к С. Я. Школьникову о написании специальных аналитических тестовых задач для сравнения с методикой Б. Л. Историка и методикой ВНИИ ГОЧС.

Одна из таких задач была реализована для случая призматического русла треугольного поперечного сечения без начального наполнения в нижнем бьефе. Общий вид задачи расчета волны прорыва (неустановившегося течения воды) в призматическом русле треугольного поперечного сечения с постоянным уклоном дна приведен на рис. 4. Задача решалась в безразмерных координатах.

Площадь поперечного сечения канала рассчитана по формуле:

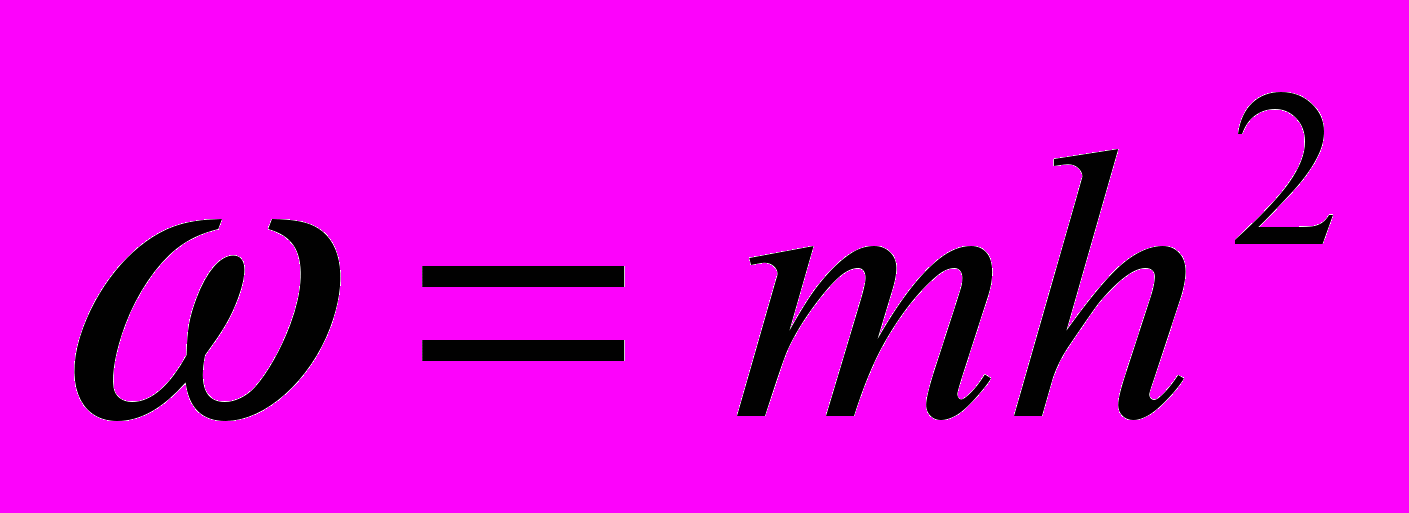, (1)

где m – заложение откосов канала; h – его высота.

Смоченный периметр рассчитан по формуле:

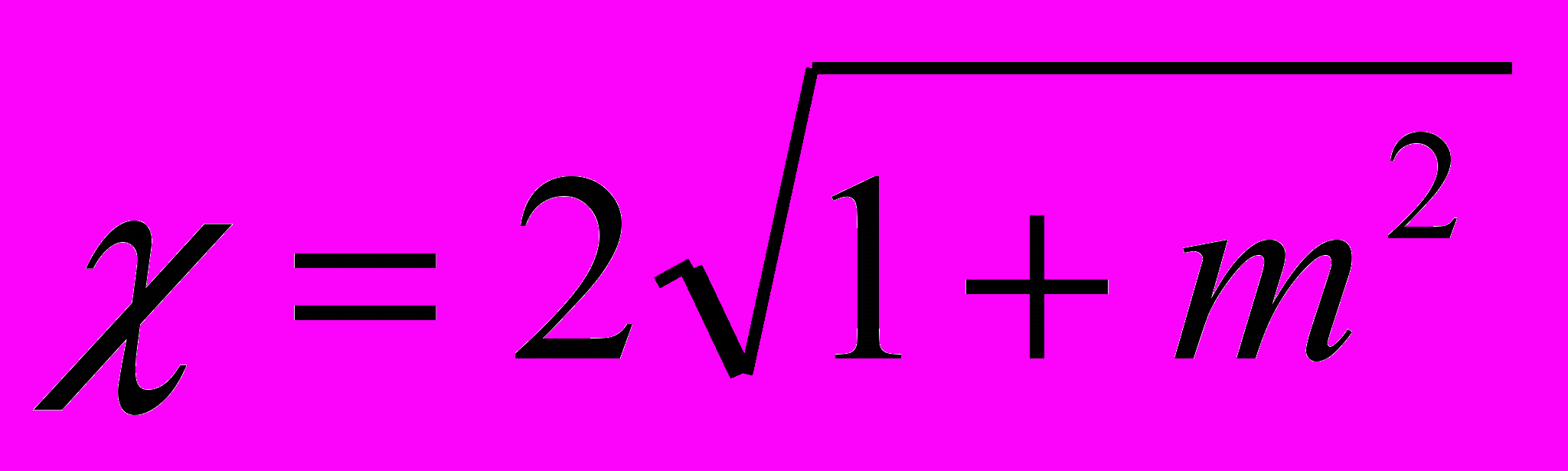(2);

а гидравлический радиус по:

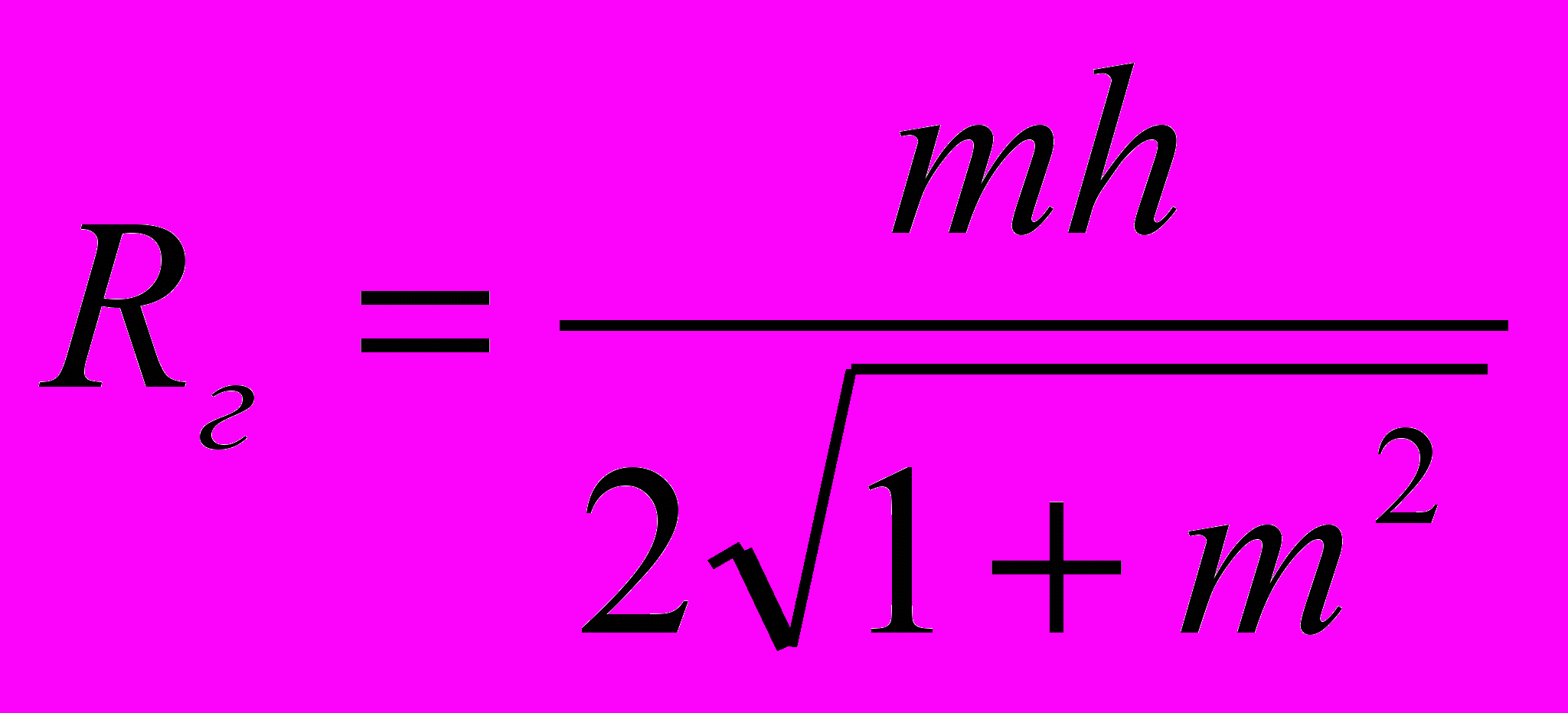(3).





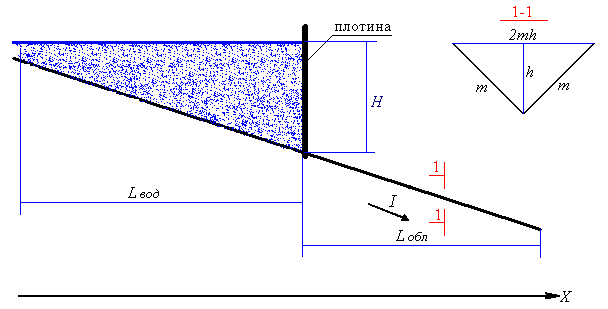
Рис. 4. Общий вид задачи расчета волны прорыва (неустановившегося течения воды) в призматическом русле треугольного поперечного сечения с постоянным уклоном дна:

Н – глубина водохранилища до начала аварии; L_вод – длина водохранилища; L_обл – длина расчетной области (расстояние от створа плотины до расчетного створа); I – уклон; m – заложение откосов канала; h – высота канала; 2mh – ширина канала поверху.


В соответствии с геометрией выбранной расчетной области имеем:

длину водохранилища:

L_вод = H/I (4);

объем водохранилища:

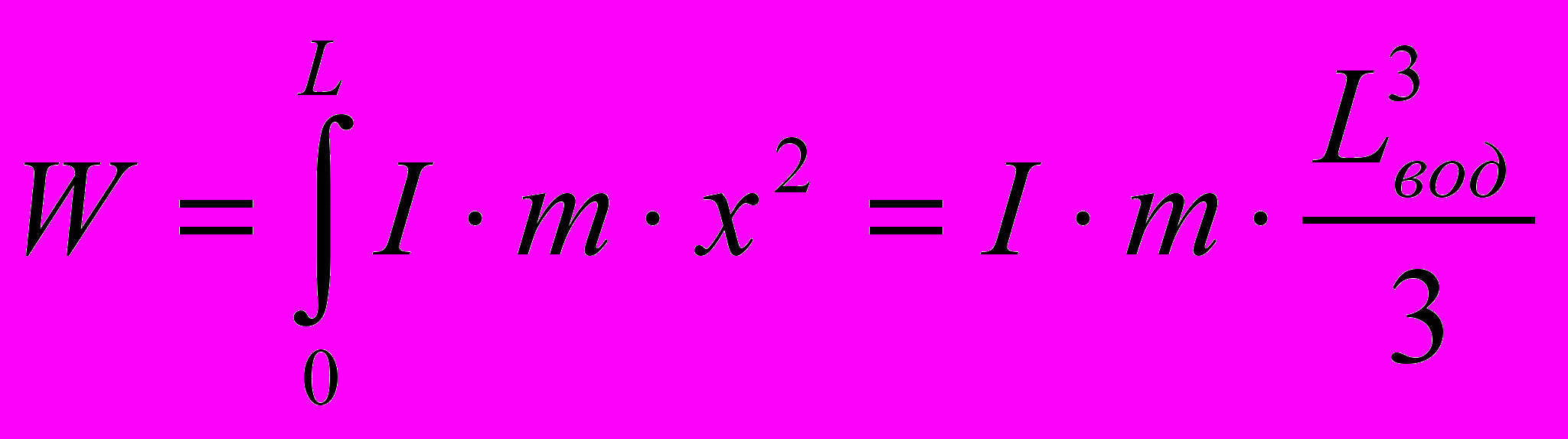(5);

высоту канала:

h(x) = I∙x (6);

площадь поперечного сечения канала:

w(x) = I∙m∙x² (7);


Для решения задачи использованы одномерные уравнения Сен-Венана:

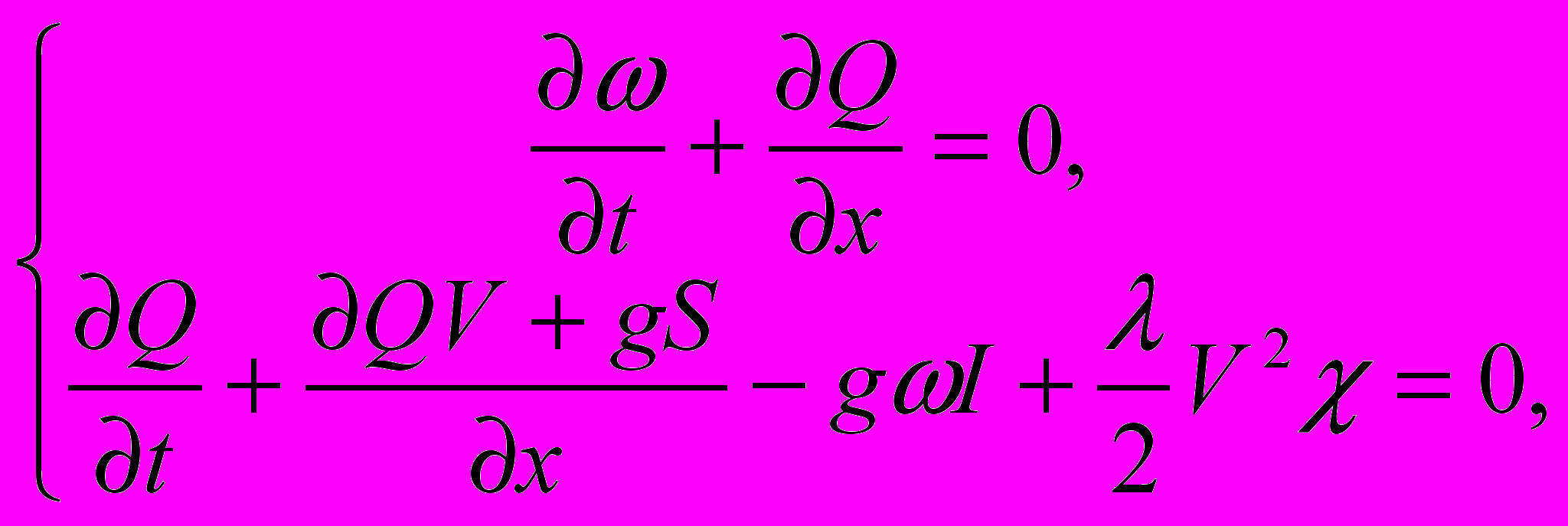(8);

где: t – время; х – длина; – площадь поперечного сечения; V – средняя по сечению скорость течения; g – ускорение силы тяжести; λ – коэффициент гидравлического трения; Q=ωV – расход; S – статический момент сечения потока относительно свободной поверхности воды; χ – смоченный периметр.

Первое уравнение системы (8) выражает закон сохранения массы воды (вода здесь несжимаема), второе – 2-й закон Ньютона для руслового потока.

Произведены некоторые преобразования с помощью ввода следующих зависимостей: .

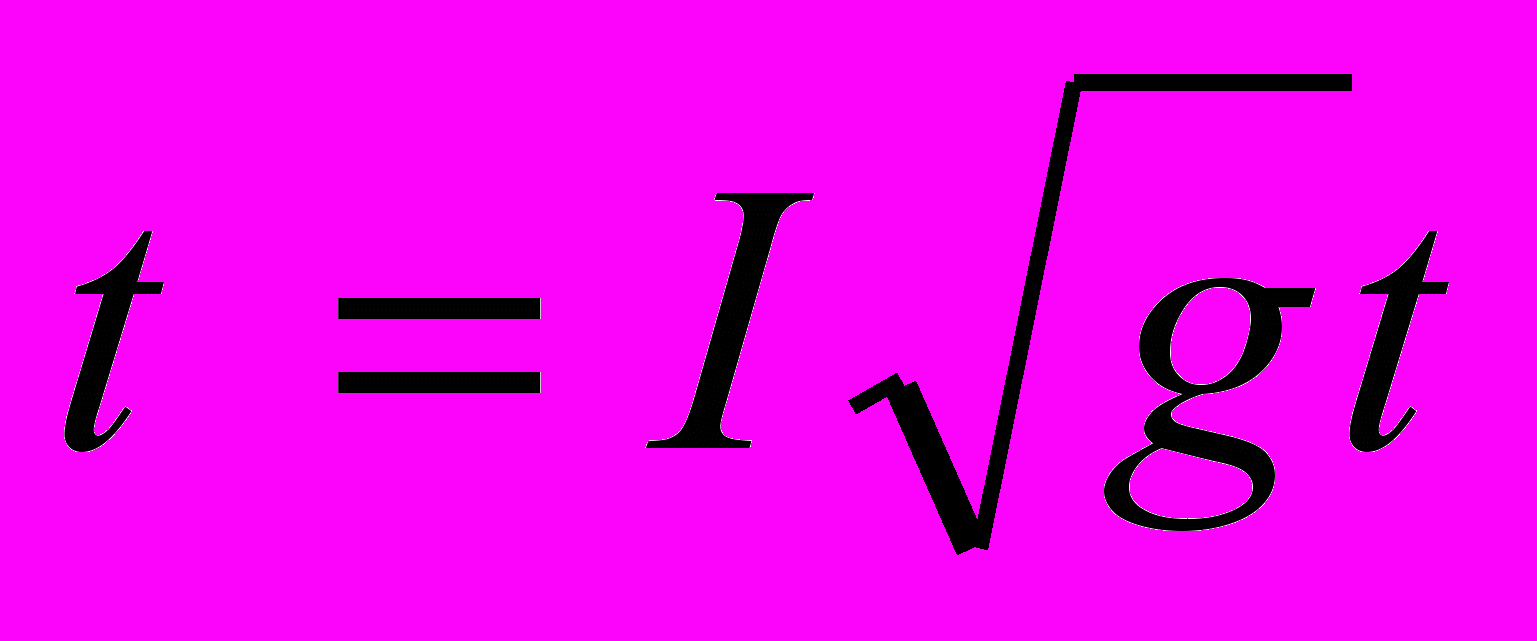
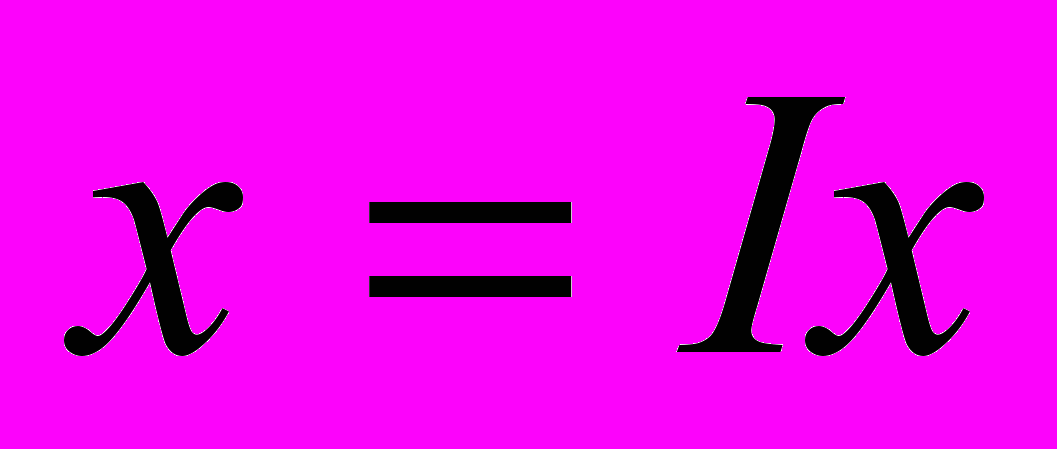
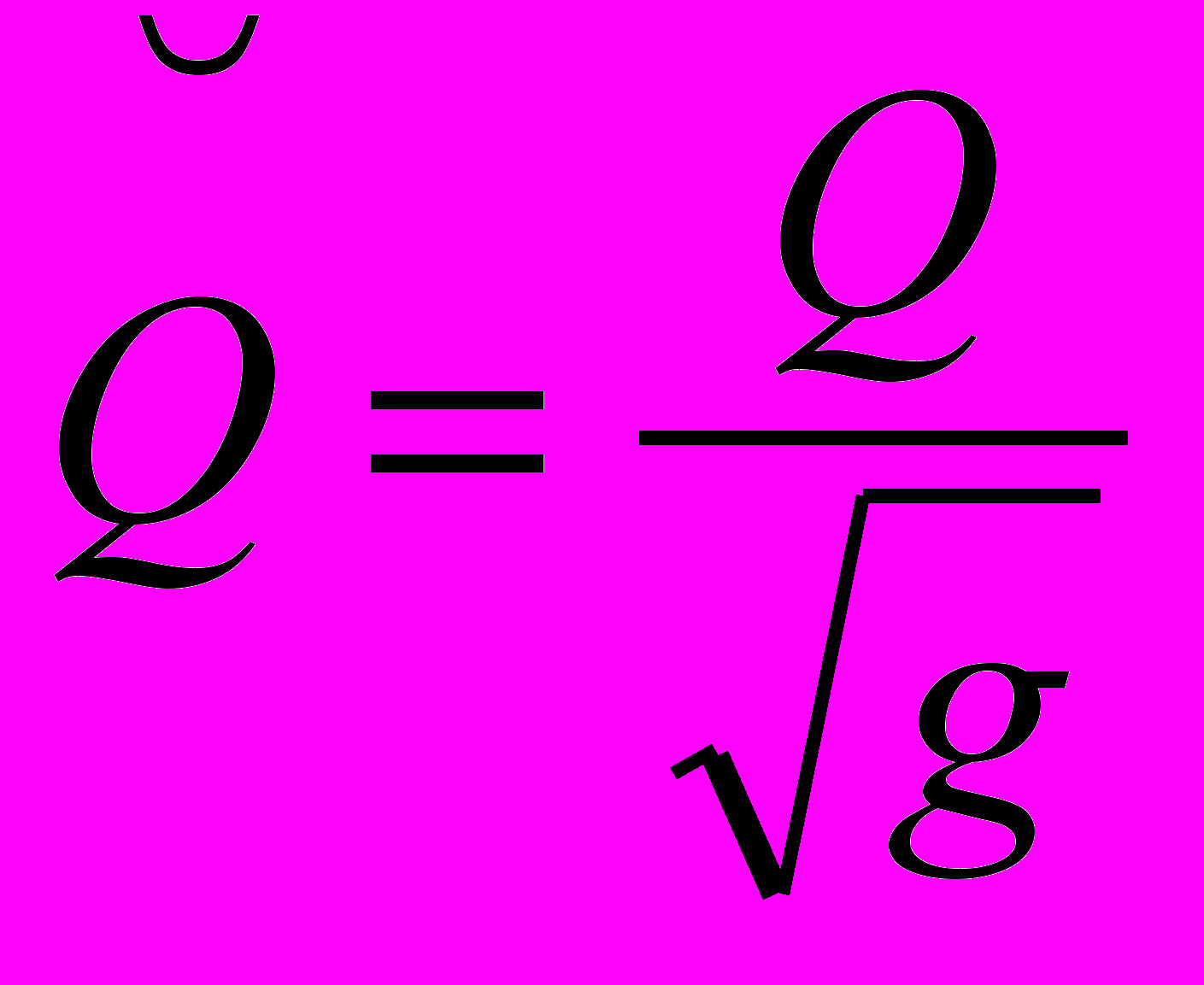
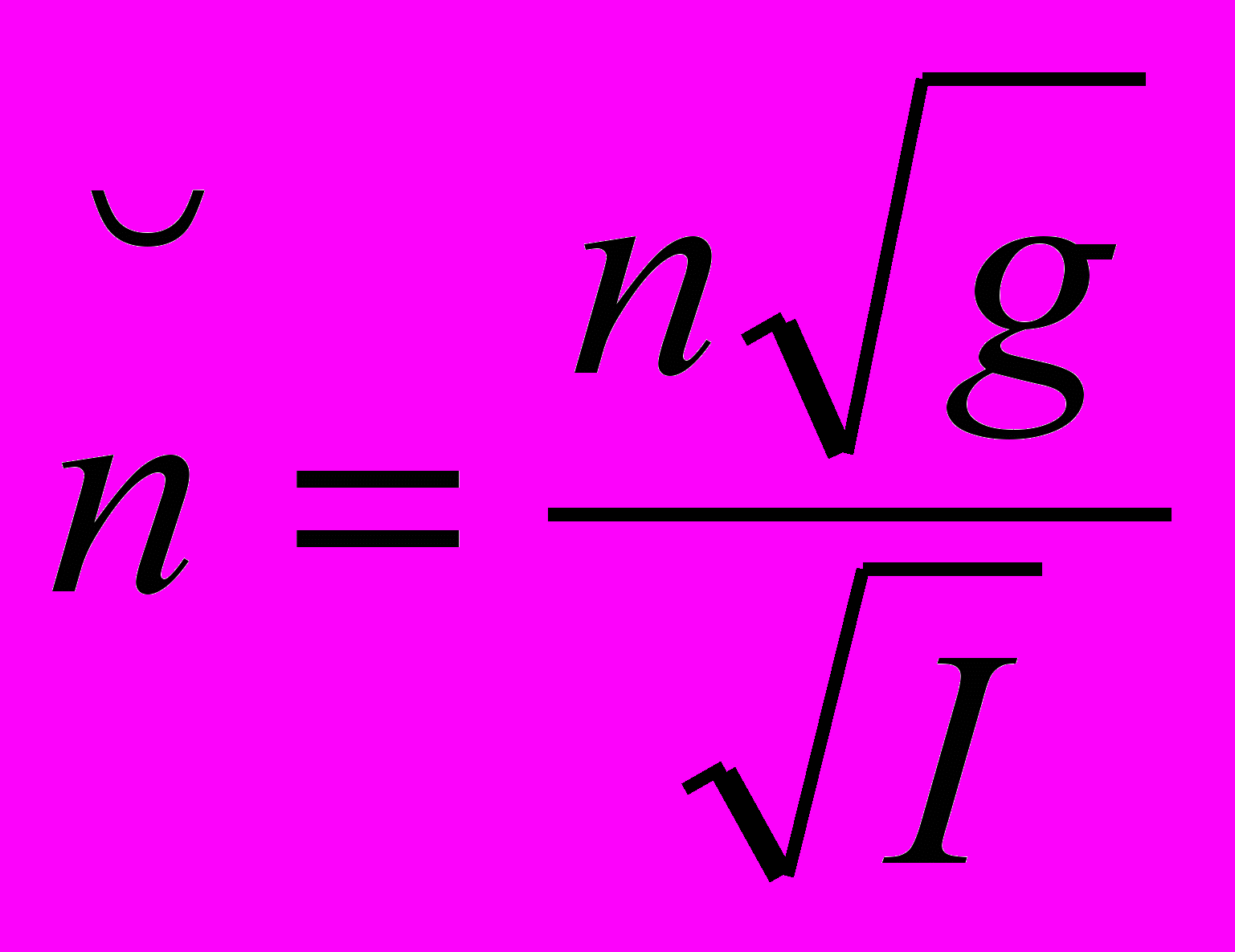(8а);

Теперь каждый член уравнения имеет размерность м². Для того, чтобы перейти к безразмерным величинам, выполнена следующая замена:



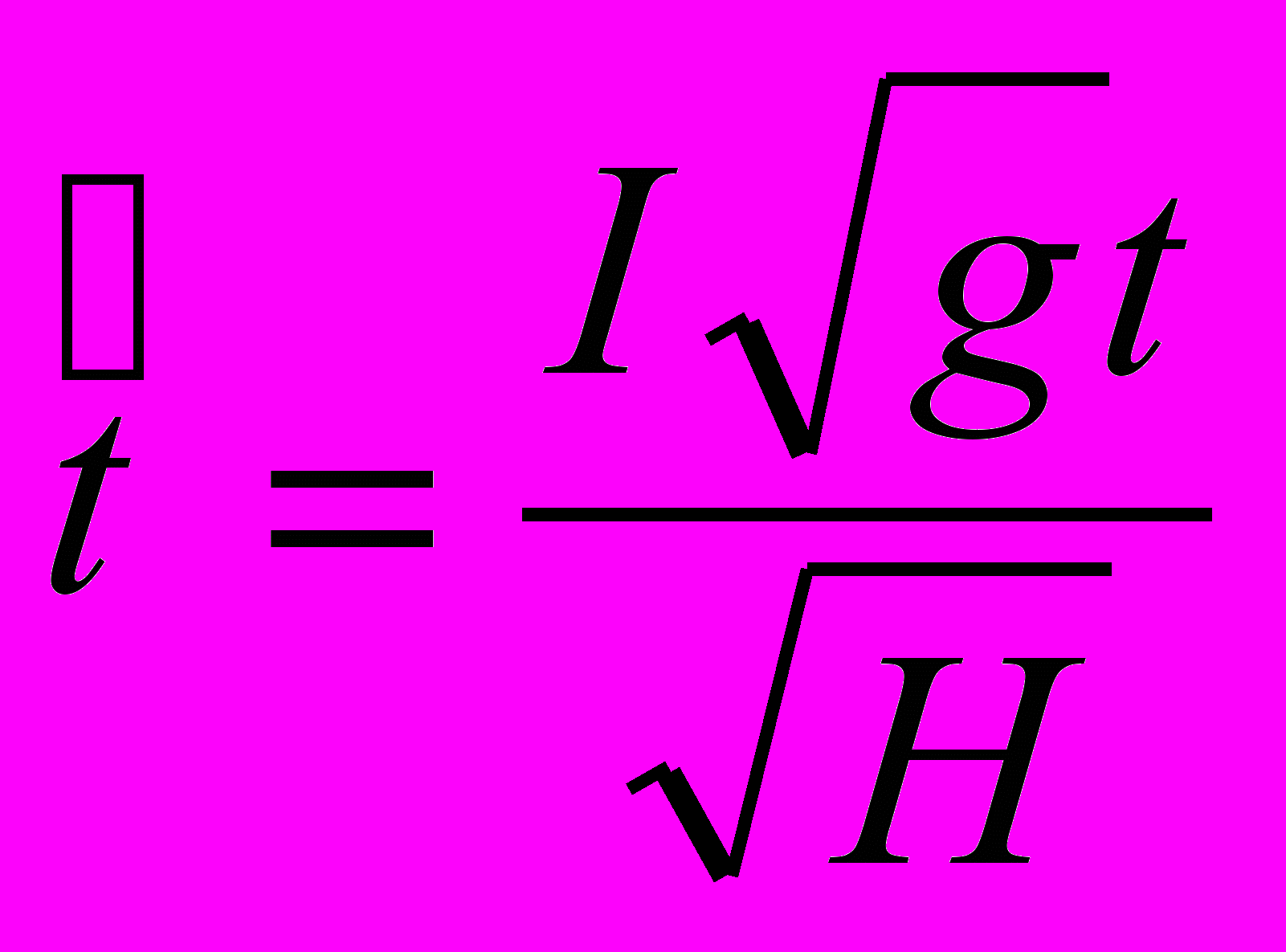
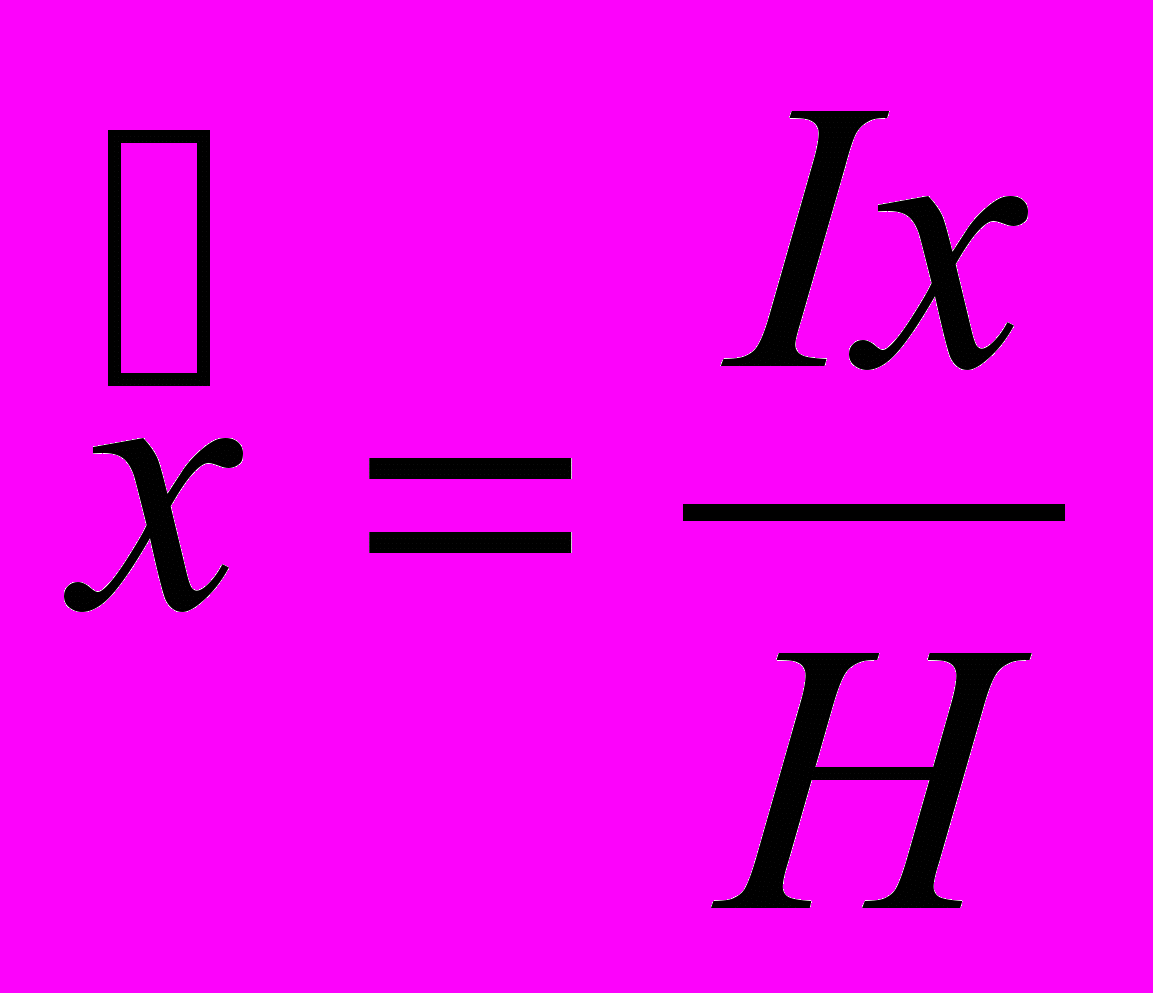
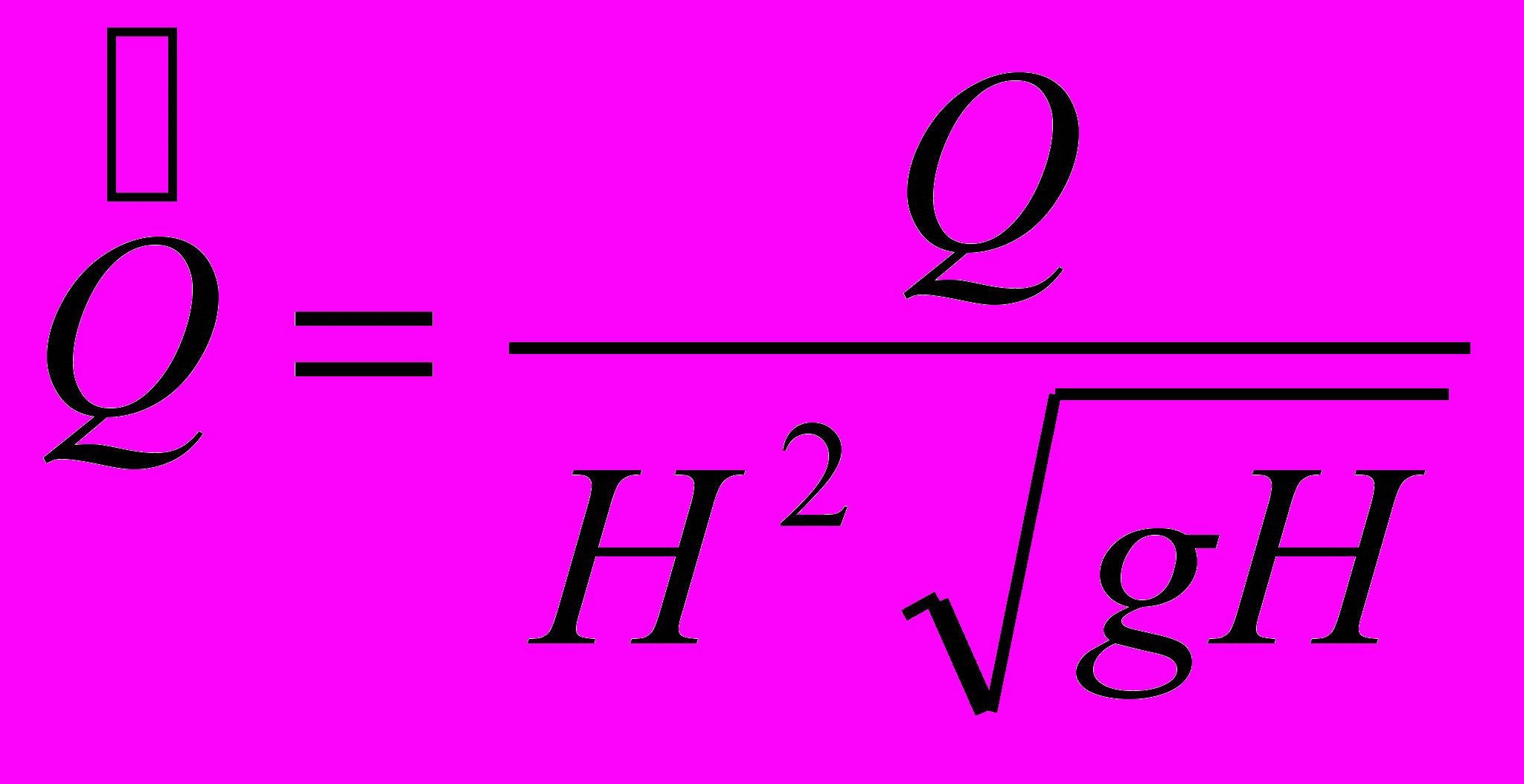
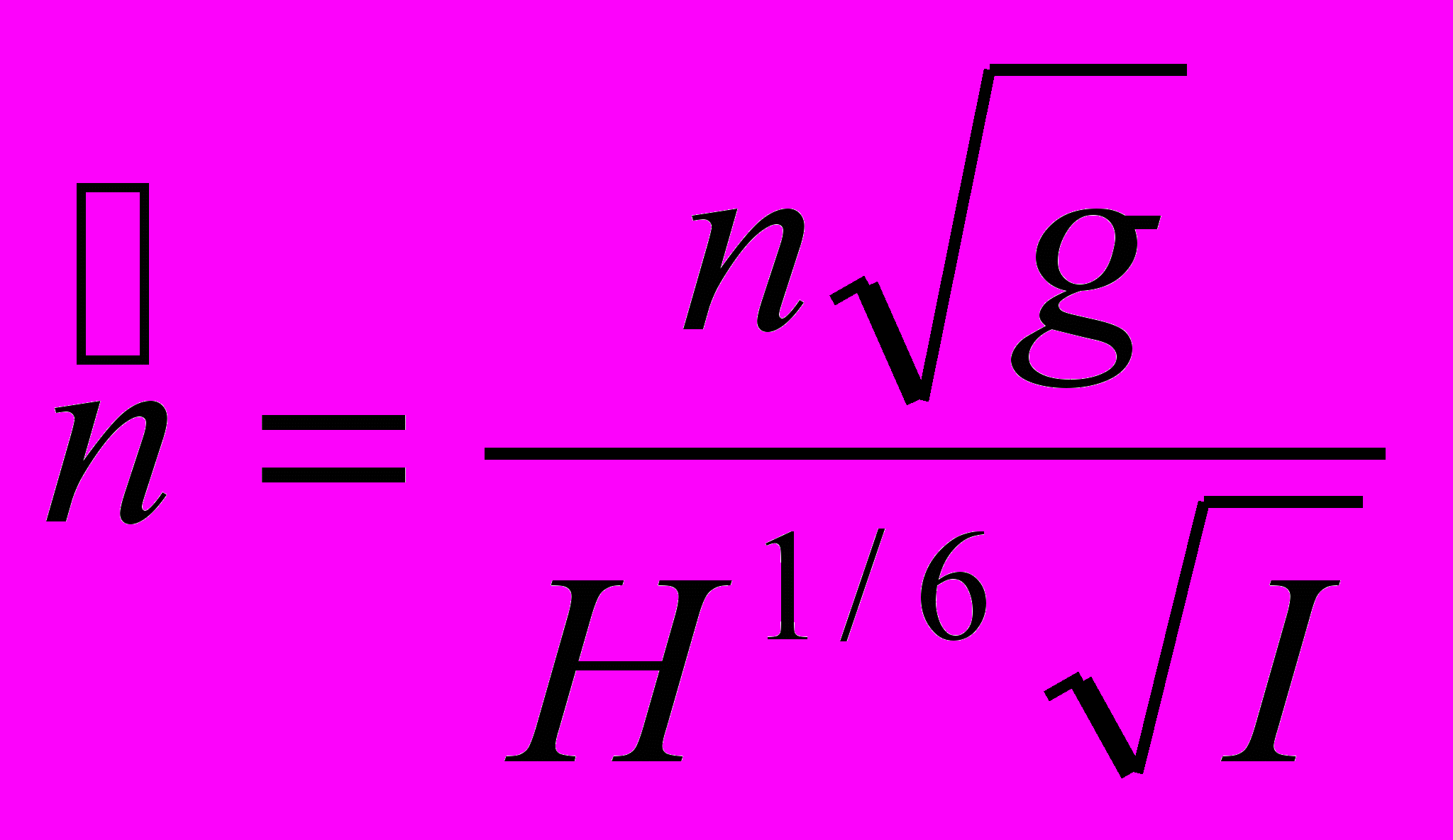
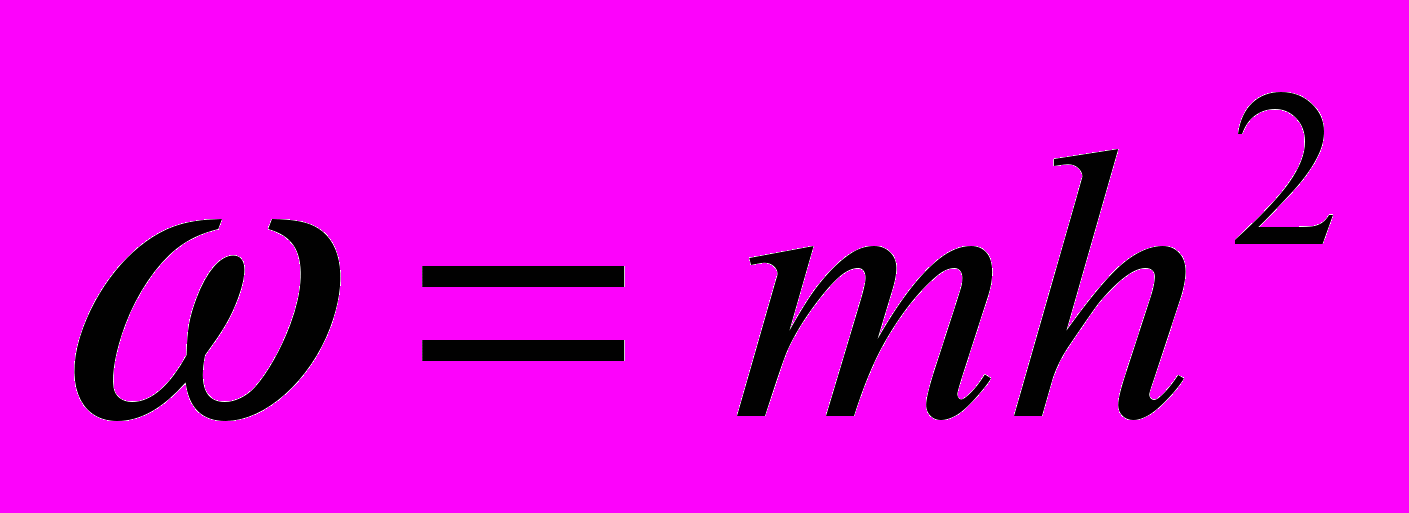
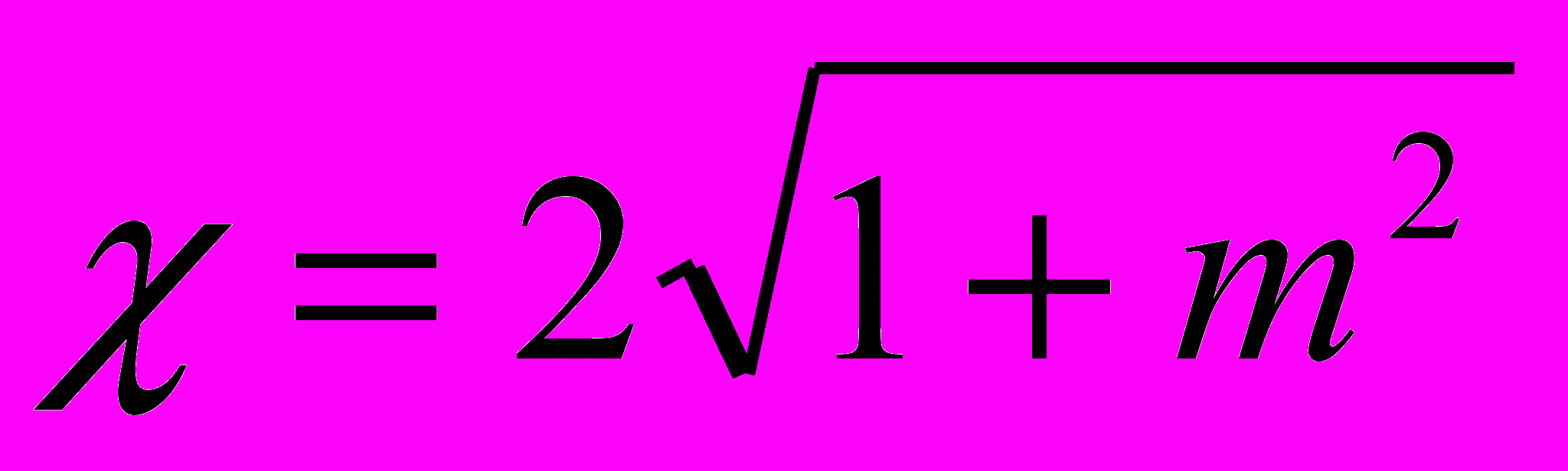
Так как для треугольного русла справедливы следующие зависимости: 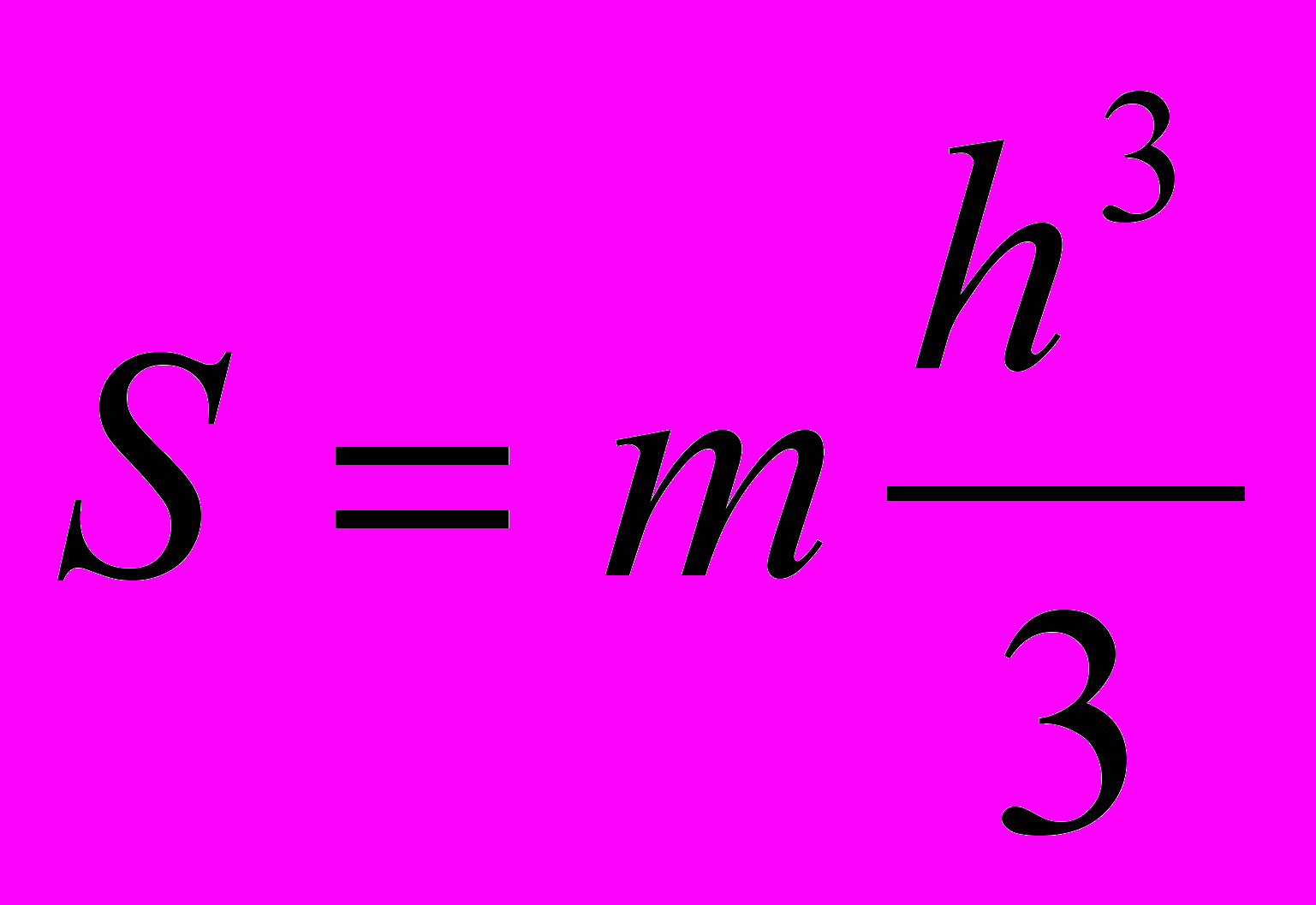, то, после подстановки их в уравнении (8а) уравнения Сен-Венана имеют в следующий вид:

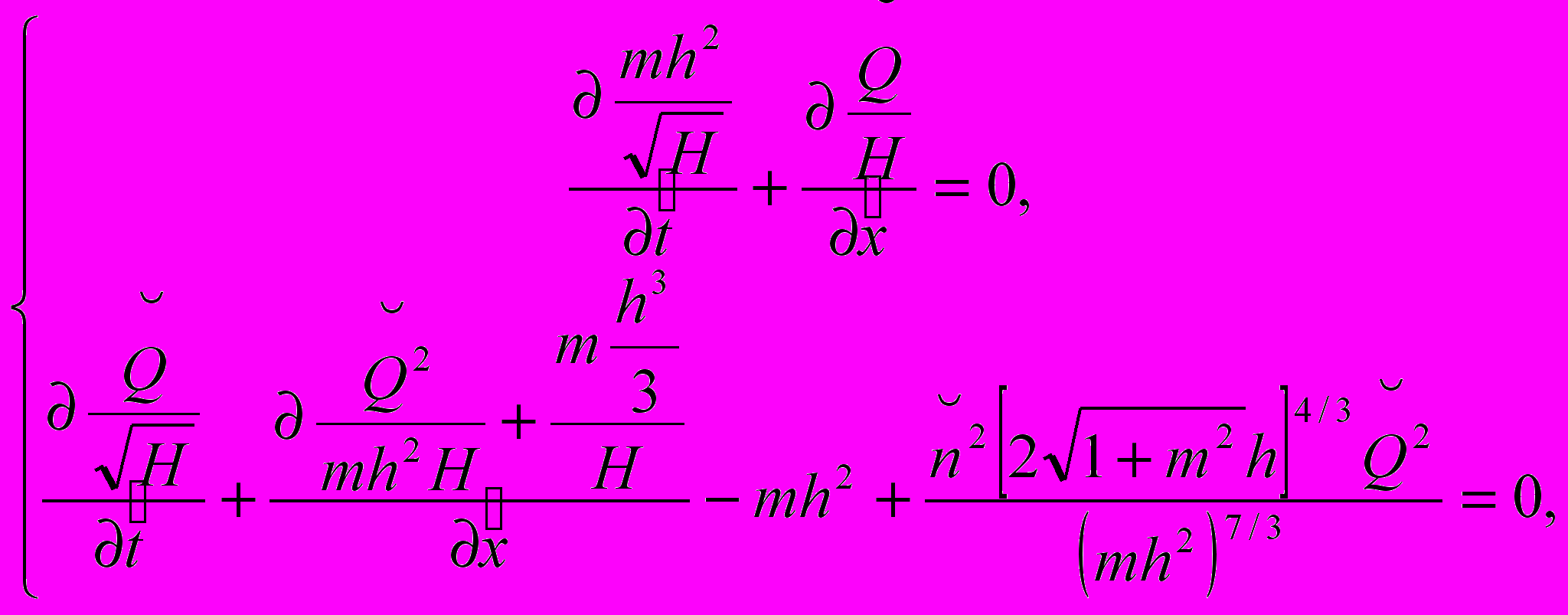(8б);

или:

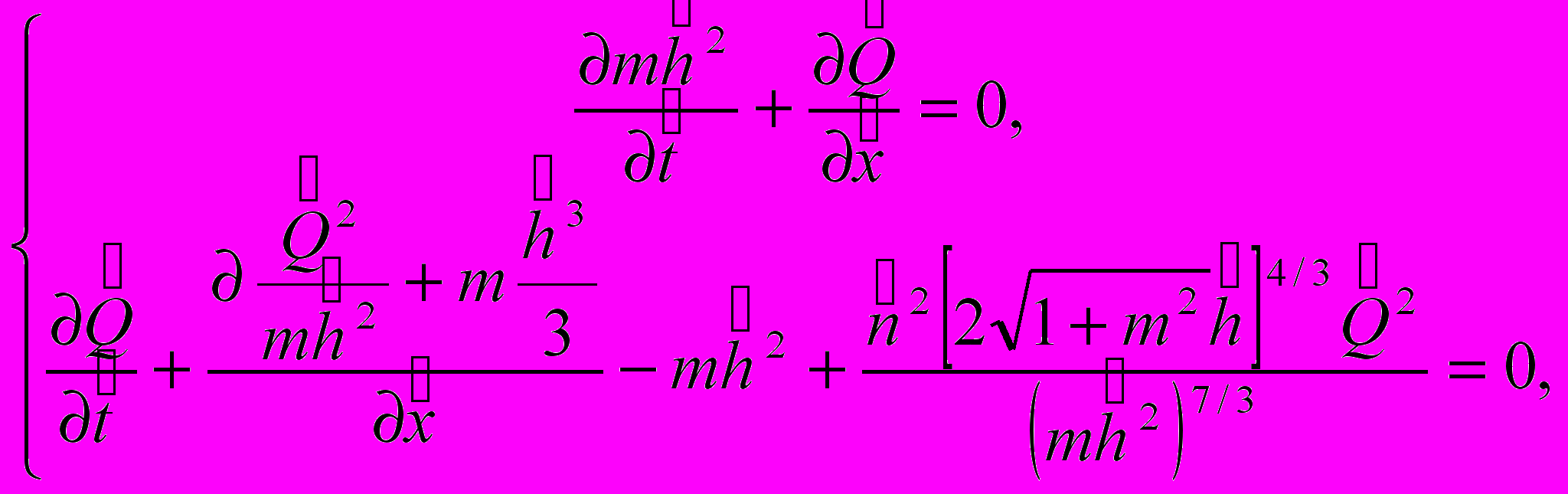(8в).

В качестве варьируемых параметров принимались следующие размерные величины:

Х₁ – уклон дна русла ( I) 0,0001 – 0,0005;

Х₂ – шероховатость русла (n) 0,02-0,06;

Х₃ – глубину воды в водохранилище до начала аварии (H) 2-10 м;

Х₄ – заложение откосов рассматриваемого канала (m) 1-5;

Х₅ – расстояние от плотины до створа наблюдения (x) 0,2 – 90 км;

Х₆ – объем воды в водохранилище до начала аварии (W)

2,7·10⁶ - 1,7·10⁹ м³;

Х₇ – длина водохранилища (L_вод) 2 – 10 км.

В качестве выхода рассматривалась максимальная глубина затопления (h_max).

Так как у нас задача с постоянным уклоном и поперечным сечением канала, это дает нам право выразить варьируемые параметры в некоторых зависимостях друг от друга [см. формулы (1-8)]. В результате преобразований получены два безразмерных варьируемых параметра, для которых составлена матрица эксперимента: = от 1,35 до 5,3 и m = от 1 до 5,

где: .

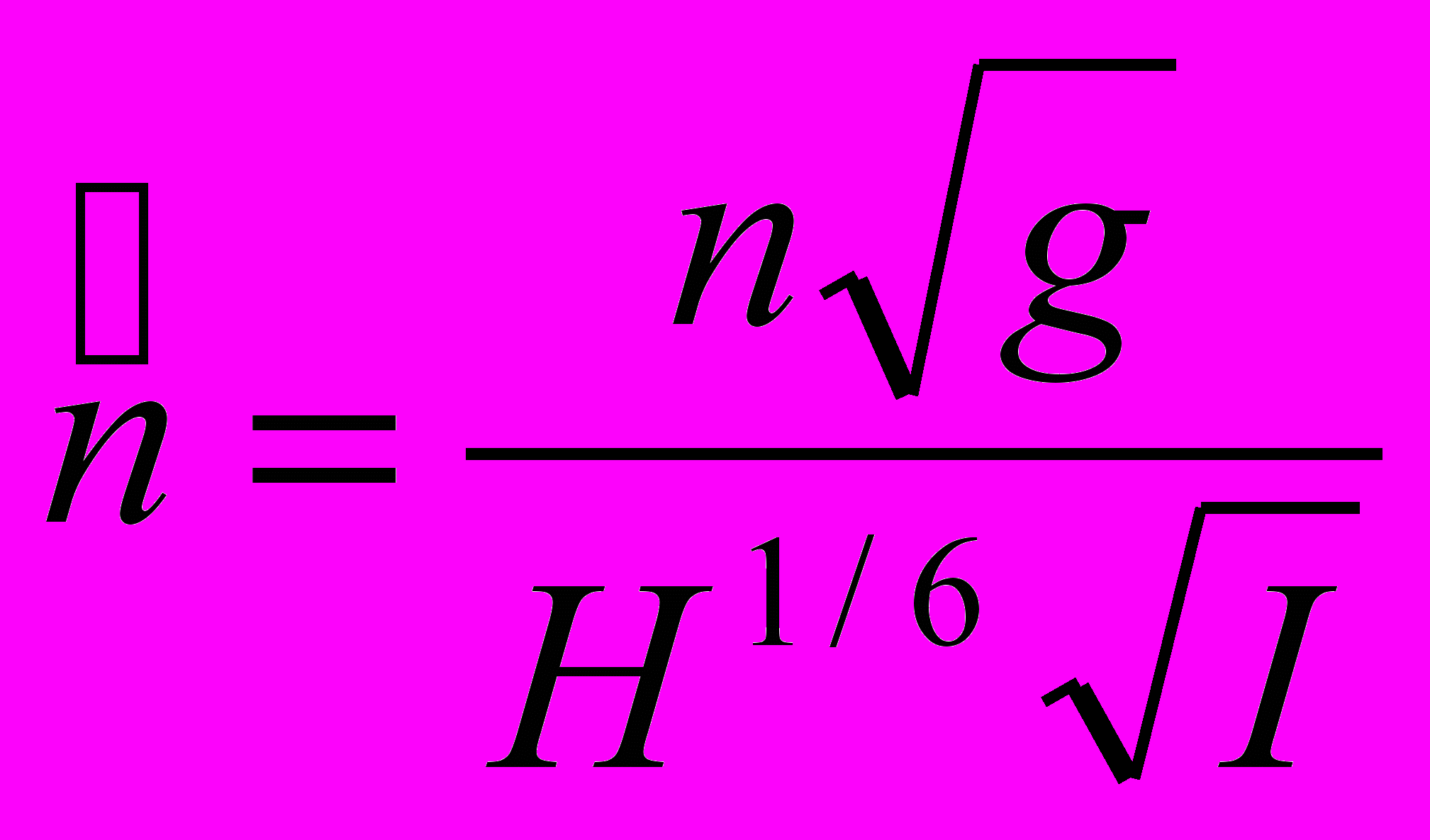Параметры варьировались на двух уровнях – минимальном (-) и максимальном (+), обозначающимися по общепринятым правилам как «-» и «+». Количество опытов полного факторного эксперимента (ПФЭ) рассчитано по формуле: N = 2^k , где N – количество опытов; 2 – количество уровней (в данном случае их два – верхний и нижний); k – количество факторов. Так как количество факторов – 2 и уровней – 2, то общее количество опытов 4. Матрица планирования эксперимента приведена в табл. 5, результаты расчетов – в табл. 6 и на рис. 5-8.

Таблица 5

Матрица планирования эксперимента

№ опыта		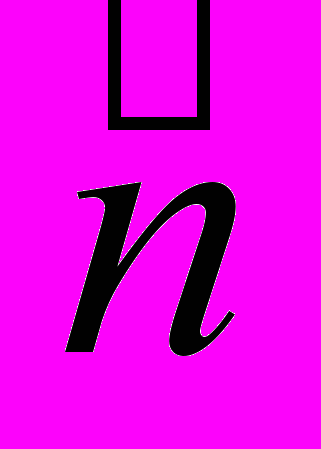m
1	-	-
2	+	-
3	-	+
4	+	+

После проведения расчетов выяснилось, что методика Историка дает достаточно точные результаты (расхождение с программой Школьникова во всех четырех опытах составляет от 1,5 до 7 %); методика же ВНИИ ГОЧС не достаточно точна - расхождение с программой Школьникова во всех четырех опытах составляет до 70 %.

В результате проведенных расчетов выяснилось, что для гидроузлов, не имеющих в нижнем бьефе других гидротехнических сооружений (плотин, мостовых переходов), а также внезапных значительных расширений русла методика Историка дает весьма достоверные результаты. Это было доказано проведением аналитической тестовой задачи. Для зон, где на параметры волны прорыва сказывается влияние таких сооружений необходимо искать пути учета гидравлических потерь напора (применение достаточно простых формул или коэффициентов пересчета и т.п.).



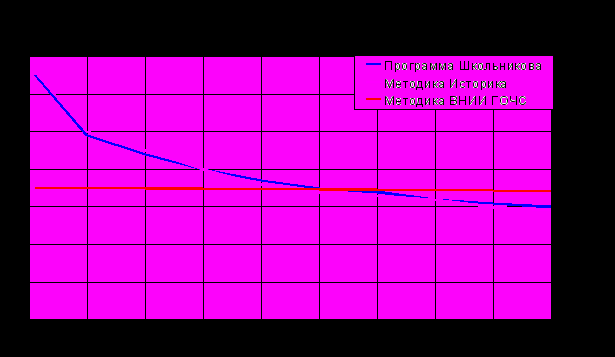
Рис. 5. Результаты расчетов, проведенных для условий опыта №1.


Таблица 6

Сравнение максимальных глубин затопления в расчетных створах, полученных различными методиками расчета

N опыта	Расстояние от гидроузла, км	Максимальная глубина затопления, м
		Методика Историка	Программа SV_1	Методика ВНИИ ГОЧС
1	1	6,5	6,6	3,51
	10	4,9	5	3,5
	22	4,4	4,5	3,49
	30	4	4	3,48
	40	3,7	3,6	3,47
	50	3,5	3,4	3,46
	60	3,4	3,3	3,45
	70	3,2	3,2	3,44
	80	3,1	3	3,43
	90	3	2,9	3,42
N опыта	Расстояние от гидроузла, км	Максимальная глубина затопления, м
		Методика Историка	Программа SV_1	Методика ВНИИ ГОЧС
2	0,2	1,34	1,49	2,97
	2	1	1,04	3,22
	4	0,88	0,88	2,8
	6	0,8	0,8	2,55
	8	0,76	0,72	2,38
	10	0,7	0,69	2,26
	12	0,68	0,66	2,16
	14	0,64	0,64	2,09
	16	0,62	0,61	2,03
	18	0,6	0,59	1,98
3	1	6,1	7,46	3,48
	10	4,9	5,06	3,5
	20	4,3	4,46	3,49
	30	4	4	3,48
	40	3,7	3,6	3,47
	50	3,5	3,47	3,46
	60	3,3	3,33	3,45
	70	3,2	3,2	3,44
	80	3,1	3,06	3,43
	90	3	2,93	3,42
4	0,2	1,38	1,49	1,99
	2	1	1,04	2,05
	4	0,88	0,88	1,98
	6	0,8	0,8	1,92
	8	0,76	0,72	1,87
	10	0,7	0,69	1,82
	12	0,68	0,67	1,78
	14	0,64	0,63	1,75
	16	0,62	0,61	1,72
	18	0,6	0,58	1,69

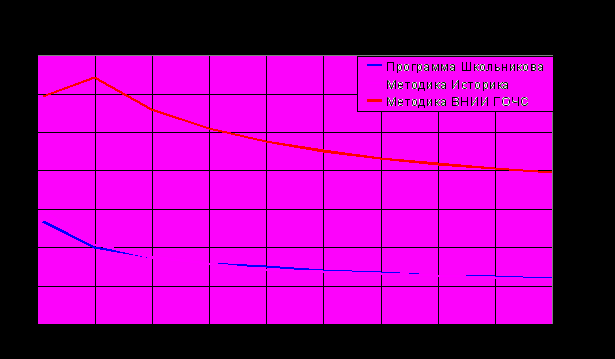
Рис. 6. Результаты расчетов, проведенных для условий опыта №2.




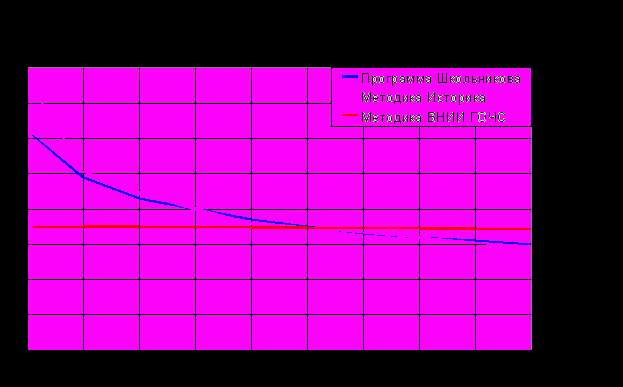
Рис. 7. Результаты расчетов, проведенных для условий опыта №3.



Рис. 8. Результаты расчетов, проведенных для условий опыта №4.