Тепловые двигатели и нагнетатели

Вид материала

Документы

Содержание 2. Насосы Центробежные насосы Действительный напор насоса Подводы и отводы центробежных машин Пересчет характеристик центробежных машин при изменении частоты вращения 1 — уплотнение колеса; 2 1 — уплотнение колеса; 2 Регулирование подачи центробежных нагнетателей Регулирование производительности дросселированием 4 — кривая КПД насоса; 5 Регулирование производительности байпасированием Hн можно считать равным изменению напора в сети H Регулирование производительности изменением частоты вращения рабочего колеса 1 (рис. 2.9) при частоте вращения n'

Подобный материал:

• Интегрированный урок «Тепловые двигатели» Цели урока, 28.56kb.
• Выбор рациональных параметров конструкции опор газотурбинных двигателей с межроторными, 218.67kb.
• Пособие по выполнению контрольных работ №1 и №2 Одобрено методической комиссией фбо, 1130.33kb.
• Учебник : С. В. Громов, Н. А. Родина 8 класс, 66.62kb.
• Совершенствование рабочего процесса дизеля с объемно-пленочным смесеобразованием при, 190.09kb.
• Конвертирование рабочего процесса транспортных двс на природный газ и водород 05. 04., 459.6kb.
• Урок по физике. 8 класс Тема: «Тепловые двигатели. Двигатель внутреннего сгорания», 113.91kb.
• Конспект урока физики в 10 классе По теме: «Тепловые двигатели и их роль в жизни человека», 37.82kb.
• Тепловые двигатели. Двигатель внутреннего сгорания, 139.75kb.
• «О структуре естественно-научного факультета», 54.97kb.

2. Насосы

Центробежные насосы

Общие закономерности работы центробежных насосов

Центробежный насос состоит из корпуса, в котором вращается рабочее колесо с лопатками. Под действием возникающего центробежного поля жидкость отбрасывается от центра к периферии, так что вблизи оси насоса возникает разрежение, а на периферии давление возрастает. Схема рабочего колеса показана на рис. 2.1 (см. также рис. 2.3). На рис. 2.2 изображены планы скоростей жидкости для идеального центробежного насоса. На рис. 2.1 и 2.2 приняты следующие обозначения: индекс «1» соответствует точке входа на лопатку колеса, индекс «2» — точке выхода с лопатки; D — диаметр входа на лопатку (выхода с лопатки); b — ширина проточной части колеса; d — толщина лопатки; n — частота вращения рабочего колеса; u — вектор абсолютной скорости частицы (элемента) жидкости; u_от — вектор относительной скорости элемента жидкости (по отношению к лопатке); u_пер — вектор переносной скорости колеса (т. е. окружная скорость колеса); u_R — радиальная составляющая вектора абсолютной скорости элемента жидкости. Углы между касательными к лопатке и к окружности колеса: на входе b₁, на выходе — b₂. Углы между вектором абсолютной скорости u и касательной к окружности колеса: на входе — a₁, на выходе — a₂.



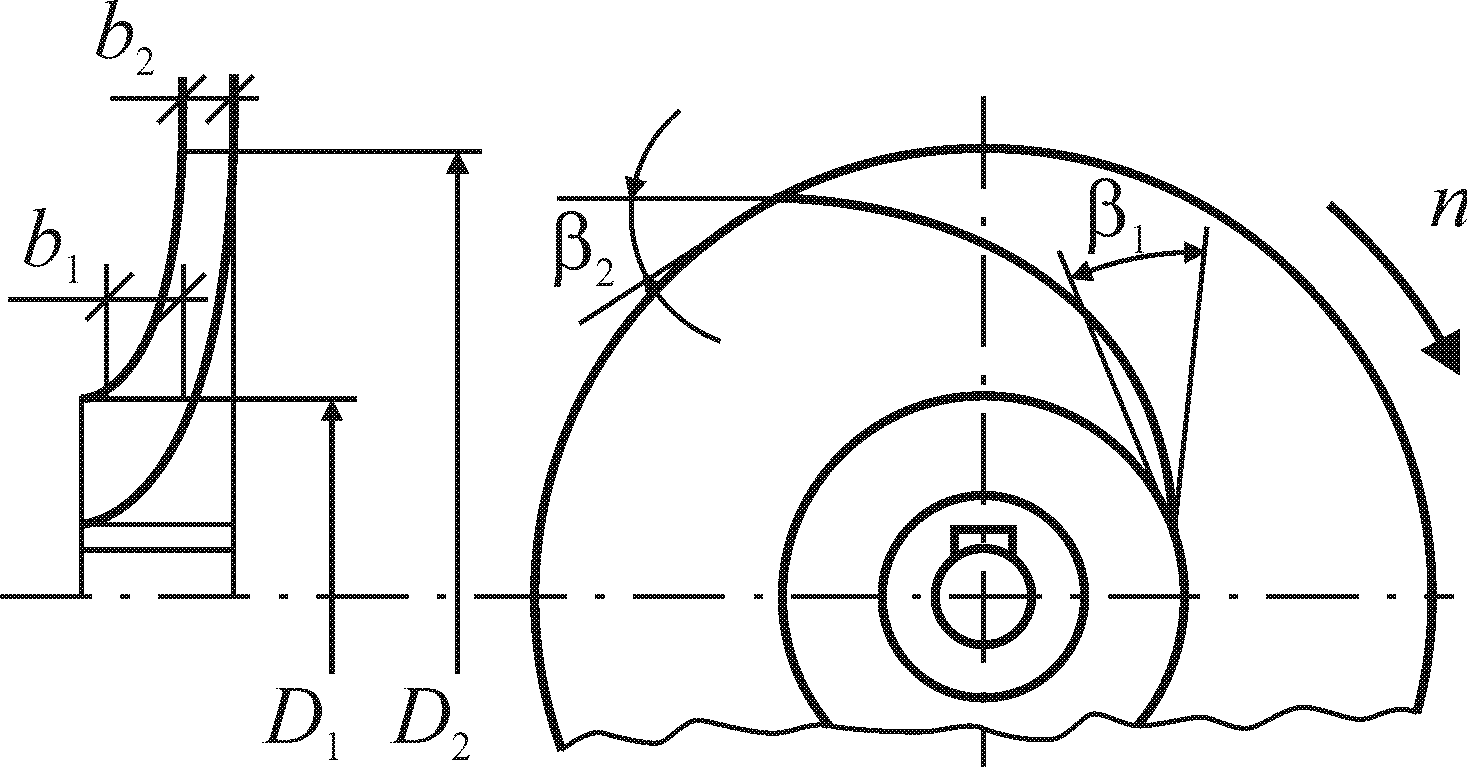
Рис. 2.1. Рабочее колесо центробежного насоса



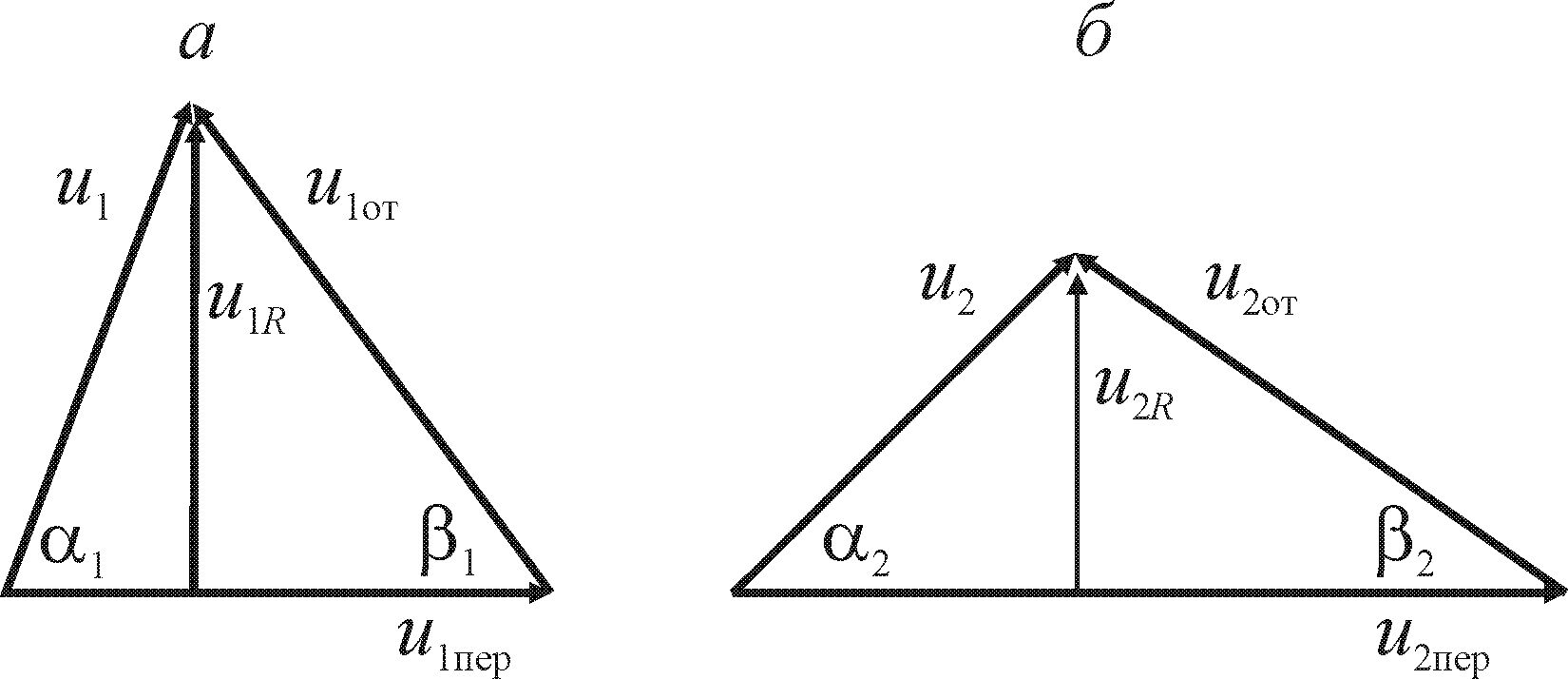
Рис. 2.2. Планы скоростей:
а) при входе жидкости в колесо;
б) при выходе жидкости из колеса

При отсутствии специальных направляющих аппаратов подкрутка жидкости перед ее входом на лопатки рабочего колеса невелика, при этом скорость u₁ направлена радиально, т. е. a₁ = 90, u₁ = u_1R. Для достижения безударного входа жидкости на лопатки при заданной оптимальной подаче при конструировании центробежного насоса выбирают соответствующий угол b₁.

При бесконечно большом количестве лопаток с бесконечно малой толщиной теоретический напор насоса (формула Эйлера)

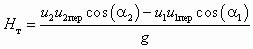. (2.1)

Если подкрутка отсутствует (a₁ = 90), то cos(a₁) = 0; тогда, используя выражение для подачи

Q_т = D₂b₂u_2R, (2.2)

теоретический напор можно выразить в виде

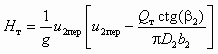. (2.3)

Действительный напор насоса меньше теоретического по следующим причинам: реальные лопатки имеют конечную толщину и их количество ограниченно, поэтому в межлопастных каналах колеса возникает циркуляция жидкости, план скоростей искажается; при течении жидкости в насосе (в межлопаточных каналах, при входе жидкости на лопатки, в улитке, во всасывающем и нагнетательном патрубках) неизбежны гидравлические потери. Первый фактор учитывают при помощи коэффициента циркуляции

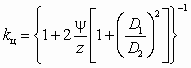, (2.4)

где — коэффициент, зависящий от шероховатости поверхности проточной части колеса (принимают y   = 0,9¸ 1,1).

Второй фактор характеризуется гидравлическим КПД — h_г, который для современных гидравлических машин колеблется в пределах 0,80–0,96.

Действительный напор насоса можно рассчитать по формуле

Н = Н_{т h г} k_ц. (2.5)

Действительная подача реального насоса с учетом толщины лопаток

Q = Q_{т h об} k₂, (2.6)

где h_об — объемный КПД насоса; k₂ — коэффициент, учитывающий стеснение проточной части насоса лопатками: k₂ = .

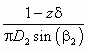Отношение статического напора к полному для идеального насоса с безударным входом на лопатки (при оптимальном угле b₁)

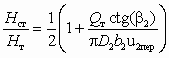, (2.7)

причем 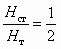при b₂ = 90. В реальных насосах для достижения высокого КПД угол b₂ выбирают в диапазоне 15–35 (лопатки загнуты назад), при этом снижается скоростной напор, а значит, и гидравлические потери внутри насоса; помимо этого, соблюдение условия b₂ < 90 позволяет избежать возникновения кавитации в зоне А (рис. 2.3). В ряде конструкций центробежных вентиляторов для достижения высоких скоростных напоров лопатки выполняют загнутыми вперед, т. е. b₂ > 90, что приводит, однако, к снижению КПД.

Подводы и отводы центробежных машин

Центробежные машины содержат помимо корпуса и рабочего колеса, закрепленного на валу привода, еще два конструктивных элемента: подводы и отводы (рис. 2.3).

Подводом называют часть проточной полости машины, подводящую перемещаемую среду к входному отверстию рабочего колеса. Подвод правильной конструкции для сохранения высокого гидравлического КПД машины должен давать равномерное, осесимметричное распределение потока по входному сечению рабочего колеса. Потери в подводе должны быть минимальными, для этого скорости в его сечениях не должны быть высокими. Поэтому диаметр подводящего патрубка центробежных насосов обычно больше диаметра нагнетательного патрубка, а сам подвод выполняют либо спиральным (при поперечном потоке), либо в виде прямолинейного конфузора (при осевом потоке) — рис. 2.3.



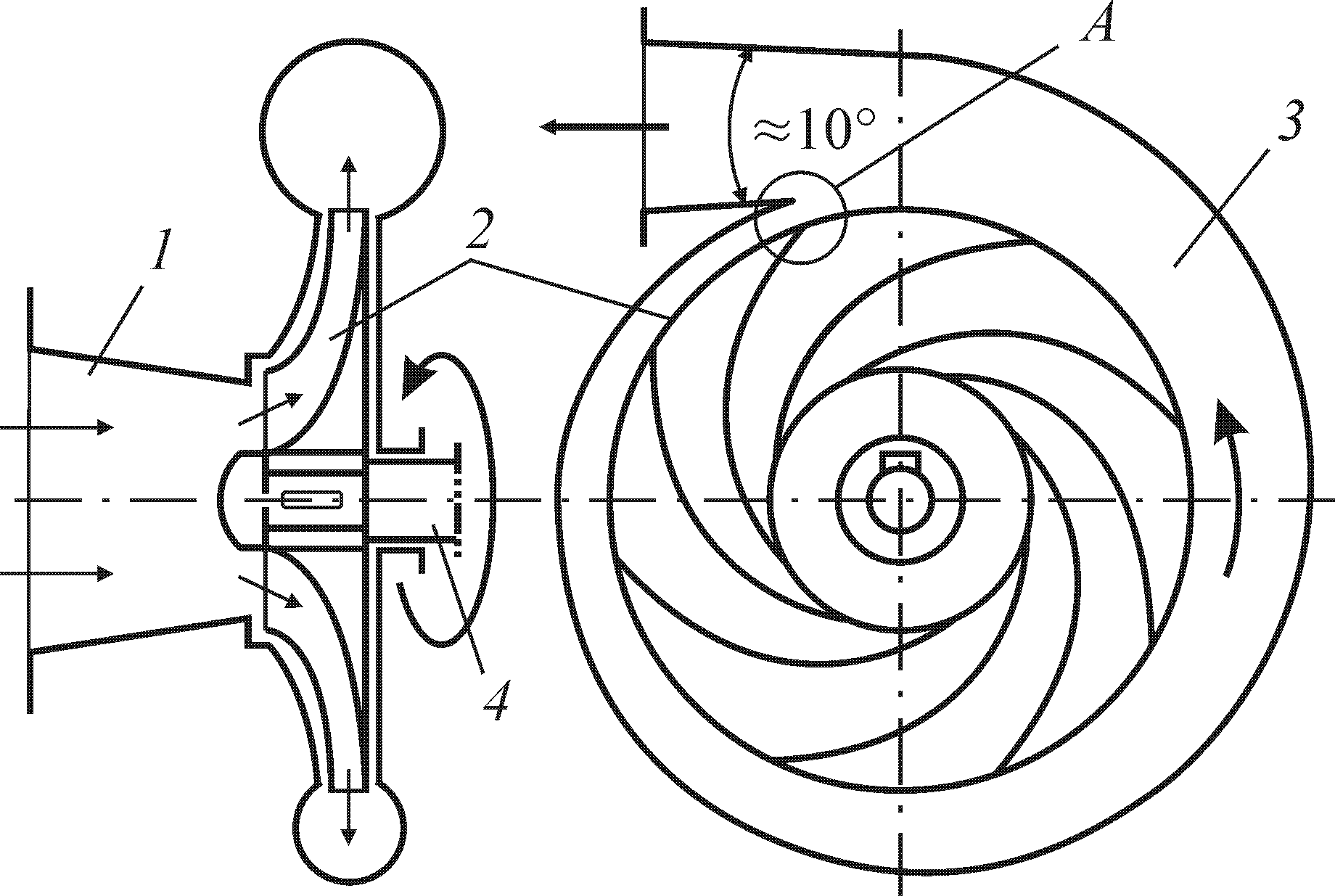
Рис. 2.3. Схема центробежной машины:
1 — подвод конфузорного типа; 2 — рабочее колесо;
3 — спиральный отвод; 4 — приводной вал;
А — зона возможной кавитации

Отводом называют часть проточной полости машины, принимающую перемещаемую среду из рабочего колеса и частично преобразующую кинетическую энергию этой среды в потенциальную.

Известны три типа отводов: кольцевой (цилиндрическое пространство постоянной ширины, охватывающее рабочее колесо), спиральный (представляет собой комбинацию криволинейного диффузора с кольцевым отводом — рис. 2.3) и лопаточный (обычно используется в многоступенчатых машинах и представляет собой систему нескольких диффузорных каналов,
окружающих рабочее колесо — рис. 2.4).



Рис. 2.4. Лопаточный отвод центробежной машины

Подобие центробежных насосов. Коэффициент быстроходности

Движение жидкостей (газов) в проточной полости машин весьма сложно и не поддается точному теоретическому описанию. Поэтому для определения (или уточнения) характеристик гидравлических машин промышленных размеров нередко используют метод физического моделирования, т. е. по результатам испытаний модели (лабораторного образца либо действующей промышленной машины) рассчитывают характеристики аналогичных машин с другими размерами, частотой вращения и т. д. при соблюдении законов подобия между ними.

Основное уравнение реального центробежного насоса (2.5) можно выразить в безразмерном виде

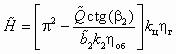, (2.8)

где 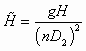— безразмерный напор насоса; 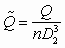— безразмерная производительность насоса; 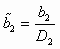— геометрический симплекс.

Для выполнения условий гидродинамического подобия необходимо, чтобы рабочие колеса подобных центробежных насосов удовлетворяли требованиям:

- геометрического подобия, т. е. 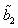= const, b₂ = const, k₂ = const;

- кинематического подобия, т. е. должны быть подобны поля скоростей и h_об = const, k_ц = const;

- динамического подобия, т. е. должны быть одинаковыми режимы течения жидкости в проточной части подобных насосов: h_г = const.

Из этих условий следует, что подобные насосы обладают тождественными характеристиками, если их представить в безразмерном виде (2.8). Ряд подобных насосов можно охарактеризовать числом подобия — соотношением оптимального напора H_опт и оптимальной подачи Q_опт, соответствующих оптимальному режиму работы, при котором наблюдается безударный вход жидкости на лопатки колеса, а значит, и максимальный КПД. В практике насосостроения в качестве такого числа подобия принят коэффициент быстроходности

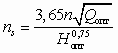, (2.9)

где n — частота вращения рабочего колеса, с^–1.

Коэффициентом быстроходности данной машины (насоса, компрессора, вентилятора) называют число, равное частоте вращения рабочего колеса машины, геометрически подобной данной, но имеющей подачу 0,075 м³/с и напор 1 м в режиме максимального КПД.

Значения коэффициента быстроходности для различных типов насосов следующие:

Центробежные	40–300
Диагональные	300–600
Осевые	600–1200

Таким образом, по мере увеличения n_s производительность насосов увеличивается, а напор снижается.

Коэффициент быстроходности практически однозначно связан с геометрическими размерами рабочего колеса (см. рис. 2.1):

ns	60	100	180
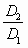	3	2	1,5
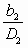	0,05	0,1	0,2

Пересчет характеристик центробежных машин при изменении частоты вращения

Пусть известны параметры H_I, Q_I, N_эфI насоса (вентилятора) при частоте вращения n_I. Требуется получить эти параметры при частоте вращения n_II. При удовлетворении условия гидродинамического подобия течения жидкости в проточной части насоса, т. е. h  = const, получены формулы пропорциональности

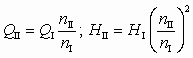, (2.10)

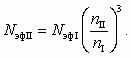(2.11)

Очевидно, что эти формулы справедливы лишь в узком диапазоне изменения n, т. к. с изменением частоты вращения изменяется скорость течения жидкости в насосе, а значит, и число Рейнольдса, т. е. нарушается условие гидродинамического подобия. На практике формулами (2.11) пользуются в области .

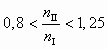Уравнение

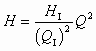. (2.12)

называют параболой подобных режимов (рис. 2.9), т. к. она характеризует зависимость H от Q с изменением частоты вращения n при условии постоянства  .

Компенсация осевых усилий в центробежных насосах

Осевые силы возникают в центробежных машинах как результат неодинакового распределения давлений, действующих на рабочие колеса с передней (обращенной к всасывающему патрубку) и задней сторон. Кроме того, осевая сила возникает и в результате динамического действия потока, входящего в рабочие колеса. В крупных многоступенчатых центробежных насосах осевые силы могут достигать нескольких тонн, приводя к преждевременному износу подшипников и уплотнений; в компрессорных машинах в силу малой плотности газа эти силы не столь значительны.



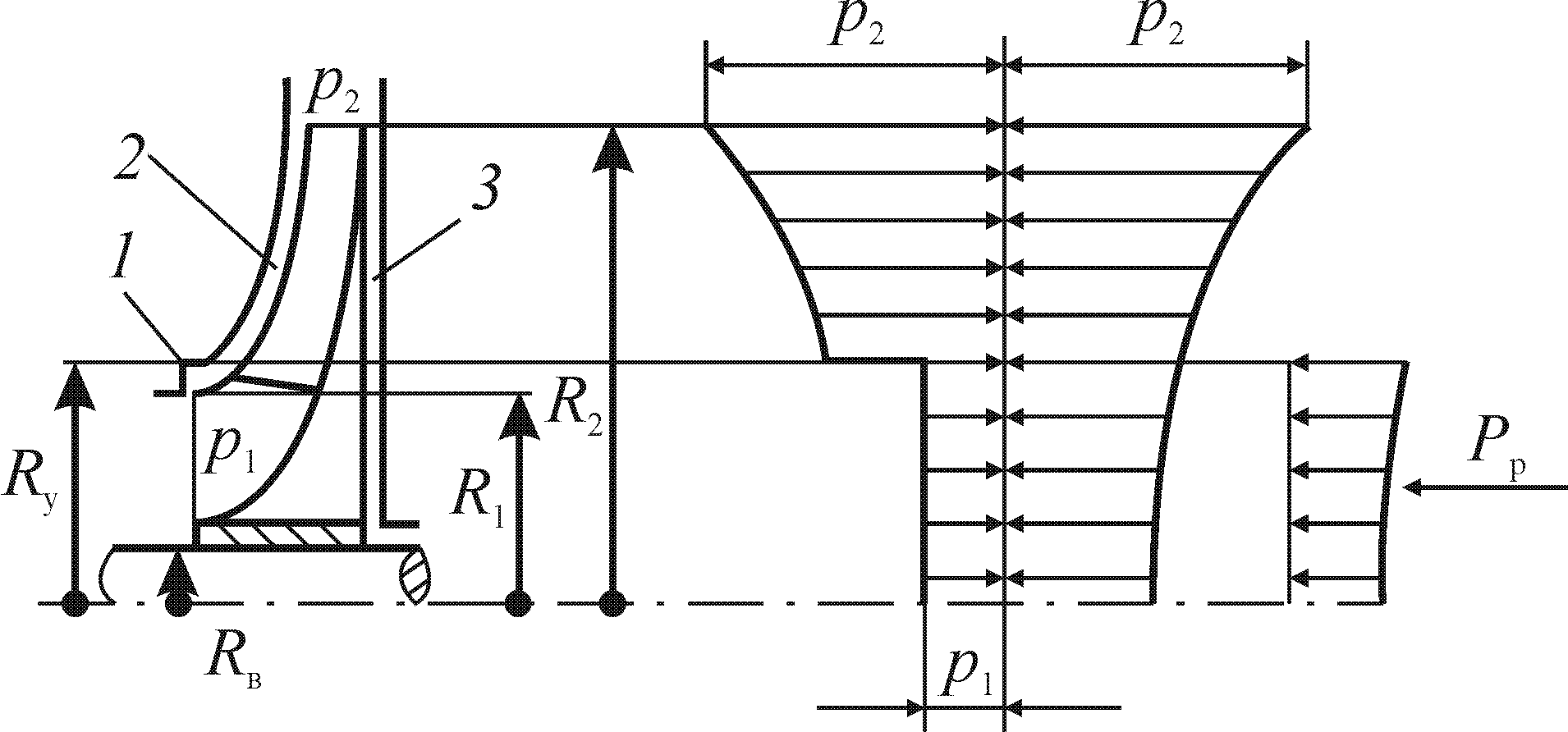
Рис. 2.5. Распределение осевых давлений по наружным поверхностям колеса
центробежной машины:
1 — уплотнение колеса; 2, 3 — зазоры

Пусть у входа в рабочее колесо давление равно р₁ (рис. 2.5). При наличии уплотнения 1 на входном диаметре колеса конечное давление р₂ распространяется через зазоры 2 и 3 между колесом и корпусом насоса. В полости закрытого рабочего колеса между входными и выходными кромками лопаток (т. е. на радиусе от R₁ до R₂) осевые силы полностью уравновешены. Действительное осевое давление в любой точке наружной поверхности колеса определяется давлением р₂ (на радиусе R₂) и центробежным давлением, обусловленным вращением жидкости в зазорах 2 и 3. В передней же стороне на радиусе R_у действует постоянное давление р₁. Вследствие этой асимметрии и возникает осевая сила Р_р (рис. 2.5). В силу малости зазоров 2 и 3 средняя угловая скорость жидкости в них вдвое меньше скорости колеса на данном радиусе, что позволило получить формулу для осевой силы:

 (2.13)

где w — угловая скорость вращения колеса, с^–1; w  = 2p n.

Сила, обусловленная динамическим давлением входящего потока на колесо:

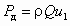. (2.14)

Суммарная осевая сила, действующая на одно рабочее колесо центробежной машины:

Р_ос = Р_р – Р_д. (6.3.2.15)

Как видно из формулы (2.13), при данных размерах колеса и частоте вращения осевая сила тем выше, чем больше давление р₂. Поэтому при дросселировании, когда р₂ возрастает, осевая сила также растет.

Компенсация осевой силы происходит благодаря следующим конструктивным решениям:

- применению рабочего колеса с двусторонним входом либо с двусторонним симметричным входом (для многоступенчатых машин);

- использованию переточных отверстий и ложной ступицы;

- выполнению импеллера на задней стороне рабочего колеса;

- в многоступенчатых насосах — установке разгрузочного диска (гидравлической пяты).

Рабочее колесо с двусторонним входом (рис. 2.6, а) не передает осевой силы на вал в силу своей симметрии; колеса такого типа широко используются в одноступенчатых центробежных насосах. При использовании переточных отверстий 2 (либо специальной соединительной трубки) и ложной ступицы 3 (рис. 2.6, б) диаметр последней выполняют таким же, как и диаметр уплотнения 1 рабочего колеса. Благодаря переточным отверстиям давления по обе стороны колеса на радиусе R_у выравниваются и сила Р_р исчезает. Динамическое усилие Р_д невелико и может восприниматься подшипником. Этот способ уравновешивания удобен и прост и поэтому широко распространен. Его недостатком является некоторое понижение объемного КПД за счет дополнительного перетекания через отверстия.



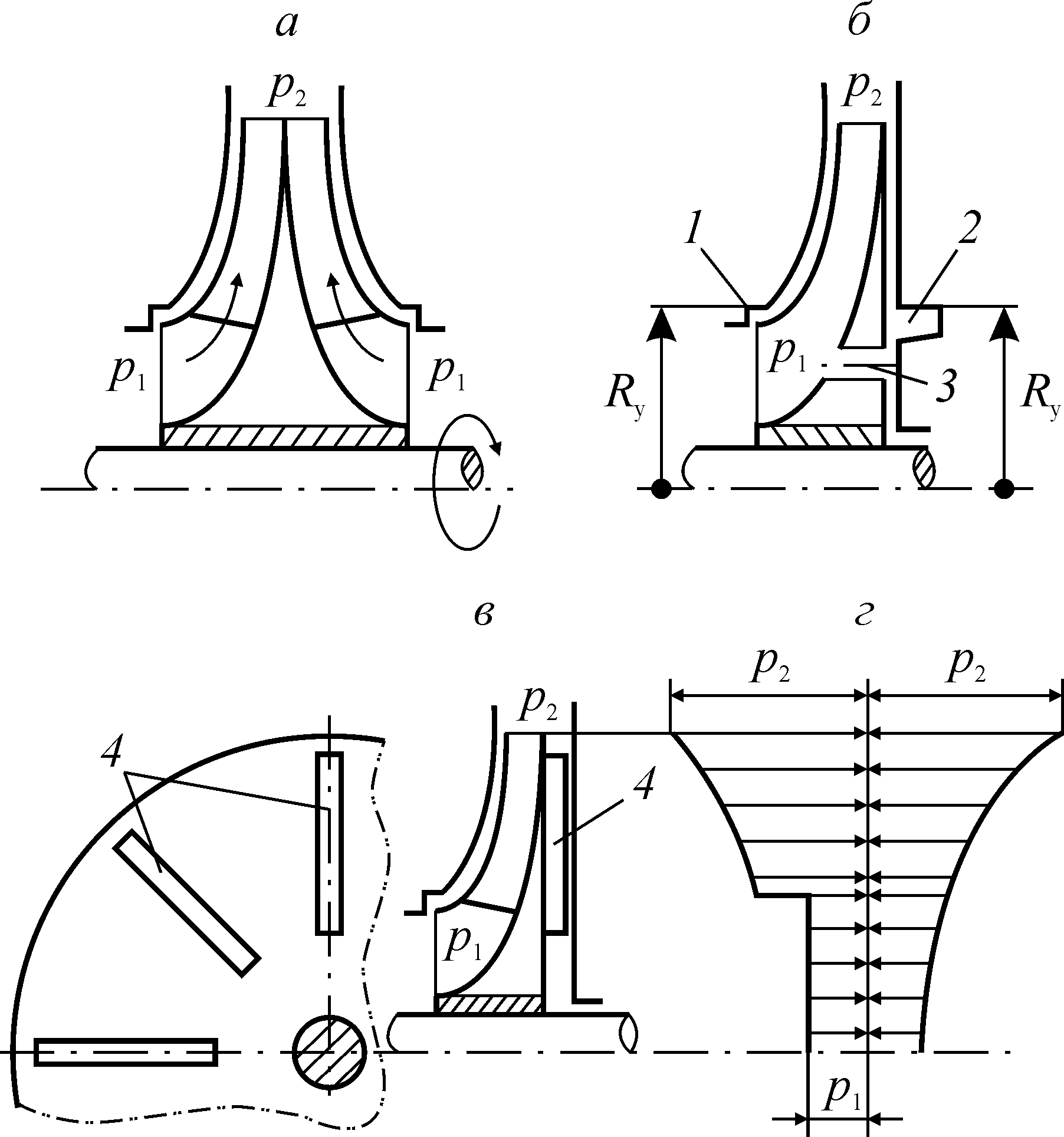
Рис. 2.6. Способы компенсации осевой силы в центробежных насосах:
а) колесо с двусторонним входом жидкости;
б) колесо с переточными отверстиями и ложной ступицей;
в) колесо с импеллером;
г) эпюра давлений для колеса с импеллером
1 — уплотнение колеса; 2 — ложная ступица;
3 — переточные отверстия; 4 — лопасти импеллера

Импеллер, состоящий из радиальных лопаток 4 на задней стороне рабочего колеса (рис. 2.6, в), при заданной частоте вращения создает такое центробежное поле давления, площадь эпюры которого (рис. 2.6, г) в точности равна площади эпюры центробежного давления в зазоре между передней частью колеса и корпусом (рис. 2.6, в). Это приводит к уравновешиванию осевой силы. Недостаток метода: при изменении частоты вращения эффект компенсации осевой силы нарушается.

Регулирование подачи центробежных нагнетателей

Основной задачей регулирования насоса является подача в сеть заданного расхода жидкости. Для этого может использоваться один из следующих способов: дросселирование; байпасирование; изменение частоты вращения рабочего колеса; регулирование поворотными направляющими на входе в рабочее колесо, т. е. подкрутка потока на входе. Первые три способа описаны ниже, четвертый обычно применяют для регулирования подачи вентиляторов и центробежных компрессоров; так, при a₁ < 90 напор, создаваемый нагнетателем, уменьшается (см. (2.1) и план скоростей на рис. 2.2), а при a₁ > 90 напор увеличивается. При включении нагнетателя в сеть соответственно будет уменьшаться или увеличиваться и подача.

Определив характеристику сети, при заданном расходе находят необходимый напор, а затем ориентировочно, с некоторым запасом, подбирают один или несколько типов насосов, способных обеспечить эти два параметра в сети. На практике характеристики насосов обычно заданы графически, поэтому задачи, связанные с подбором наиболее экономичного насоса либо системы параллельно или последовательно включенных насосов, а также способа его (их) регулирования, удобно решать также графически.

Регулирование производительности дросселированием

Метод заключается в том, что в сети последовательно с насосом устанавливается устройство с переменным (регулируемым) живым сечением, именуемое дросселем, в котором рассеивается (диссипируется) часть напора насоса (рис. 2.7).



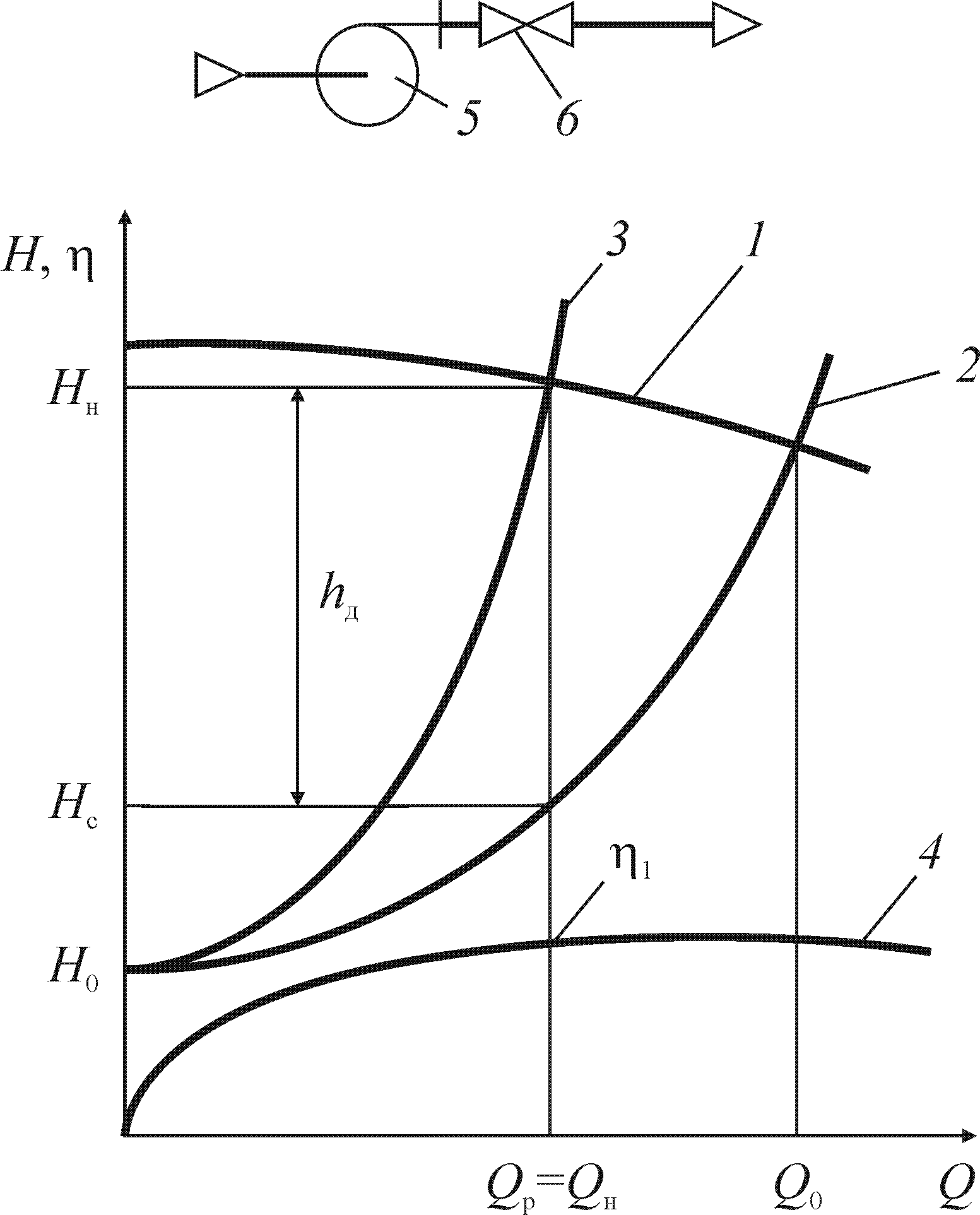
Рис. 2.7. Регулирование производительности лопастных насосов дросселированием:
1 — характеристика насоса;
2 — исходная характеристика сети;
3 — характеристика сети с дросселем;
4 — кривая КПД насоса;
5 — насос лопастного типа; 6 — дроссель

В качестве таких дросселей используется запорно-регулирующая арматура, т. е. задвижки, вентили, а в воздуховодах — заслонки (поворотного типа и шиберные).

Место установки дросселей для насосов лопастного типа — линия нагнетания, поскольку в случае их установки на линии всасывания давление на входе в насос уменьшается (за счет появления потерь на дросселе), в результате возрастает риск появления кавитации в насосе.

На рис. 2.7 показана совмещенная характеристика сети и центробежного насоса при дросселировании. Из графиков видно, что если включить насос в сеть без регулирующих устройств, то рабочая точка, являющаяся пересечением характеристики насоса 1 и характеристики 2 сети, будет иметь абсциссу Q₀, лежащую значительно правее абсциссы заданной рабочей производительности Q_р.

После включения дросселя в сеть ее сопротивление возрастет. Это означает, что кривая характеристики сети станет круче. Характеристику сети можно плавно регулировать путем изменения степени закрытия дросселя. Таким путем и достигается настройка системы на требуемую производительность Q_р. Характеристика сети 3 при этом будет пересекать характеристику насоса 1 в точке с абсциссой Q_р. Ордината этой точки Н_н есть напор насоса. Из графиков видно, что этот напор складывается из двух частей: падения напора в сети Н_с и потерь напора в дросселе h_д. Величина Н_с находится как ордината точки пересечения вертикальной линии Q = Q_р = const с исходной характеристикой 2 сети; значение h_д — как разность h_д = Н_н – Н_с.

Особенностью регулирования производительности дросселированием является последовательное соединение насоса, сети и дросселя. Поэтому расходы в них будут одинаковыми: Q_р = Q_н. Все характеристики насоса (напор, КПД, эффективная мощность, кавитационный запас) обычно задаются графически как функции расхода. Поэтому в данном случае КПД насоса легко находится как значение h₁ = h(Q_н). Однако общий КПД установки будет меньше, поскольку часть энергии, сообщаемой насосом жидкости, рассеется в дросселе. По определению КПД установки h есть отношение полезной мощности N_пол = rgQ_рH_с к затраченной (эффективной) 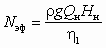, т. е. КПД установки при дросселировании

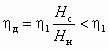. (2.16)

В насосах объемного типа способ дросселирования использовать нельзя (см. ниже).

Регулирование производительности байпасированием

Метод заключается в том, что в сети параллельно с насосом устанавливается байпасная (обходная, by pass [англ.] — посредством перепуска, обхода) линия с дросселем, через которую пропускается избыточная часть жидкости (рис. 2.8), т. е. производительность насоса Q_н может быть представлена как сумма

Q_н = Q_с  Q_б,

где Q_с = Q_р — расход жидкости в сети (рабочий расход); Q_б — расход жидкости через байпасную линию.

В схеме регулирования производительности байпасированием полный напор насоса H_н можно считать равным изменению напора в сети H_с:

H_н = H_с.

На рис. 2.8 показана совмещенная характеристика сети и насоса при байпасировании. Из графиков видно, что если включить насос в сеть при закрытом дросселе на байпасной линии, то рабочая точка, являющаяся пересечением характеристики 1 насоса и характеристики 2 сети, будет лежать правее заданной рабочей производительности Q_р; при этом Q_б = 0. По мере открывания байпасной линии расход через нее Q_б возрастает, а напор в системе снижается (байпасная линия как бы «шунтирует» источник энергии — насос). При этом благодаря наклону характеристик сети и насоса производительность сети будет уменьшаться, а подача насоса — увеличиваться. Этот процесс регулирования продолжается до тех пор, пока расход в сети Q_с не станет равным рабочему расходу Q_р.



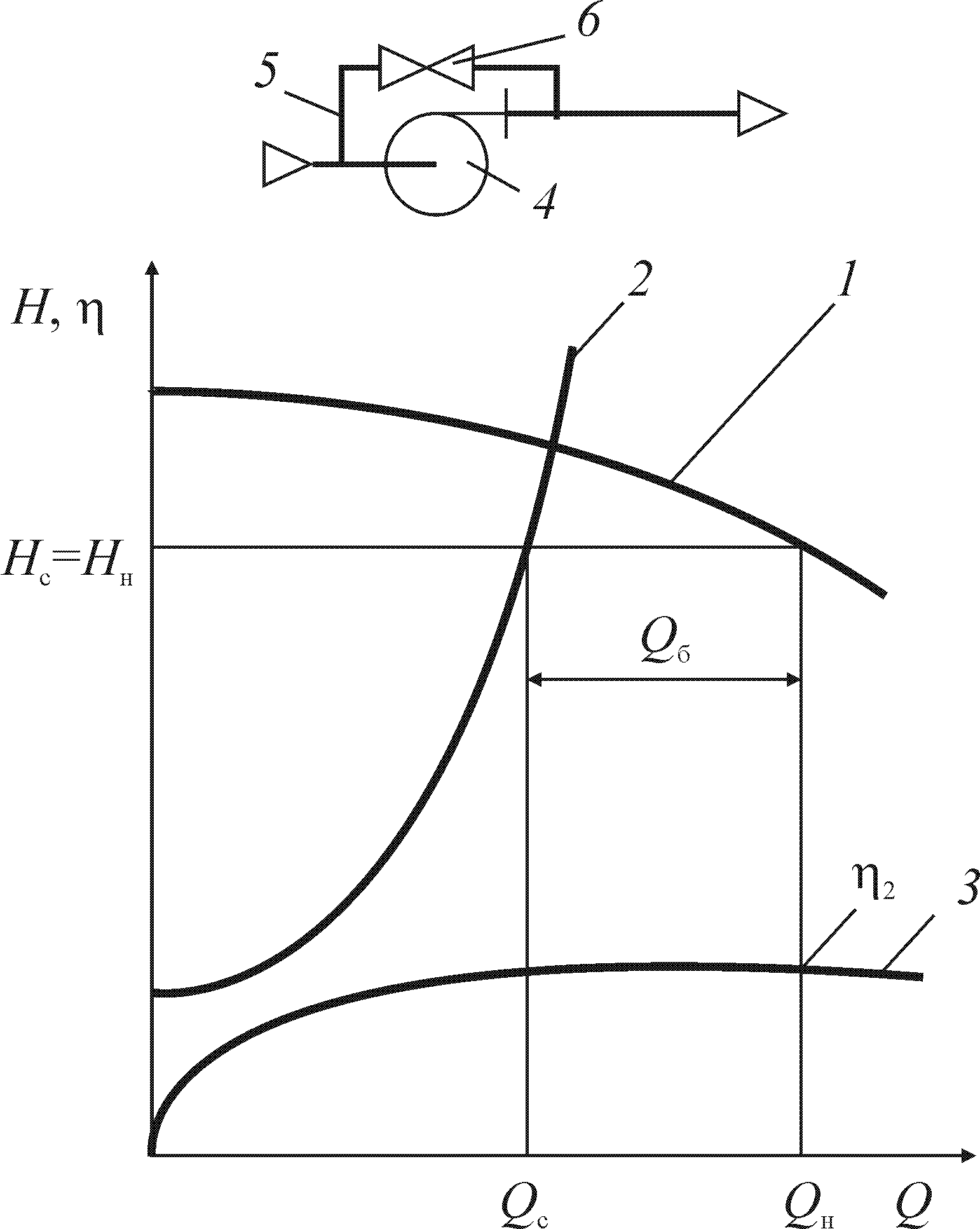
Рис. 2.8. Регулирование производительности насосов байпасированием:
1 — характеристика насоса; 2 — характеристика сети;
3 — кривая КПД насоса; 4 — насос;
5 — байпасная линия;
6 — байпасный регулятор расхода

Не вся энергия, передаваемая насосом жидкости, будет использоваться в сети, поскольку часть жидкости с высоким давлением возвращается через байпасную линию на всасывающую сторону насоса с низким давлением, теряя энергию. Коэффициент полезного действия насоса h ₂ определяется по его производительности Q_н (рис. 2.8). КПД установки h есть отношение полезной мощности N_пол = gQ_рH_с к затраченной (эффективной)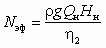, откуда, учитывая равенство H_н = H_с, находим КПД установки при байпасировании:

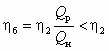. (2.17)

Сравнивая КПД при дросселировании и байпасировании, выбирают наиболее экономичный способ регулирования.

Регулирование производительности изменением частоты вращения рабочего колеса

Изменение частоты вращения, как и геометрических размеров гидравлических машин, должно проводиться с учетом теории гидродинамического подобия (см. выше).

Пусть известна характеристика насоса 1 (рис. 2.9) при частоте вращения n', а также характеристика сети 3. Необходимо обеспечить производительность Q_С, т. е. рабочей точкой должна стать точка С. Построим параболу подобных режимов 5, описываемую выражением

.



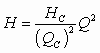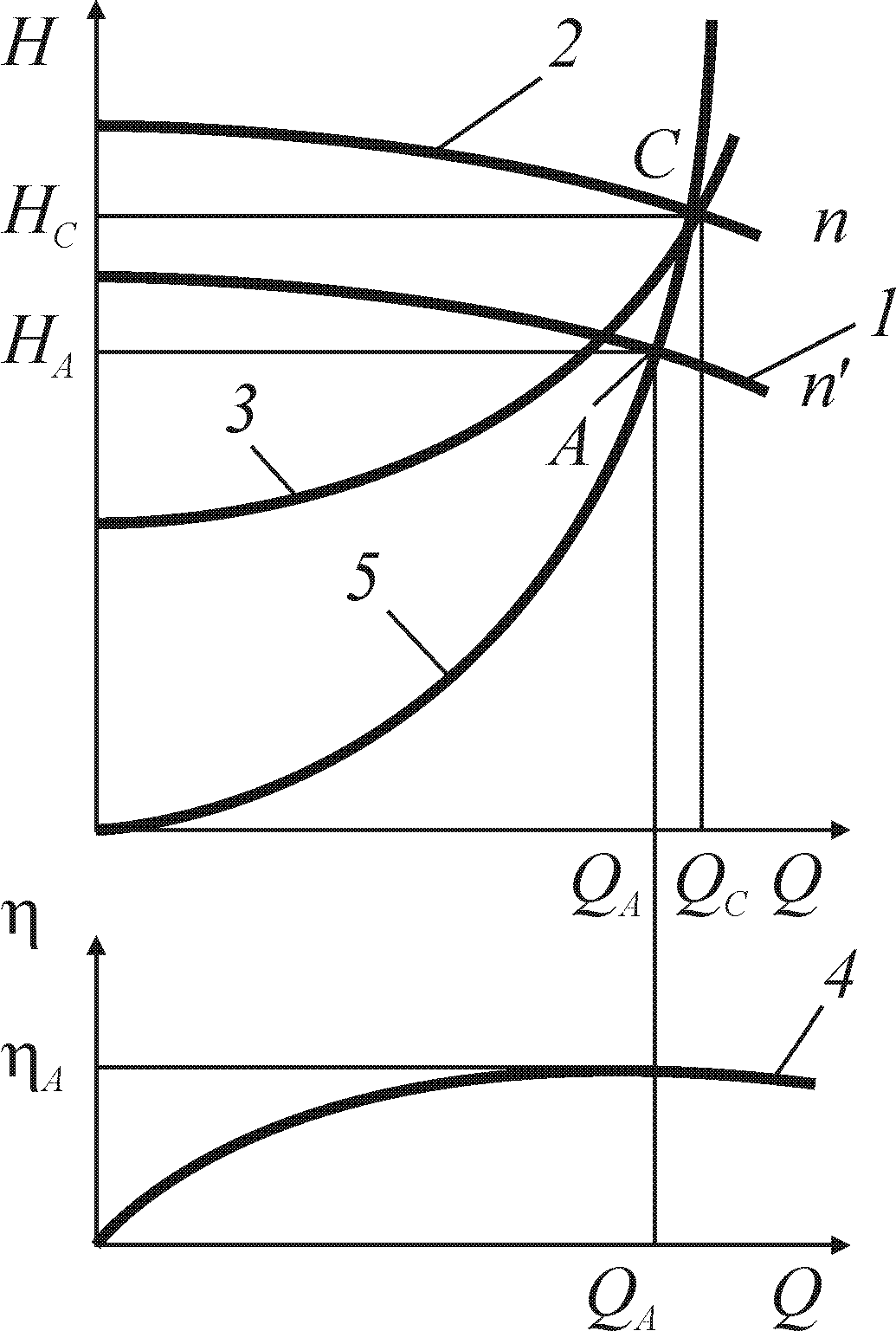
Рис. 2.9. Регулирование производительности насосов изменением частоты вращения рабочего колеса;
1 — характеристика насоса при частоте n';
2 — характеристика насоса при частоте n;
3 — характеристика сети; 4 — кривая КПД насоса;
5 — парабола подобных режимов

Пересечение линий 1 и 5 даст точку А, параметры в которой подобны параметрам в точке С, а КПД одинаковы. Искомая частота вращения n рабочего колеса определяется по любой из формул (2.10, 2.11). Учитывая постоянство размеров колеса насоса, можно записать



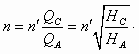
Этот способ регулирования производительности является теоретически наиболее экономичным, однако далеко не всегда используется на практике из-за относительно высокой стоимости регулируемого привода.