Конспект открытого урока по теме «Закон всемирного тяготения»

Вид материала

Урок

Подобный материал:

• Урок по теме «Закон всемирного тяготения», 42.5kb.
• Урок по физике в 9 классе Тема урока: закон всемирного тяготения, 114.37kb.
• Самостоятельная работа по теме: "Закон всемирного тяготения"., 92.26kb.
• Тема урока: «Закон всемирного тяготения» 9 класс Тип урока, 44.28kb.
• Горбуновой Натальи Сергеевны Информатика: Раздел: Представление о системе объектов, 39.63kb.
• План-конспект открытого урока в 5 «В» классе по теме «Семья», 43.36kb.
• Конспект Открытого урока по алгебре и началам анализа в 10 классе (для слушателей мрио), 49.21kb.
•  - высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз,, 99.34kb.
• А. А. Гришаев этот «цифровой» физический мир в 5-ти разделах с Дополнением Раздел организация, 975.13kb.
• Закон всемирного тяготения, 34.95kb.

План - конспект открытого урока по теме

«Закон всемирного тяготения»

Современный уровень развития науки и техники не мыслим без использования компьютерных технологий в преподавании физики и астрономии в школе. Одно из направлений использования компьютера на уроках – .составление и показ презентации учащимися.

Тип урока – комбинированный

Цель урока – Изучить закон всемирного тяготения, показать его практическую значимость. Шире раскрыть понятие взаимодействия тел на примере этого закона и ознакомить учащихся с областью действия гравитационных сил.

Задачи урока:

1. Образовательные:
   

• сформировать понятие гравитационных сил, добиться усвоения закона всемирного тяготения, познакомить с опытным определением гравитационной постоянной;
  

2. Воспитательные:
   
   • формирование системы взглядов на мир;
     
3. Развивающие:
   
   • развитие речи, мышления;
     
   • совершенствование умственной деятельности: анализ, синтез, классификация, способность наблюдать, делать выводы, выделять существенные признаки объектов, выдвигать гипотезы, проверять результаты.
     

Оборудование к уроку:

• Компьютер, с рекомендуемыми техническими требованиями: Windows 95/98/ME/NT/2000/XP, Internet Explorer 5.0, Pentium-150, 100 Мб свободного дискового пространства, 64 Мб оперативной памяти, СD-ROM, SVGA 800x600
  
• интерактивный курс «Физика, 7–11 классы»
  
• видеопроектор, экран
  
• презентация учащихся
  

Домашнее задание: §15,упр15

План урока:

1. Организация начала урока, объявление темы и цели урока – 3 мин.
   
2. Повторение пройденного материала по теме «Три закона Ньютона»– 7 мин.
   
3. Новый материал– 20 мин.
   
4. Просмотр интерактивного урока и презентации -12 мин.
   
5. Подведение итогов урока – 3 мин.
   

Ход урока:

1. Цель урока – Сегодня на уроке мы с вами изучим закон всемирного тяготения, покажем его практическую значимость. Шире раскроем понятие взаимодействия тел на примере этого закона и ознакомимся с областью действия гравитационных сил.
   
2. Повторение. Проверка домашнего задания. Начнем с того, что мы уже знаем. Вспомним и ответим на следующие вопросы:
   

• Что называется свободным падением тела?
  
• Что такое ускорение свободного падения?
  
• Почему в воздухе кусочек ваты падает с меньшим ускорением, чем железный шарик?
  
• Кто первым пришел к выводу о том, что свободное падение является равноускоренным движением?
  
• Действует ли сила тяжести на подброшенное вверх тело во время его подъема.
  
• С каким ускорением движется подброшенное вверх тело при отсутствии сопротивления воздуха?
  
• Первый закон Ньютона.
  
• Второй закон Ньютона.
  

3. Изучение нового материала.

На доске помещены портреты ученых и приготовлен план беседы с учащимися об исторических фактах, предшествующих открытию закона всемирного тяготения:

1).Гипотеза Коперника о том, что все планеты движутся вокруг Солнца

2).Сбор эмпирических данных (тщательные измерения положения планет, выполненные астрономом Тихо Браге)

3).Анализ данных и их обобщение в эмпирических законах, сделанное Кеплером.

4).Построение теории, объясняющей все общие закономерности и предсказывающей многие новые следствия, сделанное Ньютоном.

После открытия Коперником гелиоцентрической системы мира начались поиски закономерностей, которым подчиняется движение планет вокруг Солнца. Датский астроном Тихо Браге, многие годы наблюдая за движением планет, накопил многочисленные данные, но не сумел их обработать. Это сделал его ученик Иоганн Кеплер. Им были открыты три закона движения планет вокруг Солнца. (Проводится работа с учебником астрономии для знакомства с этими законами). Но причину, определяющую эти общие для всех планет закономерности, Кеплеру найти не удалось. Существует легенда, что, постоянно думая над этим вопросом и наблюдая за падением яблока с ветки дерева, Ньютон выдвинул гипотезу о том, что движение планет по орбитам вокруг Солнца и падение тел на Землю вызваны одной и той же причиной - тяготением, которое существует между всеми телами. Теперь исследования историков показывают, что такая догадка высказывалась учеными и до Ньютона. Однако именно он из этой гипотезы сделал частный, но очень важный вывод: между центростремительным ускорением Луны и ускорением свободного падения на Земле должна существовать связь. Эту связь нужно было установить численно и проверить. Именно этим соображения Ньютона отличались от догадок других ученых, например от догадок Гука, который тоже считал, что между телами действуют силы тяготения.

Далее вводится закон всемирного тяготения.

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния R между ними: F=Gm₁m₂/R²

где G = 6,67·10^–11 м³/кг·с² –гравитационная постоянная.

Закон всемирного тяготения справедлив для точечных, а также сферически симметричных тел. Приближенно он выполняется для любых тел, если расстояние между ними значительно больше их размеров.

Одним из проявлений закона всемирного тяготения является сила тяжести. Сила тяжести направлена к центру Земли и на поверхности Земли равна F=mg

Просмотр фрагмента о законе всемирного тяготения с диска Интерактивный курс «Физика, 7–11 классы»

Содержание данного фрагмента:

Ц
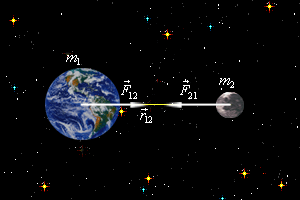
ентростремительное ускорение Луны можно определить из чисто кинематических соображений, поскольку период обращения Луны вокруг Земли известен: T=27,3 суток. Известно было во времена Ньютона и расстояние от Земли до Луны. Оно равно 385 000 км. Обозначим его буквой R. Подставляя эти данные в формулу центростремительного ускорения, получим

a_л.=4π²R/T²=2,7·10^-3м/с²

Но как сопоставить это ускорение с ускорением свободного падения на поверхности Земли?
Если природа тяготения общая, то центростремительное ускорение Луны можно определить и из динамических соображений, используя общую закономерность для движения всех планет, найденную Кеплером, следующим образом.

Силу, удерживающую Луну на орбите, можно определить по второму закону Ньютона: F=ma_л.=4π²mR/T². Но по третьему закону Кеплера T²=R³/K, где K - некоторая постоянная, которую надо определить. Значит, F=4πmK/R², где m - масса Луны; R - расстояние от Земли до Луны.

Следовательно, сила тяготения обратно пропорциональна квадрату расстояния. Значит, отношение центростремительного ускорения Луны к ускорению свободного падения на поверхности Земли должно быть равно отношению квадрата радиуса Земли R_З. к квадрату расстояния от центра Земли до Луны, т. е.

a_л./g=R_З.²/R²

Поскольку И. Ньютон знал, что расстояние от Земли до Луны равно приблизительно шестидесяти земным радиусам, то он получил тот же результат: a_л.=2,7·10^-3м/с². Гипотеза была доказана, поскольку теоретический вывод совпал с результатом, полученным из наблюдений. Говорят, что Ньютон был так взволнован своим открытием, что был не в силах довести вычисления до конца и поручил это сделать своим ученикам. Сам Ньютон писал о своем открытии так: «И в тот же год (ему было всего 24 года) я начал думать о притяжении, как о чем-то относящемся к орбите Луны и, ...пользуясь правилом Кеплера, нашел, что силы, которые удерживают планеты на их орбитах, должны меняться обратно пропорционально квадратам расстояний от центров, вокруг которых они вращаются; и в связи с этим я сравнил силу, требуемую для того чтобы удержать Луну на ее орбите, с силой тяготения на поверхности Земли и нашел, что они весьма близки». Однако Ньютон установил не только существование всемирного тяготения и обратную пропорциональность силы тяготения квадрату расстояний между телами, но и зависимость этой силы от масс тяготеющих тел. Однако из полученной формулы F=4π²Km/R² не ясно, от чего зависит величина K. Тогда Ньютон сделал предположение, что она пропорциональна массе второго тяготеющего тела. Заметим, что это вытекает из третьего закона Ньютона. В самом деле, по третьему закону сила, с которой Луна притягивает Землю, равна по модулю силе, с которой Земля притягивает Луну:F_Л.=F_З., или 4π²K_З.m_З./R²=4π²K_Л.m_Л./R²
  Отсюда следует K_З./m_Л.=K_Л./m_З.=G, где G - некая постоянная величина. Подставив K_Л.=Gm_З. в формулу, определяющую силу притяжения между Луной и Землей, получим F=Gm_Л.m_З./R².
  Очевидно, что такой же результат окажется справедливым для взаимодействия всех планет с Солнцем и, более того, для взаимодействия любых тел.
  Окончательно закон всемирного тяготения формулируется так: два тела притягиваются друг к другу силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними:

F=Gm_Л.m_З./R²


  Дальнейший ход астрономических наблюдений и лабораторных измерений подтвердил найденное выражение для силы взаимного притяжения тел. Оказалось, что G - это универсальная константа, названная гравитационной постоянной. Она численно равна силе притяжения двух тел массой по 1 кг, расположенных на расстоянии 1 м друг от друга. Лабораторные измерения дали результат:

G=6,67·10^-11Нм²/кг²


  Следует обратить внимание на то, что сформулированный закон всемирного тяготения справедлив лишь для материальных точек. Ньютон также доказал, что закон справедлив для шаров, плотность которых распределена симметрично относительно их центров. В этом случае R - это расстояние между центрами шаров. Для тел более сложной формы расчет силы взаимодействия достаточно сложен. Мы эту проблему рассматривать не будем.

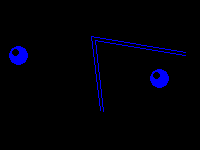  В лабораторных условиях закон всемирного тяготения удалось проверить лишь сто лет спустя после его открытия. Это сделал лорд Г. Кавендиш в 1798г. Опыты проводились при помощи крутильных весов (рис. 1). На длинном стержне 1 уравновешивались два маленьких шарика одинаковой массы m. Стержень был подвешен на тонкой проволоке 2. К маленьким шарикам с противоположных сторон стержня подставлялись на близком расстоянии большие свинцовые шары. Масса каждого большого шара была равна M. При сближении шаров проволока закручивалась. Угол закручивания проволоки регистрировался на шкале 3 по повороту светового пучка 4, отраженного от зеркальца 5. По углу закручивания проволоки определялся момент силы упругости, равный моменту пары сил, возникающих при притяжении маленьких шариков к большим.
  Результаты опыта позволили определить гравитационную постоянную по формуле

G=FR²/mM

  Получилось очень маленькое значение этой величины, которое удалось измерить только благодаря большой чувствительности крутильных весов.

Показ учащимися класса презентации к уроку. Презентация составлена с использованием следующих дисков

1С: Репетитор

1С: Школа. Физика, 7–11 классы

Физика 7–11 классы

Интерактивный курс «Физика, 7–11 классы»

«Живая физика»

«Открытая физика» 1.1 ФИЗИКОН

Материал для презентации:

Презентация

Закон всемирного тяготения

1.Презентация на тему «Закон всемирного тяготения»


2.


3. Закон всемирного тяготения.

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния r между ними:    где G = 6,67·10–11 м3/кг·с2 –гравитационная постоянная.


4.Закон всемирного тяготения справедлив для точечных, а также сферически симметричных тел. Приближенно он выполняется для любых тел, если расстояние между ними значительно больше их размеров.


5. Сила тяжести на различных расстояниях от Земли. При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения убывают.


6. Сила, с которой тело действует на горизонтальную опору или подвес, называется весом тела  По третьему закону Ньютона с той же по модулю силой опора или подвес действует на тело; эта сила называется реакцией опоры  При неподвижной опоре или подвесе эта сила равна силе тяжести Следует помнить, что эти силы приложены к разным телам. Вес тела и сила реакции опоры – следствия силы всемирного тяготения


7. Ньютоновская теория тяготения и ньютоновская механика явились величайшим достижением естествознания. Они позволяют описать с большой точностью обширный круг явлений, в том числе движение естественных и искусственных тел в Солнечной системе, движения в других системах небесных тел: в двойных звёздах, в звёздных скоплениях, в галактиках. На основе теории тяготения Ньютона было предсказано существование неизвестной ранее планеты Нептун и спутника Сириуса и сделаны многие другие предсказания, впоследствии блестяще подтвердившиеся. В современной астрономии закон тяготения Ньютона является фундаментом, на основе которого вычисляются движения и строение небесных тел, их эволюция, определяются массы небесных тел


8. Солнечная система – это комплекс небесных тел, объединенных происхождением, упорядоченностью движения и общностью физических свойств. Центральным телом Солнечной системы является Солнце. Вокруг него по эллиптическим орбитам вращаются девять больших планет; периоды T их обращения связаны с большими полуосями орбит a третьим законом Кеплера:


9. Обычно для измерения расстояний, сопоставимых по масштабам с радиусами планетных орбит, применяется астрономическая единица – длина большой полуоси земной орбиты. 1 а. е. = 149 млн км.


10. Помимо обращения вокруг Солнца каждая планета вращается вокруг своей оси.


11. По характеристикам планеты делятся на две группы. К планетам земной группы, состоящим, в основном, из скалистых и металлических пород и имеющим небольшие размеры, относятся Меркурий, Венера, Земля и Марс. Планеты-гиганты – Юпитер, Сатурн, Уран и Нептун – расположены дальше от Солнца; их металлические ядра окутывает плотная атмосфера из водорода, гелия и других газов.


12. Нет текста


13. Помимо больших планет в Солнечную систему входят малые планеты (астероиды), составляющие два пояса; один из них находится между орбитами Марса и Юпитера, а второй – пояс Койпера, – за орбитой Нептуна. В настоящее время полагают, что Плутон является одним из объектов пояса Койпера. Далеко за поясом Койпера находится еще одно пылевое облако – облако Оорта. Кроме того, в Солнечную систему входят многочисленные кометы, облетающие Солнце по сильно вытянутым орбитам, межпланетная пыль и газ.


14. Солнечная система – не единственная планетная система во Вселенной. В последние годы обнаружено более 70 внесолнечных планет с массами 0,15–17 масс Юпитера, вращающихся вокруг расположенных недалеко от Солнца звезд


15. Солнце – ближайшая к нам звезда. Расстояние от Земли до Солнца равно 1 а. е. (149,6 млн км) – свет идет до Солнца всего 8 минут


16. Нет текста


17. Цикл солнечной активности повторяется в среднем через 11 лет


18. Звезды – наиболее распространенные из всех наблюдаемых космических объектов Вселенной.

Важнейшим параметром звезд является масса. Звездами называются газовые шары, масса которых превосходит 0,08 масс Солнца.

Изучая свечение звезд, их спектры, установили, что атмосферы звезд состоят из водорода, гелия и примеси некоторых других элементов. Именно в звездах имеются условия для формирования более тяжелых элементов, чем гелий.


19. Сравнительные размеры звезд


20. Стадии эволюции звезд.


21. Галактики – это большие звездные системы, в которых звезды связаны друг с другом силами гравитации. В них сосредоточено все видимое вещество во Вселенной. Масса нашей Галактики равняется приблизительно 2·1011M, а диаметр составляет 30 кпк.


22. Эллиптическая галактика, спиральная галактика, неправильная галактика


23. Наблюдаемую часть Вселенной обычно называют Метагалактикой. Ее составляют различные наблюдаемые структурные элементы: галактики, звезды, сверхновые, квазары и т. д. Размеры Метагалактики ограничены нашими возможностями наблюдений и в настоящее время приняты равными 1026 м.

4. Закрепление нового материала. Ответы на проблемные вопросы:

1).Чем ограничиваются размеры животных на Земле?

Фактически насекомые обитают в условиях сильно пониженной по сравнению с более крупными животными гравитации. Поэтому вопрос о том, какой вес смог бы поднять муравей, если бы был размером со слона, просто не имеет смысла. Строение тела насекомых и вообще всех мелких животных оптимально именно для пониженного тяготения, и ноги у муравья просто не выдержат веса тела, не говоря уже о каком-то дополнительном грузе. Так сила тяжести накладывает ограничения на размеры наземных животных, и самые крупные из них (например, динозавры), по-видимому, существенную часть времени проводили в воде.

2) Чему равен вес самых тяжелых из земных птиц?

Летательные способности в животном мире также ограничены массой тела. Не только сила мышц, но и площадь крыльев растет пропорционально квадрату линейных размеров, т.е. для при некоторой предельной массе тела полеты становятся невозможными. Эта критическая масса составляет примерно 15-20 кг, что соответствует весу самых тяжелых из земных птиц. Поэтому очень сомнительно, что древние гиганские ящеры действительно могли летать; скорее всего, их крылья позволяли им только планировать с дерева на дерево.

3) Почему среди тяжелоатлетов так много низкорослых? ( ПОДНЯТИЕ ГИРИ ДВУМЯ УЧЕНИКАМИ)

Достаточно распространено мнение, что занятия тяжелой атлетикой замедляют рост спортсменов, поэтому, мол, среди тяжелоатлетов так много низкорослых. На самом деле низкорослость штангистов действительно наблюдается, но только в ограниченных весовых категориях, особенно среди легковесов. В одной книжке по атлетизму приводится даже пояснение, что низкорослые побеждают чаще оттого, что им приходится поднимать штангу на меньшую высоту. На мой взгляд, такой довод совершенно неубедителен. Я же предлагаю следующее объяснение. Каждый тип ткани (мышцы, кости, кожа, жировая прослойка и т.д.), из которых состоит тело, составляет определенный процент от его общего веса. И если предположить, что эти пропорции одинаковы для двух человек разного роста, то более низкий человек, естественно, будет весить меньше. Однако если он за счет мышц наберет такую же массу тела, что и высокий, то это будет означать, что абсолютная мышечная масса у него больше (поскольку немышечной ткани у него просто меньше по определению). А больше мышечная масса - больше сечения мышц, и, следовательно, в этих условиях при равной массе тела низкий тяжелоатлет действительно сильнее высокого, поэтому последние просто отсеиваются.

5. Подведение итогов урока. Рефлексия.

6. Задача на дом для желающих:

Определить массу Земли.