В. А. Сухомлинский «Знания, даваемые насильно, душат разум.»

Вид материала

Документы

Содержание Актуальность и перспективность опыта Ведущая педагогическая идея Теоретическая база опыта Концептуальная модель данного опыта Высокий уровень мотивации учения, преобладание внутренних мотивов над внешними, рост качества знаний учащихся Технология опыта. Создание учебно-проблемной ситуации Постановка и формулирование основной учебной задачи. Самоконтроль и самооценка возможностей предстоящей деятельности по изучению данной темы. Игровой замысел Игровые действия Познавательное содержание Результат игры. Зашифрованные задания. Задание с продолжением. Найди ошибку. Результативность опыта

Подобный материал:

• Крылова Наталья Викторовна Список литературы Абелюк Е. С. Миф или сказка, 27.67kb.
• В. А. Сухомлинский жил и трудился в то время, когда в педагогике ни о чем не говорили, 35.71kb.
• В. А. Сухомлинский Сердце отдаю детям Издание четвертое Издательство «Радянська школа», 3941.79kb.
• Тової війни, колишний в`язень концтабору під час Другої світової війни та особа, яку, 24.47kb.
• М. В. Ломоносова Факультет журналистики Рациональные концепции понимания бытия. Платон, 368.24kb.
• Тематический план 2011-2012 уч год 1-й семестр Что такое философия? (4 часа), 13.07kb.
• В. А. Сухомлинский писал, что такие родители похожи на садовника, который, не зная,, 99.15kb.
• Реферат на тему "Вселенная, жизнь, разум", 263.67kb.
• Е. Лазарев. Тибетское сказание об Иисусе Тибетское Евангелие, 344.09kb.
• Долга, которая лежит в основе такого размышления: разум познает природу, ее явления, 347.67kb.

«Создание условий для формирования у учащихся внутренней мотивации учения через организацию их самостоятельной деятельности в процессе изучения математики»

ОПИСАНИЕ

ОПЫТА


«Все наши замыслы, все поиски

и построения превращаются

в прах, если нет у ученика

желания учиться.»

В. А. Сухомлинский

«Знания, даваемые насильно,

душат разум.»

А. Франс

Условия возникновения, становления опыта

Современный мир переживает радикальные изменения: на смену техногенного типа общества идет посттехногенное общество. Главное отличие последнего состоит в изменении отношения к человеку. Техногенному обществу, где человек есть объект, вещь, средство, свойственна так называемая «традиционная» система образования. Посттехногенному типу общества, где человек есть субъект и главная цель (отсюда и признание прав человека и создание максимальных условий для его развития и самореализации), необходима принципиально новая система образования – так называемое «личностно-ориентированное образование».

В связи с этим изменяются цели и задачи современной школы. В «Концепции модернизации Российского образования на период до 2010 года» преобразование общеобразовательной школы предполагает ориентацию образования не только на усвоение обучающимися определенной суммы знаний, но и на развитие их личности, их познавательных и созидательных способностей.

Автор данного опыта является сторонником не разрушения традиционной системы, а ее глубинного, постепенного и последовательного преобразования. Естественно на первый план выдвигается проблема обеспечения новых подходов к организации педагогической деятельности, акценты в которой должны быть сделаны на воспитание саморазвивающейся личности.


Переход к личностно-ориентированному образованию повлек за собой изменения и в целях обучения математике, которые направлены на формирование четырех групп компетентностей выпускника:

• математической (прагматической);
  
• социально-личностной;
  
• общекультурной;
  
• предметно-мировоззренческой.
  

Образовательная область «Математика» выступает как предмет общего образования, ведущей целью которого является интеллектуальное воспитание, развитие мышления подрастающего человека, необходимое для свободной и безболезненной его адаптации к условиям жизни в современном обществе. Математика должна предстать перед учащимися не как набор разрозненных фактов, а как цельная, развивающаяся и в то же время развивающая дисциплина общекультурного характера.


Около четырех лет назад, когда из организатора внеклассной воспитательной работы автор данного опыта стал «полноценным» учителем математики с нагрузкой 25 часов, перед ним встали неожиданные проблемы. Раньше, когда не было достаточного опыта в преподавании, казалось, что обучить математике можно практически любого ученика: главное – грамотно и доступно преподнести ему учебный материал. Тем более это легко сделать в сельской школе, где наполняемость классов невысока. А ребята не «обучались»! Они готовы были заниматься любой деятельностью, но только не учебной. Кроме того, помощи от большинства родителей в создании соответствующего «настроя» на учебу ждать не приходилось. Низкий образовательный уровень ( 10-15% родителей с высшим образованием, 20 - 25% не имели среднего образования), неполные семьи, пьянство не способствовали пониманию многими родителями своей роли в интеллектуальном развитии своих детей.

Как показало анкетирование, при переходе учащихся от школы первой ступени ко второй уменьшается интерес ребят к учению, снижается внутренняя мотивация обучения. Около 70% учащихся имели морально-дисциплинарный мотив учения (чувство долга перед родителями, ожидание одобрения со стороны учителей).

Справедливой оказалась древняя восточная мудрость, многократно цитируемая применительно к школе: можно привести коня к водопою, но заставить его напиться нельзя. Овладения математическими знаниями, развития качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, не произойдет без пробуждения интереса, без внутренней мотивации учения.

Как же пробудить у ребят желание «напиться из источника знаний»? Как сформировать у них внутреннюю мотивацию учения? Над решением этой проблемы и предстояло работать автору данного опыта.

Актуальность и перспективность опыта

Учебная мотивация является одним из критериев эффективности педагогического процесса, источником активности и успешности в обучении. Поэтому формирование мотивации учения можно назвать одной из основных задач современной школы.

Актуальность этой проблемы вытекает из анализа противоречий, сложившихся в настоящее время в современном образовании. Выделим те из них, которые определяют проблему данного опыта:

• противоречие между знаниево-просветительским традиционным обучением и ориентацией современного образования на развитие личности;
  
• между демотивированностью основной массы школьников и необходимостью достижения ими определенного уровня обученности и воспитанности;
  
• между снижением интереса учащихся к изучению математики и формированием качеств мышления, характерных для математической деятельности и необходимых для жизни в обществе;
  
• между пассивностью школьников и формированием у них приемов самостоятельного приобретения знаний, развития активности;
  
• между потребностью ученика в эмоциональных переживаниях успеха и слабо развитыми способностями к самонаблюдению, саморегуляции, самосовершенствованию, самооценке.
  

Таким образом, можно сформулировать основную проблему данного педагогического опыта:

Создание условий для формирования у учащихся внутренней мотивации учения через организацию их самостоятельной познавательной деятельности в процессе изучения математики.

Данная целевая установка конкретизируется в следующих задачах:

• овладение учащимися конкретными математическими знаниями, необходимыми для применения в практической деятельности, продолжения образования;
  
• развитие познавательных умений учащихся (выделять главное, составлять план и др.);
  
• развитие навыков рефлексии (самонаблюдения, самооценки);
  
• активизация учебного процесса путем внедрения интерактивных технологий и форм обучения.
  

Ведущая педагогическая идея


Как уже отмечалось, традиционная школа плохо вписывается в современные реалии жизни. В настоящее время идет процесс перехода школы в новое качественное состояние. В этом контексте главной педагогической идеей для автора данного опыта становится гуманно-личностный подход к ребенку, где в центр школьной образовательной системы становится развитие всей целостной совокупности качеств личности. Главная задача педагога в этом случае – разбудить, вызвать к жизни внутренние силы и возможности учащихся, использовать их для более полного и свободного развития личности.


Данный подход объединяет следующие основные положения:

• взгляд на личность как цель образования, личностная направленность учебно-воспитательного процесса;
  
• гуманизация и демократизация педагогических отношений;
  
• отказ от прямого принуждения, как метода, не дающего результатов в современных условиях;
  
• содержание обучения рассматривается как средство развития личности;
  
• обучение ведется обобщенным знаниям, умениям и навыкам и способам мышления;
  
• развитие творческих способностей ребенка;
  
• активизация познавательных сил ребенка.
  

Таким образом, каждый ученик должен владеть не только систематическими знаниями по основам важнейших наук и углубленными познаниями в тех областях, которые его интересуют, но также системой способов деятельности по отношению к себе, семье, обществу, природе, миру вообще.


Теоретическая база опыта


В классической педагогике и школьной практике можно найти немало примеров непрерывного педагогического поиска, направленного на облегчение школьной жизни ребенка, на увлечение учащихся процессом познания, на организацию обучения и воспитания, основанных на обоюдном доверии. В своей работе автор данного опыта опирается на научные исследования и экспериментальную работу таких известных педагогов, как А.С. Макаренко, В.А. Сухомлинского, В.В. Давыдова, Д.Б. Эльконина, В.Ф. Шаталова и др. Важное значение для знания теоретических основ формирования мотивации учения школьников имеют работы Марковой А.К. Фундаментальные теоретические изыскания в области обучения математике Л.М. Фридмана помогают автору в разработке и обеспечении условий внутреннего включения обучающихся в познавательный процесс, организации учения на основе интереса к самому процессу постижения знаний. При составлении занимательных заданий используется опыт М.Ю. Шубы.

Человек, ученик есть деятельностное существо. Он всегда что-то делает, участвует в какой-то деятельности. Но ученик участвует во многих различных видах деятельности, совершает разные действия. Для того, чтобы ученик эффективно учился, он должен совершать не любые действия, а вполне определенные. Встает вопрос: почему ученик совершает именно эти действия, а не другие, что побуждает его совершать эти действия, что направляет и регулирует его деятельность в процессе обучения?

Иными словами, что мотивирует – побуждает и направляет – деятельность ученика? Разобраться в этом необходимо прежде всего потому, что учитель должен организовывать деятельность учащихся в процессе обучения, а для этого он должен уметь формировать у них нужную мотивацию.

Так что же такое мотивация?

Под мотивацией обычно понимают «совокупность побуждений к деятельности» (Л. М. Фридман). Основным видом побуждений являются различного рода потребности. Потребности имеют две функции: во-первых, они являются предпосылкой деятельности; во-вторых, они направляют и регулируют конкретную деятельность человека. Для того, чтобы потребность вызвала определенную деятельность, должен найтись соответствующий ей предмет. Этот предмет, который отвечает данной потребности, становится побуждением к конкретной деятельности и называется мотивом .Следующим видом побуждений, входящих в мотивацию деятельности, является интерес. Когда интерес служит побуждением к деятельности, то его следует рассматривать как потребность в определенных предметах и видах деятельности как источниках положительных эмоциональных переживаний.

Каким же образом потребность, мотив, интерес вызывают определенную деятельность? Когда человек получает информацию об определенных побуждениях – потребности, мотиве, интересе, она перерабатывается с помощью мышления и эмоций. И только после этого дается «команда» к деятельности, предварительно установив ее цель.


Процесс формирования мотивации может быть представлен в следующем виде:



целеполагание

Деятельность может быть организована на основе внешней и внутренней мотивации. Главная особенность внешне мотивированной деятельности связана с побуждением к активности за счет внешних атрибутов, не связанных с самим процессом деятельности (хорошая отметка, одобрение родителей и т.д.). Внутренняя мотивация характеризуется интересом к самому процессу познания и его результату, стремлением развить какие либо умения, качества. Если, например, ученики решают задачу, то внешними мотивами этой деятельности могут быть: желание получить хорошую отметку, добиться похвалы учителя и т.д. Внутренними – интерес к процессу решения, к поиску наиболее рационального способа, к результату и т.д.

Итак, внутренняя мотивация учения формируется в процессе самой деятельности.

Активизация внутренних саморегулирующихся механизмов развития личности – основная идея личностно-ориентированного развивающего обучения. Поэтому организация самостоятельной деятельности учащихся по добыванию и усвоению знаний есть главное средство для решения современных проблем образования, в том числе и для формирования мотивации учения. Таким образом, наиболее эффективное формирование учебных мотивов обеспечивается благодаря такому построению обучения, которое направлено на развитие познавательных умений учащихся, включение в процесс обучения элементов историзма и занимательности.

В своей работе по формированию учебной мотивации автор данного опыта опирается на следующие общепедагогические принципы:

• гуманизации (отношение к человеку, как к субъекту)
  
• гуманитаризации (изменение смысла образования в сторону «человеческого измерения», приобщение школьников к методам научного поиска);
  
• деятельностной активности;
  
• успешности.
  

Новизна опыта.

Механизмы формирования мотивации общеизвестны и рассматривались многими учеными и практиками. Новизна данного педагогического опыта реализуется на уровне усовершенствований: существующая традиционная система обучения подвергается модернизации. Учебный процесс строится таким образом, что в режиме перехода к развивающему обучению, исходя из сложившихся условий, конструируется авторская методика преподавания и воспитания, которая объединяет в себе ряд элементов различных инновационных методик и технологий на основе приоритета авторской ведущей идеи.

Концептуальная модель данного опыта

Цель

обоснована

Ведущая

идея

опирается на




Принципы

определяют


Содержание

обучения


достигается через

Средства

зависит от

Ограничения

и ресурсы

приводит к



Высокий уровень мотивации учения, преобладание внутренних мотивов над внешними, рост качества знаний учащихся




Результат


Технология опыта.


Данный педагогический опыт опирается на вышеизложенную идею гуманно-личностного отношения к ребенку. Исходя из сложившихся условий и анализа противоречий в образовании, была сформулирована цель (проблема) данного опыта: создание условий для формирования у школьников 5-9 классов внутренней мотивации учения через организацию их самостоятельной познавательной деятельности. Эта цель была конкретизирована в задачах (см. выше). Исходя из данных целей и задач, содержание математического образования складывается из следующих содержательных компонентов: «Числа и вычисления», «Выражения и их преобразования», «Уравнения», «Функции», «Геометрические фигуры. Измерение геометрических величин». В содержание образования кроме традиционных знаний, умений и навыков, специфичных для математики, входят методики приобщения учащихся к самостоятельной познавательной деятельности, элементы историзма и занимательности, которые способствуют формированию мотивации изучения математики.

В основе рассматриваемого учебно-воспитательного процесса лежат следующие общедидактические принципы:

• единства воспитания, обучения и развития;
  
• научности;
  
• наглядности и моделирования;
  
• связи теории с практикой, обучения с жизнью;
  
• доступности;
  
• систематичности и последовательности;
  
• самостоятельности и активности учащихся;
  
• целенаправленности и мотивации обучения;
  
• индивидуального и дифференцированного подхода к учащимся.
  

В обучении используется «Примерная программа по математике для основной школы» под ред. Дорофеева Г.В., которая реализуется с помощью следующих учебников: «Математика,5» и «Математика,6» (авт. Н.Я.Виленкин идр.); «Алгебра,7», «Алгебра,8», «Алгебра, 9»(авт. Ю.Н.Макарычев и др.); «Геометрия,7-9»(авт. Л.С.Атанасян и др.).

В соответствии с поставленными целями и задачами ведущими методами учебно-воспитательного процесса являются активные формы обучения, повышающие субъектную позицию ученика: частично-поисковый метод, метод проблемного обучения, дидактические игры.

Организуя учебно-воспитательный процесс, формирование мотивации осуществляется через:

• создание атмосферы эмоционального комфорта;
  
• использование исторического и занимательного материала;
  
• выявление практической значимости изучаемого материала;
  
• организацию самостоятельной деятельности учащихся;
  
• подведение итогов и поощрение достижений в учебной деятельности.
  

Например, создание атмосферы эмоционального комфорта можно реализовать, если на каждом уроке и во внеурочное время заботиться о преобладании положительных эмоций, которые связаны со школой, ровными взаимоотношениями с учителями и одноклассниками, отсутствием конфликтов, активным участием в жизни классного и школьного коллектива, с успешностью учебы, с радостью преодоления трудностей.

Особое место в ряду средств формирования мотивации учения занимает организация самостоятельной деятельности учащихся по добыванию знаний, так как «нужные потребности и мотивы могут быть сформированы у учащихся только в процессе их собственной деятельности»(Фридман Л.М.). Как же эту деятельность организовать? Автор данного опыта предлагает следующее решение.

Процесс обучения математике строится как процесс взаимодействия учителя и учащихся по осуществлению целей и задач обучения. Учитель выступает как организатор и руководитель этого процесса и совместной деятельности учителя и учащихся в разных ее формах.

Усовершенствовать традиционную классно-урочную систему можно, если за самостоятельную, законченную единицу учебного процесса взять не урок а систему уроков по изучению темы. Деятельность учителя начинается с подготовки к изучению очередной темы программы. Анализируется содержание учебного материала; составляется перечень тех знаний и умений, которыми должны овладеть учащиеся; определяются те общеучебные приемы деятельности, которые возможно развивать средствами данной темы. На основе этого анализа составляются тематические и поурочные планы изучения предстоящей темы программы. (См. Приложение 1.).

В соответствии с планом учитель готовит все необходимые пособия, дидактические материалы. Особое внимание уделяется подбору заданий, направленных на формирование мотивации учения. Можно выделить следующие блоки таких заданий:

• исторические задачи;
  
• задачи с практической и профессиональной ориентацией;
  
• занимательные задачи;
  
• задания с зашифрованными ответами и др.
  

В процессе обучения создается «банк» таких заданий (См. Приложение 2.).

Деятельность учителя в ходе изучения темы неотделима от деятельности учащихся и проходит в форме совместной деятельности с ними. Эту совместную деятельность можно представить в виде схемы-модели:

I этап : «Ориентировка» (мотивационный)

1. Создание учебно-проблемной ситуации
   
2. Постановка и формулирование основной учебной задачи
   
3. Самоконтроль и самооценка возможностей предстоящей деятельности.
   

II этап : «Исполнение» (операционально-познавательный)

1. Познание и освоение содержания учебного материала
   
2. Овладение учебными действиями и операциями, входящими в это содержание.
   

III этап : «Контроль» (рефлексивно-оценочный)

1. Анализ собственной деятельности
   
2. Сопоставление результатов деятельности с поставленной учебной задачей
   
3. Оценка и самооценка деятельности
   
4. Прогнозирование новых целей и задач.
   

Эта схема универсальна и может быть «наложена» на любой вид учебной деятельности. Рассмотрим данные этапы подробнее.

На этапе «Ориентировка» ученики должны осознать, почему и для чего им нужно изучать данную тему, что именно им придется изучить и освоить, какова основная учебная задача предстоящей работы. Учащиеся под руководством учителя должны выяснить, готовы ли они к изучению этой темы, чего им не достает, что именно должны проделать ученики, чтобы с успехом выполнить учебную задачу. Этот этап состоит из следующих учебных действий:

1. Создание учебно-проблемной ситуации, вводящей учащихся в предмет изучения предстоящей темы. Учебно-проблемная ситуация может быть создана разными приемами: а) постановка перед учащимися задачи, решение которой возможно лишь на основе изучения данной темы; б) беседой, рассказом учителя о теоретической и практической значимости предстоящей темы; в) рассказом учителя (ученика) об истории возникновения и развития основных понятий данной темы и др.
   
2. Постановка и формулирование основной учебной задачи. Обсуждение основной проблемы в созданной учебно-проблемной ситуации завершается формулированием основной учебной задачи, которая должна быть решена в процессе изучения данной темы. Учебная задача показывает учащимся тот ориентир, на который они должны направить свою деятельность в процессе изучения данной темы. Она тем самым создает основу для целеполагания.
   
3. Самоконтроль и самооценка возможностей предстоящей деятельности по изучению данной темы. После того, как основная учебная задача сформулирована, понята и принята учащимися, переходят к обсуждению того, что необходимо знать и уметь для изучения темы. Завершается это обсуждение тем, что учащиеся дают самооценку своих возможностей, указывают, что они повторят и что еще сделают для подготовки к предстоящей работе.
   

Так, например, при изучении темы «Проценты» учебно-проблемная ситуация может быть создана рассказом учителя об истории возникновения понятия «процент». После этого учитель с ребятами на простейших примерах разбирает содержательное понимание термина «процент». На дом учащимся предлагается такое домашнее задание: «Подберите и выпишите примеры задач из газет, книг, в которых встречаются проценты. Поинтересуйтесь у своих родителей, сестер, братьев, с какими задачами на проценты они сталкивались в своей жизни». На следующем уроке идет обсуждение домашней работы. При этом были выделены три основных типа задач на проценты и определены этапы дальнейшей работы:

• научиться решать простейшие задачи на проценты;
  
• найти область применения этого понятия (в химии, медицине, банковском деле, сельском хозяйстве и др.).
  

Совместно с учителем ребята выяснили, что им необходимо повторить темы «Как найти дробь от числа», «Число по его дроби», «Умножение и деление дробей».

Итак, первый этап изучения темы очень важен для организации самостоятельной познавательной деятельности учащихся, направленной на формирование мотивации учения.

На этапе «Исполнение» учащиеся познают и осваивают содержание темы и овладевают учебными действиями и операциями, входящими в это содержание. От того, как будет организована деятельность учащихся, зависит эффективность всего учебно-воспитательного процесса и в том числе достижение высокого уровня мотивации учения. Организовать самостоятельную познавательную деятельность учащихся можно в различных формах. Автор данного опыта применяет в своей практике следующие из них: индивидуальную, групповую, фронтальную.

На данном этапе изучения темы основной является индивидуальная форма организации учебной деятельности школьников, так как усвоение знаний, овладение умениями и навыками, развитие творческих способностей есть сугубо индивидуальный процесс (с точки зрения, что никто другой не может этого сделать за данного человека). Ученик должен выработать у себя свои собственные взгляды и убеждения, только в этом случае они будут направлять его деятельность.

Самостоятельная индивидуальная деятельность ученика происходит главным образом во время выполнения домашней работы, которая складывается из выполнения им обязательных заданий учителя и работы, выполняемой по собственной инициативе. Желательные или свободные задания даются учащимся в форме пожелания их выполнения. Например: «Из задач (называются номера задач по учебнику) решите столько, сколько считаете нужным, и какие хотите». Также используются следующие виды домашних заданий: практические (изготовление моделей, пособий, проведение измерительных и вычислительных работ); индивидуальные задания(для учащихся разного уровня ); задания для обобщения изученного учебного материала (составить задачу на определенную тему, составить контрольную работу для проверки пройденного и т.д.); творческие задания (написать доклад или сочинение на математические или историко-математические темы) и т.д.

На уроках индивидуальные виды учебной деятельности используются при самостоятельной работе ученика по индивидуальным и дифференцированным заданиям. Учитель применяет различные приемы, активизирующие мыслительную деятельность и направленные на мотивацию учения. Приведем примеры некоторых из них.

Многовариативная обучающая самостоятельная работа. Ее основу составляет одно задание. Индивидуальная ориентация задания на различные группы учащихся осуществляется с помощью специальных указаний. Так, при изучении темы «Рациональные дроби» (8 кл.) проводится следующая самостоятельная работа:

Вариант 1. Упростите выражение




у+3 у+3 у²

2у+3 у – 3 9 – у²


Вариант 2. Упростите выражение


у+3 у+3 у²

2у+3 у – 3 9 – у²

У к а з а н и е. Упростите выражение, предварительно умножив на (-1) числитель и знаменатель дроби.


Вариант 3. Упростите выражение



у+3 у+3 у²

2у+3 у – 3 9 – у²


У к а з н и е. 1) Разложите выражение 9 – у² на множители; 2) приведите к общему знаменателю выражение в скобках, предварительно умножив числитель и знаменатель второй дроби на (-1).


Вариант 4. Заполните пропущенные места:

у+3 у+3 у² у+3 у+3 у² у+3

2у+3 у – 3 9 – у² 2у+3 у – 3 … 2у+3


(у+3)² – у² у+3 … … 1

… 2у+3 (у – 3)(у+3) … у – 3


Количество вариантов может быть различным в зависимости от изучаемой темы и уровня подготовки учащихся. Общее задание записывается на доске, а указания даются на карточках индивидуально.


Индивидуальное изучение темы. Этот прием используется при изучении некоторых тем по геометрии. После мотивационного этапа изучения темы каждый ученик получает карточку с легким заданием по первому параграфу. Выполнив это задание, ученик получает следующее, посложнее предыдущего и т.д. Первые три карточки содержат задачи, подобные тем, которые решены либо в классе, либо в тексте учебника. Остальные задачи более сложные, требующие самостоятельного поиска информации и самостоятельных рассуждений. На каждый параграф для каждого ученика готовится обычно по 6 карточек. Например, серия заданий (карточек), адресованная слабым учащимся по теме «Смежные углы» (7кл.), выглядит следующим образом:

1) Величина угла  на рисунке равна 35⁰ . Найдите остальные углы.







2) Градусная мера одного из смежных углов 60^о. Найдите градусную меру второго угла и постройте эти углы.

3) Один из смежных углов больше другого на 30^о. Найдите эти углы.

4) Найдите смежные углы, если один из них в 4 раза меньше другого.

5) Найдите смежные углы, если их градусные меры относятся как 2:3 .

6) Составьте задачу про смежные углы.

Для средних учащихся используются по существу те же самые задачи, но с менее удобными числовыми данными. Первая задача серии средним учащимся вовсе не предлагается. Но зато предпоследней в списке идет задача: «Найдите величину угла, если величины двух смежных с ним углов составляют 100^о.». Сильным учащимся даются задачи, которые требуют догадки. Например: «Две прямые пересекаются. Известно, что два угла из тех, что образуют эти прямые, в сумме составляют 50^о. Найдите градусные меры этих углов».

Те учащиеся, которые выполнили все задания и получили от учителя «добро», могут переходить к изучению следующего параграфа из учебника.


Чтобы поддерживать познавательный интерес учащихся, их учебную мотивацию на достаточно высоком уровне, необходимо разнообразие форм организации обучения. Поэтому, наряду с индивидуальными, используются групповые способы обучения. Например.

Парная работа учащихся при изучении темы носит двусторонний характер и основана на принципе взаимообучения. Два ученика, обычно сидящие за одной партой, вместе изучают теоретическую часть темы по учебнику, разбирают примеры. Затем они обсуждают содержание, т.е. один пересказывает, а другой дополняет. Затем они сообщают учителю о том, что теоретический материал изучен, и получают карточки с парой однотипных заданий по данной теме. Допустим, требуется решить неравенства:

Карточка 1

а) (х – 5)(х – 2) >0


б) (х+ 7)(х – 4) < 0

Карточка 2

а) х²+ 3х – 48 >0


б) –2х²+ 2х + 15 <0




Каждый ученик в паре самостоятельно решает задание а). Затем первый ученик объясняет второму решение задания а) из своей карточки. При этом, если есть необходимость, он дает теоретические объяснения и отвечает на все вопросы соседа по парте. Затем таким же образом второй ученик объясняет первому, как решается задание а) из своей карточки. Потом первый ученик приступает к решению задания б) из Карточки 2, а второй – задания б) из Карточки 1. Проверив друг у друга правильность решения задания, они сообщают об этом учителю.

Работа учащихся в малых группах. Класс делится на несколько небольших групп по 4-5 человек. При комплектовании групп учитывается характер межличностных отношений учащихся. Приведем пример. При изучении теоремы о сумме внутренних углов выпуклого п-угольника эффективным оказывается частично-поисковый метод доказательства этой теоремы. Учащиеся класса разбиваются на четыре гетерогенные группы, каждая из которых «ищет свое доказательство» теоремы, получив от учителя на листах задание с некоторыми указаниями. Характер и полнота указаний зависят от состава конкретной группы. Учащиеся первой группы доказывают теорему методом математической индукции: при п=3 формула ^ п – 2) справедлива в силу теоремы о сумме углов треугольника; далее предполагается истинность данной формулы при п =k и доказывается ее справедливость при п = k + 1.

Учащиеся второй группы проводят доказательство с опорой на рисунок 1. Учащиеся замечают, что если п – количество сторон многоугольника, то п – 2 - количество образовавшихся треугольников. И так как сумма внутренних углов треугольника равна 180⁰, то  = ^ п – 2) .

Третья группа учащихся находит доказательство теоремы, исходя из рисунка 2.

 = 180⁰п – 360⁰ = ^ п – 2).

Четвертая группа, изучая основной рисунок 3 и выполняя дополнительный рисунок 4, приходят к выводу, что  = 180⁰п – 360⁰ = ^ п – 2).


А₁ А₂ А₁ А₂




А_п А₃


А_п А₃

А_п-1


А_п-1


Рис.1 рис.2





2




1 1 3

2 4

5

5


3

4

Рис.3 рис.4

Учитель участвует в работе каждой группы, консультируя ее и побуждая к активному поиску. После вывода необходимой формулы представитель группы на доске демонстрирует всему классу найденное доказательство теоремы. Затем решаются задачи на применение этой теоремы.

Итак, групповая работа помогает активизировать учебный процесс, создает положительный эмоционально-психологический климат, что способствует формированию мотивации.

Еще одной эффективной формой организации самостоятельной познавательной деятельности учащихся является дидактическая игра, которая зачастую объединяет в себе элементы индивидуальной, групповой и фронтальной форм обучения.

«Учебные игры (по Эрлиху и Рейнольдсу):

• позволяют учащимся самим решать трудные проблемы, а не просто быть наблюдателями;
  
• создают потенциально более высокую возможность переноса знаний и опыта деятельности из учебной ситуации в реальную;
  
• обеспечивают учебную среду, незамедлительно реагирующую на действия учащихся;
  
• позволяют «сжимать» время;
  
• психологически привлекательны для учащихся».
  

Основными структурными элементами дидактической игры являются : игровой замысел, правила, игровые действия, познавательное содержание, оборудование, результат игры.

Например, при изучении темы «Произведение суммы и разности двух одночленов» (7кл.) можно провести игру «Математический поединок ».

Игровой замысел состоит в том, чтобы на основе созданной проблемной ситуации и соревнования команд активизировать мышление учащихся, превратить весь урок в процесс активной поисковой деятельности.

Для проведения игры класс делится на две команды. Выбираются капитаны, которые следят за порядком и дисциплиной в команде и сами участвуют в игре .

При проведении урока должны соблюдаться правила игры:

1. За правильные ответы команде начисляются очки; неправильный ответ, нарушение дисциплины приводят к штрафным очкам.
   
2. Каждый член команды может вновь отвечать только после того, как ответят все члены команды.
   
3. Вопросы и задания дает учитель. Счет соревнования записывается на доске.
   
4. После постановки общего задания разрешаются консультации внутри команд.
   
5. Все необходимые записи по указанию учителя заносятся в тетрадь.
   
6. На определенном этапе работы сначала одна команда является «первопроходцем». Деятельность второй команды состоит в том, чтобы внимательно следить за правильностью ответов, а после завершения изучения некоторой части материала ответить на вопросы, предложенные учителем и командой соперников, и выполнить задания, аналогичные рассмотренным. Затем роли команд меняются.
   
7. За правильные дополнения ответов учащихся из другой команды каждый может получить дополнительно 2 очка.
   

Игровые действия состоят в том, чтобы быстро и без ошибок отвечать на вопросы учителя, выполнять нужные записи и построения в тетрадях, следить за правильностью ответов своих товарищей из своей и другой команды, решать примеры и задачи у доски, во время объявленной консультации консультировать соседей по парте или при необходимости самому брать консультацию, не нарушать дисциплину, быть внимательным и активным.

Познавательное содержание состоит в том, чтобы учащиеся усвоили формулу сокращенного умножения (а – b)(а + b) = а² – b² и могли применять ее при умножении чисел и двучленов определенного вида (См. Приложение 3).

Результат игры. Учащиеся обогатились знаниями и умениями применять формулу сокращенного умножения для умножения чисел и двучленов. В процессе игры происходило развитие самостоятельных познавательных умений учащихся, вырабатывается целеустремленность, организованность, положительное отношение к учебе.

Математическая сторона игры отчетливо выдвигается на первый план. Только тогда игра будет выполнять свою роль в математическом развитии детей и воспитании интереса их к математике.

На последнем этапе изучения темы – «Контроль» - школьники учатся рефлексировать, анализировать свою собственную деятельность, оценивать ее, сопоставляя результаты этой деятельности с поставленными основными и частными учебными задачами. Для этого необходимо так организовать работу по подведению итогов изучения пройденного материала, чтобы учащиеся могли испытать чувство эмоционального удовлетворения от проделанной работы, радость победы над трудностями, ими преодоленными в процессе изучения темы, счастье познания нового, интересного. Тем самым будет формироваться ориентация на переживание таких чувств в будущем, что приведет к формированию потребности в творчестве, познании, в упорной самостоятельной работе, т.е. к устойчивой высокой мотивации учения.

В организации этого этапа используются разнообразные методы и приемы, дающие учащимся возможность проявить самостоятельность и инициативу. Внешний контроль со стороны учителя над деятельностью ученика пока еще имеет место . Но этот тип контроля постепенно передается учащимся и выполняется в процессе взаимо- и самоконтроля. Эти типы контроля наиболее отвечают идеям личностно-ориентированного обучения.

Один из приемов взаимоконтроля был описан выше (см. «Парная работа учащихся»). Еще одним приемом взаимоконтроля и самоконтроля является сверка решения задачи с образцом ее решения на доске или в тетради товарища, взаимообмен тетрадями.

По мере прохождения учащимися очередной темы учебного материала эффективным бывает контроль, проводимый при помощи ассистентов или консультантов. Ими становятся учащиеся того же класса, но уже освоившие учебный материал и отчитавшиеся перед учителем. Например, по окончании изучения темы «Наибольший общий делитель. Взаимно простые числа» (6кл.) учащиеся должны ответить на следующие вопросы:

1. Какое число называют наибольшим общим делителем нескольких натуральных чисел? Приведи пример.
   
2. Какие числа называют взаимно простыми? Приведи пример.
   
3. Объясни, как используется разложение на простые множители для нахождения наибольшего общего делителя чисел 360 и 250.
   
4. Сформулируйте правило нахождения наибольшего общего делителя. Объясни, как нужно найти наибольший общий делитель чисел 42, 60 и 75.
   

Отчитавшиеся до урока перед учителем учащиеся назначаются ассистентами, и на уроке они принимают ответы других учеников. Такая форма взаимоконтроля развивает математическую речь школьников, воспитывает чувство взаимопомощи, стимулирует познавательную активность.

Организация обучения в условиях перехода к развивающему обучению связана с обеспечением саморегуляции личности, основанной на самооценке. Умению адекватно оценивать собственные достижения и возможности, делать необходимые выводы относительно собственного самосовершенствования необходимо учить также, как мы стремимся вооружить детей знаниями, умениями и навыками, научить самостоятельно мыслить. Формированию навыков рефлексии способствует технология «Портфель ученика» (Полот Е.С.).Принципы этой технологии можно сформулировать следующим образом:

1. Самооценка результатов (промежуточных, итоговых) овладения определенными видами познавательной деятельности.
   
2. Систематичность и регулярность самомониторинга.
   
3. Структуризация материалов «Портфеля», логичность и лаконичность всех письменных пояснений.
   
4. Аккуратность и эстетичность оформления «Портфеля».
   
5. Целостность, тематическая завершенность представленных в «Портфеле» материалов.
   
6. Наглядность и обоснованность презентации «Портфеля» учеником.
   

«Портфель ученика» - это комплект документов, самостоятельных работ ученика, который разрабатывается учителем совместно с учениками в самом начале изучения темы и предусматривает:

• задания ученику по отбору материала в «Портфель»(имеется в виду не конкретное указание, какой материал следует отобрать, а по каким параметрам следует его отбирать);
  
• анкеты для рецензентов (родителей, учителей и др.), которые предполагают внимательное ознакомление с работами ученика, параметры и критерии оценки вложенных в «Портфель» работ;
  
• анкеты для экспертной группы на презентации для объективной оценки представленного «Портфеля».
  

Ученик по собственному выбору отбирает наиболее интересные, с его точки зрения, самостоятельные работы в свое «досье», организует их в предусмотренную структуру. Его задача – тщательно проанализировать эти работы, составить собственный краткий отчет самооценки: что, на его взгляд, ему удалось в этой работе, что не удалось, на что следует обратить внимание. По истечении срока, предусмотренного на составление «Портфеля», ученик выставляет его на презентацию, где должен показать свое продвижение в данной области, доказать, что он приложил максимум усилий для этого, сделать выводы в отношении своей дальнейшей познавательной деятельности (см. Приложение 4).

Этапы рассматриваемой технологии опыта взаимосвязаны и «взаимопроникаемы», поэтому многие методические приемы можно использовать на разных ее стадиях. Вот еще несколько таких приемов, направленных на формирование мотивации учения.

Зашифрованные задания. Этот прием известен давно. Ценность его заключается в том, что он позволяет в «пустыню однообразных упражнений»(необходимых, однако, для выработки какого-либо навыка), вставлять зашифрованные задания, которые повышают интерес к этой, иногда однообразной, но нужной деятельности, развивают логическое мышление учащихся. Например, произведение разности двух выражений и их суммы выполняется по формуле разности квадратов. Закрепляется навык применения этой формулы. Требуется восстановить равенство:

 с²с).

Чтобы восстановить это равенство, надо уловить связи между объектами, проявить некоторую сообразительность.


Задание с продолжением. Главное достоинство этих заданий – экономия времени на уроке. На доске записана задача, ученики решают ее. Затем учитель дописывает два-три символа – получается вторая задача. Потом учитель опять дописывает ее и т. д.

З а д а н и е : Разложите на множители многочлен а²  21ах ас хс.

1. Если изменить знак каждого коэффициента на противоположный, получится многочлен а² ах ас хс. Можно ли его разложить на множители?
   
2. Если изменить все знаки, кроме одного, можно ли разложить?
   
3. Если изменить только два знака, можно ли разложить?
   



Успешно решенные предыдущие задачи стимулируют ученика на решение последующих задач.

Найди ошибку. Этот прием помогает провести своеобразную профилактику ошибок в занимательной для учеников форме. Например. «Некто Витя Верхоглядкин, выполняя домашнее задание, решил уравнение так: 15х30 = 12х – 24; 15(х – 2) = 12(х – 2); 15 = 12. Ответ: решения нет. В чем его ошибка?». Как задания, так и способы их предъявления могут быть самыми разнообразными. Этот прием доказал свою эффективность с методической точки зрения: вырабатываются навыки самоконтроля, критического мышления и др.

Резюме. Данный прием используется в конце урока с целью помочь учащимся подытожить свои знания по теме, оценить собственную деятельность и дать учителю информацию о предварительной результативности урока. Учащиеся письменно отвечают на серию следующих вопросов:

1. Что понравилось на уроке?
   
2. Что не понравилось?
   
3. Проявился ли интерес к математике на данном уроке?
   
4. Что нового ты узнал на уроке?
   
5. Важны ли для тебя знания, полученные на уроке?
   
6. Задай вопрос, на который ты не получил ответа на уроке.
   
7. Поставь себе отметку за урок. Обоснуй ее.
   

Рассмотренная технология педагогического опыта, направленная на организацию самостоятельной познавательной деятельности учащихся в сотрудничестве с учителем, способствует формированию внутренней мотивации учения в процессе изучения математики.


Результативность опыта


Для того, чтобы оценить результативность данного опыта, необходимо провести анализ основных показателей учебной мотивации. Изучение мотивационной сферы учащихся можно провести, опираясь на методики диагностики, разработанные М. Лукьяновой (зав. лабораторией психолого-педагогической и социальной диагностики Ульяновского ИПК работников образования). Данная методика включает в себя анкеты для учащихся 7-го, 9-го и 11-го классов. Исходя из того, что в различных возрастных группах школьников мотивация проявляется по-разному и для полноты описания результатов автором данного опыта, были разработаны анкеты для учащихся 5-го класса (см. Приложение 5).


Анкета для учащихся содержит четыре содержательных блока, каждый из которых характеризует тот или иной показатель мотивации:

1. личностный смысл учения
   
2. способность к целеполаганию
   
3. различные виды мотивов
   
4. преобладание внутренних или внешних мотивов
   

Для примера возьмем диагностику по двум параллельным классам за два года.



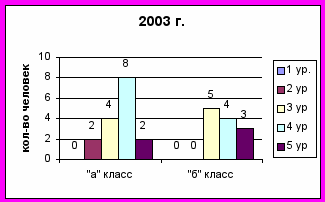
Первый, второй и третий содержательные блоки выявляют итоговый уровень мотивации учения:


1 ур. – очень высокий уровень мотивации учения;

2 ур. – высокий уровень мотивации учения;

3 ур. – нормальный (средний) уровень мотивации учения;

4 ур. – сниженный уровень мотивации учения;

5 ур. – низкий уровень мотивации учения.


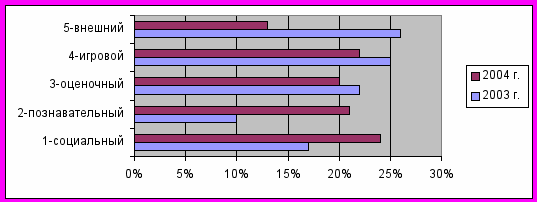
В третьем блоке анкеты оценивается также характер выбранных мотивов.


Из диаграммы видно, что в выборах мотивов учащихся преобладают познавательный и социальный – значит у учителя с учениками хорошие взаимоотношения, ребята с удовольствием занимаются математикой. Это свидетельствует и о том, что школьники не испытывают перегрузки, что задания им доступны, а потому и учебная деятельность успешна, что и порождает внутреннюю мотивацию.




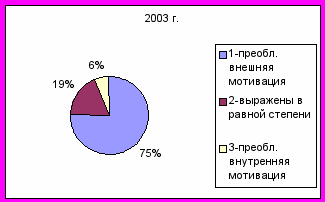
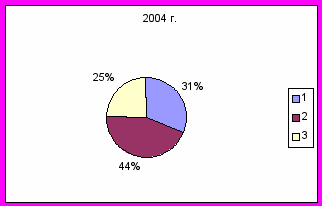
Четвертый блок анкеты позволяет выявить преобладание у школьников внутренней или внешней мотивации учения.


Анализируя данный мониторинг, можно сделать вывод, что число ребят с высоким и очень высоким уровнем мотивации растет. Также увеличивается количество ребят с преобладанием внутренней мотивации учения.




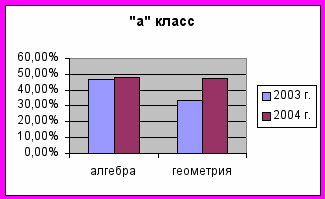
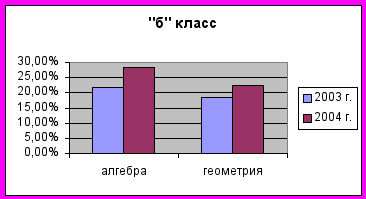
Как следствие этой положительной динамики можно рассматривать рост качественной успеваемости в этих классах.

Анализ анкет «Мой любимый предмет» показал, что около 50% учащихся отдают предпочтение математике (можно было отметить два предмета).

Для того, чтобы и дальше способствовать повышению познавательного интереса и учебной мотивации учащихся и всвязи с переходом к профильному и предпрофильному обучению, автором данного опыта была разработана программа элективного курса для предпрофильной подготовки учащихся 9 класса «Теория графов и ее применение». Основная цель курса – углубление знаний учащихся по математике и расширение их кругозора в областях знаний, тесно связанных с математикой, через задачи прикладного характера. Этот курс дополняет базовую программу, не нарушая ее целостности. Связь теории графов с различными школьными дисциплинами способствует формированию у учащихся понимания роли математики при изучении других наук. Данный элективный курс будет также способствовать тому, что учащиеся смогут более адекватно оценить свои способности и сделают сознательный выбор математического профиля обучения (см. Приложение 6).


Итак, анализируя результативность данного педагогического опыта, можно говорить о том, что цель, сформулированная автором как «создание условий для формирования у учащихся внутренней мотивации учения через организацию их самостоятельной деятельности в процессе изучения математики», достигается при помощи описанной технологии. В результате все больше и больше ребят испытывают желание «напиться из источника знаний», задумываются о своем самосовершенствовании.

В итоге можно сделать вывод о том, что данный педагогический опыт достаточно эффективен, что, конечно же, не исключает возможностей его дальнейшего усовершенствования.