Литература

Вид материала

Содержание

I. Психолого-педагогическое обоснование проблемы реализации дифференцированного подхода в обучении младших школьников общему при
Первый этап
Второй этап
Третий этап
Четвёртый этап
1.2. Виды дифференцированной работы при обучении общему приёму решения текстовых задач.
II. Практическое описание опыта реализации дифференцированного подхода в обучении младших школьников решать текстовые задачи

Подобный материал:

МОУ «Гремячинская средняя общеобразовательная школа»

«Использование разноуровневых заданий при обучении общему приёму решения текстовых задач»

(индивидуальный творческий проект)

Учитель начальных классов:

Романова Татьяна Валентиновна

Научный руководитель:

Чудова Ольга Владимировна,

преподаватель Центра образовательных

ресурсов и технологий

ГОУ СПО «Вологодский педагогический

колледж»

2010 год

Содержание

Введение …………………………………………………………2-3

Психолого-педагогическое обоснование проблемы реализации дифференцированного подхода в обучении младших школьников общему приёму решению текстовых задач…………………4- 12
1. Сущность общего приёма решения текстовых задач…………4-9
2. Виды дифференциации работы при обучении общему приёму решения текстовых задач………………………………………….9-12
Практическое описание опыта реализации дифференцированного подхода в обучении младших школьников общему приёму решения текстовых задач………………………………………………….12-21
Описание результатов……………………………………………22-23

Заключение……………………………………………………….23

Литература………………………………………………………..24-25

Приложение………………………………………………………..26-27

Введение

Одной из приоритетных целей обучения младших школьников математике является формирование осознанного умения решать текстовые задачи. Одна из наиболее сложных проблем, с которой сталкивается учитель при обучении детей математике./1/ В традиционной методике предполагалось « научить учащихся решать набор так называемых стандартных задач, используя многократное повторение задач каждого типа вплоть до выработки и запоминания образца решения»

Новые стандарты начального общего образования по математике ориентируют на практические жизненные потребности человека в умении решать разные задачи. Таким целям отвечает не частный, а общий подход в обучении решению текстовых задач. Надо заботиться о творческом подходе к решению задач, ведь жизнь наполнена решением самых разнообразных проблем, которые необходимо решать. Постепенно школа начинает осознавать недостатки традиционного подхода к овладению учащимися умения решать задачи, заключающегося в формировании частных умений решения задачи. При формировании общего умения решать задачи предметом изучения являются задачи; процесс решения задач; методы и способы решения задач, приёмы, помогающие осуществлению каждого этапа и всего процесса решения задач.

Но методика работы над задачей рассчитана на среднего ученика. Возникает противоречие : опыт показывает, что научить всех детей с разным уровнем обучаемости в одинаковые сроки невозможно, т.е система работы над задачей рассчитана не на конкретного ученика. Дети с низким уровнем обучаемости не справляются с решением задач, особенно составных. У них возникает боязнь выполнения задания, исчезает вера в свои силы, а порой школьники отказываются от решения задач вообще. Объективно существующие различия учащихся приводят к снижению уровня знаний у всех учащихся, не способствуют развитию ребят с ярко выраженными способностями. Следовательно, необходима такая организация работы над задачей, которая позволила бы учитывать различия между учащимися и создавать оптимальные условия для эффективной учебной деятельности всех школьников, то есть возникает необходимость изменения содержания, методов, форм обучения. Подходом, который реализуется с учётом данных особенностей, является дифференциация в обучении и овладение общим приёмом решения любых текстовых задач.

Исходя из данной проблемы наметила цель: разработать варианты реализации дифференцированного подхода в обучении младших школьников общему приёму решения текстовых задач. Достижению цели предполагает выполнение совокупности задач:

Изучить и проанализировать психолого-педагогическую литературу о данной проблеме
Разработать разноуровневые задания для овладением детьми общего приёма решения текстовых задач
Апробировать систему дифференцированных заданий в формировании умения решать текстовые задачи

I. Психолого-педагогическое обоснование проблемы реализации дифференцированного подхода в обучении младших школьников общему приёму решения текстовых задач.

Сущность общего приёма решения текстовых задач.

В Федеральном государственном стандарте общего образования, разработанном творческой группой учёных под руководством А. М. Кондакова, чётко сформулирована цель начального общего образования – « развитие личности обучающегося на основе освоения универсальных учебных действий, познания и освоения мира».

Для достижения данной цели в процессе обучения используются личностные, регулятивные, познавательные и коммуникативные универсальные учебные действия.

Результат образовательной деятельности начальной школы фиксируется в следующем портрете выпускника:

- любознательный, интересующийся, активно познающий мир;

- владеющий основами умения учиться, способный к организации собственной деятельности;

- любящий свой край и свою Родину;

- уважающий и принимающий ценности семьи и общества;

- готовый самостоятельно действовать и отвечать за свои поступки перед семьёй и школой;

- доброжелательный, умеющий слушать и слышать партнёра, умеющий высказывать своё мнение;

- выполняющий правила здорового и безопасного образа жизни для себя и окружающих./16/

Но полноценно развить личность ребёнка в процессе обучения, основанного на усвоении готовой информации, практически невозможно. Именно поэтому внимание педагогов обращается к поиску способов обучения, побуждающих школьников к самостоятельному разрешению учебных проблем, в результате которого происходит как освоение субъективно новых знаний, так и овладение способами продуктивной мыслительной деятельности.

Формирование умения решать текстовые задачи – одна из важнейших задач обучения математике. Новые государственные стандарты начального общего образования по математике ориентируются на практические жизненные потребности человека в умении решать разные задачи. Таким целям отвечает не частный, а общий подход в обучении решению текстовых задач. Общий подход к решению задач по математике для начальной школы был разработан ещё в 80-е годы, но в действующем учебнике математики оставался частный подход к решению задач. Логика изложения материала была такова, что учащимся предлагались вначале задачи одного вида, затем другого, третьего, при этом решение первого вида задач многими школьниками забывалась. Как следствие, формировалось частное умение решать задачи. В последнее десятилетие общий подход к решению задач, предполагающий деление процесса решения задач на этапы, постепенно становится приоритетным и в практике. Существенный вклад в наметившиеся перемены внесли работы Л. М. Фридман, С. Е. Царёвой, А. В. Белошистовой, Р. Н. Шиковой.

«Обучение общему умению решать задачи - это:

- формирование знаний о задачах, методах и способах решения, приёмах, помогающих решению, о процессе решения задачи, этапах этого процесса, назначения и содержания каждого этапа;

- выработка умения расчленять на составные части, использовать различные методы решения, адекватно применять приёмы, помогающие понять задачу, составить план решения, выполнить его, проверить решение,

умения выполнять каждый из этапов решения».

Существуют различные подходы при анализе процесса решения задачи: логико- математический ( выделяют логические операции , входящие в этот процесс), психологический (анализируются мыслительные операции , на основе которых он протекает ) и педагогический (приёмы обучения, формирующие у учащихся умения решать задачи). При всём многообразии подходов к обучению решению задач основными считаются четыре этапа решения задачи, которые вычленил Д. Пойа. Каждый этап есть сложное умственное действие, входящее в состав ещё более сложного – решения задачи.

Первый этап- восприятие и осмысление задачи. Цель этапа - понять задачу, то есть выделить все множества и отношения, величины и зависимости между ними, числовые данные, лексическое значение слов. Основные приёмы работы на этом этапе:

- разбивка текста на смысловые части;

- постановка специальных вопросов;

-переформулировка, перефразирование, заменить описание термином, синонимом, убрать несущественные слова, конкретизировать;

- построить модель

Второй этап- поиск плана решения. Цель: связать вопрос и условие. Приёмы:

- рассуждения от условия к вопросу (синтетический способ), от вопроса к условию (аналитический способ), составление уравнения, рассуждение по модели, по словесному заданию отношений;

- название вида задачи;

- знание способа решения «таких» задач

Третий этап- выполнение плана решения задачи. Цель: выполнить операции в соответствующей математической области устно или письменно. Приёмы:

- оформление решения в виде записи решения: по действиям без пояснения, по действиям с пояснением, выражением, по действиям с вопросами, с помощью уравнения;

- выполнение алгоритма решения «таких» задач;

- название вида задачи

Четвёртый этап- проверка. Цель: убедиться в истинности выбранного плана и выполненных действий, после чего сформулировать ответ.

Приёмы - до решения: прикидка ответа или установление границ с точки зрения здравого смысла математики. Во время решения: по смыслу полученных выражений; осмысление хода решения по вопросам. После решения: решение другим способом, другим методом, подстановка результата в условие; сравнение с образцом; проверка на малых числах; составление и решение обратной задачи.

Общий приём решения задач должен быть предметом специального усвоения с последовательной отработкой каждого из составляющих этапов. Овладение этим приёмом позволит учащимся самостоятельно анализировать и решать различные типы задач.

Универсальные учебные действия можно сгруппировать в четыре блока: личностные, регулятивные, познавательные (включая логические, знаково-символические и познавательные), коммуникативные.

Общий приём решения задач - является универсальным учебным действием познавательного характера, так как в его этапах можно выделить постановку и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблемы поискового и творческого характера. Познавательные действия включают в себя исследование, поиск, отбор и структурирование необходимой информации, моделирования изучаемого содержания, логические действия и операции, способы решения задач. Для успешного обучения в начальной школе должны быть сформированы следующие познавательные универсальные учебные действия: общеучебные, логические, действия постановки и решения проблемы.

Общеучебные универсальные действия:

-знаково-символическое моделирование- преобразование объекта из чувственной формы в модель;

- умение структурировать знания;

-выбор наиболее эффективных способов решения задачи в зависимости от конкретной задачи;

-рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. Рефлексия одна из важнейших особенностей, которая начинает складываться в младшем школьном возрасте./12/.

-постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера

Универсальные логические действия:

- анализ объектов с целью выделения признаков (существенных, несущественных)

-синтез как составление целого из частей, в том числе с самостоятельным достраиванием , восполнением недостающих компонентов;

- выбор оснований и критериев для сравнения, сериации, классификации объектов;

-установление причинно-следственных связей;

-построение логической цепи рассуждения;

- доказательство

-выдвижение гипотез и их обоснование

Одно из важнейших познавательных универсальных действий – умение решать проблемы или задачи. Усвоение общего приёма решения задач базируется на сформированности логических операций – умение анализировать объект, осуществлять сравнение, выделять общее и различное, осуществлять классификацию, сериацию, логическую мультипликацию, устанавливать аналогии. В силу сложного системного характера общего приёма решения задач данное универсальное учебное действие может рассматриваться как модельное для системы познавательных действий. Решение задач выступает и как цель, и как средство обучения. Умение ставить и решать задачи является одним из основных показателей уровня развития учащихся, открывает им пути овладения новыми знаниями.

1.2. Виды дифференцированной работы при обучении общему приёму решения текстовых задач.

Приоритетной задачей начальной ступени образования является сохранение индивидуальности ребёнка, создание условий для его самовыражения. Эта задача решается посредством дифференцированного обучения, которое учитывает темп деятельности школьника, уровень его обученности, сформированность у него умений и навыков. В практике внутриклассная дифференциация представлена различными заданиями, дозированием учебной помощи ученикам. Чаще всего на уроках используются задания различного уровня сложности, рассчитанные на группы учащихся, отличающиеся по своим психофизическим признакам: особенностям памяти, внимания, мышления, восприятию информации. Важно создать условия для того, чтобы каждый ученик мог полностью реализовать себя, стать подлинным субъектом, желающим и умеющим учиться. В практике существуют различные способы дифференциации: по уровню творчества, трудности, объёму. Используются разные способы организации деятельности детей: по степени самостоятельности, характеру помощи, форме учебных действий. Предмет «математика» наиболее сложный, потому что он включает в себя решение задач. Решение задач – процесс, с которым справится не каждый ребёнок. Если учащиеся затрудняются в решении задач, им необходима специально организованная помощь. Могут быть предложены следующие виды помощи учащимся: стимулирующая ( в начале и в конце работы), направляющая (в процессе работы), обучающая ( от начала и до конца работы, отдельным ученикам). В учебнике М. И. Моро не разработаны приёмы оказания дидактической помощи ученикам. Поэтому нужно разработать виды помощи для каждого этапа работы над задачей, используя разные способы дифференциации. Учащимся предлагаются разноуровневые по сложности задания.

Требования к подбору разноуровневых заданий:

-по содержанию материал подбирается в соответствии с индивидуальными особенностями учащихся;

-объём заданий, необходимый и достаточный, соответствует индивидуальным особенностям учащихся;

- прослеживается преемственность и перспективность изучаемого материала.

Рассмотрим различные виды дифференциации на каждом этапе решения текстовых задач.

Работа над задачей начинается с прочтения, понимания задачи и выделения её структурных элементов, т.к именно невнимательно прочитанная задача, отсутствие анализа её текста становится причиной ошибок в процессе решения задач. Поэтому при работе с задачей важно уделить как можно больше внимания первому этапу решения задачи- усвоению содержания её текста. А. В. Белошистова подчёркивает, что с «методической точки зрения, для полноценной работы над этим этапом работы с задачей ребёнок должен:

а) уметь хорошо читать и понимать смысл прочитанного;

б) уметь анализировать текст задачи, выявляя его структуру и взаимоотношения между данными и искомым;

в) моделировать заданную в задаче ситуацию/9/

Ученики достаточно хорошо справляются с решением задачи если при разборе и поиске решения использовался чертёж т.е модель задачи. Как и всякому учебному действию, действию моделирования надо учиться специально. Можно предложить следующие виды работы по формированию действия моделирования:

-дорисовать схему, чтобы она соответствовала задаче;

-обозначить на схеме известные и неизвестные в задаче величины;

-выбрать схему, которая соответствует задаче;

- используя данную схему, вставить пропущенные в задаче слова и числа»

- используя схему, закончить решение задачи различными способами;

- используя данную схему или таблицу, вставить пропущенные в условии числа и сформулировать вопрос;

-используя данную схему, записать, что обозначает выражение;

- соединить условия с соответствующими схемами;

- выбрать схему, соответствующую данному условию, обозначить на ней известные и неизвестные величины;

- составить по схеме задачу.

Второй этап- поиск плана решения задачи - требует рассуждений обучающихся. Рассуждение можно строить двумя способами: идти от вопроса задачи к числовым данным или же от числовых данных к вопросу.

Во втором классе легче усваивается синтетический способ разбора, если он сопровождается наглядностью или схемой. Учащимся, испытывающим трудности в составлении плана решения можно предложить следующие дифференцированные задания:

- по данной модели записать решение задачи;

- деформированный план решения привести в соответствие с ходом решения задачи;

- закончить начатый план решения задачи;

- выбрать верный план решения из предложенных вариантов.

На третьем этапе решения задачи – выполнение плана решения задачи –учащиеся, как правило , не сталкиваются с большими трудностями. Но ребятам менее успешным в решении текстовых задач полезно предлагать карточки с разной степенью помощи учителя. Это могут быть следующие виды дифференцированной помощи:

- выбрать выражение, которое является решением задачи;

- закончить запись решения задачи и написать пояснение к каждому действию решения задачи;

- по данной модели записать решение задачи;

- записать пояснение к каждому действию решения задачи;

- записать решение задачи по вопросам;

- записать решение задачи, пользуясь пояснением;

- выбрать выражения, которые имеют смысл, и записать к ни м пояснение;

- написать, что обозначает каждое выражение, затем записать решение задачи по действиям с пояснением.

Четвёртый этап – проверка решения. Виды дифференцированной помощи:

- сравнить с образцом;

- решить другим способом;

- проверка на малых числах;

- составление и решение обратной задачи:

- подстановка результата в условие.

Использование данных приёмов и способов обучения младших школьников решению текстовых задач поможет преодолеть затруднения, позволит учителю сделать этот процесс успешным, организовать деятельность детей так, чтобы они сумели справляться с проблемами, возникающими в процессе обучения.

II. Практическое описание опыта реализации дифференцированного подхода в обучении младших школьников решать текстовые задачи

Приоритетной целью современного российского образования становится не репродуктивная передача знаний, умений и навыков от учителя к ученику, а полноценное формирование и развитие способностей ученика самостоятельно ставить учебную проблему, формулировать алгоритм её решения, контролировать процесс и оценивать полученный результат, т.е научиться учиться. Это станет залогом успешной адаптации в стремительно меняющемся обществе.

Решение задач в учебном предмете «Математика» выступает как цель и как средство обучения. Умение ставить и решать задачи является одним из основных показателей уровня развития учащихся, открывает им пути овладения новыми знаниями. В результате мной была поставлена задача: организовать процесс обучения общему приёму текстовых задач для успешного развития каждого ребёнка.

Успешность процесса учения решению текстовых задач зависит от многих факторов, среди которых не последнюю роль играет обучение соответственно способностям и возможностям ребёнка, т. е дифференцированное обучение./15/

Большую роль при этом играет организация групповых форм обучения, которые основаны на учебном сотрудничестве младших школьников и позволяют учащимся работать без пошагового руководства и контроля со стороны учителя. Работая в группе, учащиеся учатся работать активно, серьёзно относиться к порученному делу, успешно взаимодействовать с любым партнёром, вежливо и доброжелательно общаться с ним, испытывать чувство ответственности не только за собственные успехи, но и за успехи своих партнёров. Работа в группах может быть организована по разному. Полезно всем учащимся предлагать разноуровневые задания. Разделить класс на группы может учитель. Главное – сделать это тактично, и тогда деление на разноуровневые группы ученики воспримут вполне адекватно, так же как, скажем, деление по вариантам, тем более что группы эти не постоянного, а сменного состава. Ученика из первой группы можно перевести во вторую, а из второй в третью. При сотрудничестве в группе у школьников не возникает боязни и стеснения, что он ошибётся или не выполнит задание, он – среди равных себе. А сколько восторга и радости вызывает правильное выполнение задания, похвала группе и перевод в другую группу. Задания первой группы направлены на фрагментное восприятие учебного материала, выполнение одношаговых и двушаговых операций, простейших действий по образцу. Во второй группе – задания на самостоятельное воспроизведение учебного материала с установлением связей между его элементами, выполнение стандартных операций, умение сопоставлять, классифицировать, делать правильный выбор. Задания третьей группы являются более сложными и оригинальными: на применение теоретических знаний для поиска ответа на вопрос в субъективно новой ситуации, решение нестандартных задач, решение задач разными способами .

Второй класс – это начальный этап решения задач. Дети знакомятся с терминами «задача», «вопрос задачи», « данные и искомые задачи». Простая и составная задачи, обратная задача, краткая запись решения задачи. Часто дети затрудняются в решении задач, им необходима организованная помощь. Предлагаются следующие виды помощи: стимулирующая ( в начале и в конце работы), направляющая (в процессе работы), обучающая (от начала и до конца работы, отдельным ученикам). Эту помощь учитель может оказать с помощью карточек-помощниц. Рассмотрим особенности работы с карточками – помощницами.

Пример №1

Математика М. И. Моро 2 класс стр. 34 №13

В киоске было 90 гвоздик. До обеда продали 40 гвоздик, а после обеда ещё 28. Сколько гвоздик осталось в киоске?

Учащимся третьей группы предлагается выполнить задание самостоятельно, а учащимся 1-й и 2-й групп оказывается помощь различного уровня. Карточки – помощницы являются либо одинаковыми для всех в группе, либо подбираются индивидуально. Ученик может получить несколько карточек с нарастанием уровня помощи при выполнении одного задания, а может работать с одной карточкой. Важно учитывать, что от урока к уроку степень помощи ученикам уменьшается.

Карточки с видами помощи:

- краткая запись, модель, схема;

- план решения;

- начало решения или частично-выполненное решение

- алгоритм решения задачи.

На уроке организую самостоятельную работу учащихся по карточкам. Работа строится таким образом, чтобы каждый выбрал задание в соответствии со своими возможностями. При выполнении заданий отмечаю отличие заданий по трудности – лёгкости.

Пример № 2

Даны задачи:

а) В автобусе было 10 пассажиров, вышло 4. Сколько пассажиров осталось?

б) В автобусе было 10 пассажиров, вышло 4, а потом ещё 2. Сколько пассажиров осталось?

в) В автобусе было 10 пассажиров, вышло 4, а потом ещё 2, а 3 человека вошло. Сколько пассажиров стало?

Делаю на доске запись:

Знаешь, как решить решай.
Решил, приступай к решению задачи следующего уровня.

У каждого ученика на парте лежит карточка с заданием трёх уровней. Класс не делится на группы. Все ученики в одинаковых условиях. Учитель даёт задание прочитать задачу первого уровня. Если ребёнок понял, как решать задачу он поднимает карточку зелёного цвета, если затрудняется поднимает карточку красного цвета. Учеников, у которых возникло затруднение я приглашаю за отдельный стол, где находятся карточки помощницы или работаю с ними индивидуально. Так с каждым уровнем решения задачи. Таким видом работы над задачей нацеливаем каждого ученика на адекватный выбор сложности задания. «Примериваем» задания к ученику: «Почему ты смог выполнить это задание», «Что помогло это сделать?» Такая организация самостоятельной работы при решении задач способствует повышению познавательного интереса учащихся, выполнивших задание только первого уровня. У учеников возникает естественное желание самостоятельно выполнить все предложенные задания. Выполнить более сложное задание становиться целью каждого ученика.

Пример самостоятельной работы над задачей с лишними данными с использованием дозированной, постепенно увеличивающейся помощи:

Пример № 3

Задача: Дядя Федор поехал с папой в Простоквашино на 5 дней. Дядя Фёдор привёз в подарок Матроскину 15 бутербродов, а папа 13 бутербродов. Сколько бутербродов съел Матроскин, если через 2 дня у него осталось 9 бутербродов?

Карточка 1

Прочитай задачу внимательно. Она не совсем обычная. Подумай, что в задаче известно и что нужно узнать. Реши задачу.

Карточка 2

Подумай, все ли числа нужно использовать при решении задачи

Карточка 3

В задаче есть лишние данные. Подумай, какие числа не нужны для решения задачи.

Карточка 4

Подумай верно ли составлена краткая запись задачи:

Привезли- ? 15 б. и 13 б.

Съел - ?

Осталось – 9 б.

Карточка 5

Подумай, как можно узнать , сколько всего бутербродов привезли Матроскину и сколько он их съел?

Карточка 6

Воспользуйся схемой и реши задачу

1

) + = (б) – привезли

2

) - = (б)

Для того чтобы организовать разноуровневую работу над задачей в одно и то же время, отведённое для этого на уроке, мы используем индивидуальные карточки задания разные по цвету, которые готовим заранее в четырёх вариантах. Карточки содержат системы заданий, связанных с анализом и решением одной и той же задачи , но на разных уровнях.

Пример 4. М. И. Моро 2 класс №4 стр26

Около школы 8 лип, а берёз на 2 больше, чем лип. Сколько всего лип и берёз посадили около школы?

Этапы	1 группа	2 группа	3 группа
Восприятие и осмысление задачи	Дан чертёж.Найди и покажи данны и искомые Л. 8 ? Б. на2 б.	Подписать данные и искомые на чертеже	Самостоятельно составить чертёж и подписать
Поиск плана решения	План решения 1) 8+ = 10 (б.) 2) + = 18 (д.)	Закончить начатый план 1) + = (б.) 2) + = (д.)	Записать план решения
Выполнение плана решения	Записать по действиям	Записать по действиям с пояснением к каждому действию	Записать по действиям и выражением
Проверка	Сравнение с образцом	Сравнение с образцом	Придумай свою задачу, которая имеет такое же решение, с такими же числами и сравни результаты.

Проанализировав задачу, учитель предлагает взять карточку зелёного цвета и выполняют задание, затем красного, жёлтого и белого. Каждый цвет обозначает этап решения задачи.

Пример № 5 М. И. Моро №3 стр. 7

На прогулку вышли 7 девочек, а мальчиков на 2 больше. Сколько мальчиков вышло на прогулку?

Этапы решения задачи	1 группа	2 группа	3 группа
Восприятие и осмысление плана решения задачи	Вставить данные и искомые в краткую запись Девочки – Мальчики -	Самостоятельно составить краткую запись решения	Самостоятельно составить краткую Запись решения
План решения	На основе рассуждения синтетическим способом составить план решения	Самостоятельно по краткой записи составить план решения	Самостоятельно по краткой записи составить план решения
Запись решения задачи	Запиши решение задачи + =	Запиши решение задачи	Запиши решение задачи
Проверка	Фронтальная	фронтальная	фронтальная

С целью формирования умения решать задачи можно использовать виды дополнительной работы над задачей.

3- группа – измени вопрос задачи так, чтобы она решалась в два действия.

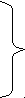2-ой группе – реши задачу, используя схему

7

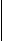на,2 б. ?

1-ая группа под руководством учителя

Пример № 6

Саша собрал с грядки 36 кг. огурцов, а Серёжа на 6 кг. больше. Сколько кг. огурцов собрали ребята?

этапы	1 группа	2 группа	3 группа
Восприятие и осмысление задачи	Дана схема 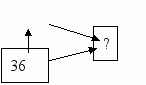6	Подписать данные и искомые	Самостоятельно сделать чертёж и подписать
Поиск плана решения	План решения 1) + = 2) + =	Выбрать правильное решение 1) - = 2) + = 1) + = 2) + =	Записать план решения
Выполнение плана решения	Записать по действиям	Записать по действиям с пояснением к каждому действию	Записать по действиям и выражением
Проверка	Ответ:78 кг.	Составь выражение по задаче +( + ) сверь ответы	Сопоставь ответы , полученные по действиям и выражением

После решения задачи на индивидуальных карточках ставится цель: продолжить формирование умения составлять задачу , обратную данной по выражению.

78- 42=

1-уровень

Рассмотри данное выражение. Оно показывает , что должно быть известно в задаче. Догадайся каким должен быть вопрос. Для выполнения этого задания используй этот текст.

Всего ребята собрали …кг. огурцов. Серёжа собрал … кг. Поставь нужные числа и запиши вопрос задачи.

2

- группа

Для выполнения задания воспользуйся чертежом. Обозначь на нём то, что

надо. Подумай каким будет вопрос задачи, и укажи его на чертеже.

3группе. Составленную тобой обратную задачу изобрази с помощью чертежа

На уроке может быть организована и групповая работа учащихся. Состав группы может быть как разноуровневый, так и одноуровневый, в зависимости от цели, которую ставит перед собой учитель. При этом дети каждой группы обсуждают и выполняют задания совместно.

Работа над текстовой задачей на уроке с помощью описанных нами карточек заданий органично вписывается в ход урока, удобна в организации, повышает самостоятельность учащихся и позволяет формировать у них умения решать текстовые математические задачи на доступном уровне сложности, - это совершенствует обучение решению задач учащихся начальных классов.

Результативность

Метод оценивания - индивидуальная работа детей.

Критерии оценивания:

- умение выделять смысловые единицы текста и устанавливать отношения между ними

- создавать схемы решения

- выстраивать последовательность операций

- соотносить результат решения с исходным условием задачи

Проанализировав таблицу (смотри приложение) видно, что большинство детей имеют средний уровень успешности в обучении решению задач. Они ещё применяют стереотипные способы решения задач, допускают ошибки в соотнесении результата решения с исходными данными задачи. Мы так же видим, что особое внимание надо уделить учащимся показавшим низкий уровень, поэтому целесообразно вести работу по использованию дифференцированных заданий для учащихся моего класса.

Но при использовании разноуровневых заданий на каждом этапе решения задач хорошо прослеживается развитие личностных универсальных учебных действий. У ребят открывается ориентация на понимание причин успеха в учебной деятельности, способность к самооценке на основе критерия успешности, воспитывается сопереживание, сознание ответственности.

Познавательные учебные действия: дети учатся использовать знаково-символические средства, в том числе модели и схемы для решения задачи, осваивают разнообразие способов решения задач, осуществляют анализ задачи с выявлением существенных и несущественных признаков, синтез как составление целого из частей, строить рассуждения, обобщать.

Ребята учатся правильно оценивать ход решения и реальность ответа на вопрос задачи, проверяют правильность хода решения, анализируют ответ к задаче с точки зрения его реальности. Использую задачи на развитие логического мышления. Исходя из данных наблюдений можно предположить динамику роста успешности детей в обучении решению текстовых задач (смотри приложение)

Метод оценивания: итоговые и текущие контрольные работы (таблицу смотри в приложении)

Заключение

В процессе работы над использованием разноуровневых заданий при формировании общего приёма решения текстовых задач была поставлена цель: разработать варианты реализации дифференцированного подхода в обучении младших школьников общему приёму решения текстовых задач.

Для достижения этой цели были решены следующие задачи: изучена и проанализирована психолого-педагогическая литература о данной проблеме; разработаны разноуровневые задания для каждого этапа решения текстовых задач, использованы на практике; проанализированы результаты своей деятельности.

Использование разноуровневых заданий при обучении общему приёму текстовых задач способствует более успешному обучению детей в старших классах, поможет детям преодолеть затруднения и улучшить свои навыки в решении задач. Позволит учителю начальных классов сделать этот процесс успешным, организовать деятельность детей так, чтобы они сумели справляться с проблемами, возникающими в процессе обучения. В целом организация процесса обучения в условиях дифференциации при условии систематического контроля за результатами обучения и развития каждого ребёнка позволяет осуществить у учащихся положительную познавательную мотивацию, способствует их развитию. Считаю, что стоит задача дальнейшего совершенствования работы по данному вопросу.

Литература

Л. С. Гугова. Дидактические затруднения учителя в обучении решению текстовых задач// Начальная школа на пути совершенствования// Вологда. - 2009 –с.59-66
Л. С. Гугова, В. В. Косарева. //Формирование обобщённых умений решения текстовых задач на основе моделирования и разноуровневых заданий у учащихся 1-2 классов //Начальная школа на пути совершенствования// Вологда -2009 – с.68-80
О. В. Баринова. Дифференцированное обучение решению математических задач//начальная школа - 1999 год- № 2-с.41-44.
С. Е. Царёва. Обучение решению задач// Начальная школа// - 1997- №11-с. 93-94.
А. Г. Асмолова. Как проектировать УУД в начальной школе// Стандарты второго поколения . //Москва «Просвещение»-2010 –с.90-93
Г. С. Ковалёва, О.Б. Логинова Планируемые результаты начального общего образования// Стандарты второго поколения //Москва- «Просвещение»-2010-с.57-63
Примерная основная образовательная программа образовательного учреждения // Москва «Просвещение»-2010- с. 100-101
Р. Н. Шикова, Е. И. Бологова. Формирование самоконтроля в процессе обучения младших школьников решению текстовых задач// Начальная школа -2000 год-№1-с37-40
А.В. Белошистова. Обучение решению текстовых задач с ориентацией на формирование учебной деятельности учащихся//Методические рекомендации по методике преподавания математики//М.МГПИ им. Ленина-1985-с. 67-73
В. В. Яровая. Организация самостоятельной работы на уроках математики в начальной школе//начальная школа-№4-2006-с.84-86
Т. И. Пинчук. Как лучше организовать обучение с одарёнными детьми.// Начальная школа//-№6-2019-с.21-22
С.С. Пичугин. Использование графа в решении задач//Начальная школа-2010-№11-с.34
С. Е. Царёва. Виды работы с задачами на уроках математики. //нач. школа//- №10- 1990 с.52-63
Осмоловская И. М. Как организовать дифференцированное обучение.// Библиотека журнала// Директор школы - 2002 -№5-
А. В. Перевезный.// Организационно- педагогические аспекты дифференцированного обучения. //Нач. школа плюс до и после -2008- №4-
Интернет www standart. edu.ru

Приложение

Ф. И.
	Умение выделять смысловые единицы текста и отношения между ними	Создавать схемы решения	Выстраивание последовательности операции	Соотношение результата решения с исходным решением задачи
Анисова Ксения	-	+	+	-
Васюкова Марина	-	-	+	+
Завьялова Анастасия	-	-	-	-
Кучин Дмитрий	+	+	+	-
Кичигин Владимир	+	+	+	+
Лукачёв Максим	-	+	+	+
Мекрюкова Наталия	+	+	+	+
Норов Дмитрий	+	+	+	+
Сарбай Даниил	-	-	-	-
Силинская Алёна	-	-	+	+
Смирнов Павел	-	+	-	+
Шилова Марина	-	+	+	+

Таблица прогнозируемых результатов

Ф. И.	Восприятие задачи	Составление модели	Построение последовательности операции	Соотношение результата с исходным
Анисова	+	+	+	+
Васюкова	-	+	+	+
Завьялова	-	-	-	-
Кучин	+	+	+	+
Кичигин	+	+	+	+
Лукачёв	+	+	+	+
Мекрюкова	+	+	+	+
Норов	+	+	+	+
Сарбай	-	-	-	-
Силинская	+	+	+	+
Смирнов	-	-	+	+
Шилова	+	+	+	+

Таблица текущих срезов

Фамилия, имя	I четверть	I четверть	II четверть
Анисова Ксения	+	+	+	В
Васюкова Марина	-	+	+	С
Завьялова Анастасия	-	-	-	Н
Кичигин Владимир	+	+	+	В
Кучин Дмитрий	+	+	+	В
Лукачё Максим	-	+	+	С
Мекрюкова Наталия	+	+	+	В
Норов дмитрий	+	+	+	В
Сарбай Даниил	-	-	-	Н
Силинская Алёна	-	+	+	С
Смирнов Павел	-	-	+	С
Шилова Марина	+	-	+	С

Blog

Литература

Содержание