Задачи моего диплома: Найти и прочитать материал по моей теме

Вид материала

Диплом

Содержание §2. Определения сечения, призмы и пирамиды.

Подобный материал:

• Доклад по гуманитарной конференции Лены Швец. «Два Диониса: в «Лягушках» Аристофана, 124.18kb.
• Для обучающихся 11 а и 11 в классов, 34.56kb.
• Скажем «нет» курению. Цель, 52.19kb.
• Урок по географии по теме «Путешествие по штатам», 36.99kb.
• Задачи: Подобрать литературу по теме «Золотое сечение». Найти информацию по теме, 164.44kb.
• Д. з учебник №575, 577, 588, 604. 7а геометрия Д. з учебник, 29.07kb.
• Цель: познакомить учащихся с традициями и обычаями празднования Нового года в России, 86.07kb.
• Задачи по теме Высокочастотные, 34.16kb.
• Значение русского языка в моей жизни, 29.35kb.
• Задачи по теории вероятностей и математической статистике, 57.05kb.

§1. Введение.

В своей деятельности человеку повсюду приходится сталкиваться с необходимостью изучать форму, размеры, взаимное расположение пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул. Раздел геометрии, в котором изучаются такие задачи, называется стереометрией (от греческого «стереос»- объемный, пространственный).

В курсе стереометрии 10-х классов были рассмотрены важные и интересные свойства плоскостей, прямых, многогранников и их взаимное расположение. Но многие интересные и действительно полезные геометрические факты не вошли в основной курс. Мой диплом посвящен глубокому изучению видов сечений и методов их построения, которые не изучаются в школьной программе.

Теме «Задачи на построение сечений», которая изучается в десятом классе, отведено 3 часа, что достаточно только для базового изучения, но недостаточно для получения хороших навыков. В тему «Задачи на построение» входят: определение сечения, методы построения простейших сечений, виды сечений. С помощью данного материала, который изучается в школьной программе, мы можем решать довольно узкий круг задач.

Задачи моего диплома:

1. Найти и прочитать материал по моей теме.
   
2. Разобрать данный материал.
   
3. Изучить методы построения сечений.
   
4. Подобрать условия задач для создания электронного пособия.
   
5. Создать электронное пособие в программе «Живая Математика», а именно пошаговое построение сечений с ссылками на определения и теоремы(свойства).
   
6. Создать электронное пособие в среде Flash для демонстрации решения задач с помощью методов построения сечений.
   

Итак, цель моего диплома– изучить методы построения сечений и продемонстрировать решение задач с помощью данных методов в среде Flash и создать пошаговое обучение построению в программе «Живая Математика». Поэтому мой диплом будет включать следующие параграфы:

1. Введение.
   
2. Определение сечения, призмы, пирамиды (призма, пирамида – основные фигуры, в которых строятся сложные сечения).
   
3. Методы построения сечений
   

1) метод следов;

2) метод вспомогательных сечений;

3) комбинированный метод.

4. Виды сечений, а также условия образования данных видов сечений.
   
5. Вывод.
   

При написании дипломной работы буду пользоваться следующей литературой:

1. Геометрия: Учебник для 10кл. с углубленным и профильным изучением математики/Е.В. Потоскуев, Л.И. Звавич.
   
2. Геометрия: Задачник для 10кл. с углубленным и профильным изучением математики/Е.В. Потоскуев, Л.И. Звавич.
   
3. "Анимация в среде Flash" С.И. Переверзев, Москва Бином 2005
   

§2. Определения сечения, призмы и пирамиды.

Определение сечения многогранника:

М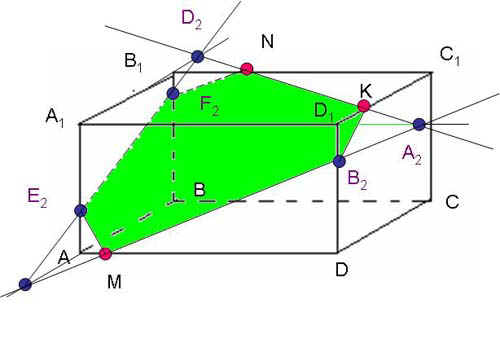ногоугольник, представляющий собой множество всех точек пространства, принадлежащих одновременно данному многограннику и плоскости, плоскость при этом называется секущей плоскостью.

Плоскость не может пересечь грань многогранника по ломанной, а имеет с ней либо общий отрезок, либо общую точку(вершину многогранника), либо не имеет с ней общих точек. Число сторон многоугольника-сечения не может превышать числа граней многогранника. Причем если пересечением плоскости и многогранника является точка (вершина многогранника) или отрезок (ребро многогранника), то эту плоскость мы не будем называть секущей.


Самые простые сечения строятся в параллелепипеде и тетраэдре. Данные построения были рассмотрены в школьной программе 10 класса. Параллелепипед и тетраэдр являются частными случаями призмы и пирамиды соответственно.


Определение n-угольной пирамиды:

М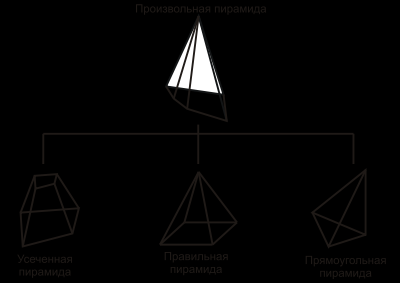ногогранник, одна грань которого, называемая основанием пирамиды, - некоторый выпуклый n-угольник, а остальные n граней – треугольники с общей вершиной. Эта общая вершина называется вершиной пирамиды, а треугольники – боковыми гранями пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами ее основания, называются боковыми ребрами пирамиды. Пирамида, в основании которой n-угольник, а боковые ребра равны между собой, называется правильной пирамидой. Пирамида, в основании которой лежит треугольник, называется треугольной пирамидой или тетраэдром.


Определение n-угольной призмы:

Многогранник, две грани которого, называемые основаниями призмы – равные n-угольники, а все остальные n грани – параллелограммы. Они называются боковыми гранями призмы. Призма может быть прямой или наклонной. У прямой призмы все боковые грани – прямоугольники, у наклонной призмы хотя бы одна грань – параллелограмм, а не являющийся прямоугольником. Призма, в основании которой лежит параллелограмм, называется параллелепипедом.