Матеріал розробила Гордієнко Марія Григорівна, учитель вищої категорії Вельбівської зош І-ІІ ст. Гадяцького району Полтавської області
| Вид материала | Документы |
СодержаниеФункція у = х Функції y = kx, y = k 1. у = k х + 1 Розв’язання 2. у = kх + b. Розв’язання |
- Пропозиції до Комплексної програми впровадження у навчально виховний процес загальноосвітніх, 78.05kb.
- Маркетингові дослідження проекту Мета, 135.94kb.
- Федорова С. М., учитель української мови та літератури зош №138, спеціаліст вищої категорії, 72.17kb.
- Програми з читання, української мови, математики для 1-10 класів спеціальної загальноосвітньої, 1141.95kb.
- Рішенням Конституційного Суду України від 22 травня 2008 р. N 10-рп закон, 128.22kb.
- Учитель вищої категорії, вчитель-методист навчально-виховного комплексу «Загально-, 2399.21kb.
- Ісакієва Людмила Вікторівна, директор Горлівського нвк «зош І ііі ст. №14 багато профільний, 173.71kb.
- «Українська мова 7 клас», 76.39kb.
- Маляренко Світлана Олексіївна, спеціаліст вищої категорії, «старший учитель». «Нестандартні, 102.6kb.
- Постановою Верховної Ради України від 11 грудня 1991 року n 1964-xii із змінами, 203.18kb.
Відділ освіти Гадяцької районної державної адміністрації
Гадяцький науково – методичний центр
ВИВЧЕННЯ МОДУЛІВ
У КУРСІ МАТЕМАТИКИ
БАЗОВОЇ ШКОЛИ
З досвіду роботи
вчителя математики
вищої категорії
Вельбівської ЗОШ І-ІІ ст.
Гордієнко М.Г.
2010р.
Матеріал розробила Гордієнко Марія Григорівна, учитель вищої категорії Вельбівської ЗОШ І-ІІ ст. Гадяцького району Полтавської області.
Посібник містить основні методи розв’язування вправ з модулями в 6-9х класах загальноосвітньої школи. викладення методів супроводжується необхідним теоретичним матеріалом і відповідними прикладами. Для кожного класу і по кожній темі наводяться приклади з детальним поясненням їх розв’язування. Посібник містить велику кількість вправ з модулями.
Рецензенти:
Ємець Т.М. – методист районного методичного кабінету.
Методичний посібник розглянутий і схвалений радою районного методичного кабінету (протокол №3 від 17.02.2009р.) як перспективний педагогічний досвід.
Однією з проблем викладання математики в загальноосвітніх школах є розв’язання вправ модулями. Якщо з модулями працювати систематично з 6-го по 11-й класи, засвоївши певні методики, алгоритми розв’язування вправ, то такий матеріал не такий уже й складний. На жаль, на вивчення модулів у середній школі відводиться одна година в 6-му класі і одна година в 11-му класі. Рівень знань модулів у 6-му класі зводиться до вміння відшукати модуль конкретного числа. Пропоную вихід з такого становища, апробований на власному досвіді, хоча б для засвоєння модулів сильнішими учнями. Ідея така – потрібно з цим матеріалом працювати в 6-9-х класах під час вивчення інших тем.
Вивчення модулів починається в 6-му класі. Учні повинні вміти знаходити модуль числа, як записано в Державному стандарті математичної освіти, але важливо, щоб вони зрозуміли означення модуля за допомогою букв, як подано в підручнику. Найбільша проблема під час вивчення модулів у старших класах – це незнання або нерозуміння означення модуля. Учні добре знають, що
5 = 5 і -5 = 5, а завдання: записати, чому дорівнює х, якщо
-3 < х < -1, викликає труднощі. Особливу увагу слід звернути на розв’язування рівнянь типу х - 1= 4. Успішне засвоєння матеріалу підручника та вміння розв’язувати найпростіші рівняння через означення модуля стане добрим підґрунтям у наступних класах. На жаль цю роботу необхідно провести за один урок. Згідно з програмою та рекомендаціями з планування навчального матеріалу наступна зустріч з модулями – в 11-му класі на одному уроці. Я хочу показати, в яких розділах шкільної програми ми можемо опрацьовувати матеріал з модулями.
У 6-му класі з перших кроків вивчення раціональних чисел у добірку вправ треба ввести вправи на відпрацювання поняття модуля та його геометричної інтерпретації.
У 6-му класі діти вчаться розв’язувати рівняння, що містять модуль:
-5 + х = 3;
-7 - у = 4;
(8,3 - х)·4,7 = 5,64 та обчислювати значення виразів типу:
-20 + 17 + -17 + 20 + -15 + 15
У 7-му класі під час вивчення лінійних рівнянь можна звернутися до найпростіших рівнянь типу х - 2 = 4, а потім розв’язати рівняння типу х - 3 = 2х. Розглядаючи це рівняння, показуємо, що за означенням модуля розв’язати його не можна, бо ми не знаємо, який знак має вираз 2х (це не число). Тому шлях його розв’язування такий.
Розглянемо два випадки, коли х – 3 > 0 і х – 3 < 0. Якщо
х – 3 > 0, х - 3 = - 3, а якщо х – 3 < 0, х - 3 = - (х – 3) (ось тут і необхідне означення модуля). У першому випадку (х – 3 > 0) маємо рівняння х – 3 = 2х. Розв’язок його х = -3. Але ми розглядали випадок, коли х – 3 > 0. Число -3 цю умову не задовольняє, тому розв’язком не буде. Можливий і інший підхід: х - 3 > 0 завжди, тому 2х > 0, х = -3 цю умову не задовольняє. Але перший підхід універсальний, другий – строго індивідуальний.
Розглянемо другий випадок: х – 3 < 0. У цьому випадку
-(х - 3) = 2х. Розв’язавши його, маємо х = 1. Це число задовольняє умову х – 3 < 0, тому є розв’язком рівняння. Складніших лінійних рівнянь у 7-му класі звичайних шкіл, на мою думку, розв’язувати не варто. Їх можна використати, готуючи учнів до олімпіади. Вони зможуть за цією методикою розв’язати і рівняння, де є кілька модулів х – 1 - 1 = 2х. Головне, щоб учні зрозуміли підхід до розв’язування (поділ числової осі на проміжки, де й шукаємо розв’язки).
Розглянемо приклади побудови графіків функції з модулями в 7-му класі.
Функція у = х
Функцію у = х та її графік доцільно розглянути вперше під час вивчення графіка прямої пропорційної залежності y = kx. Необхідно звернути увагу учнів на те, що у формулі у = х коефіцієнт k =1. далі вчитель пропонує учням пригадати означення модуля, наголошуючи на тому, що саме на основі цього означення будують графік функції у = х. Розглядають два випадки:
1. у = х, коли х 0.
Графік – промінь, який є бісектрисою першого координатного кута;
2. у = - х, коли х < 0. Графік – промінь, який є бісектрисою другого координатного кута.
Отже, графік функції у = х складається з двох променів, які виходять з початку координат.
Областю визначення функції у = х є уся числова пряма.
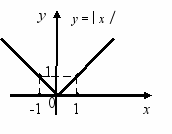
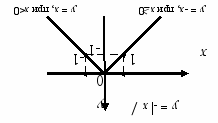
У ході подальшого вивчення відомостей про функцію доцільно побудувати графік залежності у = -х.
Учні повинні самостійно дійти висновку, що графік функції
у = -х проходить через початок координат, складається з двох півпрямих, симетричних відносно осі у, розміщених у нижній півплощині.
Функції y = kx, y = k x + b (k 0)
Для закріплення і поглиблення матеріалу учні будують графіки функцій y = 3x і y = - 3x, y = 0,5x та
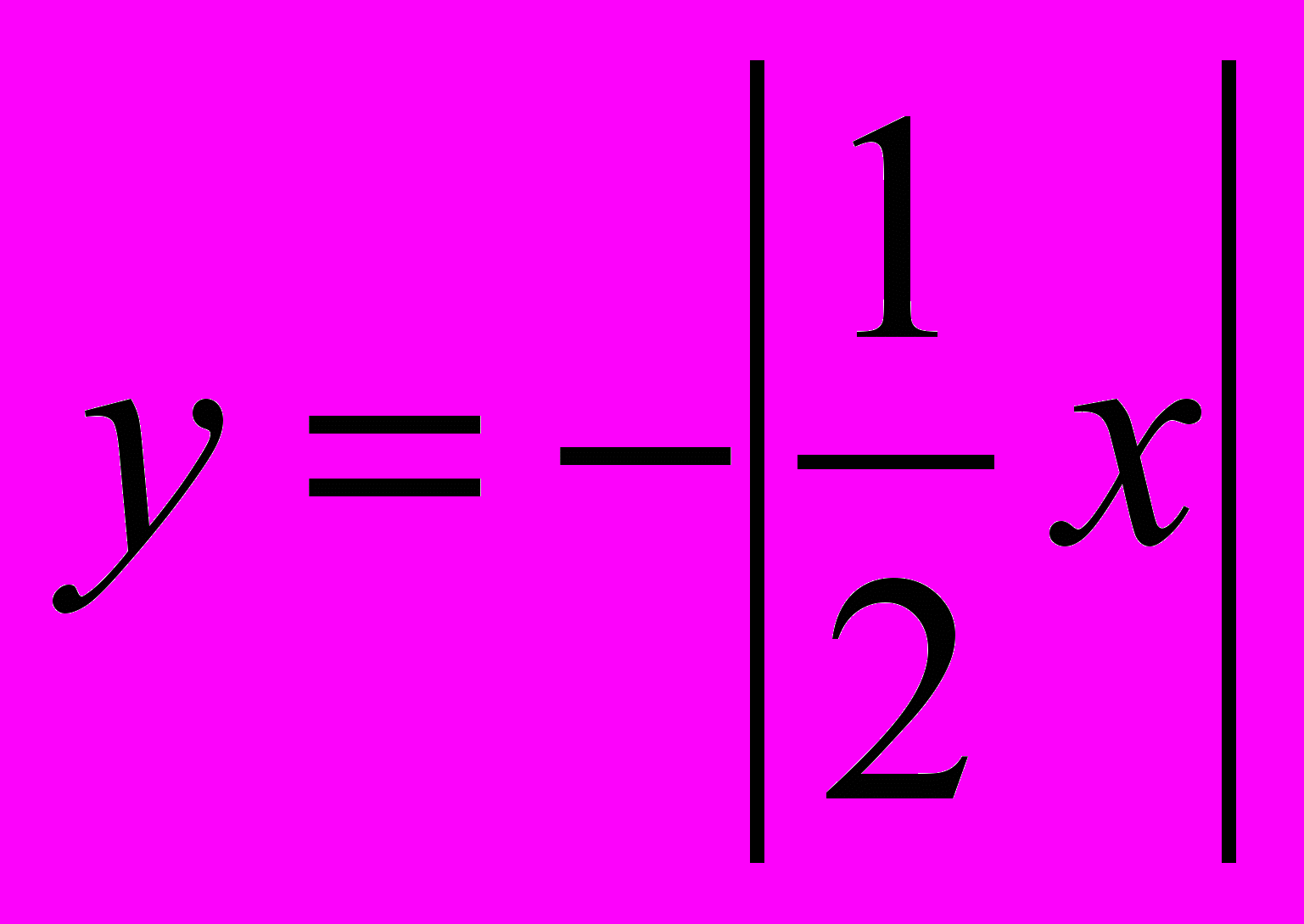 і подібних.
і подібних.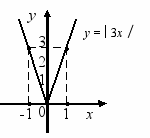
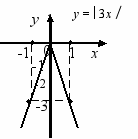
Дослідним шляхом учні переконуються, що на одній півпрямій графіка більшому значенню х відповідає більше значення у (тобто функція зростає), а на другій – більшому значенню х відповідає менше значення у (тобто функція спадає).
Доцільно розглянути і графіки таких залежностей:
х = 1 та у = 1.
Спираючись на означення модуля, замінимо рівняння х = 1 двома такими:
х = 1, якщо х 0,
х = - 1, якщо х < 0.
Шуканий графік є сукупністю цих двох півпрямих.
Міркуючи аналогічно, побудуємо графік у = 1; у = 1, якщо
у 0 і у = - 1, якщо у < 0.
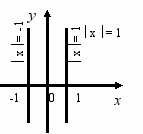

Розгляд таких вправ ще раз проілюструє учням властивість модуля числа х = -х, сприятиме кращому усвідомленню понять парної і непарної функцій. Учні роблять висновок, що функція у = х – непарна, а отже, графік її симетричний відносно осі у. Виходячи з цього, можна сформулювати більш загальне правило побудови графіка функції у = х: щоб побудувати графік функції
у = х, досить побудувати графік функції у = х для х 0, і відобразити його симетрично відносно осі у.
Варто звернути увагу учнів також на те, що коли коефіцієнт
k > 1, то півпрямі звужують ламану, а коли коефіцієнт k < 1, то півпрямі розширюють її.
У 7-му класі під час вивчення лінійної функції варто ознайомити дітей з поняттям осьової симетрії і почати вивчати побудову графіків, що містять знак модуля. Під час побудови таких графіків доцільно розглянути різні види лінійних функцій з модулем. Розглянемо перетворення графіків лінійних функцій, що містять модуль.
1. у = k х + 1
Розв’язання
Будуємо графік функції у = kх + b і частину графіка, що знаходиться в правій площині, відображаємо симетрично відносно осі координат.
2. у = kх + b.
Розв’язання
Функція набуває тільки додатних значень, отже, будуємо графік функції у = kх + b і ту частину графіка, що розміщена нижче від осі Ох, відображаємо симетрично їй.
3. у = kх + b.
Розв’язання
Будуємо графік функції у = kх + b. Оскільки права частина рівності набуває тільки додатних значень або дорівнює 0, то залишаємо частину графіка, яка знаходиться вище від осі абсцис, і відображаємо її симетрично осі Ох.
Розглянемо ці перетворення н прикладах.
1
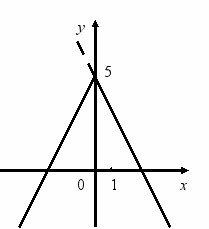
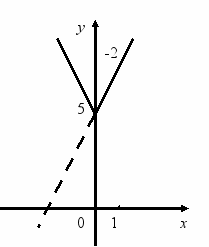 . у = -2 х + 5. 2. у = 2 х + 5.
. у = -2 х + 5. 2. у = 2 х + 5.3. у = 2х + 5 . 4. у = -2х + 5 .
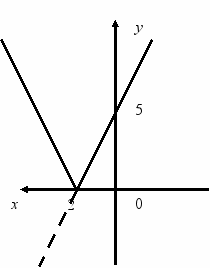
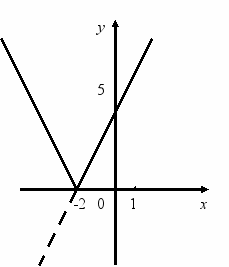
5. у = 2х + 5. 6. у = -2х + 5.
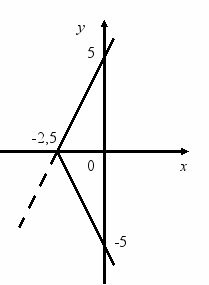
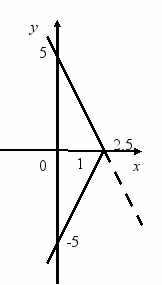
Приклади.
Записати формулу за графіком, поданим на малюнку:
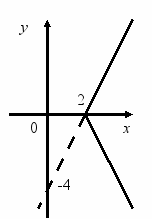
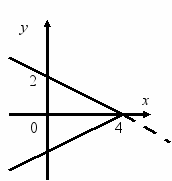
Відповідь. у = 2х – 4 Відповідь. у = -0,5х + 2
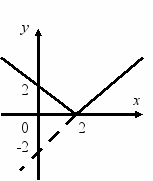
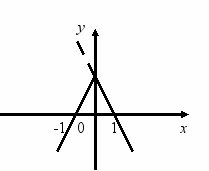
Відповідь. у = х - 2 Відповідь. у = -2 х + 2.
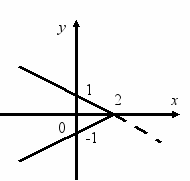
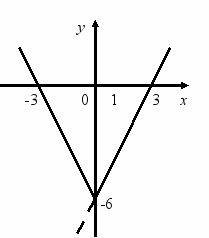
Відповідь. у = -0,5 х + 1. Відповідь. у = -2 х - 6.
Коли учні набудуть досвіду побудови і читання графіків функцій, слід продовжити розгляд вправ, де аргумент входить під знак модуля. Графік функції y = k x + b можна побудувати так: будуємо графік функції y = k x + b для х > 0 і відображаємо його симетрично осі у. У загальному вигляді графік функції y = k x + b – ламана, що складається з двох ланок.
Приклад. Побудувати графік функції y = x + 2.
Виконаємо побудову, використовуючи означення модуля: накреслимо пряму y = x + 2 (для х 0), а потім пряму y = -x + 2 (для
х < 0).
Пам’ятаючи, що функція y = x + 2 – парна, тобто її графік симетричний відносно осі у, можна обмежитися побудовою за двома точками прямої y = x + 2 (для х 0) і відобразити її симетрично відносно осі у.
Приклад. Побудувати графік функції y = 1 – 2 x.
Виконаємо побудову графіка функції y = 1 – 2 x (для х 0) і відобразимо його симетрично відносно осі у.
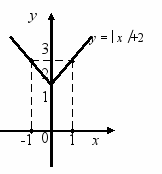
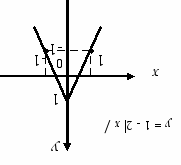
Після розв’язування подібних вправ корисно запропонувати учням зробити деякі узагальнення, а саме:
а) коли перед х стоїть знак плюс, то півпрямі направлені вгору, а коли стоїть знак мінус – униз;
б) коли в формулі y = k x + b число b – додатне, то графік функції y = k x переміщується на b одиниць вгору вздовж осі у, а коли b число від’ємне, то – на b одиниць униз.
Функція y = k x + b
Під час повторення і систематизації відомостей про лінійну функцію у сильних класах доцільно ознайомити учнів з графіком функції y = k x + b, наголошуючи на відмінностях функцій y = k x і
y = k x + b та їх графіків.
Підкреслимо, що з перших кроків вивчення функцій, заданих формулами з вживанням знака модуля, треба чітко розрізняти функції виду у = f(х) і у = f(х).
По-перше, функція у = f(х) не є парною, тому не можна застосовувати симетричне відображення відносно осі у частини графіка. По-друге, з формули, якою задана функція у = f(х), ясно, що вона набуває лише невід’ємних значень, отже, її графік розміщується лише у першому і другому координатних кутах. По-третє, оскільки з означення модуля випливає, що
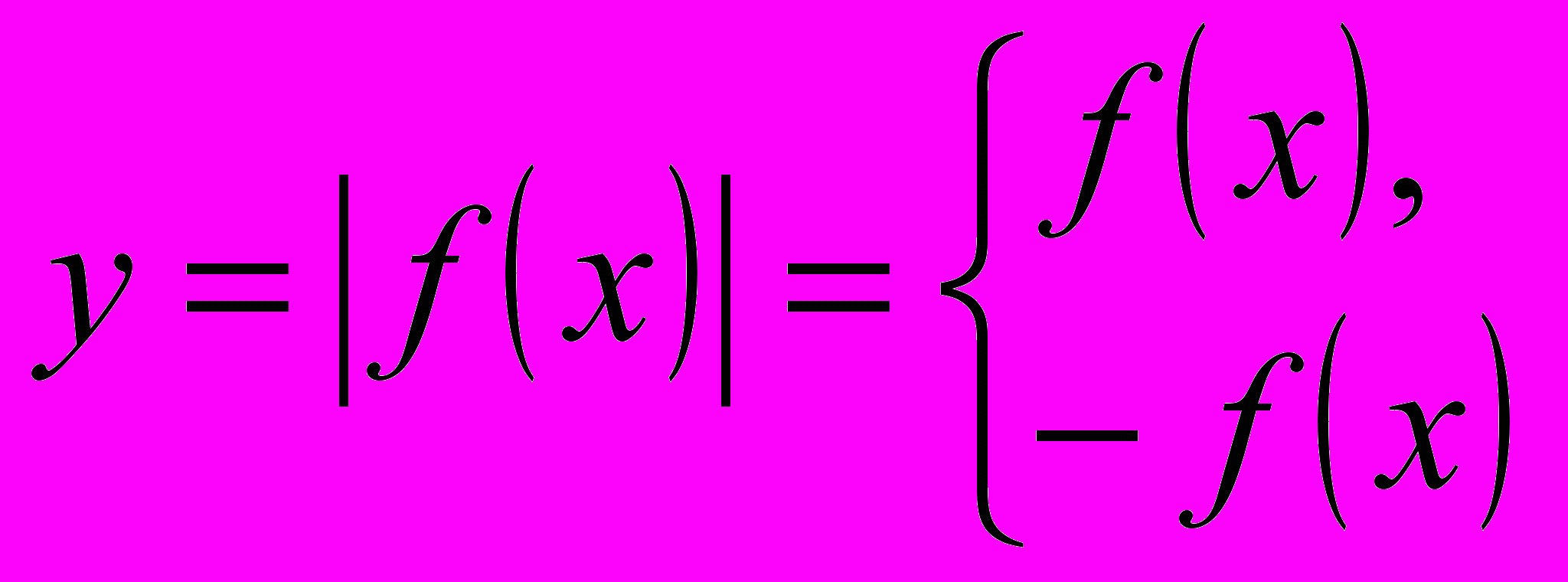
коли f(х) 0
коли f(х) < 0,
т
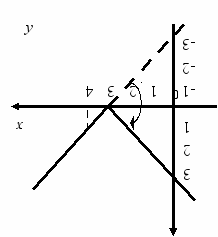 о очевидна симетричність графіків функцій у = f(х) і
о очевидна симетричність графіків функцій у = f(х) і у = - f(х) відносно осі х. Спираючись на ці міркування, приходимо до висновку: щоб побудувати графік функції y = k x + b досить побудувати пряму y = k x + b (для kx + b 0,
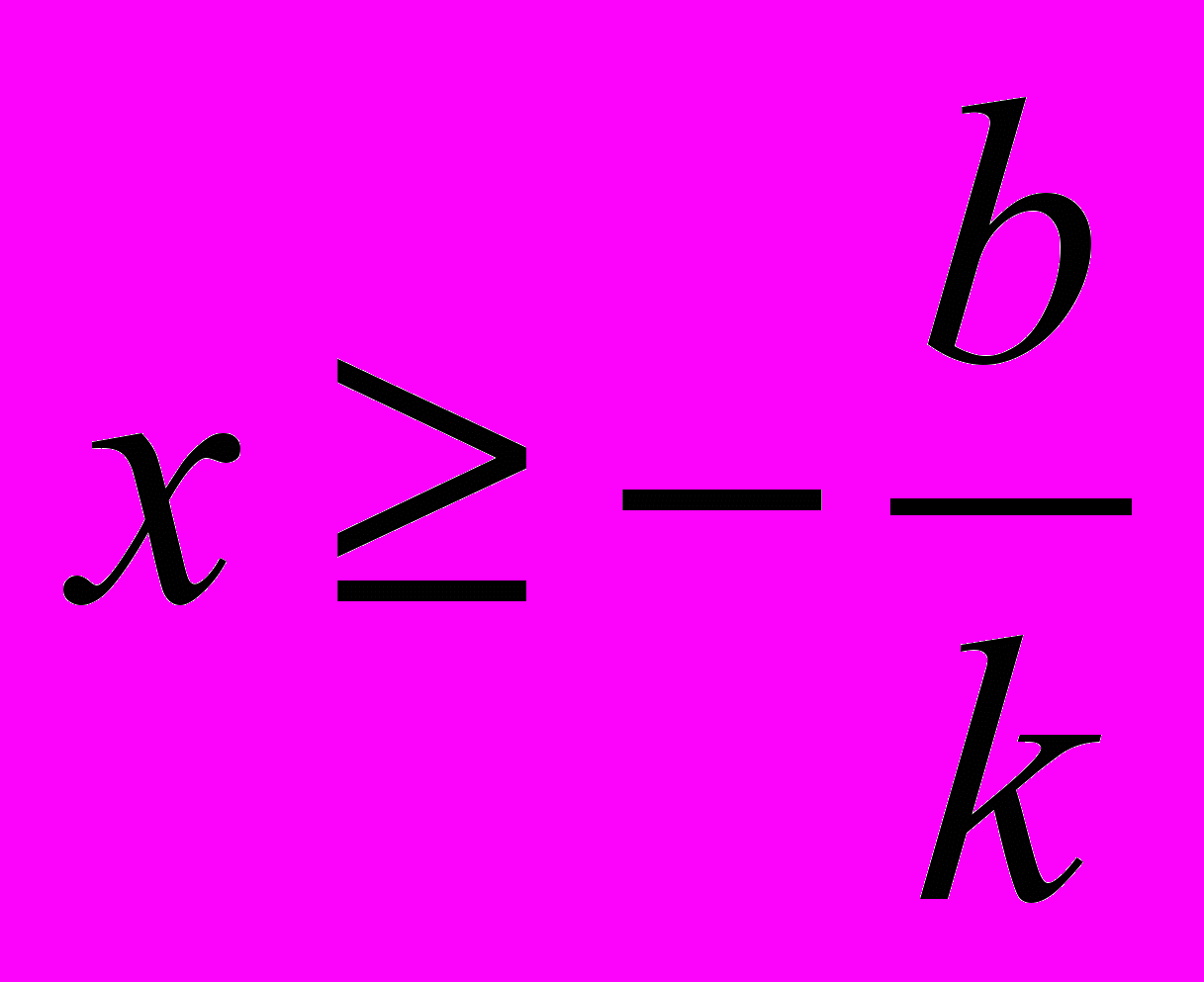 ). Потім ту частину прямої, якій відповідають від’ємні значення у, відобразити симетрично відносно осі х.
). Потім ту частину прямої, якій відповідають від’ємні значення у, відобразити симетрично відносно осі х.Приклад. Побудувати графік функції y = x – 3.
Побудуємо за двома точками пряму y = x – 3 і ту її частину, якій відповідають від’ємні значення у, відобразимо симетрично відносно осі х. Варто запропонувати учням визначити, чи має графік вісь симетрії, записати її рівняння х = 3.
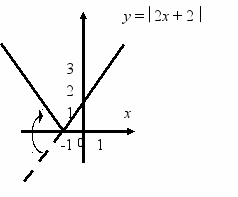
Приклад. Побудувати графік функції y = 2x + 2.
Побудуємо пряму y = 2x + 2 і відобразимо ту її частину, якій відповідають від’ємні значення у, симетрично відносно осі х.
Приклад. Побудувати графік функції y = - x + 1.
Р
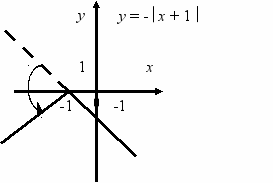 озпочнемо з побудови графіка y = - (x + 1).
озпочнемо з побудови графіка y = - (x + 1).Другим кроком буде відображення частини прямої y = – x – 1, якій відповідають додатні значення у, симетрично відносно осі х (тому, що за умовою у набуває лише від’ємних значень). Звертаємо увагу учнів на те, що віссю симетрії графіка буде пряма
у = -1.
П
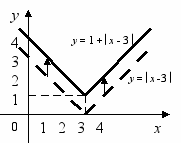 риклад. Побудувати графік функції y = 1 + x - 3.
риклад. Побудувати графік функції y = 1 + x - 3.Для побудови цього графіка треба виконати переміщення графіка функції
y = x - 3 на одну одиницю вгору відносно осі х.
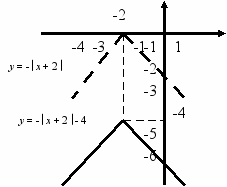
Приклад. Побудувати графік функції
y = - x + 3 - 4.
Аналогічно до попереднього виконаємо переміщення графіка
y = - x + 3 на 4 одиниці униз відносно осі у.
П
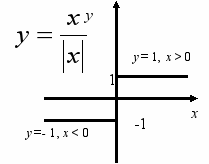 риклад. Побудувати графік функції
риклад. Побудувати графік функції 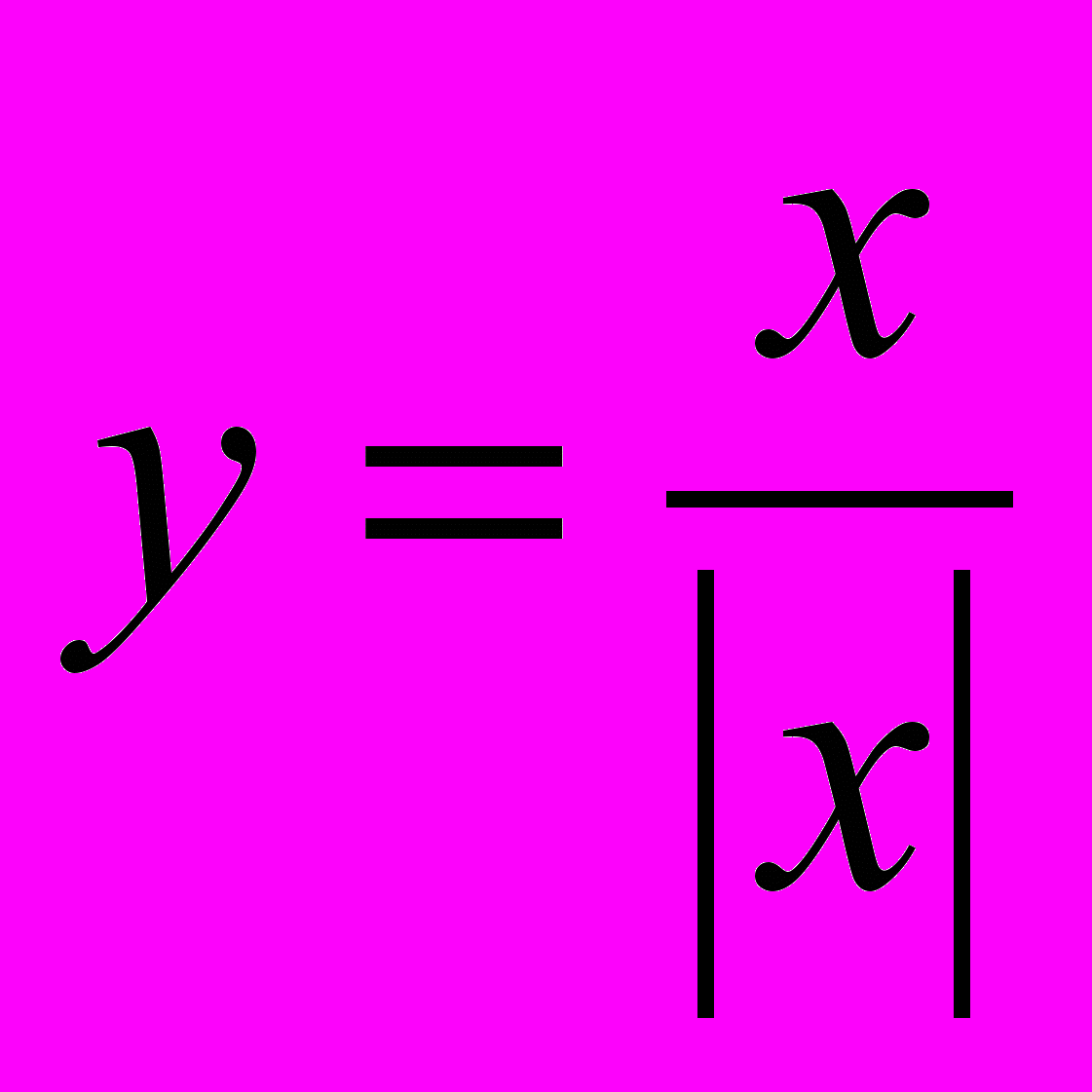
Перш за все визначимо ОДЗ:
х 0. За означенням модуля
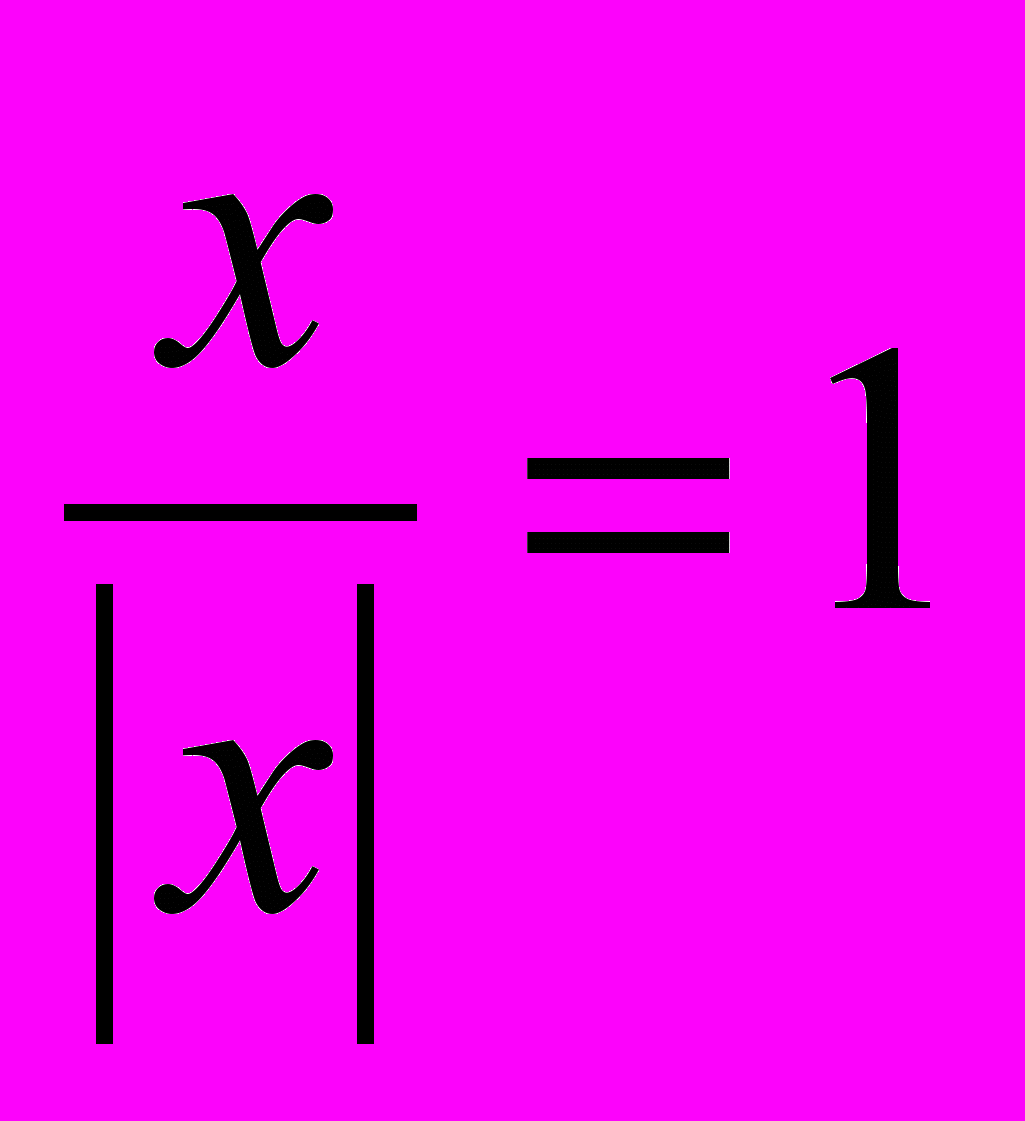 , якщо x > 0 і
, якщо x > 0 і 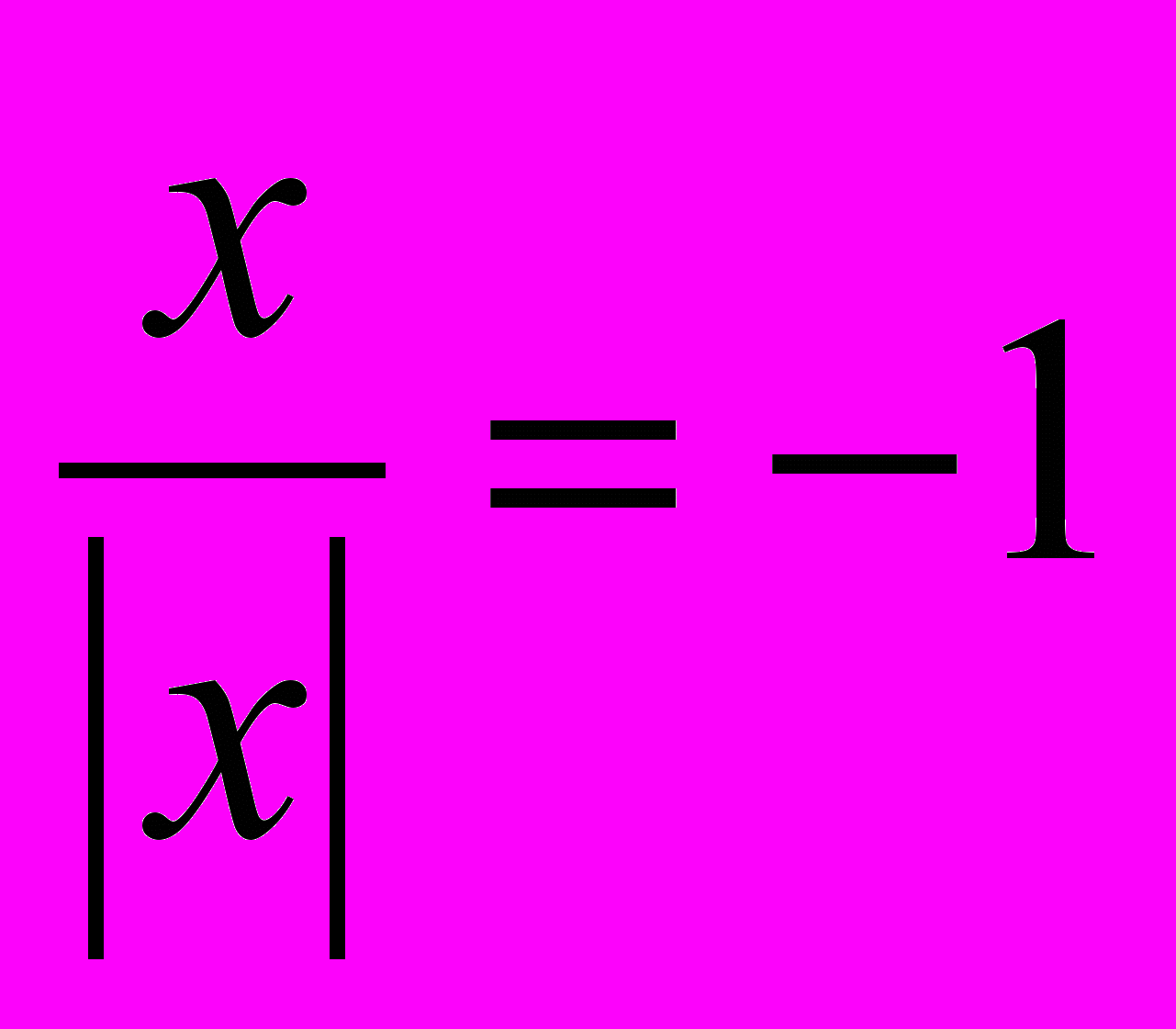 , якщо х < 0.
, якщо х < 0.Графік матиме розрив у точці нуль і складається із двох півпрямих.
Наступний етап роботи – побудова графіків функцій, що містять кілька модулів. Добірка завдань може бути такою.
Побудувати графіки функцій:
- у = 2 х + 5;
- у = 1 - 4х + 8;
- у = - 0,2 х + 1;
- у = 5х + 1;
5)
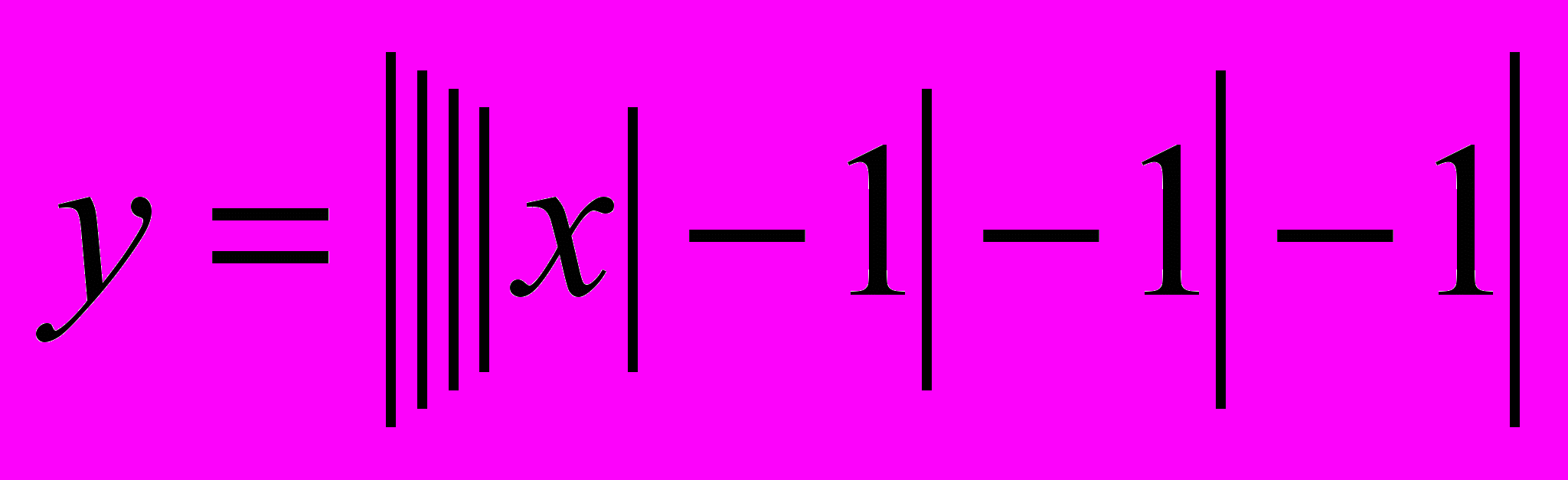
Останній графік учні 7-го класу можуть побудувати. Перед цим доцільно відпрацювати побудову графіка функції у = kх + b + а.
Пропедевтично можна ознайомити учнів з поняттям „паралельне перенесення” і прийти до висновку, що з додаванням декого числа l > 0 до правої частини рівняння графік „піднімається вгору” на таку саму кількість одиниць, або вісь абсцис опускається вниз і навпаки, коли l < 0.
Приклад. Побудувати графік рівняння
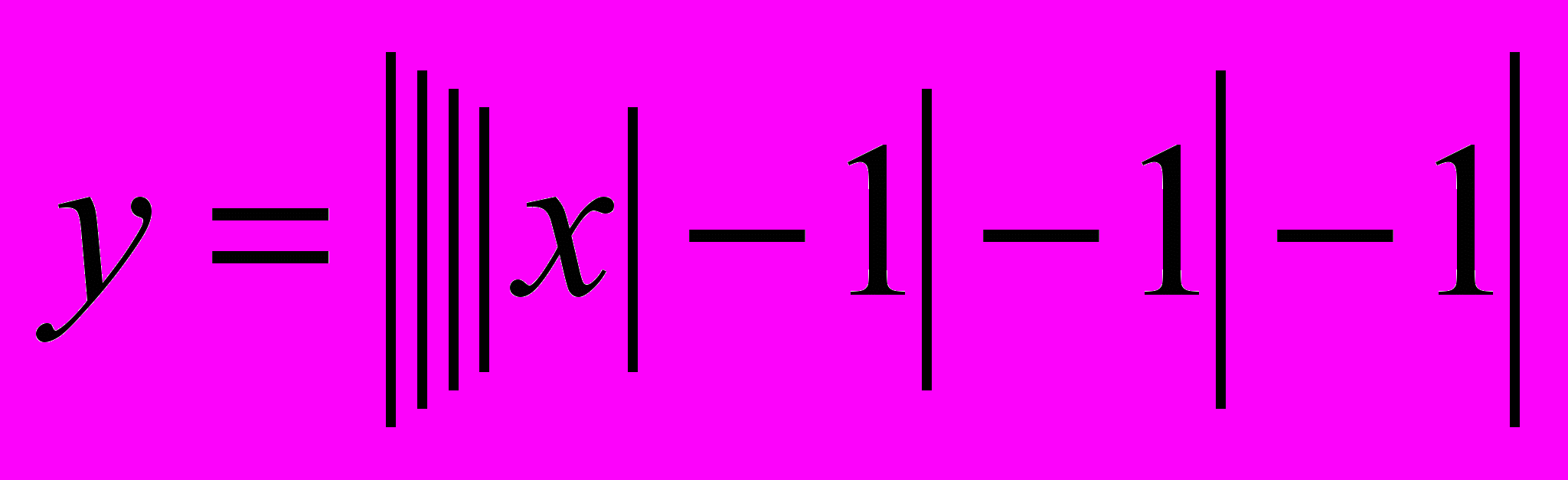
Розв’язання
Графік будуємо в такій послідовності:
- у = х -1;
- у
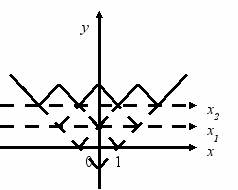 = х -1 – відображаємо симетрично відносно осі Ох від’ємну частину графіка;
= х -1 – відображаємо симетрично відносно осі Ох від’ємну частину графіка;
- у = х -1 -1 – піднімаємо вгору вісь абсцис на одну одиницю (одержимо вісь х2);
- у = х -1 -1 – відображаємо симетрично відносно осі Ох від’ємну частину графіка;
- у = х -1 -1 -1 – піднімаємо вгору вісь абсцис на одну одиницю (одержимо вісь х3);
- у = х -1 -1 -1 – відображаємо симетрично відносно осі Ох від’ємну частину графіка.
Широке поле для ознайомлення учнів з модулями в курсі алгебри 8-го класу. Під час вивчення квадратних коренів слід звернути увагу учнів на те, що
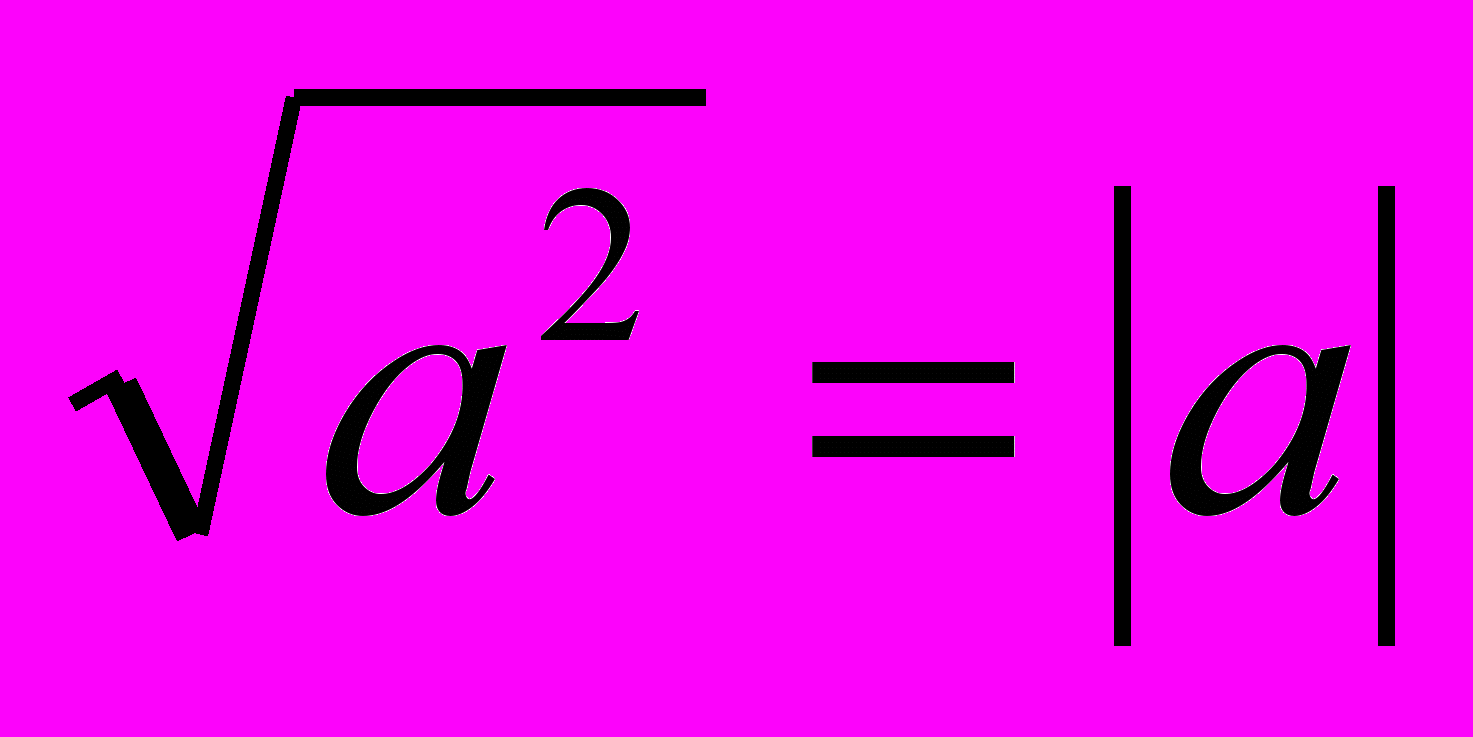 і виконати завдання типу: спростити вираз,
і виконати завдання типу: спростити вираз, 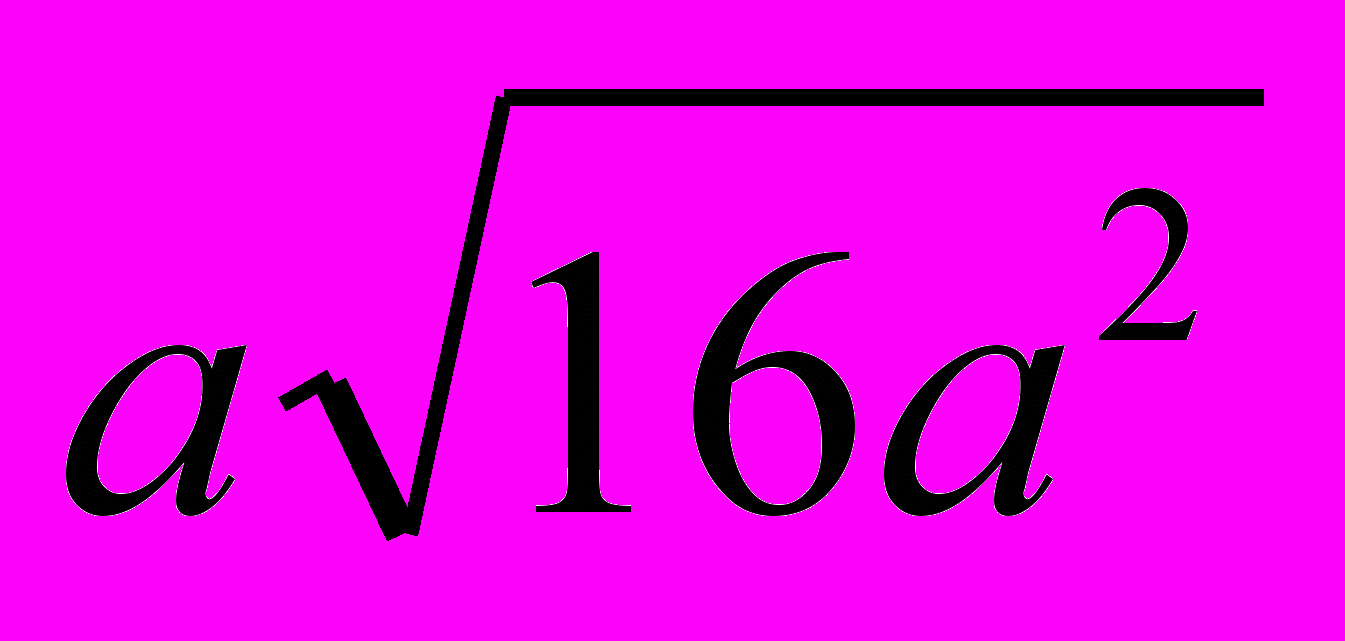 , якщо а < 0. Вивчаючи квадратні рівняння, потрібно показати і розв’язування рівняння типу х2 - 3х - 4 = 0. Знову слід пригадати метод розв’язування шляхом поділу числової осі на проміжки (а при утрудненнях розв’язати найпростіше лінійне рівняння цим методом). Згадане рівняння учні розв’язують так: якщо х 0, х = х, і рівняння має вигляд х2 – 3х – 4 = 0. Корені цього рівняння: х = 4 та х = -1. Але х = -1 не задовольняє умову x > 0, тому тут тільки один розв’язок х = 4. Якщо х < 0, х = -х, і рівняння має вигляд:
, якщо а < 0. Вивчаючи квадратні рівняння, потрібно показати і розв’язування рівняння типу х2 - 3х - 4 = 0. Знову слід пригадати метод розв’язування шляхом поділу числової осі на проміжки (а при утрудненнях розв’язати найпростіше лінійне рівняння цим методом). Згадане рівняння учні розв’язують так: якщо х 0, х = х, і рівняння має вигляд х2 – 3х – 4 = 0. Корені цього рівняння: х = 4 та х = -1. Але х = -1 не задовольняє умову x > 0, тому тут тільки один розв’язок х = 4. Якщо х < 0, х = -х, і рівняння має вигляд:х2 + 3х – 4 = 0. Звідки маємо: х = -4 та х = 1. але х = 1 умови
х < 0 не задовольняє, тому розв’язком цього рівняння є
х = 4 та х = -4.
Для сильних учнів можна запропонувати і таке рівняння:
х2 – 3х = 4. Це рівняння складніше, оскільки знак модуля залежить від знака виразу х(х - 3). Краще ці проміжки зобразити графічно.

Якщо х 3, х(х - 3) = х2 – 3х. З рівняння х2 – 3х – 4 = 0 маємо х = 4 та х = -1. Перевіривши умову х > 3, відкидаємо х = -1.
Якщо 0 х < 3, х2 – 3х = - (х2 – 3х). Рівняння х2 – 3х + 4 = 0 розв’язків не має.
Якщо х < 0, х2 – 3х = х2 – 3х. З рівняння х2 – 3х – 4 = 0 маємо х = 4 та х = -1. Умову задовольняє тільки х = -1.
У 8-му класі після ознайомлення учнів з параболою доцільно повторити всі вивчені прийоми в процесі побудови таких графіків:
П
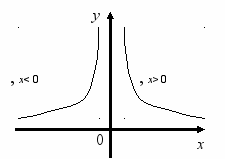 риклад. Побудувати графік функції
риклад. Побудувати графік функції 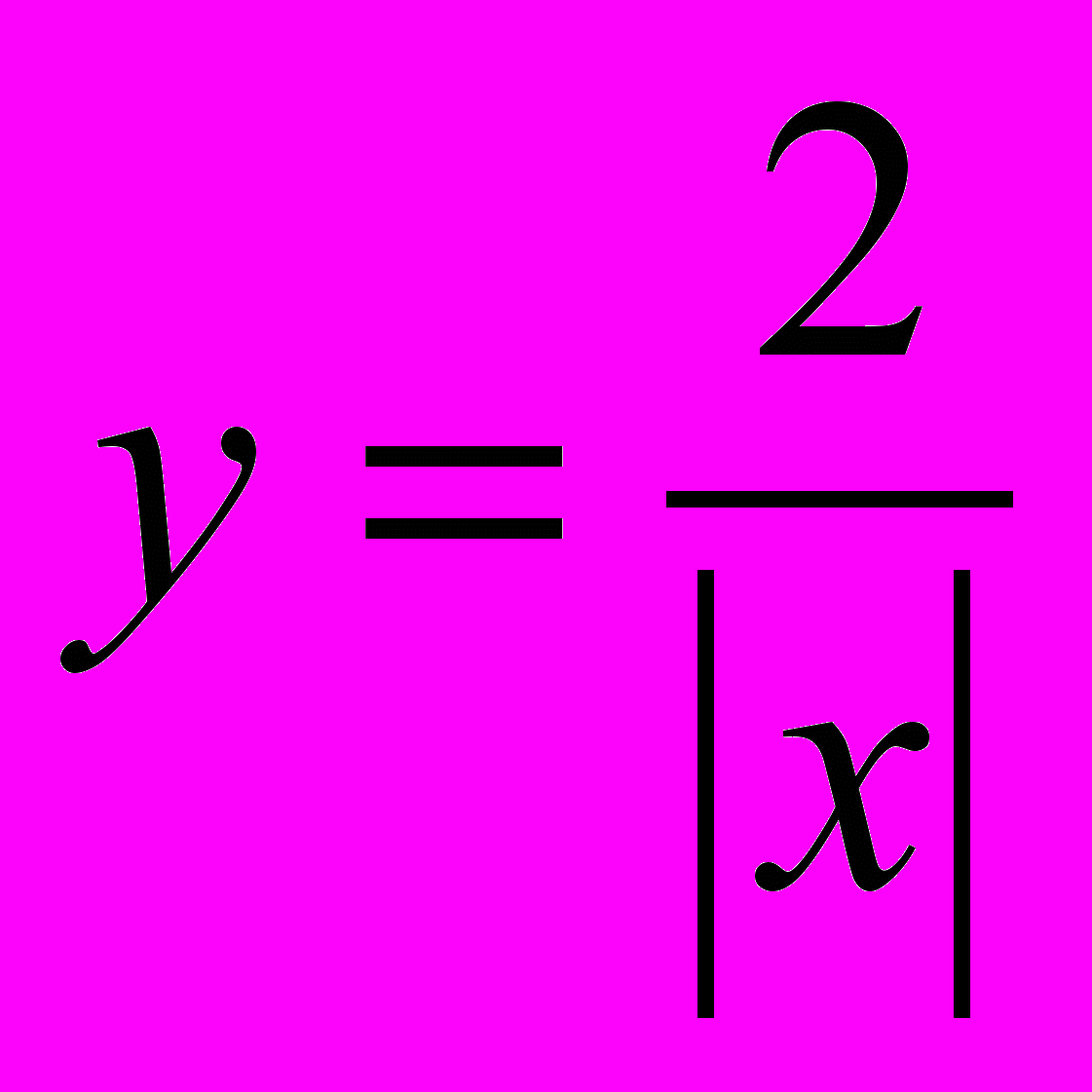
Графік оберненої пропорційності
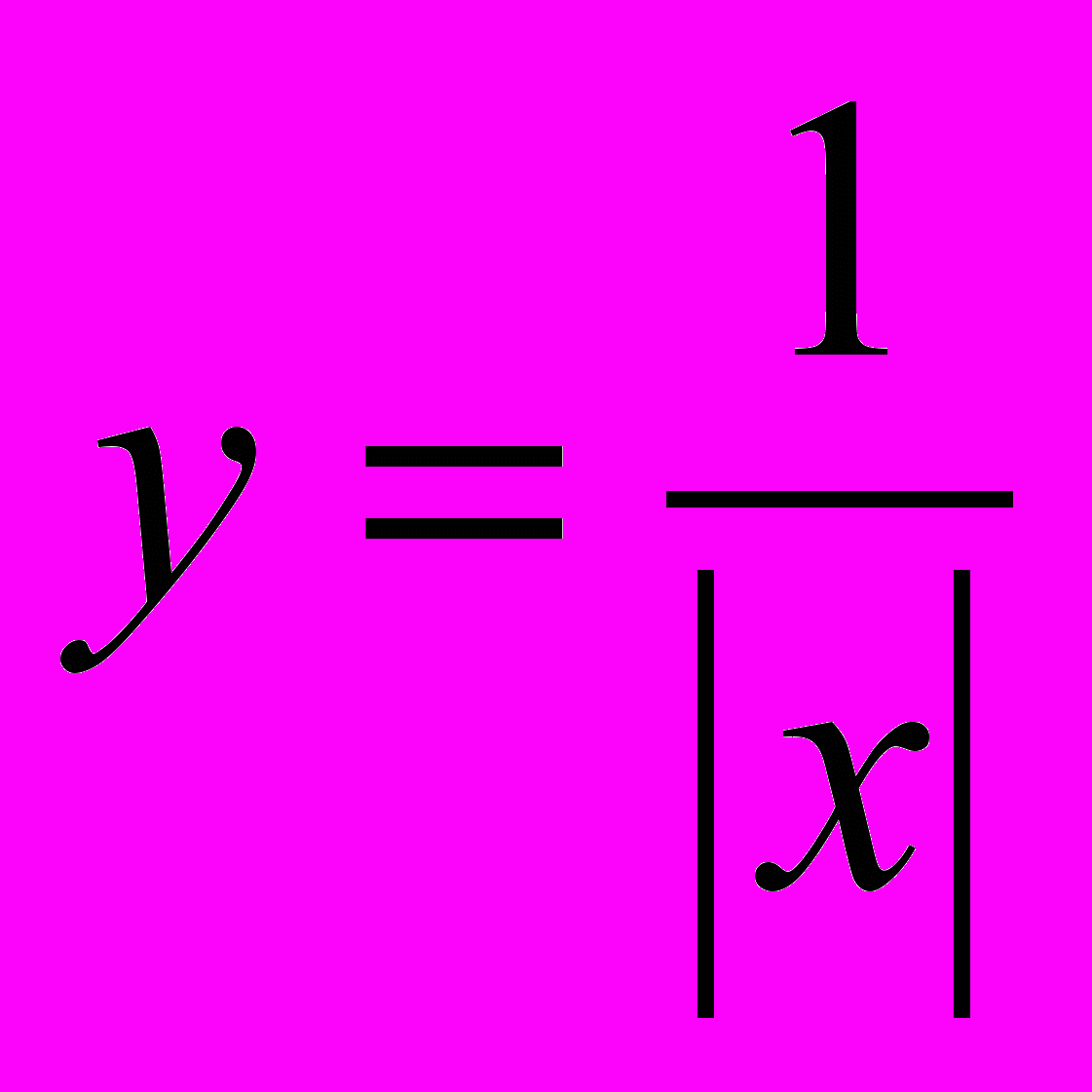 (х 0) добре відомий учням. Позбувшись знака модуля, дістанемо:
(х 0) добре відомий учням. Позбувшись знака модуля, дістанемо: 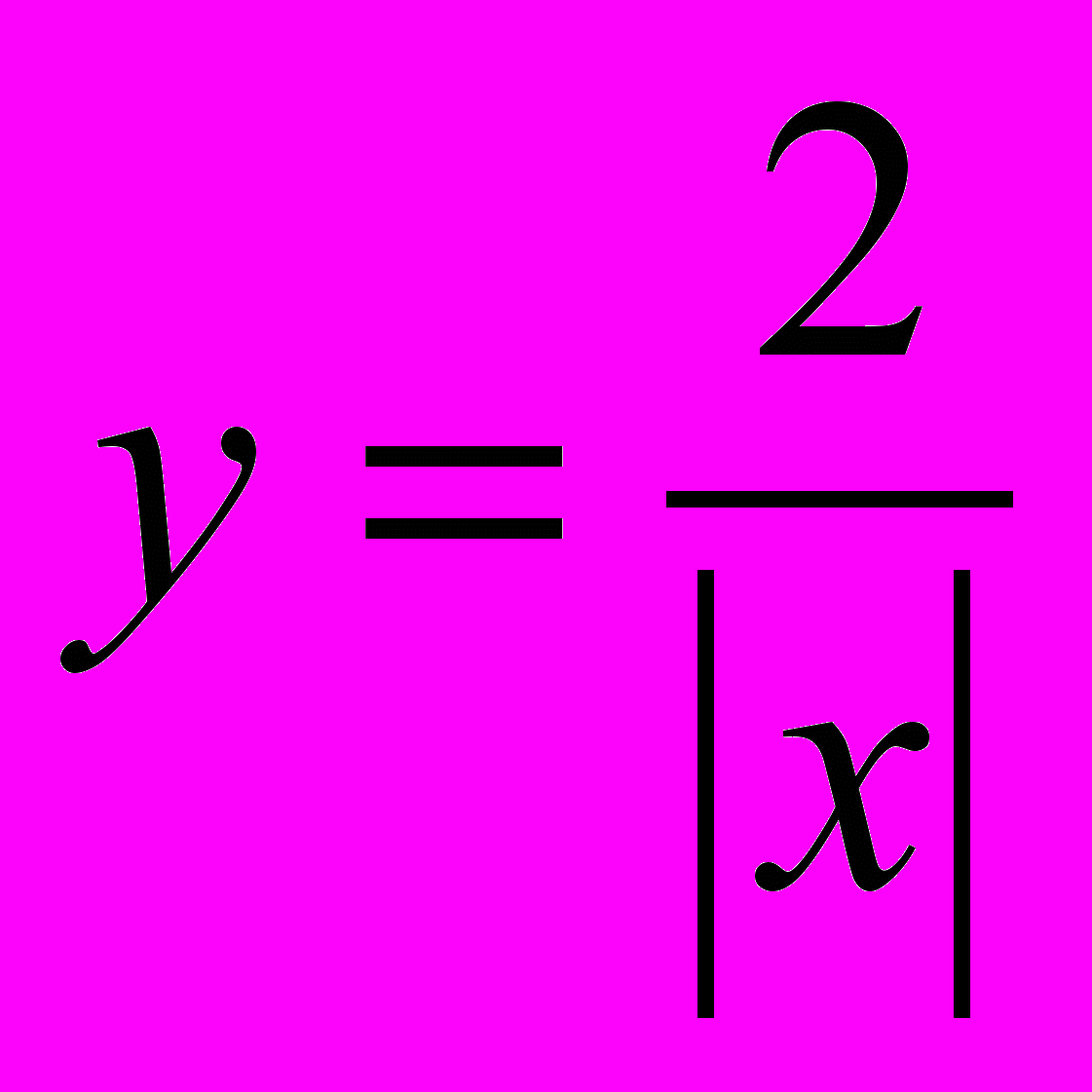 , якщо x > 0,
, якщо x > 0,  , якщо х < 0.
, якщо х < 0.Побудувати графіки залежностей:
1)
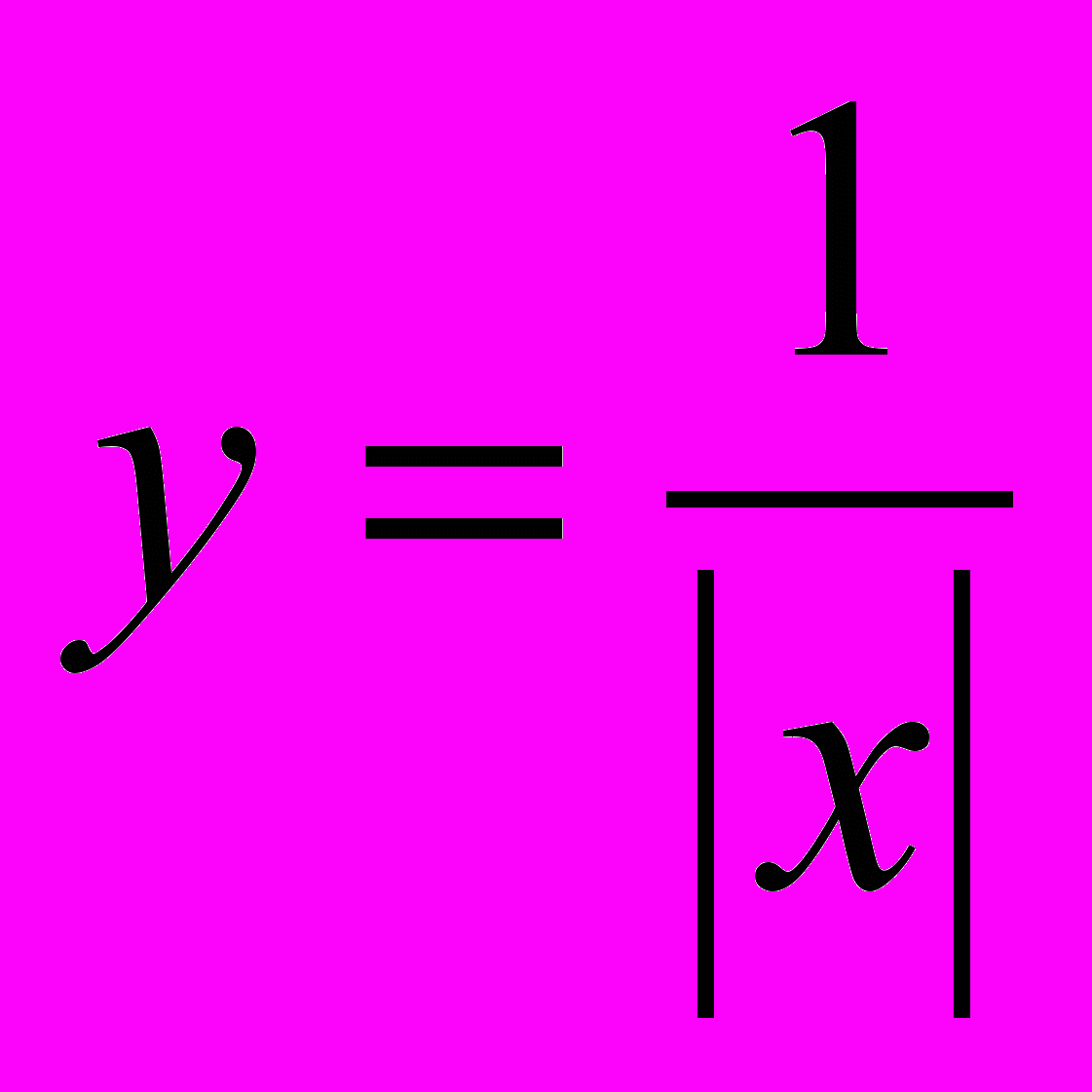 ;
;2)
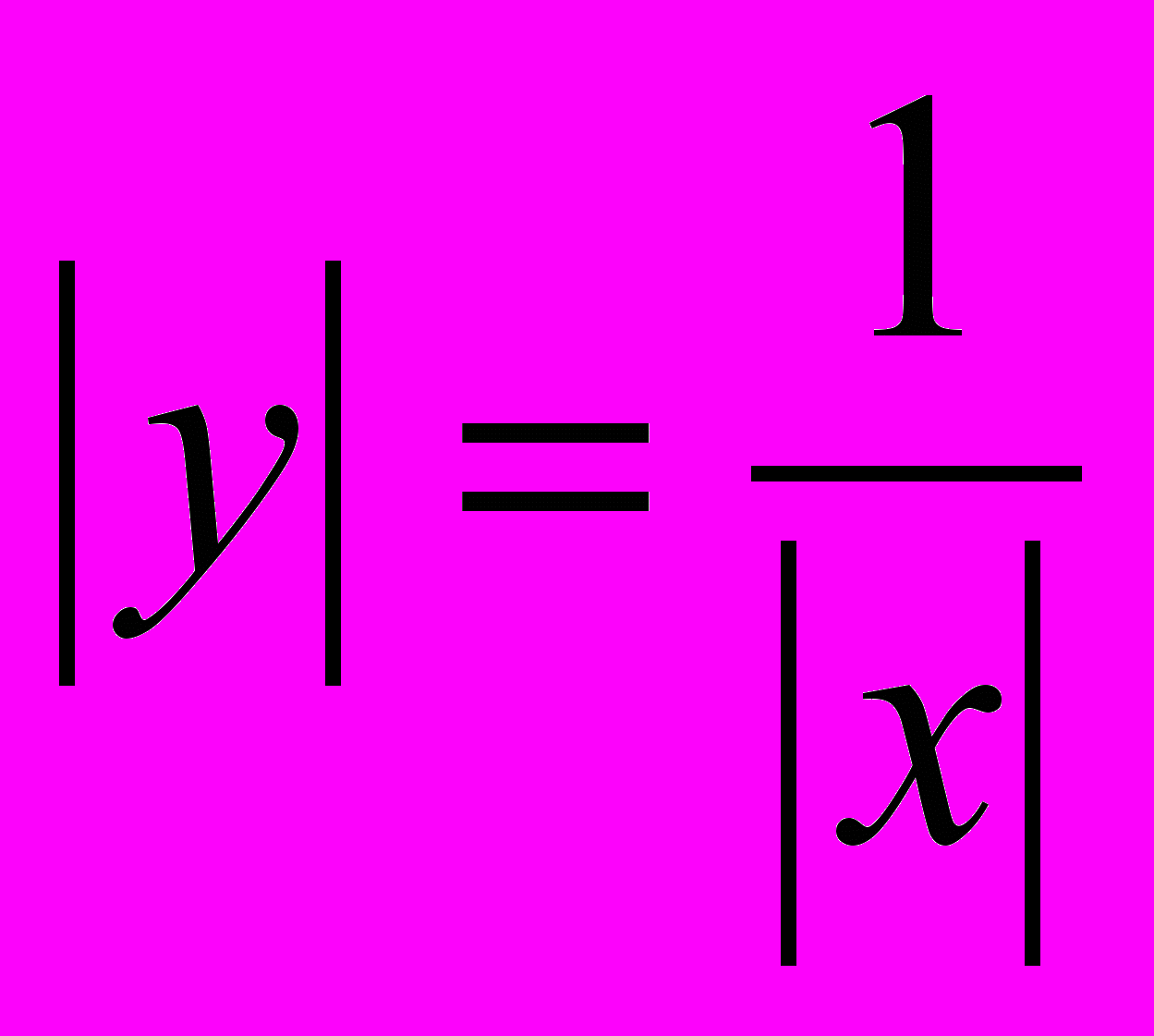 ;
;3) 1 = у ·х;
4)
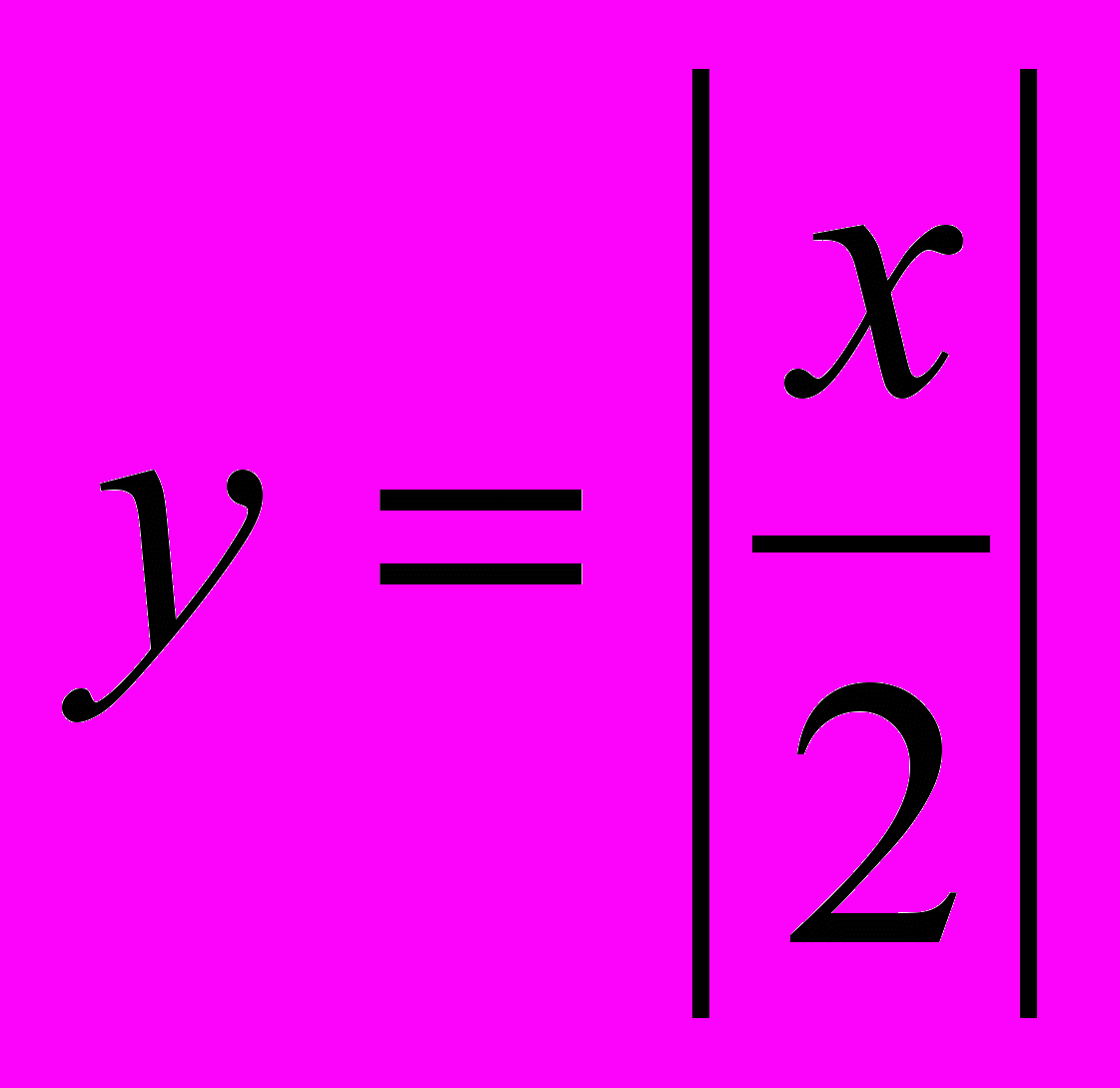 ;
;5)
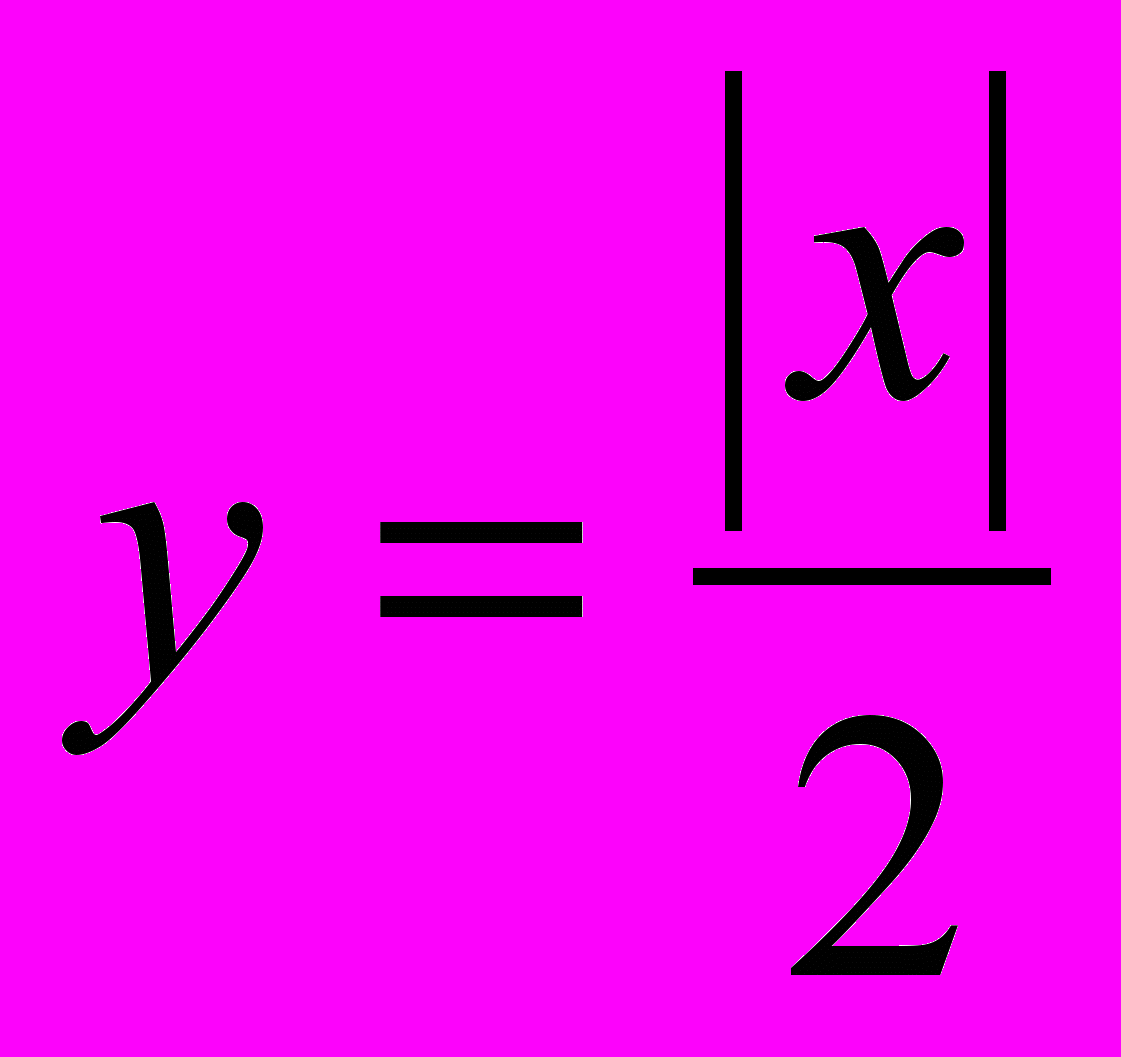 ;
;6) у = х3 - 1;
7) у = х2 - 4;
8) у = х2 + 4;
9) у = х2;
10) у = х2 - 2;
11) у = - х2 + 3;
12) у = х2 - 3.
У 9-му класі можна розв’язувати найпростіші нерівності з модулями під час вивчення теми „Нерівності”. Починаємо з найпростіших нерівностей типу х < а та х > b. Важливо, щоб учні зрозуміли підхід до їх розв’язування. Ці найпростіші нерівності можна розв’язувати і через означення, але універсальним є метод проміжків. У цій темі розглядаємо нерівності типу х - 2 > 5. Паралельно, особливо при утрудненнях, слід пригадати і розв’язування відповідних рівнянь. Як і у 8-му класі, сильним учням запропонувати і детально розглянути нерівності типу х - 2 > 2х або х - 2 < х + 6, які за означенням розв’язати неможливо.
Розглянемо другий приклад.
Якщо х – 2 0, х - 2 = х – 2 і х – 2 < х + 6, звідки
-2 < 6. це свідчить про те, що умова х 2 є розв’язком нерівності. Якщо х < 2, х – 2 = - (х - 2) і -х + 2 < х + 6, звідки х > -2. За цієї умови розв’язок має вигляд: -2 < х < 2. Об’єднуючи розв’язки, маємо
х > -2.
Наступне спірне питання – розв’язування квадратичних нерівностей. Спірне з точки зору підходів до методики розв’язування. Ознайомити учнів з графічним способом, який подано в підручнику, і який потім не використовується в старших класах, чи ознайомити учнів з методом інтервалів? Але, без сумніву, подати учням нерівності виду х2 - 5х + 6 > 0 необхідно. Методика їх розв’язування через числові проміжки, а це вже ближче до методу інтервалів. У даній нерівності слід розглянути два проміжки х 0 та х < 0. якщо х 0, маємо нерівність х2 - 5х + 6 > 0. Розв’язок її х < 2 або х > 3. Враховуючи умову х 0, маємо розв’язок 0 х < 2 або х > 3. Якщо х < 0, розв’язком нерівності х2 + 5х + 6 > 0 є х < -3 або х > -2. Разом з умовою буде х < -3 або -2 < х < 0. Об’єднуючи розв’язки, одержуємо відповідь х < -3, або -2 < х < 2, або х > 3.
Розглянемо рівняння, які в курсі 9-го класу успішно розв’язуються графічно. Наприклад, якщо розв’язувати рівняння
х3 = х - 2 аналітично, то одержимо сукупність систем, з якою учень 9-го класу не справиться. Проте рівняння легко розв’язується графічно. Для цього треба побудувати графіки у = х3 і у = х - 2 та знайти абсцису точки їх перетину.
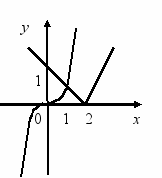
Відповідь. 1.
П
 риклад. Побудувати графік функції у = х2 – 4.
риклад. Побудувати графік функції у = х2 – 4.Графіком функції у = х2 – 4 є парабола, алгоритм побудови якої добре відомий. Побудуємо графік і позначимо штриховою лінією. Виконаємо рівносильні перетворення, щоб позбутися модуля:
а) у = х2 – 4, якщо х2 4, або х 2, звідки х 2, х -2.
Отже, коли х2 4, графіком функції є вітки параболи, які розміщені у проміжках
(-; -2 і 2; +).
б) у = – х2 + 4, якщо х2 < 4, або х < 2, звідки -2 < х < 2. Отже, коли х2 < 4, графіку функції відповідає частина дуги параболи (проміжок (-2; 2)), дзеркально відображена відносно осі х.
Приклад. Побудувати графік функції
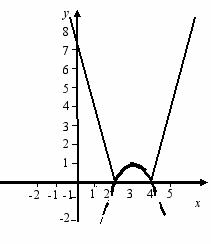 у = – х2 + 6х – 8.
у = – х2 + 6х – 8.Побудуємо параболу
у = – х2 + 6х – 8. Її вітки, що відповідають від’ємним значенням у з проміжків (-; 2) та (4; +),відобразимо симетрично відносно осі х, тобто виконаємо дзеркальне відображення. Дістанемо шукану параболу.
П
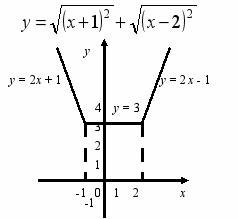 риклад. Побудувати графік функції
риклад. Побудувати графік функції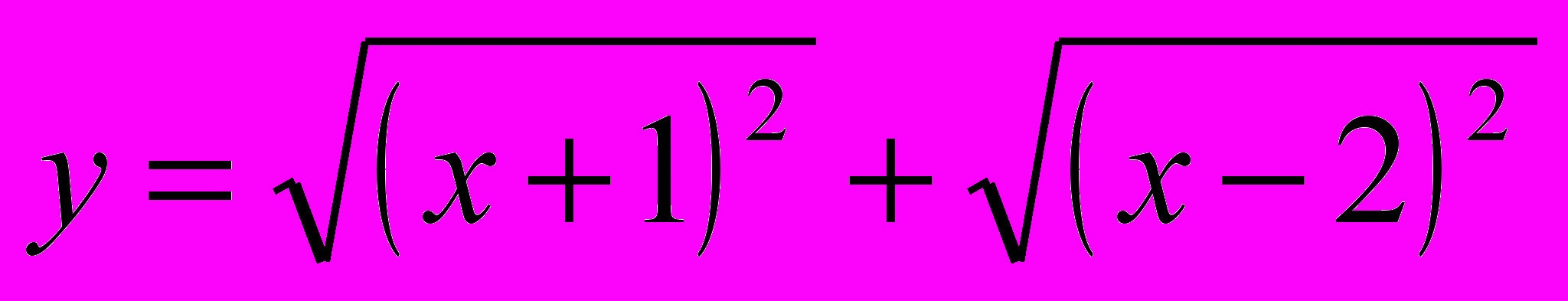 . Скориставшись залежністю
. Скориставшись залежністю  =х, матимемо у = х + 1 + х – 2.
=х, матимемо у = х + 1 + х – 2.Розглянемо такі випадки:
а) у = х + 1 + х – 2 = 2х – 1, якщо х + 1 0 і х – 2 0, тобто х 2;
б) у = х + 1 – х + 2 = 3, якщо х + 1 0 і х – 2 < 0, тобто -1 х < 2;
в) у = – х – 1 + х – 2 = –3, якщо х + 1< 0 і х – 2 0, тобто х < -1 і
х 2 (це неможливо);
г) у = – х – 1 – х + 2 = –2х + 1, якщо х + 1 < 0 і х – 2 < 0, тобто
х < –1.
Отже, розіб’ємо вісь х на такі проміжки: (-; -1) -1; 2) і 2; +) і на кожному з них побудуємо графік відповідної лінійної функції. Матимемо ламану, що складається з трьох ланок.
Приклад. побудувати графік функції
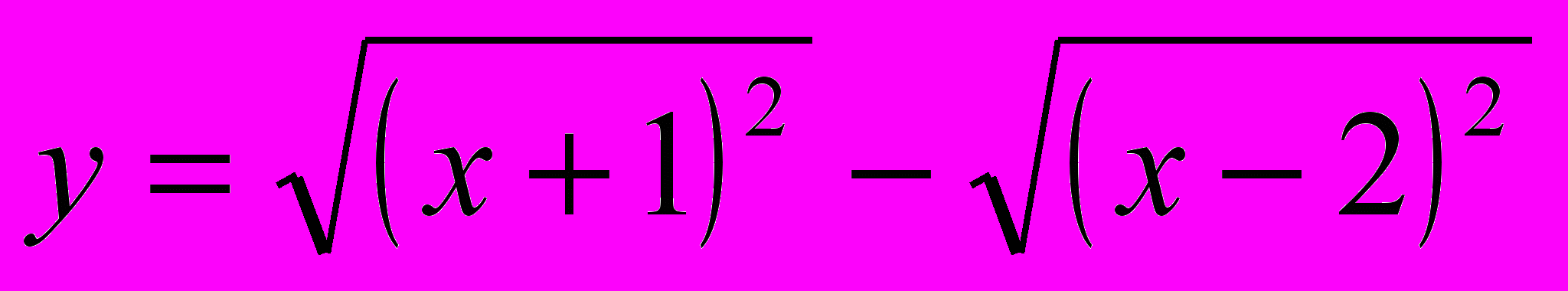 .
.Маємо: у = 1 + х – 1 – х.
Можливі випадки:
а) у = х + 1 – 1 + х = 2х, якщо х + 1 0 і 1 – х 0, тобто -1 х 1;
б) у = 1 + х + 1 – х = 2, якщо х + 1 0 і 1 – х < 0, тобто – х > 0;
в) у = – 1 – х – 1 + х = – 2, якщо х + 1< 0 і х – 2 0, тобто х < -1;
г) у = – 1 – х + 1 – х = – 2х, якщо х + 1< 0 і 1 – х < 0 – прийшли до суперечності, отже, цей випадок до уваги не беремо.
Вісь х розділена на 3 проміжки: (-; -1), -1; 1 і (1; +). Накреслимо відповідні ланки ламаної для кожного з проміжків.
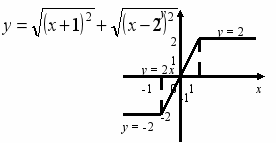
Приклад. Побудувати графік функції у = х – 1.
Г
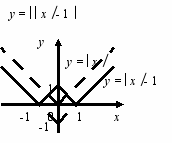 рафіки, що містять кілька знаків модуля, починаємо будувати поетапно: спочатку накреслимо штриховою лінією графік функції у = х, потім у = х – 1, тобто графік у = х перенесемо на одну одиницю вниз уздовж осі у. Нарешті, частину графіка функції у = х – 1, якій відповідають від’ємні ординати дзеркально відобразимо відносно осі х. Графіком є ламана.
рафіки, що містять кілька знаків модуля, починаємо будувати поетапно: спочатку накреслимо штриховою лінією графік функції у = х, потім у = х – 1, тобто графік у = х перенесемо на одну одиницю вниз уздовж осі у. Нарешті, частину графіка функції у = х – 1, якій відповідають від’ємні ординати дзеркально відобразимо відносно осі х. Графіком є ламана.Можна запропонувати учням розв’язати графічно такі
рівняння:
- х - 1 = 4 + х;
- х + 4 = -2 х - 8;
- 3 - 2х = 2 - х - 3;
- 4х + 2 =
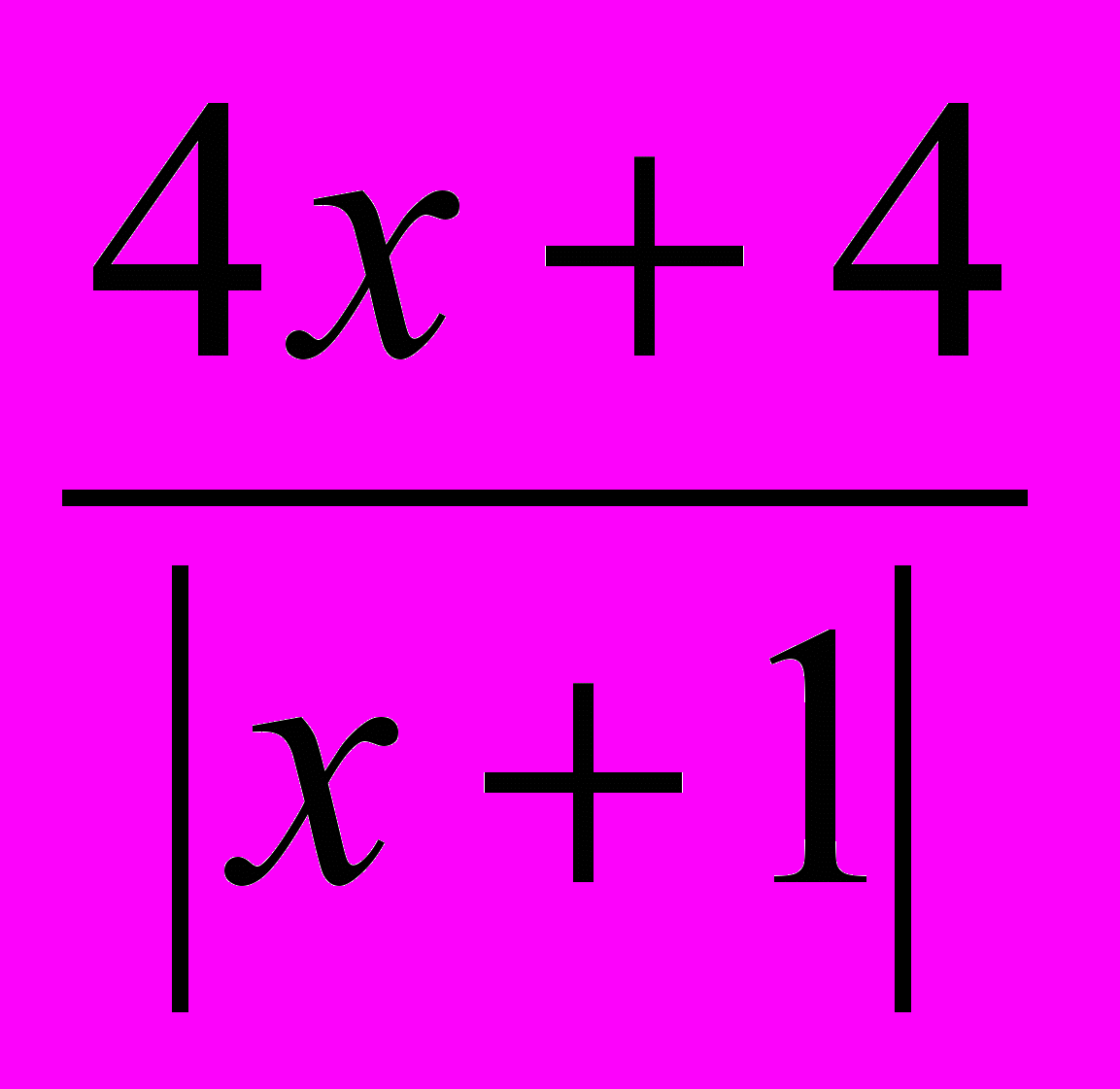 ;
;
-
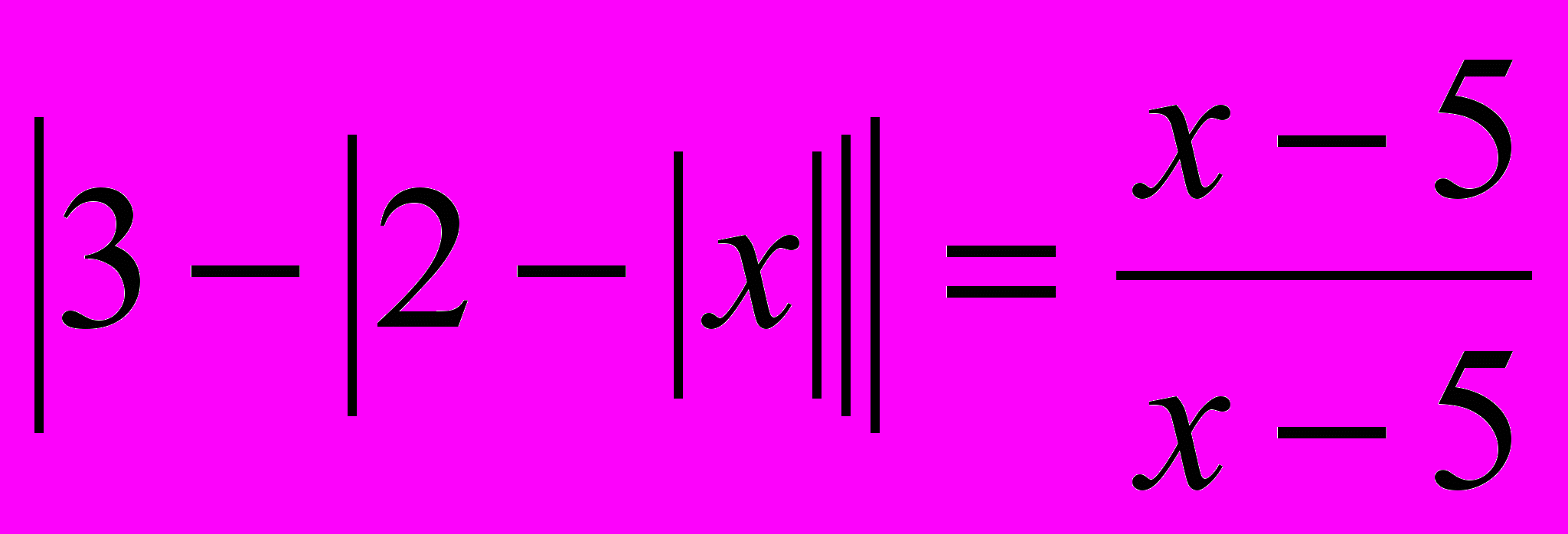 ;
;
-
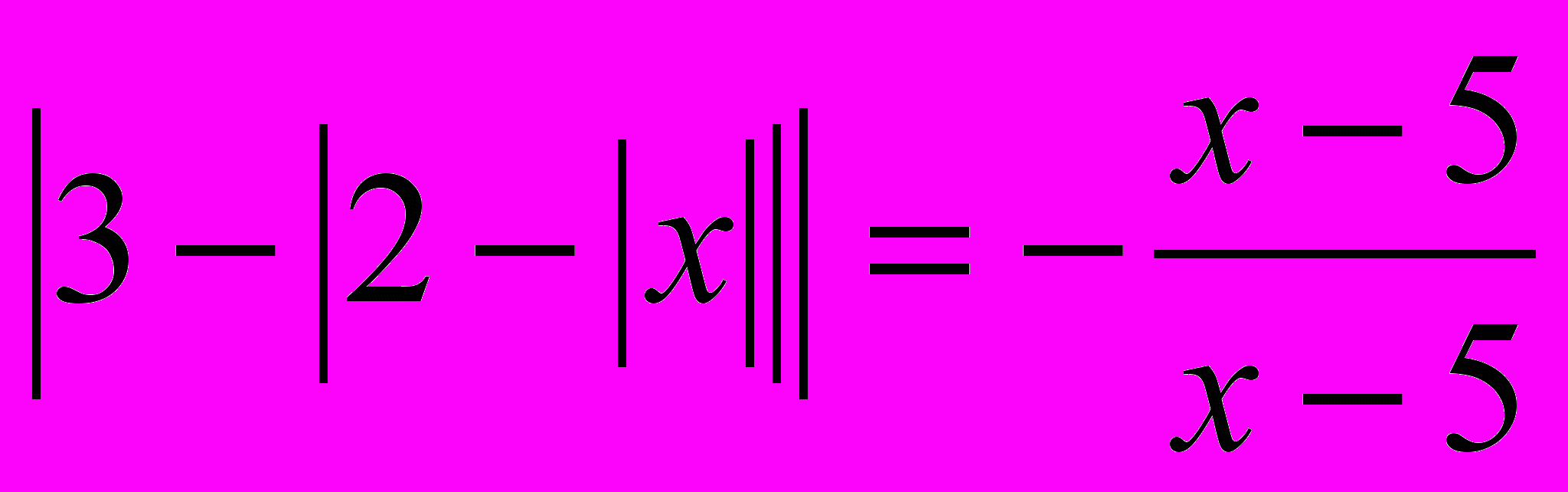 ;
;
-
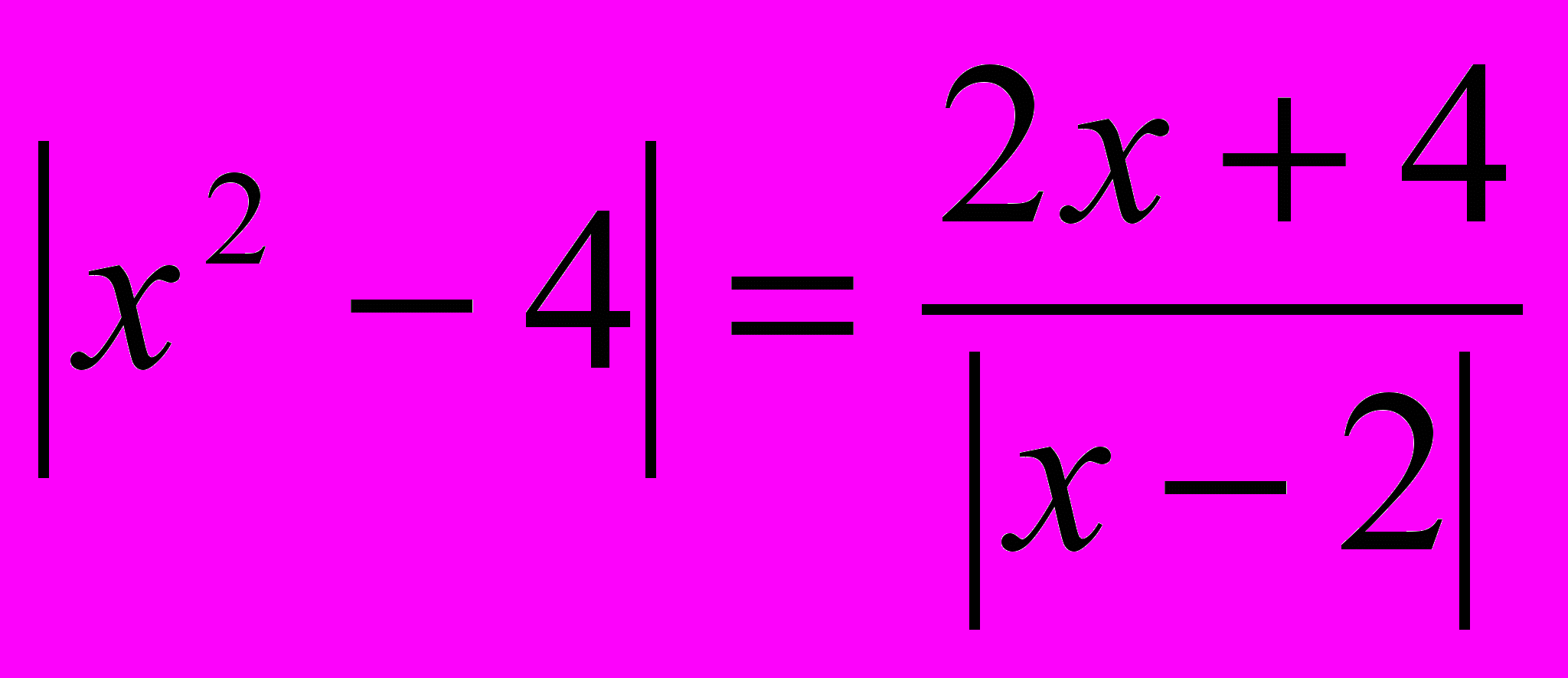 ;
;
- 2х - 5 = 3х – 10;
- х + х + 4 = х + 1;
- х2 - 1 =
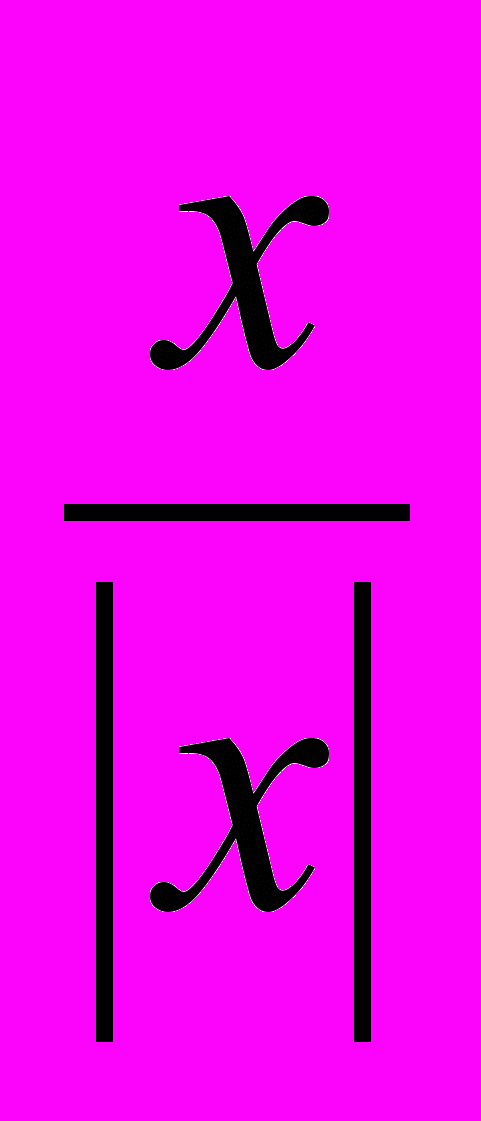 ;
;
- х2 - 2 =
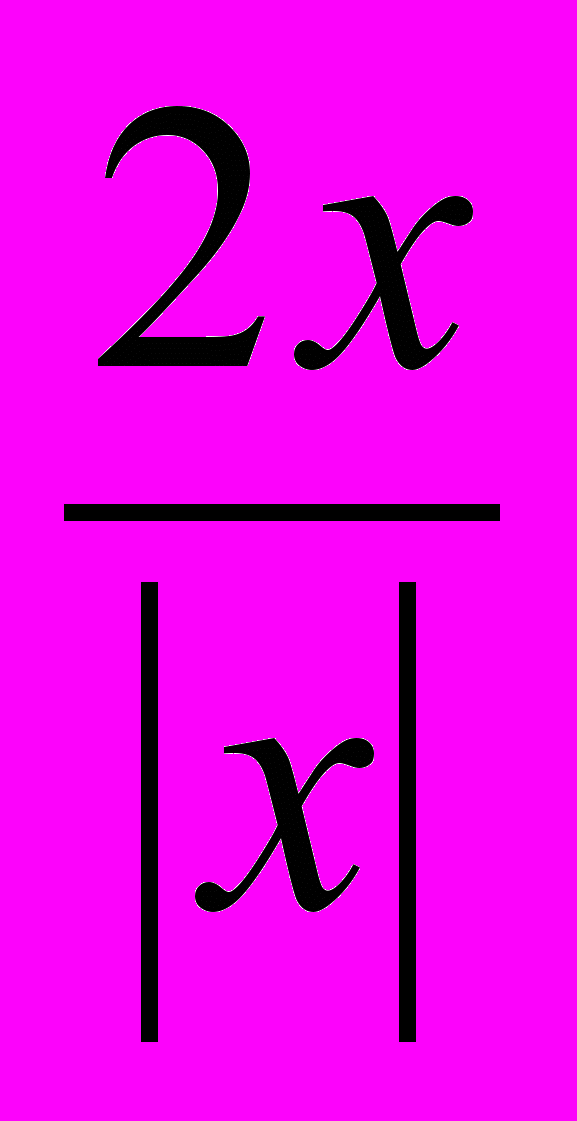 ;
;
- –х х = -
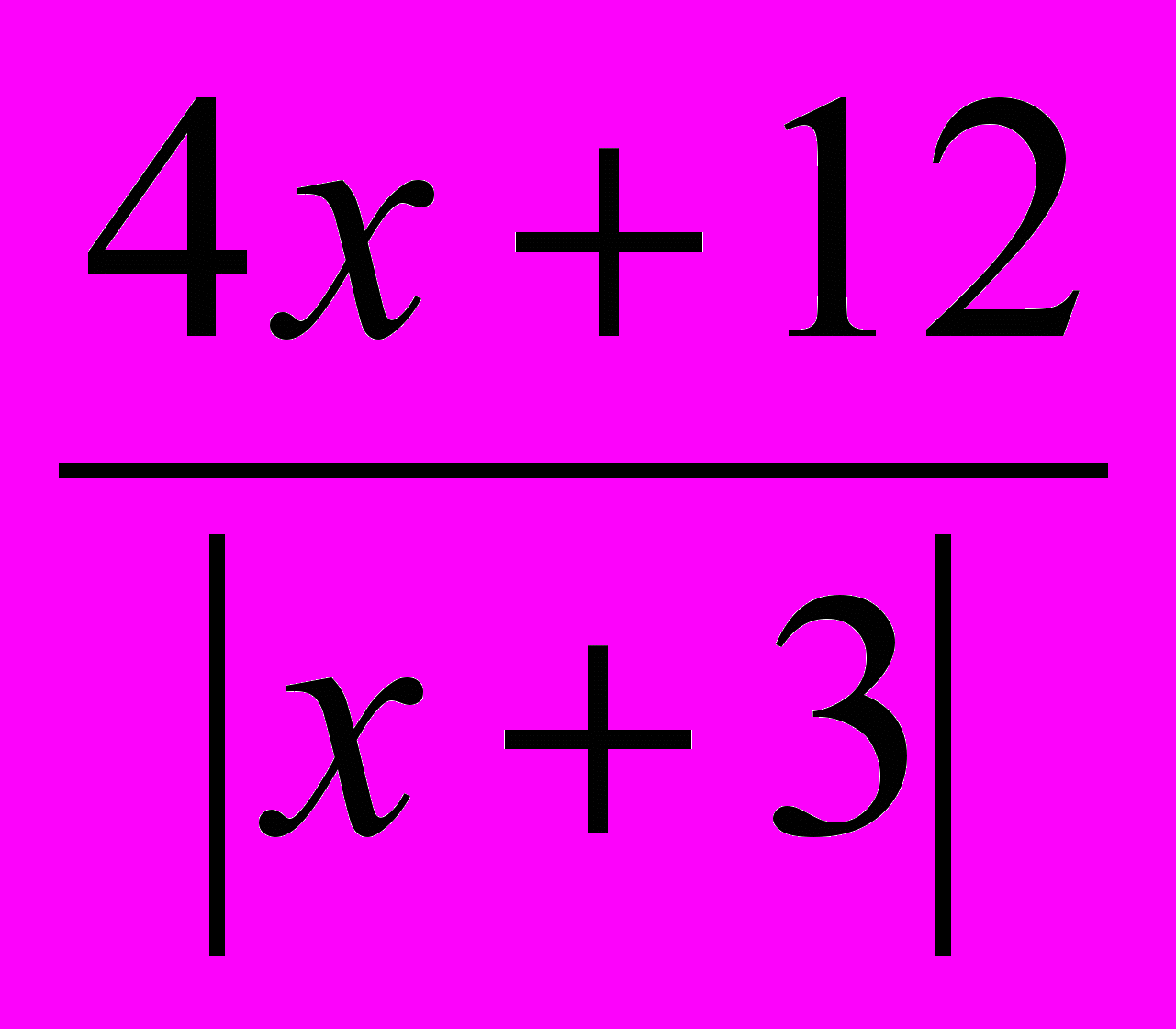 ;
;
Зауважимо, що під час розв’язування таких рівнянь спочатку треба будувати той графік, що передбачає зміщення осей координат.
З учнями 9-го класу можна графічно розв’язати такі системи рівнянь:
1)

2)
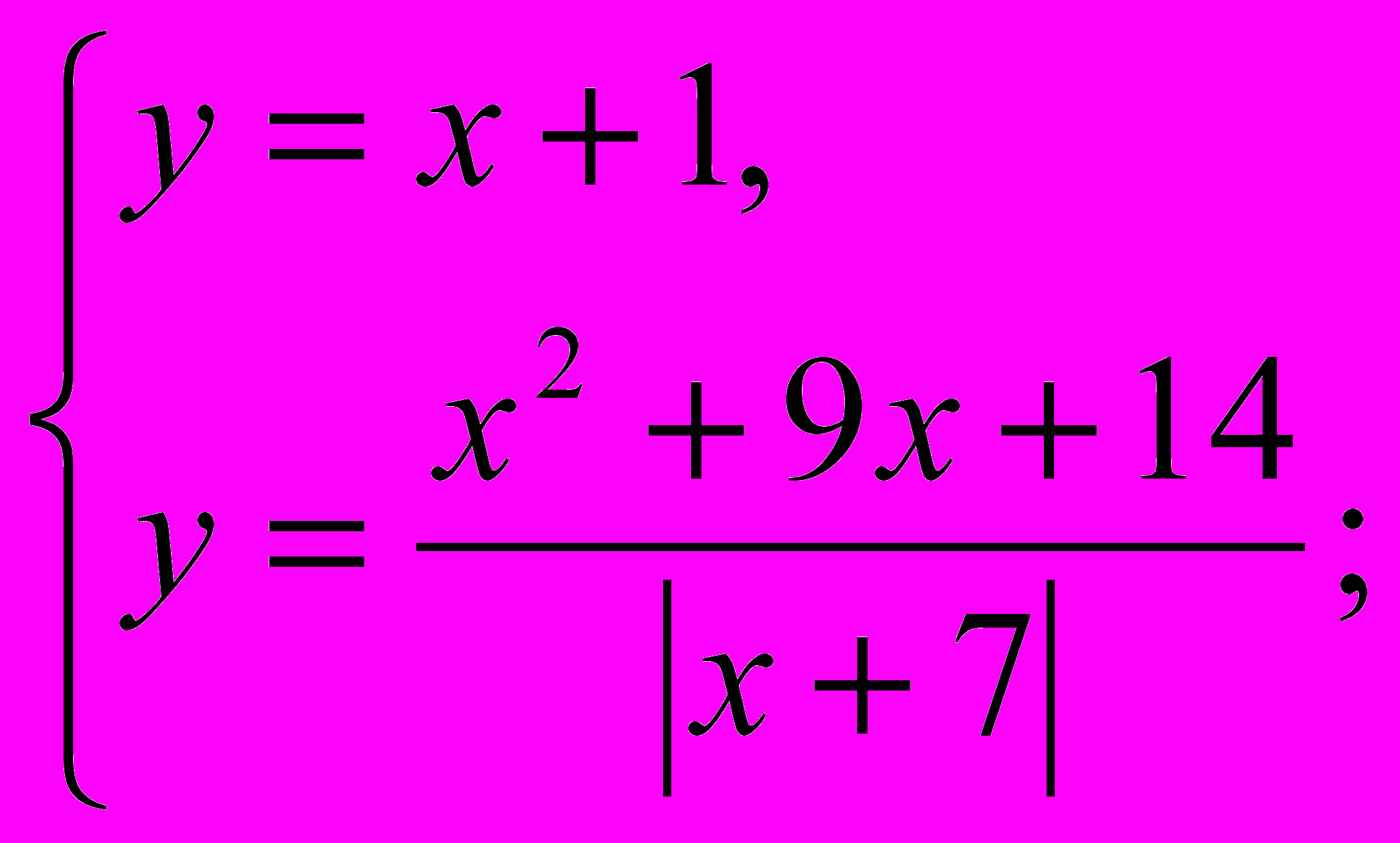
3)
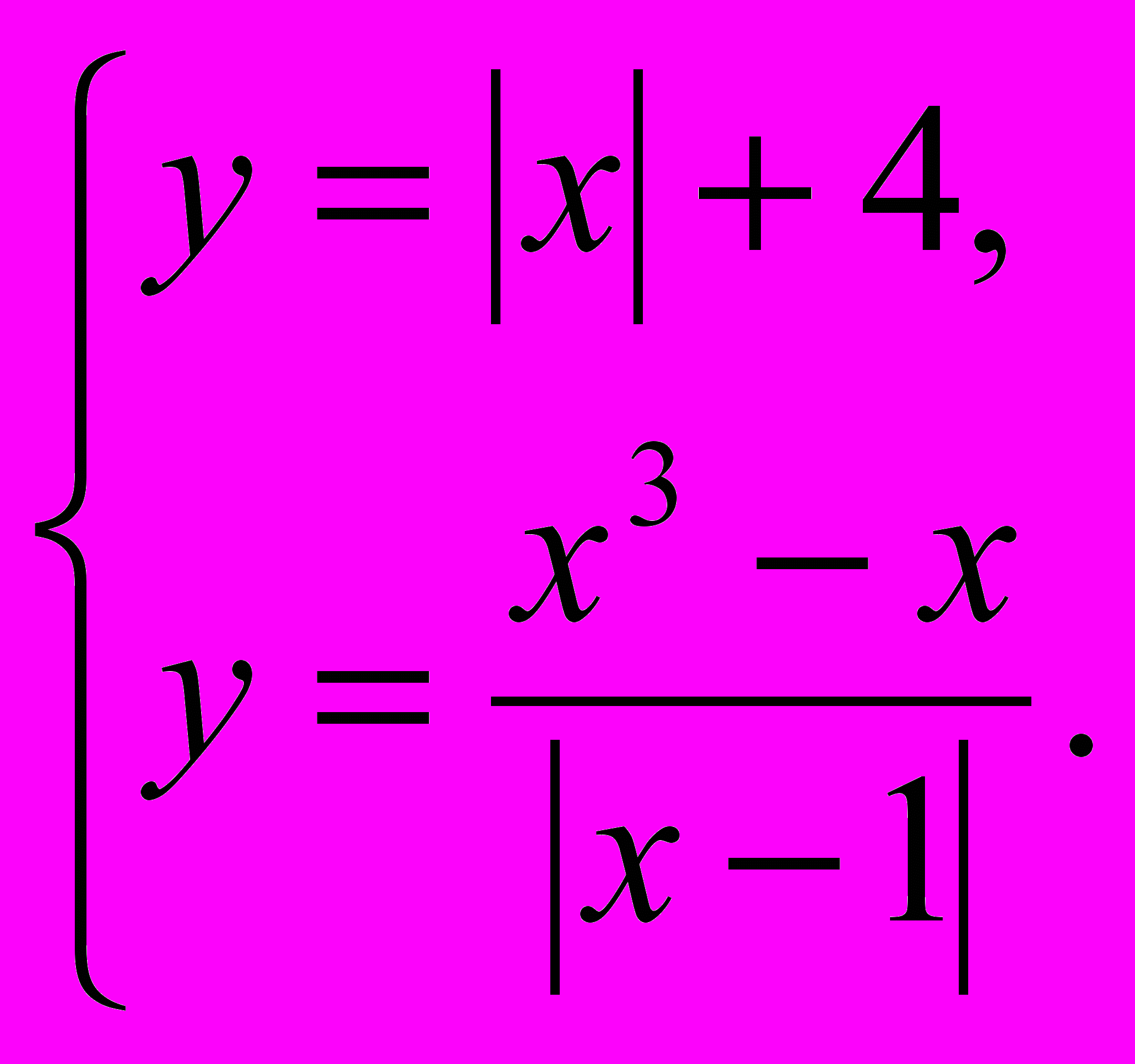
Вважаю, що кожного півріччя в підсумкову контрольну роботу слід включати завдання, які вимагають побудови графіків з модулями.
Наприклад
Розв’язати графічно рівняння:
1)
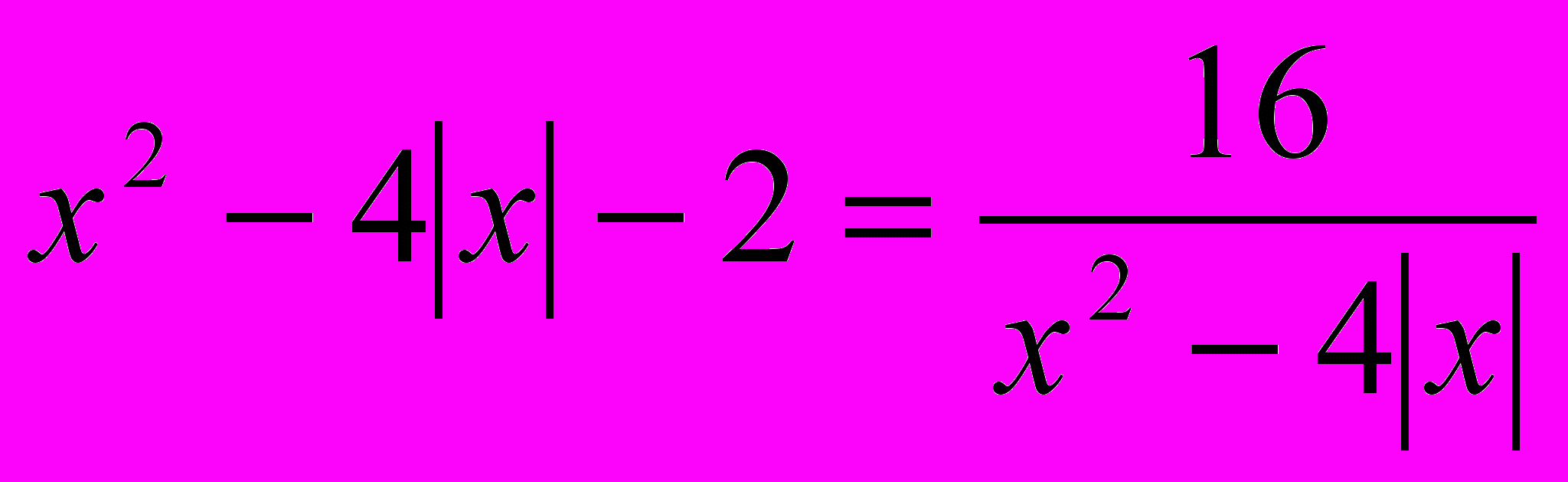 ;
;2)
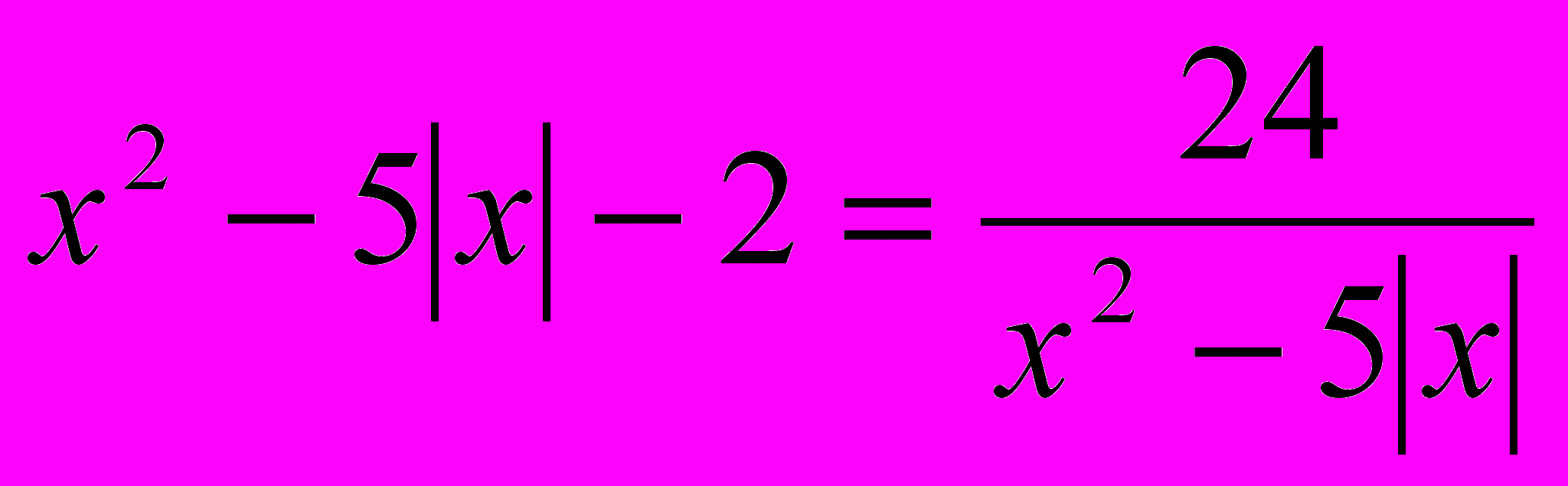 .
.Література
- Горделадзе Г., Кухарчук М. Збірник задач з математики. – «Вища школа», 1992.
- Дубинчук О.С., Мальований Ю.І., Дичек Н.П. Методика викладання алгебри в 7-9 класах: Посібник для вчителя. – К., 1991. – 254с.
- Колесник Б.М. Алгебраїчні задачі на дослідження. – Київ, 1992.
- Математика // Шкільний світ, 2004.
- Математика // Шкільний світ, 2005.
- Математика // Шкільний світ, 2008.
- Чашечников С.М., Чашечникова Л.Г., Чертков И.Я. Вивчення алгебри в 6-8 класах., 1998.
