Методы отбора инвестиционных проектов для финансирования (доп. материал, краткий

Вид материала

Документы

Содержание Методы сравнительной оценки и выбора объектов инвестиций (лекция) 12 Методы отбора инвестиционных проектов для финансирования (доп. материал, краткий вариант) Методы показателей и приведенных затрат ПЗ — приведенные затраты; З Метод экспертных оценок Модель экономического равновесия В. Парето Методы отбора инвестиционных проектов для финансирования (доп. материал, полный вариант) 1 вариант экспертной оценки Рисунок 1 — Связь ЧДД и ВНД 2 вариант экспертной оценки K — общее количество подготовленных анкет; n Выбор наилучшего проекта при помощи методов векторной оптимизации Методы сравнительной оценки и выбора объектов инвестиций (лекция) Метод объективной оценки Таблица 1 — Таблица значений показателей (правило Парето) Таблица 2 — Таблица ранжирования проектов (правило Парето) Таблица 3 — Таблицы предпочтений (правило Парето) Таблица 4 — Таблица ранжирования проектов (правило Борда) Таблица 5 —Таблица рангов проектов (правило Борда) Метод линейного программирования ... Полное содержание

Подобный материал:

• Рассматриваются вопросы отбора и экспертизы проектов в случае наличия нескольких альтернативных, 77.74kb.
• Совершенствование системы финансирования инвестиционных проектов банками Казахстана, 539.22kb.
• Техническое задание на оказание консультационных услуг по построению финансовой модели, 56.01kb.
• Техническое задание на оказание консультационных услуг по построению финансовой модели, 50.72kb.
• Постановлением Правительства Российской Федерации от 30 декабря 2009 г. N 1166 Собрание, 287.39kb.
• Вестник Брянского государственного технического университета. 2006. №1 (9), 88.23kb.
• РешениЕ от 22. 09. 11г. №14/613 г. Краснодон Опроведении Конкурсного отбора инвестиционных, 354.08kb.
• Методические рекомендации по оценке эффективности инвестиционных проектов и их отбору, 1579.29kb.
• В. А. Кулаков московский инженерно-физический институт (государственный университет), 28.6kb.
• Контрольная работа по курсу: Инвестиции на тему: Оценка эффективности инвестиционных, 305.17kb.

Содержание

Методы отбора инвестиционных проектов для финансирования (доп. материал, краткий вариант)

Наиболее часто применяемые методы отбора инвестиционных проектов можно условно разделить на четыре группы:

• методы, связанные с выбором проекта по наилучшему значению какого-либо одного показателя экономической эффективности инвестиций (чистой текущей стоимости, внутренней нормы доходности, индекса прибыльности, периода окупаемости);
  
• выбор наилучшего проекта при помощи показателя приведенных затрат;
  
• выбор наилучшего проекта при помощи какой-либо разновидности метода экспертных оценок;
  
• выбор наилучшего проекта при помощи метода Парето.
  

Методы показателей и приведенных затрат

При выборе самого эффективного (самых эффективных) проекта производится сравнение значений показателей разных проектов, рассчитанных методами чистой текущей стоимости, внутренней нормы доходности, индекса прибыльности, периода окупаемости. Лучшим (лучшими) признается проект или проекты, имеющие оптимальные значения этих показателей по сравнению с другими, либо с эталонными значениями подобных показателей.

Необходимость приведения текущих и единовременных затрат при оценке экономической эффективности инвестиционных сложений обусловлена:

• с одной стороны, разновременностью поступлений и затрат в процессе реализации инвестиционных проектов;
  
• с другой стороны, потребностями определения сравнительной экономической эффективности различных вариантов инвестиционных решений и инвестиционных проектов.
  

При расчетах сравнительной эффективности необходимо привести к сопоставимости текущие издержки на производство продукции или услуг и единовременные капитальные вложения на создание необходимых производственных мощностей. Для этого используется категория приведенных затрат, которые определяются по выражению:

,

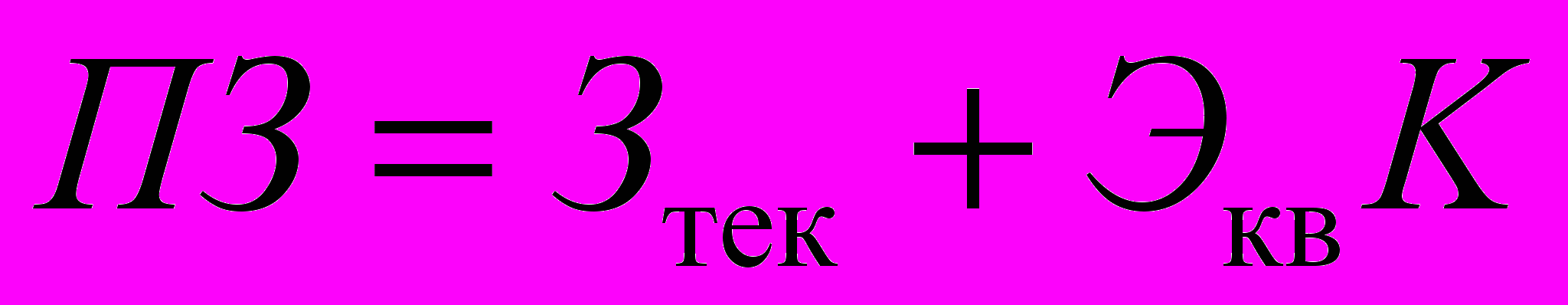где ПЗ — приведенные затраты;

З_тек — текущие производственно-эксплуатационные издержки;

K — единовременные капитальные вложения в основные производственные фонды;

Э_кв — коэффициент эффективности капитальных вложений.

Экономическая сущность приведения единовременных капитальных и других затрат к текущим затратам состоит в распределении их по инвестиционным периодам (отрезкам) срока реализации инвестиционного решения Величина коэффициента экономической эффективности капитальных вложений представляет собой величину, обратную среднеотраслевому сроку их окупаемости.

Метод экспертных оценок

В случае использования метода экспертных оценок лучший (лучшие) проект(ы) выбирается экспертами, путем присвоения различных оценок заранее определенным качествам проектов. Данные оценки определенным образом обрабатываются, после чего формируется окончательная оценка проекта. На основе интегральных, окончательных оценок возможно ранжирование проектов.

Экспертная оценка любого инвестиционного проекта состоит из следующих этапов:

1. Подбор группы экспертов.

Для решения данной задачи формируется группа экспертов, состоящая из нечетного числа участников (чем больше участников группы, и чем более разнятся их интересы, тем достовернее будет конечная оценка). Оптимальный состав группы 7—13 участников для небольших и среднемасштабных проектов, и 13—25 участников для крупномасштабных.

2. Определение набора факторов.

Чем шире набор факторов для экспертной оценки, и чем более полно (комплексно) эти факторы описывают окружение проекта, тем достовернее конечный результат оценки. (Поскольку внешние и внутренние факторы, влияющие на успешность реализации инвестиционного проекта зачастую необходимо не только количественно оценить, но и ранжировать, то для каждого из перечисленных выше факторов определена была степень его значимости в общей совокупности).

3. Обработка результатов экспертного опроса. Производится с использованием следующих формул:

; .

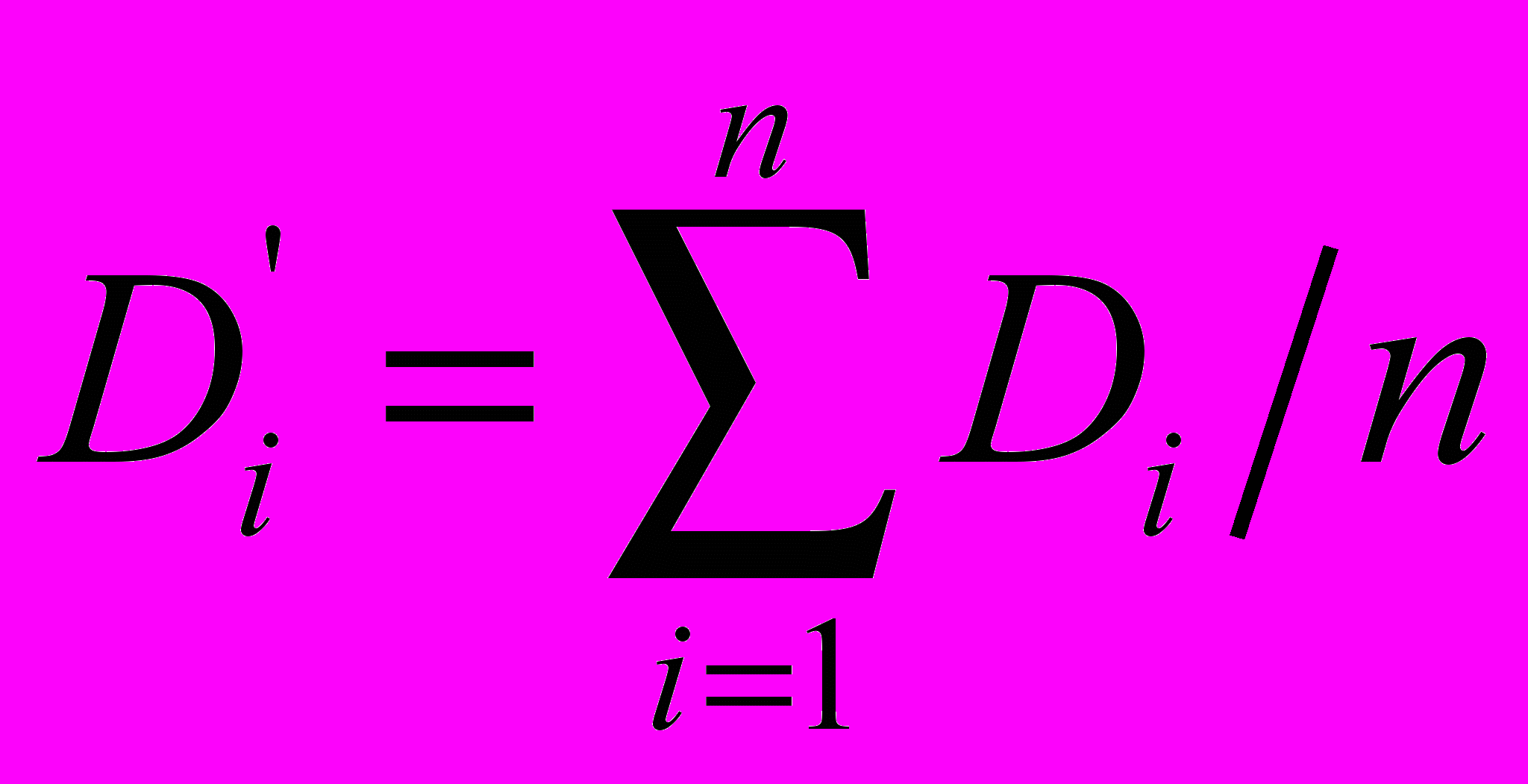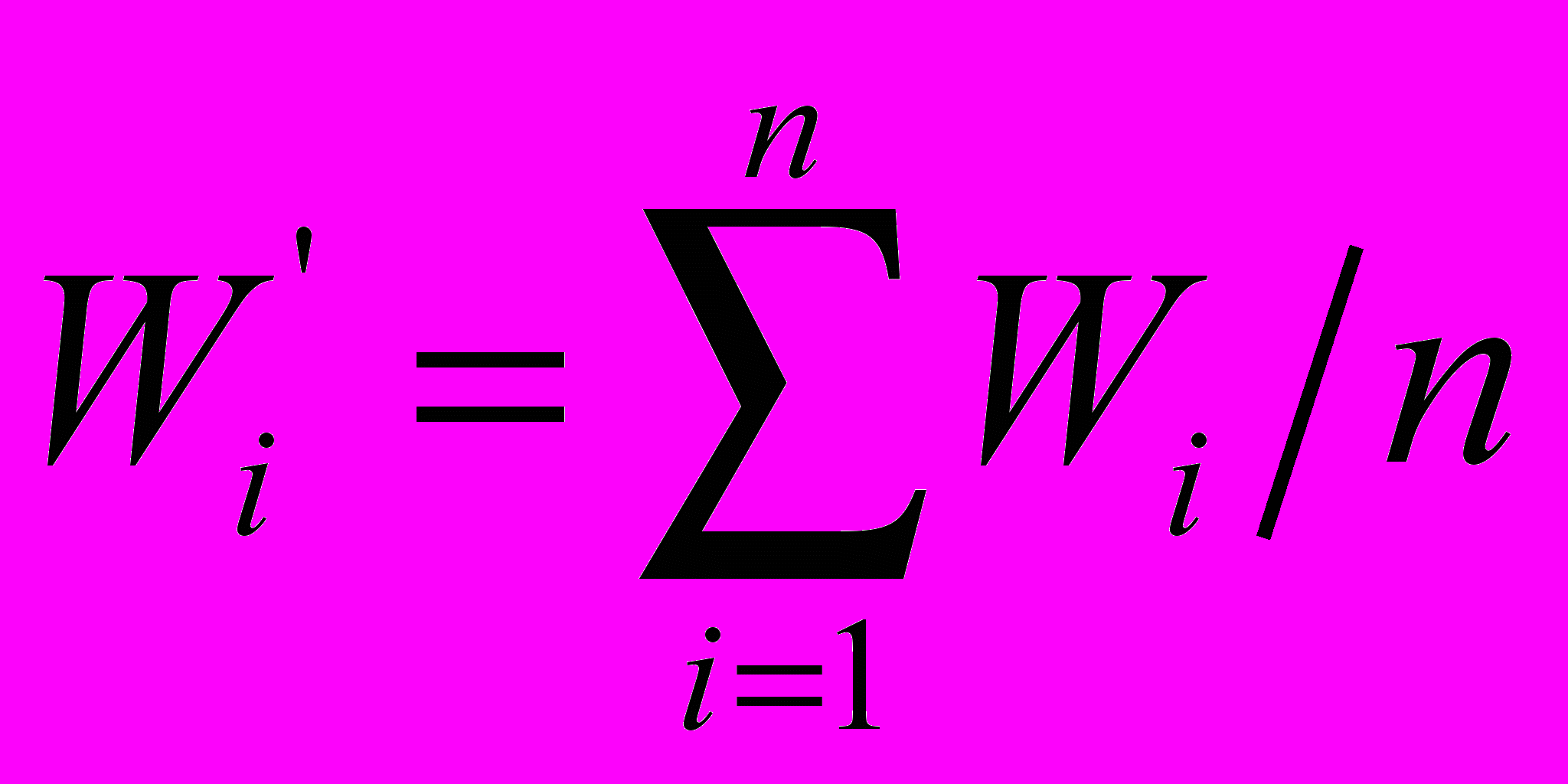Для удобства расчетов веса всех факторов приводятся к значениям, составляющим в сумме единицу. Формула приведения имеет следующий вид:

,

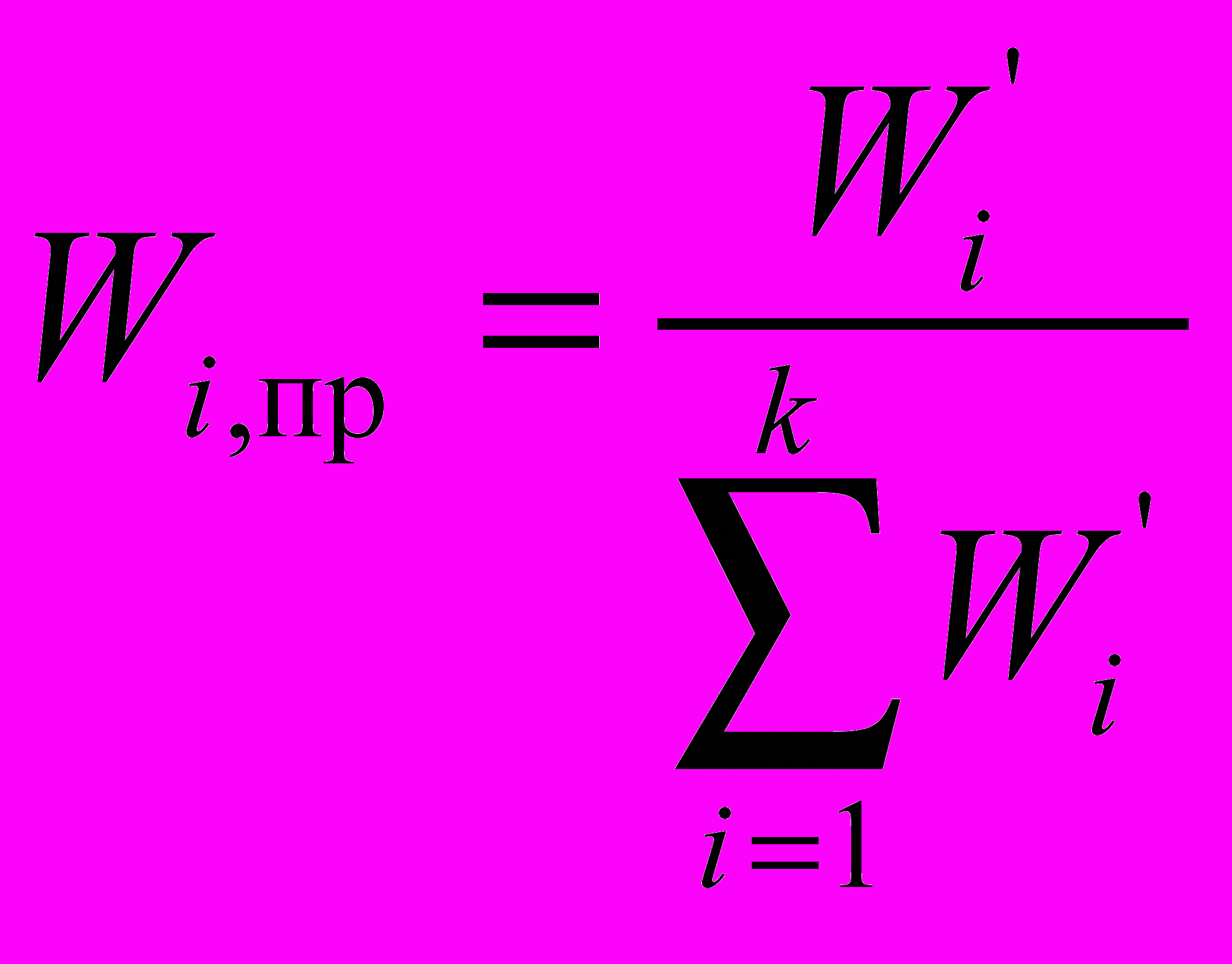где 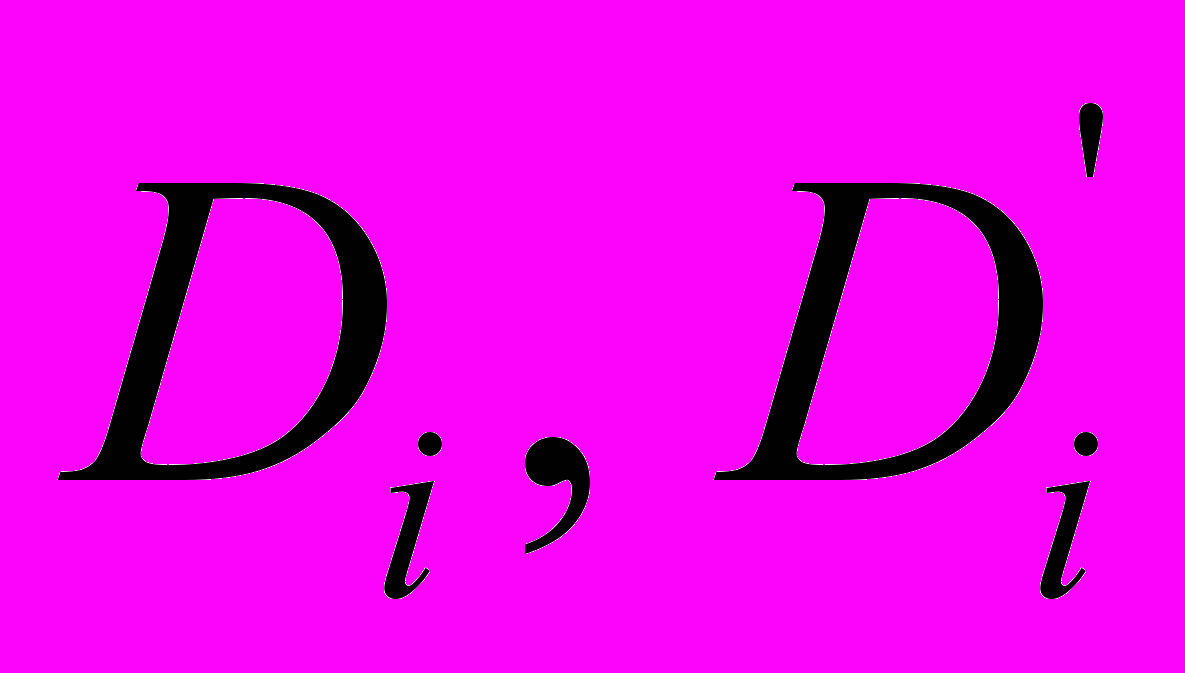— численное значение фактора в i-й анкете и итоговая численная оценка i-го фактора соответственно;

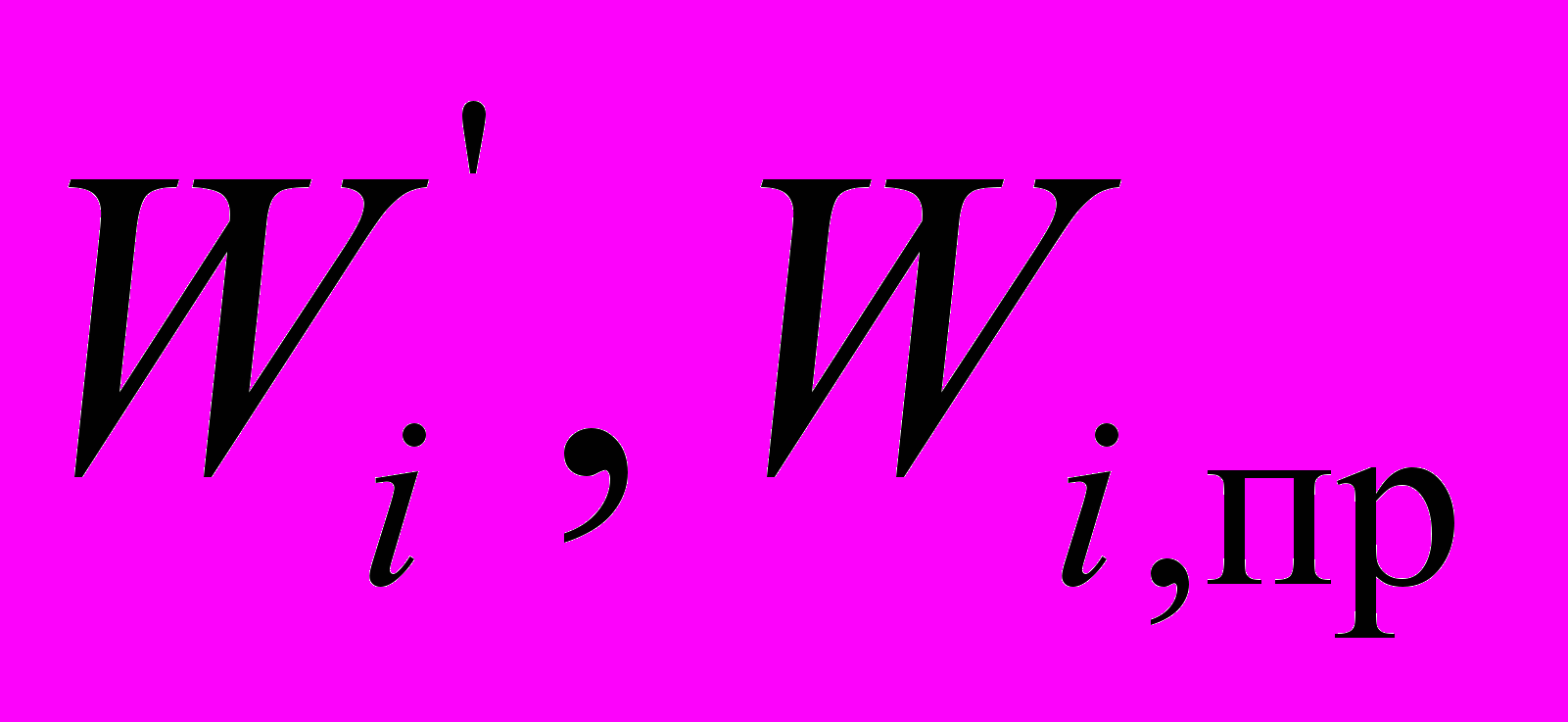— среднее и приведенное значение веса i-го фактора соответственно;

n — общее количество подготовленных анкет;

k — количество факторов в каждой анкете.

Модель экономического равновесия В. Парето

Итальянский экономист В. Парето сформулировал один из самых распространенных экономических критериев оптимальности. Он формулируется очень просто: «Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым пользу, является улучшением». Критерий Парето имеет весьма широкий экономический смысл и очень часто используется при решении сложных экономических задач. Его можно использовать тогда, когда оптимизация одной совокупности показателей, характеризующих объект, не должна ухудшать другую совокупность не менее важных показателей. Критерий Парето не применим к тем ситуациям, когда экономический эффект одних связан с убытками других.

Область решений, оптимальных по Парето, получила название области компромиссов.

С понятием оптимальности по Парето тесно связано другое очень важное понятие — экономическое равновесие. Экономическое равновесие дает возможность методологически согласовать противоречивые экономические интересы взаимодействующих элементов системы.

Алгоритм выделения области Парето:

1. Выбрать проект П_i, полагая i = 1.

2. Проект П_i сравнивается с остальными по всем показателям и отмечаются те из них, которые строго хуже, чем П_i.

3. Отмеченные проекты не могут принадлежать области Парето и из дальнейшего рассмотрения исключаются.

4. Полагаем i = i + 1.

5. Если 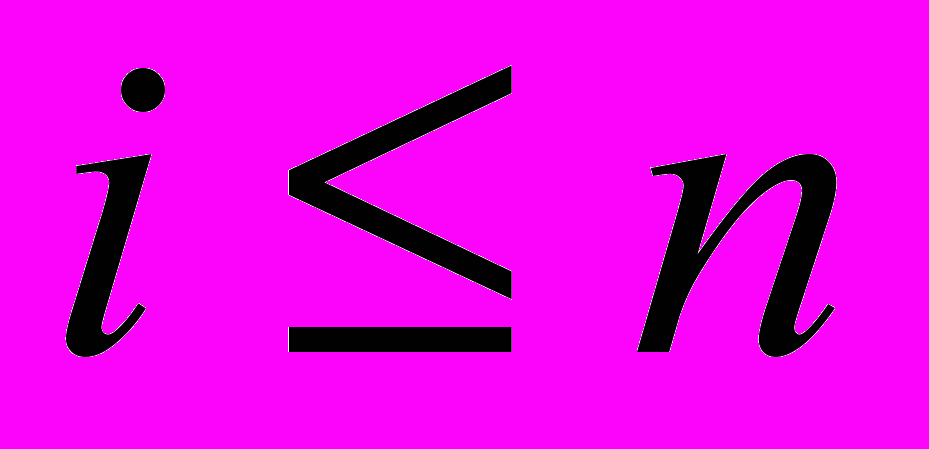и проект П_i уже был отмечен на предыдущих итерациях, то выполняется переход к п.4.

6. Если 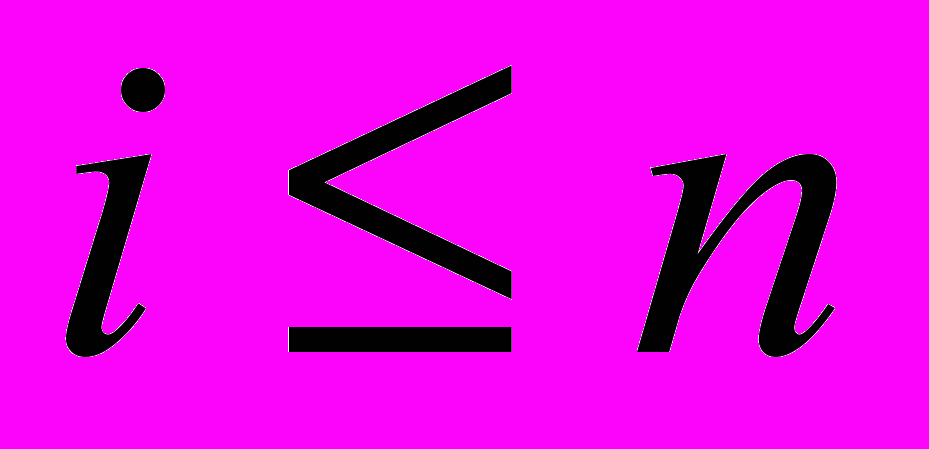и проект еще не помечен, то производится переход к п. 2.

7. Если 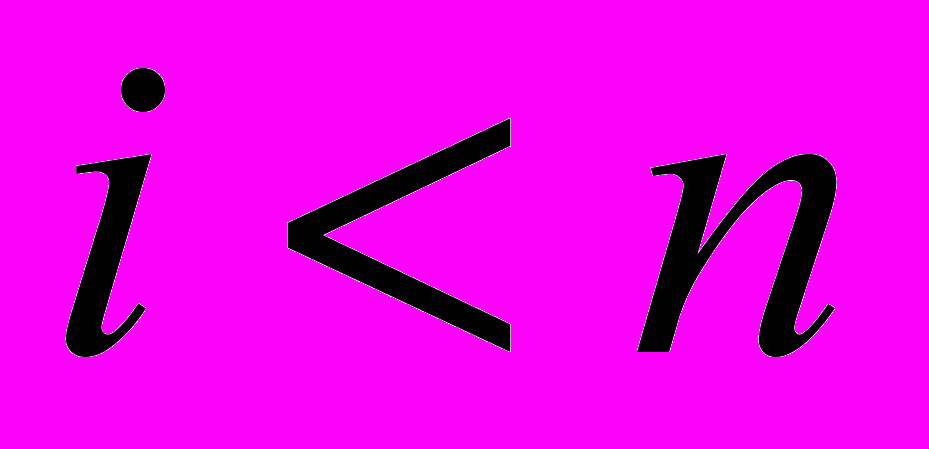, где n — число сравниваемых проектов, то осуществляется переход к п. 8.

8. Оставшиеся не отмеченными проекты образуют множество эффективных решений (область Парето).

В рамках полученной в результате работы алгоритма информации дальнейшее уточнение мест, занимаемых проектами внутри группы, невозможно. Если использовать дополнительную информацию, например, об относительной важности показателей, то можно получить дальнейшее уточнение мест проектов.

Методы отбора инвестиционных проектов для финансирования (доп. материал, полный вариант)

Методы отбора инвестиционных проектов (по эффективности инвестиций) можно условно разделить на следующие группы:

• методы, связанные с выбором проекта по наилучшему значению какого-либо одного показателя экономической эффективности инвестиций (чистого дисконтированного дохода, внутренней нормы доходности, индекса доходности, периода окупаемости),
  
• выбор наилучшего проекта при помощи какой-либо разновидности метода экспертных оценок
  
• выбор наилучшего проекта при помощи методов векторной оптимизации (метод Парето)
  

При выборе самого эффективного (самых эффективных) проекта(ов) производится сравнение значений показателей разных проектов, рассчитанных методами чистой текущей стоимости, внутренней нормы доходности, индекса прибыльности, периода окупаемости. Лучшим (лучшими) признается проект или проекты, имеющие оптимальные значения этих показателей по сравнению с другими, либо с эталонными значениями подобных показателей.

1 вариант экспертной оценки

В случае использования метода экспертных оценок лучший (лучшие) проект(ы) выбирается заранее сформированной группой экспертов, путем присвоения различных оценок определенным заранее качествам проектов. Данные оценки определенным образом обрабатываются, после чего формируется окончательная оценка значения этих показателей по сравнению с другими, либо с эталонными значениями подобных показателей.

Такой подход к отбору является весьма логичным, поскольку позволяет в процессе выбора учесть особенности конкретного инвестиционного проекта С точки зрения крупного инвестора — предпочтителен критерий ЧДД, показывающий массу получаемой от проекта чистой прибыли, средние и мелкие инвесторы заинтересованы в уменьшении времени оборота капитала, следовательно для них весьма важен срок окупаемости инвестиций В пользу подобного подхода к отбору инвестиционных проектов для финансирования говорит и тот факт, что и ЧДД, ВНД, ИД, ИДД и срок окупаемости инвестиций определяются на основе общих исходных данных — притоков и оттоков финансового плана.

Т

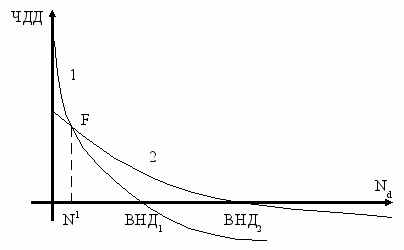
Рисунок 1 — Связь ЧДД и ВНД

ем не менее выбор проекта по наилучшему значению какого-либо одного показателя экономической эффективности инвестиций не всегда корректен, ибо опирается на информацию только об «одной стороне» эффективности проекта. На практике нередки ситуации, когда, несмотря на высокие значения чистого дисконтированного дохода, внутренней нормы доходности, индексов доходности проект не может быть принят из-за неудовлетворительного срока окупаемости инвестиций. Кроме того выбор по наибольшему значению ВНД в ряде случаев может быть некорректен На рисунке 1 приведены графики зависимости ЧДД от нормы дисконта для двух инвестиционных проектов. Осуществляя выбор по наибольшему значению внутренней нормы доходности, следует предпочесть проект № 2. Однако выбор будет правильным только в том случае, если в расчетах экономической эффективности инвестиций была использована норма дисконта большая, чем N¹, в противном случае объективно эффективнее по критерию чистого дисконтированного дохода будет проект № 1, ЧДД которого будет больше.

Трудности оценки проекта с использованием данного метода связаны не только с тем, что некорректен выбор проекта по максимальной величине ВНД, но и с тем. что некоторые инвестиционные проекты могут иметь инвестиционный этап, разбитый на несколько периодов, когда по окончании одного периода знак денежного потока меняется с «минуса» на «плюс» В этом случае график, отображающий ЧДД проекта (где по оси OY — откладывается значение ЧДД, а по оси ОХ — значение нормы дисконтирования) будет иметь несколько точек пересечения с горизонтальной осью координат, и соответственно, несколько значений ВНД.

Вышесказанное не означает полную непригодность метода выбора проекта по наилучшему значению какого-либо одного показателя экономической эффективности инвестиций. Лучший вариант проекта зачастую выбирается именно так.

2 вариант экспертной оценки

Как и в 1 варианте, лучший (лучшие) проект(ы) выбирается заранее сформированной группой экспертов, путем присвоения различных оценок определенным заранее качествам проектов. Данные оценки определенным образом обрабатываются, после чего формируется окончательная оценка проекта на основе интегральных, окончательных оценок, при этом возможно ранжирование проектов.

Поскольку предложенные факторы для более точной оценки инвестиционных проектов необходимо не только количественно оценить, но и ранжировать, для каждого из них определяется степень его значимости в общей совокупности.

Для удобства расчетов веса всех факторов обычно приводятся к значениям, составляющим в сумме единицу. Формула приведения имеет следующий вид:

.

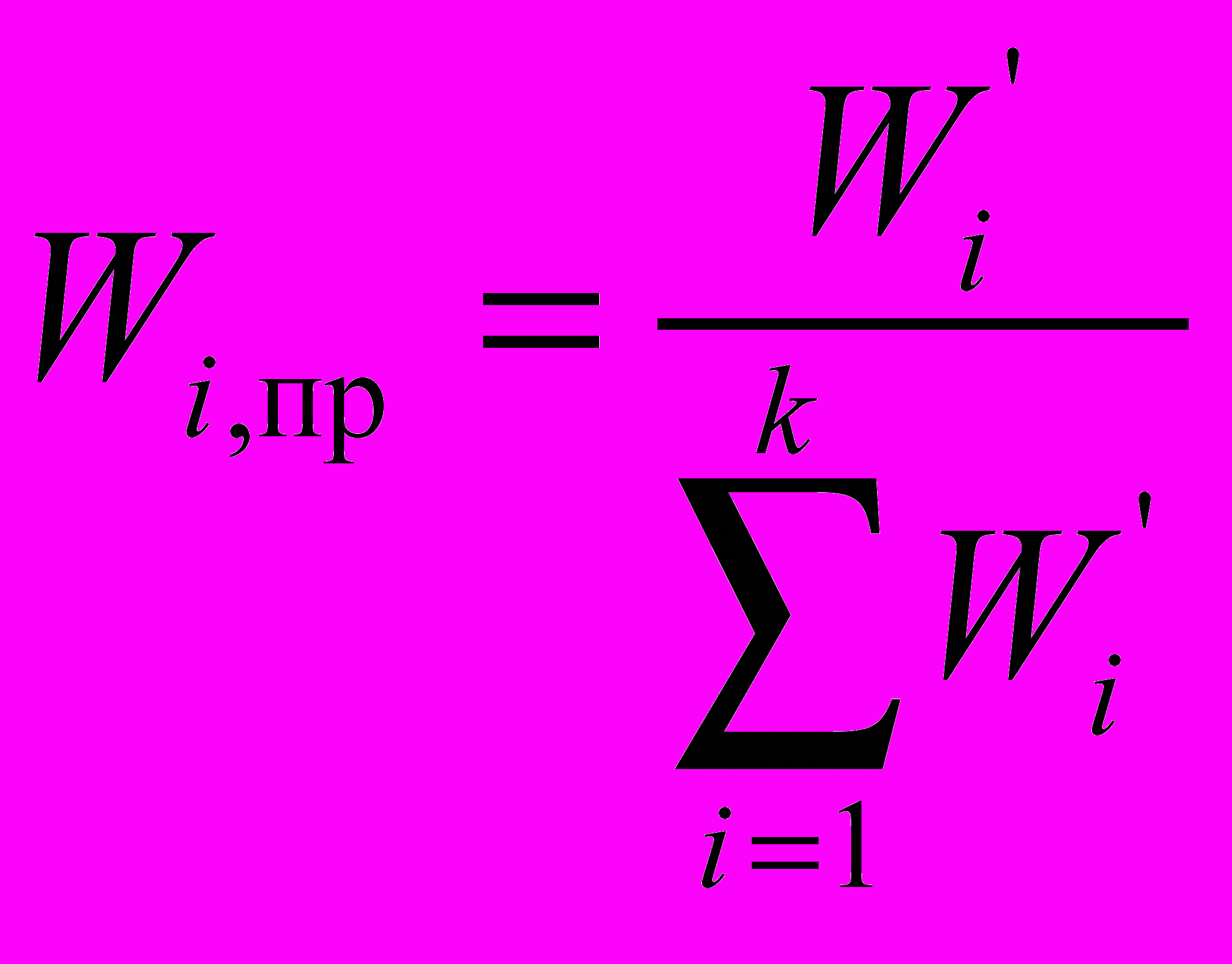Обработка результатов экспертного опроса производится с использованием следующих формул:

, 

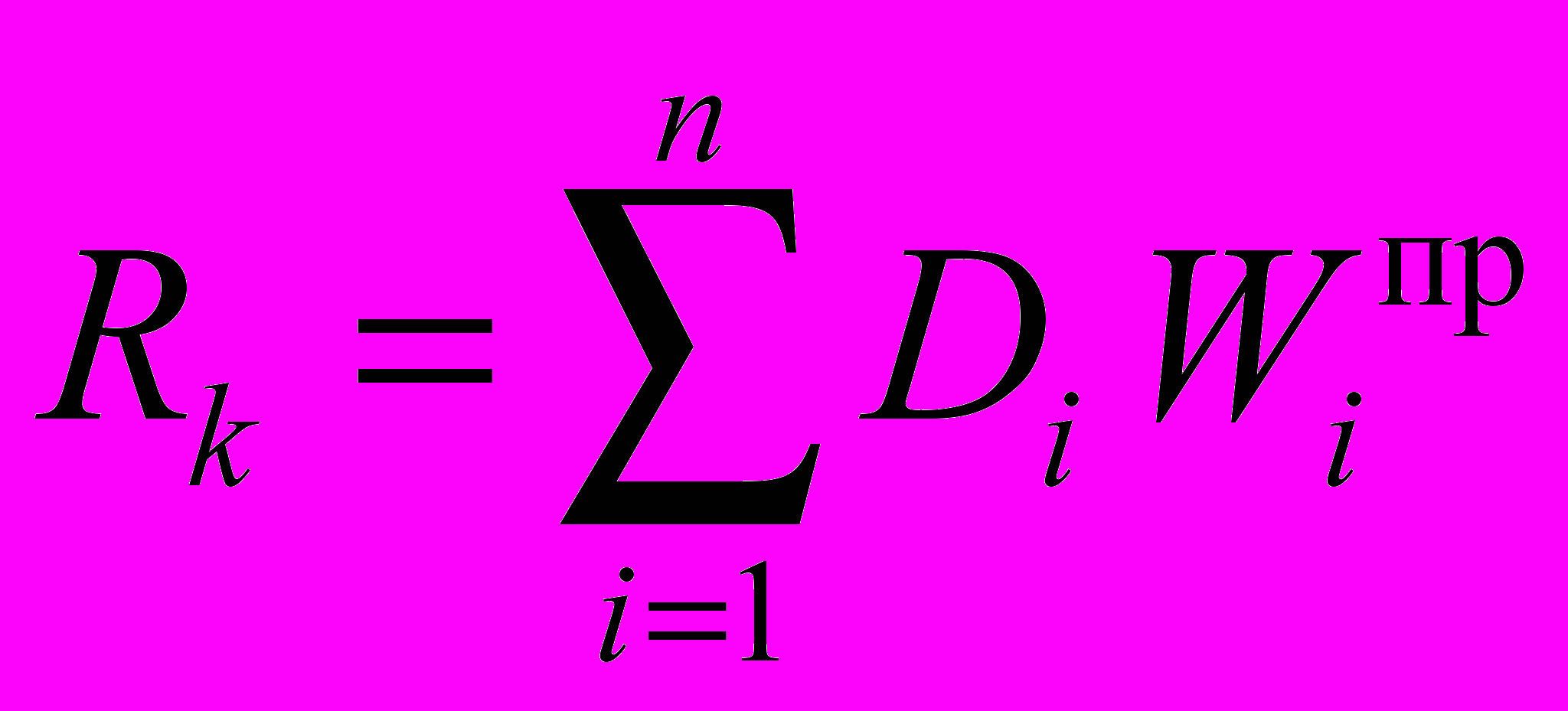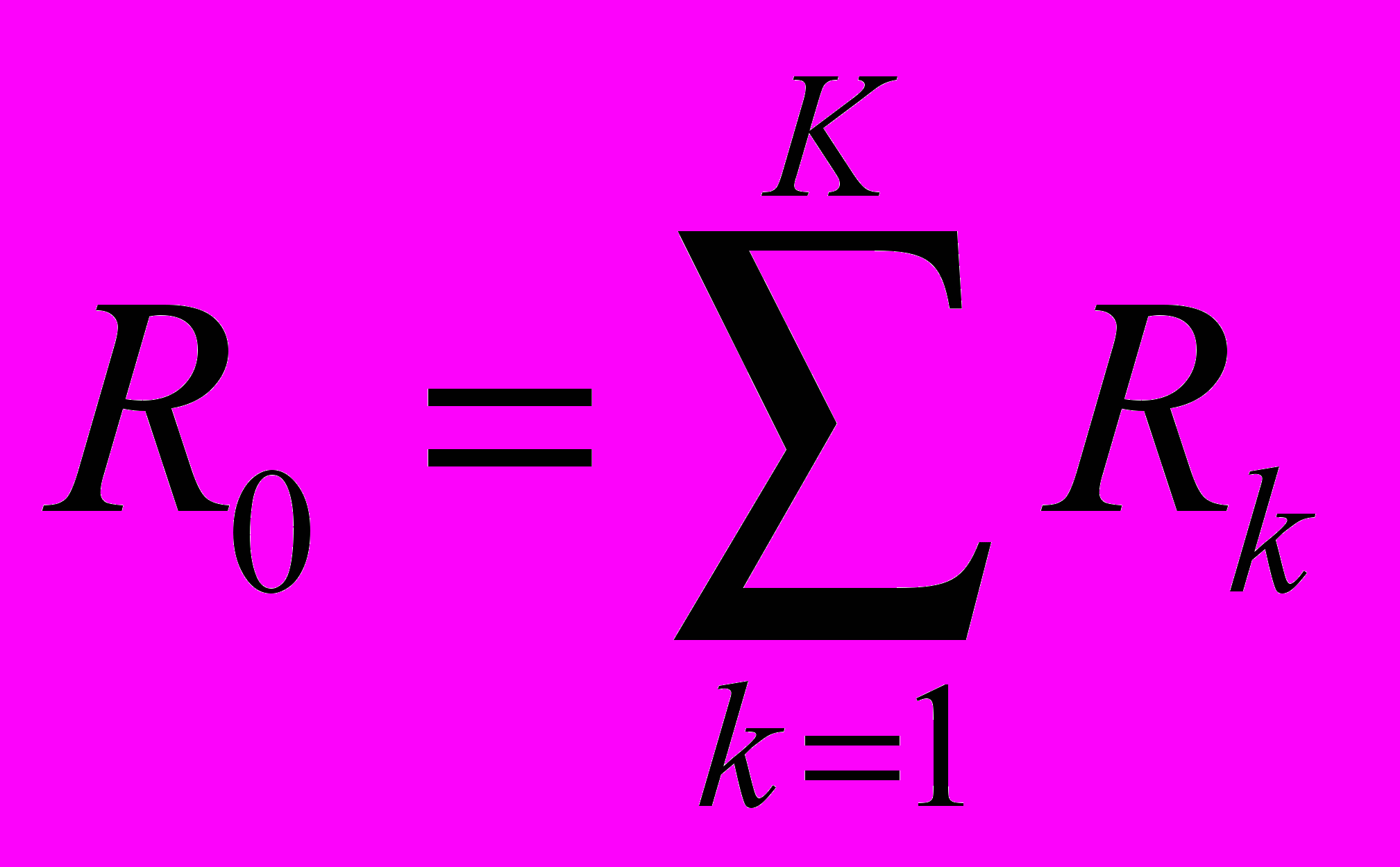
где R_k — интегральная оценка инвестиционного проекта по k-й анкете

D_i — численная оценка i-го фактора;

W_i — вес i-го фактора;

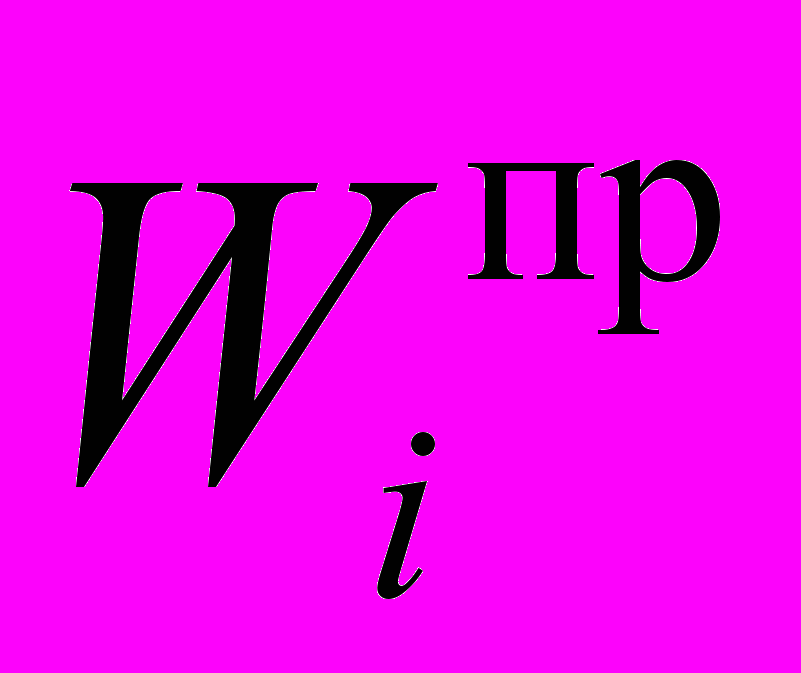— приведенный вес i-го фактора;

K — общее количество подготовленных анкет;

n — количество факторов в каждой анкете.

Метод экспертных оценок, однако, имеет ряд недостатков, которые привели к существенному сужению области его применения. Наиболее значительные из них:

• трудность формирования такой группы экспертов, которая могла бы объективно оценить преимущества и недостатки предложенных им для оценки инвестиционных проектов;
  
• трудность проведения самой процедуры экспертного опроса;
  
• получение необъективных оценок экспертов.
  

Однако один из самых существенных недостатков метода экспертных оценок заключается в несовершенстве самих методов обработки, заполненных экспертами анкет. При получении некоторой интегральной оценки проекта R_k, на основе которой и будет сделан выбор лучшего проекта, (см. приведенные ранее формулы) автоматически предполагается, что низкое значение оценки абсолютно любого фактора может быть скомпенсировано высоким значением оценки какого-либо другого фактора, что на практике не соответствует истине (например, высокое значение ЧДД не компенсирует длительный срок окупаемости).

Если от экспертов требуется отдать однозначное предпочтение какому-либо инвестиционному проекту попарно сравнивая все проекты совокупности, то может возникнуть ситуация, когда будет нарушен принцип транзитивности (проект А лучше проекта В, проект В лучше проекта С, следовательно, проект А лучше проекта С).

Поясним возможность возникновения подобной ситуации на следующем примере. Допустим, 35 экспертов должны оценить три инвестиционных проекта, при этом каждый из них должен дать заключение в виде: «проект А лучше проекта В». Мнения экспертов вполне могут распределиться следующим образом:

• проект А лучше проекта В — 25
  
• проект В лучше проекта А — 10
  
• проект В лучше проекта С — 21
  
• проект С лучше проекта В — 14
  
• проект А лучше проекта С — 15
  
• проект С лучше проекта А — 20
  

В результате нарушен принцип транзитивности — проект А лучше проекта В, проект В лучше проекта С, следовательно, проект А лучше проекта С.

Выбор наилучшего проекта при помощи методов векторной оптимизации

Очевидно, что в процессе отбора проектов желательно иметь такую ситуацию, в которой выбираемый для финансирования инвестиционный проект будет иметь первенство по всем показателям. На практике такие ситуации если не невозможны, то встречаются настолько редко, что могут быть рассмотрены в качестве редчайших исключений. Однако в этом случае, когда необходимо выбрать лучший проект именно по совокупности показателей, могут быть использованы методы векторной оптимизации.

Итальянский экономист В. Парето сформулировал один из самых распространенных экономических критериев оптимальности. Он формулируется очень просто: «Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым пользу, является улучшением». Критерий Парето имеет весьма широкий экономический смысл и очень часто используется при решении сложных экономических задач. Его можно использовать тогда, когда оптимизация одной совокупности показателей, характеризующих объект, не должна ухудшать другую совокупность не менее важных показателей. Критерий Парето не применим к тем ситуациям, когда экономический эффект одних связан с убытками других.

Область решений, оптимальных по Парето, получила название области компромиссов. С понятием оптимальности по Парето тесно связано другое очень важное понятие — экономическое равновесие. Экономическое равновесие дает возможность методологически согласовать противоречивые экономические интересы взаимодействующих элементов системы. Методику отбора проектов по методу Парето целесообразно разделить на два этапа и можно представить с помощью следующего алгоритма.

Этап 1. Алгоритм выделения области Парето.

1. Выбрать проект П_i, полагая i = 1.

2. Проект П_i сравнивается с остальными по всем показателям и отмечаются те из них, которые строго хуже, чем П_i.

3. Отмеченные проекты не могут принадлежать области Парето и из дальнейшего рассмотрения исключаются.

4. Полагаем i = i + 1.

5. Если 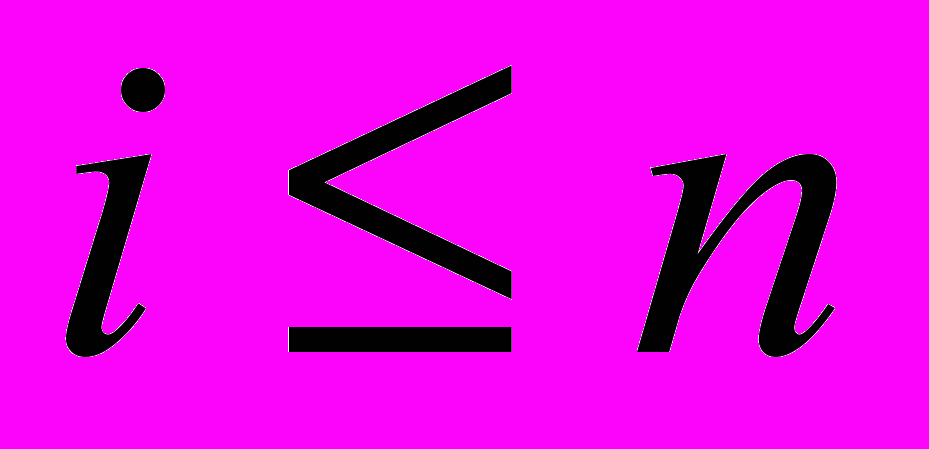и проект П_i уже был отмечен на предыдущих итерациях, то выполняется переход к п.4.

6. Если 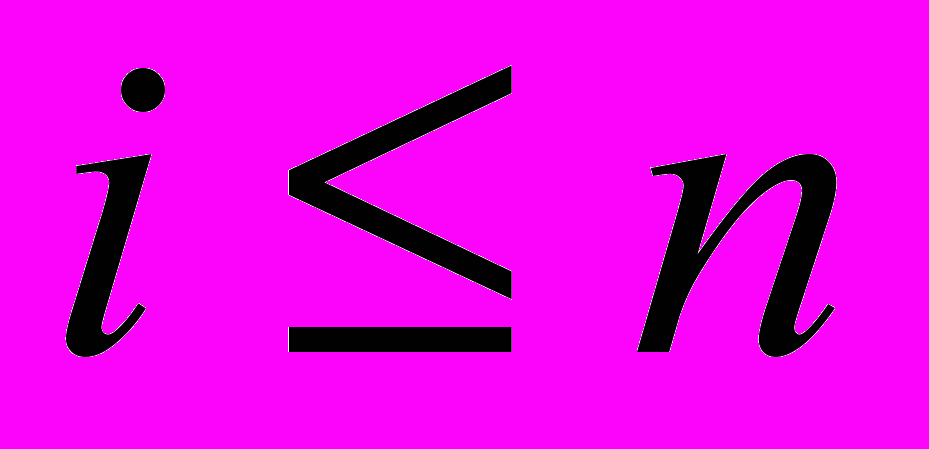и проект еще не помечен, то производится переход к п. 2.

7. Если 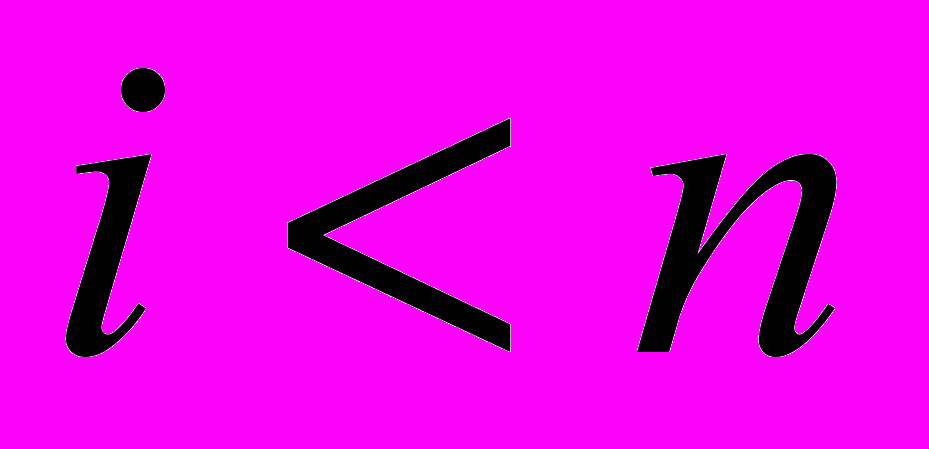, где n — число сравниваемых проектов, то осуществляется переход к п. 8.

8. Оставшиеся не отмеченными проекты образуют множество эффективных решений (область Парето).

Этап 2. В рамках полученной в результате работы алгоритма информации дальнейшее уточнение мест, занимаемых проектами внутри группы, невозможно. Если использовать дополнительную информацию, например, об относительной важности показателей, то можно получить дальнейшее уточнение мест проектов.

Таким образом, вышесказанное позволяет сделать вывод, что наиболее правильный ответ на вопрос «какой проект эффективнее?» позволяет ответить процедура, использующая метод В. Парето. Именно эта процедура позволяет вначале — на этапе 1 — отсеять наименее эффективные инвестиционные проекты, а затем — на этапе 2 —корректно выбрать лучшие проекты, сформулировав дополнительные критерии отбора.

Методы сравнительной оценки и выбора объектов инвестиций (лекция)

Формирование инвестиционного портфеля предприятия производится в предположении, что:

• общий объем инвестиционных ресурсов ограничен;
  
• имеется ряд объектов инвестиций (проектов), по отдельности удовлетворяющих условиям доходности, и по общему объему превышающих имеющийся объем инвестиций (т. е. возникает задача выбора некоторых из набора).
  

Требуется составить портфель инвестиций, обеспечивающий максимально возможный прирост капитала предприятия и/или соответствующий иным критериям.

Описанная выше ситуация может также возникнуть и в следующих случаях:

• проведение конкурсов инвестиционных проектов;
  
• определение направлений развития крупных предприятий, организаций;
  
• формирование кредитного портфеля для крупного инвестора;
  
• поиск перспективных направлений вложения средств для инвестора, входящего на новый рынок.
  

В общем случае задача не имеет прямого аналитического решения. В практике оценка инвестиционных решений ведется по всем показателям, причем ранжирование объектов и формирование портфеля осуществляется на основе различных методов, включая следующие:

1) Субъективные методы:

• методы субъективного предпочтения;
  
• метод экспертных оценок (принципы рассмотрены выше, см. также таблицы 2, 3, 4);
  
• способы неформализуемого выбора;
  

2) Объективные методы:

• метод выбора по Парето, когда наилучшим считается тот объект инвестиций, для которого нет ни одного объекта по критериальным показателям не хуже указанного, а хотя бы по одному показателю лучше.
  
• метод выбора по Борда, при котором объект инвестиций ранжируется по значениям каждого показателя в порядке убывания с присвоением соответствующего значения ранга, а затем подсчитывается суммарный ранг для каждого объекта инвестиций. Наилучшим считается объект с максимальным значением суммарного ранга.
  
• метод выбора по удельным весам показателей, при котором сами критериальные показатели ранжированы по значимости для инвестора. Каждому критериальному показателю присваивается удельное значение веса (в долях единицы) при сумме весов всех показателей, равной единице. Значения рангов показателей для каждого проекта взвешиваются по удельным весам самих показателей и суммируются. Результирующие ранги сравниваются между собой и лучшим считается объект с наибольшим значением такого взвешенного ранга.
  
• методы линейного программирования — наиболее сложная группа методов, с помощью которых решается задача максимизации доходности портфеля при заданных ограничениях.
  

Метод объективной оценки

Если из пакета проектов необходимо выбрать несколько лучших, общая сумма финансирования по которым соответствует инвестиционным возможностям инвестора, применяется правило выбора по Парето.

Рассмотрим 5 проектов со следующими значениями основных показателей: чистого дисконтированного дохода (ЧДД), индекса доходности (ИД), внутренней нормы доходности (ВНД), срока окупаемости (СО), рентабельности инвестиций (Р_И).

Таблица 1 — Таблица значений показателей (правило Парето)

Проект	ЧДД, тыс. долл.	ИД	ВНД, %	СО, лет	РИ, %
А	900	1,10	25	2,0	27
В	800	1,15	40	1,5	30
С	1000	1,20	30	1,8	35
D	1010	1,25	20	1,0	25
Е	300	1,40	15	1,2	2

Таблица 2 — Таблица ранжирования проектов (правило Парето)

Ранг	ЧДД, тыс. долл.	ИД	ВНД, %	СО, лет	РИ, %
1	D	Е	В	D	С
2	С	D	С	Е	В
3	А	С	А	В	А
4	В	В	D	С	D
5	Е	А	Е	А	Е

Для удобства рассмотрения составим таблицы предпочтений, в которых сравниваются все проекты попарно так, что в таблице для проекта B в клетку пересечения строки ЧДД и столбца «С» ставится «+», если значение ЧДД по проекту больше, чем по проекту С, знак «–», если меньше, и знак «0», если значения равны.

Таблица 3 — Таблицы предпочтений (правило Парето)

А	B	C	D	Е
ЧДД	+	–	–	+
ИД	–	–	–	–
ВНД	–	–	+	+
СО	–	–	–	–
РИ	–	–	+	+

В	А	С	D	Е
ЧДД	–	–	–	+
ИД	+	–	–	–
ВНД	+	+	+	+
СО	+	+	–	–
РИ	+	–	+	+

С	А	B	D	Е
ЧДД	+	+		+
ИД	+	+	–	–
ВНД	+	–	+	+
СО	+	–	–	–
РИ	+	+	+	+

D	А	В	С	Е
ЧДД	+	+	+	+
ИД	+	+	+	–
ВНД	–	–	–	+
СО	+	+	+	+
РИ	–	–	–	+

Е	А	В	С	D
ЧДД	–	–	–	–
ИД	+	+	+	+
ВНД	–	–	–	–
СО	+	+	+	–
РИ	–	–	–	–

Принимая во внимание приведенное выше правила выбора по Парето, в настоящем случае проект выбирается (выигрывает у других вариантов), если в таблице, составленной для него нет ни одного столбца, в котором отсутствует знак «–». Наличие в таблице для проекта С столбца А, не имеющего ни одного знака «–», означает, что проект С имеет по всем показателям лучшие значения, чем проект А. В рассматриваемом случае только для проекта А есть проект, имеющий преимущество, поэтому по правилу Парето выбираются все проекты, кроме А.

Правила выбора по Парето нередко дают больше выигрышных значений, чем это необходимо. В таких случаях применяется более строгое правило выбора — правило выбора по Борда.

Для применения правила Борда берется таблица ранжирования проектов Парето и вводится специальный столбец, значения в котором соответствуют рангу строки. Таким образом, проект, имеющий наилучшее значение по какому-либо показателю, имеет по данному показателю ранг «5», а ранг «1» соответствует наихудшему значению.

Таблица 4 — Таблица ранжирования проектов (правило Борда)

Ранг	ЧДД	ИД	ВНД	СО	РИ
5	D	Е	В	D	С
4	С	D	С	Е	В
3	А	С	А	В	А
2	В	В	D	С	D
1	Е	А	Е	А	Е

Составим таблицу рангов по всем проектам.

Таблица 5 —Таблица рангов проектов (правило Борда)

Ранг	ЧДД	ИД	ВНД	СО	РИ	Сумма
А	3	1	3	1	3	11
В	2	2	5	3	4	16
С	4	3	4	2	5	18
D	5	4	2	5	2	18
Е	1	5	1	4	1	13

Наилучшим при выборе, согласно правилу Борда, являются варианты, набравшие наибольшую сумму. Наибольшие суммы в данном случае имеют проекты С и D.

Надо отметить, что процедура выбора может содержать комбинированные методы. Для этого выбор проводится в несколько этапов, на каждом из которых применяется одно из правил с последующим исключением выбранных вариантов из дальнейшего рассмотрения.

Метод линейного программирования

Постановка задачи методом линейного программирования имеет следующий вид:

Пусть имеется L объектов предполагаемых инвестиций объемов И_i (i = 1, L) с соответствующими показателями эффективности ЧДД_i, BHД_i, ИД_i, C_Oi, a также прочими показателями объектов, являющимися критериальными для предприятия- Предполагается, что общий объем инвестиций предприятия меньше, чем совокупный объем инвестиций в предполагаемые объекты, что означает необходимость выбора комплекта объектов из всего множества рассматриваемых объектов.

Пусть также имеется набор ограничений, включающих:

• общий объем инвестиций предприятия И_п, выделенных на формирование инвестиционного портфеля;
  
• цену капитала СК;
  
• удовлетворяющий предприятие минимальный уровень чистого дисконтированного дохода предприятия от всего объема выделяемых инвестиций ЧДД_п;
  
• требуемую норму доходности (НД) или цену капитала, выделяемого на финансирование инвестиций СС (СК);
  
• установленный предприятием предельный уровень доходности объекта инвестиций ИД;
  
• установленный предприятием предельный уровень срока окупаемости инвестиций С_Оп;
  
• прочие критериальные показатели, существенные для предприятия.
  

На первом этапе следует ранжировать объекты инвестиций методами, приведенными выше. Предположим, что объекты ранжированы в порядке убывания инвестиционной привлекательности (например в порядке убывания ЧДД или ИД).

Требуется сформировать инвестиционный портфель предприятия, который обеспечивает максимизацию минимального индекса доходности объектов инвестиционного портфеля



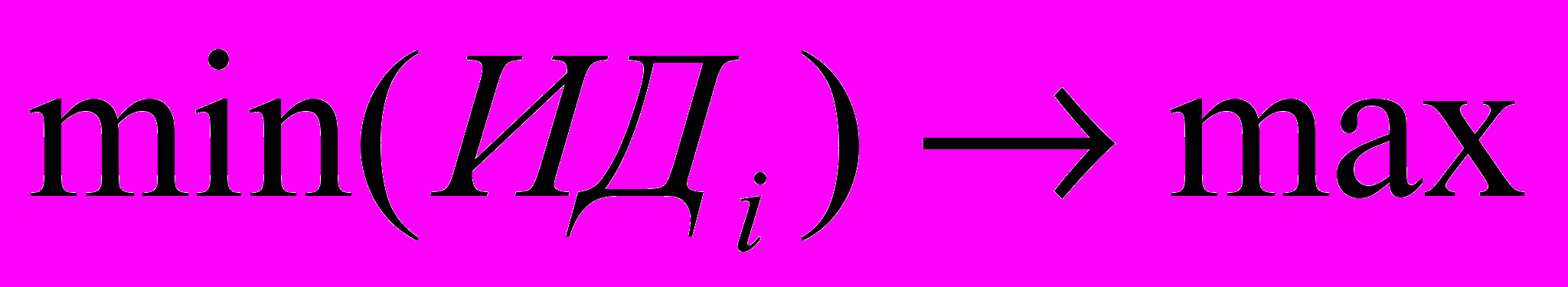
при выполнении условий:

1) Объем инвестиций по объектам, включенным в инвестиционный портфель, не превышает общего объема выделенных средств:

.

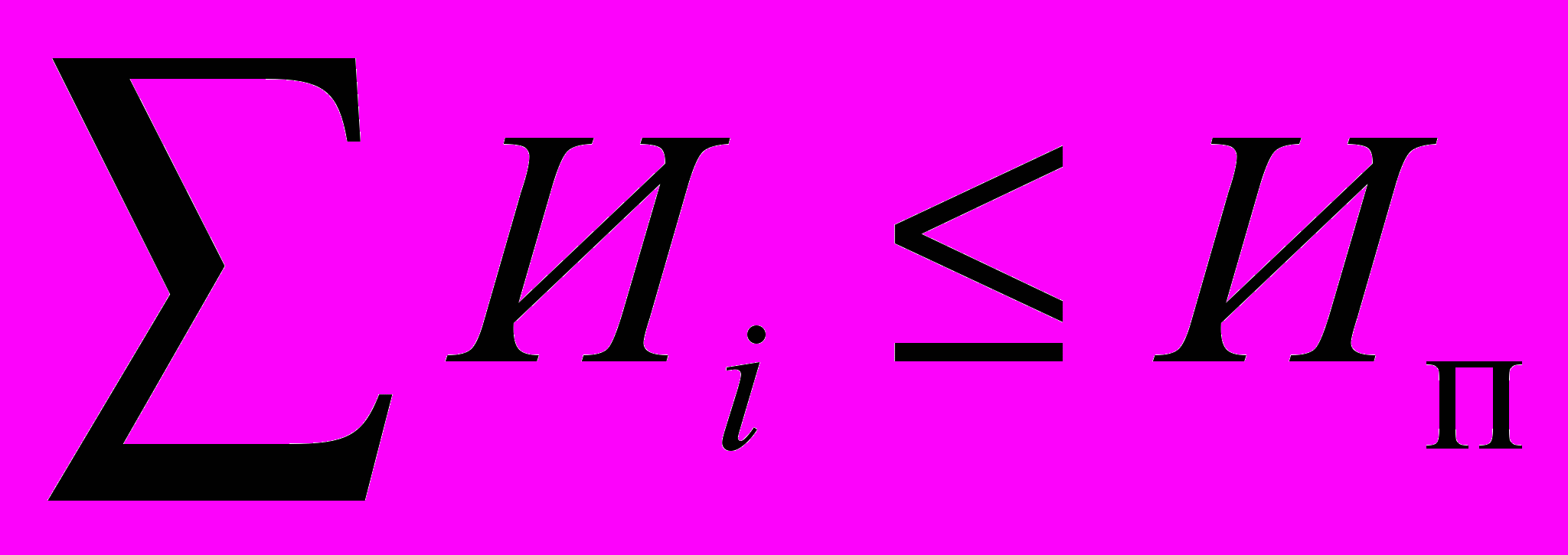2) Суммарный чистый дисконтированный доход инвестиционного портфеля не меньше установленной предприятием величины:

.

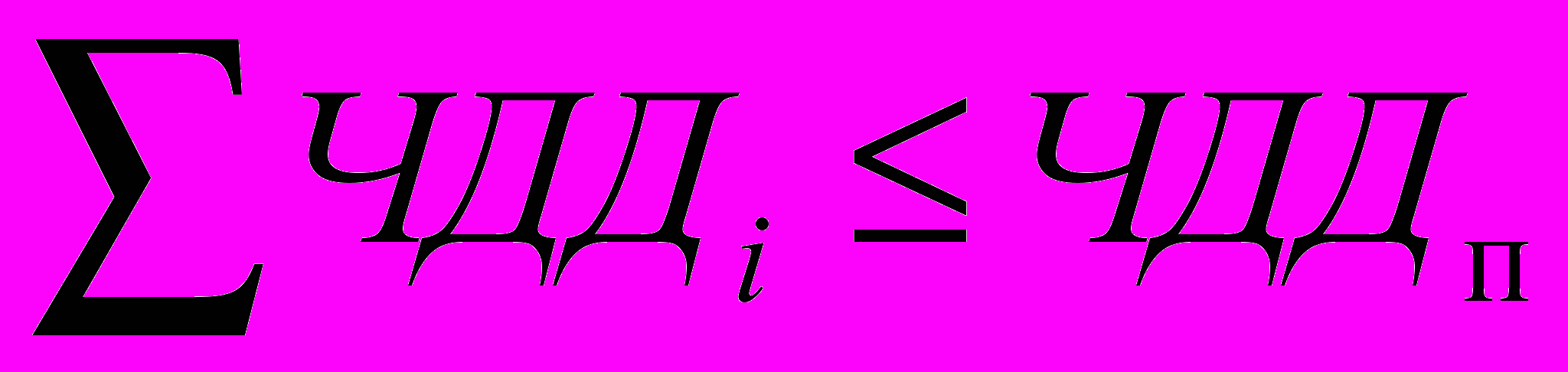3) Минимальная внутренняя норма доходности по объектам (ВНД), включенным в инвестиционный портфель, не меньше установленной предприятием нормы дисконта НД, или не меньше цены капитала предприятия или цены капитала, выделенного на инвестиции, соответственно:

.

4) Максимальный срок окупаемости по объектам, включенным в инвестиционный портфель, не больше установленного предприятием ограничения:

.

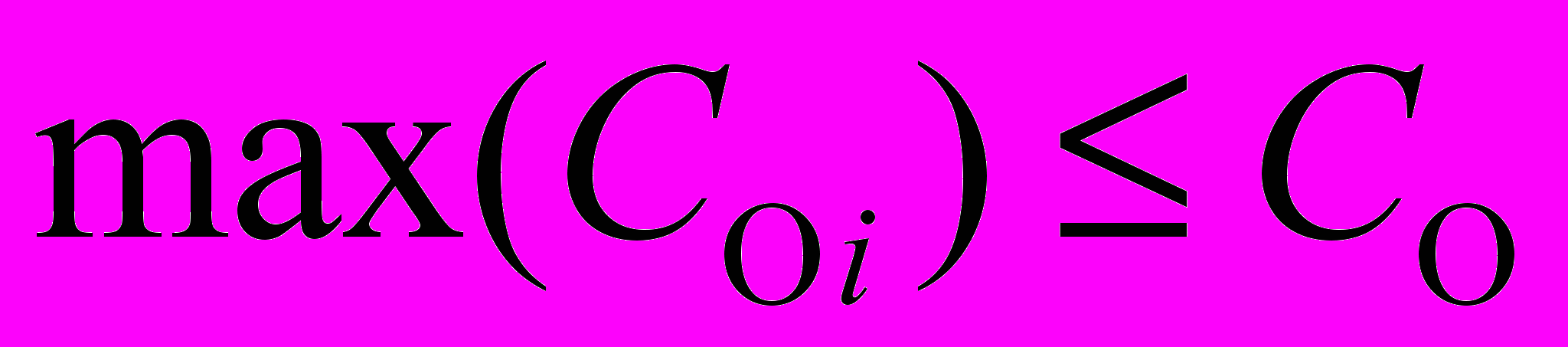В реальной практике формирования инвестиционного портфеля могут быть дополнительные условия, а также отсутствовать имеющиеся.

Алгоритм решения представленной задачи заключается в том, что при формировании инвестиционного портфеля в него включаются последовательно объекты в порядке убывания ранга объекта до тех пор, пока они могут инвестироваться в полном объеме при выполнении установленных ограничений.