Отчет по лабораторным работам фтпу 1-21/1
| Вид материала | Отчет |
СодержаниеМетод дихотомии «базы данных» |
- Методические указания по лабораторным работам Факультет: электроэнергетический, 554.73kb.
- Методические указания к лабораторным работам по курсу, 438.32kb.
- Методические указания к электронным лабораторным работам по курсу физической химии, 2388.82kb.
- Методические указания к лабораторным работам по дисциплине «Материаловедение и ткм», 215.09kb.
- Методические указания к лабораторным работам для студентов специальности 210100 "Автоматика, 536.56kb.
- Методические указания к лабораторным работам №1-5 для студентов специальности 210100, 363.6kb.
- Методические рекомендации к лабораторным работам по курсу «Основы проектирования, 616.07kb.
- Методические указания к лабораторным работам по физике по практикуму «Вычислительная, 138.12kb.
- Название дисциплины, 52.28kb.
- Методические указания к лабораторным работам по теме: «Технология обработки текстовой, 139.7kb.
| «Информатика» (2 семестр) Отчет по лабораторным работам | | ФТПУ 7.1-21/1 |
Министерство образования Российской Федерации
Томский политехнический университет
__________________________________________________________
Кафедра И.П.С.
Отчет по лабораторным работам
«ИНФОРМАТИКА» (2 семестр)
Разработала: ст. гр. 2Б53 Гуцалюк Е.К.
Принял: преп. Хамухин А.А.
Томск - 2005
Содержание
Лабораторная работа №1__________________________________________________
Лабораторная работа №2__________________________________________________
Лабораторная работа №3__________________________________________________
Лабораторная работа №4__________________________________________________
Лабораторная работа №5__________________________________________________
Лабораторная работа №1
«Интерполяция и экстраполяция».
Цель работы: научиться применять формулы полиномиальной и сплайн-интерполяции для восстановления отсутствующих (дефектных) значений в массивах экспериментальных данных.
Порядок работы
- Подготовить исходный «массив экспериментальных данных» на листе Excel в виде 2-х столбцов (А3:В13) для X и Y. Где X – аргумент, изменяющийся с некоторым шагом, Y – некоторая функция от Х ,например, Y=SIN(X) и представить этот массив на графике, например, - один период синусоиды.
- Скопировать исходный массив в соседние справа столбцы (C3:D13) и «потерять» при этом значение одной точки в соответствии с вариантом индивидуального задания. «Дефектный» массив также представить в виде графика (на отдельной диаграмме).
- Набрать программу по формулам полиномиальной (формула Лагранжа для N узлов) и сплайн-интерполяции (в качестве сплайна использовать полином Лагранжа для соседних узлов) для восстановления значения «потерянной» точки. Исходные данные считывать из столбцов (C3:D13), результаты записывать соответственно в столбцы (E3:F13) и (G3:H13).
- Под столбцами результатов разместить кнопки «Пуск» и «Очистка», а сами результаты представить в виде графиков на отдельных диаграммах.
- Зная точно значение потерянной точки (А3:В13), вычислить относительную погрешность для каждой из формул и сделать вывод.
- Изменять порядок сплайна в программе (1,3), повторить расчеты и по изменению погрешности сделать вывод.
Расчетные формулы
Формула Лагранжа для N узлов:
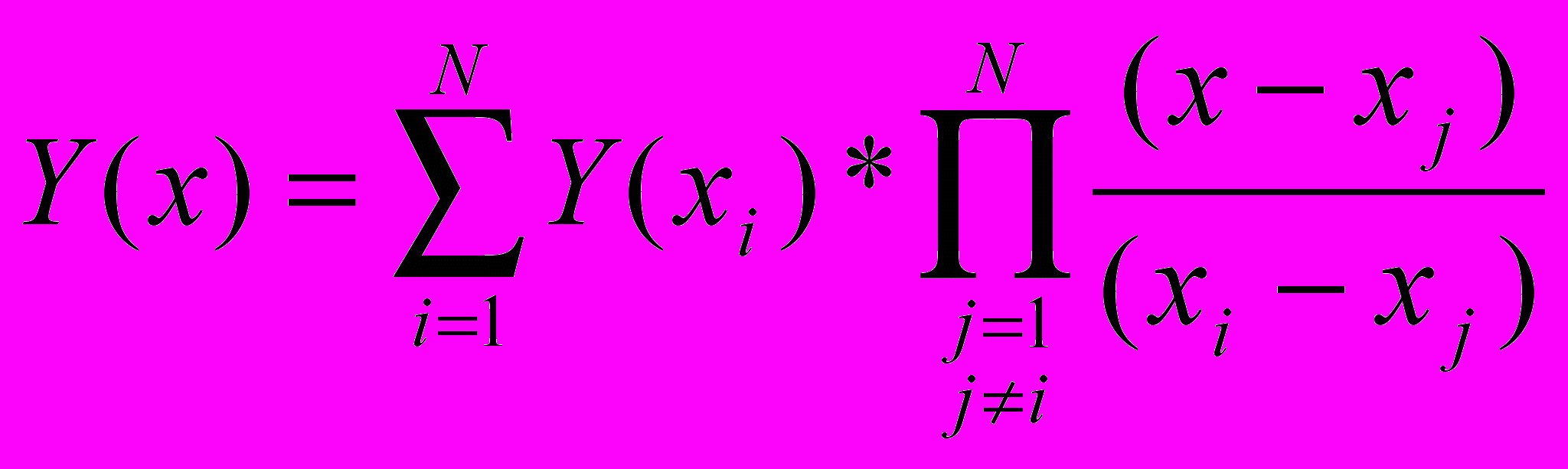
Формула Лагранжа
S = 0
For i = 0 To N
p = 1
For j = 0 To N
If j <> i And j <> Nz Then p = p * ((z - x(j)) / (x(i) - x(j)))
Next j
If i <> Nz Then S = S + y(i) * p
Next i
y(Nz) = S '
Формула расчета погрешности
Pogr = Abs((yt - y(Nz)) / yt)
Формула сплайн-интерполяции
S = 0
For i = Nz - Nspline To Nz + Nspline
p = 1
For j = Nz - Nspline To Nz + Nspline
If j <> i And j <> Nz Then p = p * ((z - x(j)) / (x(i) - x(j)))
Next j
If i <> Nz Then S = S + y(i) * p
Next i
y(Nz) = S
Индивидуальное задание для интерполяции
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Пример программы
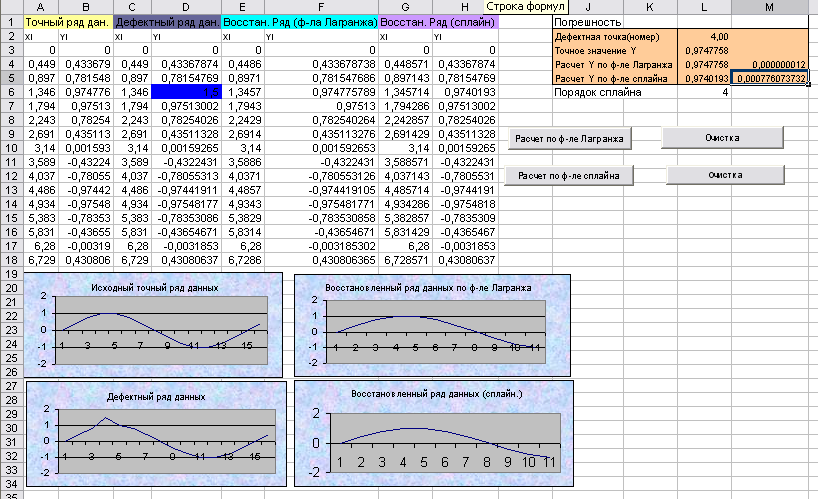
Выводы и результаты
При подстановки точки № 4 по варианту 15 получаем:
- При порядке сплайна 5 формула Лагранжа = 0,000000012 сплайн – инт = 0,000516621698
- При порядке сплайна 4 формула Лагранжа = 0,000000012 сплайн – инт = 0,000001422684
- При порядке сплайна 3 формула Лагранжа = 0,000000012 сплайн – инт = 0,006525084773
- При порядке сплайна 2 формула Лагранжа = 0,000000012 сплайн – инт = 0,000023967258
- При порядке сплайна 1 формула Лагранжа = 0,000000012 сплайн – инт = 0,098932437348
Погрешность по формуле Лагранжа составляет 0,000000012 % - это намного меньше, чем погрешность при использовании формулы сплайн-интерполяции. Поэтому для восстановления дефектных точек лучше пользоваться формулой Лагранжа.
Индивидуальное задание для экстраполяции
| Количество точных точек | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Восстановить точки | 4, 5,6 | 5, 6,7 | 6, 7,8 | 7, 8,9 | 8, 9,10 | 9, 10,11 | 10, 11,12 | 11, 12,13 | 12, 13,14 | 13, 14,15 |
Пример работы программы
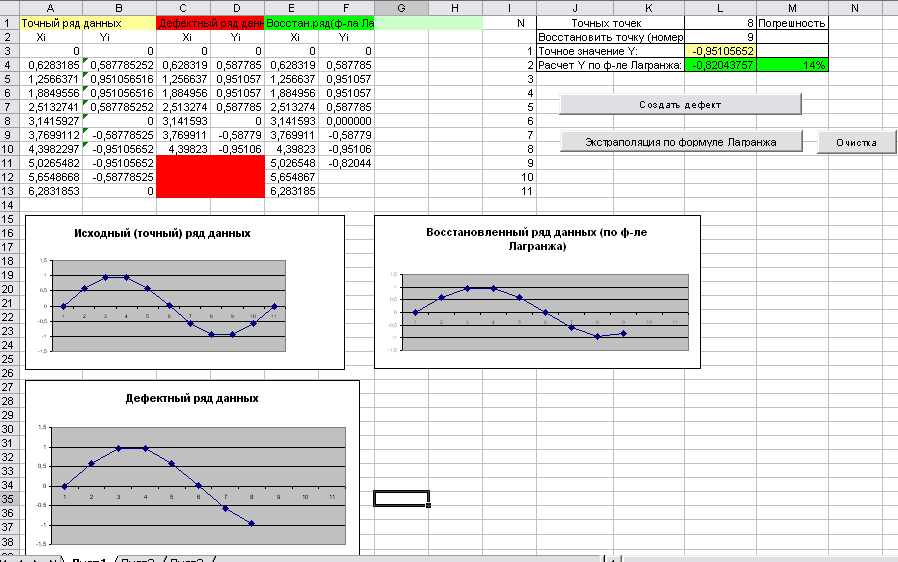
Лабораторная работа №2
«АППРОКСИМАЦИЯ».
Цель работы: научиться применять формулы метода наименьших квадратов для функционального описания массива экспериментальных данных.
Порядок работы
- Подготовить исходный «массив экспериментальных данных» на листе Excel в виде 2-х столбцов (А3:В13) для X и Y. Где X – аргумент, изменяющийся с некоторым шагом, Y – линейная функция от Х ( Y=Aточн*X+Bточн). Добавить в столбец Y случайные отклонения (например, за счет погрешности измерений), и записать этот «дефектный» массив в столбцы C3:D13. Представить массивы на графиках.
- Набрать программу для расчета коэффициентов линейной зависимости Yрасч=Aрасч*Х+Bрасч по формулам метода наименьших квадратов.
- Вычислить по этим коэффициентам расчетное значение Y и занести в столбцы (E3:D13). Под столбцом разместить кнопки «Пуск» и «Очистка». Результаты представить в виде графика на той же диаграмме.
- Сделать проверку «равноудаленности» построенной расчетной линии от экспериментальных точек визуально и с помощью «линии тренда» (в меню Excel).
- Взять исходные данные из предыдущей лабораторной работы (Экстраполяция), поместить их на место «дефектного» массива и повторить расчет. Рассчитать погрешность восстановления «потерянной» точки и сделать выводы.
Расчетные формулы
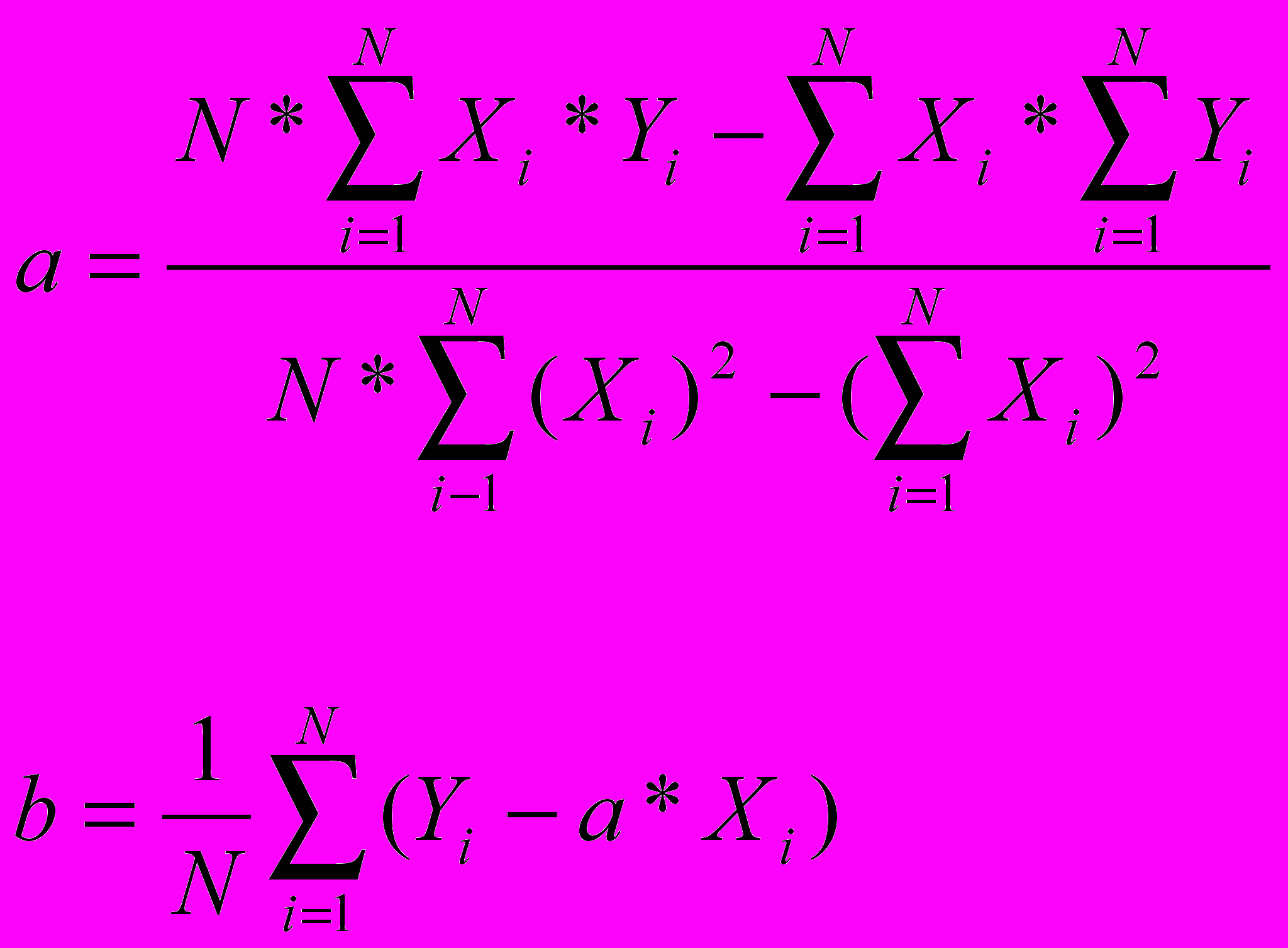
Пример работы программы
s1 = 0
s2 = 0
s3 = 0
s4 = 0
For i = 0 To N
s1 = s1 + x(i) * y(i)
s2 = s2 + x(i)
s3 = s3 + y(i)
s4 = s4 + x(i) 2
Next i
a = ((N + 1) * s1 - s2 * s3) / ((N + 1) * s4 - s2 2)
Worksheets(1).Cells(22, 2).Value = a
s5 = 0
For i = 0 To N
s5 = s5 + (y(i) - a * x(i))
Next i
b = s5 / (N + 1)
Worksheets(1).Cells(23, 2).Value = b
For i = 0 To N
y(i) = a * x(i) + b
Worksheets(1).Cells(i + 3, 5).Value = x(i)
Worksheets(1).Cells(i + 3, 6).Value = y(i)
Next i
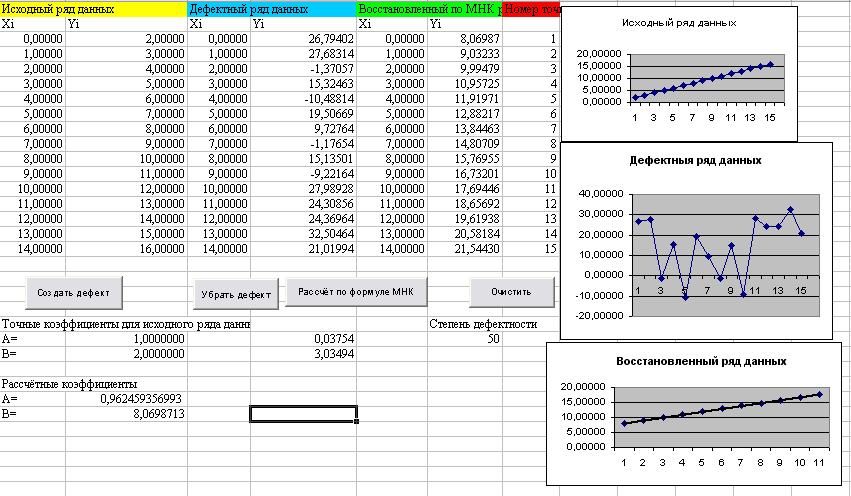
Индивидуальное задание
| Aточн | -11 | 12 | 11 | -12 | -13 | -13 | 10.5 | -10.5 | -12 | -18 |
| Bточн | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 2 | 1 |
| Степень дефектности | Расчеты значений Аи В | Погрешность |
| 5 | А=1,0298581 В=1,1095026 | А=2,99% В=44,52% |
| 4 | А=1,1682917 В=0,3837320 | А=16,83% В=80,81% |
| 50 | А=1,0689 В=1,6551724 | А=6,9% В=17,24% |
Лабораторная работа №3
«ИНТЕГРИРОВАНИЕ»
Цель работы: научиться применять формулы численного интегрирования для вычисления площадей под функционально или таблично заданными экспериментальными зависимостями.
Порядок работы
- Подготовить исходный «массив экспериментальных данных» на листе Excel в виде 2-х столбцов (А3:В13) для X и Y. Где X – аргумент, изменяющийся с некоторым шагом, Y – некоторая функция от Х, описывающая уравнение границы заданной фигуры (рекомендуется четверть круга) и представить этот массив на графике.
- Набрать программу вычисления площади заданной фигуры по формулам: 1)прямоугольников, 2)трапеций, 3)Симпсона. Результаты записать соответственно в ячейки: C1, D1, E1. Для запуска расчета по каждой формуле разместить на листе кнопки «Пуск» и одну кнопку общего сброса.
- Для определения погрешностей вычислить площадь заданной фигуры аналитически и записать ее в ячейки C2, D2, E2. Набрать программу расчета погрешности и занести результаты в ячейки C3, D3, E3. Сделать вывод.
- Для той же фигуры на листе 2 подготовить в 2 раза больший массив исходных данных с в 2 раза меньшим шагом (A3:B23).
- Для новых данных повторить пп. 2) и 3) и сделать вывод.
Расчетные формулы
Уравнение границы четверти круга (для 10 точек):
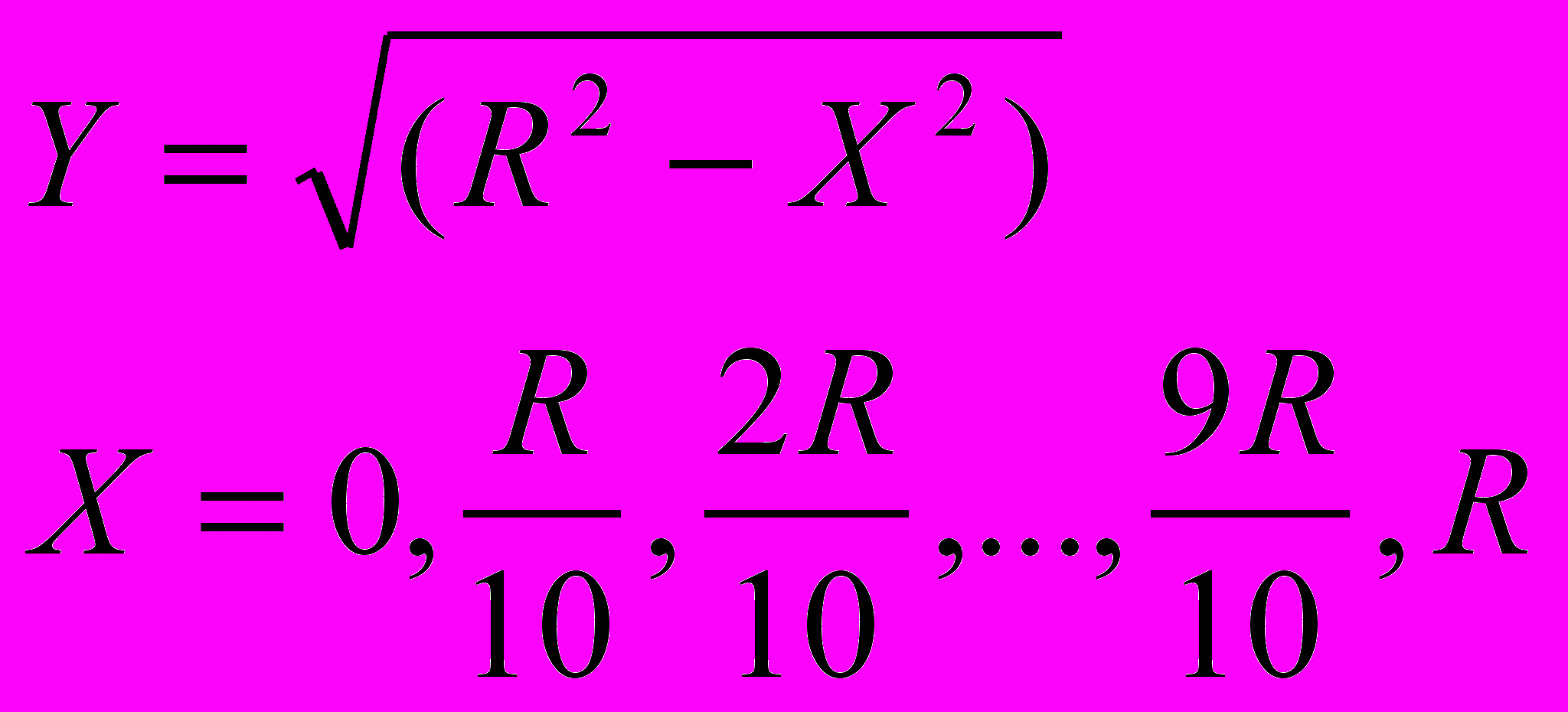
Формулы прямоугольников:
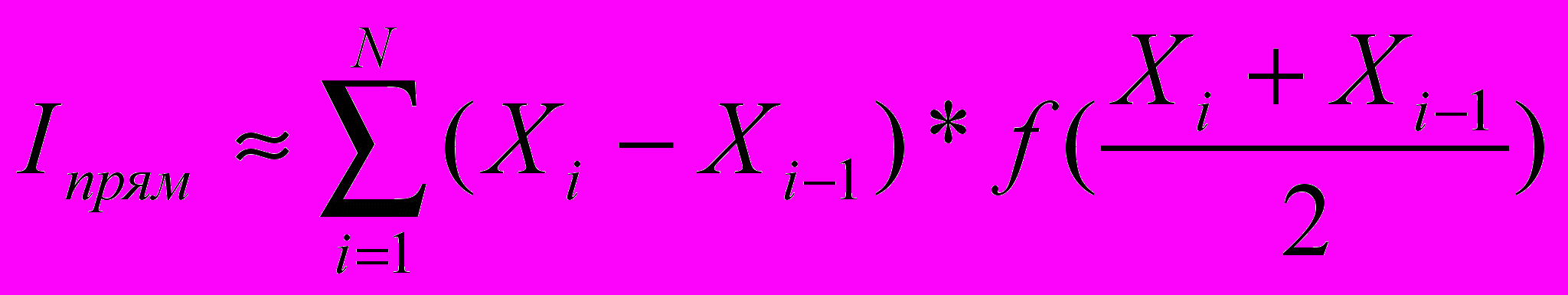
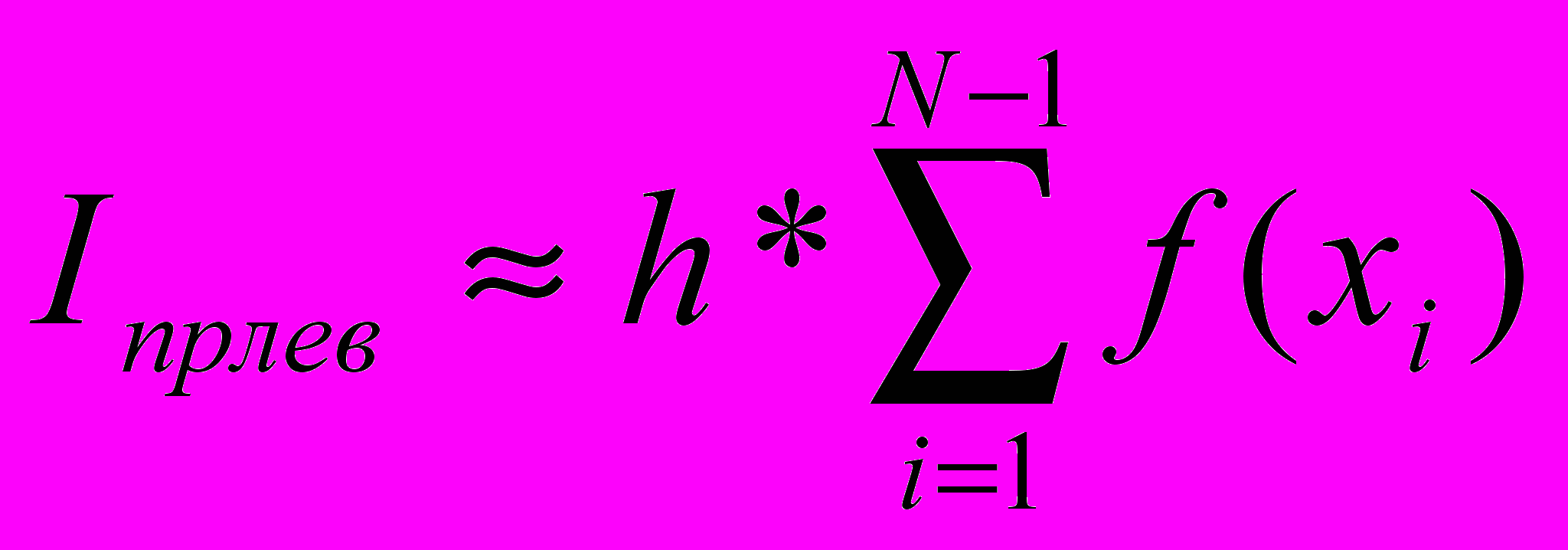
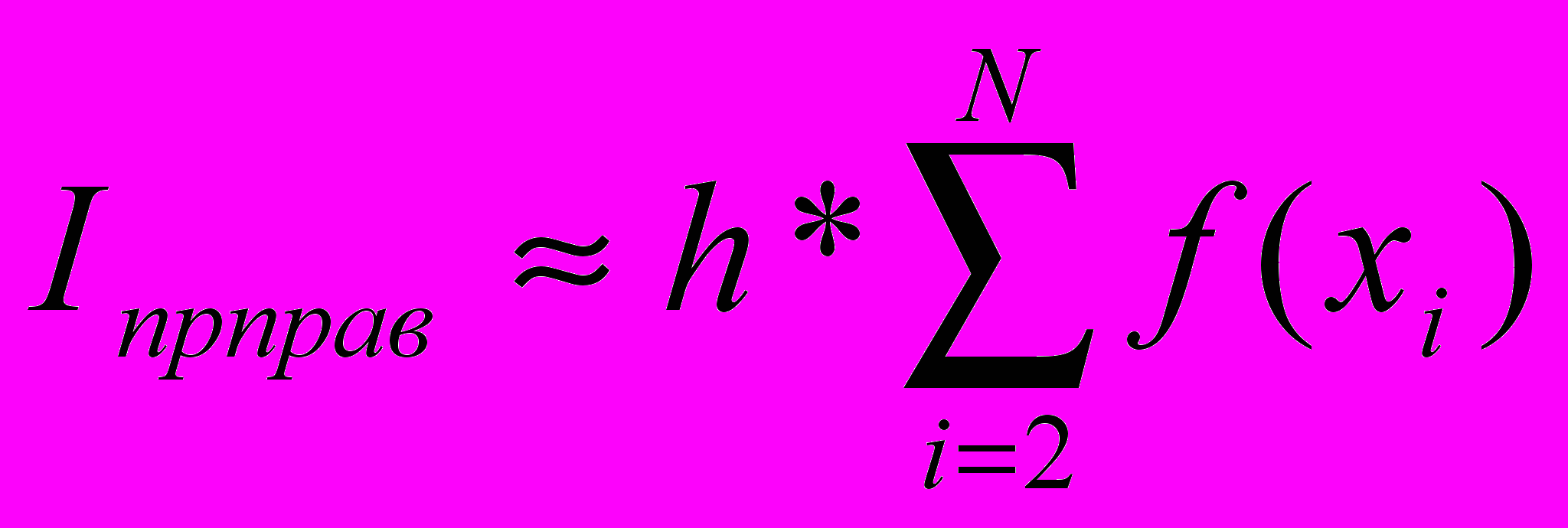
Формула трапеций:
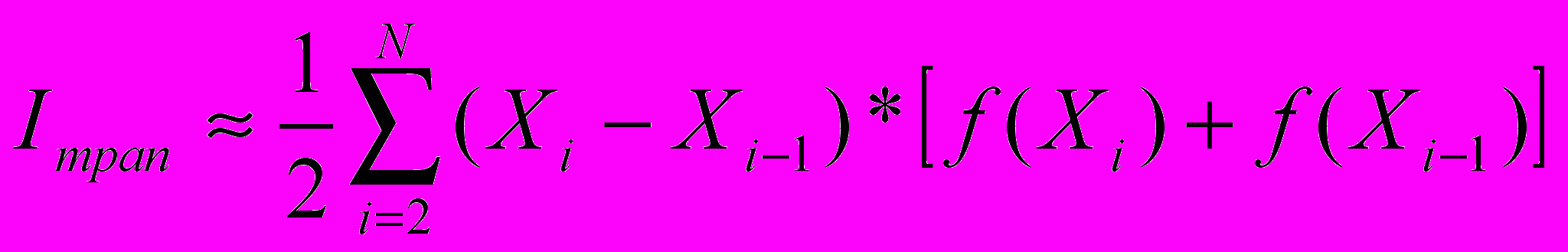
Формула Симпсона:
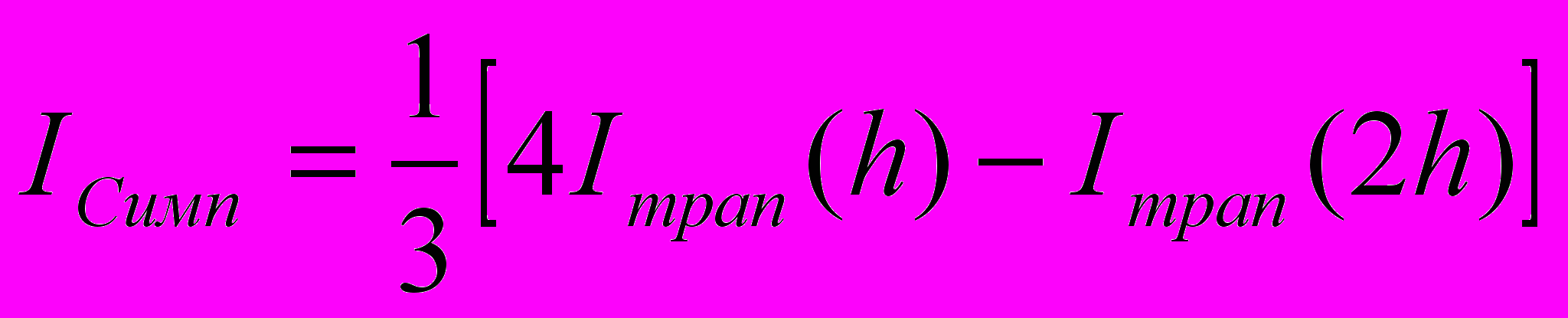
Пример программы
Private Sub Кнопка2_Щелкнуть()
'расчет по формуле трапеций
N = Worksheets(1).Cells(2, 11).Value
For i = 0 To N
x(i) = Worksheets(1).Cells(i + 3, 1).Value
y(i) = Worksheets(1).Cells(i + 3, 2).Value
Worksheets(1).Cells(i + 3, 5).Value = x(i)
Worksheets(1).Cells(i + 3, 6).Value = y(i)
Next i
s = 0
For i = 1 To N - 1
s = s + Abs((x(i) - x(i - 1)) * y(i))
Next i
s = s + y(0) * (x(1) - x(0)) / 2 + y(N) * (x(N) - x(N - 1)) / 2
Worksheets(1).Cells(16, 6).Value = s
stochn = Worksheets(1).Cells(16, 2).Value
Pogr = Abs((s - stochn) / s)
Worksheets(1).Cells(17, 6).Value = Pogr
End Sub
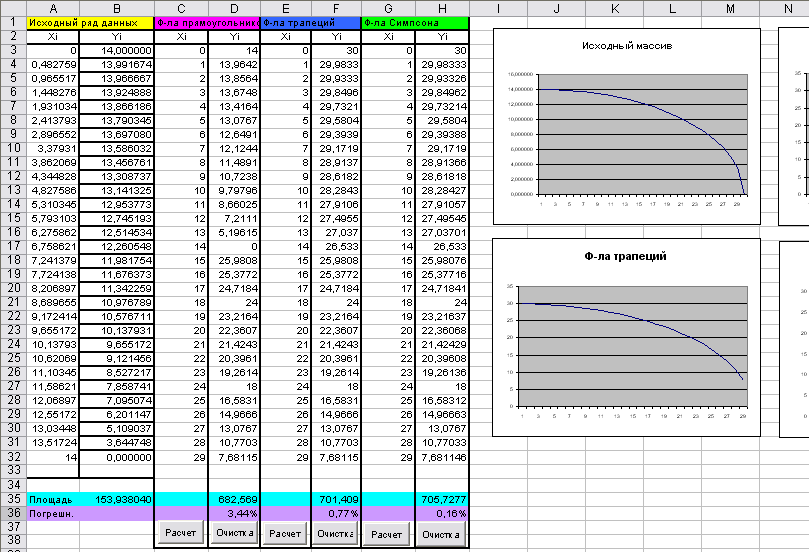
Выводы и результаты
Часть А
| Количество точек в исходном ряде данных | 7 | 9 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
| Радиус | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Радиус | Кол-во точек | Ф-ла треугольников | Ф-ла трапеций | Ф-ла Симпсона |
| 14 | 15 | 3,44% | 0,77% | 0,16% |
| 14 | 14 | 5,26% | 0,71% | 0,28% |
| 14 | 13 | 8,64% | 4,09% | 3,78% |
| 14 | 12 | 13,32% | 8,77% | 7,9% |
При увеличении числа точек процент погрешности уменьшается. Расчет более точен.
Часть Б
Шаг =14/29
| Радиус | Кол-во точек | Ф-ла треугольников | Ф-ла трапеций | Ф-ла Симпсона |
| 14 | 30 | 3,44% | 0,77% | 0,16% |
| 14 | 29 | 2,43% | 0,24% | 0,18% |
При расчете необходимо использовать формулу Симпсона, так как при ней погрешность расчетов минимальна.
Лабораторная работа №4
«Поиск особых точек»
Цель работы: научиться применять формулы итерационного поиска нулей функционально заданных экспериментальных зависимостей.
Порядок работы
- По заданной функции Y=Ao+A1*X+A2*X*X (коэффициенты взять по номеру варианта индивидуального задания) подготовить массив исходных экспериментальных данных на листе Excel в виде 2-х столбцов (А3:В13) для X и Y. Где X – аргумент, изменяющийся с некоторым шагом, Y – заданная функция. Представить его на графике.
- Визуально выбрать пары точек, между которыми функция проходит через 0 (пересекает ось Х).
- Набрать программу «деление отрезка пополам»(дихотомии) и применить ее для каждой выбранной в п. 2) пары точек с заданной на листе погрешностью.
- Выполнить проверку, подставив найденные Х-ы в заданную функцию.
- Уменьшить заданную погрешность, повторить пп. 3), 4) и сделать вывод.
- Дополнительное задание: в п.3 заменить формулы метода дихотомии на формулы метода хорд и повторить расчет. Сравнить с методом дихотомии по погрешности и количеству шагов.
Расчетные формулы
Метод дихотомии
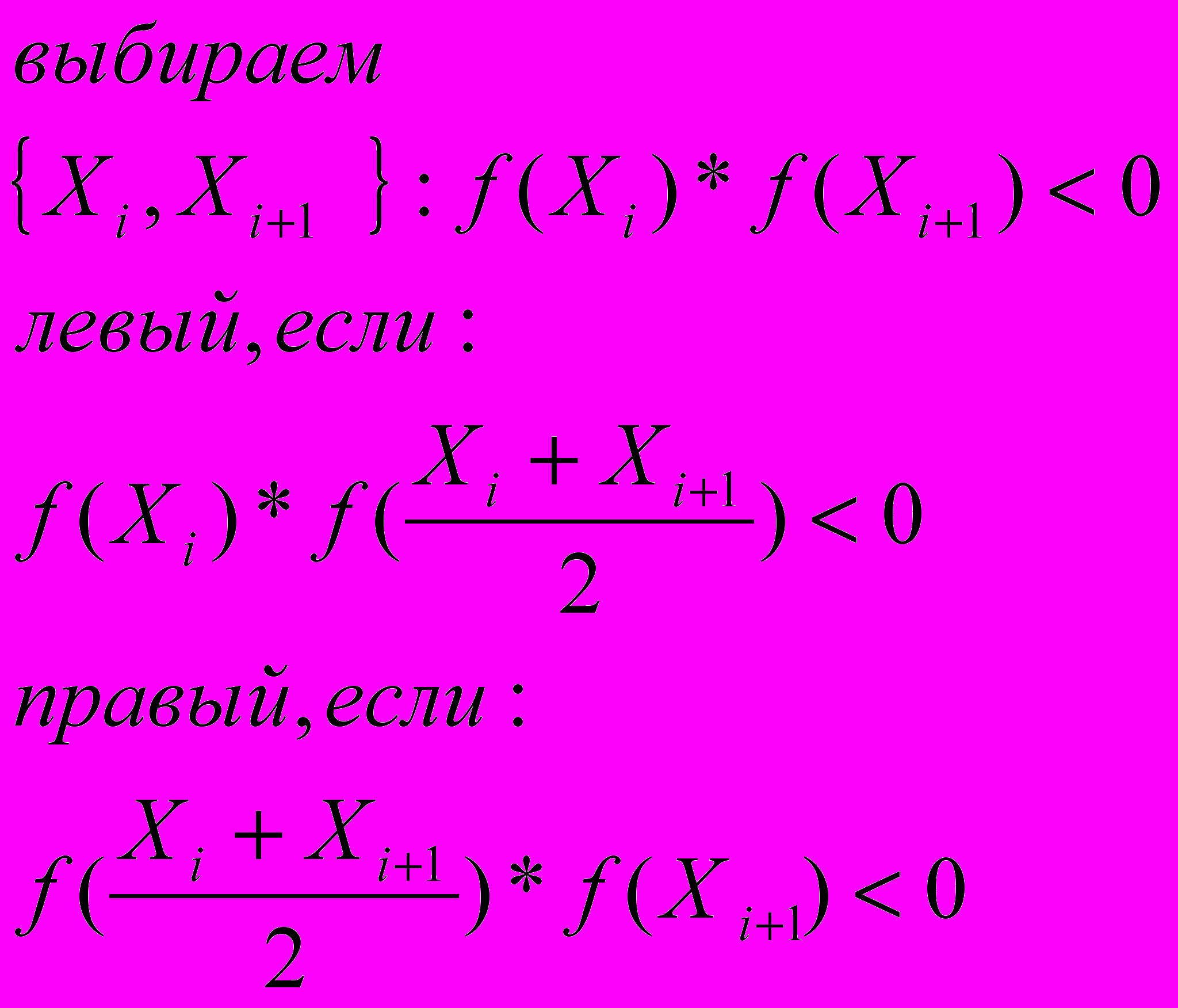
Метод хорд-секущих
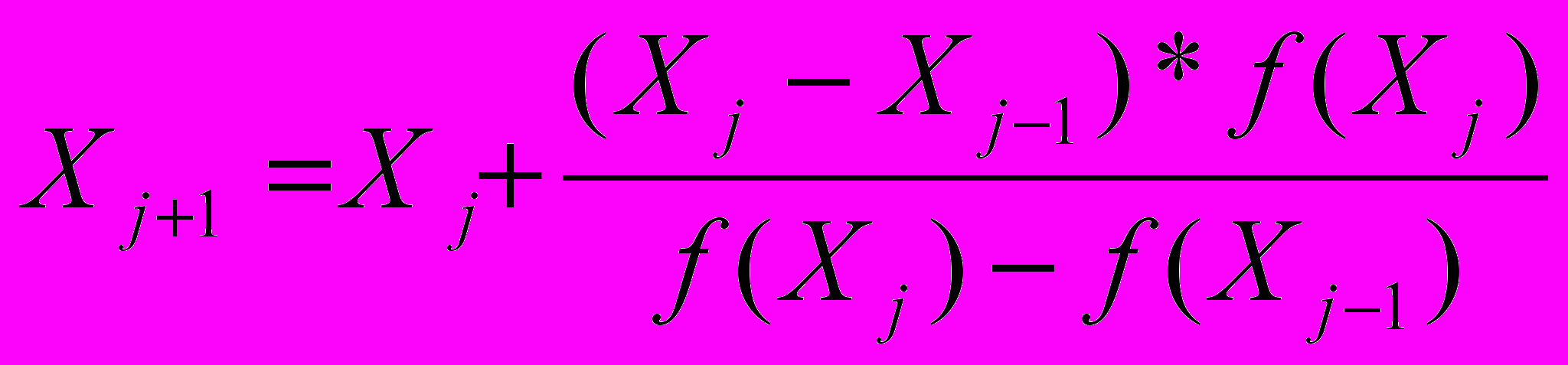
Пример работы программы
Nleft = Worksheets(1).Cells(3, 3).Value
Nright = Worksheets(1).Cells(3, 4).Value
If Nleft >= Nright Then
MsgBox "неправильно задана пара точек"
Exit Sub
End If
Worksheets(1).Cells(4, 3).Value = Worksheets(1).Cells(Nleft + 2, 1).Value
Worksheets(1).Cells(4, 4).Value = Worksheets(1).Cells(Nright + 2, 1).Value
Xleft = Worksheets(1).Cells(4, 3).Value
Xright = Worksheets(1).Cells(4, 4).Value
Xpol = (Xleft + Xright) / 2
Fpol = FUNC(Xpol)
While Abs(Fpol) > eps
Xleft = Worksheets(1).Cells(4, 3).Value
Xright = Worksheets(1).Cells(4, 4).Value
Xpol = (Xleft + Xright) / 2
Fleft = FUNC(Xleft)
Fright = FUNC(Xright)
Fpol = FUNC(Xpol)
If Fleft * Fpol < 0 Then
Worksheets(1).Cells(4, 3).Value = Xleft
Worksheets(1).Cells(4, 4).Value = Xpol
Else
Worksheets(1).Cells(4, 3).Value = Xpol
Worksheets(1).Cells(4, 4).Value = Xright
End If
Wend
Worksheets(1).Cells(15, 3).Value = Xpol
Worksheets(1).Cells(15, 4).Value = Fpol
Case 3
'метод хорд
Nnach = Worksheets(1).Cells(3, 5).Value
Xpred = Worksheets(1).Cells(Nnach + 2, 1).Value
Xtek = Xpred + 100 * eps
Ftek = FUNC(Xtek)
Fpred = FUNC(Xpred)
Worksheets(1).Cells(4, 5).Value = Xtek
While Abs(Ftek) > eps
Ftek = FUNC(Xtek)
Fpred = FUNC(Xpred)
Xsled = Xtek - ((Xtek - Xpred) * Ftek) / (Ftek - Fpred)
Xpred = Xtek
Xtek = Xsled
Worksheets(1).Cells(4, 5).Value = Xtek
Wend
Worksheets(1).Cells(15, 5).Value = Xtek
Worksheets(1).Cells(15, 6).Value = Ftek
Case Else
MsgBox "Ошибка"
End Select
End Sub
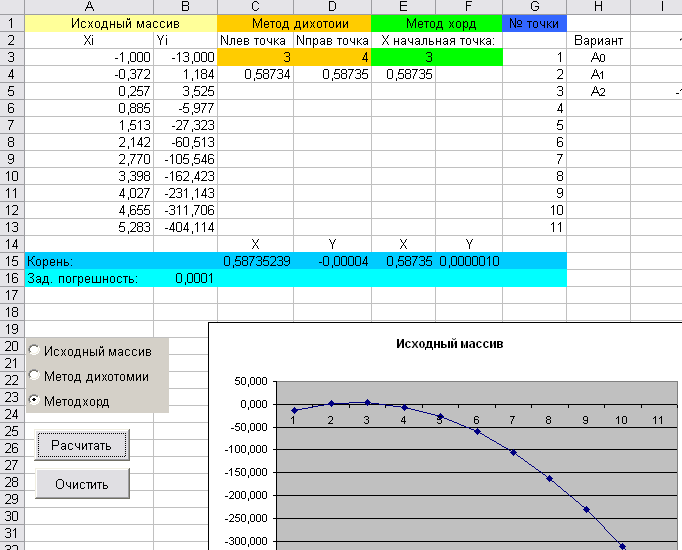
Индивидуальные задание
Функция f(X) = Ao + A1*X + A2*X2
| Ao= | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A1= | 3 | 2 | 1 | 2 | 3 | 4 | 1 | 2 | 5 | 6 |
| A2= | -15 | -8 | -9 | -15 | -14 | -16 | -12 | -19 | -21 | -22 |
Вывод: я научилась применять формулу интеграционного поиска нулей.
Лабораторная работа №5
«БАЗЫ ДАННЫХ»
Цель работы: научиться строить связанные таблицы данных предметной области в среде реляционной СУБД (MS Access), заполнять эти таблицы, формировать по ним запросы и отчеты.
Порядок работы
- Разработать модель данных предметной области, например, - «Учебный процесс в ВУЗе» (см. лекцию). Определить перечень таблиц данных, например, - «предметы», «преподаватели», «группа», «студенты», «успеваемость».
- С помощью Мастера БД создать эти таблицы в MS Access и связать их по ключевым данным (см. Пример). Контроль осуществлять по диагностике целостности данных.
- Создать простые и подчиненные формы для заполнения всех таблиц. С помощью этих форм занести во все таблицы по 3-4 записи (придумать самим, учесть будущие запросы).
- К заполненным таблицам с помощью Мастера БД сформировать запросы в соответствии с выданным преподавателем индивидуальным заданием.
- Экспериментально проверить работу запросов и форм.
- Пополнить таблицы и повторить п. 5, сделать вывод.
Расчетные формулы
Нет
Пример программы
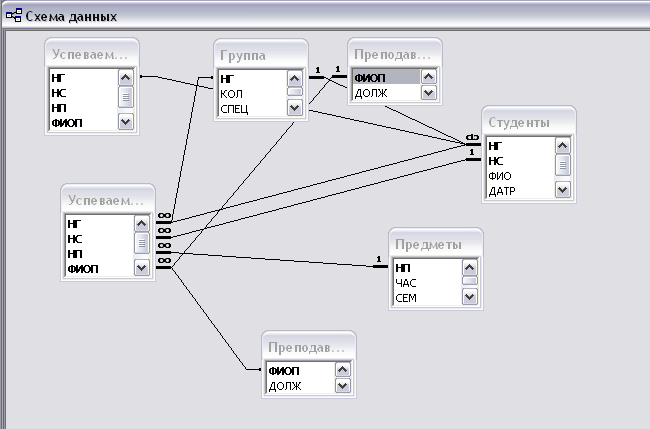

Вывод: в ходе работы была создана база данных, я ознакомилась с возможностями программы Microsoft Access.
Разработала ст. гр. 2Б53 Гуцалюк Е.К.
Принял преп. Хамухин А.А.

