Лабораторная работа №3 Численные методы решения скалярных уравнений

Вид материала

Лабораторная работа

Подобный материал:

• Методические материалы для студентов, 104.19kb.
• «Численные методы», 64.5kb.
• Секция “Краевые задачи механики сплошной среды, численные и численно-аналитические, 67.85kb.
• Аннотация рабочей программы дисциплины «Численные методы решения инженерных задач», 29.99kb.
• Рабочая программа по разделу «Численные методы в строительстве», 71.92kb.
• Рабочая программа учебной дисциплины численные методы Направление подготовки 210400, 273.35kb.
• Реферат по математике. На тему: «основные методы решения систем уравнений с двумя переменными», 140.92kb.
• Пример оформления тезисов докладов сравнение решений некоторых интегральных уравнений, 13.4kb.
• Реализация алгоритмов решения задач газовой динамики на многопроцессорных вычислительных, 9.14kb.
• Лабораторная работа 1 Методы решения задач линейной алгебры, 32.21kb.

Лабораторная работа №3

Численные методы решения скалярных уравнений

Цель работы: сформировать у студентов представление о применении уравнений в различных областях деятельности, привить знания об основных этапах решения уравнения, выработать навыки использования различных методов для уточнения корня уравнения и выбора того или иного программного средства для проверки правильности найденного результата.

1. Метод хорд.
   

Пример. Решить уравнение 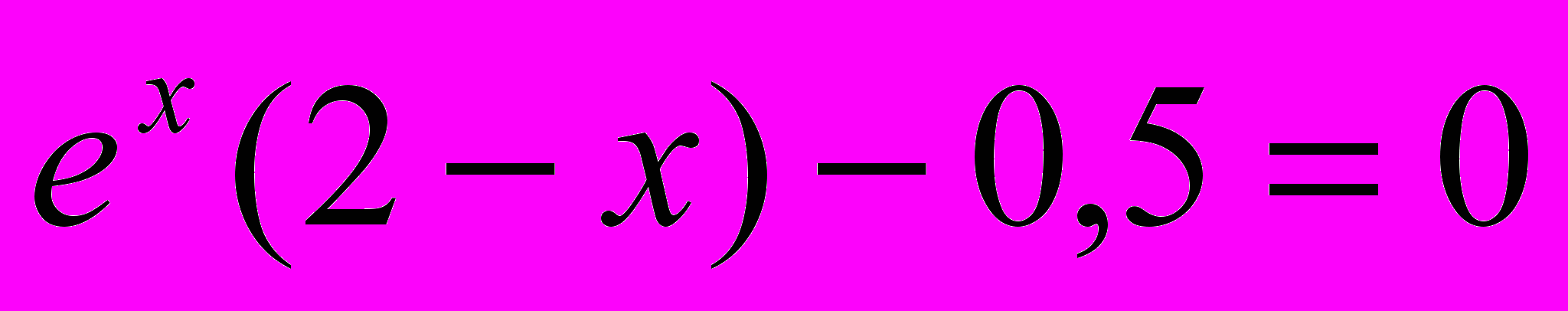методом хорд с точностью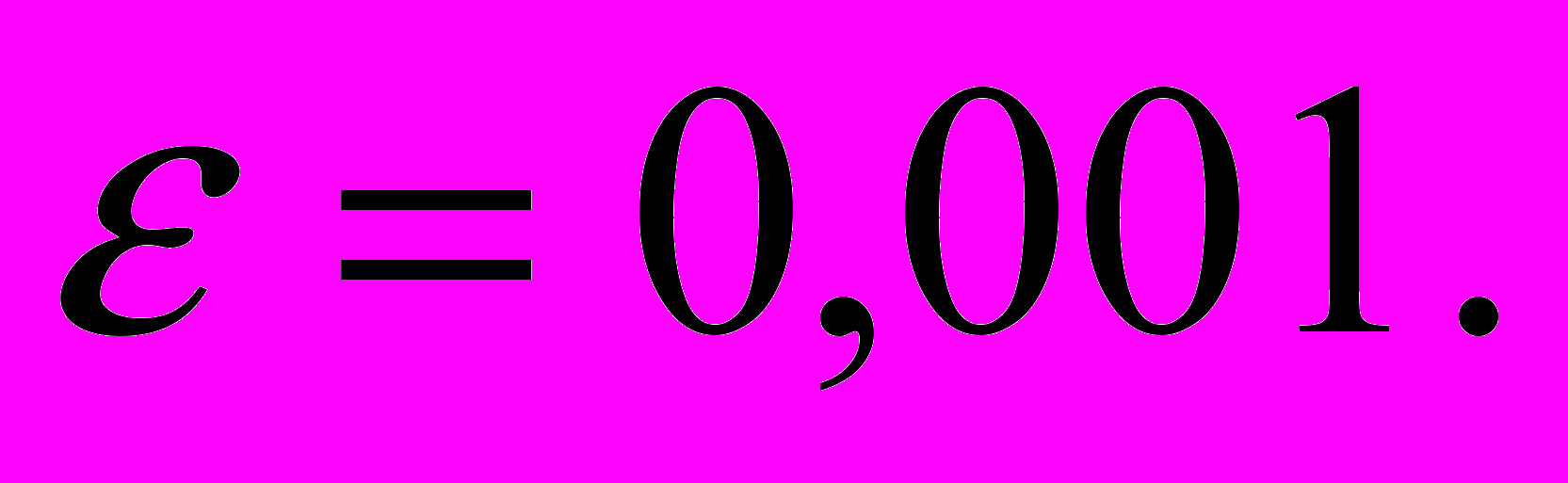

Решение.

1. Отделяем корни. Этот этап вычислений осуществляется с помощью аналитического или графического метода. После того как корень, подлежащий уточнению, отделен, за начальное приближение может быть выбрана любая точка [a,b] (начало отрезка, его середина и т.д.).Воспользуемся графическим методом. Построим график функции и найдем точки пересечения его с осью 0x.
   
   
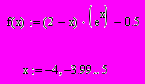
   Получили два интервала [-3;-2], [1,5;2,5]. Интервал, в котором мы будем уточнять корень – [1,5;2,5].
   
2. Уточняем корни. Находим первую производную функции f(x)= :
   
   
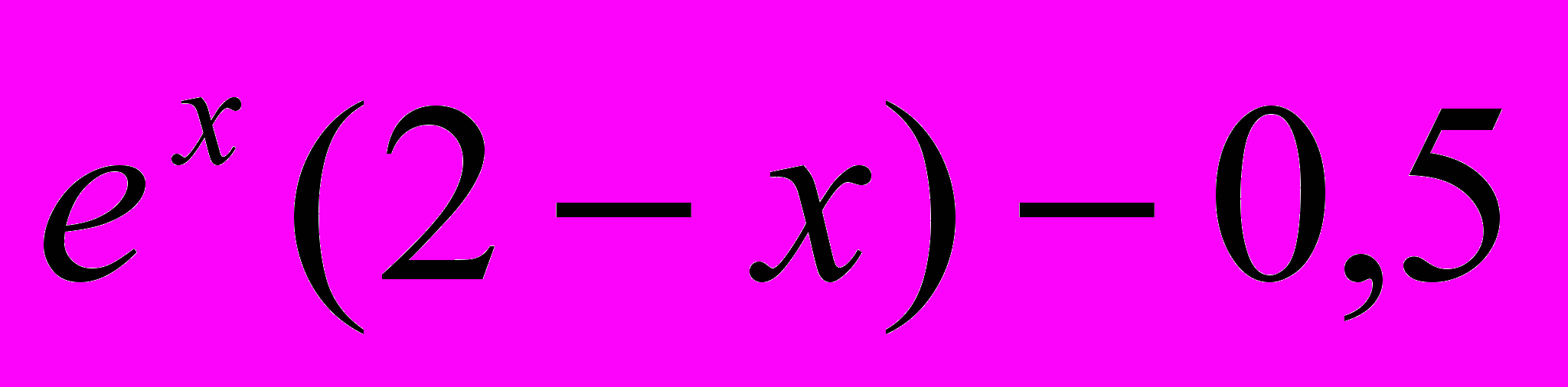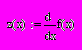
3. Определяем знаки функции f(x) на отрезке [1,5;2,5].
   
   Значит, на данном отрезке действительно существует корень нашего уравнения.
   
4. Строим последовательность значений с использованием рекуррентной формулы метода хорд и проанализируем результаты вычисленных значений последовательности x_n. Для этого рассмотрим значение функции dz(x_n) – эта величина является критерием достижения заданной точности
   
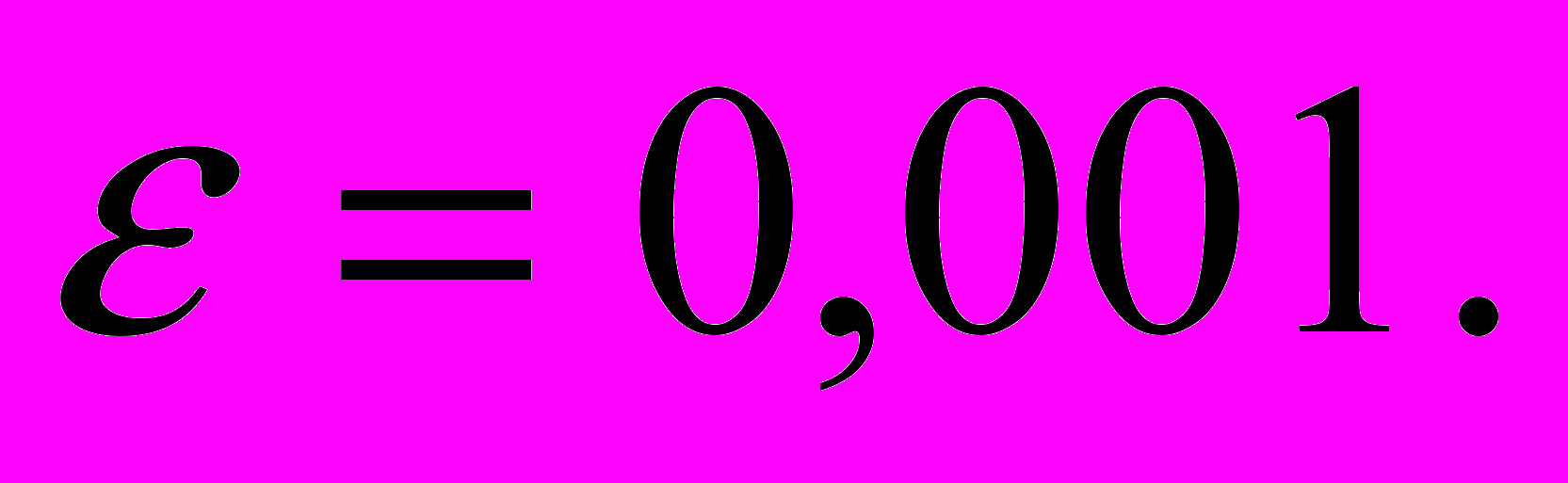
   Начиная с n=8, значения x_n удовлетворяют критерию достижения заданной точности, значит, x₈=1,927 является решением данного уравнения.
   
5. Создаем функцию, реализующую вычисления корня уравнения 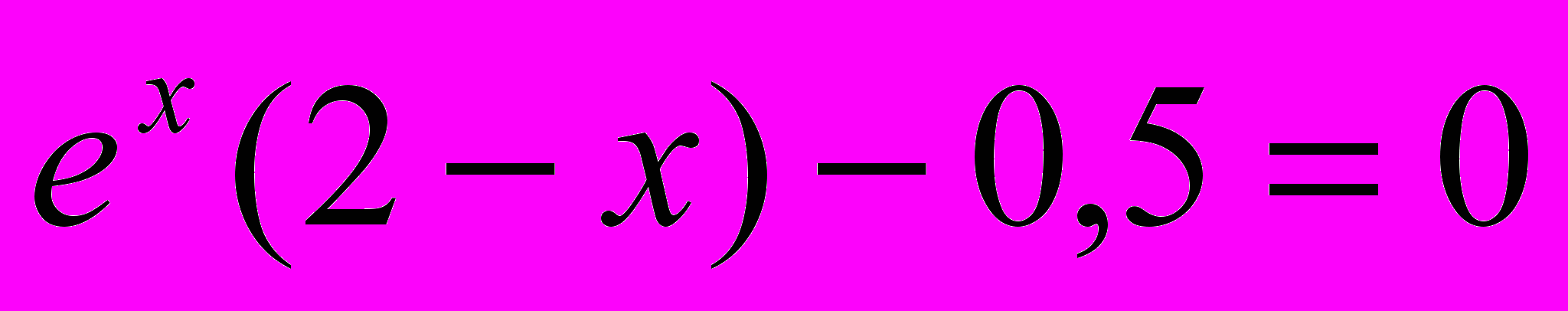на отрезке [1,5;2,5] с точностью методом хорд. Решением будет являться число 1,927, получившееся на третьем шаге решения.
   
   
   

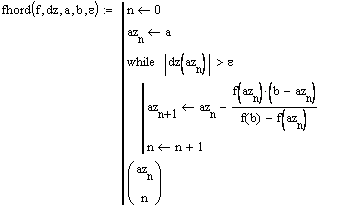
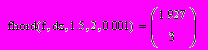
6. Проверяем решение
   
   

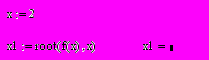
Ответ: корень уравнения по методу хорд равен 1,927 с точностью 0,001, найденный на третьем шаге.

2. Метод касательных
   

Пример: Вычислить методом касательных корень уравнения 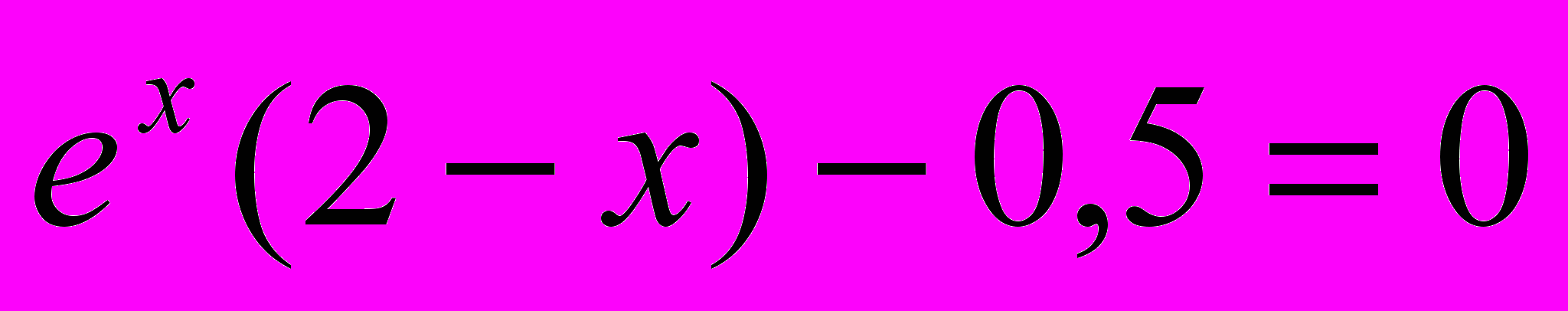на отрезке [1,5;2,5] с точностью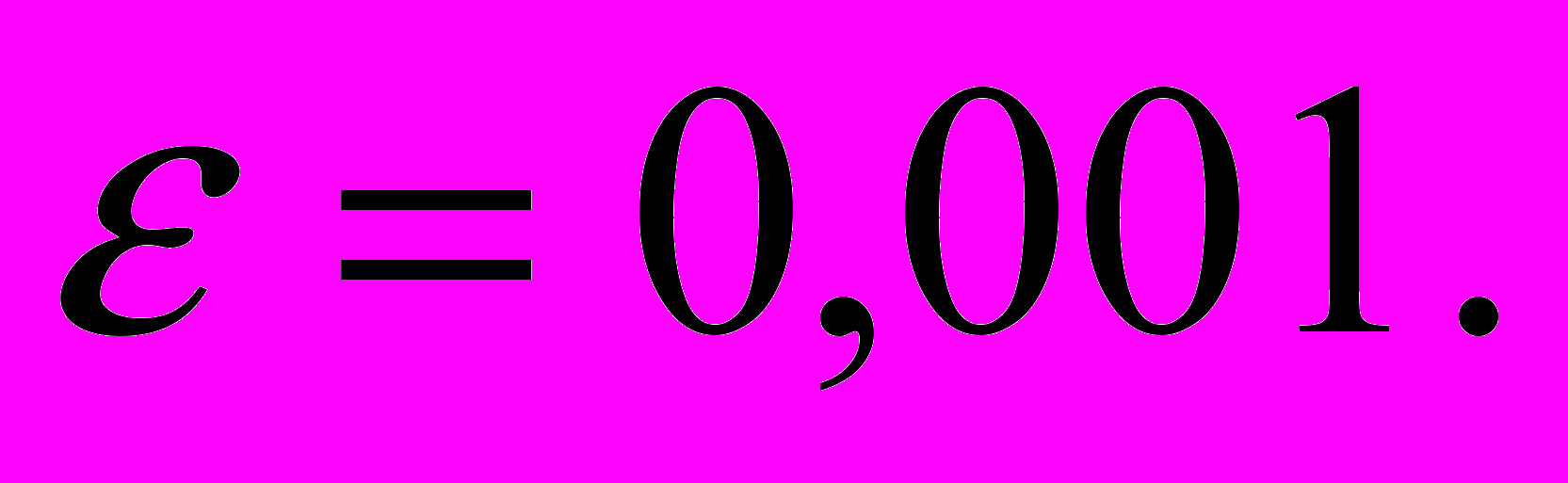

Решение.

1. Отделяем корни уравнения.
   
2. Определяем неподвижную точку. Для этого определяем знаки функции и второй производной на отделенном интервале [1,5;2,5]. Для этого составим функцию, проверяющую условие неподвижности точки
   

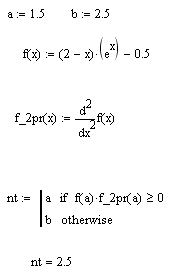
Тогда подвижной точкой будет точка a=1,5.

3. Вычисляем значение итерационной последовательности с использованием рекуррентной формулы метода касательных
   
   
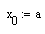
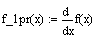
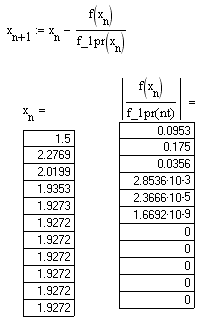
   Анализируя полученные значения для достижения критерия заданной точности, можно сказать, что решением уравнения будет значение x4=1,927 при n=4, т.к. 2,36710^-5<0,001.
   
4. Создаем функцию, реализующую метод касательных (аналогично методу хорд).
   
5. Проверяем полученные результаты.
   

Замечание: В пакете Mathcad имеется еще несколько функций, позволяющих решать уравнения, например функция solve, вызываемая с панели Symbolic.

3. Метод простой итерации
   

Пример: Решить уравнение 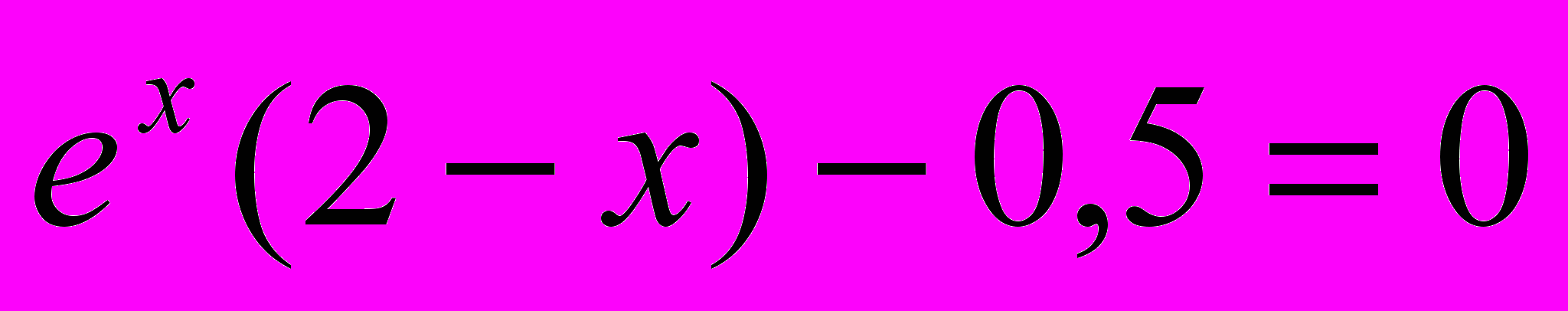методом простой итерации с точностью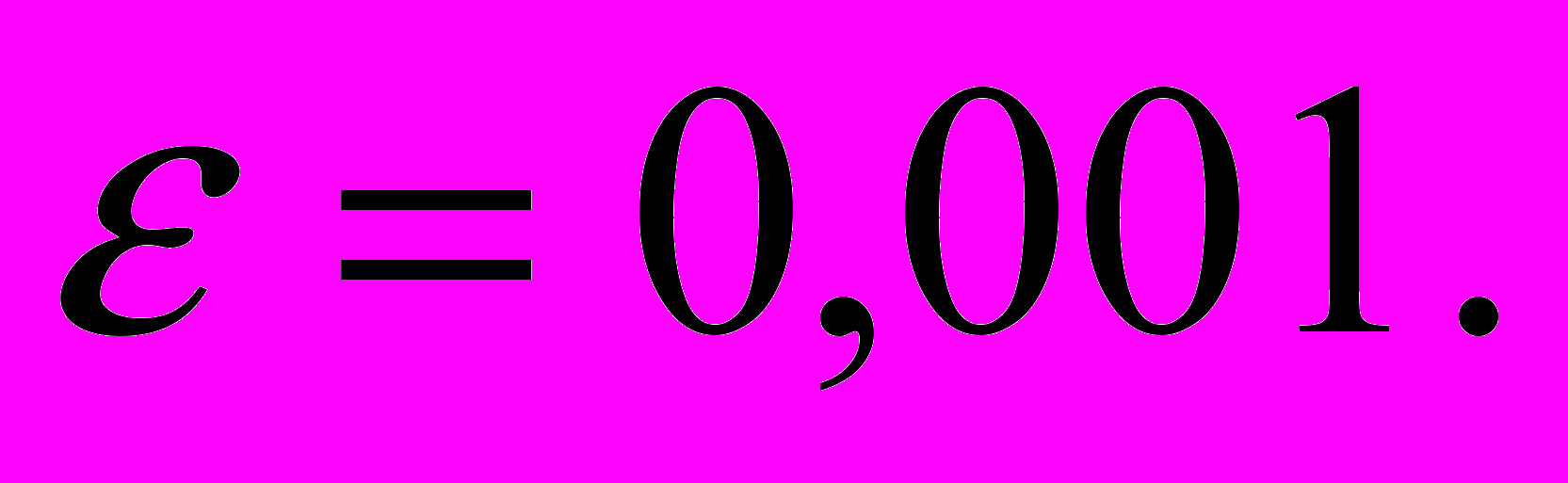

Решение:

1. Отделяем корни уравнения.
   
2. Приводим исходное уравнение к виду x=f(x).
   Заменим уравнение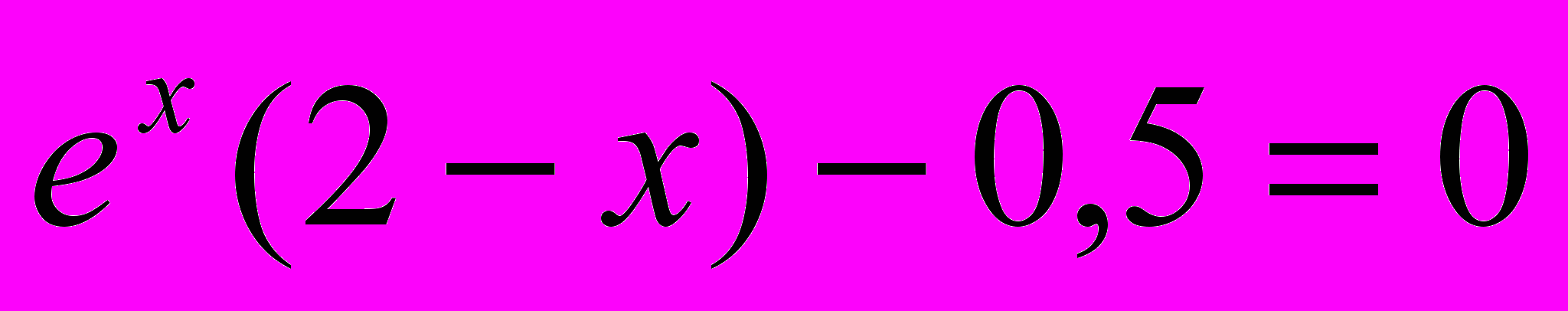 уравнением вида f(x)=x-mF(x). Здесь величина m должна быть подобрана так, чтобы для функции f(x) выполнялись условия теоремы 2.2 о достаточном условии сходимости итерационного процесса.
   Производная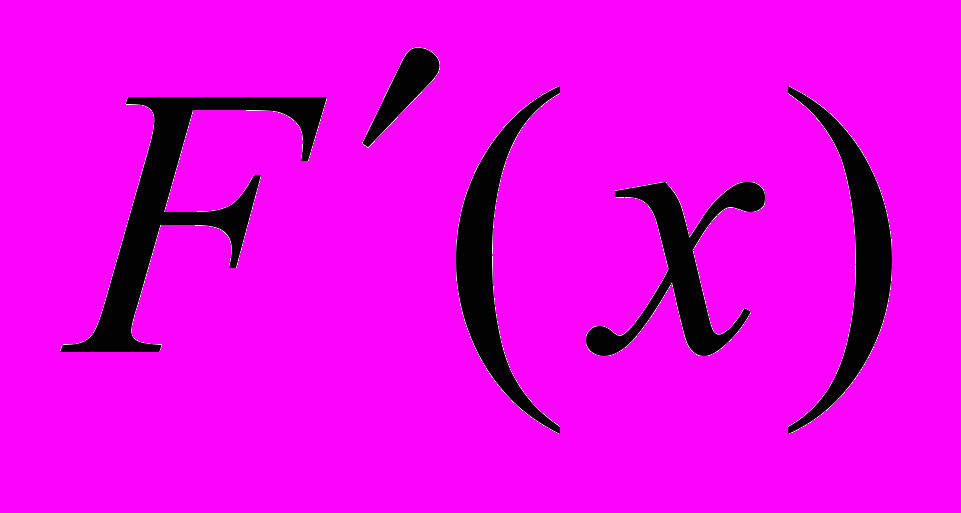 на отрезке [1,5;2,5] отрицательна, следовательно, функция F(x) на этом отрезке монотонно убывает. Ее значения представлены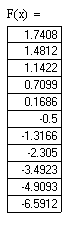
   
   
3. Тогда значения функции f(x) будут равны:
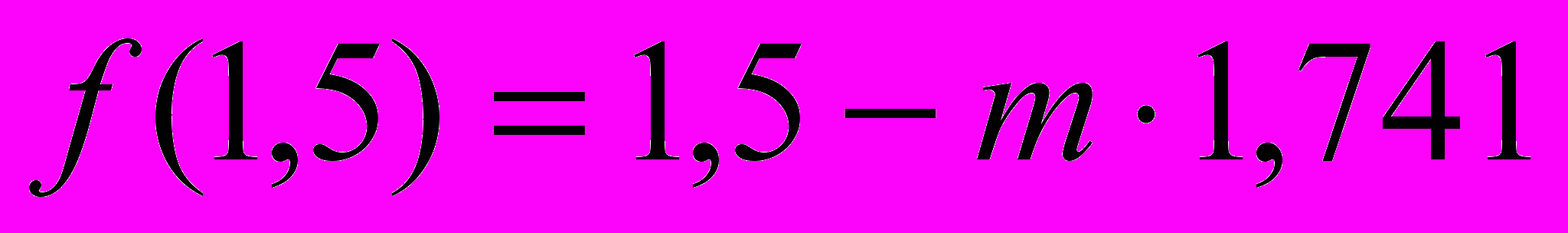   и .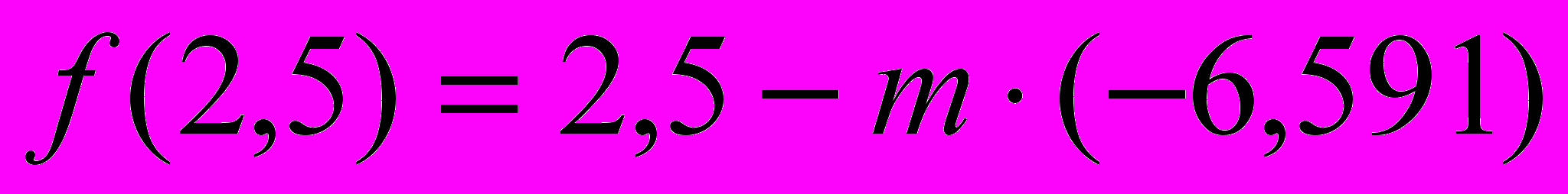
   Учитывая, что монотонность функции f(x), из последних равенств легко заметить, что условие 2 теоремы будет заведомо выполнено, если m – правильная отрицательная дробь
   
   

Поскольку производная 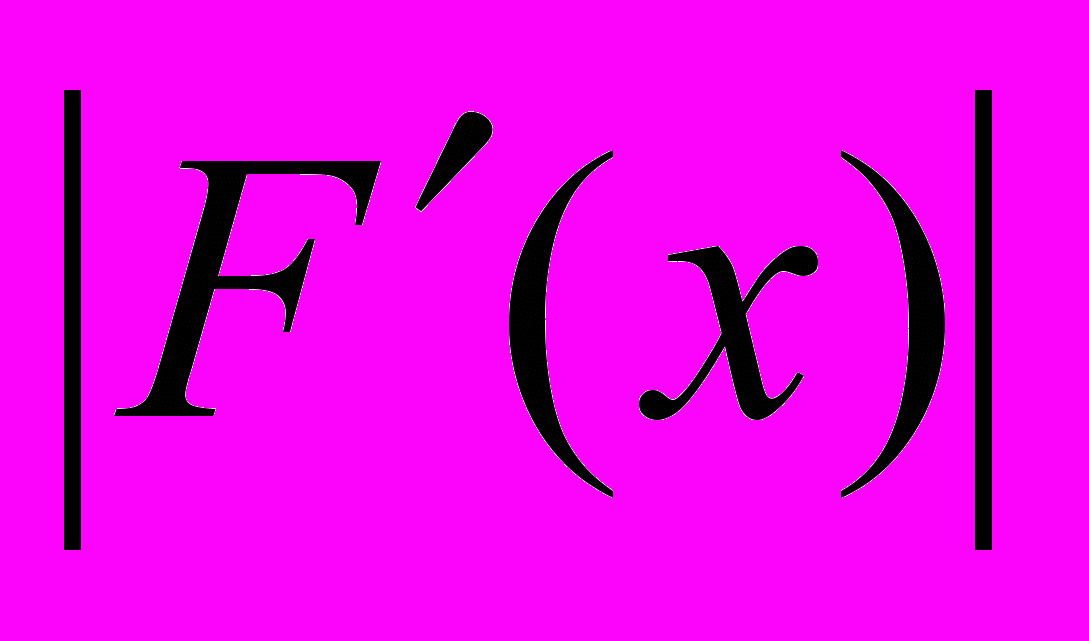на концах интервала [1,5;2,5] положительна (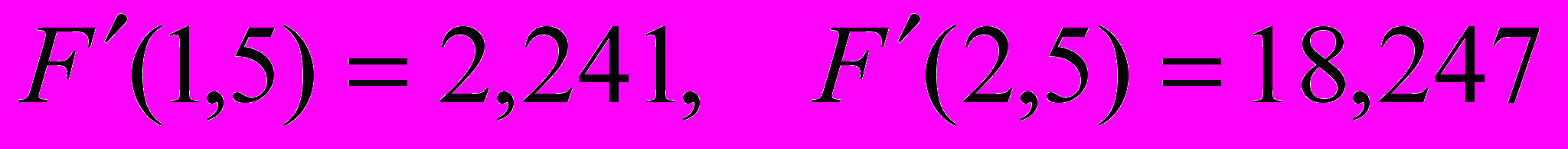) и монотонно возрастает, ее модуль имеет максимум на правом конце отрезка. Тогда, если за m принять число , то условие 2 теоремы выполнено.

Для выполнения условия 3 теоремы 2.2 найдем производную преобразованной функции и ее значения на концах отрезка [1,5;2,5].



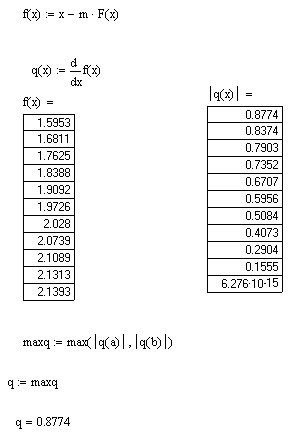
3. Вычисляем значения итерационной последовательности x_n=f(x_n-1). В качестве начального приближения возьмем, например начало отрезка, точку x₀=1,5.

Критерием достижения заданной точности при решении уравнения методом простой итерации является величина A, равная



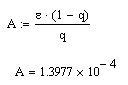
4. Строим итерационную последовательность. Один метод описан в лекции.

Второй метод:



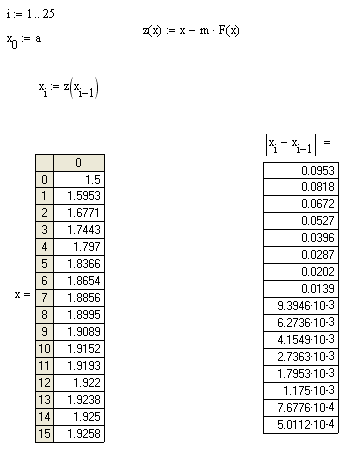
Для 24 приближения получили, что |x₂₃–x₂₄|<1,39810^-5x₂₃=1,92718 является приближенным решением нашего уравнения.

Вопросы по теме

1. Что означает решить уравнение?
   
2. Каковы этапы решения уравнения с одной неизвестной численными методами?
   
3. Какие существуют методы решения уравнения с одной неизвестной?
   
4. В чем заключается этап отделения корней при использовании численных методов решения уравнения?
   
5. Суть метода хорд. Графическая интерпретация метода.
   
6. Суть метода касательных. Графическая интерпретация метода.
   
7. Суть метода простой итерации.
   
8. Какое уравнение можно решать методом простой итерации?
   
9. каковы достаточные условия сходимости итерационного процесса при решении уравнения x=f(x) на отрезке[a,b], содержащего корень, методом простой итерации?
   
10. Какое условие является критерием достижения заданной точности при решении уравнения x=f(x) методом хорд, касательных, итераций?
    
11. Записать формулу нахождения значений последовательности при решении уравнения методом: хорд, касательных.
    
12. Как строится итерационная последовательность точек при решении методом простой итерации?