Программа дисциплины по кафедре Автоматики и системотехники Теория автоматического управления

Вид материала

Программа дисциплины

Содержание Содержание отчета 2. Лабораторный практикум 6 семестр Общие сведения Общие сведения Порядок выполнения работы Содержание отчета Цель работы Порядок выполнения работы Содержание отчета Рекомендации и вопросы для подготовки к защите Исследование линейной системы. Время выполнения лабораторной работы 6 час Общие сведения Порядок выполнения работы Лабораторная работа 2-7 Время выполнения лабораторной работы 2час. Время выполнения лабораторной работы 2 час 6. Практические занятия Содержание отчета Исследование устойчивости методом гармонической линеаризации ... Полное содержание

Подобный материал:

• Программа дисциплины по кафедре Автоматики и системотехники микропроцессорные системы, 453.35kb.
• Программа дисциплины по кафедре Автоматики и системотехники моделирование систем, 250.13kb.
• Рабочая программа учебной дисциплины "теория автоматического управления" Цикл, 168.41kb.
• Программа наименование дисциплины Теория автоматического управления Рекомендуется для, 218.73kb.
• Программа дисциплины по кафедре автоматики и системотехники схемотехника, 375.75kb.
• Программа дисциплины "Теория автоматического управления" Направление, 86.24kb.
• Теория автоматического управления Общая трудоемкость изучения дисциплины составляет, 25.58kb.
• Примерная программа дисциплины теория автоматического управления Рекомендуется Минобразованием, 169.51kb.
• Рабочей программы дисциплины Теория автоматического управления по направлению подготовки, 19.98kb.
• Рабочая программа учебной дисциплины "теория автоматического управления" Цикл, 208.81kb.

Содержание отчета:

• матрица Гурвица
  
• определители Гурвица
  
• критерий Гурвица
  
• определение апериодической границы устойчивости
  
• определение колебательной границы устойчивости
  
• расположение корней в комплексной плоскости
  

асимптотически устойчивой, устойчивой и неустойчивой

систем


9.Построение характеристических полиномов и синтез

систем управления


Содержание отчета:

• структурная схема системы управления (комбинированного регулятора),
  

обеспечивающего стабилизацию объекта второго порядка в точке y = y* с заданными показателями качества

- время переходного процесса

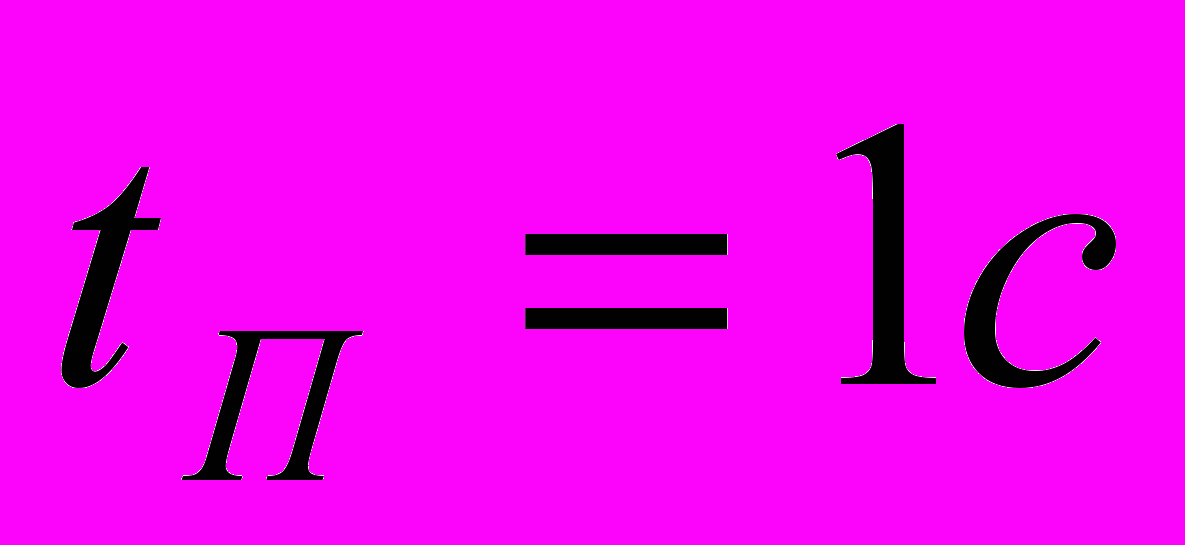
- перерегулирование

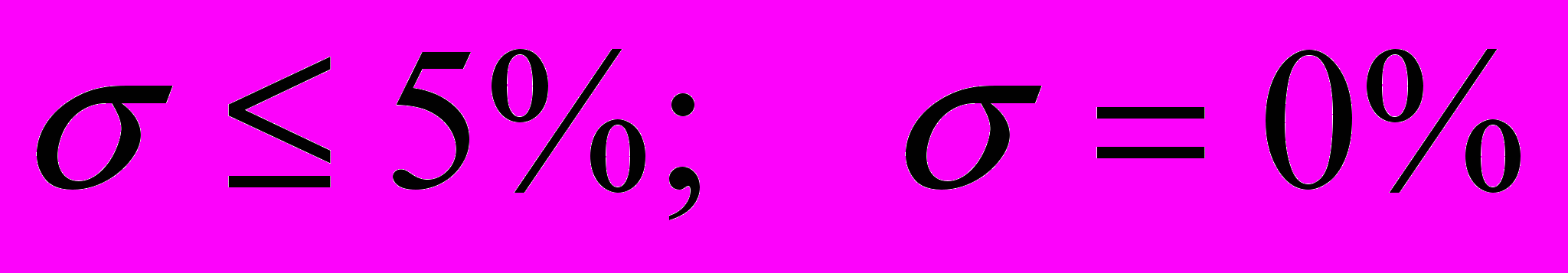
- биноминальное разложение и переходные функции

• полином Баттерворта
  

10.Исследование П- регулятора и ПД – регулятора

Содержание отчета:

• структурная схема объекта второго порядка с управлением
  

по отклонению и возмущению с П- регулятором

• передаточные функции по каналу управления и
  

возмущения

• передаточные функции замкнутой системы с П – регулятором
  
• переходные процессы системы с П- регулятором при постоянном и линейно нарастающем задающем воздействии
  
• структурная схема объекта второго порядка с управлением
  

по отклонению и возмущению с ПД- регулятором

- переходные процессы системы с ПД- регулятором при

постоянном и линейно нарастающем задающем

воздействии

- структурная схема объекта второго порядка с управлением

по отклонению и возмущению с ПИ- регулятором

- переходные процессы системы с ПИ- регулятором при

постоянном и линейно нарастающем задающем

воздействии

- структурная схема объекта второго порядка с управлением

по отклонению и возмущению с ПИД- регулятором

- переходные процессы системы с ПИД- регулятором при

постоянном и линейно нарастающем задающем

воздействии

5. 2. ЛАБОРАТОРНЫЙ ПРАКТИКУМ 6 СЕМЕСТР
   

Лабораторная работа 1.2.


МОДЕЛИРОВАНИЕ СТАЦИОНАРНЫХ

НЕЛИНЙНОСТЕЙ


Цель работы: Изучение характеристик блоков стационарных

нелинейностей (Nonlinear) MATLAB –Simulink

включенных в схемы для исследований .

1. Общие сведения
   

Состав блоков раздела библиотеки Nonlinear и их краткие характеристики. Блоки (Backlash, Couljmb & Viscous Friction, Dead Zone, Rate Limiter, Manual Switch, Quantizer, Relay, Saturation, Switch).

2. Порядок выполнения работы. Собирать функциональную схему и исследовать нелинейность при подаче на вход ее регулярных воздействий .
   
3. Содержание отчета:
   

• функциональные схемы;
  
• переходные характеристики;
  
• анализ этих характеристик.
  

Время выполнения работы – 4 часа


Рекомендации и вопросы для подготовки к защите

лабораторной работы:

• дать определение верхнего порога насыщения;
  
• дать определение нижнего порога насыщения;
  
• дать определение зоны нечувствительности;
  
• привести пример физического устройства с люфтом;
  
• привести пример физического устройства с гистерезисом;
  
• привести схему “шага квантования по уровню”.
  

Лабораторная работа 2.2.


Процессы управления в автоколебательных системах


Цель работы: изучение автоколебательных процессов в нелинейных САУ при различных воздействиях на систему.

Общие сведения

Автоколебательные системы часто встречаются среди нелинейных САУ и САР , в том числе и в системах , включающими отдельные звенья с характеристиками релейного типа. Будем считать, что частота автоколебаний в рассматриваемых системах лежит много выше возможных частот процесса управления.

Порядок выполнения работы:

Собрать структурную схему нелинейной САУ в состав которой входит нелинейный элемент с идеальной релейной характеристикой. Подобрать параметры входных и возмущающих воздействий и определить экспериментально частоту и амплитуду автоколебаний и смещение на выходе системы. Сравнить полученные параметры с расчетными.


Содержание отчета:

• структурная схема системы с включенной в прямую цепь звена с идеальной релейной характеристикой;
  
• переходные процессы при различных параметрах входных и возмущающих воздействий;
  
• анализ переходных процессов.
  

Время выполнения работы – 4 часа


Рекомендации и вопросы для подготовки к защите

лабораторной работы:

• дайте оценку формы сигнала на входе релейного элемента при отсутствии возмущающего воздействия;
  
• оцените влияние жесткой местной обратной связи на форму выходного сигнала;
  
• изобразите идеальную релейную характеристику;
  
• изобразите физическую модель представленной структурной схемы с идеальной релейной характеристикой в прямой цепи.
  

Лабораторная работа 2.3.


Нелинейные корректирующие устройства


Цель работы: изучение нелинейностей специального вида, которые вводятся в линейную систему в качестве корректирующих устройств.

Общие сведения

В результате такого ввода линейная система становится нелинейной. Нелинейная коррекция обладает более широкими возможностями, чем линейная, так как она, во-первых, большее разнообразие форм частотных характеристик и, во-вторых, она позволяет менять форму частотных характеристик в зависимости от величины амплитуды сигнала.


Порядок выполнения работы:

Собрать структурную схему нелинейной САУ в состав которой входит нелинейная обратная связь , сигнал которой уменьшается с возрастанием ошибки. Напряжение пропорциональное модулю ошибки, подается на вход умножителя , а затем вычитается из выходного напряжения. Задача нелинейной коррекции заключается в достижении желаемых свойств процессов управления, причем предусматривается возможность изменения этих свойств с изменением величины отклонения. По ходу исследования найти возможность преодоления известного из линейной теории противоречия между требованиями точности и требованиями устойчивости системы, а также значительно усиливать регулирующее воздействие при больших отклонениях.


Подобрать параметры входных и возмущающих воздействий и определить экспериментально частоту и амплитуду автоколебаний и смещение на выходе


Содержание отчета:


-структурная схема системы с включенной в цепь обратной

связи нелинейность, сигнал которой уменьшается с

возрастанием ошибки;

• из анализа переходных процессов определить убыстрение
  

больших отклонений и уменьшение скорости отработки в

конце процесса;

- привести уравнения описывающие динамику процесса .


Рекомендации и вопросы для подготовки к защите

лабораторной работы:

• привести пример специального вида нелинейностей;
  
• по какой причине линейная система становится нелинейной?
  
• как меняется форма частотных характеристик в зависимости от величины амплитуды сигнала?
  

Лабораторная работа 2.4.


Импульсные САР с цифровым регулятором

(программа impuls. exe)


Цель работы: изучение дискретного раздела “импульсные САУ”


Общие сведения: приводится структурная схема авторегулирования:

• W – приведенная непрерывная часть системы , задаваемая
  

передаточной функцией W(p) из библиотеки передаточных

функций системы;

• с блоком квантования сигнала рассогласования по времени с периодом квантования Т (преобразователь аналог-код);
  
• D – дискретный блок , преобразующий числовую последовательность (решетчатую функцию) e(nT) , в соответствии с законом регулирования , в числовую последовательность x(nT). Блок D задается передаточной функцией D(z) из библитотеки Z- передаточных функций программы;
  
• П – блок преобразования числовой последовательности x(nT) c выхода цифрового D в аналоговый сигнал v(t). В основном режиме h(0) блок выполняет функцию амплитудно-импульсного модулятора (экстраполятора нулевого порядка). Сигнал v(t) на его выходе равен числу x(nT) в течение промежутка времени от nT (n + 1)T, а затем принимает значение x((n + 1)T). В дополнительном режиме (h>0) блок осуществляет нелинейные преобразования, обусловленные ограниченностью разрядной сетки преобразователя аналог- код;
  
• N – блок , который при исследовании линейных систем осуществляет тождественное u = v. В другом случае является нелинейным звеном типа “насыщение”;
  
• H – безинерционная обратная связь;
  
• f,g – задающее и возмущающее воздействия;
  
• e, u,v - дополнительные точки , выход из которых может отслеживаться при построении переходного процесса;
  
• у – выходной сигнал.
  

Порядок выполнения работы:


Работа с программой начинается с диалога. Студенту предлагается установить базовый вариант или повторить последний отсчет.

В первом случае будет установлено : D = 1, N = 1, H = 1, f = 1, g = 0.

П – в основном режиме (h>0), W и не определены и их нужно выбрать, т.е. требуется задать передаточную функцию W(p) и период квантования Т.

Главное меню программы и мет вид:

• формирование элементов схемы;
  
• просмотр выбранных параметров;
  
• исследование линейной системы;
  
• процесс регулирования;
  
• поиск минимума;
  
• выход из программы F 10.
  

После окончания формирования структурной схемы , иследователь возвращается в главное меню с помощью команды “просмотр выбранных вариантов и проверяет правильность ввода”

Следующий этап работы :


Исследование линейной системы.


В программе предусмотрены следующие методы исследования:

• построение фрагмента корневого годографа характеристического уравнения САР;
  
• построение АФХ (кривой Найквиста) для исследования устойчивости по критерию Найквиста;
  
• вычисление числа неустойчивых корней; характеристического уравнения (т.е. расположенных вне единичного круга) по критерию Рауса. Число неустойчивых корней определяется в зависимости от одного или двух параметров системы;
  
• построение процесса регулирования, т.е. графиков функций y(t), e(t), u(t) или v(t) в зависимости от задающего или возмущающего воздействий f(t),g(t).
  

Содержание отчета:

• привести cтруктурную схему импульсной САР;
  
• графики переходных процессов с различными структурами непрерывной части;
  
• получить заданные показателей качества;
  
• Анализ расположения корней на комплексной z – плоскости;
  
• aнализ годографа Найквиста;
  
• aнализ таблицы корней в меню “годограф”;
  
• анализ особенностей расчета нелинейной системы.
  

Рекомендации и вопросы для подготовки к защите

лабораторной работы:

• дать определение критерия Найквиста;
  
• назвать параметры цифрового ПИД – регулятора;
  
• Критерии выбора шага квантования;
  

- указать передаточные непрерывной части импульсно САР

функции;

• дать определение устойчивости импульсной САР по
  

расположению корней в единичном круге;

• оценить влияние нелинейных элементов на процесс регулирования в САР.
  

Время выполнения лабораторной работы 6 час


Лабораторная работа 2-5


Исследование адаптивной следящей системы с

неявной эталонной моделью


Цель работы : изучение адаптивной следящей системы в которой эталонная модель выступает не в виде реализуемого динамического звена, а виде некоторого “эталонного ” уравнения


Общие сведения: приводится структурная схема адаптивной следящей системы с неявной эталонной моделью (рис.4.16. Т.3). Предполагается, что возмущение n(t) является стационарным случайным процессом и моделируется как реакция формирующего фильтра с передаточной функцией 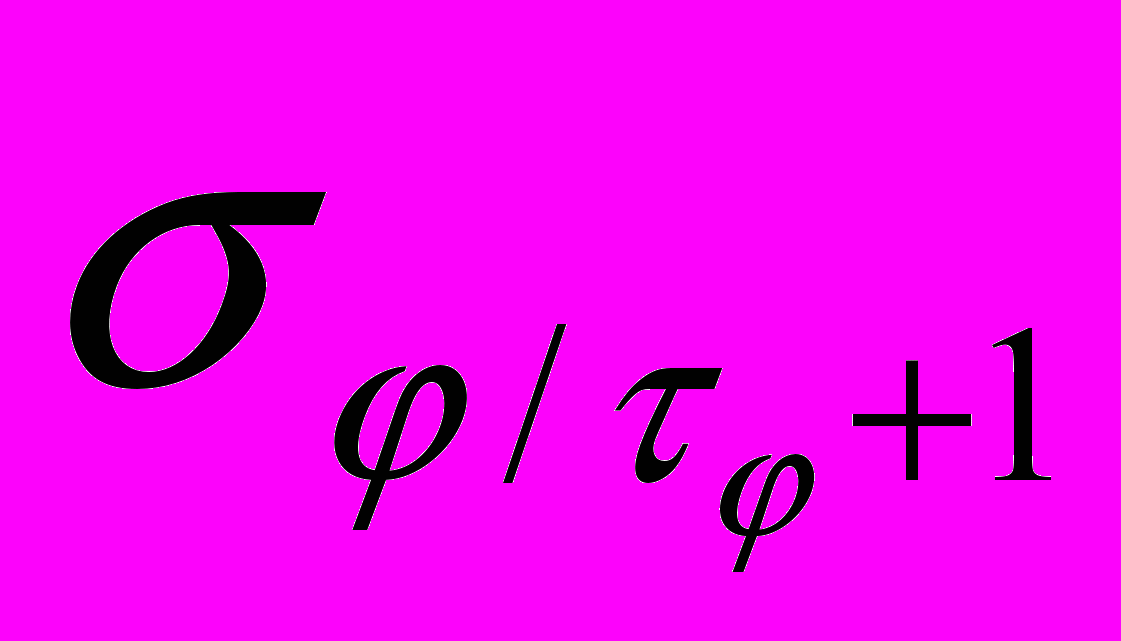на белый шум ()


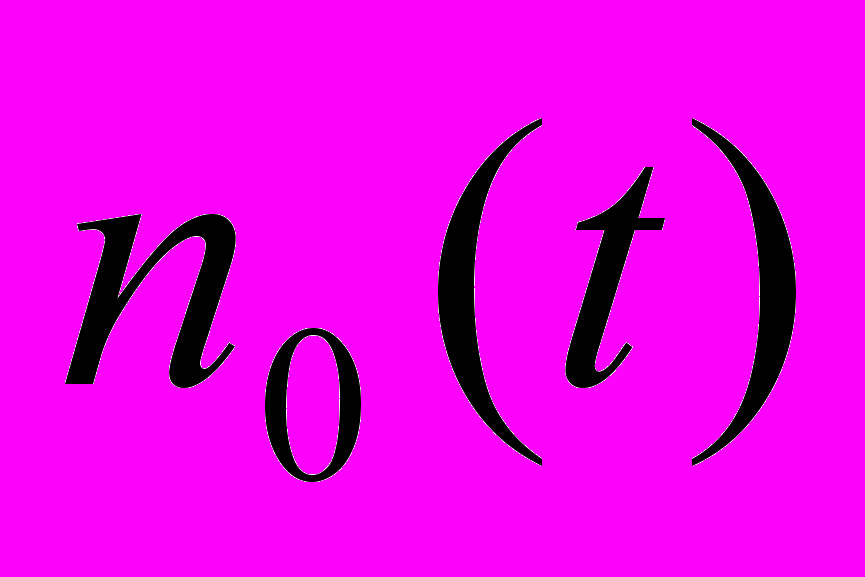Порядок выполнения работы:


Собрать структурную схему в MATLAB – Simulink адаптивной следящей системы с неявной эталонной моделью. Целью управления является приближение вектора состояния X(t) объекта управления к состоянию равновесия X* системы с “идеальными” коэффициентами регулятора, вычисленными в предположении, что задающее воздействие установилось на уровне y(t).

Неявная эталонная модель получается из равенства 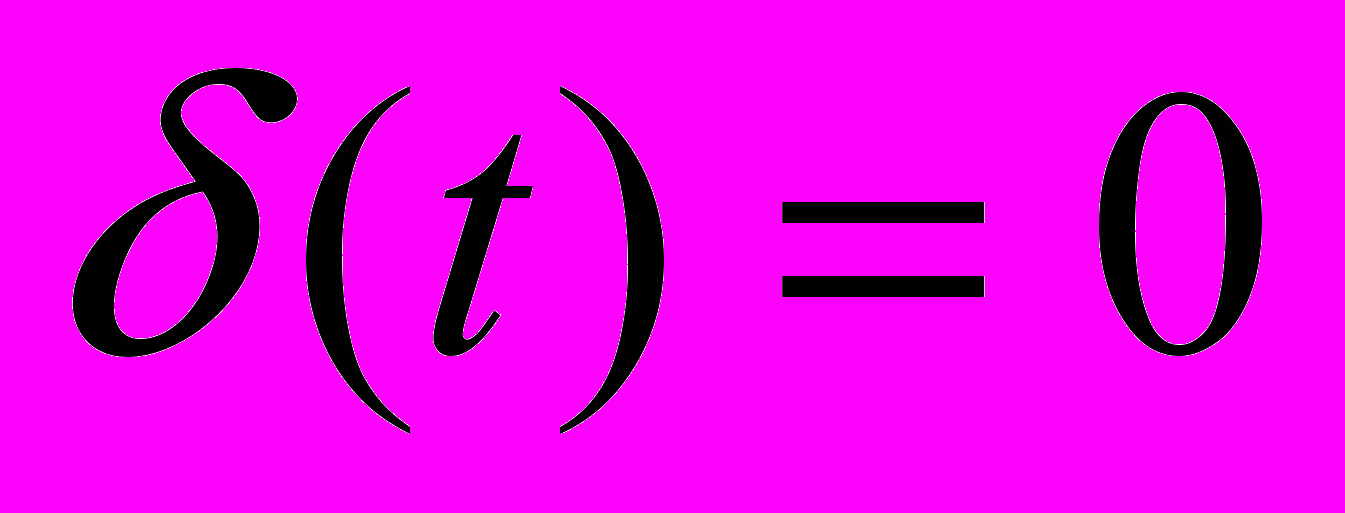и имеет следующий вид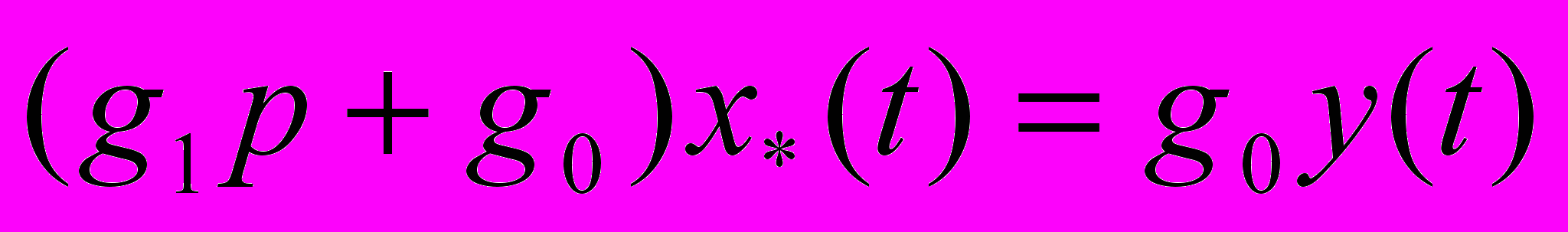





Введение отрицательной обратной связи позволяет использовать алгоритм адаптивного управления в дискретной форме. Выполнить этот алгоритм с помощью s-функции


Содержание отчета:

• привести cтруктурную схему адаптивной следящей системы с неявной эталонной моделью
  
• привести алгоритм адаптивного управления в неперывной и дискретной формах
  
• привести результаты моделирования во временной области
  
• добиться, чтобы время переходного процесса не превышало 3,6 с при отсутствии возмущения (n(t) = 0).
  

Рекомендации и вопросы для подготовки к защите

лабораторной работы:

• определение адаптивной системы;
  
• определение самоорганизующихся адаптивных систем;
  
• определение самонастраивающихся адаптивных систем;
  
• определение явной модели;
  
• определение неявной модели;
  
• определение явной-неявной модели;
  
• определение цели управления адаптивной системы;
  
• определение поисковых адаптивных систем.
  

Время выполнения лабораторной работы 4 час


Лабораторная работа 2-6


Структуры реализации цифровых фильтров


Содержание отчета :

• показать общую структуру последовательной реализации цифрового фильтра через звенья первого и второго порядков
  
• показать общую структуру параллельной реализации цифрового фильтра через звенья первого и второго порядков
  
• через заданную структуру системы дискретного временив виде z-образа передаточной функции H(z) запишите в виде, удобном для построения последовательной структуры с использованием звеньев второго порядка
  
• через заданную структуру системы дискретного временив виде z-образа передаточной функции H(z) запишите в виде, удобном для построения параллельной структуры с использованием звеньев второго порядка
  

Лабораторная работа 2-7


Операции z- преобразования с помощью

программного пакета MATLAB


Содержание отчета:

• укажите известные Вам операции z- преобразования;
  
• для каких целей используется функция deconv?;
  
• для каких целей используется функция residues?;
  
• дано z- преобразование X(z) , найти первые шесть членов обратного z - преобразования x(n) с помощью метода разложения в степенной ряд (деления многочленов) и программного пакета MATLAB;
  
• получить z – образ, выраженный как разложение на элементарные дроби;
  
• с помощью функции MATLAB zplane рассчитать и вывести на экран диаграмму нулей и полюсов заданной системы дискретного времени, которая характеризуется передаточной функцией.
  

Время выполнения лабораторной работы 2час.

Лабораторная работа 2-8


Разработка цифровых фильтров


Содержание отчета:

• при заданной передаточной функции аналогового фильтра (числитель равен 1 , знаменатель имеет 3-й порядок)вычислите подходящие коэффициенты цифрового фильтра с использованием билинейного метода
  
• записать передаточную функцию цифрового фильтра
  
• организовать каскадную реализацию цифрового фильтра(факторизация производится с использование элементарных дробей с порядком не выше второго)
  
• организовать параллельную реализацию цифрового фильтра(факторизация производится с использование элементарных дробей с порядком не выше второго)
  

Время выполнения лабораторной работы 2 час.


Лабораторная работа 2 - 9

Разработка КИХ – фильтра с помощью MATLAB


Содержание отчета:

• описать метод взвешивания
  
• задать необходимую частотную характеристику
  
• выбрать весовую функцию и оценить число коэффициентов фильтра, N
  
• получить идеальную частотную характеристику 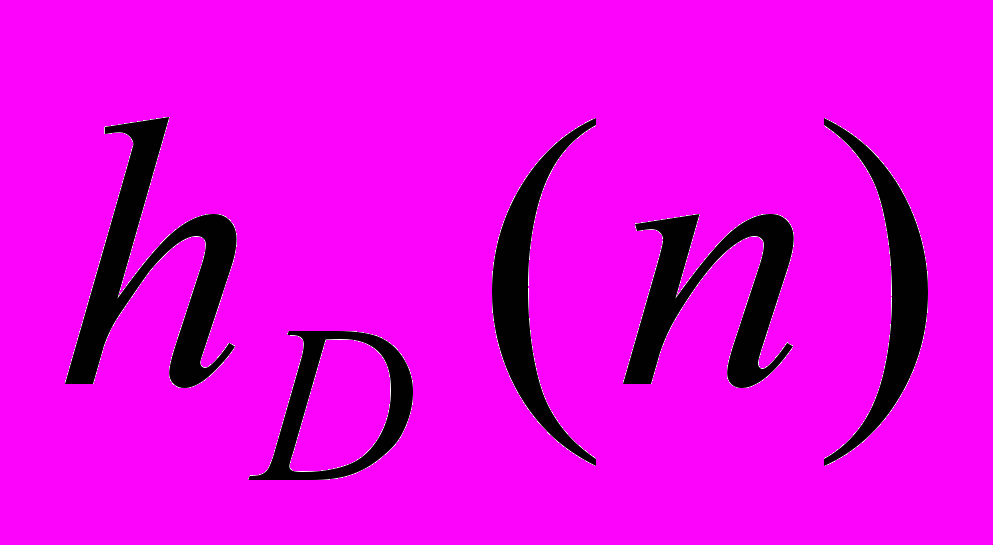, усеченную до N значений
  
• получить N коэффициентов весовой функции,
  
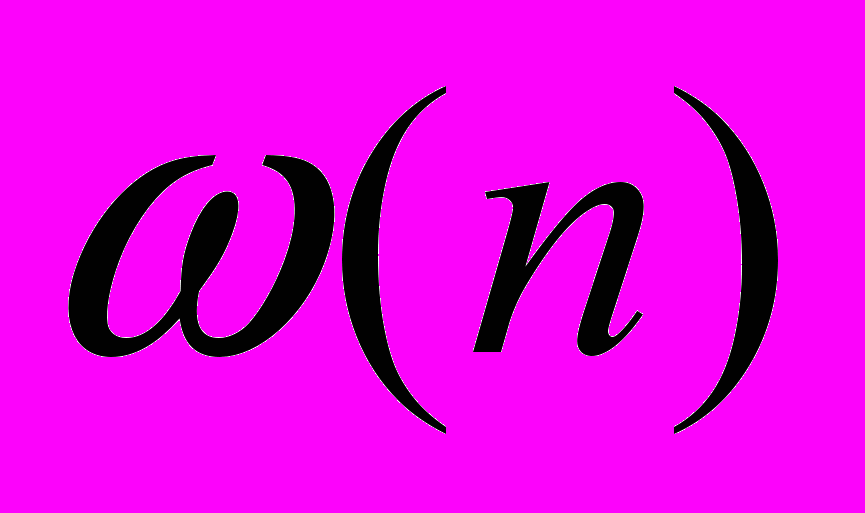
• получить коэффициенты КИХ – фильтра, воздействовав на частотную характеристику весовой функцией,
  
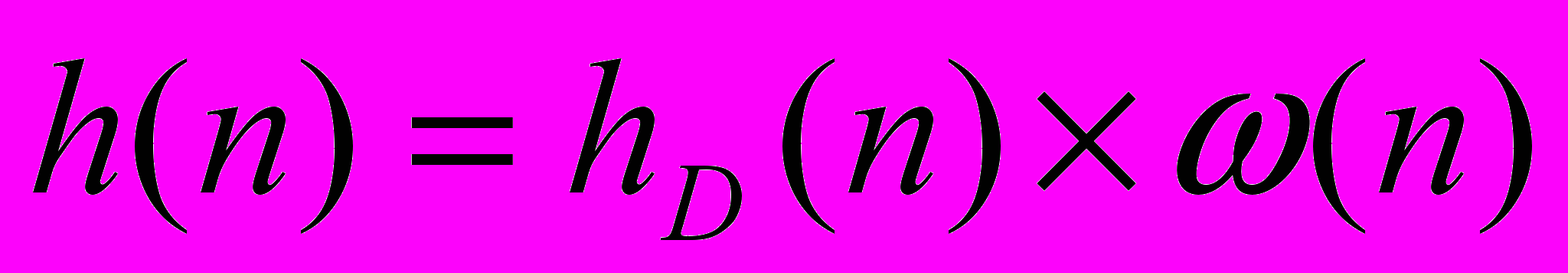
• использовать команду высокого уровня в Toolbux является команда fir1
  

Время выполнения лабораторной работы 2 час.


Лабораторная работа 2 - 10


Разработка БИХ – фильтра с помощью MATLAB


Содержание отчета:

• Аналоговый фильтр нужно преобразовать в эквивалентный цифровой, который будет работать с частотой дискретизации 256 Гц. Например, аналоговый фильтр имеет следующую передаточную функцию:
  

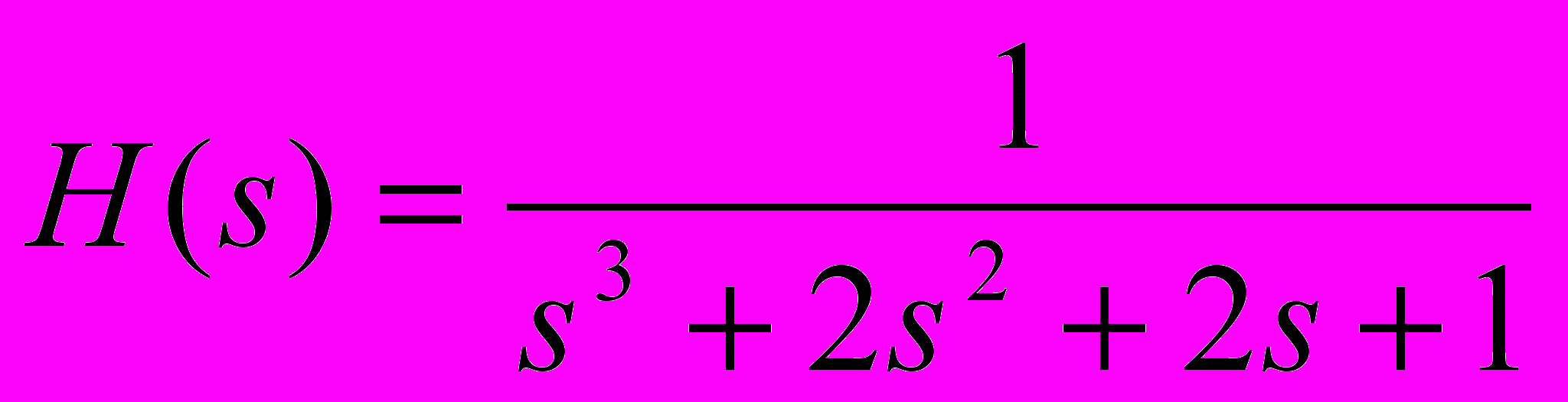
• получите подходящие коэффициенты для цифрового фильтра;
  
• цифровой фильтр нужно реализовать с помощью каскадной структуры, изобразите блок-схему реализации и выведете разностное уравнение;
  
• а также цифровой фильтр нужно реализовать с помощью параллельной структуры, изобразите блок-схему реализации и выведете разностное уравнение;
  
• испытайте разработанный цифровой фильтр в системе, состоящей из достаточно инерционного объекта управления при зашумленном входном воздействии.
  

Время выполнения лабораторной работы 2 час


6. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ


1. Исследование систем со скользящим процессом на примере САР с включением нелинейности в прямую цепь и получением фазовых траекторий в виде параболы. Положение вершины параболы определяется начальными условиями переходного процесса.

Содержание отчета:

- собрать структурную схему САР в MATLAB-Simulink;

-построить линию переключения;

-построить линию движения изображающей точки к началу координат.

2. Исследование устойчивости методом гармонической линеаризации
   

Содержание отчета

-определение границ устойчивости, как граница области существования периодических собственных колебаний в системе (К = Кгр);

-организовать появление пары чисто мнимых корней в характеристическом уравнении гармонически линеаризованной системы?

-определение границы устойчивости по Гурвицу.

-представить графики .

2. Исследование устойчивости нелинейной САУ путем разделения на линейную и линейную части.
   

Содержание отчета:

• определение точки пересечения линейной и нелинейной частей;
  
• определение по графикам амплитуды автоколебаний и частоты при различных типах нелинейностей;
  
• выполнение расчетной части (составление
  

характеристического уравнения).