Geum.ru

Вестник Брянского государственного технического университета. 2007. №4(16)

Вид материалаИсследование

Содержание


Список литературы
Подобный материал:

ISBN 5-89838-309-3 Вестник Брянского государственного технического университета. 2007. № 4(16)


УДК 519.624

Б.Г. Кеглин, Е.Г. Гайворонский


ПРИМЕНЕНИЕ МЕТОДА РУНГЕ-КУТТА С ПРИПАСОВЫВАНИЕМ
ДЛЯ РЕШЕНИЯ ЗАДАЧ ФРИКЦИОННЫХ АВТОКОЛЕБАНИЙ
В РАСПРЕДЕЛЕННЫХ СИСТЕМАХ


Описан вариант метода Рунге-Кутта, приспособленный для решения задач фрикционных автоколебаний с остановками. Показаны сложности синтеза метода припасовывания и численного решения дифференциальных уравнений с переменной структурой. Приведена количественная оценка преимущества данного метода по сравнению с классическим методом Рунге-Кутта при исследовании фрикционных автоколебательных процессов в системах с распределенными параметрами.


Исследование процессов фрикционных автоколебаний в континуальных системах при наличии силы трения, зависящей от продолжительности неподвижного контакта
[1, 2] (далее реологической силы трения), привело к необходимости создания метода, четко описывающего смену состояний в такой системе.

Коэффициент трения во время движения fск(v) описывается зависимостью Крагельского-Щедрова [3], или кубическим законом трения. В момент остановки трение начинает зависеть от времени остановки t:

fпок(t) = f∞ – (f∞ – f0)e– n t,

где f∞ – коэффициент силы трения при бесконечно большом времени контакта; f0 – коэффициент силы трения при нулевом времени контакта; n – инкремент увеличения силы трения.

Реологическая сила трения порождает модель трения, в которой дифференциальные уравнения движения имеют переменную структуру, т.е. они в зависимости от значения скорости скольжения трущихся частей, составляющих модель, предстают в виде разных наборов дифференциальных уравнений – дифференциальных уравнений с переменной структурой (ДУсПС). Система ДУсПС с двумя структурами получается в задачах фрикционных автоколебаний в сосредоточенном и распределенном случаях. Приведем систему уравнений для одномассовой задачи.

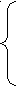
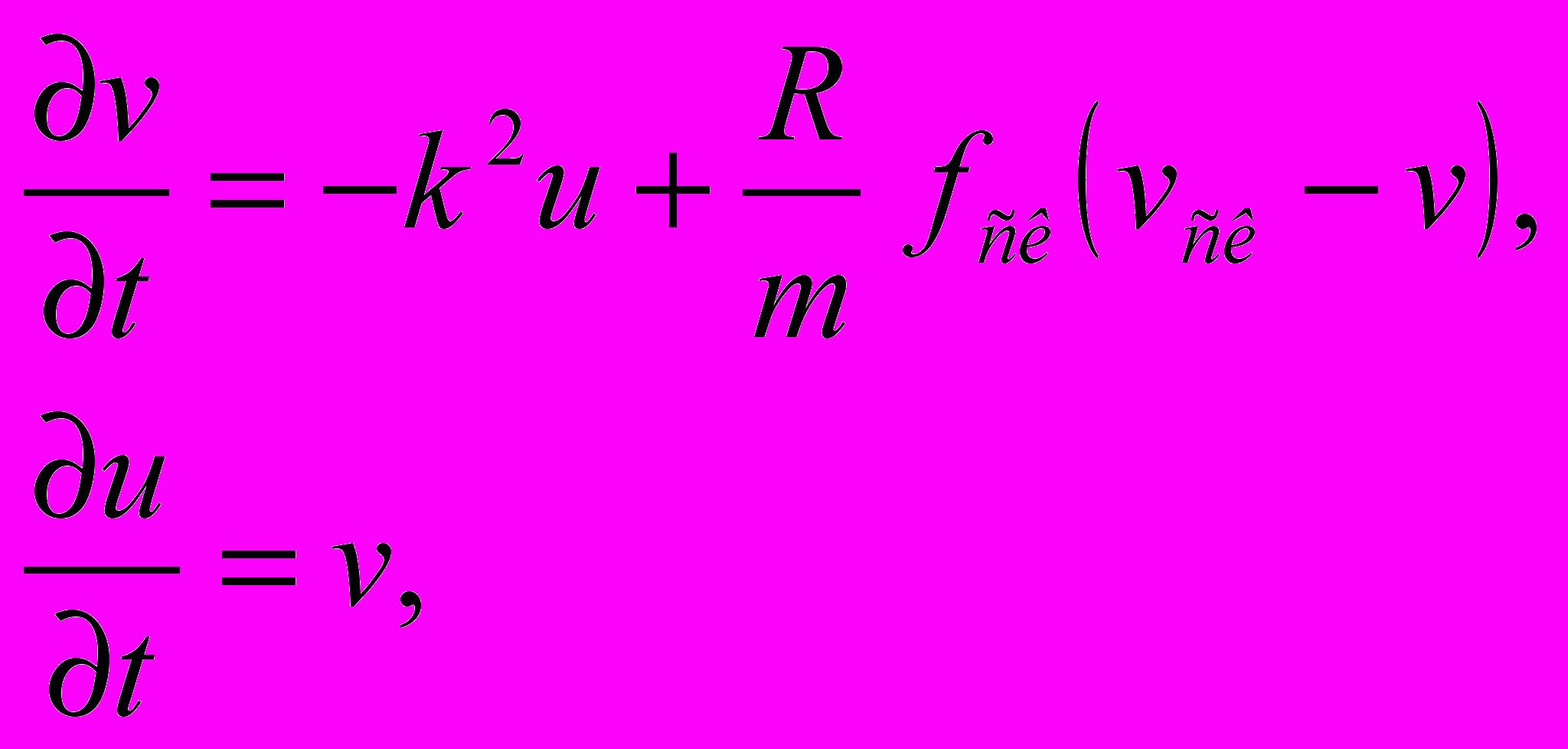пока Усл1(t, u, v) = ложь; (1)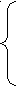

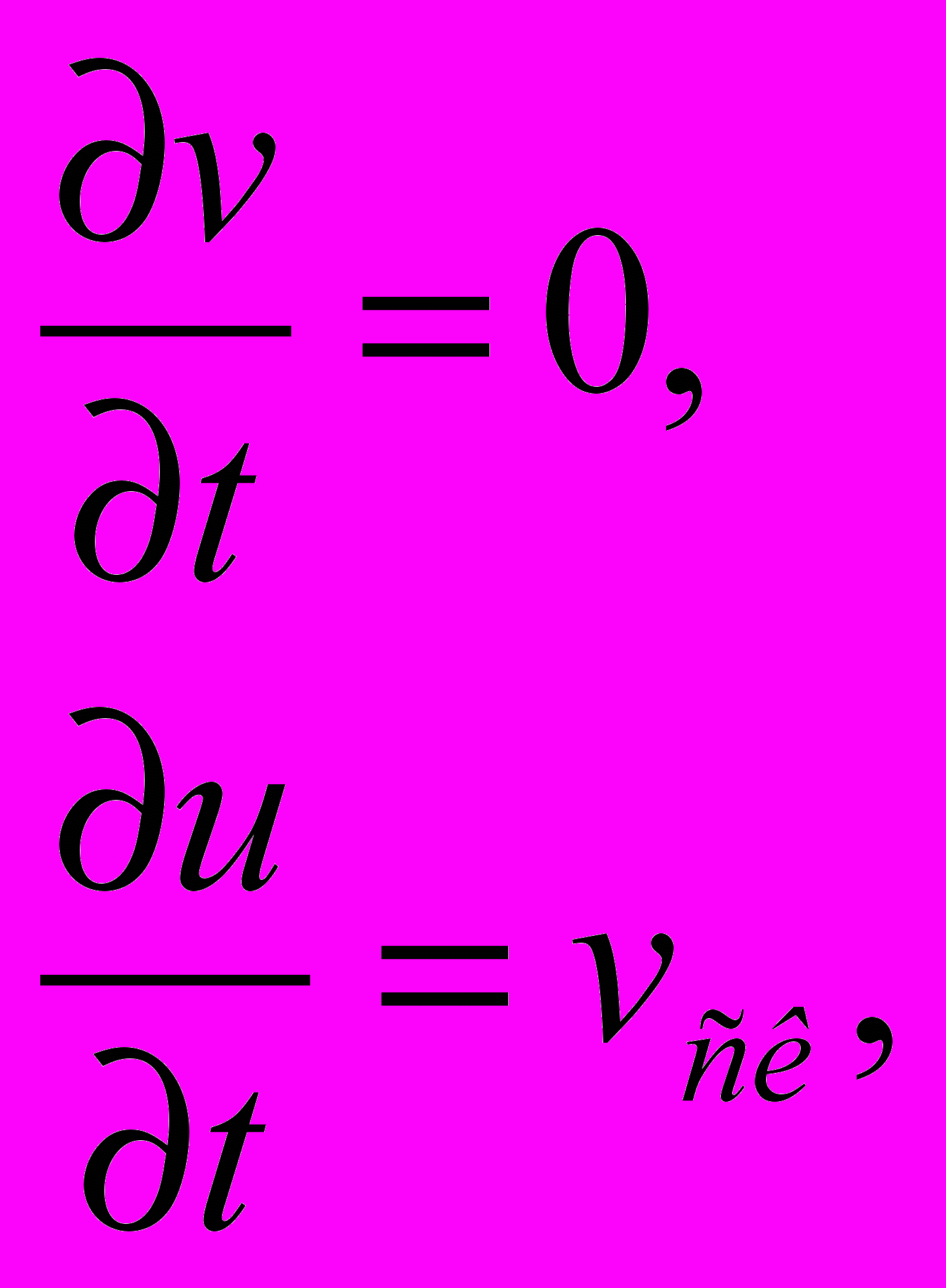пока Усл2(t, u, v) = ложь; (2)

¬  (t, u, v): (Усл1(t, u, v) Усл2(t, u, v)) = истина,

где vск – скорость скольжения трущихся частей в стационарном состоянии системы; k – частота свободных колебаний системы; 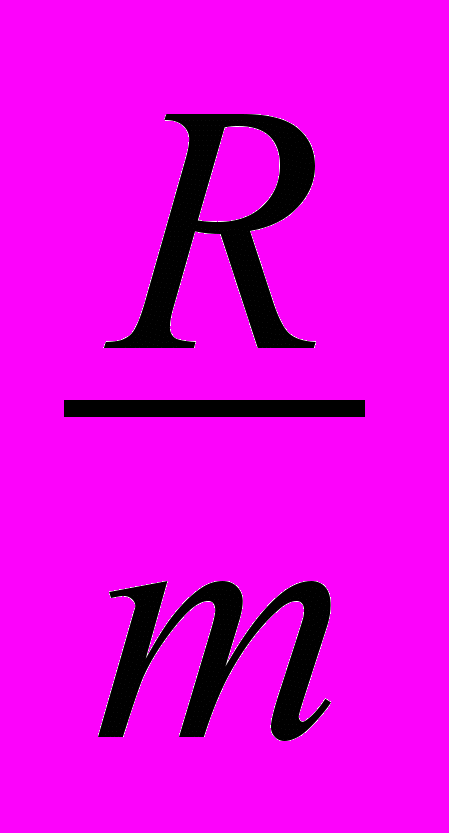– показатель, соотносящий силу трения с силами инерции. Условия перехода от одной системы уравнений к другой: от скольжения к покою – Усл1(t, u, v), от покоя к скольжению – Усл2(t, u, v).

Линеаризация систем с реологическим трением и другие подходы, заменяющие решение ДУсПС на решение обычных дифференциальных уравнений [4], имеют один общий недостаток: они явно не учитывают сууществующую в действительности смену законов движения автоколебательных систем. Так, некоторые режимы релаксационных колебаний, как показали вычислительные эксперименты, могут иметь квазигармоническую форму или быть стохастическими с суперпозицией квазигармонических форм (в многомассовой задаче). Установить, что имеет место именно релаксационный процесс, а не остаточные колебания или безостановочные автоколебания, может только анализ последовательности смены структур решения.

Общим подходом в исследовании уравнений с переменной структурой является метод припасовывания [5]. Обычно он используется для точного описания уравнений движения, но теоретически можно соединить его, например, с методом Рунге-Кутта. Для создания такого комбинированного метода необходимо разрешить ряд трудностей, возникающих в ходе реализации данной идеи.

Для получения возможности работы с ДУсПС надо внести изменения в метод Рунге-Кутта, которые позволят не выходить при решении за границы одной структуры. При реализации этого подхода были обнаружены эффекты, которые обусловливаются численным характером решения:
  1. В областях перехода от одной структуры уравнений к другой может проявляться самоограничение решения из-за скачкообразного изменения коэффициента трения скольжения fск(v) при смене знаков скорости. Это приводит к тому, что в момент фактического перехода от скольжения к покою не выполняется условие смены структуры дифференциального уравнения Усл1(t, u, v) (это условие может вообще никогда не выполняться). В результате получается решение, в котором отсутствует релаксационный автоколебательный процесс.
  2. Неустойчивость решения вследствие неопределенности коэффициента трения при v = vск приводит к ошибкам в определении ускорения на шаге срыва – при выполнении условия Усл2(t, u, v). Масштаб этой ошибки гораздо больше масштаба шага интегрирования . Эффект приводит к заметному (более 2% – на конкретных примерах) падению точности решения.
  3. Существует еще один механизм потери точности вычислений, который непосредственно связан с дифференциалом (1,2): в области, где v = vск, смена скольжения на покой – выполнение условия Усл2(t, u, v) – происходит при какой-то близкой к vск скорости, но не равной ей. При этом на графике скорости мы будем видеть, что у каждого периода колебаний своя скорость остановки. Это приводит, например, к погрешности вычисления периода колебаний (более 3%).

Для решения перечисленных проблем предусмотрено следующее:
  1. Для борьбы с самоограничением решения предусмотрена задержка появления скачка трения на один шаг интегрирования уравнения. Это можно сделать, если добавить к зависимости коэффициента трения от скорости fск(v) дополнительную вспомогательную переменную:

fск(v, v2) = f'ск(v), если v2 > 0;

fск(v, v2) = – f'ск(v), если v2 < 0.

Переменные v и v2 таковы, что v на предыдущем шаге равняется v2 на последующем. Функция f'ск(v) должна описывать коэффициент трения только в области положительных значений v, а в области перехода к отрицательным значениям должна быть аналитической функцией. Таким образом, при решении ДУсПС удается задержать скачкообразное изменение коэффициента трения на один шаг, система «заходит» за скачок и улавливает условие изменения структуры.
  1. Для верного нахождения изначальной величины ускорения применяется (на первом с момента срыва шаге) метод Эйлера для решения дифференциальных уравнений, при этом шаг разбивается на N частей. При таком подходе система решения ДУсПС сама определяет величину ускорения. Мы не видим в решении ошибок на шагах от 1 до N, а видим только значение в N-й точке. N определяется из соотношения порядка ошибки определения ускорения и шага .
  2. Избавиться от эффекта потери точности вычислений, непосредственно связанного с дифференциалом, можно, если заменить выражение (2) на выражение

;

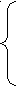
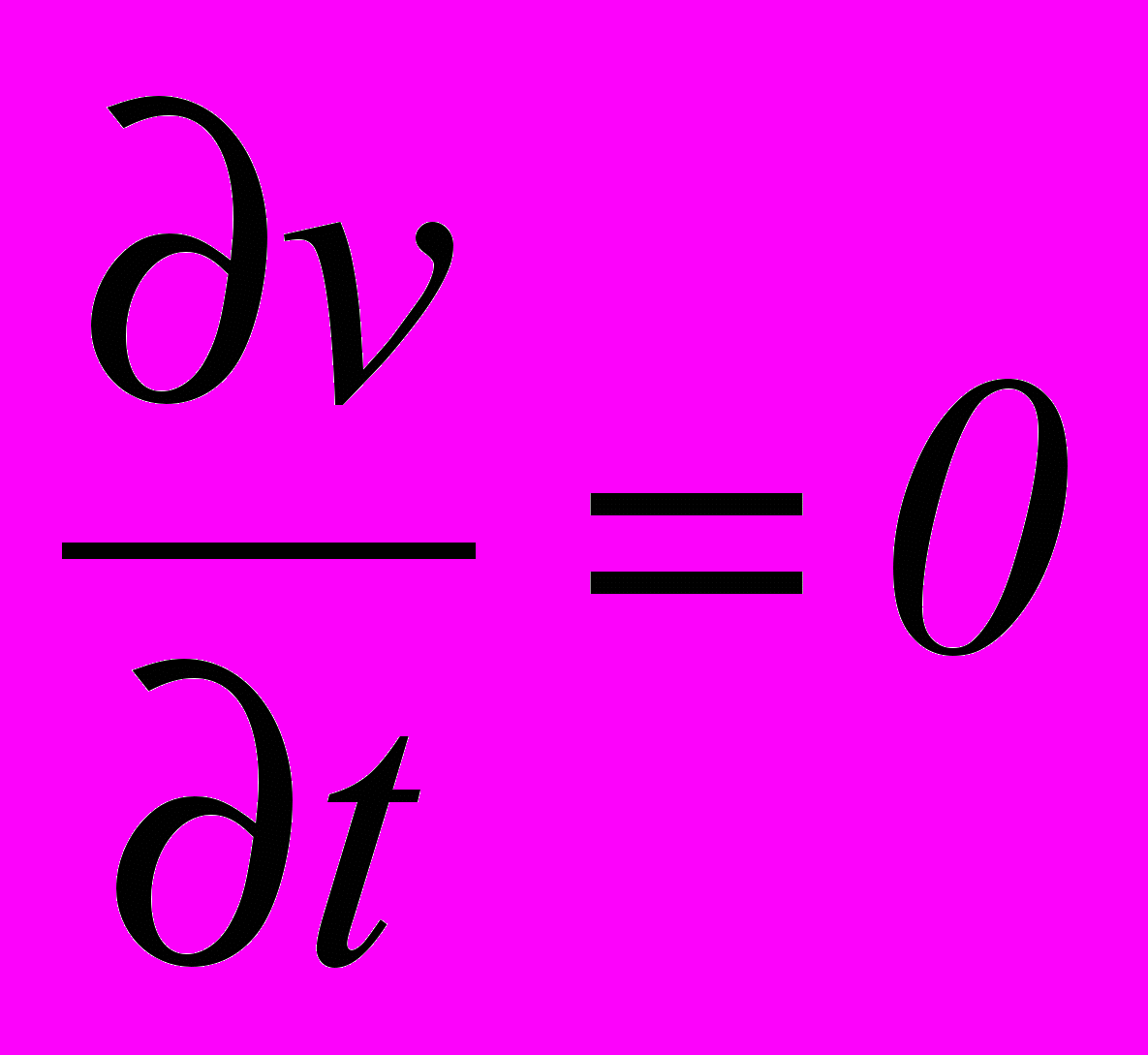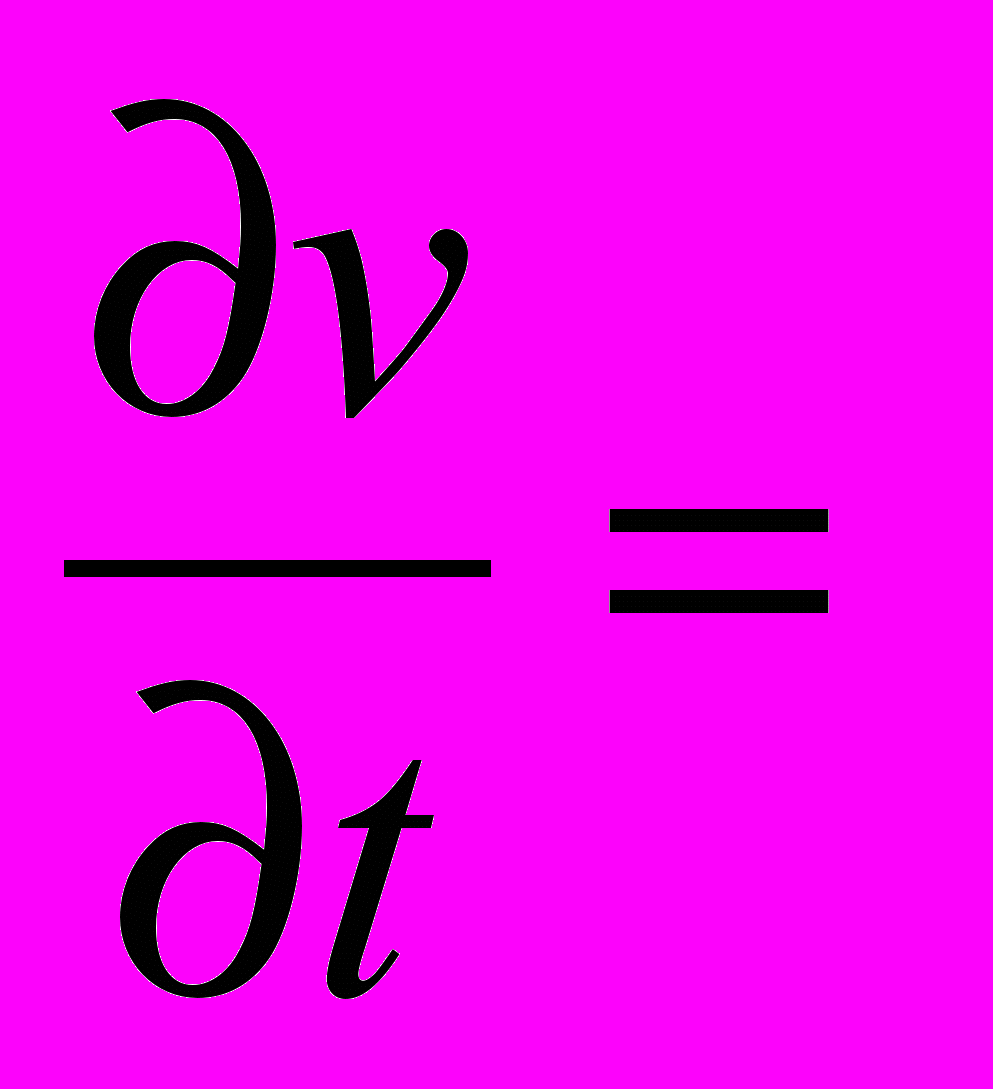
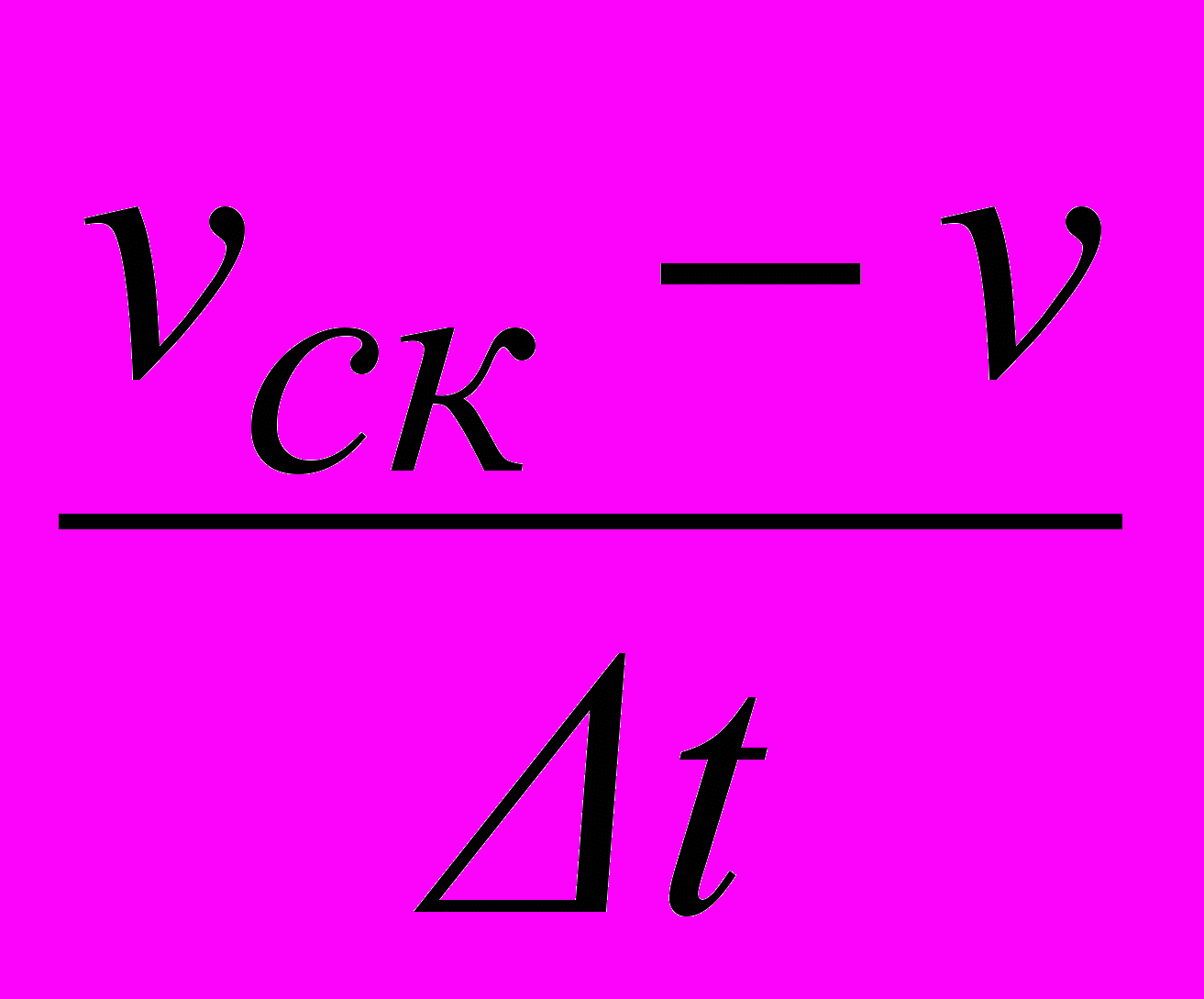, если 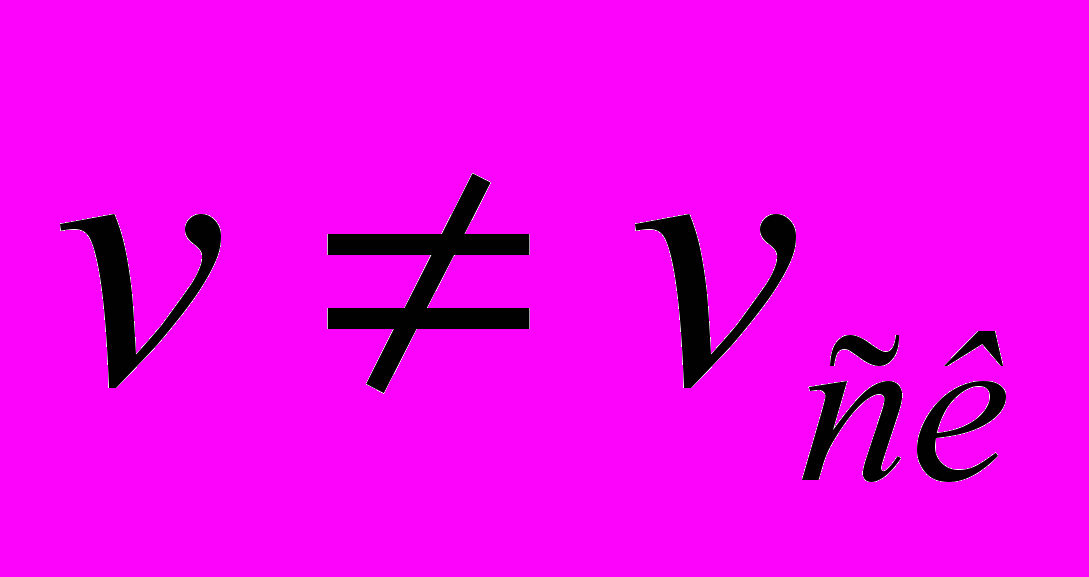; 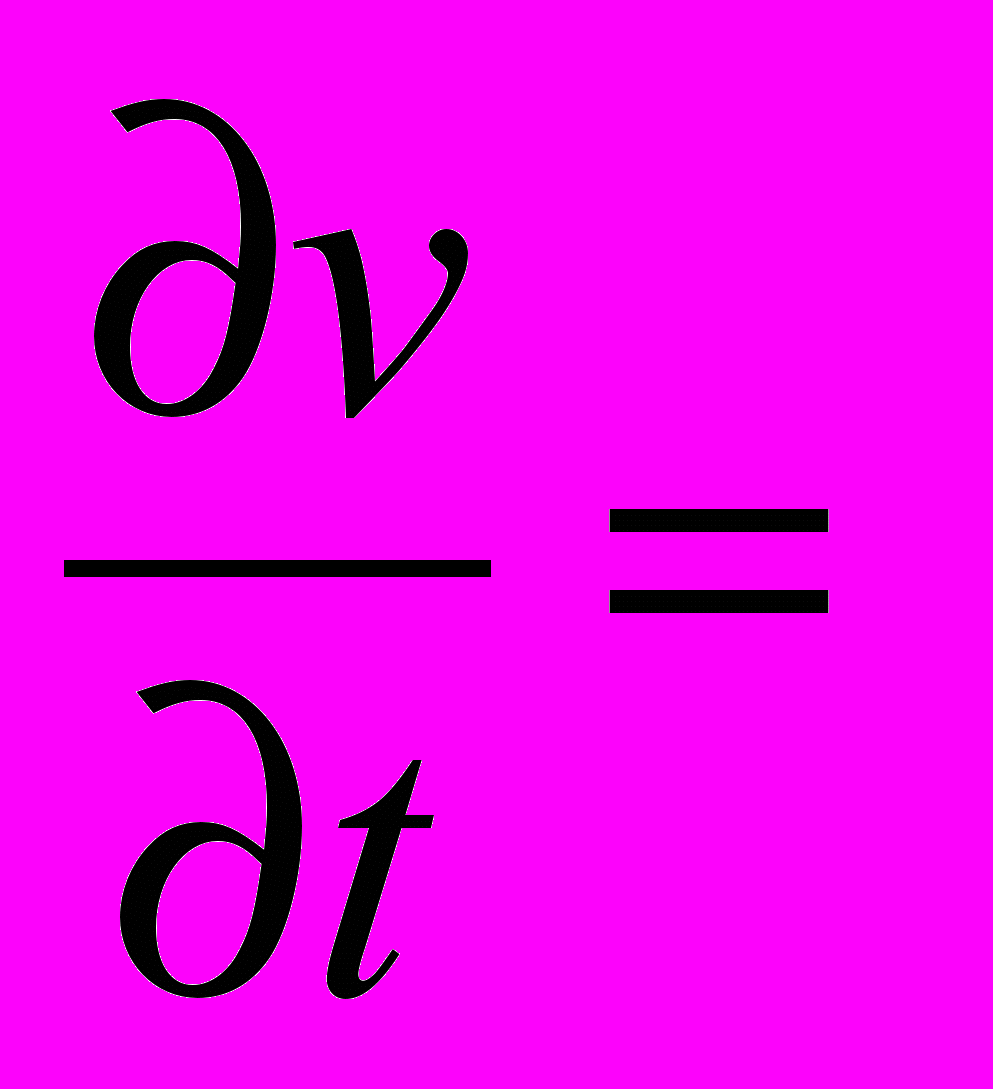0 если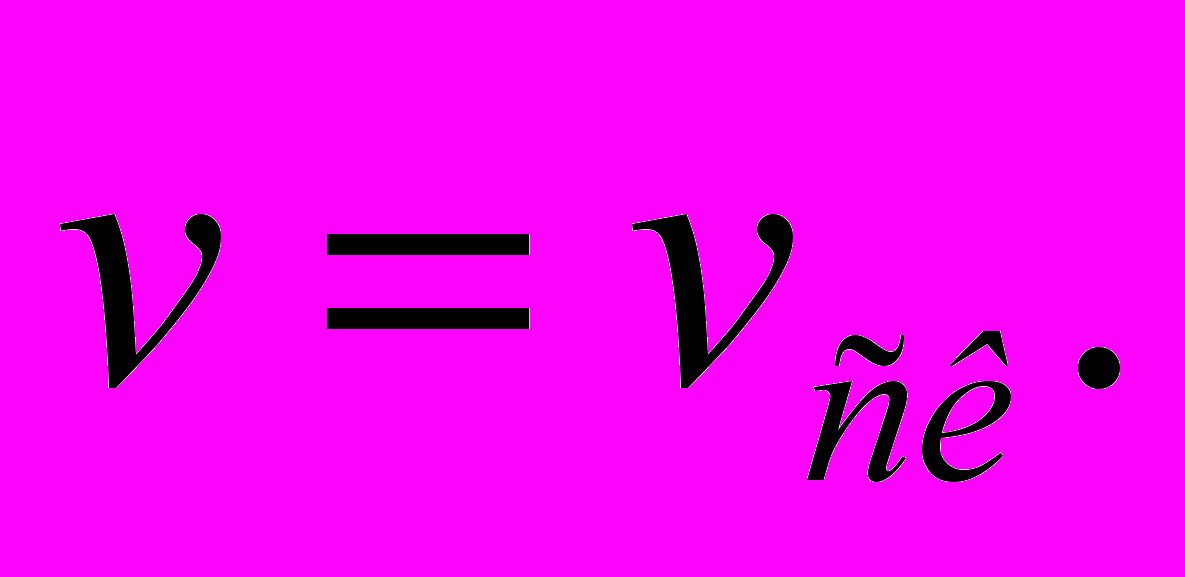

В случае интегрирования многомассовых систем, которые получаются, например, вследствие дискретизации континуальных задач, с ростом точности дискретизации и – соответственно количества узлов возникает проблема зацикливания решения ДУсПС. Это связано с появлением циклов в условиях перехода системы из одного состояния в другое, т.е. когда последующее состояние системы способствует ее переходу в предыдущее состояние. Выход из данного положения был найден в управляемом снижении точности решения в местах перехода от одной системы уравнений к другой.

С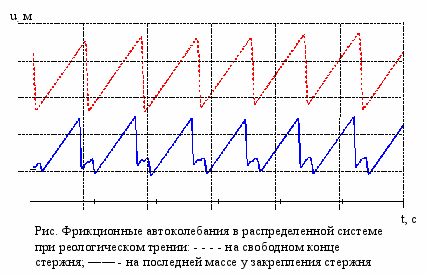равнение решений некоторых задач автоколебаний методом Рунге-Кутты с припасовыванием и классическим методом Рунге-Кутты (если этим методом задача могла быть решена) показало, что одинаковой точности решения последний метод достигал приблизительно при в 2,5 раза меньшем количестве точек. Это очень важно, ведь при решении задач автоколебаний в распределенных системах путем их дискретизации (рисунок) и исследовании решений, например методом корреляционного анализа, можно быстро достичь предела возможностей современных ЭВМ.

СПИСОК ЛИТЕРАТУРЫ
  1. Крагельский, И.В. Коэффициенты трения / И.В. Крагельский, И.Э. Виноградова. - М.: Машгиз, 1955. - 188 с.
  2. Кудинов, В.А. Динамика станков / В.А. Кудинов. - М: Машиностроение, 1967. - 360 с.
  3. Крагельский, И.В. Трение и износ / И.В. Крагельский. - М.: Машиностроение, 1968. - 480 с.
  4. Никольский, Л.Н. Амортизаторы удара подвижного состава / Л.Н. Никольский, Б.Г. Кеглин. - М.: Машиностроение, 1986. - 144 с.
  5. Бидерман, В.Л. Теория механических колебаний: учеб. для вузов / В.Л. Бидерман. - М.: Высш. шк., 1980. - 408 с.


Материал поступил в редколлегию 20.09.07.