Лабораторная работа №1

Вид материала

Лабораторная работа

Содержание Тригонометрическая форма комплексного числа Формула Эйлера e = (cos + isin). (3)Формула Муавра-Лапласа Элементарные функции комплексных переменных

Подобный материал:

• Методические указания к лабораторным работам Лабораторная работа, 357.24kb.
• Лабораторная работа №3 кпк лабораторная работа №3 Тема: карманный персональный компьютер, 173.34kb.
• Методические возможности стенда Особенности работы на стендах уилс-1 Ознакомительное, 1487.3kb.
• Лабораторная работа по курсу «Физические основы микроэлектроники», 136.21kb.
• Лабораторная работа, 166.92kb.
• Самостоятельная работа по учебным пособиям, 471.48kb.
• Конспект урока в 9 классе по теме: «Магний», 84.54kb.
• Лабораторная работа №1 Введение в Windows. Работа с окнами и приложениями в Windows, 67.41kb.
• Знакомство c Excel, 1212.51kb.
• Лабораторная работа, 105.21kb.

Лабораторная работа № 3.1

АРИФМЕТИКА КОМПЛЕКСНЫХ ЧИСЕЛ

Комплексным числом называется сумма вида z = x + iy,

где

i – мнимая единица: i² = -1;

x, y – вещественные числа: x = Rez; y = Imz.

Комплексные числа



называются комплексно сопряженными.


Операции над комплексными числами.

Пусть

z₁ = x₁ + iy₁; z₂ = x₂ + iy₂

тогда

z₁  z₂ = (x₁  x₂) + i(y₁  y₂);


z₁ * z₂ = (x₁x₂ – y₁y₂) + i(x₁y₂ + y₁x₂); (1)





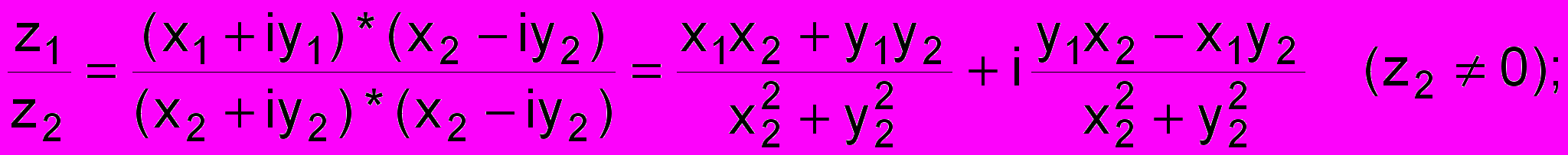
Тригонометрическая форма комплексного числа

z = x + iy = r (cos + i sin),

где

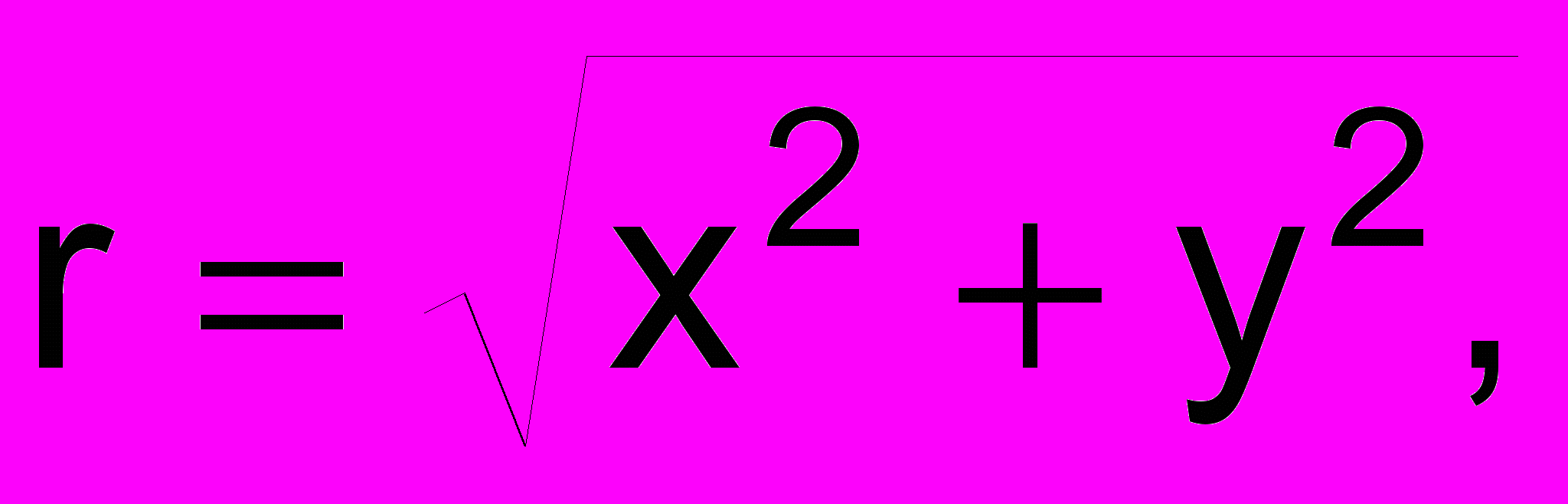число r называется модулем (абсолютной величиной) комплексного числа, r = z;

угол  определяется из условий



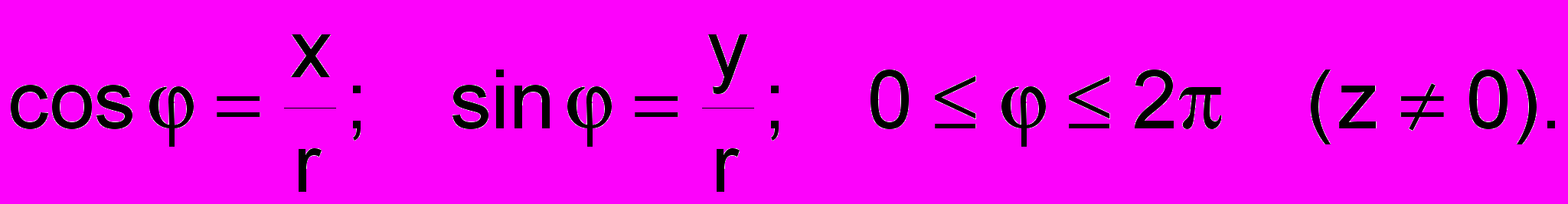
Угол  называется аргументом комплексного числа:  = argz. Аргумент  определяется с точностью до угла, кратного 2.

Пусть

z₁ = r₁(cos₁ + isin₁); z₂ = r₂(cos₂ + isin₂);

тогда

z₁*z₂ = r₁*r₂(cos(₁+₂) + isin(₁+₂)); (2)

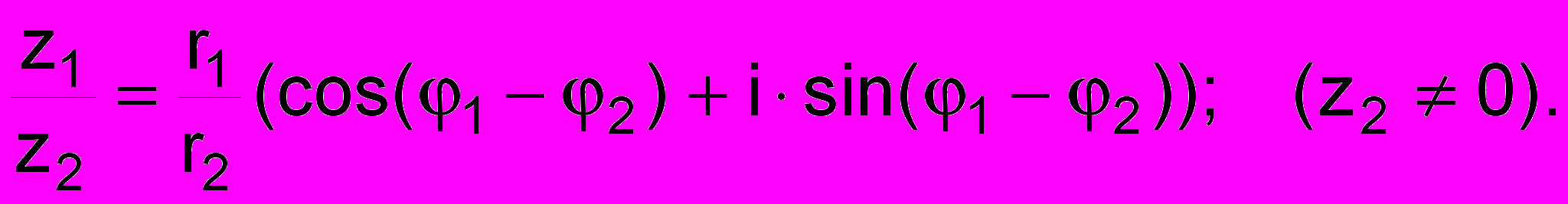
Формула Эйлера

e^i = (cos + isin). (3)

Формула Муавра-Лапласа

(r(cos + isin))ⁿ = rⁿ(cosn + isinn) (n – целое); (4)

zⁿ = rⁿ(cosn + isinn).

Элементарные функции комплексных переменных

z = x + iy = re^i;

e^z = e^x+iy = e^x(cosy + isiny); (5)

shz = (e^z – e^-z)/2 = shxcosy + ichxsiny; (6)

chz = (e^z + e^-z)/2 = chxcosy + ishxsiny; (7)

sinz = (e^iz - e^-iz)/2i = sinxchy + icosxshy; (8)

cosz = (e^iz + e^-iz)/2 = cosxchy - isinxshy; (9)

lnz = ln(re^i) = lnr + i( + 2k), k = 0, 1, 2,  (10)

Напомним, что аргумент  определяется с точностью до угла, кратного 2.

ЗАДАНИЯ

1. Сформировать модуль для работы с комплексными числами. Используя модуль написать программу решения системы линейных алгебраических уравнений порядка n (n  10) с комплексными коэффициентами методом Гаусса (Жордана) с выбором главного элемента.

Порядок и коэффициенты системы вводятся из файла. В файл результатов выдаются: исходная система; решение системы; результат подстановки решения в систему в виде “левая часть = правая часть”.


2. Сформировать модуль для работы с комплексными числами. Используя модуль написать программу обращения матрицы порядка n (n  10) с комплексными коэффициентами методом Гаусса (Жордана) с выбором главного элемента.

Порядок и коэффициенты матрицы вводятся из файла. В файл результатов выдаются: исходная матрица; обратная матрица; произведение исходной матрицы на обратную.


3. Сформировать модуль для работы с комплексными числами. Используя модуль написать программу вычисления определителя матрицы порядка n (n  10) с комплексными коэффициентами методом Гаусса с выбором главного элемента.

Порядок и коэффициенты матрицы вводятся из файла


4. Сформировать модуль для работы с комплексными числами. Используя модуль написать программу вычисления определителя трехдиагональной матрицы порядка n (n  40) с комплексными коэффициентами методом Гаусса.

Порядок и коэффициенты матрицы (главная и соседние с ней диагонали) вводятся из файла.


5. Сформировать модуль для работы с комплексными числами. Используя модуль написать программу решения системы линейных алгебраических уравнений порядка n (n  40) для трехдиагональной матрицы с комплексными коэффициентами методом прогонки. Предусмотреть экономное использование памяти.

Порядок и коэффициенты матрицы (главная и соседние с ней диагонали), вектор правых частей вводятся из файла. В файл результатов выдаются: исходная система; решение системы; результат подстановки решения в систему в виде “левая часть = правая часть”.


6. Сформировать модуль для работы с комплексными числами. Используя модуль написать программу обращения трехдиагональной матрицы порядка n (n  40) с комплексными коэффициентами методом прогонки. предусмотреть экономное использование памяти.

Порядок и коэффициенты матрицы (главная и соседние с ней диагонали) вводятся из файла. В файл результатов выдаются: исходная матрица; обратная матрица; произведение исходной матрицы на обратную.


7.Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления



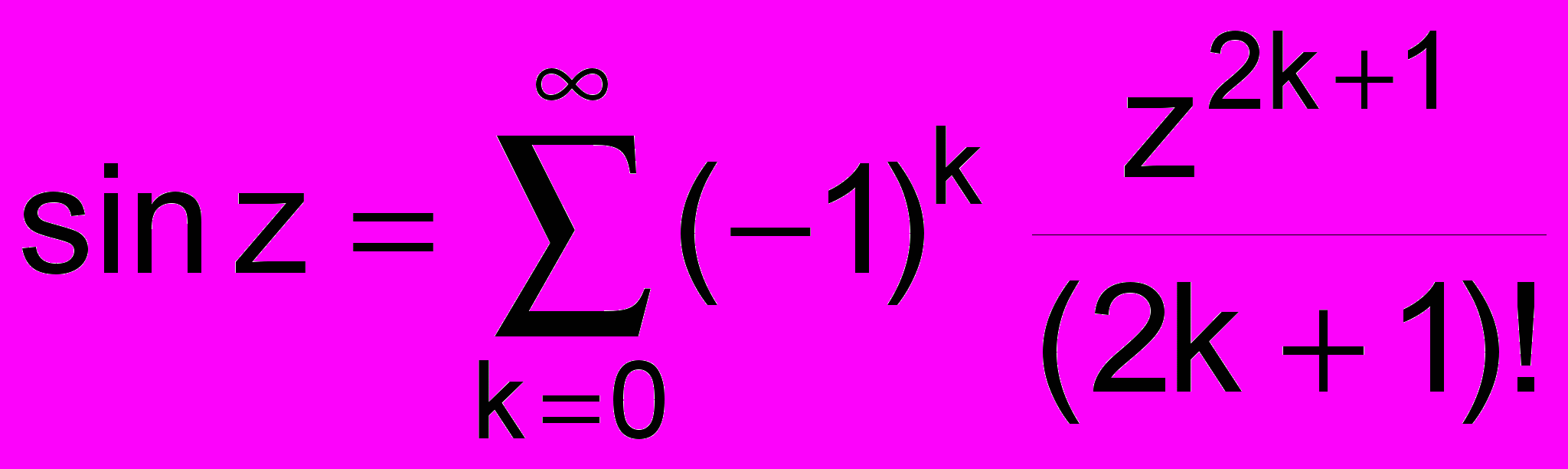
с точностью до . С помощью этой функции проверить справедливость равенства

sin(x+iy) = sinxchy + icosxshy.

Выполнить расчеты для

z = re^i, r = 0.5,  = 0, /8, 2/8, , 2.

Результаты расчетов представить в виде

“z=; левая часть = правая часть”.


8.Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления



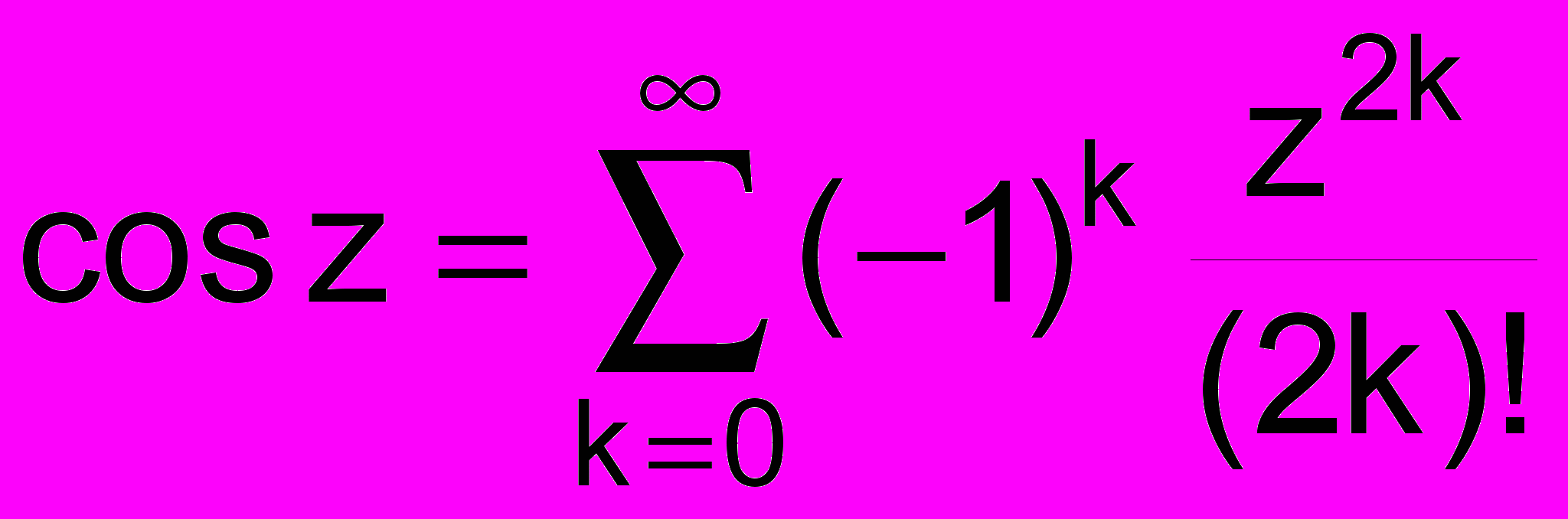
с точностью до . С помощью этой функции проверить справедливость равенства

cos(x+iy) = cosxchy - isinxshy.

Выполнить расчеты для

z = re^i, r = 0.5,  = 0, /8, 2/8, , 2.

Результаты расчетов представить в виде

“z=; левая часть = правая часть”.


9.Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления



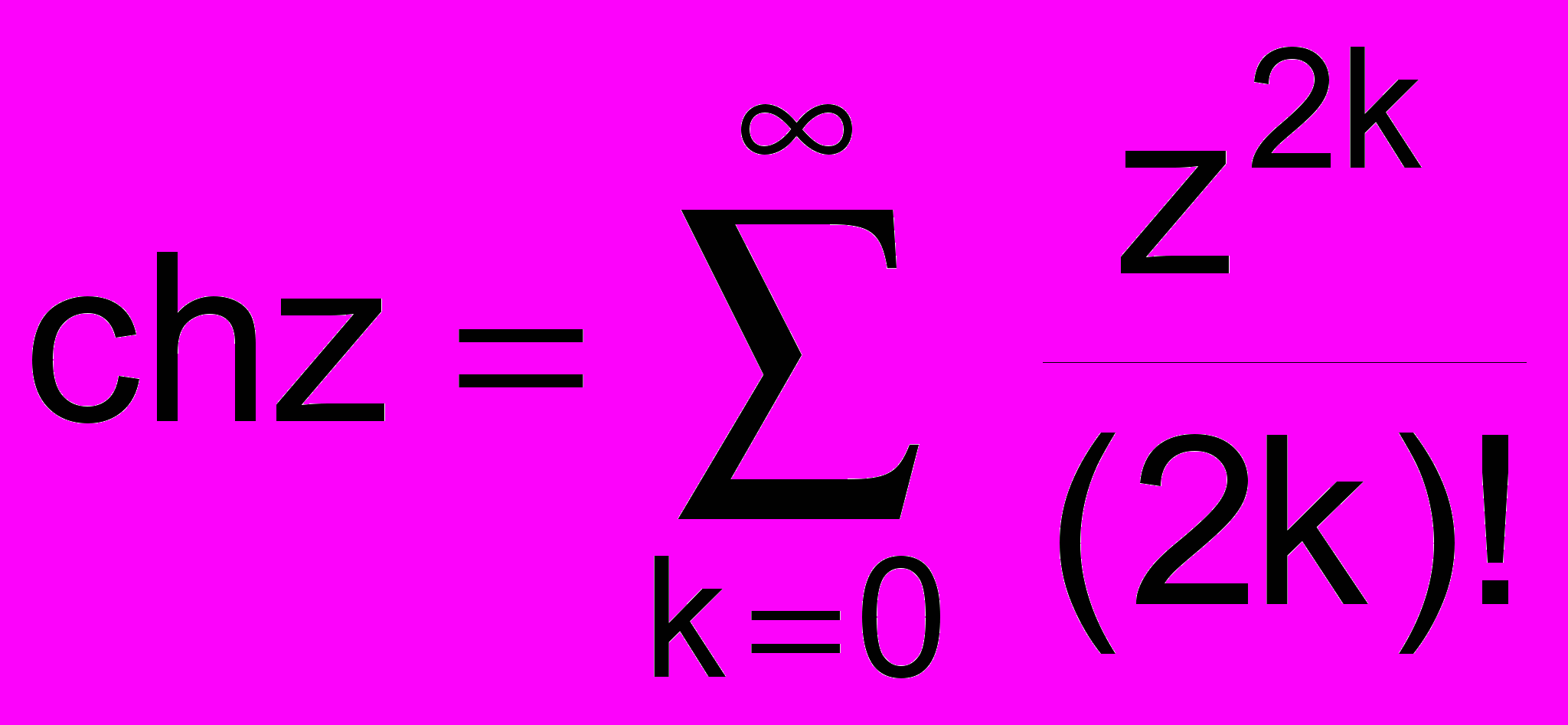
с точностью до . С помощью этой функции проверить справедливость равенства

ch2z = 2ch²z - 1.

Выполнить расчеты для

z = re^i, r = 0.5,  = 0, /8, 2/8, , 2.

Результаты расчетов представить в виде

“z=; левая часть = правая часть”.


10.Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления





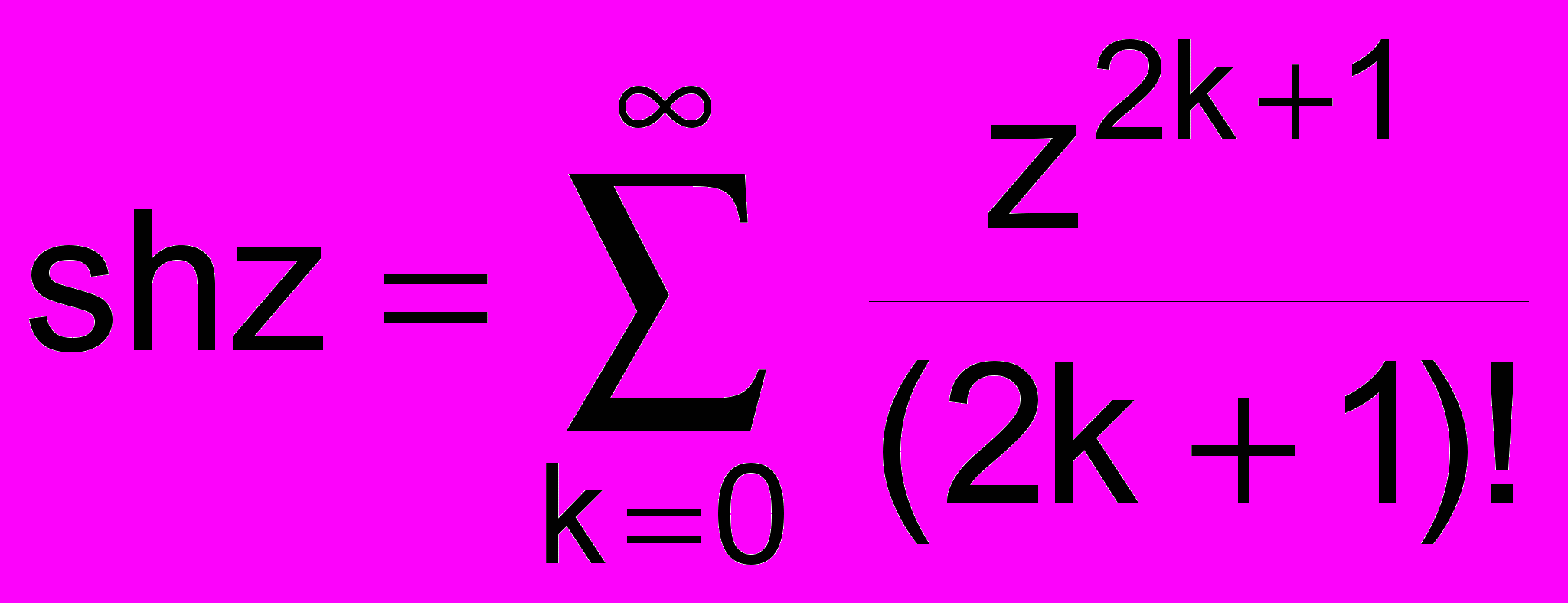
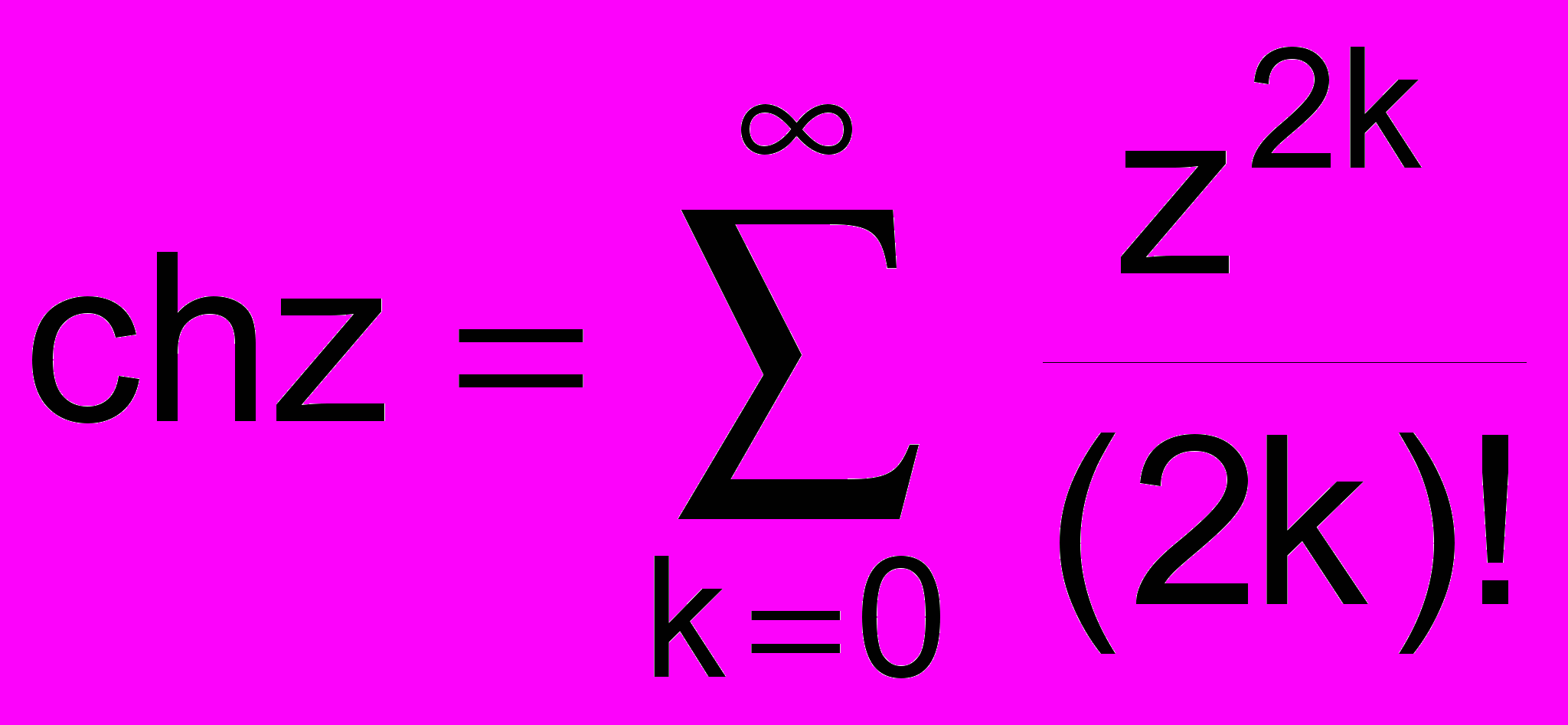
с точностью до . С помощью этой функции проверить справедливость равенства

sh2z = 2shzchz.

Выполнить расчеты для

z = re^i, r = 0.5,  = 0, /8, 2/8, , 2.

Результаты расчетов представить в виде

“z=; левая часть = правая часть”.


11. Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию с аргументами z, n для вычисления zⁿ (n – целое) методом сокращенного умножения:

- определяем двоичное разложение числа n


n = p_kp_k-1p₁p₀₍₂₎; p_i=0,1, i=0, 1, , k;


n = p₀2⁰ + p₁2¹ +  +p_k-12^k-1 + p_k2^k;


- полагаем u = z; v = 1;

- для i = 0, 1, , k вычисляем

если p_i  0, то v := v*u; u := u²;

- полагаем zⁿ = v.

Например, для вычисления z¹⁹ полагаем

19 = 10011₍₂₎, (k=4);

u = z; v = 1;

для i = 0, 1, 2, 3, 4 вычисляем

v = vu; u = uu; v = vu; u = uu; u = uu; u = uu; v = vu; u = uu;

полагаем z¹⁹ = v.

Всего потребовалось 8 умножений – вместо 18.

Выполнить расчеты для n = 16, 17, 18, z = re^i, r = 2,  = 0, /4, 2/4, , 2. Результаты расчетов сравнить с расчетом по формуле Муавра-Лапласа.


12.Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления lnz (z<1) c точностью до .

Воспользоваться разложением



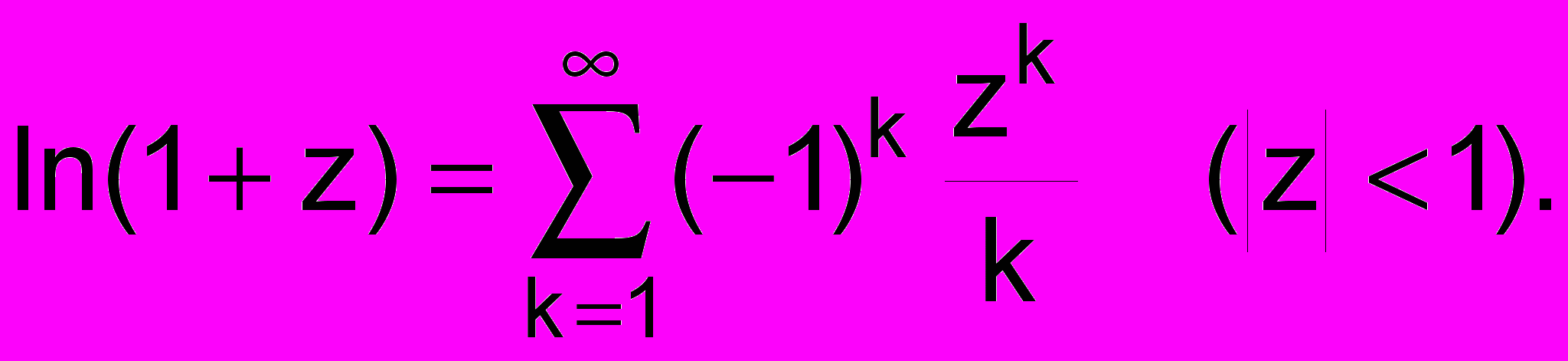
Выполнить расчеты для z = re^i, r = 0.5,  = 0, /8, 2/8, , 2. Сравнить со значениями полученными по формуле (10).


13.Сформировать модуль для работы с комплексными числами. Используя модуль построить изолинии функции zⁿ - 1 в квадрате -2  x  2, -2  y  2.

Указание: Изолинией (линией уровня) функции f(x,y) называется линия, являющаяся решением уравнения

f(x,y) = c (c – заданная константа).

Для получения точек изолинии можно использовать следующий метод: задаем значения одной из переменных и решаем уравнение относительно другой переменной.

Например, для построения изолинии функции f(x,y) в прямоугольнике a  x  b, c  y  d:

полагаем y = y_i = a + ih, i = 0, 1, , k, h = (d – c)/k;

для каждого y_i ищем корни уравнения f(x,y_i) = c на отрезке a  x  b.

Выполнить расчеты для c = c₁, c₂, , c_m, например, c = 0.1, 0.5, 1, 2, 4, 6.


14. Сформировать модуль для работы с комплексными числами. Используя модуль построить изолинии функции z + 1/z для 0 < x  2, 0 < y  2 (см. указание к задаче 13).

Выполнить расчеты для c = c₁, c₂, , c_m, например, c = 0.1, 0.5, 1, 2, 4, 6.

15. Сформировать модуль для работы с комплексными числами. Используя модуль построить изолинии функции chz для -2  x  2, -2  y  2 (см. указание к задаче 13).

Выполнить расчеты для c = c₁, c₂, , c_m, например, c = 0.05, 0.1, 0.2, 0.5, 1, 2, 3.

16. Сформировать модуль для работы с комплексными числами. Используя модуль построить изолинии функции cosz для -2  x  2, -2  y  2 (см. указание к задаче 13).

Выполнить расчеты для c = c₁, c₂, , c_m, например, c = 0.05, 0.1, 0.2, 0.5, 1, 2, 3.

17. Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления значений полинома

P_n(z) = a₀zⁿ + a₁z^n-1 +  +a_n

с комплексными коэффициентами по схеме Горнера. С помощью этой функции построить изолинии функции P_n(z) в квадрате -M  x,y  M, M = (a₁ + a₂ +  + a_n|)/a₀ (см. указание к задаче 13).

Степень и коэффициенты полинома вводятся из файла. Выполнить расчеты для c = c₁, c₂, , c_m, например, c = 0.1, 0.5, 1, 2, 

18. Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления



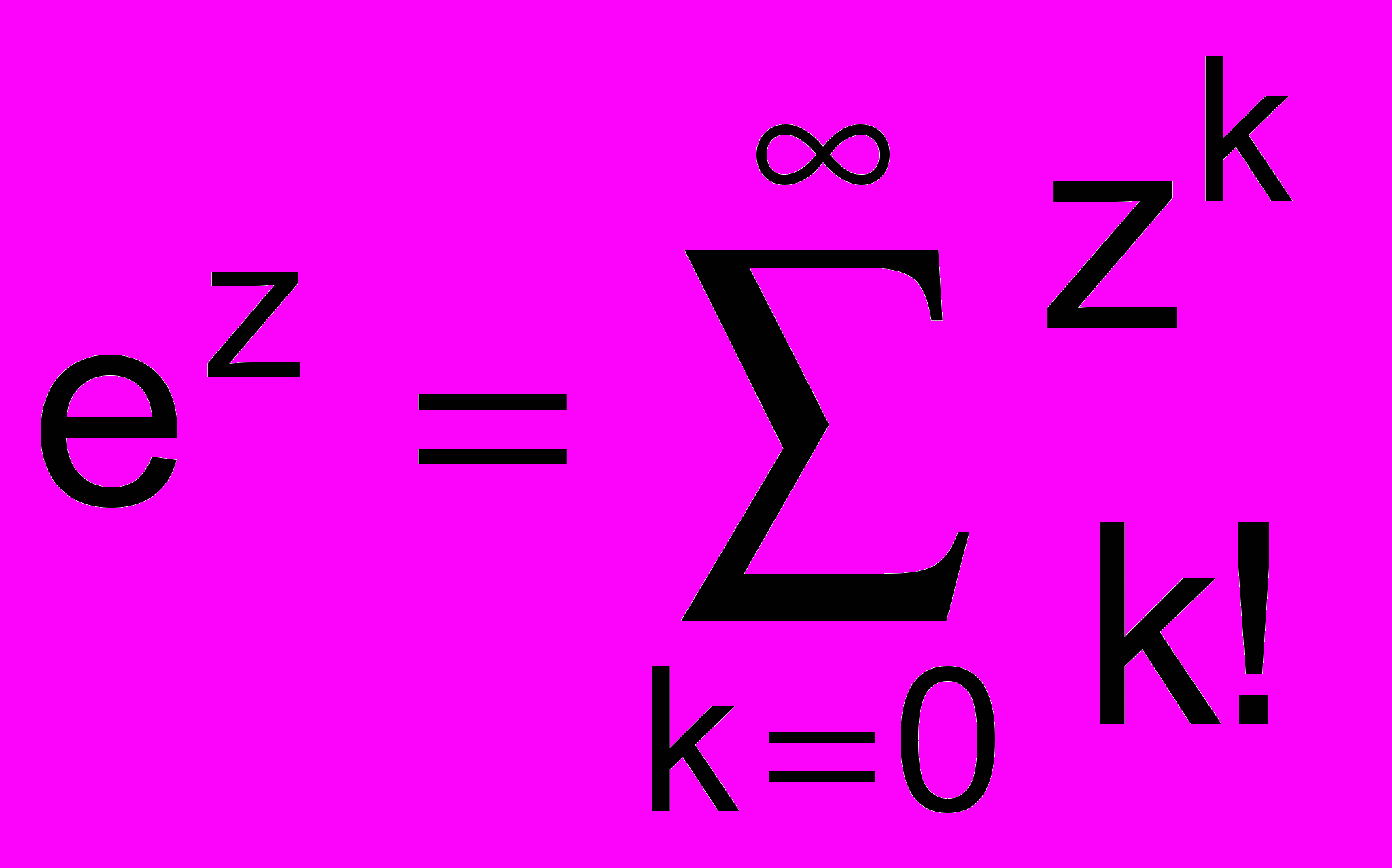
с точностью до . С помощью этой функции проверить справедливость формулы



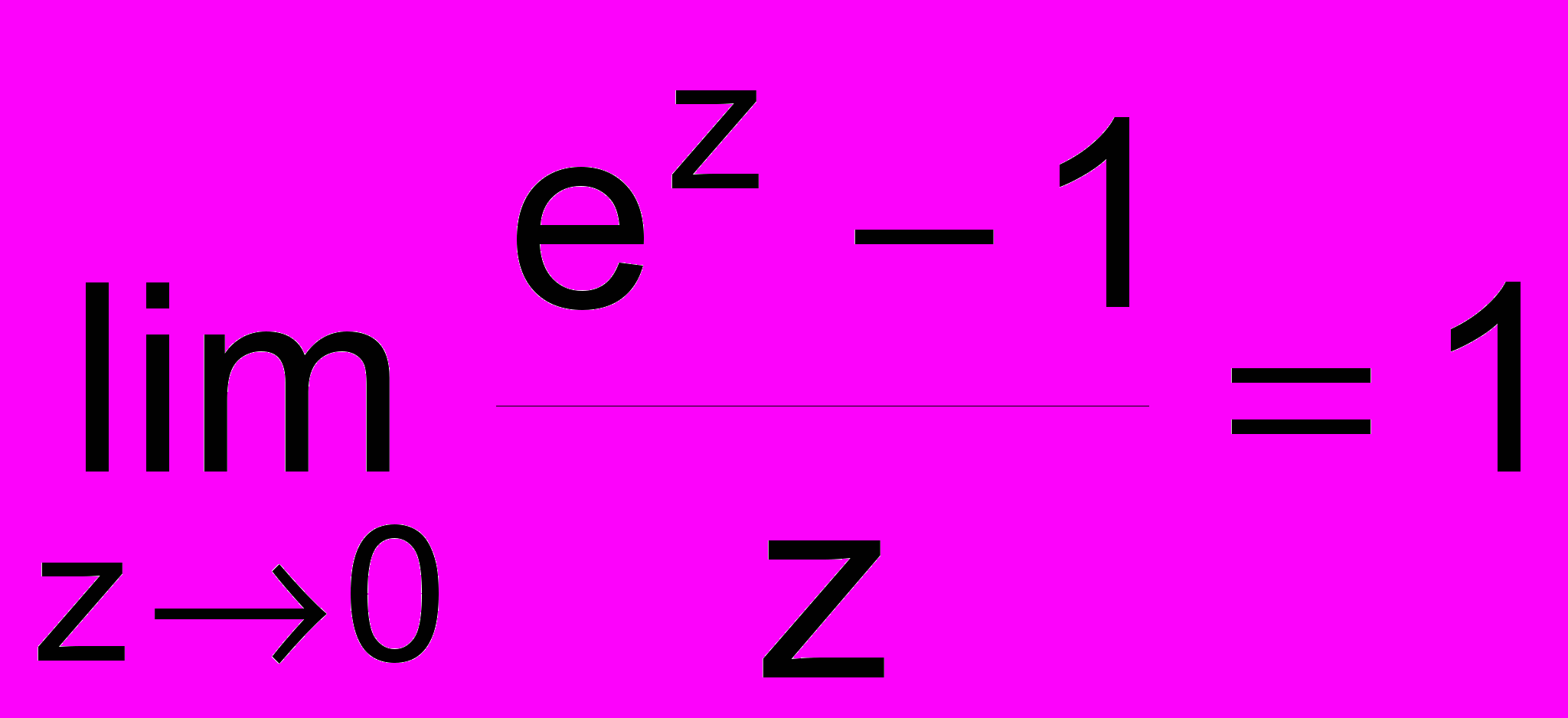
Предел вычислять вдоль луча z = re^i (r₀ = 1; r_i = r_i-1/2), угол  вводится с экрана.

19. Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления



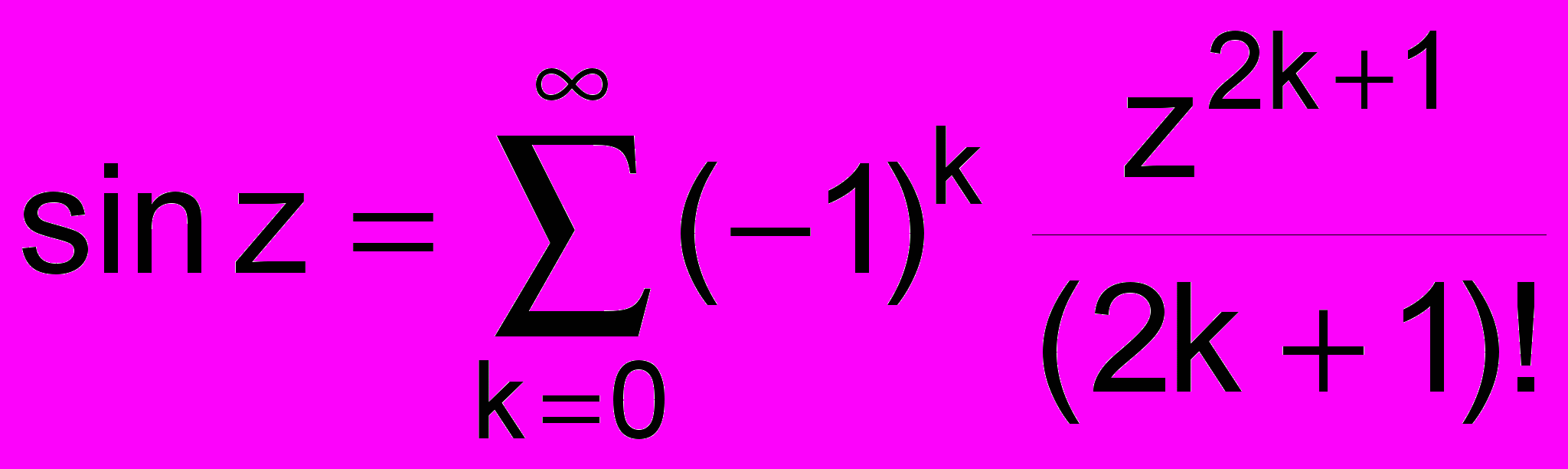
с точностью до . С помощью этой функции проверить справедливость формулы



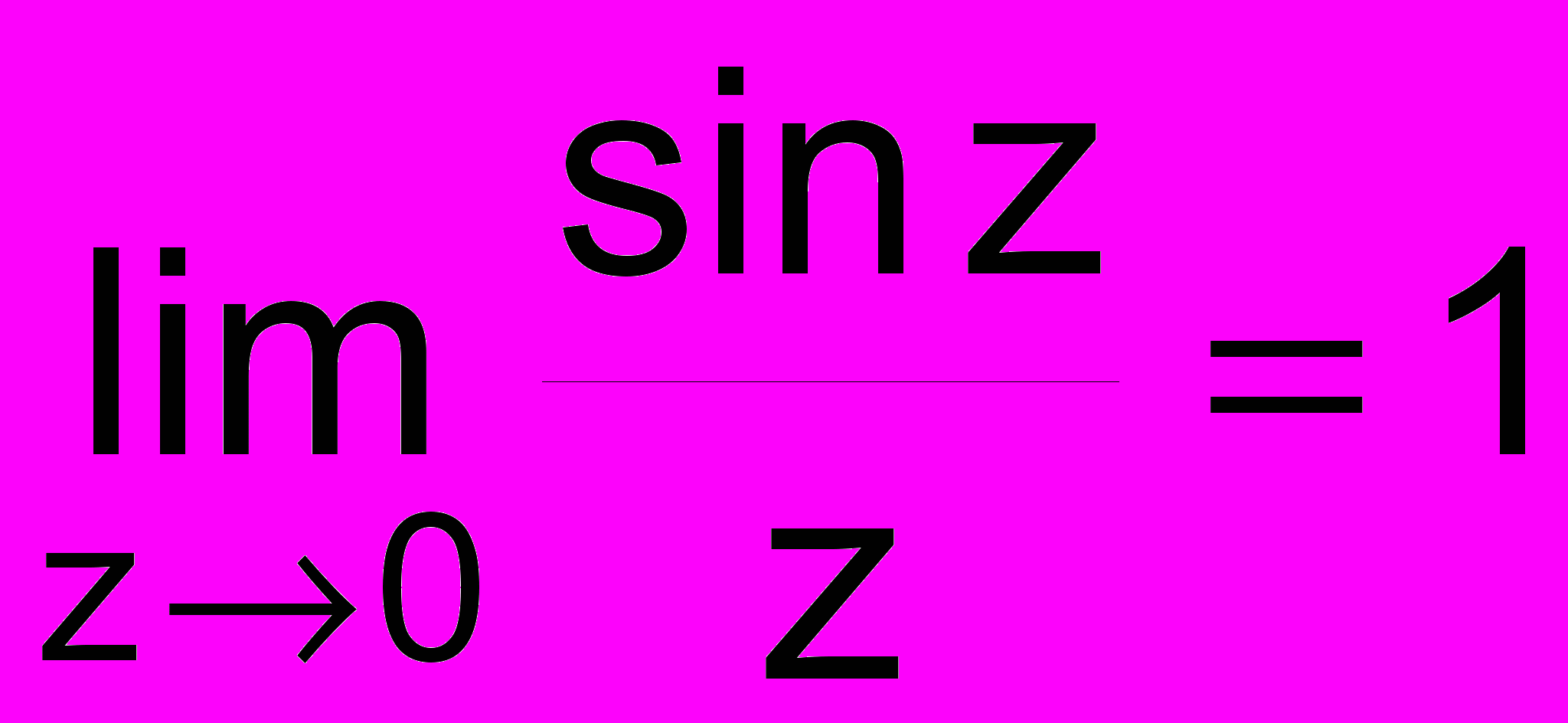
Предел вычислять вдоль луча z = re^i (r₀ = 1; r_i = r_i-1/2), угол  вводится с экрана.

20. Сформировать модуль для работы с комплексными числами. Используя модуль написать функцию для вычисления



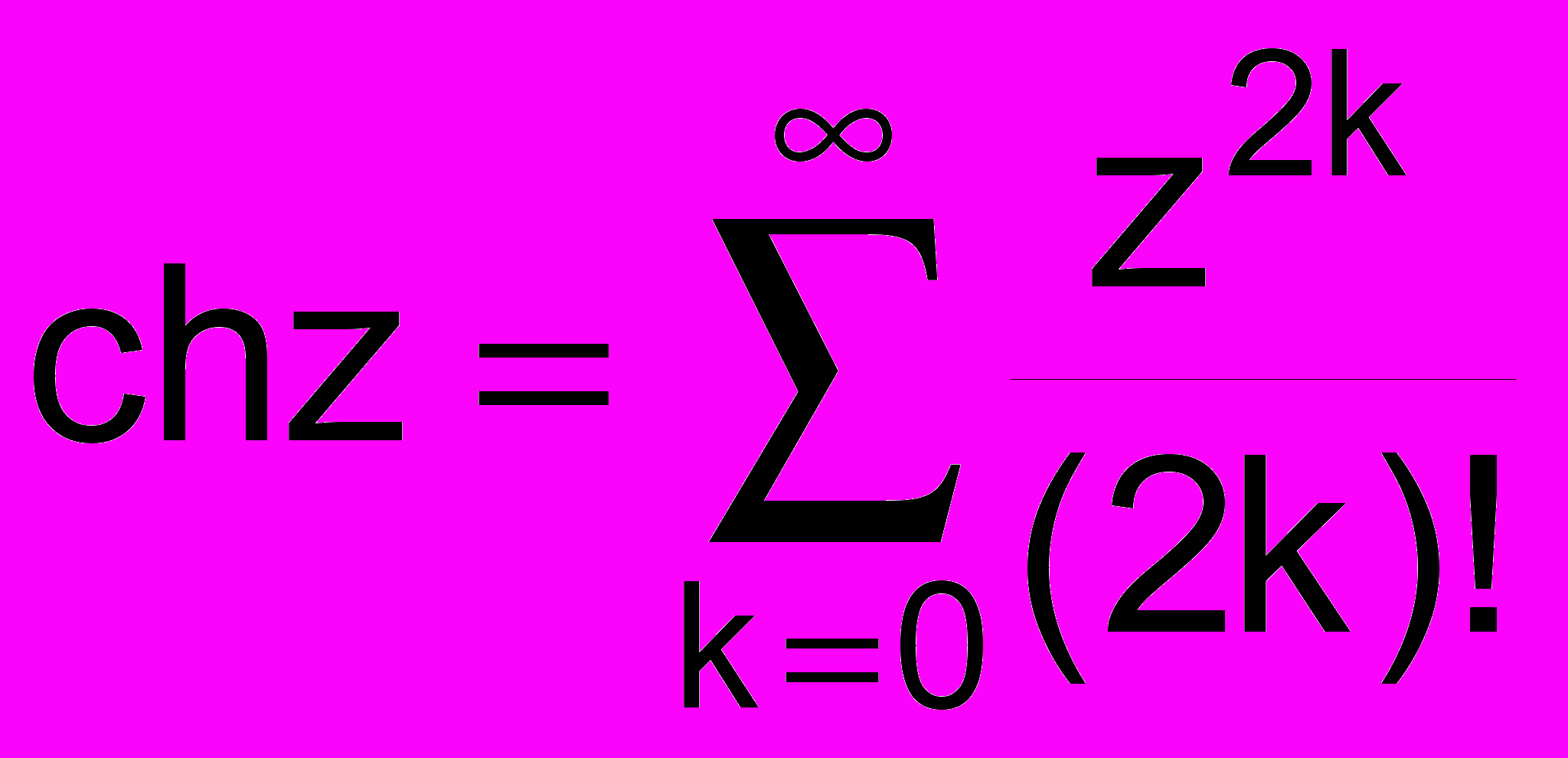
с точностью до . С помощью этой функции проверить справедливость формулы



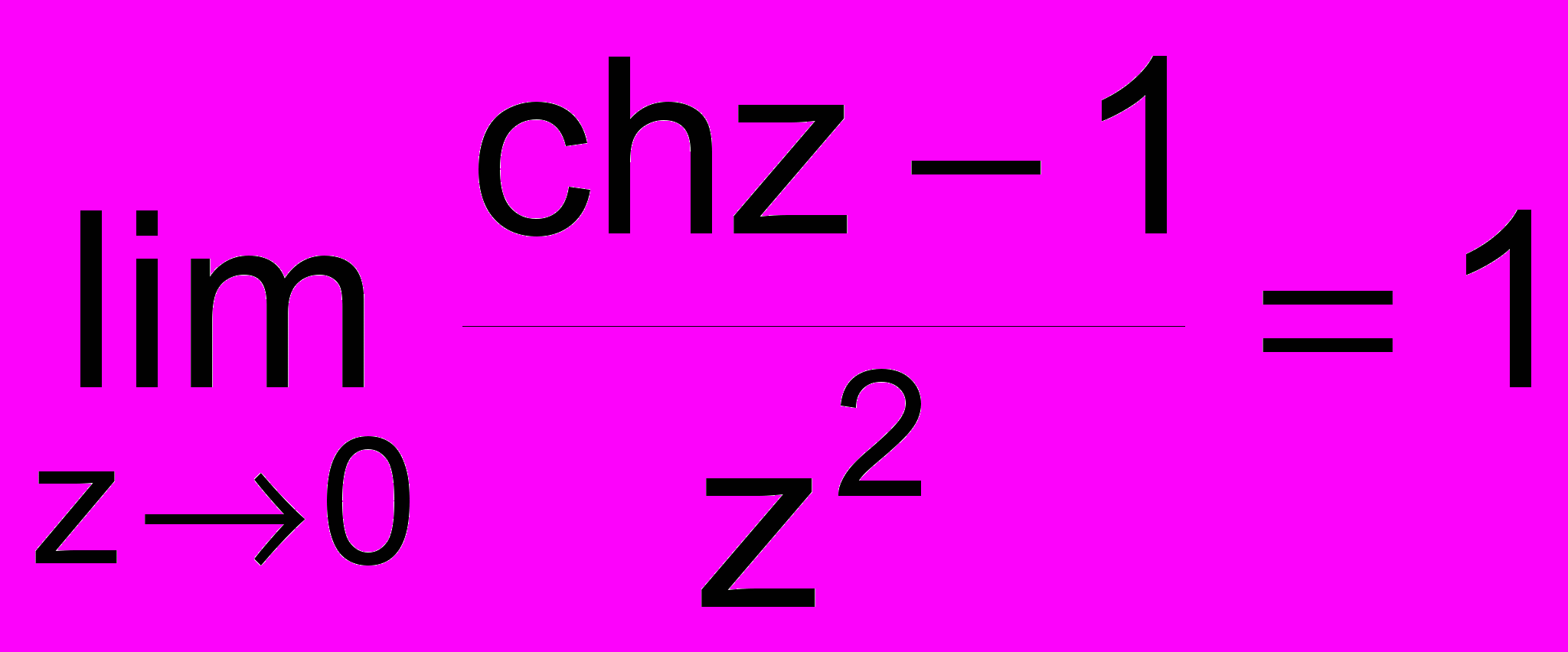
Предел вычислять вдоль луча z = re^i (r₀ = 1; r_i = r_i-1/2), угол  вводится с экрана.

21.Сформировать модуль для работы с комплексными числами. используя модуль решить задачу:

Из файла вводятся целое n (n  100), комплексные z₁, z₂, , z_n. Найти на комплексой плоскости точки z_i, z_j (i,j = 1, , n; i  j), расстояние между которыми минимально. Дать графическое представление задачи.

22.Сформировать модуль для работы с комплексными числами. используя модуль решить задачу:

Из файла вводятся целое n (n  100), комплексные z₁, z₂, , z_n. Найти на комплексой плоскости точки z_i, z_j (i,j = 1, , n; i  j), расположенные на одном луче, выходящим из точки z = 0. Если таких точек нет, найти точки, расположенные на лучах, максимально “близких” друг к другу – с минимальным углом между ними. Дать графическое представление задачи.

23.Сформировать модуль для работы с комплексными числами. используя модуль решить задачу:

Из файла вводятся целое n (n  100), комплексные z₁, z₂, , z_n. В точках z_i, i = 1, …, n вычисляются значения функции



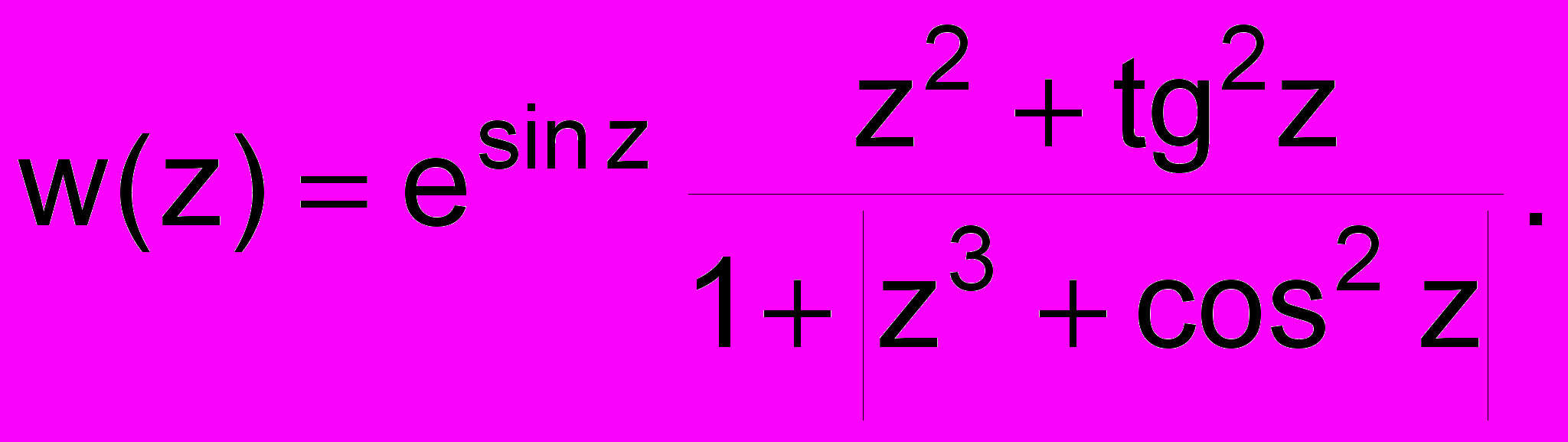
Найти точку, в которой Imw принимает максимальное значение.

24.Сформировать модуль для работы с комплексными числами. используя модуль решить задачу:

Из файла вводятся целое n (n  100), комплексные z₁, z₂, , z_n. Упорядочить последовательность z_i методом сортировки выбором по неубыванию абсолютной величины числа, если абсолютные величины совпадают, - по неубыванию аргументов чисел. (Указание: в качестве ключа для сортировки выбирается величина 2z + argz).

В файл результатов выдаются исходная последовательность и упорядоченная последовательность с указанием абсолютной величины и аргументов чисел.

25.Сформировать модуль для работы с комплексными числами. используя модуль решить задачу:

Из файла вводятся целое n (n  100), комплексные z₁, z₂, , z_n. Упорядочить последовательность z_i методом “пузырька” по неубыванию абсолютной величины числа, если абсолютные величины совпадают, - по неубыванию аргументов чисел. (Указание: в качестве ключа для сортировки выбирается величина 2z + argz).

В файл результатов выдаются исходная последовательность и упорядоченная последовательность с указанием абсолютной величины и аргументов чисел.

26.Сформировать модуль для работы с комплексными числами. используя модуль решить задачу:

Из файла вводятся целое n (n  100), комплексные z₁, z₂, , z_n. Упорядочить последовательность z_i методом сортировки разделением по неубыванию абсолютной величины числа, если абсолютные величины совпадают, - по неубыванию аргументов чисел. (Указание: в качестве ключа для сортировки выбирается величина 2z + argz).

В файл результатов выдаются исходная последовательность и упорядоченная последовательность с указанием абсолютной величины и аргументов чисел.

27. Сформировать модуль для работы с комплексными числами. Используя модуль сравнить по времени исполнения алгоритмы сортировки выбором и сортировки разделением. Для этого:

• написать процедуры сортировки массива комплексных чисел по неубыванию величины 2z + argz (массив упорядочивается по неубованию абсолютных величин чисел, при совпадении абсолютных величин – по неубыванию аргументов чисел);
  
• используя датчик случайных чисел, равномерно распределенных на отрезке [-1, 1], сформировать массив из N комплексных чисел;
  
• Упорядочить массив (! один и тот же исходный массив !) каждым из алгоритмов, засекая время исполнения.
  

Выполнить расчеты для N = 10 (контрольный просчет) и N > 1000 (основной расчет).

28. Сформировать модуль для работы с комплексными числами. Используя модуль сравнить по времени исполнения алгоритмы сортировки выбором, сортировки методом “пузырька” и сортировки перестановками:

для i = 1, …, n-1 выполнить

для j = i+1, …, n выполнить

если x_i > x_j, то переставить x_i, x_j.

Для этого:

• написать процедуры сортировки массива комплексных чисел по неубыванию величины 2z + argz (массив упорядочивается по неубованию абсолютных величин чисел, при совпадении абсолютных величин – по неубыванию аргументов чисел);
  
• используя датчик случайных чисел, равномерно распределенных на отрезке [-1, 1], сформировать массив из N комплексных чисел;
  
• Упорядочить массив (! один и тот же исходный массив !) каждым из алгоритмов, засекая время исполнения.
  

Выполнить расчеты для N = 10 (контрольный просчет) и N > 1000 (основной расчет).