Учебно-методический комплекс «Вычислительная математика» для студентов отделения высшего образования специальности «Вычислительные машины, комплексы, системы и сети»

Вид материала

Учебно-методический комплекс

Содержание Шифр и наименование дисциплины Объём дисциплины 2. Материалы к промежуточному и 9 1. Программа курса дисциплины «Вычислительная математика» 1.1. Тематический план дисциплины Цели курса. ТЕМАТИЧЕСКИЙ ПЛАН УЧЕБНОЙ ДИСЦИПЛИНЫ (2 к, ДО) 1.2. Содержание учебной дисциплины (дидактические единицы) ДЕ I (48 часов) Тема 3. Методы численного решения уравнений и систем нелинейных уравнений. ДЕ II (38 часов) ДЕ III (54 часа) Лабораторные работы 2. Материалы к промежуточному и итоговому контролю 3. Методические рекомендации по освоению учебного материала 4. Основная и дополнительная литература

Подобный материал:

• Автор Ридель Валерий Вольдемарович учебно-методический комплекс, 620.31kb.
• Программа сквозной практической подготовки для студентов направления 654600 специальности, 176.46kb.
• Курс лабораторных работ для студентов специальностей 230101 "Вычислительные машины,, 318.37kb.
• Методические указания и контрольные задания для студентов заочников Специальности 230101, 135.39kb.
• Программа-минимум кандидатского экзамена по специальности 05. 13. 15 «Вычислительные, 126.11kb.
• Учебно-методический комплекс по дисциплине вычислительные системы, сети и телекоммуникации, 287.7kb.
• Микропроцессорные системы, 177.83kb.
• Рабочая программа, 258.96kb.
• Компьютерная графика, 205.26kb.
• Автор Карпухин Владимир Борисович учебно-методический комплекс, 473.72kb.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

РУБЦОВСКИЙ ИНСТИТУТ


«Утверждаю»

Директор РИ (филиала) АлтГУ

_____________ К.Г. Анисимов

«_____» _____________2010 г.


Учебно-методический комплекс


«Вычислительная математика»

для студентов отделения высшего образования специальности

«Вычислительные машины, комплексы, системы и сети»

Рубцовск 2010

Кафедра	Математики и прикладной информатики
Шифр и наименование дисциплины	Вычислительная математика
Статус дисциплины	общепрофессиональная
Специальности	Вычислительные машины, комплексы, системы и сети
Объём дисциплины	140 часов (4,7 зачетных единиц)

Зав. кафедрой математики и прикладной информатики

_________ к.т.н., доцент Жданова Е.А.

Зам. директора по учебной работе

_____________ Жданова Е.А.


Автор: Анисимова Е.А., к.т.н., доцент преподаватель кафедры математики и прикладной информатики,

Ибрагимова А.С., преподаватель кафедры математики и прикладной информатики.


Содержание УМК

1. Программа курса дисциплины

«Вычислительная математика»

1.1. Тематический план дисциплины

«Вычислительная математика»

Пояснительная записка: Первый и главный этап математического моделирования — собственно построение модели — очень часто опирается на некоторые имеющиеся исходные данные. При этом широко применяются вычислительные методы обработки данных: методы интерполяции, аппроксимации и др. Основная задача моделирования различного рода процессов и систем с целью исследования объектов, прогнозирования их поведения или поиска наилучших условий функционирования сводится к расчету анализируемых показателей по математической модели при тех или иных значениях (или функциях) входных величин. Важное значение при этом приобретают вычислительные алгоритмы, с помощью которых можно получить при моделировании решение конкретной математической задачи.

Цели курса.

Знакомство с идеями и алгоритмами решения наиболее распространенных задач вычислительной математики, применяющихся при математическом моделировании и получение практических навыков их применения

Задачи курса.

• Дать основы знаний по каждому разделу вычислительной математике.
  
• Привить общие навыки решения конкретных задач по основным разделам вычислительной математики.
  
• Получить общее представление о приложениях вычислительной математики.
  

Задачи лабораторных работ

• Соединить теоретические знания, полученные студентом при осмыслении основ вычислительной математики, с конкретными их приложениями в процессе выполнения лабораторных работ на языке Турбо Паскаль.
  
• Научить студента корректной постановке вычислительных задач и правильному выбору методов их решения.
  
• Развить у студента навыки самостоятельной работы при решении вычислительных задач.
  

Курс «Вычислительная математика» опирается на знания, полученные при изучении математического анализа, алгебры, аналитической геометрии, дифференциальных уравнений, информатики (турбо-паскаль).


ТЕМАТИЧЕСКИЙ ПЛАН УЧЕБНОЙ ДИСЦИПЛИНЫ (2 к, ДО)

Дидактические единицы (ДЕ)	Наименование тем	Макс. учебная нагрузка студента, час	Количество аудиторных часов при очной форме о6учения			Самост. работа студ.
			Всего	Лекции	Лабораторные раб.
1	2	3	4	5	6	7
ДЕ I. 25 баллов	1. Понятие линейного нормированного пространства.	4	2	2		2
	2. Методы численного решения систем линейных алгебраических уравнений.	20	8	4	4	12
	3. Методы численного решения уравнений и систем нелинейных уравнений.	24	8	4	4	16
Промежуточный контроль		Коллоквиум
ДЕ II 30 баллов	4. Среднеквадратичное приближение функций.	38	18	8	10	20
Промежуточный контроль		Контрольная работа
ДЕ III 45 баллов	5. Интерполирование функций.	10	4	2	2	6
	6. Численное дифференцирование.	10	8	4	4	2
	7. Численное интегрирование.	16	8	4	4	8
	8. Численное решение обыкновенных дифференциальных уравнений.	18	8	4	4	10
Промежуточный контроль		Контрольная работа
Итоговый контроль		Зачет
Итого часов		140	64	32	32	76

1.2. Содержание учебной дисциплины

(дидактические единицы)

ДЕ I (48 часов)

Тема 1. Понятие линейного нормированного пространства.

Примеры линейных нормированных пространств. Сходимость последовательностей в линейных нормированных пространствах.

Тема 2. Методы численного решения систем линейных алгебраических уравнений.

Метод Гаусса. Метод итераций.

Тема 3. Методы численного решения уравнений и систем нелинейных уравнений.

Отделение корней. Метод половинного деления. Метод итераций для одного уравнения с одним неизвестным. Метод итераций для системы двух нелинейных уравнений.

ДЕ II (38 часов)

Тема 4. Среднеквадратичное приближение функций.

Интегральное среднеквадратичное приближение функций обобщенными многочленами. Среднеквадратичное приближение функций тригонометрическими многочленами. Точечное среднеквадратичное приближение функций ортогональными многочленами. Ортогональные многочлены Чебышева. Метод наименьших квадратов.

ДЕ III (54 часа)

Тема 5. Интерполирование функций.

Интерполяционная формула Лагранжа.

Тема 6. Численное дифференцирование.

Вычисление производной по ее определению. Конечно-разностные аппроксимации производных.

Тема 7. Численное интегрирование.

Квадратурные формулы прямоугольников, трапеций и Симпсона. Квадратурные формулы Гаусса.

Тема 8. Численное решение обыкновенных дифференциальных уравнений.

Метод Эйлера. Метод Рунге-Кутта.

Лабораторные работы

1. Решение СЛАУ методом Гаусса .-2 ч.
   
2. Решение СЛАУ методом простых итераций.-2 ч.
   
3. Численное решение уравнений. Метод половинного деления. Метод итераций. – 2 ч.
   
4. Численное решение систем уравнений. Метод итераций для системы двух нелинейных уравнений. – 2 ч.
   
5. Среднеквадратичное приближение функций тригонометрическими многочленами. Построение тригонометрического многочлена, аппроксимирующего заданную функцию. – 4 ч.
   
6. Точечное среднеквадратичное приближение функций ортогональными многочленами. Вычисление ортогональных многочленов Чебышева на заданном множестве точек. – 2 ч.
   
7. Вычисление многочленов наилучшего среднеквадратичного приближения функций ортогональными многочленами. – 2 ч.
   
8. Метод наименьших квадратов. Определение параметров эмпирической формулы с двумя параметрами методом наименьших квадратов. – 2 ч.
   
9. Интерполирование функций. Построение интерполяционного многочлена Лагранжа. – 2 ч.
   
10. Вычисление производной по ее определению. – 2 ч.
    
11. Вычисление производных первого и второго порядков. – 2 ч.
    
12. Вычисление определенного интеграла по квадратурным формулам прямоугольников, трапеций и Симпсона. – 2 ч.
    
13. Вычисление определенного интеграла методом двойного по формуле Гаусса с тремя узлами. – 2 ч.
    
14. Численное решение задачи Коши для дифференциального уравнения первого порядка методами Эйлера, Эйлера-Коши и Рунге-Кутта. – 4 ч.
    

2. МАТЕРИАЛЫ К ПРОМЕЖУТОЧНОМУ И

ИТОГОВОМУ КОНТРОЛЮ

Задача 1. Методом половинного деления с точностью =10^-2 найти корень уравнения

1. .
   
2. .
   

Задача 2. Методом итераций с указанной точностью найти корень уравнения.

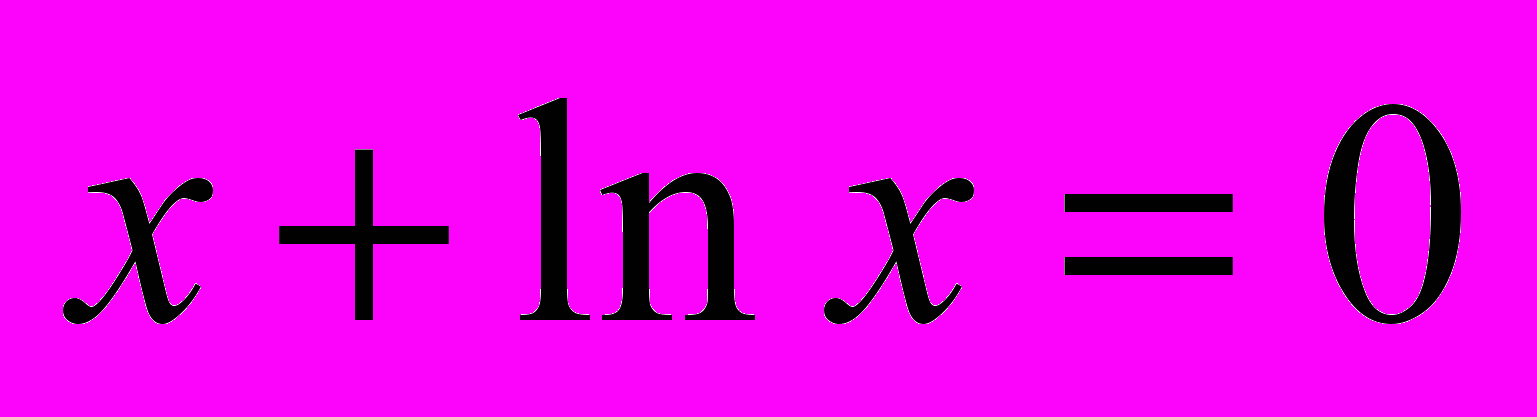1. , =10^-3.
   
2. , =10^-2.
   

Задача 3. Найти с точностью =10^-3 решения системы уравнений, расположенные в первой четверти Ох₁х₂.

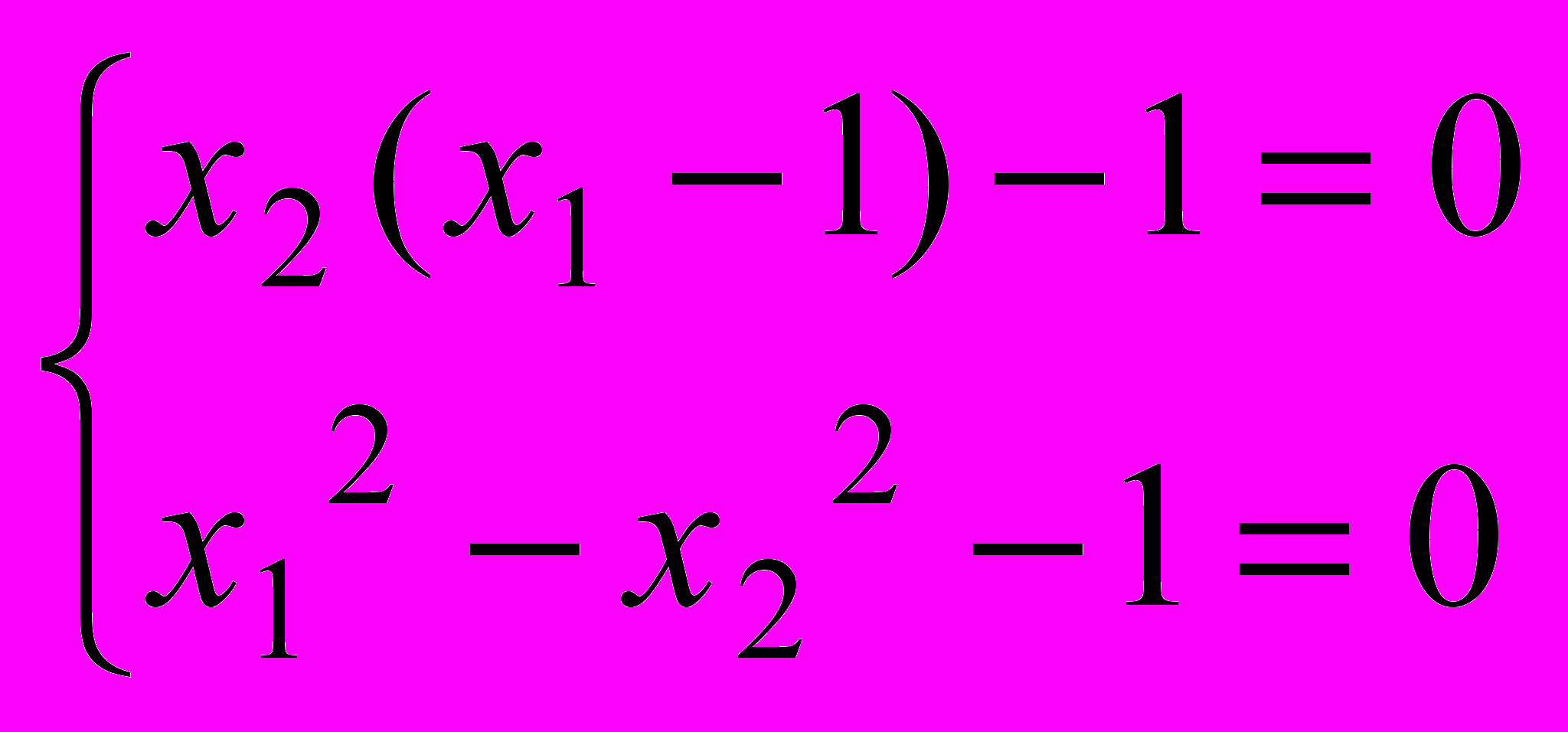1. . 2. .
   

Задача 4. Найти ряд Фурье для функции 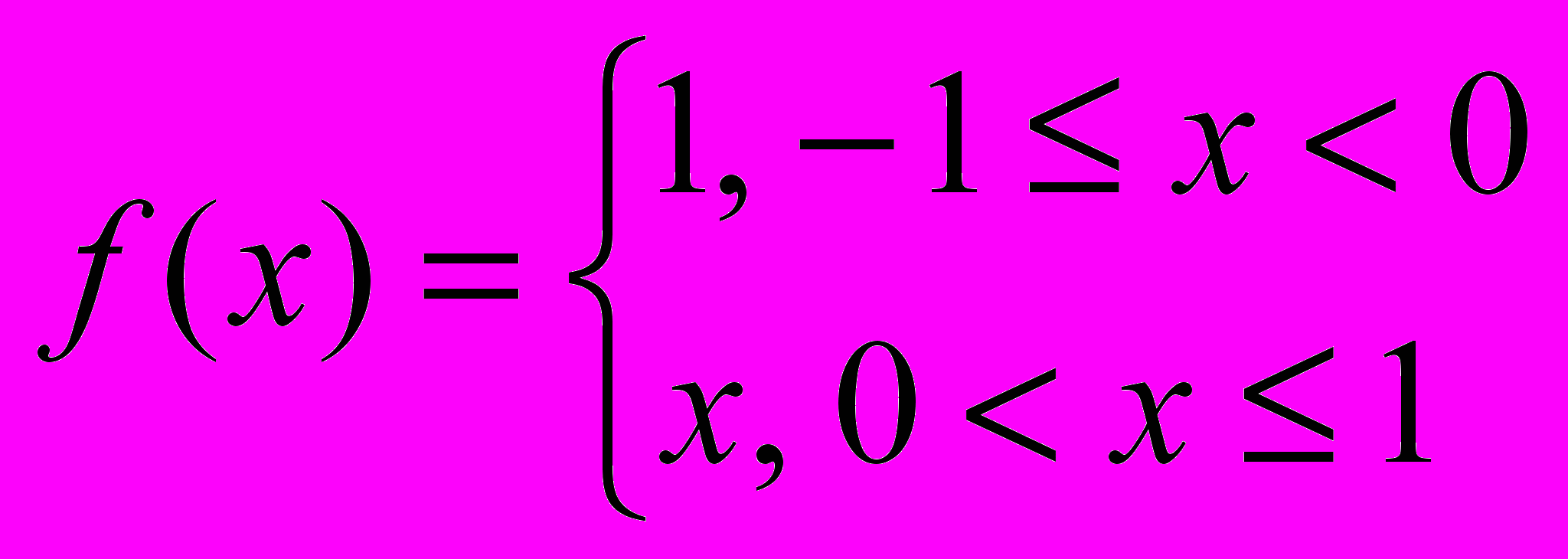. Представить графически приближение этой функции с помощью тригонометрических многочленов степеней n₁=1, n₂=3. Оценить погрешность среднеквадратичного приближения .

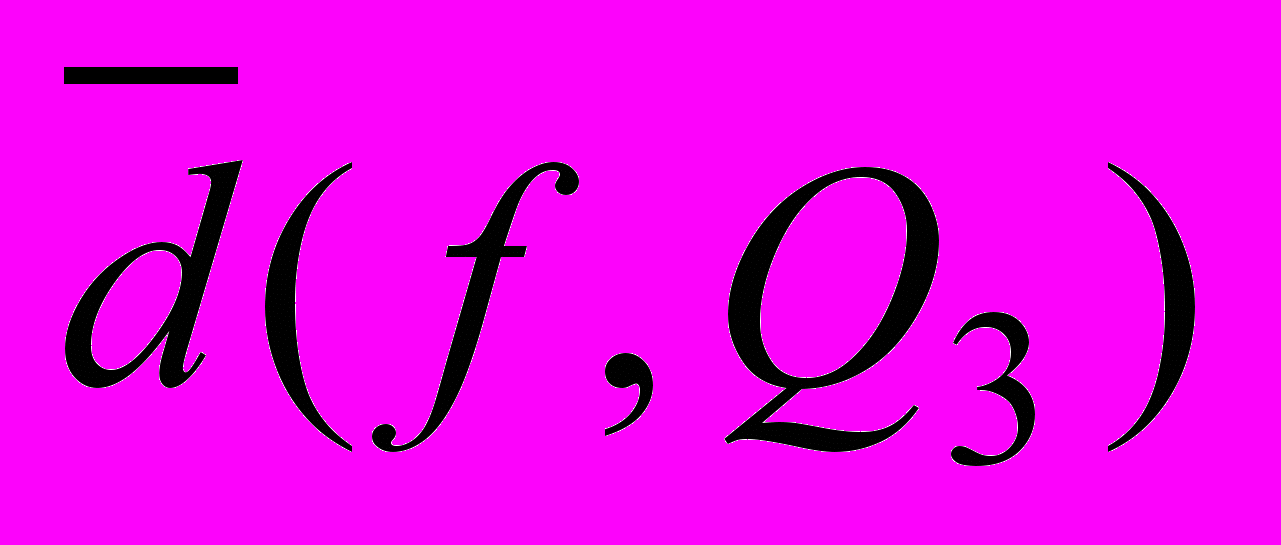Задача 5. Функцию 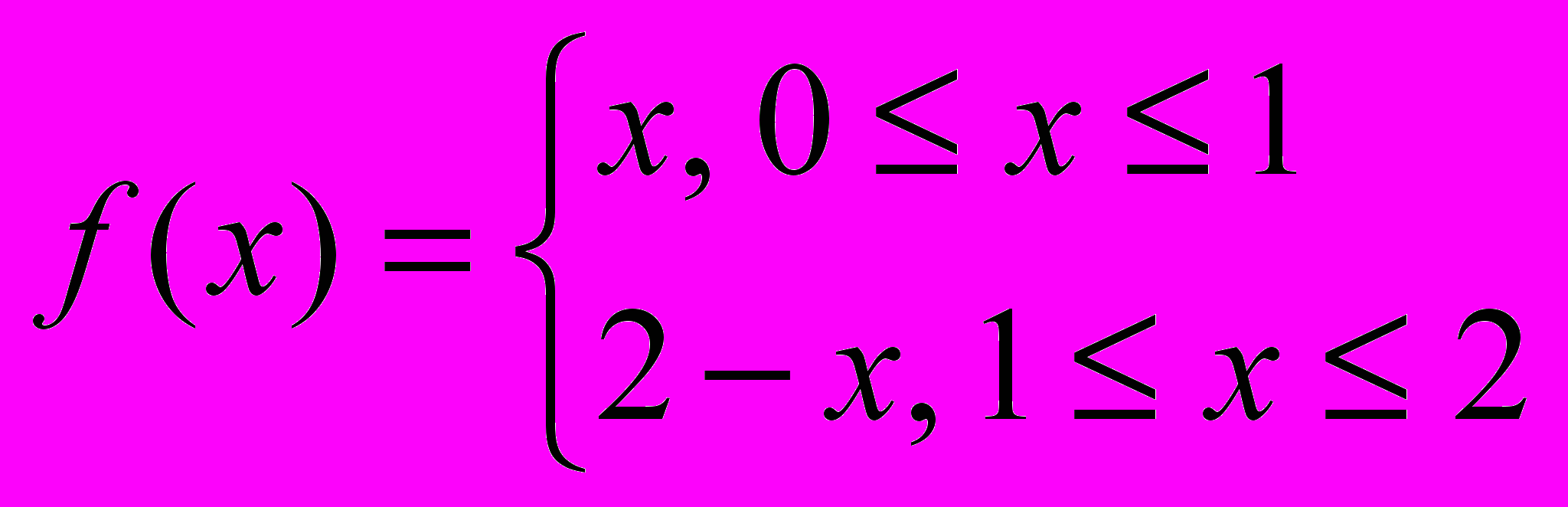разложить в ряд Фурье по синусам. Представить графически приближения этой функции с помощью тригонометрических многочленов степеней n₁=1, n₂=5. Оценить погрешности среднеквадратичного приближения 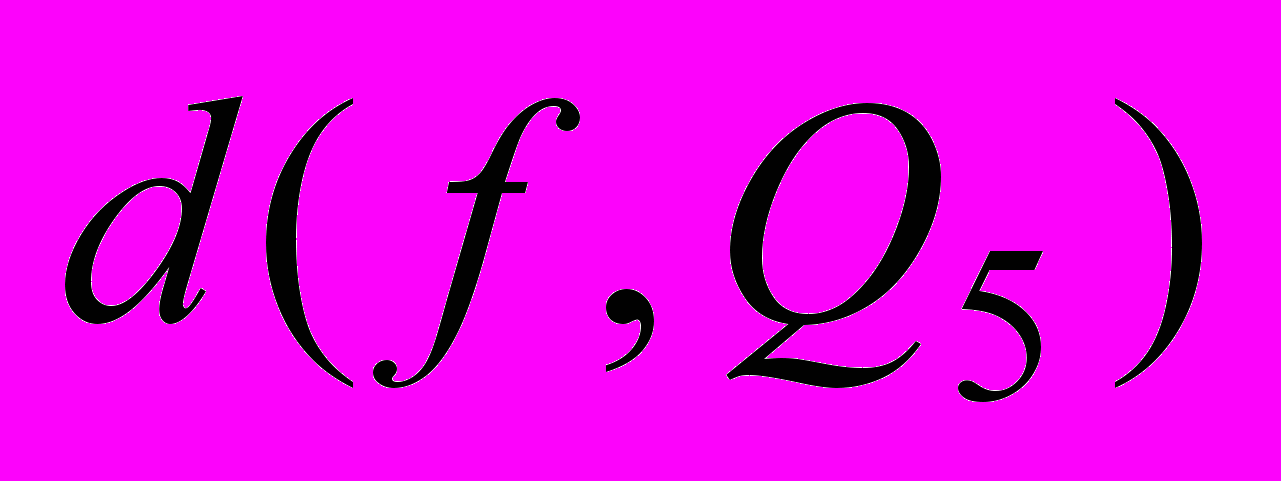и .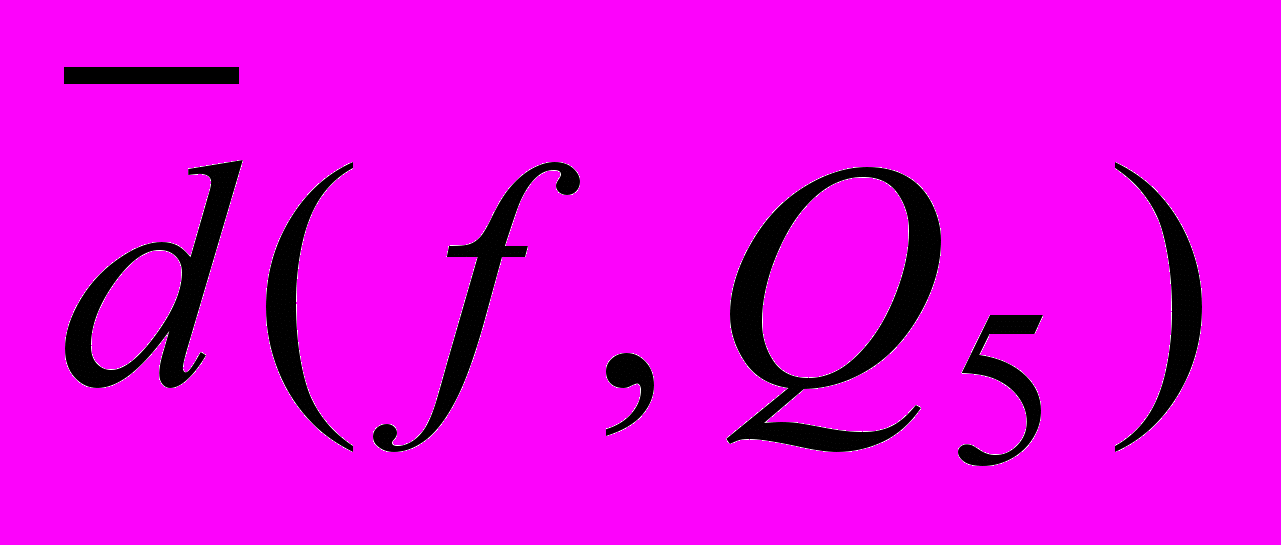

Задача 6. На множестве двух точек 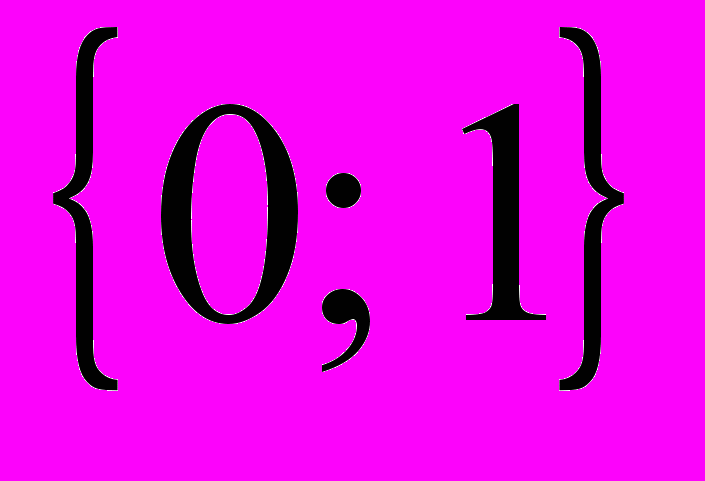определить ортогональные многочлены Чебышева и вычислить их нормы.

Задача 7. Функция 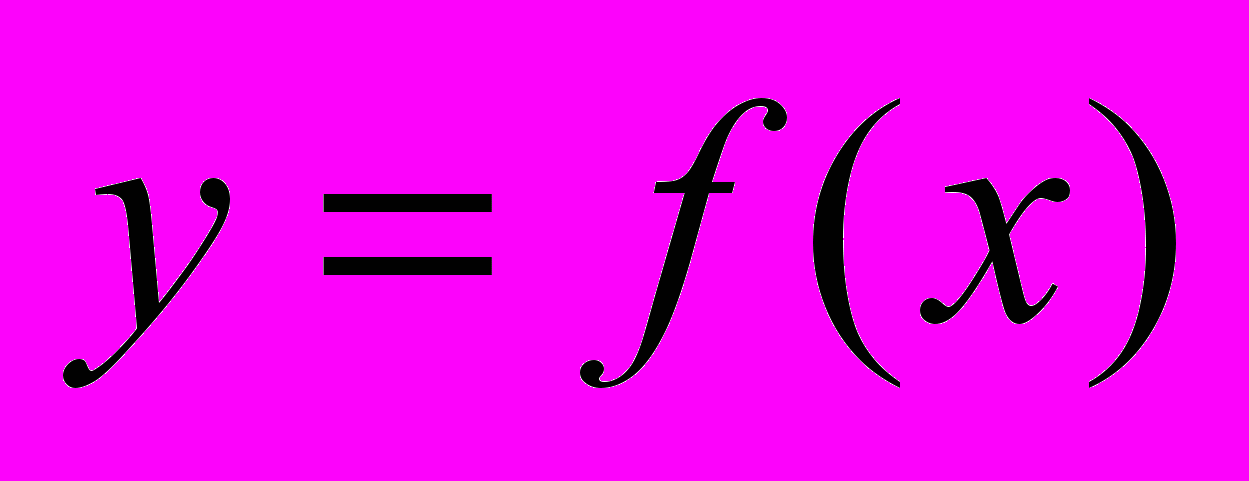определена таблицей. Требуется аппроксимировать функцию 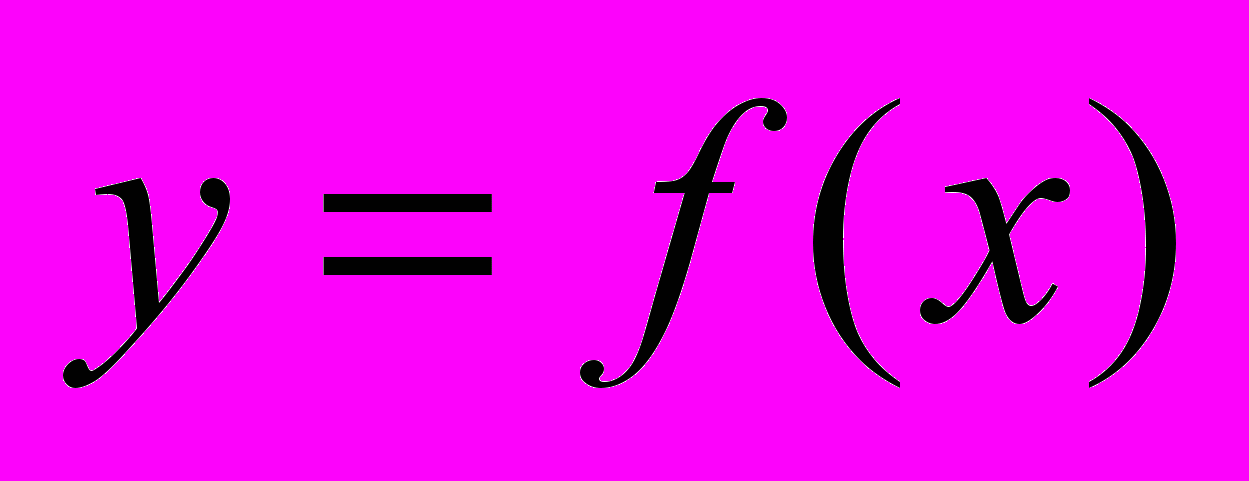алгебраическими многочленами наилучшего среднеквадратичного приближения 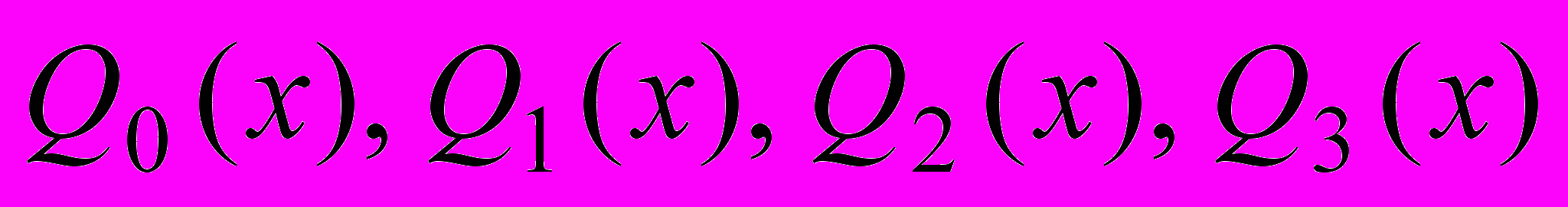и оценить погрешности каждого приближения 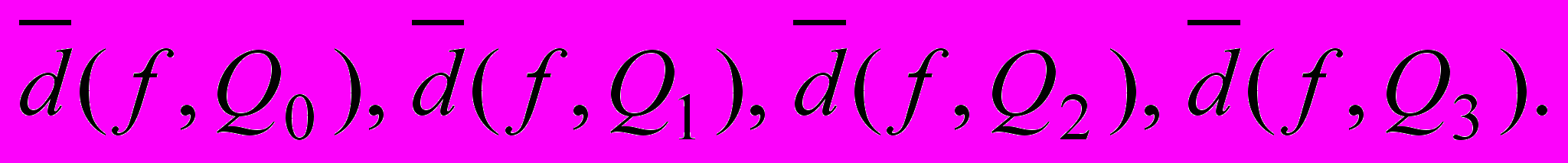Изобразить графики функций 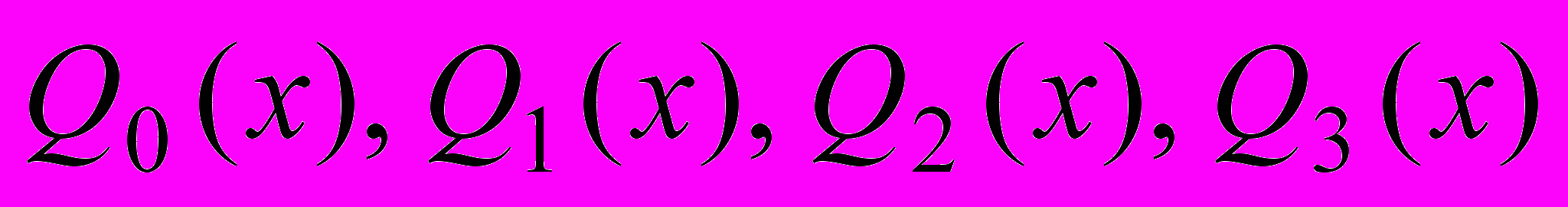и отметить экспериментальные точки в той же системе координат.

i	1	2	3	4
xi	0	1	3	4
yi	4	0	1	2

Задача 8. Установить вид эмпирической формулы 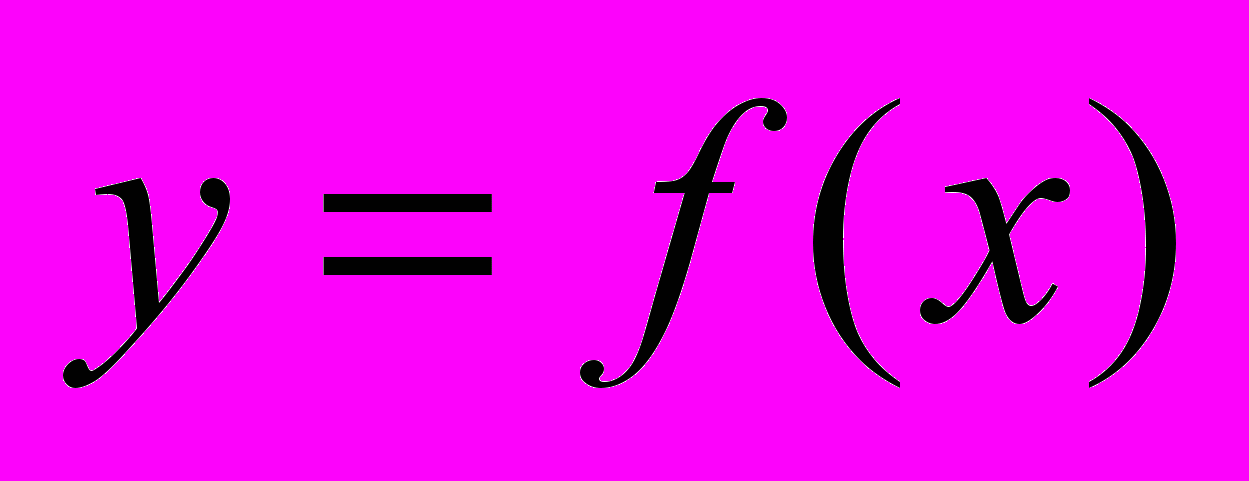используя аппроксимирующие зависимости с двумя параметрами и .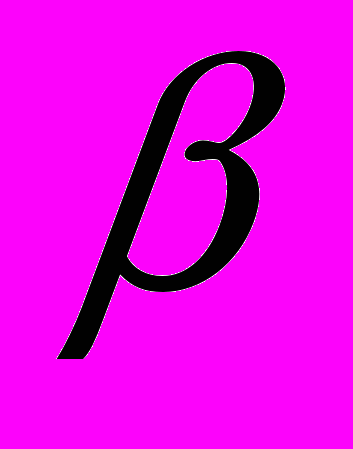

xi	1	2	3	4	5
yi	7,1	27, 8	62,1	110	161

Задача 9. Найти интерполяционный многочлен Лагранжа для функции, заданной таблицей:

x	-1	0	1	2	3
y	17	7	5	11	49

Задача 10. Найти приближенные значения интеграла 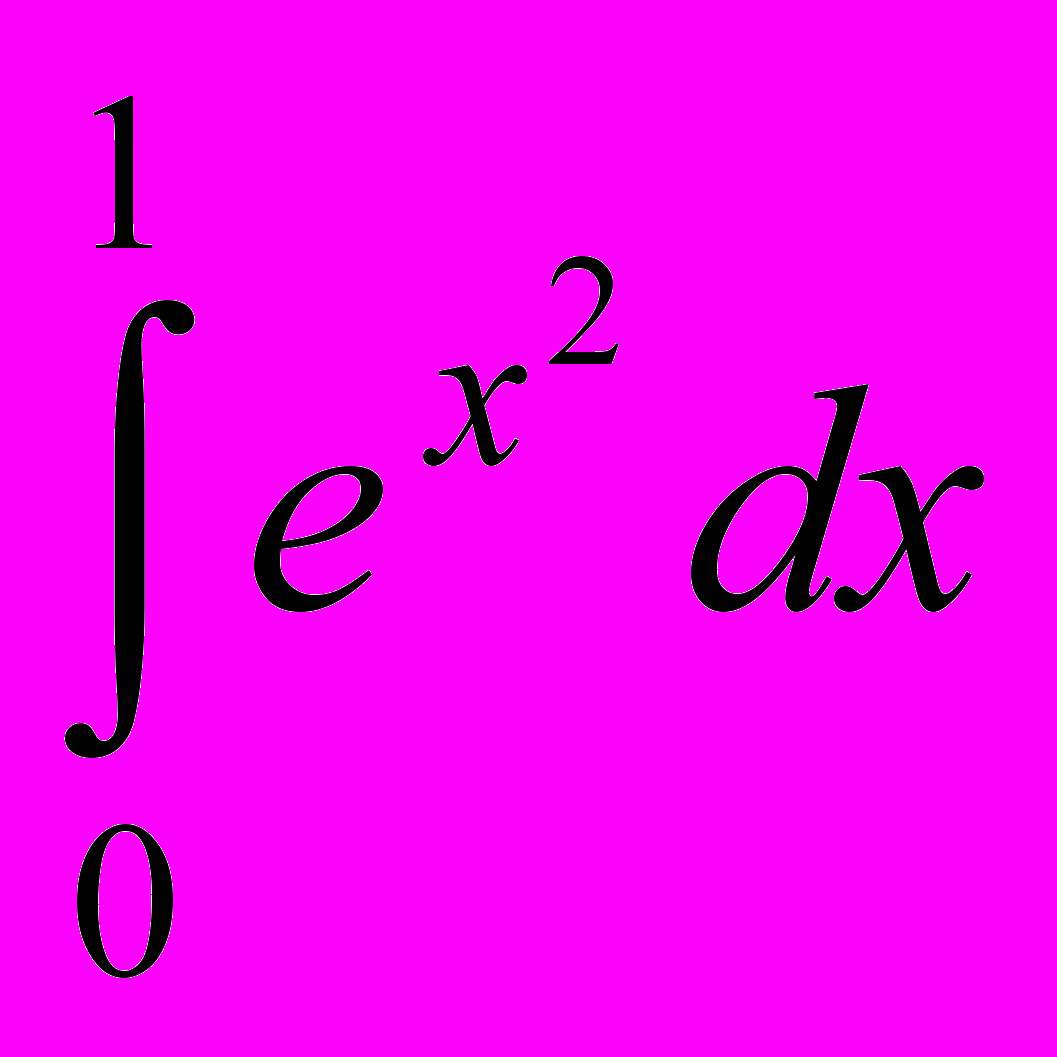с помощью квадратурных формул прямоугольников, трапеций и парабол, если отрезок интегрирования разбит на n=2; 4; 10 равных частей. Оценить величину погрешности полученных результатов в каждом случае.

Задача 11. Вычислить заданный интеграл по формулам прямоугольников, трапеций и парабол, если отрезок интегрирования разбит на n=2 и n=4 равные части. Оценить погрешность результата и сравнить приближенные значения интеграла с точным.

.

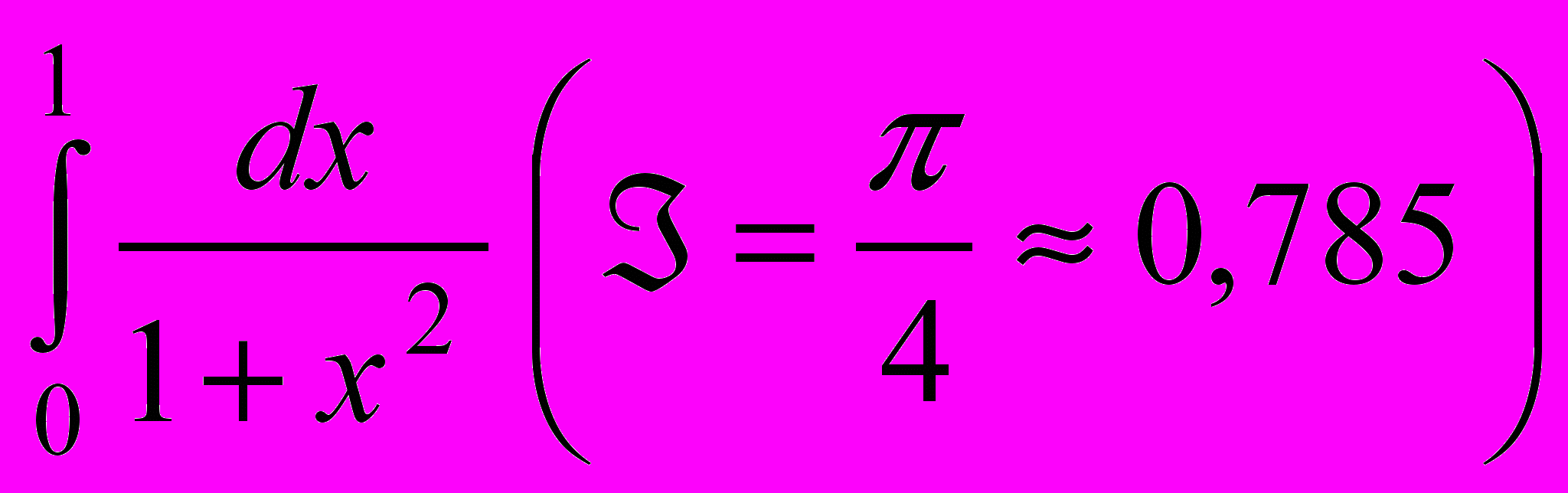Задача 12. Найти приближенное значение интеграла 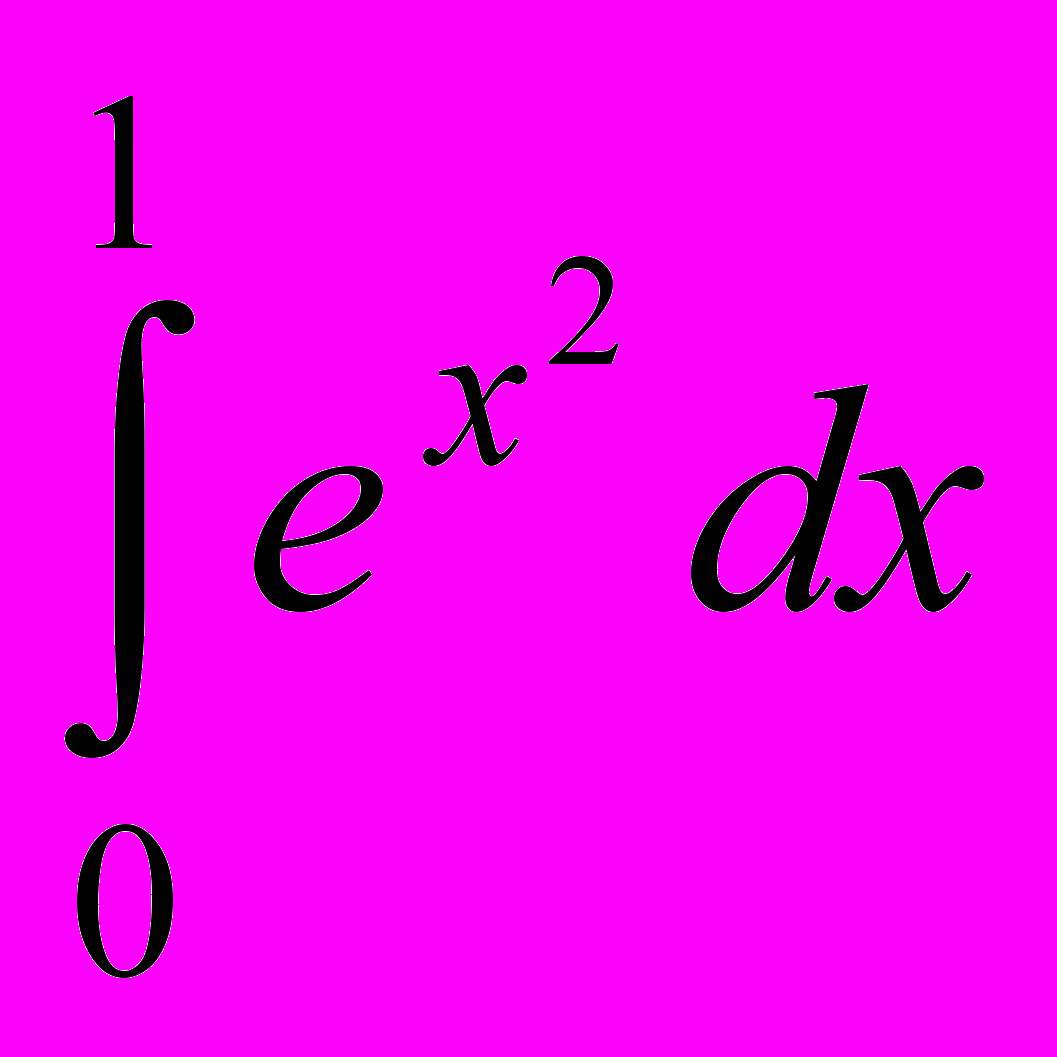по квадратурной формуле Гаусса с тремя узлами для n=1.

Задача 13. Решить задачу Коши 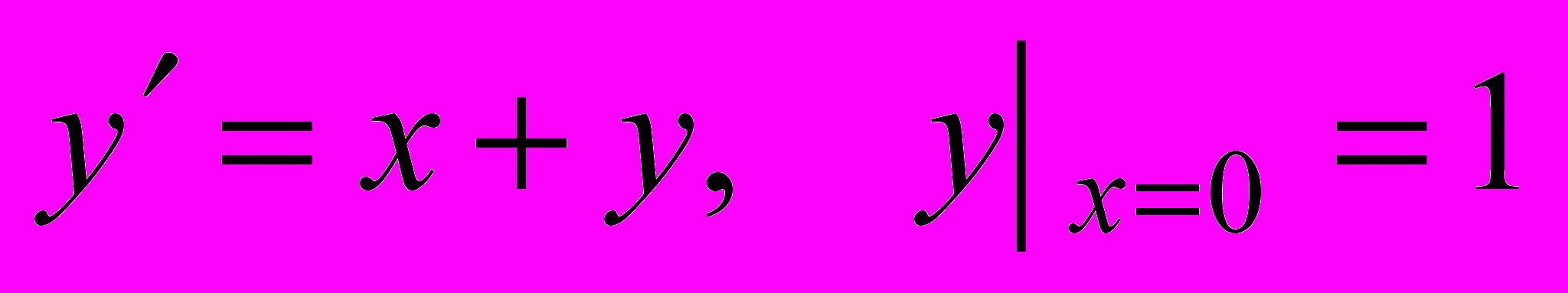методом Эйлера и методом Рунге-Кутта на отрезке [0; 0,4]. Найти решение на равномерной сетке с шагом h=0.1 в четырех узловых точках. Аналитическое решение задачи имеет вид .

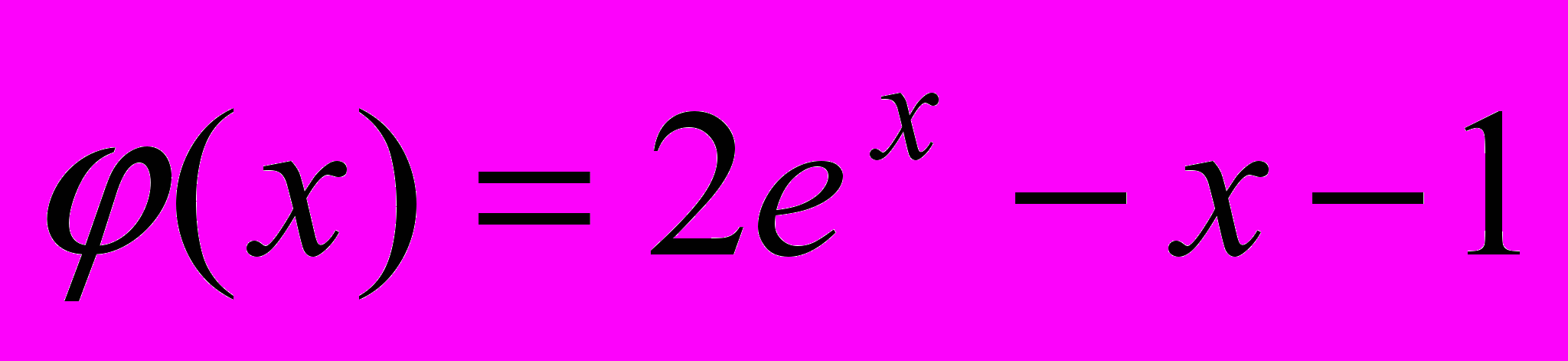Задача 14. Найти решение задачи Коши для дифференциального уравнения первого порядка на равномерной сетке отрезка [a, b] один раз с шагом h=0.2, другой – с шагом 0.1 методами Эйлера, Эйлера–Коши и методом Рунге-Кутта. Оценить погрешность численного решения. Сравнить численное решение с точным.

, , ,

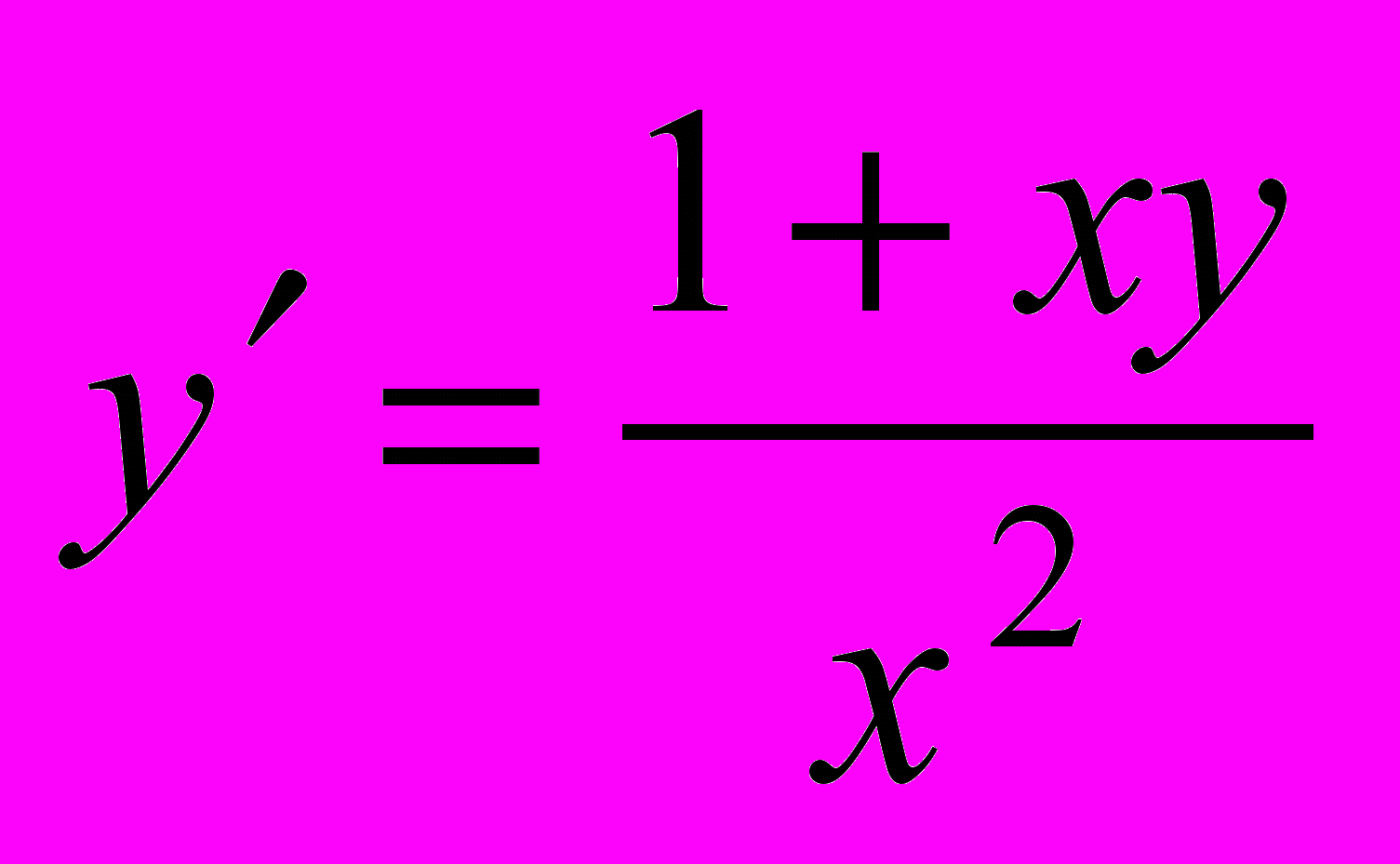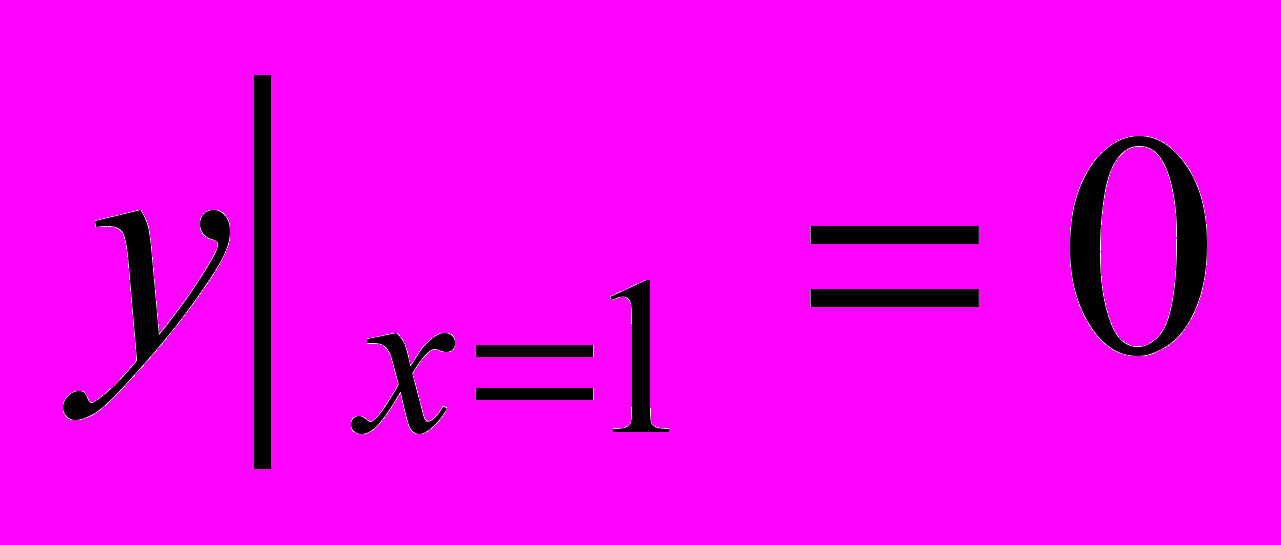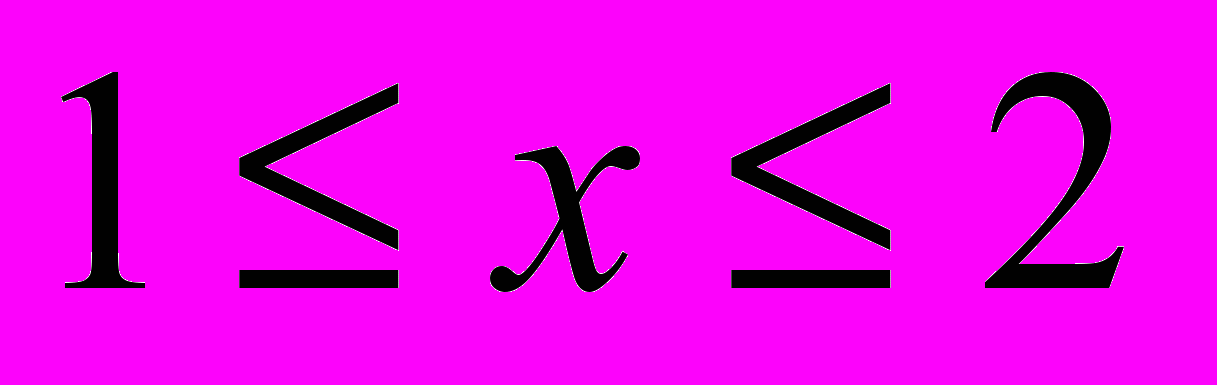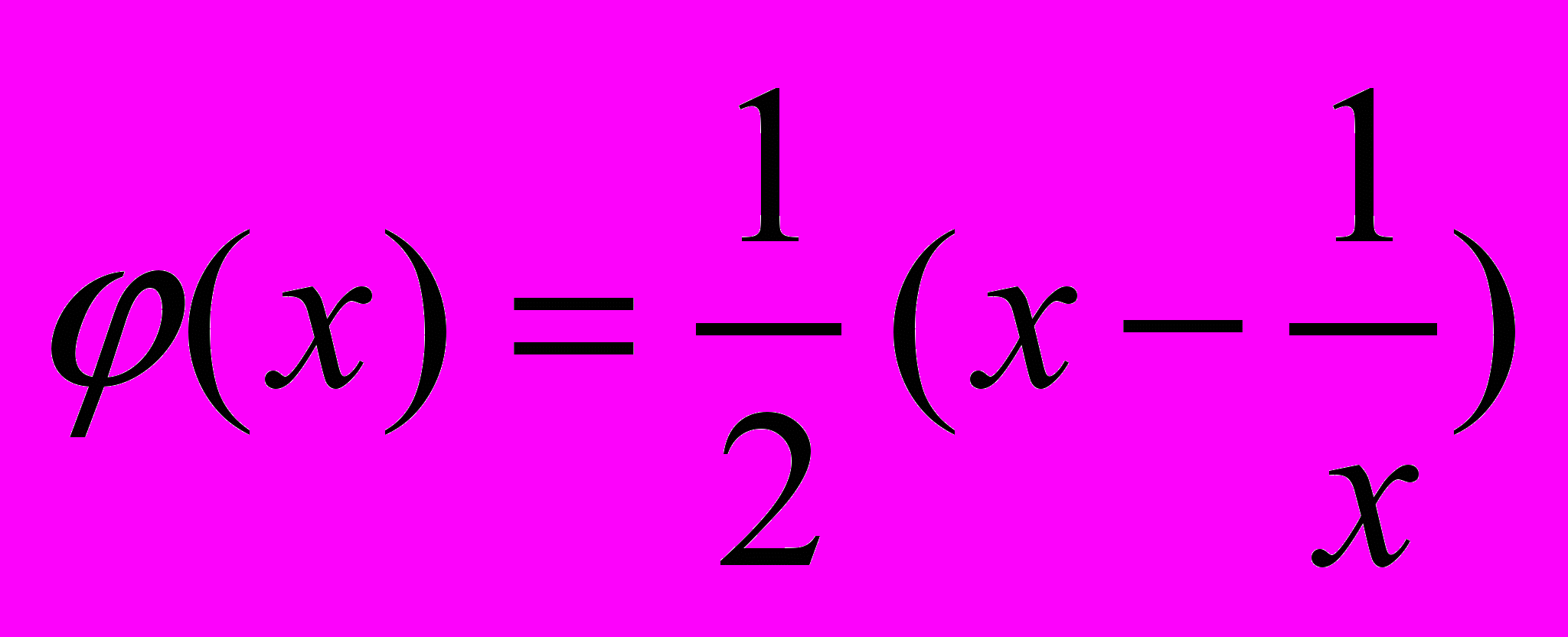
Вопросы к зачету:

1. Примеры линейных нормированных пространств.
   
2. Метод Гаусса.
   
3. Метод итераций.
   
4. Интегральное среднеквадратичное приближение функций обобщенными многочленами.
   
5. Среднеквадратичное приближение функций тригонометрическими многочленами.
   
6. Точечное среднеквадратичное приближение функций ортогональными многочленами.
   
7. Ортогональными многочлены Чебышева.
   
8. Метод наименьших квадратов.
   
9. Интерполяционная формула Лагранжа.
   
10. Вычисление производной по ее определению.
    
11. Конечно-разностные аппроксимации производных.
    
12. Квадратурные формулы прямоугольников, трапеций и Симпсона.
    
13. Квадратурные формулы Гаусса.
    
14. Полиномом какой степени является интерполяционный полином Лагранжа при n+1 узлах?
    
15. Может ли метод Лагранжа применяться для экстраполяции?
    
16. Что влияет на точность интерполяции в методе Лагранжа?
    
17. Можно ли добавлять новые узлы интерполяции при использовании метода Лагранжа?
    
18. Можно ли располагать узлы интерполяции произвольно при использовании метода?
    
19. К какому классу функций относится функция, задаваемая интерполяционной формулой Лагранжа?
    
20. Как повлияет дополнительная точка исходных данных внутри отрезка на точность интерполяции?
    
21. Как определить погрешность интерполяции в узле?
    
22. Как влияет количество узлов интерполяции на точность интерполяции?
    
23. Каким путем в общем случае можно повысить точность интерполяции?
    
24. В чем заключается геометрический смысл метода половинного деления?
    
25. Всегда ли позволяет метод половинного деления вычислить отделенный корень уравнения с заданной погрешностью?
    
26. Как выбираются концы отрезка следующего интервала в методе половинного деления?
    
27. Какими свойствами должна обладать функция f(x), чтобы методом половинного деления можно было гарантированно решить уравнение f(x)=0?
    
28. Что необходимо для нахождения хотя бы одного действительного корня уравнения f(x)=0 методом половинного деления?
    
29. Можно ли найти корень методом половинного деления, если он находится на границе интервала?
    
30. В чем основное отличие точных и приближенных методов решения систем линейных уравнений?
    
31. Каким методом лучше всего решать систему уравнений невысокого порядка, например третьего?
    
32. В каких случаях предпочтительны итерационные методы решения систем линейных уравнений?
    
33. От чего зависит скорость сходимости метода итераций?
    
34. Что является решением дифференциального уравнения?
    
35. Необходим ли поиск начальных условий в методе Эйлера?
    
36. К какой группе относится модифицированный метод Эйлера?
    
37. Метод Рунге — Кутта
    
38. Как можно оценить погрешность решения дифференциального уравнения при использовании метода Рунге — Кутта?
    

3. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ОСВОЕНИЮ УЧЕБНОГО МАТЕРИАЛА

Дисциплина «Вычислительная математика» изучается в течение одного семестра на втором курсе специальности «Вычислительные машины, комплексы, системы и сети».

Вся дисциплина разбита на три ДЕ, по итогам каждой имеется промежуточная аттестация. Итоговой контрольной точкой является зачет.

4. ОСНОВНАЯ И ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Бахвалов Н.С. Численные методы.– М.: Наука, 2007.
   
2. Воеводин В.В. Вычислительные основы линейной алгебры. – М.: Наука, 1977.
   
3. Волков Е.А. Численные методы. – М.: Наука, 1982. – 254 с.
   
4. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. – М.: Физматгиз, 1962.
   
5. Дьяченко В.Ф. Основные понятия вычислительной математики. – М.: Наука, 1977.
   
6. Калиткин Н.Н. Численные методы. – М.: Наука; 1978.
   
7. Самарский А.А. Задачи и упражнения по численным методам. М. 2007.
   
8. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы, т. 1. – М.: Наука, 1976; т.2. – М.: Наука, 1977.
   
9. Фаронов В.В. Турбо Паскаль 7.0 Начальный курс. М, 2000, 576 с.