Geum.ru

Контрольная работа №2. Резерв времени 2 час

Вид материалаКонтрольная работа

Содержание


Первый модуль
Второй модуль.
Резерв времени
Содержание обучения.
Второй модуль.
Тема модуля
Резерв времени
Примерный план урока.
Цель урока
Задачи урока
Ход урока
Подобный материал:


ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ МАТЕМАТИЧЕСКИХ ЗАДАЧ



Колотова И.В., учитель информатики МОУ «Медико-биологический лицей» г. Саратова


Пояснительная записка.

Программа цикла элективных курсов в рамках предпрофильной подготовки «Численные методы решения математических задач» адресована учащимся 9 класса, овладевшим базовым курсом информатики, или учащимся 8 класса в условиях «мягкой» модели введения программы предпрофильной подготовки и профильного обучения.

Тематика данного цикла элективных курсов призвана расширить класс изучаемых задач и продемонстрировать ученикам, как задачи, которые невозможно решить известными алгебраическими методами, могут быть решены с помощью численных методов.

Цикл элективных курсов «Численные методы решения математических задач» состоит из двух модулей, каждый из которых может рассматриваться как отдельный, самостоятельный курс. Учитель может использовать целиком предложенный цикл или отдельные его модули в зависимости от цели и задачи обучения.

В зависимости от уровня обученности модули цикла могут изучаться в 9 классе (если предпрофиль осуществлялся с 8 класса и учащиеся овладели знаниями основ языка Pascal) или в 10 классе при наличии подготовки по информатике в объёме базового курса 9 класса.

Предлагаемые задачи послужат хорошим практикумом по программированию на языке Turbo Pascal.

Первый модуль. (8 час.) Схема Горнера для вычисления значения многочлена любой степени. Метод отделения корней алгебраического уравнения. Численное решение алгебраических уравнений. Точность приближенного решения.

Контрольная работа №1.

Второй модуль. (8 час.) Алгоритм Евклида нахождения НОД. Бинарный алгоритм нахождения НОД. Сравнение алгоритмов. Вычисление корня n-ой степени из числа.

Контрольная работа №2.

Резерв времени - 2 час.

В результате изучения цикла элективных курсов «Численные методы решения математических задач» учащиеся должны иметь представление:

- о методе отделения корней алгебраических уравнений;

- о точности приближенного решения алгебраического уравнения;

- об алгоритме Евклида нахождения НОД;

- о бинарном алгоритме нахождения НОД;

- о вычислении корня n-ой степени из числа и точности метода вычисления.

уметь:

- применять схему Горнера для вычисления значения многочлена:

- использовать для отделения корней алгебраического уравнения написанную на уроке программу на Pascal’е;

- использовать для нахождения приближенных значений корней алгебраических уравнений написанную на уроке программу на Pascal’е;

- использовать программу нахождения НОД по алгоритму Евклида и бинарному алгоритму;

- использовать программу приближенного нахождения корня n-ой степени из числа.


Содержание обучения.

Первый модуль.

Схема Горнера для вычисления значения многочлена.

Алгоритм отделения корней алгебраического уравнения на заданном отрезке (a, b). Составление блок-схемы и программы.

Программа и блок-схема приближенного вычисления корня алгебраического уравнения методом половинного деления. Понятие точности вычислений.

Алгоритм численного решения алгебраических уравнений методом хорд.

Блок-схема и программа на Pascal’е приближенного вычисления корня алгебраического уравнения методом хорд. Понятие точности вычислений.

Второй модуль. Алгоритм Евклида нахождения НОД. Бинарный алгоритм нахождения НОД. Алгоритм нахождения НОК. Составление блок-схем и программ нахождения НОД методом Евклида и бинарным методом. Сравнение методов.

Программа нахождения НОК (наименьшее общее кратное). Алгоритм вычисления корня n-ой степени. Блок-схема и программа вычисления корня n-ой степени. Вычисление квадратного корня из данного числа как частный случай предложенного алгоритма. Точность вычисленного значения.


№
Тема модуля
Кол-во часов
Формы работы
Образовательный продукт
Формы контроля
Литература для учителя
Литература для учащихся

1
Модуль 1. Схема Горнера для вычисления значения многочлена любой степени. Метод отделения корней алгебраического уравнения. Численное решение алгебраических уравнений. Точность приближенного решения
8
Лекции.

Практикум по решению задач.

Составление и отладка программ на Pascal’е для решения поставленных задач.
Опорный конспект.

Блок-схемы решения задач и программы на Pascal’е с подробными комментариями.

Подборка задач с решениями.
Контрольная работа №1.
1. В.М. Заварыкин, В.Г. Житомирский и др. Численные методы. М., Просвещение, 1990 г.

2. С.А. Немнюгин. Turbo Pascal. Санкт-Петербург, «Питер», 2002 г.
1. В.М. Заварыкин, В.Г. Житомирский и др. Численные методы. М., Просвещение, 1990 г.

2
Модуль 2. Алгоритм Евклида нахождения НОД. Бинарный алгоритм нахождения НОД. Сравнение алгоритмов. Вычисление корня n-ой степени из числа.
8
Лекции.

Практикум по решению задач. Составление и отладка программ для решения поставленных задач.
Опорный конспект.

Блок-схемы решения задач и программы на Pascal’е с подробными комментариями.

Подборка задач с решениями.
Контрольная работа №2.
1. В.М. Заварыкин, В.Г. Житомирский и др. Численные методы. М., Просвещение, 1990 г.

2. Д. Кнут. Искусство программирования для ЭВМ. т.2
1. В.М. Заварыкин, В.Г. Житомирский и др. Численные методы. М., Просвещение, 1990 г.

3
Резерв времени
2
















Примерный план урока.

Тема: алгоритм приближенного вычисления корней алгебраического уравнения на заданном отрезке методом половинного деления.

Цель урока: составить пошаговый алгоритм приближенного вычисления корней алгебраического уравнения методом половинного деления с выбранной точностью.

Задачи урока:

а) изучить и понять алгоритм приближенного вычисления корней алгебраического уравнения методом половинного деления;

б) создать блок-схему задачи;

в) решить конкретную задачу по составленной блок-схеме.

Ход урока


1. Проверка домашнего задания.

2. Рассказ об алгоритме приближенного вычисления корней алгебраического уравнения методом половинного деления.

Пусть f(x)=0 – алгебраическое уравнение, т.е. уравнение, в левой части которого стоит многочлен n-ой степени. Основная теорема алгебры, изучаемая в курсе высшей алгебры, говорит о том, что такое уравнение имеет столько корней, какова его степень.

Пусть требуется найти корень алгебраического уравнения f(x)=0 на отрезке [a, b]. Для начала следует выяснить, имеет ли алгебраическое уравнение f(x)=0 корни на [a, b]. Для этого подсчитаем значения f(x) в нескольких точках из [a, b] и построим приближённый график f(x), соединив полученные точки. Если на отрезке [a, b] график хотя бы один раз пересекает ось x, то это означает, что на отрезке [a, b] имеется корень алгебраического уравнения f(x)=0. Далее применим алгоритм отделения корней алгебраического уравнения, изученный на предыдущих уроках, задав точность достаточно малой. В результате уменьшим отрезок [a, b] так, чтобы на нем осталось не более одного корня.

Далее предлагается следующий алгоритм приближенного вычисления корня алгебраического уравнения f(x)=0.

1. Выяснить, являются ли концы отрезка a и b корнями алгебраического уравнения f(x)=0. Если хотя бы одно из значений a или b обращает функцию f(x) в нуль, то выводим на экран значение корня и заканчиваем задачу.

2. Если f(a) 0 и f(b) 0, то проверяем: f(a)·f(b)<0? Если да, то это значит, что на отрезке [a, b] функция меняет знак.

3. Рассмотрим точку c=(b-a)/2. Опять проверяем: f(a)·f(с)<0? Если да, то b:=c. Если нет, то a:=c. Т.о., отрезок [a, b] уменьшился, и мы вновь проверяем неравенство: f(a)·f(b)<0? Корень остается внутри уменьшенного отрезка.

Так будем делить отрезок до тех пор, пока его длина не станет совсем малой, т.е. до тех пор, пока |b-a| не станет меньше ε. Число ε называется точностью вычислений и задавать его будем сами. Например, пусть ε = 0,001. Когда отрезок [a, b] станет меньше ε, то за корень алгебраического уравнения, т.е. его приближенное значение, принимают x=(b-a)/2. составим по приведенному алгоритму блок-схему:








+





—

+




—

+




—








— +




—


+


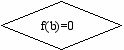
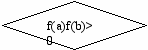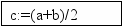
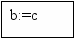
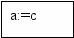
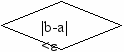
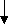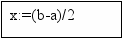
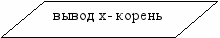
Далее работа с блок-схемой:

Задача 1. Найти корень алгебраического уравнения 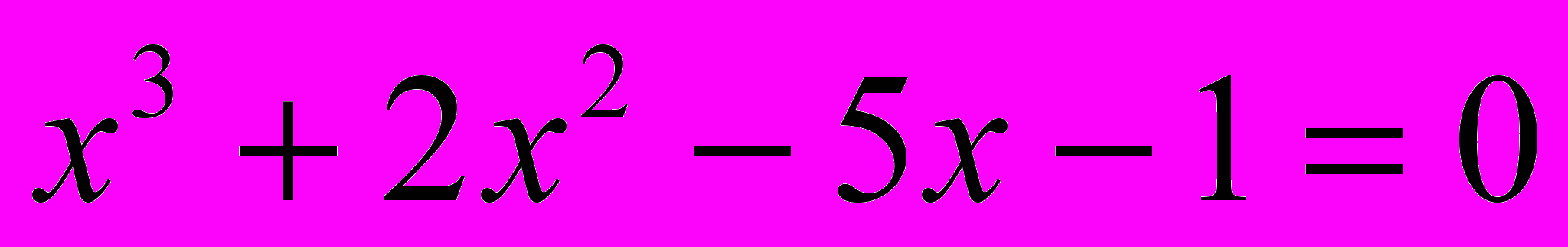на отрезке [-1, 0] с точностью 0,2.

Здесь a = -1, b = 0.

1. Проверяем: f(-1)≠0, f(0)≠0; f(0)=-1, f(-1)=5.

2. f(0)∙f(-1)<0, следовательно, корень на интервале [-1, 0] есть.

3. c:=(-1-0)/2; с=-0,5. Проверяем:f(-0,5)=+1,875, т.о. f(-0,5)>0, следовательно, f(a)∙f(c)<0, тогда b:=c, т.е. b:=-0,5.

4. Проверяем точность: ‌‌ b-a‌=0,5 т.е. ‌‌ b-a‌>0,2.

5. Повторяем шаг 3: c:=(0-0,5)/2; c=-0,25; f(-0,25)=0,359375, f(-0,25)>0, следовательно, f(a)∙f(c)<0; тогда b:=c, т.е. b:=-0,25.

6. Проверяем точность: ‌‌ b-a‌=0,25; ‌‌ b-a‌>0,2.

7. Повторяем шаг 3: c:=(0-0,25)/2; c=-0,125; f(-0,125)=-0,346, f(c)<0, следовательно, f(a)∙f(c)>0; тогда a:=c, т.е. a:=-0,125.

8. Проверяем точность: ‌‌ b-a‌=0,125; ‌‌ b-a‌<0,2.

9. Находим приближенное значение корня: x=(-0,25+0,125)/2; x=0,0625.

Домашнее задание. Найти корни алгебраического уравнения 2x3+x2-16x-15=0 на отрезке [-3,-2] и на отрезке [2, 3.5].