Фігури на площині. Методи розрізання та розфарбовування фігур. Основні поняття

Вид материала

Задача

Содержание Теорема Жордана Ф є опуклою фігурою; б) Ф Ф є перетином кількох півплощин. Для довільної скінченної множини точок площини існує її (єдина) опукла оболонка AB – одна із її сторін. Усі інші вершини занумеруємо в порядку зростання кутів, під якими видно з них відрізок AB Теорема Хеллі Ф, так і точки, які не належать цій фігурі, називається межовою Задачі для самостійного розв’язання

Подобный материал:

• 1. Вступ. Основні поняття та методологія до історія розвитку та використання методів, 102.84kb.
• Тема Фігури мовлення, 25.89kb.
• Тема предмет вивчення курсу, основні поняття, методи та основні цілі курсу Предмет, 60.95kb.
• Назва модуля: Теорія ймовірностей та математична статистика. Код модуля, 16.22kb.
• Програма Комплексного вступного іспиту на окр «Спеціаліст», 814.3kb.
• Урок № дата клас тема: Об’єкти технологічної діяльності. Методи проектування, 1706.97kb.
• Програма комплексного вступного іспиту на окр «Спеціаліст» за спеціальністю «Правознавство», 84.74kb.
• Урок з геометрії у 9 класі. Тема уроку. Поняття про перетворення фігур, 72.42kb.
• Програма фахового вступного випробування освітньо-професійний рівень „спеціаліст, 127.32kb.
• Найбільш важливі закон, 9288.95kb.

Фігури на площині.

Методи розрізання та розфарбовування фігур.

Основні поняття

Множина точок площини називається фігурою. При цьому ця множина точок може бути скінченною або нескінченною. У шкільних задачах найчастіше зустрічаються многокутники (багатокутники) – фігури, обмежені замкненими ламаними. Щодо розміщення многокутників на площині необхідно окремо виділити теорему Жордана, суть якої, на перший погляд, здається цілком очевидною, однак яка дозволяє виконувати доведення багатьох задач набагато формальніше та чіткіше.

Теорема Жордана. Довільна замкнена без самоперетинів ламана ділить площину на дві області – внутрішню (обмежену) та зовнішню (необмежену), причому довільний шлях із точки, яка лежить у внутрішній області, у точку, яка лежить у зовнішній області, перетинає цю ламану, а довільні дві точки кожної з цих областей можна з’єднати шляхом, який не перетинає ламаної.

Фігура називається опуклою, якщо разом з кожними своїми двома точками вона містить також весь відрізок з кінцями в цих точках.

Опуклим многокутником називається многокутник Ф, який має одну з таких рівносильних властивостей:

а) Ф є опуклою фігурою;

б) Ф розміщений в одній півплощині відносно прямої, яка містить будь-яку із його сторін;

в) усі його кути менші за 180°;

г) Ф є перетином кількох півплощин.

Для довільної скінченної множини точок площини існує її (єдина) опукла оболонка – найменший опуклий многокутник, який містить всі ці точки. Розв’язання деяких задач варто розпочинати саме з розгляду опуклої оболонки певної множини точок. Часто це дозволяє значно прискорити процес розв’язання та спростити його.

Задача 1. На площині дано 2n + 3 точок, жодні три з яких не лежать на одній прямій та жодні чотири з яких не лежать на одному колі. Довести, що з цих точок можна обрати три точки так, що серед необраних точно n точок лежать всередині кола, проведеного через обрані точки, а точно n – зовні цього кола.

Розв’язання. Розглянемо опуклу оболонку множини даних точок. Нехай AB – одна із її сторін. Усі інші вершини занумеруємо в порядку зростання кутів, під якими видно з них відрізок AB, тобто (оскільки жодні чотири точки не лежать на одному колі, то всі такі кути різні). Проведемо коло через точки A, B, C_n+1. Точки C₁, C₂, …, C_n лежать зовні цього кола, а точки C_n+2, C_n+3, …, C_2n+1 – всередині нього, чого і потрібно було досягти.

Методом математичної індукції доводиться (спробуйте зробити це самостійно) таке, цікаве для подальших застосувань, твердження.

Теорема Хеллі. Нехай на площині дано n опуклих фігур, кожні три з яких мають спільну точку. Тоді всі ці n фігур мають спільну точку.

Якщо об’єднання фігур D₁, D₂, …, D_n містить дану фігуру Ф, то говорять, що фігури D₁, D₂, …, D_n утворюють покриття фігури Ф. При цьому фігури D₁, D₂, …, D_n можуть перетинатися.

Множина точок, відстань від яких до точки A менша, ніж (додатне) число ɛ (читається – епсілон), називається ɛ-околом точки A. Точка, яка належить фігурі Ф разом з деяким своїм околом, називається внутрішньою точкою фігури Ф. Якщо всі точки фігури Ф є її внутрішніми точками, то ця фігура називається відкритою.

Точка, довільний (навіть дуже-дуже маленький) окіл якої містить як точки, що належать фігурі Ф, так і точки, які не належать цій фігурі, називається межовою (або граничною) точкою цієї фігури. Множина всіх межових (граничних) точок фігури називається межею (або границею) цієї фігури.

Покриття фігури Ф фігурами D₁, D₂, …, D_n, що не мають спільних внутрішніх точок, називається розрізанням фігури Ф. Як правило, прийнято розглядати такі розрізання, що об’єднання фігур D₁, D₂, …, D_n дає точно фігуру Ф.

При розв’язуванні задач, пов’язаних з покриттями та розрізаннями, найчастіше використовуються загальні властивості фігур, пов’язані з їх розташуванням та орієнтацією на площині.

Задача 2. Чи можна даний правильний трикутник покрити двома меншими правильними трикутниками?

Розв’язання. Кожен з менших трикутників може покрити тільки одну вершину більшого, тому одна з вершин обов’язково залишиться не покритою.

У деяких задачах спрацьовує ідея розфарбовування. При цьому вважають, що фігура розфарбована у декілька кольорів, якщо кожній її точці поставлено у відповідність один із цих кольорів. Зустрічаються задачі, де розфарбування уже дано. Однак найчастіше розфарбування з певними властивостями потрібно придумати самостійно.

Пам’ятайте, що ваше розфарбування має спростити та формалізувати шлях розв’язання, а не ускладнити його. Тому спершу підберіть таке розфарбування, яке, на перший погляд, буде зручним у даному випадку, а вже потім використовуйте його властивості для подальшого розв’язання. Якщо у процесі подальшого розв’язання ви помітили, що розфарбування можна було виконати простіше, перейдіть до нього. Адже чим простішим буде ваше розв’язання (розфарбування), тим менша вірогідність того, що ви заплутаєтесь у своїх думках.

Задача 3. Дно коробки розміром 10х10 вимощене плитками розміром 1х4 та 2х2. Одну з цих плиток розміром 1х4 загубили, але в запасі є плитка розміром 2х2. Чи можна наявними плитками знову вимостити дно коробки?

Розв’язання. Розіб’ємо дно коробки на квадрати та зафарбуємо деякі клітинки так, як показано на рисунку. Тоді кожна плитка 2х2 покриває рівно одну зафарбовану, а кожна плитка 1х4 покриває дві або нуль (не покриває жодної) зафарбованих клітинок. Оскільки було загублено плитку, яка покривала дві або нуль зафарбованих клітинок, то ми не можемо замінити її (навіть при будь-якому іншому розміщенні плиток) плиткою, яка може покривати лише одну зафарбовану клітинку. Тому знову вимостити дно коробки наявними плитками не можна.

Задача 4. У кожній клітинці дошки розмірами 5х5 сидить жук. За свистком кожен жук переповзає в одну із сусідніх по діагоналі клітин. При цьому в деяких клітинах може виявитися по кілька жуків, а деякі клітини стануть незайнятими. Знайдіть найменше можливе число незайнятих клітин.

Розв’язання. Пофарбуємо вертикалі дошки у білий та чорний кольори так, щоб сусідні вертикалі мали різний колір. Якщо перша зліва вертикаль – чорна, то ми отримаємо 15 чорних та 10 білих клітин. Переповзаючи, кожен жук змінює колір клітини, на якій він сидить. На чорні клітини можуть переповзти лише жуки з білих клітин. Тому не менше 5 чорних клітин стануть вільними. Для завершення розв’язання необхідно навести конкретний приклад, у якому залишаються незайнятими 5 клітин. Спробуйте зробити це самостійно.

Задача 5. На папері в клітинку задано довільні n клітинок. Доведіть, що з них можна вибрати не менше, ніж 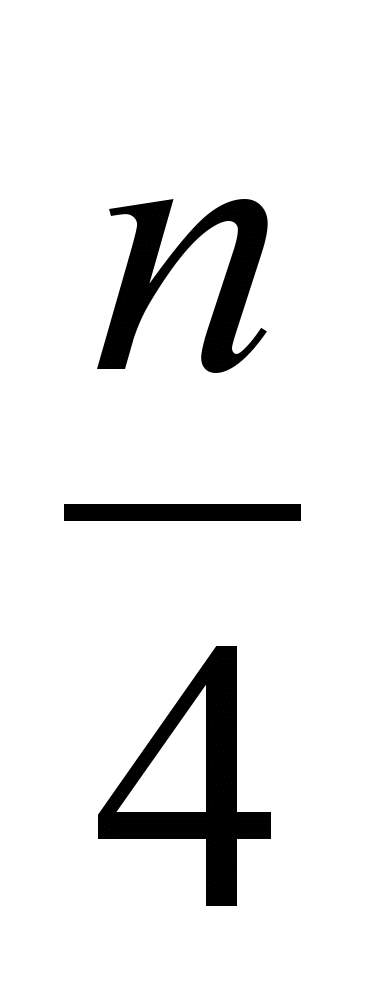клітинок, що не мають спільних точок.

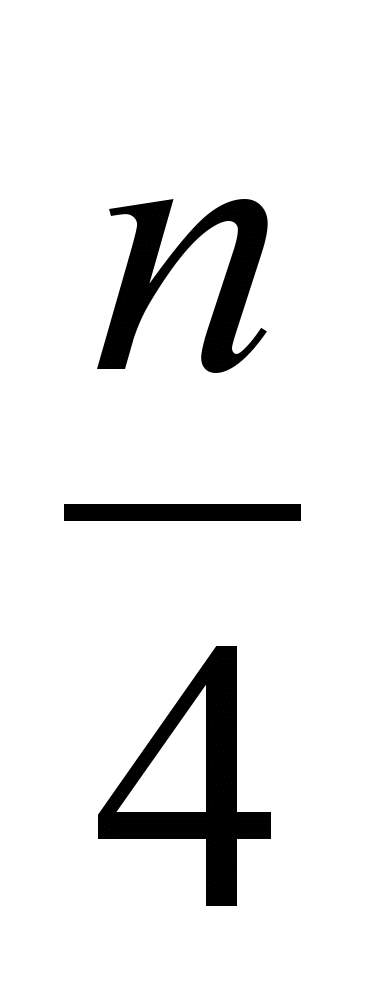Розв’язання. Розфарбуємо клітинки в 4 кольори таким чином, щоб клітинки одного кольору не мали спільних точок (наприклад, як показано на рисунку – розфарбований фрагмент паперу в клітинку). Серед n клітинок знайдуться не менше, ніж однокольорових, а однокольорові клітинки за властивістю виконаного розфарбування спільних точок не мають.

Зауважимо, що в усіх наведених прикладах задач розфарбування дозволяє значно спростити як сам хід розв’язання, так і пояснення до нього. Саме це і є однією з головних цілей методу розфарбовування.


Задачі для самостійного розв’язання

1. Доведіть теорему Хеллі, використовуючи метод математичної індукції (або інші відомі вам методи).
   

2. Довести, що всередині довільного опуклого семикутника є точка, яка не належить жодному з чотирикутників, утворених четвірками його сусідніх вершин.
   

Вказівка. Скористайтесь теоремою Хеллі.

3. Куб розбито на 27 однакових кубиків. У початковий момент жук знаходиться в центральному кубику. З кожного кубика жук може переходити до сусіднього, що має з ним спільну грань. Чи зможе жук обійти всі кубики, побувавши в кожному по одному разу?
   

4. Король обійшов дошку розмірами 9х9, побувавши точно один раз на кожному полі. Маршрут короля не замкнений і, можливо, самоперетинається. Яка найбільша можлива довжина такого маршруту, якщо довжина ходу по діагоналі дорівнює , а по вертикалі чи горизонталі – 1?
   

5. Правильний трикутник зі стороною n розбито прямими, паралельними сторонам трикутника, на n² правильних трикутників зі стороною 1. По сторонах отриманих трикутників проведена незамкнена ламана, що проходить через всі вершини трикутників точно по одному разу. Доведіть, що не менше, ніж n пар сусідніх ланок ламаної утворюють між собою гострий кут.
   

6. Чи можна шашкову дошку розмірами 10х10 замостити плитками розмірами 1х4?
   

7. Площина розбита на однакові шестикутні кімнати. В деяких стінах зроблено двері так, що для будь-якої вершини, в якій сходяться три стіни (сторони шестикутників) двері є точно в двох. Доведіть, що будь-який замкнений шлях цим лабіринтом проходить через парну кількість дверей.
   

Вказівка. Кімнати, як і будь-які інші об’єкти, також можна у розв’язанні розфарбувати певним чином.

8. Є квадратний лист паперу в клітинку розмірами 100х100. Проведено кілька ламаних без самоперетинів, що йдуть по сторонах клітинок та не мають спільних точок. Ці ламані лежать всередині квадрата, лише їхні кінці лежать на його межі. Довести, що крім вершин, знайдеться вузол (всередині або на межі), який не належить жодній ламаній.